机械设计 第2章 平面连杆机构
- 格式:doc
- 大小:103.50 KB
- 文档页数:6
第2章平面连杆机构2.1平面连杆机构的特点和应用连杆机构是由若干刚性构件用低副连接组成的机构,又称为低副机构。
在连杆机构中,若各运动构件均在相互平行的平面内运动,称为平面连杆机构;若各运动构件不都在相互平行的平面内运动,则称为空间连杆机构。
平面连杆机构被广泛应用在各类机械中,之所以广泛应用,是因为它有较显著的优点:(1)平面连杆机构中的运动副都是低副,其构件间为面接触,传动时压强较小,便于润滑,因而磨损较轻,可承受较大载荷。
(2)平面连杆机构中的运动副中的构件几何形状简单(圆柱面或平面),易于加工。
且构件间的接触是靠本身的几何约束来保持的,所以构件工作可靠。
(3)平面连杆机构中的连杆曲线丰富,改变各构件的相对长度,便可使从动件满足不同运动规律的要求。
另外可实现远距离传动。
平面连杆机构也存在一定的局限性,其主要缺点如下:(1)根据从动件所需要的运动规律或轨迹设计连杆机构比较复杂,精度不高。
(2)运动时产生的惯性力难以平衡,不适用于高速的场合。
(3)机构中具有较多的构件和运动副,则运动副的间隙和各构件的尺寸误差使机构存在累积误差,影响机构的运动精度,机械效率降低。
所以不能用于高速精密的场合。
平面连杆机构具有上述特点,所以广泛应用于机床、动力机械、工程机械等各种机械和仪表中。
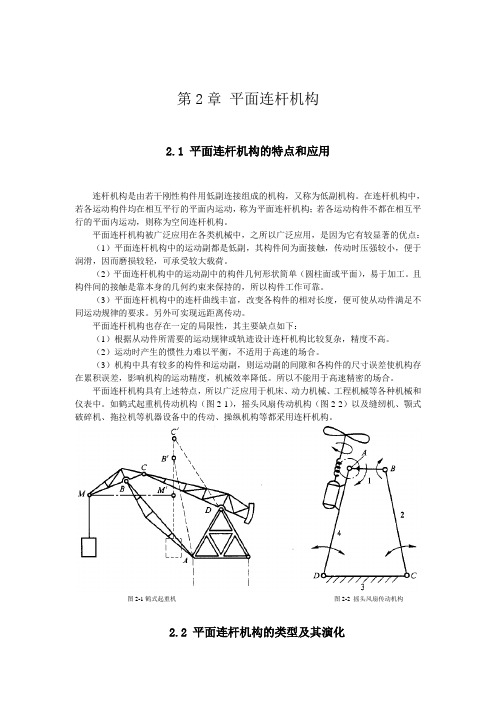
如鹤式起重机传动机构(图2-1),摇头风扇传动机构(图2-2)以及缝纫机、颚式破碎机、拖拉机等机器设备中的传动、操纵机构等都采用连杆机构。
图2-1鹤式起重机图2-2 摇头风扇传动机构2.2平面连杆机构的类型及其演化2.2.1 平面四杆机构的基本形式全部用转动副组成的平面四杆机构称为铰链四杆机构,如图2-3所示。
机构的固定件4称为机架;与机架相联接的杆1和杆3称为连架杆;不与机架直接联接的杆2称为连杆。
能作整周转动的连架杆,称为曲柄。
仅能在某一角度摆动的连架杆,称为摇杆。
按照连架杆的运动形式,将铰链四杆机构分为三种基本型式:曲柄摇杆机构、双曲柄机构和双摇杆机构。






《机械设计基础》第2章_平面连杆机构解析机械设计基础第2章介绍了平面连杆机构的解析方法,本文将详细探讨平面连杆机构的基本概念以及运动规律,并通过实例分析解算过程。
平面连杆机构是由几个连杆和连接件组成的机械装置,常见于各种机械设备和机器人中,具有重要的机械传动功能。
解析平面连杆机构的目的是求解机构中各个连杆的位置、速度和加速度等运动参数,在设计和优化机构的过程中起到关键作用。
首先,我们需要了解平面连杆机构的基本构件和运动方式。
平面连杆机构包括刚性连杆、铰链、曲轴和悬臂等,在运动过程中,这些构件之间通过铰链连接,可以实现不同形式的运动传动。
平面连杆机构中常见的运动有转动运动、直线运动和复合运动。
其次,我们需要了解平面连杆机构的运动规律。
平面连杆机构的运动规律可以通过几何方法或者代数方法进行求解。
几何方法主要是通过建立连杆的几何关系来求解连杆的位置和速度,而代数方法则是通过建立连杆的运动学方程来求解连杆的加速度。
几何方法中常用的解析方法有正弦定理和余弦定理。
通过应用这些定理,可以获得连杆的长度和角度关系,从而求解出连杆的位置和速度。
例如,在一个平面连杆机构中,已知一根连杆的长度和角度,可以利用余弦定理求解出另一根连杆的长度和角度。
代数方法中常用的解析方法有速度、加速度和加加速度分析法。
这些方法是通过建立连杆的运动学方程,并对方程进行求导得到速度、加速度和加加速度的表达式。
例如,在一个平面连杆机构中,已知连杆的运动学方程,可以对其进行求导,得到连杆的速度和加速度表达式。
最后,我们通过一个实例来详细解析平面连杆机构的运动规律。
假设我们有一个平面连杆机构,包括两根等长的连杆和一个铰链。
已知一根连杆的长度为L,角度为θ,我们希望求解另一根连杆的位置、速度和加速度。
首先,利用余弦定理求解另一根连杆的长度。
根据余弦定理,可以得到连杆的长度与角度的关系式。
然后,利用连杆长度与角度的关系式,可以求解出连杆的长度。
接下来,利用几何方法求解连杆的速度。

第2章平面连杆机构2.1复习笔记平面连杆机构是由若干构件用低副连接组成的平面机构。
优点:构件的运动形式多样,可以实现给定运动规律或运动轨迹;低副以圆柱面或平面相接触,承载能力高,耐磨损,制造简单,易获得较高的制造精度。
缺点:不易精确实现复杂的运动规律,且设计较为复杂;当构件数和运动副数较多时,效率较低。
一、平面四杆机构的基本类型及其应用按照所含移动副数目的不同,可分为3类:全转动副的铰链四杆机构、含一个移动副的四杆机构以及含两个移动副的四杆机构。
1.铰链四杆机构图2-1全部用转动副相连的平面四杆机构称为平面铰链四杆机构,简称为铰链四杆机构,如图2-1所示。
其中,机构的固定构件4称为机架,与机架用回转副相连接的杆1和杆3称为连架杆,不与机架直接连接的杆2称为连杆,能作整周转动的连架杆1称为曲柄,仅能在某一角度摆动的连架杆3称为摇杆。
按照连架杆是曲柄还是摇杆,铰链四杆机构分为三种基本形式:曲柄摇杆机构、双曲柄机构和双摇杆机构。
2.含一个移动副的四杆机构此类型的四杆机构主要有四种形式:曲柄滑块机构、导杆机构、摇块机构和定块机构,分别如图2-2所示。
曲柄滑块机构导杆机构摇块机构定块机构图2-23.含两个移动副的四杆机构含有两个移动副的四杆机构称为双滑块机构。
按照两个移动副所处位置的不同,又可分为四种形式:(1)正切机构:两个移动副不相邻;(2)正弦机构:两个移动副相邻且其中一个移动副与机架相关联;(3)两个移动副相邻且均不与机架相关联;(4)两个移动副都与机架相关联。
正切机构正弦机构两移动副相邻且均不与机架相关联的机构两个移动副都与机架相关联的机构图2-34.具有偏心轮的四杆机构该种机构如图2-4(a)、(b)所示,相对应的机构简图分别如图2-4(c)、(d)所示。
(a)(b)(c)(d)图2-4偏心轮广泛应用于传力较大的剪床、冲床、颚式破碎机、内燃机等机械中。
5.四杆机构的扩展实际生产应用中的某些多杆机构是由若干个四杆机构组合扩展形成的,如图2-5和图2-6所示。








2.6设计一偏置曲柄滑块机构。
已知滑块的行程H =50mm ,行程速比系数K =1.5,导路的偏距e =20mm 。
试求曲柄的长度l AB 和连杆的长度l BC ,并求作最大压力角αmax 。
解:行程速比系数K=1.5,则机构的极位夹角为︒=+-︒=+-︒=3615.115.118011180K K θ选定作图比例,先画出滑块的两个极限位置C 1和C 2,再分别过点C 1、C 2作与直线成︒=-︒5490θ的射线,两射线将于点O 。
以点O 为圆心,OC 2为半径作圆,最后再作一条与直线C 1C 2相距为mm e 20=的直线,该直线与先前所作的圆的交点就是固定铰链点A。
作图过程如题2.6图所示。
直接由图中量取mm AC 251=,mm AC 682=,所以曲柄AB 的长度为mm AC AC l AB 5.2122568212=-=-=连杆BC 的长度为mm AC AC l BC 5.4622568221=+=+=2.7试设计一曲柄摇杆机构,已知行程速比系数K =1.2,摇杆长L CD =300mm ,其最大摆2B 1B 2C 1C Aeθ21C C θ-︒90题2.6图O角ψmax =35°,曲柄长L AB =80mm 。
求连杆长L BC ,并验算最小传动角γmin 是否在允许的范围内。
解:简要作图步骤:作圆η。
以O 为圆心,OC 1为半径作圆,再以C 2为圆心,2l AB 为半径作圆,两圆交于S 点;●连接C 2S 延长交圆η于A 点;❍⏹机构在AB ′C′D 位置时有γmin =430<[γ]2.8图所示为脚踏轧棉机的曲柄摇杆机构。
铰链中心A 、B 在铅垂线上,要求踏板DC 在水平位置上下各摆动10°,且l DC =500mm ,l AD =1000mm 。
试求曲柄AB 和连杆BC 的长度l AB 和l BC ,并画出机构的止点位置。
mmml 005.0=μ20125.1125.118011180=+-=+-=θK K η212AC AC AB l l l -=212AC AC BC l l l +=D1C 2C ψA1B 2B Pθθ- 90SminγB 'C 'O解:1取长度比例尺做机构图mmmml20=μ()()mmAC AC l l AB752205.5260212=-=-=μ()()mmAC AC l l BC11252202.5260212=+=+=μ2.9图所示为一实验用小电炉的炉门装置,在关闭时为位置E 1,开启时为位置E 2,试设计一四杆机构来操作炉门的启闭(各有关尺寸见图)。

第二章平面连杆机构
案例导入:通过雷达天线、汽车雨刮器、搅拌机等实际应用的机构分析引入四杆机构的概念,介绍四杆机构的组成、基本形式和工作特性。
第一节铰链四杆机构
一、铰链四杆机构的组成和基本形式
1.铰链四杆机构的组成
如图1-14所示,铰链四杆机构是由转动副将各构件的头尾联接起的封闭四杆系统,并使其中一个构件固定而组成。
被固定件4称为机架,与机架直接铰接的两个构件1和3称为连架杆,不直接与机架铰接的构件2称为连杆。
连架杆如果能作整圈运动就称为曲柄,否则就称为摇杆。
2.铰链四杆机构的类型
图2-3 搅拌机
铰链四杆机构根据其两个连架杆的运动形式的不同,可以分为曲柄摇杆机构、双曲柄机构和双摇杆机构三种基本形式。
图2-4 惯性筛工作机构
图2-1 雷达天线调整机构图2-2 汽车雨刮器
(1 曲柄摇杆机构。
在铰链四杆机构中,如果有一个连架杆做循环的整周运动而另一连架杆作摇动,则该机构称为曲柄摇杆机构。
如图 2-1 所示曲柄摇杆机构,是雷达天线调整机构的原理图,机构由构件 AB 、 BC 、固连有天线的 CD 及机架 DA 组成,构件 AB 可作整圈的转动,成曲柄;天线 3 作为机构的另一连架杆可作一定范围的摆动,成摇杆;随着曲柄的缓缓转动,天线仰角得到改变。
如图 2-2 所示汽车刮雨器,随着电动机带着曲柄 AB 转动,刮雨胶与摇杆 CD 一起摆动,完成刮雨功能。
如图 2-3 所示搅拌器,随电动机带曲柄 AB 转动,搅拌爪与连杆一起作往复的摆动,爪端点 E 作轨迹为椭圆的运动,实现搅拌功能。
图2-6 平行双曲柄机构的应用
图2-5 平行双曲柄机构
对以曲柄为主动件的摆动导杆机构,因为滑块对导杆的作用力始终垂直于导杆,其传动角γ恒为90°,即γ = γmin = γmax =90°,表明导杆机构具有最好的传力性能。
2.止点
图2-20 平面四杆机构的止点位置
从F t = F cosα 知,当压力角α = 90 °时,对从动件的作用力或力矩为零,此时连杆不能驱动从动件工作。
机构处在这种位置称为止点,又称死点。
如图 2 -20a 所示
的曲柄摇杆机构,当从动曲柄 AB 与连杆 BC 共线时,出现压力角α = 90 °,传动
角γ = 0 。
如图 2-20b 所示的曲柄滑块机构,如果以滑块作主动,则当从动曲柄 AB 与连杆 BC 共线时,外力F无法推动从动曲柄转动。
机构处于止点位置,一方面驱动力作用降为零,从动件要依靠惯性越过止点;另一方面是方向不定,可能因偶然外力的影响造成反转。
四杆机构是否存在止点,取决于从动件是否与连杆共线。
例如上述图2-20a所示的曲柄摇杆机构,如果改摇杆主动为曲柄主动,则摇杆为从动件,因连杆BC与摇杆CD不存在共线的位置,故不存在止点。
又例如前述图2-20b所示的曲柄滑块机构,如果改曲柄为主动,就不存在止点。
图2-21 机构止点位置的应用
止点的存在对机构运动是不利的,应尽量避免出现止点。
当无法避免出现止点时,一般可以采用加大从动件惯性的方法,靠惯性帮助通过止点。
例如内燃机曲轴上的飞轮。
也可以采用机构错位排列的方法,靠两组机构止点位置差的作用通过各自的止点。
在实际工程应用中,有许多场合是利用止点位置来实现一定工作要求的。
如图2-21a)所示为一种快速夹具,要求夹紧工件后夹紧反力不能自动松开夹具,所以将夹头构件1看成主动件,当连杆2和从动件3共线时,机构处于止点,夹紧反力N 对摇杆3的作用力矩为零。
这样,无论N有多大,也无法推动摇杆3而松开夹具。
当我们用手搬动连杆2的延长部分时,因主动件的转换破坏了止点位置而轻易地松开工件。
如图2-21b所示为飞机起落架处于放下机轮的位置,地面反力作用于机轮上使AB件为主动件,从动件CD与连杆BC成一直线,机构处于止点,只要用很小的锁紧力作用于CD杆即可有效地保持着支撑状态。
当飞机升空离地要收起机轮时,只要用较小力量推动CD,因主动件改为CD破坏了止点位置而轻易地收起机轮。
此外,还有汽车发动机盖、折叠椅等。
第四节平面四杆机构运动设计简介
四杆机构的设计方法有图解法、试验法、解析法三种。
本节仅介绍图解法。
图2-22 按连杆的三个预定位置设计四杆机构
一、按给定的连杆长度和位置设计平面四杆机构
1.按连杆的预定位置设计四杆机构
【例2-2】已知连杆BC的长度和依次占据的三个位置B1C1、B2C2、B3C3 ,如图2-22所示。
求确定满足上述条件的铰链四杆机构的其它各杆件的长度和位置。
解:显然B点的运动轨迹是由B1、B2、B3三点所确定的圆弧,C点的运动轨迹是由C1、C2、C3三点所确定的圆弧,分别找出这两段圆弧的圆心A和D,也就完成了本四杆机构的设计。
因为此时机架AD已定,连架杆CD和AB也已定。
具体作法如下:
(1确定比例尺,画出给定连杆的三个位置。
实际机构往往要通过缩小或放大比例后才便于作图设计,应根据实际情况选择适当的比例尺,见式(1-1)。
(2连结B1B2、B2B3 ,分别作直线段B1B2和B2B3的垂直平分线b12和b23(图中细实线),此两垂直平分线的交点A即为所求B1、B2、B3三点所确定圆弧的圆心。
(3连结C1C2、C2C3,分别作直线段C1C2和C2C3的垂直平分线c12、c23(图中细实线)交于点D,即为所求C1、C2、C3三点所确定圆弧的圆心。
(4以A点和D点作为连架铰链中心,分别连结AB3、B3C3、C3D(图中粗实线)即得所求四杆机构。
从图中量得各杆的长度再乘以比例尺,就得到实际结构长度尺寸。
在实际工程中,有时只对连杆的两个极限位置提出要求。
这样一来,要设计满足条件的四杆机构就会有很多种结果,这时应该根据实际情况提出附加条件。
【实训例2-3】如图2-23所示的加热炉门启闭机构,图中Ⅰ为炉门关闭位置,使用要求在完全开启后门背朝上水平放置并略低于炉口下沿,见图中Ⅱ位置。
图2-23 加热炉门四杆机构设计
解:把炉门当作连杆BC,已知的两个位置B1C1和B2C2 ,B和C已成为两个铰点,分别作直线段B1B2、C1C2的平分线得b12和c12 ,另外两铰点A和D就在这两根平分线上。
为确定A、D的位置,根据实际安装需要,希望A、D两铰链均安装在炉的正壁面上即图中yy位置,yy直线分别与b12、c12相交点A和D即为所求。
二、按给定的行程速比系数设计四杆机构
设计具有急回特性的四杆机构,一般是根据运动要求选定行程速比系数,然后根据机构极位的几何特点,结合其他辅助条件进行设计。
【实训例2-4】已知行程速比系数K,摇杆长度l CD,最大摆角,请用图解法设计此曲柄摇杆机构。
解:设计过程如图2-24所示,具体步骤:
(1由速比系数K计算极位角θ。
由式(2-2)知
(2选择合适的比例尺,作图求摇杆的极限位置。
取摇杆长度l CD除以比例尺得图中摇杆长CD,以CD为半径、任定点D为圆心、任定点C1为起点做弧C,使弧C所对应的圆心角等于或大于最大摆角,连接D点和C1点的线段C1D为摇杆的一个极限位置,过D点作与C1D夹角等于最大摆角的射线交圆弧于C2点得摇杆的另一个极限位置C2D。
图2-24按行程速比系数设计四杆机构
(3 求曲柄铰链中心。
过 C 1 点在 D 点同侧作 C 1 C 2 的垂线 H ,过 C 2 点作与 D 点同侧与直线段 C 1 C 2 夹角为( 90 0-θ)的直线 J 交直线 H 于点 P ,连接 C 2 P ,在直线段 C 2 P 上截取 C 2 P/2 得点 O ,以 O 点为圆点、 OP 为半径,画圆
K ,在 C 1 C 2 弧段以外在 K 上任取一点 A 为铰链中心。
(4求曲柄和连杆的铰链中心。
连接A、C2点得直线段AC2为曲柄与连杆长度之和,以A点为圆心、AC1为半径作弧交AC2于点E,可以证明曲柄长度AB =
C2E/2,于是以A点为圆心、C2E/2为半径画弧交AC2于点B2为曲柄与连杆的铰接中心。
(5计算各杆的实际长度。
分别量取图中AB2、AD、B2C2的长度,计算得:
曲柄长l AB =AB2,连杆长l BC =B2C2 ,机架长l AD =AD。
习题二
图2-25
2-1 铰链四杆机构按运动形式可分为哪三种类型?各有什么特点?试举出它们的应用实例。