复习练习题

高考语文复习《劝学》练习题班级考号姓名总分一、重点实词释义君子曰：学不可以已（）。

青，取之于（）蓝而（）青于（）蓝；冰，水为（）之而寒于水。

（句式：）木直中（）绳，輮（）以为轮，其曲（）中规。

虽（）有（）槁暴，不复挺者，輮使之然也。

故木受绳则直（），金就（）砺则利（），君子博学而日（）参（）省（）乎（）己，则知（）明而行无过矣。

吾尝终日而（）思矣，不如须臾（）之所学（）也；吾尝跂（）而望矣，不如登高之博见也。

登高而招，臂非加长也，而见者远；顺风而呼，声非加疾（）也，而闻者彰（）。

假（）舆（）马者，非利足也，而致（）千里；假舟楫者，非能水（）也，而绝（）江河。

君子生（）非异也，善假于物也。

积土成山，风雨兴焉（）；积水成渊，蛟龙生焉；积善（）成德，而神明自得，圣心备焉。

故不积跬步（），无以（）至千里；不积小流，无以成江海。

骐骥（）一跃，不能十步；驽马（）十驾，功在不舍（）。

锲而舍之，朽木不折；锲而不舍，金石可镂。

蚓无爪牙之利，筋骨之强，（句式：）上（）食埃土，下（）饮黄泉，用心一也。

蟹六跪而二螯，非蛇鳝之穴无可寄托者，用（）心躁也。

（句式：）二、理解性默写（一）真题1.（2020年高考新课标Ⅱ卷）《荀子·劝学》中举例说，笔直的木材如果“___________”，就会弯曲到符合圆规的标准；即使再经暴晒也不会挺直，因为“___________”。

2.（2020年高考天津卷）在“停课不停学”期间的云班会上讨论“学习和思考的关系”，你想强调学习的重要性，可以引用荀子《劝学》中的“______________，_____________”。

3.（2018年高考新课标Ⅲ卷）《荀子·劝学》中举例论证借助外物的重要性时说，终日殚精竭虑思考，却“_________________”，踮起脚极目远望，也“_________________”。

（二）模拟1.刘禹锡诗云“芳林新叶催陈叶，流水前波让后波”，这与荀子《劝学》中的“______________，_____________”表达的思想一致。

中考数学总复习《圆的综合题》练习题（附答案）班级:___________姓名：___________考号：_____________一、单选题1．在平面直角坐标系xOy中以点(3,4)为圆心，4为半径的圆（）A．与x轴相交，与y轴相切B．与x轴相离，与y轴相交C．与x轴相切，与y轴相交D．与x轴相切，与y轴相离2．如图，在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点，则弦BC的长的最小值为()A．22B．24C．10√5D．12√33．如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DCB等于（）A．90°B．100°C．130°D．140°4．如图，在正五边形ABCDE中连接AD，则∠DAE的度数为（）A．46°B．56°C．36°D．26°5．如图，PA、PB为∠O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交∠O 于点D．下列结论不一定成立的是（）A．△BPA为等腰三角形B．AB与PD相互垂直平分C．点A，B都在以PO为直径的圆上D．PC为△BPA的边AB上的中线6．如图，四边形ABCD内接于半径为6的∠O中连接AC，若AB＝CD，∠ACB＝45°，∠ACD＝12∠BAC，则BC的长度为（）A．6 √3B．6 √2C．9 √3D．9 √27．如图，点A，B，D，C是∠O上的四个点，连结AB，CD并延长，相交于点E，若∠BOD=20°，∠AOC=90°，则∠E的度数为()A．30°B．35°C．45°D．55°8．∠ABC中∠C=Rt∠，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB，BC分别交于点E，D，则AE的长为()A．95B．125C．185D．3659．如图，AB为∠O的直径，点C在∠O上，若∠B=60°，则∠A等于（）A．80°B．50°C．40°D．30°10．两个圆的半径分别是2cm和7cm，圆心距是5cm，则这两个圆的位置关系是() A．外离B．内切C．相交D．外切11．已知正三角形的边长为12，则这个正三角形外接圆的半径是()A．B．C．D．12．一个扇形的弧长为4π，半径长为4，则该扇形的面积为（）A．4πB．6πC．8πD．12π二、填空题13．在Rt∠ABC中∠C=90°，AB=5，BC=4，求内切圆半径14．如图，∠C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内弧OB上一点，∠BMO=120°，则∠C的半径为．15．一个立体图形的三视图如图所示，根据图中数据求得这个立体图形的侧面积为.16．一个半径为5cm的球形容器内装有水，若水面所在圆的直径为8cm，则容器内水的高度为cm.17．如图，在直角坐标系中以点P为圆心的圆弧与x轴交于A，B两点，已知P（4，2）和A（2，0），则点B的坐标是．18．下面是“作一个30°角”的尺规作图过程．已知：平面内一点A．求作：∠A，使得∠A=30°．作法：如图①作射线AB；②在射线AB取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；③以C为圆心，OC C为半径作弧，与⊙O交于点D，作射线AD．则∠DAB即为所求的角．请回答：该尺规作图的依据是．三、综合题19．如图，在△ABC中AC=BC=BD，点O在AC边上，OC为⊙O的半径，AB是⊙O 的切线，切点为点D，OC=2，OA=2√2．（1）求证：BC是⊙O的切线；（2）求阴影部分的面积．20．如图，△ABC内接于⊙O，CD是直径，∠CBG=∠BAC，CD与AB相交于点E，过点E作EF⊥BC，垂足为F，过点O作OH⊥AC，垂足为H，连接BD、OA．（1）求证：直线BG与⊙O相切；（2）若BEOD=54，求EFAC的值．21．如图，四边形ABCD 内接于∠O，BD是∠O的直径，过点A作∠O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE∠CD；（2）已知AE=4cm，CD=6cm，求∠O的半径．22．如图，∠O是∠ABC的外接圆，BC为∠O的直径，点E为∠ABC的内心，连接AE并延长交∠O 于D点，连接BD并延长至F，使得BD=DF，连接CF、BE．（1）求证：DB=DE；（2）求证：直线CF为∠O的切线．23．公元前5世纪，古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱，在狱中他对方铁窗和圆月亮产生了兴趣．他不断变换观察的位置，一会儿看见圆比正方形大，一会儿看见正方形比圆大，于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了：作一个正方形，使它的面积等于已知圆的面积（1）设有一个半径为√3的圆，则这个圆的周长为，面积为，作化圆为方得到的正方形的边长为(计算结果保留π)（2）由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图)，包括化圆为方在内的几何三大问题都已被证明是不可能的．但若不受标尺的限制，化圆为方并非难事。

九年级语文中考考点复习《文学常识》练习题（附答案解析）[一题组]1．下列关于文化文学常识的表述有误的一项是（）A．在古代，山的北面江河的南面叫阴，山的南面江河的北面叫阳。

B．《岳阳楼记》的作者范仲淹，北宋著名文学家，是“唐宋八大家”之一。

C．我国古代的史书有不同的体例。

《史记》是纪传体，《资治通鉴》《左传》是编年体，《战国策》是国别体。

D．《威尼斯商人》是英国著名戏剧大师莎士比亚的一部喜剧作品，文中的夏洛克是外国文学作品中“四大吝啬鬼”之一。

【答案】B【考点定位】识记文学常识。

能力层级为识记A。

2．下列关于名著知识及文学常识的表述，有误．．的一项是（）（2分）A．一篇新闻，主要包括标题、导语和主体三部分。

新闻的基本特征是用事实说话，但有时也可以在叙事过程中插入简要的议论。

B．“铭”“说”“记”“表”“书”“序”都是古代的一种文体，其中“说”既可以说明议论，也可以记叙事物，但都是用来阐述作者对各种问题的见解，如《爱莲说》《马说》等。

C．《西游记》中，朱紫国的王后被妖怪赛太岁掳去，妖怪的金刚镯厉害无比，让悟空费尽周折，最后还是观音菩萨出面带走了妖怪，悟空才救回王后娘娘。

D．《论语》是记录孔子和他的弟子言行的一部书，《孟子》是孟子及其门人所作。

《论语》《孟子》均为儒家经典，与《大学》《中庸》合称“四书”。

【答案】C【解析】试题分析：此题考查学生对名著《西游记》中的重要人物的了解，并分析出人物性格特点，要求学生在阅读的过程中分析主要人物的性格，识记其相关的故事情节。

赛太岁的宝贝是：三个金铃。

【考点定位】识记文学常识。

能力层级为识记A。

3．下列各项说法有误的一项是（）A．孟子，名轲，战国时期思想家、教育家、散文家。

《孟子》一书由孟子弟子和再传弟子收集编纂而成，共有七篇，文章逻辑严密而富于辞采，是儒家经典之一。

B．古人擅以花言志：东晋陶渊明喜菊，“采菊东篱下”表达的是对自己田园生活的满足；北宋周敦颐爱莲，“花之君子”是对自己高洁品质的期许；南宋陆游赞梅，仰慕的是“只有香如故”的孤傲。

高考数学一轮复习《统计》练习题（含答案）一、单选题1．已知条件p ：11x -<<，q ：x >m ，若p 是q 的充分不必要条件，则实数m 的取值范围是（ ） A ．[)1,-+∞B ．(),1-∞-C ．()1,0-D ．(],1-∞-2．下表为随机数表的一部分：08015 17727 45318 22374 21115 78253 77214 77402 43236 00210 45521 64237已知甲班有60位同学，编号为00~59号，规定：利用上面的随机数表，从第1行第4列的数开始，从左向右依次读取2个数，则抽到的第8位同学的编号是（ ） A ．11B ．15C ．25D ．373．一组数据的方差为()20S S ≥，将该组数据都乘以2，所得到的一组新数据的标准差为（ ）A ．22S B ．SC ．2SD ．2S4．甲、乙两所学校的男女生比例如图所示，已知甲校学生总数为1500，乙校学生总数为1000，下列结论错误的是（ ）A ．甲校女生比乙校女生多B ．乙校男生比甲校男生少C ．乙校女生比甲校男生少D ．甲校女生比乙校男生少5．某校共有学生3000人，为了解学生的身高情况，用分层抽样的方法从三个年级中抽取容量为100的样本，其中高一抽取40人，高二抽取30人，则该校高三学生人数为（ ） A ．600B ．800C ．900D ．12006．设某高中的男生体重y （单位：kg ）与身高x （单位：cm ）具有线性相关关系，根据一组样本数据()(12)i i x y i n =,，，，，用最小二乘法建立的回归方程为ˆ0.8580.71y x =-，则下列结论中不正确的是（ ） A ．y 与x 有正的线性相关关系B ．回归直线过样本点的中心(),x yC ．若该高中某男生身高增加1cm ，则其体重约增加0.85kgD ．若该高中某男生身高为170cm ，则可断定其体重必为63.79kg 7．x 是12100,,,x x x 的平均值，5为4120,,,x x x 的平均值，10为4142100,,,x x x 的平均值，则x =（ ） A ．8B ．9C ．15D ．1528．某学校有男生400人，女生600人．为调查该校全体学生每天睡眠时间，采用分层抽样的方法抽取样本，计算得男生每天睡眠时间均值为7.5小时，方差为1，女生每天睡眠时间为7小时，方差为0.5．若男、女样本量按比例分配，则可估计总体方差为（ ）． A ．0.45B ．0.62C ．0.7D ．0.769．某样本点)()(,1,2,,i i x y i n =⋅⋅⋅的经验回归方程为ˆ0.50.7yx =+，当8x =时，y 的实际值为4.5，则当8x =时，预测值与实际值的差值为（ ）． A ．0.1B ．0.2C ．0.3D ．0.410．若数据9，m ，6，n ，5的平均数为7，方差为2，则数据11，9，21m -，17，21n -的平均数和方差分别为（ ） A ．13，4B ．14，4C ．13，8D ．14，811．2021年起，我市将试行“3+1+2”的普通高考新模式，即除语文、数学、外语3门必选科目外，考生再从物理、历史中选1门，从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科，某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制，绘制成雷达图.甲同学的成绩雷达图如图所示，下面叙述一定不正确的是（ ）A ．甲的化学成绩领先年级平均分最多.B ．甲有2个科目的成绩低于年级平均分.C ．甲的成绩最好的前两个科目是化学和地理.D ．对甲而言，物理、化学、地理是比较理想的一种选科结果.12．冬末春初，乍暖还寒，人们容易感冒发热，若发生群体性发热，则会影响到人们的身体健康，干扰正常工作生产，某大型公司规定：若任意连续7天，每天不超过5人体温高于37.3℃，则称没有发生群体性发热，下列连续7天体温高于37.3℃人数的统计特征数中，能判定该公司没有发生群体性发热的为（ ）（1）中位数为3，众数为2 （2）均值小于1，中位数为1（3）均值为3，众数为4 （4）均值为2 A ．（1）（3）B ．（3）（4）C ．（2）（3）D ．（2）（4）二、填空题13．某校高一、高二、高三年级的学生人数之比为5:5:4，现按年级用分层抽样的方法抽取若干人，若抽取的高三年级的学生人数为20，则抽取的样本容量为______.14．已知具有线性相关的变量x 、y ，设其样本点为()(1,2,,,8)i i i A x y i =，回归直线方程为1ˆ2yx b =+，若128(6,2)OA OA OA +++=(O 为原点），则b =_______.15．已知一组数据按顺序排列为：12，16，20，n ，46，51，58，60.若这组数据的第30百分位数的两倍与这组数据的第50百分位数相等，则n 的值为___________.16．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：由表中的数据得线性回归方程为y bx a =+，其中20b =-，预测当产品价格定为9.5(元)时，销量约为__________件．三、解答题17．某区政府组织了以“不忘初心，牢记使命”为主题的教育活动，为统计全区党员干部一周参与主题教育活动的时间，从全区的党员干部中随机抽取n 名，获得了他们一周参与主题教育活动时间（单位：h ）的频率分布直方图如图所示，已知参与主题教育活动时间在(]12,16内的人数为92．(1)求n 的值；(2)以每组数据所在区间的中点值作为本组的代表，估算这些党员干部参与主题教育活动时间的中位数（中位数精确到0.01）．(3)如果计划对参与主题教育活动时间在(]16,24内的党员干部给予奖励，且在(]16,20，(]20,24内的分别评为二等奖和一等奖，那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动，再从这5人中随机抽取2人作为主宣讲人，求这2人均是二等奖的概率．18．由于疫情影响，今年我们学校开展线上教学，高一年级某班班主任为了了解学生上网学习时间，对本班40名学生某天上网学习时间进行了调查，将数据（取整数）整理后，绘制出如图所示频率分布直方图，已知从左到右各个小组的频率分别是0.15，0.25，0.35，0.20，0.05，则根据直方图所提供的信息：（1）这一天上网学习时间在100~119分钟之间的学生有多少人？（2）估计这40位同学的线上平均学习时间（同一组中的数据用该组区间的中点值为代表）以及中位数分别是多少？（精确到0.1）（3）如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间，这样推断是否合理？为什么？19．省政府坚持以习近平新时代中国特色社会主义思想为指导，落实全国、全省教育大会部署，坚持社会主义办学方向，落实立德树人根本任务，发展素质教育，推进育人方式变革，引导全社会树立科学的教育质量观和人才培养观，切实减轻有损中小学生身心健康的过重学业负担，遵循教育教学规律，促进中小学生健康成长，培养德智体美劳全面发展的社会主义建设者和接班人．从某市抽取1000名一年级小学生进行调查，统计他们每周做作业的时长（单位：小时），根据结果绘制的频率分布直方图如下：（1）根据频率分布直方图，求所有被抽查小学生每周做作业的平均时长和中位数；（同一组中的数据用该组区间的中点值作代表）（2）①为了进一步了解，现采用分层抽样的方法从[8,10]和[10,12]组中抽取50名学生，则两组各抽取多少人？②再利用分层抽样从抽取的50人中选5人参加一个座谈会．现从参加座谈会的5名学生中随机抽取两人发言，求[8,10]小组中恰有2人发言的概率？20．为了调查某地区高中女生的日均消费情况，研究人员随机抽取了该地区5000名高中女生作出调查，所得数据统计如下图所示．(1)求a 的值以及这5000名高中女生的日均消费的平均数（同一组数据用该组区间的中间值代替）；(2)在样本中，现按照分层抽样的方法从该地区消费在[)15,20与[)20,25的高中女生中随机抽取9人，若再从9人中随机抽取3人，记这3人中消费在[)15,20的人数为X ，求X 的分布列以及数学期望．21．道德与法律的联系：法律､道德都是行为规范，都是为规范人们的行为而规定的行动准则.1.法律需要道德的奠基和撑持；2.道德的实施需要法律的强制保障.某校进行了一次道德与法律的相关测试（满分：100分），并随机抽取了50个统计其分数，得到的结果如下表所示： 成绩/分 [)0,20[)20,40[)40,60[)60,80[)80,100人数/个 44102210(1)若同一组数据用该区间中点值作代表，试估计这次测试的平均分和中位数（所得结果四舍五入保留整数）；(2)假设处于[)20,40的4个人的成绩分别为20，26，35，38，求表中成绩的10%分位数； (3)以频率估计概率，若在这个学校中，随机挑选3人，记3人的成绩在[)80,100间的数量为随机变量X ，求X 的分布列和数学期望()E X .22．某校从高三年级学生中随机抽取100名学生的某次数学考试成绩，将其成绩分成[)50,60，[)60,70，[)70,80，[)80,90，[]90,100的5组，制成如图所示的频率分布直方图.(1)求图中x 的值；(2)估计这组数据的平均数；(3)若成绩在[)50,60内的学生中男生占40%.现从成绩在[)50,60内的学生中随机抽取2人进行分析，求2人中恰有1名女生的概率.23．某校从高三学生中选取了50名学生参加数学质量检测，成绩（单位：分）分组及各组的频数如下：[40,50)，2；[50,60)，3；[60,70)，10；[70,80)，15；[80,90)，12；[90,100]，8．(1)列出频率分布表；(2)画出频率直方图及频率折线图．24．某农业科学研究所为检验某农作物种子的培育有效率，进行了如下试验：一是对该农作物的10000粒种子进行培育，发现有20粒种子未发芽；二是将未进行培育的该农作物的2500粒种子种植在5块试验田中，各试验田种植的种子数及未发芽数如下表：（1）求y 关于x 的回归直线方程； （2）在上述试验下，若以1nN-表示该农作物种子的培育有效率，其中n 为进行培育的10000粒种子的未发芽数，N 为依据上述回归方程估算的未进行培育的10000粒种子的未发芽数，请估计该农作物种子的培育有效率（结果保留3位有效数字）．参考公式；在回归方程ˆˆˆy bx a =+中，1221ˆni ii nii x y nx ybxnx==-⋅=-∑∑，ˆˆa y bx=-参考答案1．D2．A3．D4．D5．C6．D7．A8．D9．B10．C11．A12．D 13．7014．18-##-0.12515．34 16．6017．（1）由已知可得，0.25(0.02500.04750.05000.0125)0.1150a =-+++=． 则0.1150492n ⨯⨯=，得922000.11504n ==⨯．（2）设中位数为x ，则0.050040.01254(16)0.11500.5x ⨯+⨯+-⨯=，得13.83x ≈．（3）按照分层抽样的方法从(16，20]内选取的人数为0.050540.05000.0125⨯=+，从(20，24]内选取的人数为0.0125510.05000.0125⨯=+．记二等奖的4人分别为a ，b ，c ，d ，一等奖的1人为A ，事件E 为“从这5人中抽取2人作为主宣讲人，且这2人均是二等奖”．从这5人中随机抽取2人的基本事件为(,)a b ，(,)a c ，(,)a d ，(,)a A ，(,)b c ，(,)b d ，(,)b A ，(,)c d ，(,)c A ，(,)d A ，共10种，其中2人均是二等奖的情况有(,)a b ，(,)a c ，(,)a d ，(,)b c ，(,)b d ，(,)c d ，共6种， 由古典概型的概率计算公式得()63105P E ==． 18．（1）因为频数=样本容量⨯频率，一天上网学习时间在100119分钟之间的学生所占频率为0.35，所以一天上网学习时间在100~119分钟之间的学生人数为400.3514⨯=（人） （2）40位同学的线上学习时间估计值为：0.1569.90.2589.90.35109.90.20129.90.05149.9104.9⨯+⨯+⨯+⨯+⨯=分钟在中位数左边和右边的小长方形的面积和是相等的，设在99.9~119.9靠近左侧长度为x ,则0.15+0.25+0.350.5x =解得0.27x ≈； 所以中位数估计值是99.9+0.27=100.17100.2≈（3）因为该样本的选取只在高一某班，不具有代表性，所以这样推断不合理. 19．（1）设抽查学生做作业的平均时长为x ，中位数为y ，0.0510.130.2550.370.1590.1110.0513 6.8x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=， 0.050.10.250.15(6)0.5y y =+++⨯-=，解得203y =即抽查学生做作业的平均时长为6.8，中位数为203． （2）①[8,10]组的人数为10000.15150⨯=人，设抽取的人数为a ，[]10,12组的人数为10000.1100⨯=人， 设抽取的人数为b ，则50150100250a b ==，解得30a =，20b = 所以在[8,10]和[]10,12两组中分别抽取30人和20人，②再抽取5人，其中[8,10]和[]10,12两组中分别抽取3人和2人，将[8,10]组中被抽取的工作人员标记为1A ，2A ，3A ，将[]10,12中的标记为1B ，2B ． 设事件C 表示从[8,10]小组中恰好抽取2人，则抽取的情况如下：{}12,A A ，{}13,A A ，{}11,A B ，{}12,A B ，{}23,A A ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B 共10种情况；其中在[8,10]中恰好抽取2人有3种，则3()10P C =． 20．（1）由题意得，()20.040.080.0651a +++⨯=，解得0.01a =，故所求平均数为17.50.427.50.332.50.0537.50.0524.25⨯0.2+22.5⨯+⨯+⨯++=（元）； （2）由题意得，消费在[)15,20，[)20,25的高中女生分别有3人和6人，故X 的可能取值为0，1，2，3，∴()6033395021C C P X C ===，()21633915128C C P X C ===，()1263393214C C P X C ===，()0363391384C C P X C ===， 故X 的分布列为：∴()515310123121281484E X =⨯+⨯+⨯+⨯=； 故答案为：1. 21．(1)估计这次测试的平均分为1043045010702290106250x ⨯+⨯+⨯+⨯+⨯==（分）；设这次测试的中位数为0x ，显然()060,80x ∈，则060441022200.550x -+++⋅=，解得066x ≈（分）. 即估计这次测试的中位数为66.(2)由于5010%5⨯=，所以表中成绩的10%分位数为2026232+=. (3)X 所有可能取值为0，1，2，3.由表中数据可知，任意挑选一人，成绩在[)80,100间的概率为101505=. 所以()346405125P X ⎛⎫=== ⎪⎝⎭，()21341481C 55125P X ⎛⎫=== ⎪⎝⎭， ()122341122C 55125P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，()31135125P X ⎛⎫=== ⎪⎝⎭， 故X 的分布列为故X 的数学期望()6448121301231251251251255E X =⨯+⨯+⨯+⨯=. 22．(1)由频率分布直方图得()0.0050.0350.0300.010101x ++++⨯=，解得0.020x =， 所以图中x 的值是0.020.(2)由频率分布直方图得这组数据的平均数： (550.005650.020750.03585x =⨯+⨯+⨯+⨯)0.030950.0101077+⨯⨯=， 所以这组数据的平均数为77.(3)数学成绩在[)50,60内的人数为0. 005101005⨯⨯=(人)，其中男生人数为540%2⨯=(人)，则女生人数为3人，记2名男生分别为1A ，2A ，3名女生分别为1B ，2B ，3B ，从数学成绩在[)50,60内的5人中随机抽取2人进行分析的基本事件为：121112132122A A A B A B A B A B A B ,,,,,,23121323A B B B B B B B ,,,，共10个不同结果，它们等可能， 其中2人中恰有1名女生的基本事件为111213212223,,,,,A B A B A B A B A B A B ，共6种结果， 所以2人中恰有1名女生的概率为为63105=. 23．（1）解：频率分布表如下：（2） 频率直方图及频率折线图如图所示．24． (1)依题意，3004005006007005005x ++++==，2466755y ++++==， 513002400450066006700713700ii i x y ==⋅+⋅+⋅+⋅+⋅=∑， 52222221(34567)100001350000i i x==++++⋅=∑， 于是得512252113700550051200ˆ0.01213500005500100000i ii i i x y nx y b x nx==-⋅-⋅⋅====-⋅-∑∑，ˆˆ50.0125001ay bx =-=-⨯=-， 所以y 关于x 的回归直线方程为ˆ0.0121yx =-； (2)由(1)知，估计未进行培育的10000粒种子的未发芽数N 约为：ˆ0.012100001119y =⨯-=，而已培育的10000粒种子有20粒种子未发芽，即20n =， 所以该农作物种子的培育有效率为209910832119119-=≈。

初三化学期末复习100道练习题1.化学变化的基本特征?有新物质生成2.化学变化的关键词（至少5个）燃烧、腐蚀、变质、酿酒、光合作用、呼吸作用、生锈3.描述水的构成奥秘①水是由水分子构成的②每个水分子由两个氢原子和一个氧原子构成③水由氢氧元素组成4.保持水化学性质的微粒是?水分子5.科学探究过程中收集证据包括哪些环节?设计实验方案、进行实验6.固体药品存放在?粉末状用什么取用?块状固体用什么取用? 广口瓶/药匙或纸槽/镊子7.酒精灯用什么点燃?如何熄灭?用哪部分加热?火柴/灯帽盖灭/外焰8.液体加热的注意事项液体体积不超过1/3试管夹夹持在离口1/3处擦干外壁再加热，先预热再加热倾斜45°9.量筒的用途?集气瓶的用途?①量度液体的体积②收集或储存少量气体10.三态变化中，水分子的情况?水分子的数目和大小不变，间隔和排列方式改变11.分子的基本性质分子的质量和体积很小；相互间有间隔；总在不停地运动12.水的天然循环通过什么实现的?三态变化13.沉降除去哪些杂质?通常加入?作用是?大颗粒不溶性杂质/明矾/加速泥沙沉降14.过滤除去哪些杂质?过滤用到的仪器?玻璃棒的作用?小颗粒不溶性杂质/烧杯、漏斗、玻璃棒、铁架台（带铁圈）/引流15.过滤后滤液浑浊的原因?滤纸破损、液面高于滤纸、仪器本身不干净16.过滤慢的原因?杂质过多、滤纸未紧贴漏斗内壁17.除去水中有颜色和异味的杂质通常加入?作用?活性炭/吸附18.如何去除可溶性杂质?蒸馏19.水中的微生物如何除?属于什么变化?杀菌消毒/化学变化20.硬水和软水如何区分?软水对应的现象?生活中如何降低水的硬度?肥皂水/泡沫丰富/煮沸21.举例说出两种混合物、两种纯净物混合物—空气、海水、石头等；纯净物—氢气、水、氧气等22.电解水过程中，正极---气体?怎么验证的?现象?说明气体的性质?氧气、带火星的木条、木条复燃、助燃性负极---气体?怎么验证的?现象?说明气体的性质?氢气、点燃的火柴、气体被点燃，火焰呈淡蓝色、可燃性23.化学变化的实质?破坏旧分子，形成新分子，即原子的重新组合24.用微观角度解释化学变化中一定不变的是?一定改变的是?可能改变的是?原子的种类和数目/ 分子的种类/ 分子的数目25.化学变化中，最小的微粒?原子26.电解水文字表达式?氢气燃烧的文字表达式?水图片氢气+氧气氢气+氧气→水27.通过电解水实验得到的结论是什么?①电解水生成氢气和氧气②正氧负氢，氢二氧一③水由氢氧元素组成28.点燃氢气前应进行什么操作？验纯29.分解反应、化合反应的特点?一变多、多变一，都是化学反应30.原子的结构，并注明各微粒的带电情况31.原子中的等量关系质子数=核电荷数=核外电子数32.决定原子种类的是?质子数33.哪些物质是由原子直接构成的?金属、稀有气体、石墨金刚石34.画出钠原子、镁原子的结构示意图35.构成物质的微粒有哪些？各列举两例分子---水和大部分气体原子---金属、金刚石、稀有气体离子---氯化钠、氧化镁36.写出钠离子、镁离子、氯离子、硫离子的符号Na+ Mg2+ Cl- S2-37.原子的化学性质由什么决定?最外层电子数38.相对原子质量的定义表达式?39.一种元素和另外一种元素的区别质子数不同40.元素符号的意义?Fe这一符号的意义一种元素，代表这种元素的一个原子铁元素、一个铁原子、铁41.元素在地壳中的分布由大到小的顺序为？氧硅铝铁钙42.列举生活中常见的溶液？至少5种糖水、茶水、啤酒、白醋、消毒酒精、碳酸饮料43.溶液的特征均一、稳定44.溶液的组成溶质、溶剂45.溶于水温度升高的是？降低的是？氢氧化钠、硝酸铵46.汽油去油污的原理？溶解47.洗涤剂去油污的原理？乳化48.托盘天平称量药品时，不能把药品直接放在托盘里，应如何做？没有腐蚀性的---纸片；有腐蚀性的---烧杯中49.量筒用来量度液体的体积，读数时应注意？视线与凹液面的最低处保持水平50.在描述饱和溶液的时候，应注意强调哪三点？一定的温度；一定量的溶剂；该物质51.溶液是否饱和的判断方法？首先看溶液中是否有未溶解的固体,如果有,则此时的溶液已经达到饱和状态如果没有，再向溶液中加入少量该溶质看是否继续溶解52.饱和溶液如何转变为不饱和溶液？加入溶剂，改变温度53.溶质质量分数的表达式？溶质质量分数=（溶质质量/溶液质量）×100%54.配制一定溶质质量分数的溶液基本步骤包括？计算---称量---溶解---装瓶存放55.配制一定溶质质量分数的溶液用到哪些仪器？托盘天平、药匙、量筒、胶头滴管、烧杯、玻璃棒56.玻璃棒在配制溶液中的作用？搅拌，加速溶解57.在配制一定溶质质量分数的溶液时，导致溶质质量分数偏小的原因可能有哪些？药品不纯；量取水时仰视；烧杯或试剂瓶内壁有水；物质和砝码放反，且使用游码58.空气中含量最多的气体是？体积分数是多少？氮气；78%59.空气中各成分由多到少排序？氮气---氧气---稀有气体---二氧化碳---其它60.测定空气中氧气含量时，可选用的药品有哪些？为什么不选择木炭？铜粉、红磷；木炭与氧气加热会生成二氧化碳气体61.铜粉加热的文字表达式/现象？铜+氧气→氧化铜 ,红色粉末变黑62.氧气含量测定时，有哪些注意事项？药品要充足、装置要密封、冷却至室温再读数63.简述空气中各成分分离的简要过程？该过程属于什么变化？通过降温加压使空气液化，然后加热液态空气，利用空气中各成分的沸点的不同，使其在不同的温度下气化，从而将各种气体分离出来。

军考复习题练习题一、单选题1. 下列哪个人物是中国古代军事家？A. 孙中山B. 毛泽东C. 岳飞D. 邓小平答案：C2. 以下哪个国家是永久中立国？A. 法国B. 瑞士C. 德国D. 意大利答案：B3. 以下哪个国家是北约成员国？A. 俄罗斯B. 英国D. 中国答案：B4. 下列哪个战争是指中国人民解放军与国民党军队之间的内战？A. 抗日战争B. 第一次国共内战C. 第二次国共内战D. 韩战答案：C5. 以下哪种武器是属于火炮类？A. 步枪B. 火箭筒C. 冲锋枪D. 加农炮答案：D二、多选题1. 以下哪些国家是联合国安全理事会的常任理事国？B. 英国C. 俄罗斯D. 巴西答案：A、B、C2. 下列哪些国家是五大洲之一？A. 中国B. 英国C. 肯尼亚D. 韩国答案：A、C3. 以下哪些是中国人民解放军军衔？A. 上将B. 中将C. 下将D. 少将答案：A、B、D4. 以下哪些是陆军兵种？A. 炮兵B. 信息兵C. 空降兵D. 守备兵答案：A、B、C、D5. 以下哪些战争是中国参与的战争？A. 朝鲜战争B. 越南战争C. 韩战D. 世界大战答案：A、B三、判断题1. 中国拥有世界上最强大的海军。

答案：错误2. 二战中，中国是同盟国之一。

答案：正确3. 中国的国旗是五星红旗。

答案：正确4. 中国的军队是志愿军制度。

答案：错误5. 陆军是军队的主力兵种。

答案：正确四、简答题1. 中国人民解放军成立于哪一年？简要描述成立的背景和意义。

答案：中国人民解放军成立于1949年。

中国共产党领导的人民解放军在国共内战中战胜国民党军队，实现了中国大陆的解放。

中国人民解放军的成立标志着中国由半殖民地半封建社会进入了社会主义革命阶段，为中国的独立、自由、平等奠定了坚实的基础。

2. 现代战争中，信息化战争的特点是什么？简要描述信息化战争对军事技术的影响。

答案：信息化战争是指利用现代信息技术对战争进行指挥、控制和作战的战争形态。

2024年高考语文复习：语用试题引用手法及表达效果专项练习题阅读下面的文字，完成下面小题。

来竹峰寺的头两天，我睡得足足的。

从来没那么困过。

那阵子心里烦闷，所谓“闷向心头瞌睡多”,有它的道理。

山中的夜静极了，____①___虫鸟啼鸣也是静的一部分。

头两天，只是睡。

白天___②___睡。

白天，寺院中浮动．．着和煦的阳光，庭中石桌石凳，白得耀眼，像自身发出洁白的柔光。

屋瓦渐渐被晒暖。

这是春夏之间。

我躺在一间仅有一床一桌的客房的床上，想象自己是个养病的病人，虚弱又安详。

多少年没睡过那样的好觉了，像往一个深潭里悠悠下沉，有时开眼看看水面动荡的光影，又闭上。

睡到下午四点多，实在不好意思了，起来吃了点面条，开始在寺中转悠。

这时他们正在做晚课。

每个寺庙的晚课内容不尽相同，竹峰寺的不算长，也不短。

三个人在大殿里嗡嗡念诵，音节密集，用密集的音节营造出一种小规模的庄严气象来，站门外听，声势颇壮，听不出__③__有三人。

忽而声调一缓，由慧灯师傅带头，曼声吟唱起来，好听极了。

听到“是日已过，命亦随减。

如少水鱼，斯有何乐……”,我__④__走出院去，四下闲逛。

1．依次填入文中横线上的词语，全都恰当的一项是（）A．连也仅就B．可也共就C．连还共才D．可还仅才2．请简要分析选文加点字“浮动”的妙处。

3．说说文中画波浪线的两处引用各有怎样的表现力。

阅读下面的文字，完成下面小题。

工匠精神从来都不是什么雕虫小技，而是一种改变世界的现实力量。

坚守工匠精神，并不是把“拜手工教”推上神坛，也不是鼓励离群索居、“躲进小楼成一统”，而是为了擦亮爱岗敬业、劳动光荣的价值原色，倡导质量至上、品质取胜的市场风尚，展现创新引领、追求卓越的时代精神，（）。

将一门技术掌握到______①_______，这固然是工匠精神，但工匠精神的内涵又远不限于此。

有人说：“没有一流的心性，就没有一流的技术。

”的确，倘若没有发自肺腑、专心如一的热爱，怎能有______②_______、尽心竭力的付出；没有臻于至善、超今冠古的追求，怎能有出类拔萃、巧夺天工的卓越；没有冰心一片、物我两忘的境界，怎能有雷打不动、______③_______的笃实。

某某省富阳市场口中学高三数学 函数复习练习一、选择题1．幂函数y ＝f (x )的图象经过点⎝ ⎛⎭⎪⎫4，12，则f ⎝ ⎛⎭⎪⎫14的值为( )． A ．1 B ．2 C ．3 D ．42．(2013·某某长郡中学一模)设函数f (x )＝⎩⎪⎨⎪⎧x ＋12，x ≤－1，2x ＋2，x >－1，若f (x )>1成立，则实数x 的取值X 围是( )．A ．(－∞，－2)B.⎝ ⎛⎭⎪⎫－12，＋∞C.⎝ ⎛⎭⎪⎫－2，－12D ．(－∞，－2)∪⎝ ⎛⎭⎪⎫－12，＋∞3．(2013·某某一模)设函数f (x )是奇函数，并且在R 上为增函数，若0≤θ≤π2时，f (m sinθ)＋f (1－m )>0恒成立，则实数m 的取值X 围是( )．A ．(0,1)B ．(－∞，0) C.⎝⎛⎭⎪⎫－∞，12D ．(－∞，1) 4．(2013·某某模拟)已知函数f (x )是奇函数，当x >0时，f (x )＝a x (a >0且a ≠1)，且f ⎝ ⎛⎭⎪⎫log 124＝－3，则a 的值为( )． A.3B ．3 C ．9 D.325．(2013·某某质检)已知a ＝2，b ＝，c ，则( )． A ．a >b >c B ．a >c >b C ．c >a >b D ．b >c >a6．(2013·某某调研)已知函数f (x )＝⎩⎪⎨⎪⎧1－x ，x ≤0，a x，x >0，若f (1)＝f (－1)，则实数a 的值等于( )．A ．1B ．2C ．3D ．47．设a >1，且m ＝log a (a 2＋1)，n ＝log a (a －1)，p ＝log a (2a )，则m ，n ，p 的大小关系为( )． A ．n >m >p B ．m >p >n C ．m >n >p D ．p >m >n8．(2013·东城区综合练习)设a ＝log 123，b ＝⎝ ⎛⎭⎪⎫13，c ＝ln π，则( )． A ．a <b <c B ．a <c <b C ．c <a <b D ．b <a <c9．(2013·某某名校模拟)设函数f (x )定义在实数集上，f (2－x )＝f (x )，且当x ≥1时，f (x )＝ln x ，则有( )．A ．f ⎝ ⎛⎭⎪⎫13<f (2)<f ⎝ ⎛⎭⎪⎫12B ．f ⎝ ⎛⎭⎪⎫12<f (2)<f ⎝ ⎛⎭⎪⎫13C ．f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13<f (2)D ．f (2)<f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13 10．设函数y ＝f (x )在(－∞，＋∞)内有定义，对于给定的正数K ，定义函数：f K (x )＝⎩⎪⎨⎪⎧f x ，f x ≤K ，K ，f x >K .取函数f (x )＝a－|x |(a >1)．当K ＝1a时，函数f K (x )在下列区间上单调递减的是( )． A ．(－∞，0) B ．(－a ，＋∞) C ．(－∞，－1) D ．(1，＋∞) 二、填空题11．(2012·某某质检)若函数f (x )＝⎩⎪⎨⎪⎧2x ，x <3，3x －m ，x ≥3，且f (f (2))>7，则实数m 的取值X围是________．12．(2013·某某质检)函数y ＝log 12(3x －a )的定义域是⎝ ⎛⎭⎪⎫23，＋∞，则a ＝________. 13．若f (x )＝1＋lg x ，g (x )＝x 2，那么使2f [g (x )]＝g [f (x )]的x 的值是________． 14．已知函数f (x )＝|log 2x |，正实数m ，n 满足m <n ，且f (m )＝f (n )，若f (x )在区间[m 2，n ]上的最大值为2，则m ＋n ＝________.15．(2012·某某高中月考)关于函数f (x )＝lg x 2＋1|x |(x ≠0)，有下列命题：①其图象关于y 轴对称；②当x >0时，f (x )是增函数；当x <0时，f (x )是减函数； ③f (x )的最小值是lg 2；④f (x )在区间(－1,0)，(2，＋∞)上是增函数； ⑤f (x )无最大值，也无最小值．其中所有正确结论的序号是________．16．若实数x 满足log3 x ＝1＋sin θ，则|x －1|＋|x －9|的值为________． 17．已知函数f(x)＝⎩⎪⎨⎪⎧log2⎝ ⎛⎭⎪⎫1x ＋1，x≥0，⎝ ⎛⎭⎪⎫12x －1，x ＜0.若f(3－2a2)＞f(a)，则实数a 的取值X 围为________．18.(2013·某某模拟)函数f(x)＝log 12(x2－2x －3)的单调递增区间是________．19．设min{p ，q}表示p ，q 两者中的较小者，若函数f(x)＝min{3－x ，log2x}，则满足f(x)＜12的集合为________．20．(2011·某某卷改编)若点(a ，b)在y ＝lg x 图象上，a≠1，则下列点也在此图象上的是________(填序号)．①⎝ ⎛⎭⎪⎫1a ，b ；②(10a,1－b)；③⎝ ⎛⎭⎪⎫10a ，b ＋1；④(a2,2b)． 21．已知点⎝ ⎛⎭⎪⎫12，2在幂函数y ＝f (x )的图象上，点⎝ ⎛⎭⎪⎫－2，14在幂函数y ＝g (x )的图象上，则f (2)＋g (－1)＝________.22．(2012·苏锡常镇四市调研)如图，已知二次函数y ＝ax 2＋bx ＋c (a ，b ，c 为实数，a ≠0)的图象过点C (t,2)，且与x 轴交于A ，B 两点，若AC ⊥BC ，则a 的值为________．23．(2012·某某模拟)已知函数f (x )＝|2x －3|，若0＜2a ＜b ＋1，且f (2a )＝f (b ＋3)，则T ＝3a 2＋b 的取值X 围为________．24．(2012·某某模拟)已知函数f (x )＝9x －m ·3x＋m ＋1在x ∈(0，＋∞)上的图象恒在x 轴上方，则m 的取值X 围为________．25．对于函数f (x )＝e x －e －x(x ∈R )，有下列结论：①f (x )的值域是R ；②f (x )是R 上的增函数；③对任意x ∈R ，有f (－x )＋f (x )＝0成立；④若方程|f (x )|＝a 有两个相异实根，则a ≥0，其中所有正确的命题序号是________． 26．函数y ＝a2x －2(a >0，a ≠1)的图象恒过点A ，若直线l ：mx ＋ny －1＝0经过点A ，则坐标原点O 到直线l 的距离的最大值为________． 三．解答题1．已知函数f (x )＝log a (3－ax )(a ＞0，且a ≠1)．(1)当x ∈[0,2]时，函数f (x )恒有意义，某某数a 的取值X 围；(2)是否存在这样的实数a ，使得函数f (x )在区间[1,2]上为减函数，并且最大值为1，如果存在，试求出a 的值；如果不存在，请说明理由．2．(2012·某某学情调查)已知函数f (x )＝log 4(4x＋1)＋kx (x ∈R )是偶函数． (1)求k 的值；(2)若方程f (x )－m ＝0有解，求m 的取值X 围．基本初等函数（2）1．已知函数f (x )＝－x ＋log 21－x1＋x .(1)求f ⎝⎛⎭⎪⎫12 014＋f ⎝ ⎛⎭⎪⎫－12 014的值；(2)当x ∈(－a ，a ]，其中a ∈(0,1)，a 是常数时，函数f (x )是否存在最小值？若存在，求出f (x )的最小值；若不存在，请说明理由．2．已知函数f (x )＝x |x －2|. (1)写出f (x )的单调区间； (2)解不等式f (x )＜3；(3)设0＜a ≤2，求f (x )在[0，a ]上的最大值．3．(2012·某某调研)已知13≤a ≤1，若f (x )＝ax 2－2x ＋1在区间[1,3]上的最大值为M (a )，最小值为N (a )，令g (a )＝M (a )－N (a )． (1)求g (a )的函数表达式；(2)判断g (a )的单调性，并求出g (a )的最小值．4．(2012·某某检测)设二次函数f(x)＝ax2＋bx＋c(a≠0)在区间[－2,2]上的最大值、最小值分别是M，m，集合A＝{x|f(x)＝x}．(1)若A＝{1,2}，且f(0)＝2，求M和m的值；(2)若A＝{1}，且a≥1，记g(a)＝M＋m，求g(a)的最小值．5．已知函数f(x)＝2x－12x(x∈R)．(1)讨论f(x)的单调性与奇偶性；(2)若2x f(2x)＋mf(x)≥0对任意的x∈[0，＋∞)恒成立，求m的取值X围．6．(2013·某某模拟)已知函数f(x)＝a x－24－a x－1(a>0且a≠1)．(1)求函数f(x)的定义域、值域；(2)某某数a的取值X围，使得当定义域为[1，＋∞)时，f(x)≥0恒成立．7．如果函数f(x)＝a x(a x－3a2－1)(a＞0，a≠1)在区间[0，＋∞)上是增函数，某某数a的取值X围．8．设函数f (x )＝ka x －a －x(a ＞0且a ≠1)是奇函数． (1)求k 的值；(2)若f (1)＞0，解关于x 的不等式f (x 2＋2x )＋f (x －4)＞0；(3)若f (1)＝32，且g (x )＝a 2x ＋a －2x－2mf (x )在[1，＋∞)上的最小值为－2，求m 的值．方程的解与函数的零点（1）一、选择题1 ．已知函数f(x)是R 上的偶函数,且f(1-x)=f(1+x),当x ∈[0,1]时,f(x)=x 2,则函数y=f(x)-log 5x 的零点个数是 （ ）A ．3B ．4C ．5D ．62 ．已知函数⎩⎨⎧>-≤-=0,120,2)(x x x a x f x (R a ∈),若函数)(x f 在R 上有两个零点,则a 的取值X围是 （ ）A ．)1,(--∞B ．]1,(-∞C ．)0,1[-D ．]1,0(3 ．设函数f (x )=x |x |+bx +c ,给出下列四个命题:①c =0时,f (x )是奇函数 ②b =0,c >0时,方程f (x )=0只有一个实根 ③f (x )的图象关于(0,c )对称 ④方程f (x )=0至多两个实根其中正确的命题是 （ ）A ．①④B ．①③C ．①②③D ．①②④4 ．已知函数()ln 38f x x x =+-的零点0[,]x a b ∈,且1(,)b a a b N +-=∈,则a b +=（ ）A ．5B ．4C ．3D ．25 ．函数21f ()log 22x x x =-+的零点个数为 ( ) （ ）A ．0B ．1C ．3D ． 26 ．函数()22x f x x =-零点的个数为（ ）A ．1B ．2C ．3D ．47 ．函数12ln )(-+=x x x f 的零点的个数是（ ）A ．0B ．1C ．2D ．38 ．奇函数()f x ,偶函数()g x 的图像分别如图1、2所示,方程(())0,(())0f g x g f x ==的实根个数分别为,a b ,则a b +=（ ）A ．14B ．10C ．7D ．39 ．实系数一元二次方程01)1(2=+++++b a x a x 的两个实根为21,x x ,若有2110x x <<<,则ab的取值X 围是（ ）A ．)21,1(-B ．)21,2(-C ．)21,1(--D ．)21,2(--10已知函数()y f x =的周期为2,当[0,2]x ∈时,2()(1)f x x =-,如果()()g x f x =-5log 1x -,则函数()y g x =的所有零点之和为（ ）A ．4B ．6C ．8D ．1011．已知0x 是xx f x1)21()(+=的一个零点,)0,(),,(0201x x x x ∈-∞∈,则 （ ）A ．0)(,0)(21<<x f x fB ．0)(,0)(21>>x f x fC ．0)(,0)(21<>x f x fD ．0)(,0)(21><x f x f提升：定义在R上的函数()g x 及二次函数()h x 满足：2()2()9,(2)(0)1x x g x g x e h h e+-=+--==且(3)2h -=-. （1）求()g x 和()h x 的解析式；（2）对于12,[1,1]x x ∈-，均有11222()5()()h x ax g x x g x ++≥-成立，求a 的取值X 围； （3）设(),(0)()(),(0)g x x f x h x x >⎧=⎨≤⎩，讨论方程[()]2f f x =的解的个数情况．方程的解与函数的零点（2）12．已知函数()()21,2,03,2,1x x f x f x a x x ⎧-⎪=-=⎨≥⎪-⎩＜若方程有三个不同的实数根,则实数a 的取值X 围（ ）A ．()0,1B ．()0,2C ．()0,3D ．()1,313．若关于x 的方程24||5x x m -+=有四个不同的实数解,则实数m 的取值X 围是（ ）A ．(2,3)B ．[2,3]C ．(1,5)D ．[1,5]14．已知函数y=f(x)的周期为2,当x∈[-1,1]时f(x)=x2,那么函数y=f(x)的图象与函数y=|lgx|的图象的交点共有 （ ）A ．10个B ．9个C ．8个D ．1个15．已知函数()()f x x ∈R 是偶函数,且()(4)f x f x =-+,当x ∈[0,2]时,()1f x x =-,则方程1()1||f x x =-在区间[-8,8]上的解的个数为（ ）A ．6B ．7C ．8D ．916．函数()22xf x a x=--的一个零点在区间()1,2内,则实数a 的取值X 围是 （ ）A ．()1,3B ．()1,2C ．()0,3D ．()0,217．如右上图:二次函数a bx x x f +-=2)(的部分图象,则函数)()(x f e x g x '+=的零点所在的区间是（ ）A ．)0,1(-B ．()1,2C ．)1,0(D ．)3,2(18．设函数2()2,()ln 3xf x e xg x x x =+-=+-,若实数,a b 满足()0,()0f a g b ==,则 （ ）A ．0()()g a f b <<B ．()()0f b g a <<C ．()0()f b g a <<D ．()0()g a f b <<19函数()ln x f x x e =+的零点所在的区间是（ ）A ．(10,e)B ．(1,1e)C ．(1,e )D ．(,e ∞)20．已知函数||()e ||x f x x =+.若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值X 围是（ ）A ．(0,1)B ．(1,)+∞C ．(1,0)-D ．(,1)-∞-21．已知()f x 是定义在(0,)+∞上的单调函数,且(0,),[()ln ]1x f f x x ∀∈+∞-=,则方程2()2()7f x x f x '+=的解所在的区间为（ ）A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)22．函数f(x)对任意x ∈R,满足f(x)=f(4-x).如果方程f(x)=0恰有2011个实根,则所有这些实根之和为 （ ）A ．0B ．2011C ．4022D ．804423．已知关于x 的方程26(0)x x a a -=>的解集为P ,则P 中所有元素的和可能是（ ）A ．3,6,9B ．6,9,12C ．9,12,15D ．6,12,15【答案】B24．函数0.5() 2 |log |1x f x x =⋅-的零点个数为A . 1B . 2C . 3D .425．函数xx x f 2)1ln()(-+= 的零点所在的大致区间是（ ）A ．(3,4) B(1, 2) C ．(2,e )D ．(0,1)【答案】B26．下列区间中,函数()=+43xf x e x -的零点所在的区间为（ ）A ．(1-4,0) B ．(0,14) C ．(14,12) D ．(12,34) 二、填空题27．已知关于x 的方程220x x m -+=(0m ≤)的解集为M ,则集合M 中所有的元素的和的最大值为____________.。

拼音复习练习题（一）一拼音：6个单韵母,23个声母，9个复韵母，5个前鼻韵母，4个后鼻韵母，16个整体认读音节二：轻声：1.名词或动词的第二个重叠音节读轻声：如：妈妈（ma）, 试试（shi）2.名词词尾和方位词，趋向动词也常读轻声：如：木头（tou）,天上（shang）走出来（chu lai）3.有一些助动词也读轻声；如：好得(de)很，快走吧（ba）4.双音节的第二个音节有时也读轻声：如：萝卜（bo），风筝（zheng）,玻璃（li）三：隔音符号：a.o.e开头的音节连在其他音节后面的时候，如果音节的界限不清，就要用隔音符号（，）隔开，以免读音混淆。

如：ku ai (酷爱) dang an （档案）pi ao（皮袄）四：儿化音：1.er加在其它韵母的后面，使这个韵母成为卷舌韵母，这种情况叫做儿化韵。

2.儿化音节一半用两个汉字表示，其写法是在后面一个韵母后面加一个r.如：花儿huar3.儿化对一些词有确定性的作用。

如：画（动词）画儿（名词），尖（形容词）尖儿（名词）练习：1、在大写字母后面的括号里写出相应的小写字母。

F （）H （）Q （）R （）U （）Y （）K （）B （）J （）A（）2、按字母表的顺序，重新排列下面字母。

X L S D C T W P Z O ----------------------------------------------------------------------------3、在全是音节的那一组后面画“√”(1) fàn qià cè ǐng kǎi tǎng ( ) (2) qiào mèng yíng júèniàng ( )(3) ǔ fǎng yuán sì làn pì ( ) (4) yīng sh xún lǜ cì chóng ( )4、下列词语的拼音，开头都要将字母大写的是：（）A,北京奥运会费俊龙B, 人民主席光荣C, 将领波兰曹操D,中国天安门训练5、给下面的词语注上拼音，注意隔音符号。

中考语文复习综合性学习习题集（语文版）（七年级上）一、《学会利用图书馆》一、在《学会利用图书馆》的综合性学习中，班上要开展一次借阅图书资料活动.1．如果你要借《童年》,①在《中国图书馆分类法》中查哪一类？②按照书名目录，应怎么查?答：①文学类。

②应查“丶”（点）类 12划2．写出借书的步骤。

答:首先进入图书馆，到目录检索处寻找自己要看的书的类别,然后根据类别找到自己所要的图书，拿着图书和借书证，到办事员处办理借阅手续。

3．综合探究.（9分）泉州市开展创建国家二类语言文字示范城市活动。

为了配合这项工作，某班决定开展“我与语文工具书"探究性学习活动，请你写成以下任务。

（1）【调查分析】下面不表格是某小组对全班51位同学使用工具书情况的调查统计。

请仔（2）【姓氏排名】班里组织了查字典比赛,其中一项内容，请你将下列名著人物的姓氏按音序重新排列。

(3人物:孙悟空林黛玉武松鲁滨逊祥子(3）【问题探究】班里就语文学习中工具书使用问题展开了辩论。

甲方认为没必要使用工具书，乙方认为应经常主动使用工具书。

你支持哪一方？请你面对全班同学，运用连贯、得体的语言，简述理由。

（40字左右）（43．（8分）（1)（2分）“大多数同学不经常使用工具书。

"或“很少有同学经常使用工具书。

”（2）（2分)林黛玉鲁滨逊孙悟空武松祥子 (3）（4分。

围绕重点，言之有理即可）示例：大家好！我支持甲方观点.因为直接可以问老师，省时高效。

或：大家好！我支持乙方观点。

因为使用工具书能比较及时地解决学习困难,养成自主学习、主动探究的好习惯.二、调查社会用字情况在《调查社会用字情况》的综合性学习中,同学们在开展社会用字调查活动中收集到下列一些带错别字的词语，请你按要求答题.①家具店门口：家俱②五金店标牌:扦坐③饭店菜单:鸡旦汤④宣传标语:严历打击⑤交通宣传标语：亍道⑥修车店门口：补胎冲气⑦车站招牌：仃车收费⑧洗车店门口:洗车打醋⑨失物广告：失物启示1．将这些带错别字的词语归类，将序号填入下边横线上，并分析出造成错别字的三条原因。

复习计数单位的练习题总复习1——数的认识一、填空。

1．在18、0.3、9.16、0、1、0.2604、0.806中整数有，自然数有，小数有，有限小数有，循环小数，纯循环小数有，混循环小数有。

2．从个位到千亿位，分成级，它们是；分别包括数位。

3．小数点左边部分叫部分，右边部分叫做部分；小数点左边第二位是，计数单位是。

4．4536100是位数，最高位是位，最高位上的数是，表示。

５．一个八位数，它的最高位上的数字是８，十万位上的数字是４，其他各位上的数字都是0，这个数写作。

6．在79648000中，7在位上，计数单位是；6在位上，计数单位是；8在位上，计数单位是。

7、、⑴6005000读作读作 80040903读作105.206读作81060050860读作 20 读作 158.⑴三十五万八千写作:⑵零点二八写作⑶四千零六万零七百写作：⑷九又十七分五写作:9.个0.1和63个0.01组成的数是10、⑴0.28有个百分之一; 1.3里有13个;.7510 有三个”6”和两个”0”能组成的最大五位数是最小五位数是,能组成两个”0”都读出来的五位数是 .二判断.1.在一个八位数中,每相邻的两个计数单位之间的进率是10.2.一个七位数,它的最高位是百万位.3..3和4.30的计数单位相同.4. 在读数或写数时,都要从高位开始.5. 小数都比整数小.6. 百分数都比1小.7. 比0.57大比0.59小的数只有一个.8. 一个数的中间连续有两个0,一定要读一个零..9. 万级的最低位是万位.110. 一根4米长的钢筋,锯成8段,米.总复习2——分数和小数一判断1. 1个百分之一等于10个千分之一.2. 四位小数一定小于五位小数.3. 最小的三位小数是 0.001.154. 如果分数单位不变,大于又小于的真分数只有3个.95. 两个自然数相除,商一定比其中较小的自然数大.6. 一个整数省略万后面的尾数后约等于20万,这个数最大的数是199999.7.整数不一定都大于小数.aa8. b 是假分数,那么b 的分子必定大于分母.二把下面各数改写成用”万”作单位的数.⑴5630000⑵6700000⑶857000⑷2345600三把下面各数写成用”亿”作单位的数.保留一位小数: ⑴273400000⑵497000000保留两位小数: ⑴248300000⑵9637800000保留三位小数: ⑴843250000⑵735115000四把下面各小数四舍五入.1. 精确到十分位:4.360.952.4762. 精确到百分位:0.75 1.48 6.9993. 精确到千分位: 3.14560.6789.3584五把下面各分数化成百分数.1131211204309六化下列各百分数为小数或整数.42% 0.6% 00%七把下列各百分数化成分数.0.9%12% 2.4%八比较大小.1.把下面每组中三个分数,用小于号连接起来.353797⑴661 1182.先通分,再比较大小,并用大于号连接起来.23549147714283. 比较下面各数并用小于号连接起来240.9529.5% 0.970.0.95总复习3——约数、公因数和公倍数一选择.1..6能①整除2②被2整除③被2除尽2.数a能被3整除,被9整除,数a能被9整除,被3整除.①一定能②不一定能③不可能只有质因数2的数是①6②③12因为63=7×9,所以7和9都是63的①约数②公约数③公倍数5.一个质数有个约数.①1 ②③无数6.成为互质数的两个数,①只有公约数1 ②都是质数③一个质数,一个合数7.两个质数的积一定是①合数②奇数③偶数8. 两个数的积一定是它们的.①公约数②公倍数③最小公倍数9.把0.068的小数点去掉后是原数的①2倍②100倍③1000倍10.的分母增加3倍,要使分数的大小不变,分子应该.①扩大2倍②扩大3倍③扩大4倍.二填空1. 最小的自然数是;既不是质数又不是合数的整数是.2.0以内最小的合数是;最大的质数是;它们的和是,这个和等于质数加上质数.４．60的所有约数是其中是质数的有。

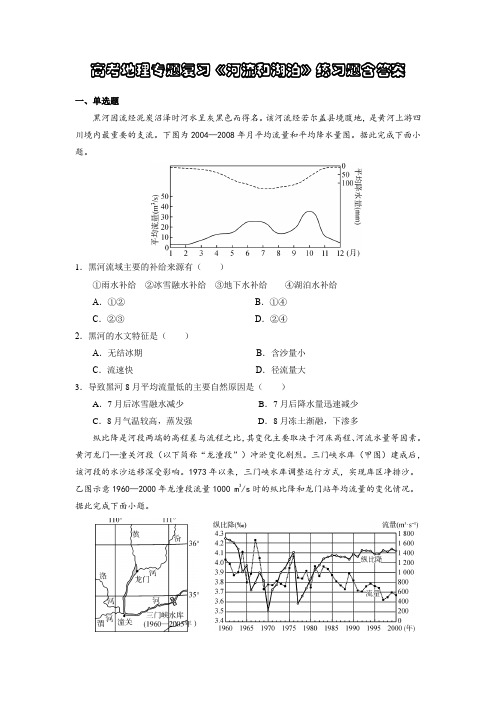
高考地理专题复习《河流和湖泊》练习题含答案一、单选题黑河因流经泥炭沼泽时河水呈灰黑色而得名。

该河流经若尔盖县境腹地，是黄河上游四川境内最重要的支流。

下图为2004—2008年月平均流量和平均降水量图。

据此完成下面小题。

1．黑河流域主要的补给来源有（）①雨水补给②冰雪融水补给③地下水补给④湖泊水补给A．①②B．①④C．②③D．②④2．黑河的水文特征是（）A．无结冰期B．含沙量小C．流速快D．径流量大3．导致黑河8月平均流量低的主要自然原因是（）A．7月后冰雪融水减少B．7月后降水量迅速减少C．8月气温较高，蒸发强D．8月冻土渐融，下渗多纵比降是河段两端的高程差与流程之比，其变化主要取决于河床高程、河流水量等因素。

黄河龙门—潼关河段（以下简称“龙潼段”）冲淤变化剧烈。

三门峡水库（甲图）建成后，该河段的水沙运移深受影响。

1973年以来，三门峡水库调整运行方式，实现库区净排沙。

乙图示意1960—2000年龙潼段流量1000 m3/s时的纵比降和龙门站年均流量的变化情况。

据此完成下面小题。

甲乙4．1960—1970年纵比降的变化趋势，反映出龙潼段（）A．河道弯曲程度降低B．潼关附近河床抬升C．雨水补给明显增多D．龙门附近侵蚀加剧5．与1968年相比，1976年（）A．潼关、龙门水位均较低B．潼关、龙门水位均较高C．潼关水位较低，龙门水位较高D．潼关水位较高，龙门水位较低6．与1976年相比，1998年龙潼段（）A．流速较快，年输沙量较少B．流速较快，年输沙量较多C．流速较慢，年输沙量较少D．流速较慢，年输沙量较多伊敏盆地位于黑龙江省大兴安岭西坡，盆地内南高北低，多年平均降水量为355 mm，年平均蒸发量为1 318 mm，盆地南部有大片露天煤矿。

盆地内多封闭性咸水湖，1983年煤矿开采前湖泊数量多且面积稳定，煤矿开采后湖泊数量减少、面积明显缩小。

下图为伊敏盆地某湖泊岩层剖面图。

据此完成下面小题。

7．煤矿开采前该湖泊的水平衡关系是（）A．降水补给＋地下水补给＝蒸发量B．降水补给＝下渗量＋蒸发量C．降水补给＋积雪融水补给＝下渗量D．降水补给＋地下水补给＝蒸发量＋径流排水量8．当地下水水位低于某一岩层或土层时，湖泊水位开始急剧下降，该土层或岩层是（）A．粉砂层B．细砂层C．淤泥层D．泥岩层俄罗斯堪察加半岛某火山口湖阶段性受到岩浆活动影响，当岩浆活动活跃时，火山蒸汽成为湖泊的重要补给水源，且岩浆中含有氯离子。

期末复习选择题练习（一）一．选择题1．下列说法中正确的是（） [单选题] *A．当车从高架桥上通过时，桥面没有发生形变B．当你对一个物体施力时，你一定也受到这个物体对你力的作用(正确答案) C．彼此接触的物体之间一定有力的作用D．只有当物体发生形变时，才能说明它受到了力的作用答案解析：当车从高架桥上通过时，对桥面有压力，桥面会发生形变，故A错误；物体间力的作用是相互的，当你对一个物体施力时，你也会受到物体对你的力，故B正确；彼此接触的物体之间不一定有力的作用，例如将水平面上竖直放置的两个长方体靠在一起，虽然接触，但两物体之间没有力的作用，故C错误；力的作用效果有两个，一是改变物体的形状，二是改变物体的运动状态，所以当物体的运动状态发生改变时，也能说明它受到了力的作用，故D错误。

2．如图所示的现象中，主要说明力可以改变物体形状的是（） [单选题] *A.(正确答案)BCD答案解析：小桌将海绵压变形，小桌的压力改变了海绵的形状，故A正确；铁球在磁铁的吸引下运动路径变弯，磁铁对铁球的吸引力使铁球的运动方向发生了改变，属于力改变物体的运动状态，故B错误；守门员接住足球，改变了球的运动状态，故C错误；运动员用力将标枪掷出，改变了标枪的运动状态，故D错误。

3．如图所示，在东京奥运会男子200米混合泳决赛中，中国选手汪顺以1分55秒的成绩成功夺冠！关于游泳过程，下列说法中错误的是（）[单选题] *A．汪顺向后划水的力大于水对他的作用力(正确答案)B．汪顺与水之间的作用力是相互的C．使汪顺向前运动的力的施力物体是水D．力改变了汪顺的运动状态答案解析：汪顺游泳过程中，他的手和脚向后划水，对水施加向后的力，由于物体间力的作用是相互的，水就会对手和脚施加向前的反作用力，人就向前运动，所以汪顺向后划水的力和水对汪顺的力是一对相互作用的力，大小相等，故A错误、B 正确；水对汪顺的力使汪顺向前运动，所以施力物体是水，故C正确；水的推力使汪顺向前运动，改变了他的运动状态，故D正确。

中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案一、单选题(共12题；共24分)1．如图是二次函数 y 1=ax 2+bx +c(a ≠0) 和一次函数 y 2=mx +n(m ≠0) 的图象.则下列结论正确的是（ ）A ．若点 M(−2，d 1)，N(12，d 2)，P(2，d 3) 在二次函数图象上，则 d 1<d 2<d 3B ．当 x <−12或 x >3 时C ．2a −b =0D ．当 x =k 2+2 （ k 为实数）时2．在平面直角坐标系中，已知抛物线与直线的图象如图所示，当y 1≠y 2时，则取y 1，y 2中的较大值记为N ；当y 1=y 2时，则N=y 1=y 2．则下列说法：①当0＜x ＜2时，则N=y 1；②N 随x 的增大而增大的取值范围是x ＜0；③取y 1，y 2中的较小值记为M ，则使得M 大于4的x 值不存在；④若N=2，则x=2﹣√2或x=1．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个3．已知抛物线y 1= 14（x ﹣x 1）（x ﹣x 2）交x 轴于A （x 1，0）B （x 2，0）两点，且点A 在点B 的左边，直线y 2=2x+t 经过点A ．若函数y=y 1+y 2的图象与x 轴只有一个公共点时，则则线段AB 的长为（ ） A ．4B ．8C ．16D ．无法确定4．如图，抛物线y ＝ax 2+bx +c 和直线y ＝kx +b 都经过点（﹣1，0），抛物线的对称轴为x ＝1，那么下列说法正确的是（ ）A ．ac ＞0B ．b 2﹣4ac ＜0C ．k ＝2a +cD ．x ＝4是ax 2+（b ﹣k ）x +c ＜b 的解5．直线y=ax ﹣6与抛物线y=x 2﹣4x+3只有一个交点，则a 的值为（ ）A ．a=2B ．a=10C ．a=2或a=﹣10D ．a=2或a=106．如图是函数y ＝x 2+bx+c 与y ＝x 的图象，有下列结论：（1）b 2﹣4c ＞0；（2）b+c+1＝0；（3）方程x 2+（b ﹣1）x+c ＝0的解为x 1＝1，x 2＝3；（4）当1＜x ＜3时，则x 2+（b ﹣1）x+c ＜0.其中正确结论的个数为（ ） A ．1B ．2C ．3D ．47．在直角坐标系中，直线y=x+2和抛物线y=x 2-x+1的若干组函数值如下表所示：x … 1 1.5 2 2.5 3 … y=x+2 … 3 3.5 4 4.5 6 … y=x 2-x+1…11.7534.7513…A ．1<x<1.5B ．1.5<Xx2C ．2<x<2.5D ．2.5<x<38．割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率．请你也用这个方法求出二次函数 y=14(x −4)2的图象与两坐标轴所围成的图形最接近的面积是（ ）A ．5B ．225C ．4D ．17﹣4π9．如图，“心”形是由抛物线 y =−x 2+6和它绕着原点O ，顺时针旋转60°的图形经过取舍而成的，其中顶点C 的对应点为D ，点A ，B 是两条抛物线的两个交点，直线AB 为“心”形对称轴，点E ，F ，G 是抛物线与坐标轴的交点，则AB=（ ）A ．6√3B ．8C ．10D ．10√310．已知一次函数y=ax+c 与二次函数y=ax 2+bx+c ，它们在同一坐标系内的大致图象是（ ）A ．B ．C ．D ．11．如图，抛物线y ＝﹣x 2+4x ﹣3与x 轴交于点A 、B ，把抛物线在x 轴及其上方的部分记作C 1，将C 1向右平移得到C 2，C 2与x 轴交于B 、D 两点．若直线y ＝kx ﹣k 与C 1、C 2共有3个不同的交点，则k 的最大值是（ ）A ．12B ．2 √5 ﹣6C ．6+4 √2D ．6﹣4 √212．在平面直角坐标系中，已知点 A(−1,4) ， B(2,1) 直线 AB 与 x 轴和 y 轴分别交于点 M ，N 若抛物线 y =x 2−bx +2 与直线 AB 有两个不同的交点，其中一个交点在线段 AN 上（包含 A ， N 两个端点），另一个交点在线段 BM 上（包含 B ， M 两个端点），则 b 的取值范围是（ ）A．1≤b≤52B．b≤1或b≥52C．52≤b≤113D．b≤52或b≥113二、填空题(共6题；共6分)13．如图，抛物线y=ax2﹣2与y轴交于点A，过点A与x轴平行的直线交抛物线y=﹣12 x2于点B，C，则S△BOC= ．14．在平面直角坐标系xOy中，函数y1＝x（x＜m）的图象与函数y2＝x2（x≥m）的图象组成图形G．对于任意实数n，过点P（0，n）且与x轴平行的直线总与图形G有公共点，写出一个满足条件的实数m的值为（写出一个即可）．15．如图，抛物线y=ax2+bx+1的顶点在直线y=kx+1上，对称轴为直线x=1，以下四个结论：①ab<0；②b<13；③a=−k；④当0<x<1其中正确的是．（填序号）16．如图，抛物线y=x2﹣2x+k与x轴交于A、B两点，与y轴交于点C（0，﹣3）．若抛物线y=x2﹣2x+k上有点Q，使△BCQ是以BC为直角边的直角三角形，则点Q的坐标为．17．已知抛物线p ：y=ax 2+bx+c 的顶点为C ，与x 轴相交于A 、B 两点（点A 在点B 左侧），点C 关于x轴的对称点为C ′，我们称以A 为顶点且过点C ′，对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线，直线AC ′为抛物线p 的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x 2+2x+1和y=2x+2，则这条抛物线的解析式为 ．18．如图，抛物线y=13x 2﹣4√33x+3与x 轴交于A ，B 两点，与y 轴交于点C ，点M 的坐标为（2√3，1）．以M 为圆心，2为半径作⊙M ．则下列说法正确的是 （填序号）． ①tan ∠OAC=√3； ②直线AC 是⊙M 的切线； ③⊙M 过抛物线的顶点； ④点C 到⊙M 的最远距离为6；⑤连接MC ，MA ，则△AOC 与△AMC 关于直线AC 对称．三、综合题(共6题；共73分)19．在平面直角坐标系中，已知A ，B 是抛物线y=ax 2（a ＞0）上两个不同的点，其中A 在第二象限，B 在第一象限．（1）如图1所示，当直线AB 与x 轴平行，∠AOB=90°，且AB=2时，则求此抛物线的解析式和A ，B 两点的横坐标的乘积；（2）如图2所示，在（1）所求得的抛物线上，当直线AB 与x 轴不平行，∠AOB 仍为90°时，则求证：A、B两点横坐标的乘积是一个定值；（3）在（2）的条件下，如果直线AB与x轴、y轴分别交于点P、D，且点B的横坐标为1 2．那么在x轴上是否存在一点Q，使△QDP为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．20．某公司成功开发出一种产品，正式投产后，生产成本为5元/件.公司按订单生产该产品（销售量=产量），年销售量y（万件）与售价x（元/件）之间满足如图1所示的函数关系，公司规定产品售价不超过15元/件，受产能限制，年销售量不超过30万件；为了提高该产品竞争力，投入研发费用P 万元（P万元计入成本），P与x之间的函数关系式如图2所示，当10≤x≤15时可看成抛物线P= 14x2−4x+m.（1）求y与x之间的函数关系式.（2）求这种产品年利润W（万元）与售价x（元/件）满足的函数关系式.（3）当售价x为多少元时，则年利润W最大，并求出这个最大值.21．如图，抛物线y＝ax2＋32 x＋c（a≠0）与x轴交于点A，B两点，其中A(－1，0)，与y轴交于点C(0，2)．（1）求抛物线的表达式及点B坐标；（2）点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．①设点E的横坐标为m，用含有m的代数式表示线段EF的长；②线段EF长的最大值是．22．已经二次函数y=ax2+bx+1 .（1）如图，其图象与x轴交于点A(−1,0)和点B，与y轴交于点C，对称轴为直线x=1 .①求二次函数解析式；②F为线段BC上一点，过F分别作x轴，y轴垂线，垂足分别为E、F，当四边形OEFG为正方形时，则求点F坐标；（2）其图象上仅有一个点的横坐标、纵坐标互为相反数，且二次函数y=ax2+bx+1函数值存在负数，求b的取值范围.23．定义符号min{a，b}的含义为：当a≥b时，则min{a，b}=b；当a＜b时，则min{a，b}=a．如：min{1，﹣2}=﹣2，min{﹣1，2}=﹣1．（1）求min{x2﹣1，﹣2}；（2）已知min{x2﹣2x+k，﹣3}=﹣3，求实数k的取值范围；（3）已知当﹣2≤x≤3时，则min{x2﹣2x﹣15，m（x+1）}=x2﹣2x﹣15．直接写出实数m的取值范围．24．某企业研发了一种新产品，已知这种产品的成本为30元/件，且年销售量y（万件）与售价x（元/件）的函数关系式为y={−2x+140，(40≤x<60)−x+80.(60≤x≤70)（1）当售价为60元/件时，则年销售量为万件；（2）当售价为多少时，则销售该产品的年利润最大？最大利润是多少？（3）若销售该产品的年利润不少于750万元，直接写出x的取值范围.参考答案1．【答案】D 2．【答案】B 3．【答案】B 4．【答案】D 5．【答案】C 6．【答案】B 7．【答案】C 8．【答案】A 9．【答案】A 10．【答案】C 11．【答案】C 12．【答案】C 13．【答案】414．【答案】1（答案不唯一） 15．【答案】①③④16．【答案】（1，﹣4）和（﹣2，5） 17．【答案】y=x 2﹣2x ﹣3 18．【答案】①②③④ 19．【答案】（1）解：如图1作BE ⊥x 轴∴△AOB 是等腰直角三角形 ∴BE=OE= 12AB=1∴A （﹣1，1），B （1，1）∴A ，B 两点的横坐标的乘积为﹣1×1=﹣1∵抛物线y=ax 2（a ＞0）过A ，B ∴a=1 ∴抛物线y=x 2 （2）解：如图2作BN ⊥x 轴，作AM ⊥x 轴 ∴∠AOB=AMO=∠BNO=90° ∴∠MAO=∠BON ∴△AMO ∽△ONB ∴AM ON =OM BN ∴AM ×BN=OM ×ON设A （x 1，y 1），B （x 2，y 2）在抛物线上 ∴AM=y 1=x 12，BN=y 2=x 22，OM=﹣x 1，ON=x 2 ∴x 12×x 22=﹣x 1×x 2 ∴x 1×x 2=﹣1∴A ，B 两点横坐标的乘积是一个定值；（3）解：由（2）得，A ，B 两点横坐标的乘积是一个定值为﹣1，∵点B 的横坐标为 12，∴点A 的横坐标为﹣2，∵A ，B 在抛物线上，∴A （﹣2，4），B （ 12 ， 14 ），∴直线AB 解析式为y=﹣ 32x+1，∴P （ 23 ，0），D （0，1）设Q （n ，0），∴DP 2= 139 ，PQ 2=（n ﹣ 23）2，DQ 2=n 2+1∵△QDP 为等腰三角形∴①DP=PQ ，∴DP 2=PQ 2，∴139 =（n ﹣ 23 ）2，∴n= 2±√133 ，∴Q 1（ 2+√133 ，0），Q 2（ 2−√133 ，0）②DP=DQ ，∴DP 2=DQ 2，∴139 =n 2+1，∴n= 23 （舍）或n=﹣ 23 ，Q 3（﹣ 23 ，0）③PQ=DQ ，∴PQ 2=DQ 2，∴（n ﹣ 23 ）2=n 2+1∴n=﹣ 512 ，∴Q4（﹣ 512 ，0），∴存在点Q 坐标为Q 1（ 2+√133 ，0），Q 2（2−√133 ，0），Q 3（﹣ 23 ，0），Q4（﹣ 512 ，0）20．【答案】（1）解：设y 与x 的函数关系式为：y=kx+b将点（5，30），（15，10）代入可得：{30=5k +b 10=15k +b解得：{b =40k =−2∴y 与x 的函数关系式为：y=-2x+40（5≤x ≤15）； （2）解：当5≤x ≤10时，则根据图像可得：P=60 ∴W=(x-5)y-P=(x-5)(-2x+40)-60=-2x 2+50x-260；当10≤x ≤15时，则P =14x 2−4x +m由图可得经过点（10，60），将其代入可得：60=14×102−4×10+m 解得：m=75∴P =14x 2−4x +75；∴W=(x-5)y-P=(x-5)(-2x+40)-(14x 2−4x +75)=−94x 2+54x −275；综上：W ={−2x 2+50x −260(5≤x ≤10)−94x 2+54x −275(10≤x ≤15)；（3）解：由（2）可得：当5≤x ≤10时W=-2x 2+50x-260=-2(x −252)2+1052∴x =252不在5≤x <10，由于开口向下在5≤x <10内随x 增大而增大 在x=10时，则取得最大值为W=40； 当10≤x ≤15时W=−94x 2+54x −275对称轴为x=−b2a=12 由于函数开口向下 ∴当x=12时，则W=49∴当x=12时，则W 取得最大值为49；综上可得：当售价为12元时，则年利润最大，最大为49万元.21．【答案】（1）解：将A(－1，0)、 C(0，2)代入y ＝ax 2＋ 32x ＋c （a ≠0）得：a ＝－ 12， c ＝2y ＝－ 12 x 2＋ 32x ＋2 当y ＝0时，则x 1＝－1，x 2＝4，故B(4，0)（2）解：设直线BC 的函数表达式为y ＝kx ＋b ，将B(4，0)、 C(0，2)代入 得：y ＝－ x ＋2，EF ＝FG －GE ＝－ m 2＋ m ＋2－(－ m ＋2) ＝－ m 2＋2m ；2 22．【答案】（1）解：①由题： {a −b +1=0−b 2a =1 解得 {a =−13b =23∴ 二次函数解析式为： y =−13x 2+23x +1 ； ②设BC 解析式为： y =kx +b 对称轴为直线 x =1 .∵ 图象与x 轴交于点 A(−1,0) 和点B ，对称轴为直线 x =1 .∴ 点 B(3,0)将 B(3,0) ， C(0,1) 代入得： {3k +b =0b =1解得： {a =−13b =1∴BC 解析式为： y =−13x +1 设点 F(m,−13m +1) ∵ 四边形 OEFG 是正方形∴EF =GF∴m =−13m +1解得 m =34∴F(34,34) （2）解：二次函数的图象其有且只有一个点横、纵坐标之和互为相反数∴−x =ax 2+bx +1 有两相等实根，即 ax 2+(b +1)x +1=0 有两相等实根 ∴{a ≠0(b +1)2−4a =0解得： a =(b+1)24>0 ，且 b ≠−1 ∵y =ax 2+bx +1 存在负值∴b 2−4a =b 2−(b +1)2>0 ，解得 b <−12综上： b <−12且 b ≠−123．【答案】（1）解：∵x2≥0∴x2﹣1≥﹣1∴x2﹣1＞﹣2．∴min{x2﹣1，﹣2}=﹣2（2）解：∵x2﹣2x+k=（x﹣1）2+k﹣1∴（x﹣1）2+k﹣1≥k﹣1．∵min{x2﹣2x+k，﹣3}=﹣3∴k﹣1≥﹣3．∴k≥﹣2（3）解：对于y=x2﹣2x﹣15，当x=﹣2时，则y=﹣7当x=3时，则y=﹣12由题意可知抛物线y=x2﹣2x﹣15与直线y=m（x+1）的交点坐标为（﹣2，﹣7），（3，﹣12）所以m的范围是：﹣3≤m≤7．24．【答案】（1）20（2）解：设销售该产品的年利润为W万元当40≤x<60时W=(x−30)(−2x+140)=−2(x−50)2+800 .∵－2<0∴当x=50时W最大=800当60≤x≤70时W=(x−30)(−x+80)=−(x−55)2+625∵−1<0∴当x=60时W最大=600∵800>600∴当x=50时W最大=800∴当售价为50元/件时，则年销售利润最大，最大为800万元.（3）解：45≤x≤55理由如下：由题意得(x−30)(−2x+140)≥750解得45≤x≤55。

高考数学一轮复习《等比数列》综合练习题（含答案）一、单项选择题1．在等比数列{}n a 中，13524610,18a a a a a a -==，则{}n a 的公比q 为（ ）A ．2-B ．12-C ．12D ．22．等比数列{an }中，若a 5＝9，则log 3a 4+log 3a 6＝（ ） A ．2B ．3C ．4D ．93．数列{}n a 满足()*331log 1log N n n a a n ++=∈，且1359a a a ++=，则()13579log a a a ++=（ ）A ．4B ．14C ．2-D ．12-4．已知各项均为正数的等比数列{}n a 满足，24a =，3424a a +=，则12233445910a a a a a a a a a a -+-+⋅⋅⋅+=（ ）A ．188(21)5+B ．188(21)5-C ．208(21)5+D ．208(21)5-5．已知数列{}n a 是等比数列，数列{}n b是等差数列，若76103a b π=，则210311sin 1b b a a +=-（ ） AB． C ．12D ．12-6．已知数列满足212323n a a a na n ++++=，设n n b na =，则数列11n n b b +⎧⎫⎨⎬⎩⎭的前2022项和为（ ） A ．40424043B ．20214043C ．40444045D ．202240457．在适宜的环境中，一种细菌的一部分不断分裂产生新的细菌，另一部分则死亡.为研究这种细菌的分裂情况，在培养皿中放入m 个细菌，在1小时内，有34的细菌分裂为原来的2倍，14的细菌死亡，此时记为第一小时的记录数据.若每隔一小时记录一次细菌个数，则细菌数超过原来的10倍的记录时间为第（ ） A ．6小时末B ．7小时末C ．8小时末D ．9小时末8．已知数列{}n a 满足()22N n n n a a n *++=∈，则{}n a 的前20项和20S =（ ）A ．20215-B ．20225-C ．21215-D ．21225-9．若数列{}n a 为等差数列，数列{}n b 为等比数列，则下列不等式一定成立的是（ ） A ．1423b b b b +≤+ B ．4132b b b b ≤-- C ．3124a a a a ≥D ．3124a a a a ≤10．已知等比数列{}n a 各项均为正数，且满足：101a <<，1718171812a a a a +<+<，记12n n T a a a =，则使得1n T >的最小正数n 为（ ）A ．36B ．35C ．34D ．3311．观察下面数阵，则该数阵中第9行，从左往右数的第20个数是（ ） A ．545B ．547C ．549D ．55112．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号.用他的名字定义的函数称为高斯函数()[]f x x =，其中[]x 表示不超过x 的最大整数，已知数列{}n a 满足12a =，26a =，2156n n n a a a +++=，若[]51log n n b a +=，为数列11000n n b b +⎧⎫⎨⎬⎩⎭的前n 项和，则[]2024S =（ ） A ．999B ．749C ．499D ．249二、填空题13．设等比数列{}n a 的前n 项和为n S ，已知3614,126S S ==，则1a =___．14．在各项均为正数的等比数列{}n a 中，若74a =，则678a a a ++的最小值为______．15．已知数列{}n a 的首项为－1，12,nn n a a +=-则数列{}n a 的前10项之和等于________.16．已知数列{}n a 满足：11a =，()*112+1n nn N a a +=∈若()1111n n b n a λ+⎛⎫=+-+ ⎪⎝⎭，1b λ=-，且数列{}n b 是单调递增数列，则实数λ的取值范围为______.三、解答题17．在等比数列{}n a 中，已知320a =，6160a =， （1）求5a ； （2）求8S .18．设{}n a 是等差数列，2d =，且312,,4a a a +成等比数列. （1）求{}n a 的通项公式；（2）记{}n a 的前n 项和为n S ，求n S 的最小值.19．已知等比数列{}n a 的首项为1a ，公比为q ，且关于x 的不等式21120a x qx -->的解集为()(),26,-∞-⋃+∞.（1）求n a ；（2）设4log n n n b a a =+，求数列{}n b 的前n 项和n T .20．已知数列{}n a 是等差数列，首项12a =，且3a 是2a 与41a +的等比中项. （1）求数列{}n a 的通项公式； （2）设14n n n b a a +=，求数列{}n b 的前n 项和n S .21．已知数列{}n a 的首项113a =，且满足1341n n n a a a +=+. (1)证明：数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列.(2)若12311112022na a a a ++++<，求正整数n 的最大值.22．已知正项等比数列{}n a 满足21372,32a a a ==，数列{}n b 的前n 项和2n S n n =-.（1）求{}n a ，{}n b 的通项公式；（2）设,,n n na n cb n ⎧=⎨⎩为奇数为偶数求数列{}nc 的前2n 项和2n T .23．设正项数列{}n a 的前n 项和为n S ，11a =，且满足___________.给出下列三个条件： ①48a =，()112lg lg lg 2n n n a a a n -+=+≥；②()1n n S pa p =-∈R ；③()()12323412nn a a a n a kn k +++⋅⋅⋅++=⋅∈R .请从其中任选一个将题目补充完整，并求解以下问题： (1)求数列{}n a 的通项公式；(2)设()22121log n nb n a =+⋅，n T 是数列{}n b 的前n 项和，求证：1132n T ≤<参考答案1．D2．C3．C4．A5．A6．D7．A8．D9．D10．B11．C12．A 13．2 14．1215．31 16．4λ<17．（1）设等比数列{}n a 的公比为q ，则3638aq a ==，所以2q，所以25320480a a q ==⨯=；（2）由（1）可得3125a a q ==， 所以818(1)5(1256)127511a q S q -⨯-===--. 18．（1）因为132+4a a a ，，成等比数列，所以2312(+4)a a a =，即1112()4(6)a a a ++=，解得18a =-，所以82(1)210n a n n =-+-=-（2）由（1）知210n a n =-， 所以2282109819()224n n S n n n n -+-=⨯=-=--； 因为N n +∈所以当4n =或者5n =时，n S 取到最小值20-19．（1）等比数列{}n a 的首项为1a ，公比为q ，且关于x 的不等式21120a x qx -->的解集为()(),26,-∞-⋃+∞.则-2和6为21120a x qx --=的两根，所以()126qa -+=，()11226a -⨯=-， 解得11a =，4q =.所以1114n n n a a q --==.（2）由（1）得14log 41n n n n b a a n -=+=+-，所以()1144121n n T n -=++⋅⋅⋅++++⋅⋅⋅+-，()141412n n n --=+-， 24132n n n--=+. 20．()23241a a a =+,()()()2111231a d a d a d +=+++, ()()()222233d d d +=++,()()()241312d d d +=++,()()144360d d d ++--=, ()()120d d +-=,∴1d =-，此时3220a d =+=, 舍,2d =,∴2n a n =; （2）()()411122111n b n n n n n n ===-⋅+++,11111122311n n S n n n ⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭. 21．（1）易知{}n a 各项均为正， 对1341n n n a a a +=+两边同时取倒数得1111433n n a a +=⋅+， 即1111223n n a a +⎛⎫-=- ⎪⎝⎭，因为1121a -=，所以数列12n a ⎧⎫-⎨⎬⎩⎭是以1为首项，13为公比的等比数列.（2）由（1）知11111233n n n a --⎛⎫-==⎪⎝⎭，即11123n n a -=+， 所以()12311311113122112313n n n f n n n a a a a ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎛⎫⎝⎭=++++=+=+- ⎪⎝⎭-， 显然()f n 单调递增，因为()10101011313110102021.52022,(1011)2023.520222323f f =-<=-⋅>，所以n 的最大值为1010.22．解：（1）由题意，设正项等比数列{}n a 的公比为()0q q >，则2237532a a a ==，故532a =.∴ 4451162a q a ===.解得2q .∴ 数列{}n a 的通项公式为1*222,n n n a n N -=⨯=∈ .当1n =时，110b S ==，当2n ≥时，()()()2211122n n n b S S n n n n n -⎡⎤=-=-----=-⎣⎦. ∴ 数列{}n b 的通项公式为*22,n b n n N =-∈（2）由（1）知，,2,,22,n n n n a n n c b n n n ⎧⎧==⎨⎨-⎩⎩为奇数为奇数为偶数为偶数.∴21234212n n n T c c c c c c -=++++++()132********n n -=++++++-()()132********n n -=+++++++-⎡⎤⎣⎦=2122222[2(42)]122n n n --⋅⋅+--212122233n n +=⋅+- 23．（1）若选①，因为()112lg lg lg 2n n n a a a n -+=+≥，所以()2112n n n a a a n -+=≥，所以数列{}n a 是等比数列设数列{}n a 的公比为q ，0q >由33418a a q q ===得2q所以12n n a -=若选②，因为()1n n S pa p =-∈R ，当1n =时，1111S pa a =-=，所以2p =，即21n n S a =- 当2n ≥时，1122n n n n n a S S a a --=-=-，所以()122n n a a n -=≥所以数列{}n a 是以1为首项，2为公比的等比数列所以12n n a -=若选③，因为()()12323412nn a a a n a kn k +++⋅⋅⋅++=⋅∈R ，当1n =时，11222a k =⋅=，所以1k =，即()12323412n n a a a n a n +++⋅⋅⋅++=⋅当2n ≥时，()1123123412n n a a a na n --+++⋅⋅⋅+=-⋅，所以()()()11122n n n a n n -+=+⋅≥，即()122n n a n -=≥，当1n =时，上式也成立，所以12n n a -=（2） 由（1）得()()()221111121log 212122121n n b n a n n n n ⎛⎫===- ⎪+⋅+⋅--+⎝⎭所以()111111111233521212221n T n n n ⎛⎫=-+-+⋅⋅⋅+-=- ⎪-++⎝⎭ ∵*N n ∈，∴()10221n >+，∴()11122212nT n =-<+ 易证*n ∈N 时，()112221n T n =-+是增函数，∴()113n T T ≥=.故1132n T ≤<。

⾼三数学复习专题练习题：解三⾓形（含答案）⾼三数学复习专题练习：解三⾓形（含答案）⼀. 填空题（本⼤题共15个⼩题，每⼩题5分，共75分）1.在△ABC 中，若2cosBsinA=sinC,则△ABC ⼀定是三⾓形.2.在△ABC 中，A=120°,AB=5,BC=7，则CBsin sin 的值为 . 3.已知△ABC 的三边长分别为a,b,c,且⾯积S △ABC =41（b 2+c 2-a 2），则A= . 4.在△ABC 中，BC=2，B=3π，若△ABC 的⾯积为23，则tanC 为 . 5.在△ABC 中，a 2-c 2+b 2=ab,则C= .6.△ABC 中，若a 4+b 4+c 4=2c 2(a 2+b 2),则C= .7.在△ABC 中，⾓A ，B ，C 所对的边分别为a,b,c ，若a=1,b=7,c=3,则B= . 8.在△ABC 中，若∠C=60°，则c b a ++ac b+= . 9.如图所⽰，已知两座灯塔A 和B 与海洋观察站C 的距离都等于a km, 灯塔A 在观察站C 的北偏东20°，灯塔B 在观察站C 的南偏东40°，则灯塔A 与灯塔B 的距离为 km.10.⼀船⾃西向东匀速航⾏，上午10时到达⼀座灯塔P 的南偏西75°距塔68海⾥的M 处，下午2时到达这座灯塔的东南⽅向的N 处，则这只船的航⾏速度为海⾥/⼩时. 11. △ABC 的内⾓A 、B 、C 的对边分别为a 、b 、c ，若c=2，b=6，B=120°,则a= .12. 在△ABC 中,⾓A 、B 、C 的对边分别为a 、b 、c ，若（a 2+c 2-b 2）tanB=3ac ，则⾓B 的值为 . 13. ⼀船向正北航⾏，看见正西⽅向有相距10 海⾥的两个灯塔恰好与它在⼀条直线上，继续航⾏半⼩时后，看见⼀灯塔在船的南偏西600，另⼀灯塔在船的南偏西750，则这艘船是每⼩时航⾏________ 海⾥.14.在△ABC 中，A=60°，AB=5，BC=7，则△ABC 的⾯积为 .15.在△ABC 中，⾓A 、B 、C 所对的边分别为a 、b 、c.若（3b-c ）cosA=acosC ，则cosA= .（资料由“⼴东考神”上传，如需更多⾼考复习资料，请上 tb ⽹搜“⼴东考神”）⼆、解答题（本⼤题共6个⼩题，共75分）1、已知△ABC 中，三个内⾓A ，B ，C 的对边分别为a,b,c,若△ABC 的⾯积为S ，且2S=（a+b ）2-c 2，求tanC 的值. （10分）2、在△ABC 中，⾓A ，B ，C 所对的边分别为a,b,c ，并且a 2=b(b+c). （11分）（1）求证：A=2B ；（2）若a=3b,判断△ABC 的形状.3、在△ABC 中，a 、b 、c 分别是⾓A ，B ，C 的对边，且C B cos cos =-ca b+2. (12分)（1）求⾓B 的⼤⼩；（2）若b=13，a+c=4，求△ABC 的⾯积.4、△ABC 中，⾓A ，B ，C 的对边分别为a ，b ，c ，且b 2+c 2-a 2+bc=0. (12分) （1）求⾓A 的⼤⼩；（2）若a=3，求bc 的最⼤值；（3）求cb C a --?)30sin(的值.5、已知△ABC 的周长为)12(4+，且sin sin B C A +=． (12分)（1）求边长a 的值；（2）若A S ABC sin 3=?，求A cos 的值．6、在某海岸A 处，发现北偏东 30⽅向，距离A 处）（13+n mile 的B 处有⼀艘⾛私船在A 处北偏西 15的⽅向，距离A 处6n mile 的C 处的缉私船奉命以35n mile/h 的速度追截⾛私船. 此时，⾛私船正以5 n mile/h 的速度从B 处按照北偏东 30⽅向逃窜，问缉私船⾄少经过多长时间可以追上⾛私船，并指出缉私船航⾏⽅向. (12分)ACB3015· ·参考答案：⼀、填空题：1、等腰；2、53；3、45°；4、33；5、60°；6、45°或135°；7、65π；8、1；9、3a ；10、2617；11、2；12、3π或32π；13、10；14、103；15、33。