离散数学 第七章:图论
- 格式:ppt
- 大小:1.81 MB
- 文档页数:80

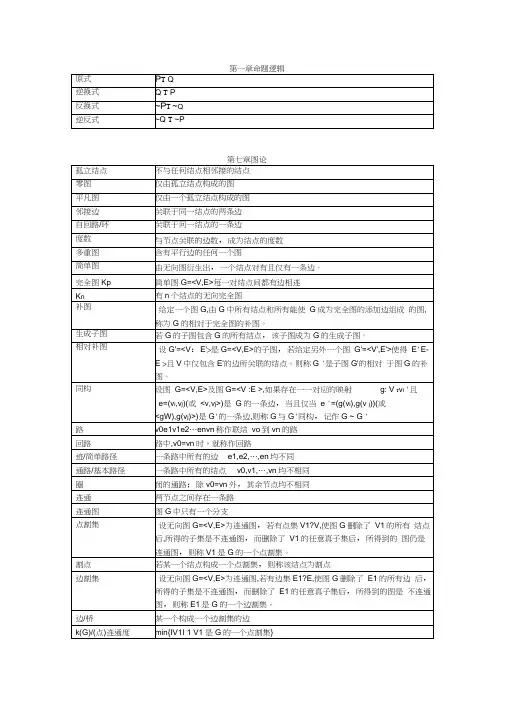
离散图论知识点总结一、基本概念图(Graph)是离散数学中的一个重要概念,它由顶点集合V和边集合E组成。
一般用G (V,E)来表示,其中V={v1,v2,…,vn}是有限非空集合,E是V中元素的无序对的集合。
图分为有向图和无向图。
无向图中的边是无序的,有向图中的边是有序的。
图中存在一些特殊的图,比如完全图、树、路径、回路等。
二、图的表示方法1. 邻接矩阵邻接矩阵是一种常见的图的表示方法,它使用一个二维数组来表示图的关系。
对于一个n 个顶点的图,邻接矩阵是一个n*n的矩阵A,其中A[i][j]表示顶点i到顶点j之间是否存在边。
对于无向图,A[i][j]=1表示顶点i与顶点j之间存在边,A[i][j]=0表示不存在。
对于有向图,A[i][j]=1表示i指向j的边存在,A[i][j]=0表示不存在。
2. 邻接表邻接表是另一种常见的图的表示方法。
它将图的信息储存在一个数组中,数组的每个元素与图的一个顶点相对应。
对于每个顶点vi,数组中储存与该顶点邻接的顶点的信息。
邻接表可以用链表或者数组来表示,链表表示的邻接表比较灵活,但是在查找某个边的相邻顶点时需要遍历整个链表。
三、图的性质1. 度图中每个顶点的度是与其相邻的边的数目。
对于无向图,顶点的度等于与其相邻的边的数目;对于有向图,则分为入度和出度。
2. 连通性对于无向图G,若图中任意两个顶点都有路径相连,则称图G是连通的。
对于有向图G,若从任意一个顶点vi到任意一个顶点vj都存在路径,则称G是强连通的。
3. 路径和回路路径是指图中一系列的边,连接图中的两个顶点;回路是指起点与终点相同的路径。
路径的长度是指路径中边的数目。
4. 树和森林一个无向图,如果是连通图且不存在回路,则称为树。
一个无向图,若它不是连通图,则称为森林。
四、图的常见算法1. 深度优先搜索(DFS)深度优先搜索是一种用于图的遍历的算法,它从图的某个顶点vi出发,访问它的所有邻接顶点,再对其中未访问的顶点继续深度优先搜索。



![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://uimg.taocdn.com/58b7923143323968011c9244.webp)


第七章图在自然界和人类社会的实际生活中,用图形来描述和表示某些事物之间的关系既方便又直观。
例如用工艺流程图来描述某项工程中各工序之间的先后关系,用网络图来描述某通讯系统中各通讯站之间信息传递关系,用开关电路图来描述IC中各元件电路导线连接关系等等。
图论起源于18世纪,它是研究由线连成的点集的理论。
一个图中的结点表示对象,两点之间的连线表示两对象之间具有某种特定关系(先后关系、胜负关系、传递关系和连接关系等)。
事实上,任何一个包含了某种二元关系的系统都可以用图形来模拟。
由于我们感兴趣的是两对象之间是否有某种特定关系,所以图形中两点之间连接与否最重要,而连接线的曲直长短则无关紧要。
由此经数学抽象产生了图的概念。
研究图的基本概念和性质、图的理论及其应用构成了图论的主要内容。
7.1 图的基本概念7.1.1图的定义7.1.1.1无向图定义7.1.1 设A,B是任意集合。
集合{(a,b)|aA且bB}称为A和B的无序积,记为A&B。
在无序积中,两个元素间的顺序是无关紧要的,即(a,b)=(b,a)。
定义7.1.2 无向图G是一个二元组<V,E>,记作G=<V,E>,其中V是一个非空有限集合,其元素称为结点(顶点)。
E是一个V&V的多重子集,其元素称为边(无向边)。
我们可用平面上的点来表示顶点,两点间的连线表示边,从而将任一个无向图用图形表示出来。
[例7.1.1]无向图G=<V,E>,其中V={a,b,c,d,e,f},E={(a,b),(a,c),(a,d),(b,b),(b,c),(b,c),(b,d),(c,d)}。
7.1.1.2有向图定义7.1.3 有向图G是一个二元组<V,E>,记作G=<V,E>,其中V是一个非空有限集合,其元素称为顶点,E是一个V V的多重子集,其元素称为有向边或弧,简称为边。
注:1)在有向图G=<V,E>中,若e=〈u,v〉,则称u和v为e的起点和终点;2)自回路既可看成是有向边又可看成是无向边;3)去掉有向图中边的方向得到的图称为该有向图的基图。

