离散数学 第七章 图论 习题课
- 格式:ppt
- 大小:552.50 KB
- 文档页数:48



离散数学图论作业7-二部图匹配Problem1证明:一个无回路的简单连通图最多只有一个完美匹配。
(完美匹配指能饱和所有顶点的匹配)Problem2从下图G=(A,B,E)中,找出相对于匹配M(粗边的集合)的任意三条交错路径(alternating path)和至少两条增广路径(augmenting path),然后利用增广路径扩大M来找到最大匹配。
a0 a1 a2 a3 a4 a5b0 b1 b2 b3 b4 b5Problem3对于哪些n值来说,下列图是存在完美匹配的二部图?a)K nb)C nc)Q n对于每一个二部图G=(A,B,E),判断G是否有饱和A的匹配。
如果没有,请说明理由。
(1)(2)(3)(4)Problem5令k为一整数。
对于任意有限集合,证明对它的任意两个k划分都存在一个相同的代表集。
•集合的k划分指划分为大小相同的互不想交的k个子集,为简便起见,设集合的大小为k的整数倍从而每个子集均有相同个元素。
•一个划分的代表集指从每个子集中取出一个元素而构成的集合。
举例:集合{1,2,3,4}的一个2划分为A:{1,2}{3,4}。
此划分的代表集有{1,3},{2,3},{1,4},{2,4},但{1,2}不是其代表集。
集合的另外一个划分为B:{2,3}{1,4}。
易见,A与B存在相同的代表集{1,3}。
Problem6假设某校计算机系学生选导师时出现了这样的情况:对于每一位学生,至少对k名导师感兴趣;对于每一位导师,至多有k名学生对他感兴趣。
假设每位导师只能指导1名学生,且每位学生也只能选择1名导师。
试证明:存在这样的匹配,使得每位学生都能选到自己感兴趣的导师。
证明一个6×6的方格纸板挖去左上角和右下角后不能用剪刀裁剪成若干1×2的小矩形。
第七章 特 殊 图 类习题7.11.解 因 m=n-1,这里m=6,所以n=6+1=7.2.解 不正确。
与平凡图构成的非连通图中有4个结点3条边,但是它不是树。
3K 3.证明 必要性。
因为G 中有n 个结点,边数m=n-1,又因为G 是连通的,由本节定理1可知,G 为树,因而G 中无回路。
再证充分性。
因为G 中无回路,又因为边数m=n-1,由本节定理1,可知G 为树,所以G 是连通的。
4.解 因 m=n-r,这里n=15,r=3,所以m=15-3=12,即G 有12条边。
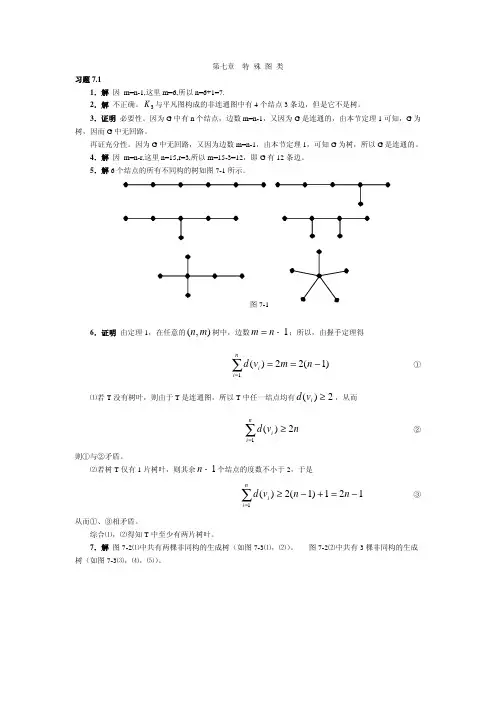
5.解6个结点的所有不同构的树如图7-1所示。
图7-16.证明 由定理1,在任意的树中,边数),(m n 1−=n m;所以,由握手定理得)1(22)(1−==∑=n m v d ni i①⑴若T 没有树叶,则由于T 是连通图,所以T 中任一结点均有,从而2)(≥i v d n v d ni i2)(1≥∑= ②则①与②矛盾。
⑵若树T 仅有1片树叶,则其余1−n个结点的度数不小于2,于是121)1(2)(1−=+−≥∑=n n v d ni i③从而①、③相矛盾。
综合⑴,⑵得知T 中至少有两片树叶。
7.解 图7-2⑴中共有两棵非同构的生成树(如图7-3⑴,⑵)。
图7-2⑵中共有3棵非同构的生成树(如图7-3⑶,⑷,⑸)。
⑵⑴⑶⑷ ⑸图7-38.解 在图7-4中共有8棵生成树,如图7-5⑴~⑻所示,第i 生成树用表示。
,,,)8,,2,1( =iT i 7)(8=T W 8)()(61==T W T W 6)()(52==T W T W )()(73==T W T W 9)(4=T W 。
其中T 2,T 5是图中的最小生成树。
9.解 最小生成树T 如图7-7所示,W (T )=18。
a bc da b cda ba bcdabc d⑴⑵⑶⑷⑸⑹⑺ ⑻图7-5图7-4图7-6图7-7习题7.21.解 不一定是。
如图7-8就不是根树.2.解 五个结点可形成3棵非同构的无向树,如图7-9⑴,⑵,⑶所示。







第6-7章一.选择/填空1、设图G 的邻接矩阵为0101010010000011100000100,则G 的边数为( D ). A .5 B .6 C .3 D .42、设有向图(a )、(b )、(c )与(d )如下图所示,则下列结论成立的是( A ).A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的3、给定无向图G 如下图所示,下面给出的结点集子集中,不是点割集的为( B ).A .{b , d }B .{d }C .{a , c }D .{b , e }4、图G 如下图所示,以下说法正确的是 ( D ) .A .{(a , c )}是割边B .{(a , c )}是边割集C .{(b , c )}是边割集D .{(a, c ) ,(b, c )}是边割集5、无向图G 存在欧拉通路,当且仅当(D ).A .G 中所有结点的度数全为偶数B .G 中至多有两个奇数度结点C .G 连通且所有结点的度数全为偶数D .G 连通且至多有两个奇数度结点6、设G 是有n 个结点,m 条边的连通图,必须删去G 的( A )条边,才能确定G 的一棵生成树.A .1m n −+B .m n −C .1m n ++D .1n m −+7、已知一棵无向树T 中有8个结点,4度,3度,2度的分支点各一个,T 的树叶数为(B ).A .8B .5C .4D .38、已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 15 . 9、连通无向图G 有6个顶点9条边,从G 中删去 4 条边才有可能得到G 的一棵生成树T .10、如右图 相对于完全图K 5的补图为(A )。
11、给定无向图,如下图所示,下面哪个边集不是其边割集( B )。
A 、;B 、{<v1,v4>,<v4,v6>};C 、;D 、。
12、设D 是有n 个结点的有向完全图,则图D 的边数为( A ) (A))1(−n n (B))1(+n n (C)2/)1(+n n (D)2/)1(−n n 13、无向图G 是欧拉图,当且仅当( C )(A) G 的所有结点的度数都是偶数 (B)G 的所有结点的度数都是奇数(C)G 连通且所有结点的度数都是偶数 (D) G 连通且G 的所有结点度数都是奇数。