最新线性代数行列式计算习题课学习资料

第一章 行列式一、教学要求1、了解行列式定义；2、掌握行列式的性质和展开法则；3、会利用化三角法和行列式展开法则计算低阶行列式以及简单n 阶行列式；4、了解克莱姆法则；重点、难点：熟练运用行列式性质，掌握行列式计算方法二、主要知识点及练习 1、 行列式性111213111112132122232121222331323331313233223=1223=223a a a a a a a a a a a a a a a a a a a a a ，则。

练习：若行列式---311234=1303=101313a b c a b c ，则。

练习：若行列式+++2、 代数余子式13122,112D x x D=则中的系数为。

练习：设行列式11111111x x 是关于的一次多项式，该式中的一次项系数是。

练习：--- 3、 行列式计算1） 对角线法------计算二阶、三阶行列式212103214111213212223313233--、a a a a a a a a a 练习：计算三阶行列式2） 利用行列式性质计算行列式------将行列式化为上三角、下三角、对角行列式222222222(1)(2)(1)(2)(2)(1)(2)11231123(3)(4)11131121(1)ab b b x x x ba b b y y y bb a b z z z b b b ax ab ac aex bd cdde x bf cfefx 练习：计算下列行列、式、、的值+++++++-+-+-+3） 利用行列式展开法计算行列式------将行列式降阶0110100111011110练习：四阶行列式。

=11121314313233441111123456224816123434D A A A A A A A A 练习：已知行列式，则，。

==+++=++--+=123,1,3D A A 练习：设三阶行列式的第二行元素分别为,,第一行元素的代数余子式的值分别为,,则。

《线性代数》课程习题第1章行列式习 题 1.11． 计算下列二阶行列式： （1）2345 （2）2163- （3）xxx x cos sin sin cos - （4）11123++-x x x x（5）2232ab b a a （6）ββααcos sin cos sin （7）3log log 1a b b a2． 计算下列三阶行列式：（1）341123312-- （2）00000d c b a （3）d c e ba 0000 （4）zy y x x 00002121（5）369528741 （6）01110111-- 3． 用定义计算行列式：（1）4106705330200100 （2）1014300211321221---（3）5000000004000300020001000 (4)dcb a 100110011001---.4.用方程组求解公式解下列方程组:(1) ⎪⎩⎪⎨⎧=-+=--=--0520322321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+-=-+=++232120321321321x x x x x x x x x习 题 1.21． 计算下列行列式：（1）123112101 (2)15810644372---- （3）3610285140 （4）6555655562.计算行列式（1）2341341241231234（2）12114351212734201----- （3）524222425-----a a a（4）322131399298203123- （5）0532004140013202527102135---- 3.用行列式的性质证明：（1）322)(11122b a b b a a b ab a -=+（2）3332221113333332222221111112c b a c b a c b a a c c b b a a c c b b a a c c b b a =+++++++++ 4.试求下列方程的根：（1）022223356=-+--λλλ（2）0913251323221321122=--x x5.计算下列行列式（1）8364213131524273------ （2）efcfbfde cd bdae ac ab---（3）2123548677595133634424355---------- （4）111110000000002211n n a a a a a a ---（5）xaaa x a a a x（6）abb a b a b a 000000000000习 题 1.31． 解下列方程组（1）⎪⎩⎪⎨⎧-=++=+--=++1024305222325321321321x x x x x x x x x （2）⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x2． k 取何值时，下列齐次线性方程组可能有非零：(1) ⎪⎩⎪⎨⎧=+-=++-=++0200321321321x x x x kx x kx x x (2)⎪⎩⎪⎨⎧=+-=++=++0300321321321x x x x kx x x x kx 习 题 五1.41．计算下列行列式（1）3010002113005004， （2）113352063410201-- （3）222111c b a c b a（4）335111243152113------， （5）nn n n n b a a a a a b a a a a D ++=+212112111112．用克莱姆法则解线性方程（1）⎪⎩⎪⎨⎧=+-=-+=--114231124342321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++=+-+=+-+=++3322212543143214321321x x x x x x x x x x x x x x3．当λ为何值时，方程组⎪⎩⎪⎨⎧=+-=+-=++0020321321321x x x x x x x x x λλ可能存在非零解？4.证明下列各等式(1) 222)(11122b a b b a a b ab a -=+(2) ))()((4)2()1()2()1()2()1(222222222c b a c a b c c c b b ba a a ---=++++++ (3) ))()()()()()((111144442222d c b a d c d b c b d a c a b a d c b a d c b a d c b a+++------=5.试求一个2次多项式)(x f ,满足1)2(,1)1(,0)1(-==-=f f f .第2章矩阵习 题 2.21．设 ⎥⎦⎤⎢⎣⎡=530142A ， ⎥⎦⎤⎢⎣⎡-=502131B ， ⎥⎦⎤⎢⎣⎡--=313210C ， 求3A -2B +C 。

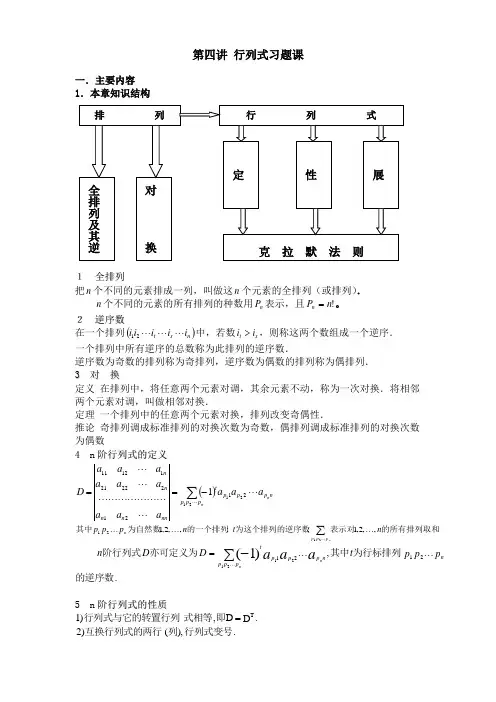
第四讲 行列式习题课一．主要内容 1．本章知识结构１ 全排列把n 个不同的元素排成一列，叫做这n 个元素的全排列（或排列）． n 个不同的元素的所有排列的种数用n P 表示，且!n P n =。

２ 逆序数在一个排列()n s t i i i i i 21中，若数s t i i >，则称这两个数组成一个逆序． 一个排列中所有逆序的总数称为此排列的逆序数．逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列． 3 对 换定义 在排列中，将任意两个元素对调，其余元素不动，称为一次对换．将相邻两个元素对调，叫做相邻对换．定理 一个排列中的任意两个元素对换，排列改变奇偶性．推论 奇排列调成标准排列的对换次数为奇数，偶排列调成标准排列的对换次数为偶数4 n 阶行列式的定义()np p p p p p tnnn n n nn n a a a a a a a a a a a a D 2121222211121121211∑-==.,,2,1;;,,2,12121的所有排列取和表示对为这个排列的逆序数的一个排列为自然数其中n t n p p p p p p n n∑.,21212121)1(的逆序数为行标排列其中亦可定义为阶行列式p p p t D D n nn p p p p p p ta aa nn∑-=5 n 阶行列式的性质.D D ,1)T =即式相等行列式与它的转置行列 .),()2行列式变号列互换行列式的两行.,)()3则此行列式等于零完全相同列如果行列式有两行. ,)()4乘此行列式等于用数一数中所有的元素都乘以同列行列式的某一行k k . )( )5面以提到行列式符号的外的所有元素的公因子可列行列式中某一行 ., )( )6则此行列式为零元素成比例列行列式中如果有两行., )( )7列式之和则此行列式等于两个行的元素都是两数之和行若行列式的某一列 ., )( , )( )8行列式的值不变对应的元素上去行然后加到另一列的各元素乘以同一数行把行列式的某一列6 行列式按行（列）展开 １） 余子式与代数余子式.,1 )1(的代数余子式叫做元素；记的余子式，记作阶行列式叫做元素列划去后，留下来的行和第所在的第阶行列式中，把元素在a A M A M a a ijijijji ijij ijij n j i n -+=-２）关于代数余子式的重要性质⎩⎨⎧≠==⎩⎨⎧≠===⎩⎨⎧≠===∑∑==.,0;,1.,0;,.,0;,11j i j i j i j i D D j i j i D D ij ijjk nk ik ij ki nk ki A a A a 当当其中 当当或当当δδδ８ 克拉默法则如果线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.,,22112222212111212111b x a x a x a b x a x a x a b x a x a x a n n nn n n n n n n 那么它有唯一解的系数行列式,0 ≠D.,,2,1,n j DD jj x ==., ,,2,11的行列式所得到，列换成常数项中第）是把系数行列式（其中２b b b n j j D n j D =二．典型例题1．计算排列的逆序数例1()()()()()., 132******** 并讨论奇偶性的逆序数求排列k k k k k k +--- 。

行列式习题及答案行列式是线性代数中的一个重要概念，它不仅可以用于求解线性方程组，还可以用于计算矩阵的逆、特征值等。

下面我们将通过几个习题来加深对行列式的理解。

# 习题1：计算二阶行列式设有一个二阶行列式：\[ \begin{vmatrix} a & b \\ c & d \end{vmatrix} \]解答：二阶行列式的计算公式为：\[ \text{det} = ad - bc \]所以，该行列式的值为 \( a \times d - b \times c \)。

# 习题2：计算三阶行列式给定一个三阶行列式：\[ \begin{vmatrix} e & f & g \\ h & i & j \\ k & l & m\end{vmatrix} \]解答：三阶行列式可以通过展开法则计算，即：\[ \text{det} = e \cdot i \cdot m + f \cdot j \cdot k + g \cdot h \cdot l - g \cdot i \cdot k - f \cdot h \cdot m - e \cdot j \cdot l \]# 习题3：利用行列式解线性方程组考虑以下线性方程组：\[ \begin{cases} x + 2y = 5 \\ 3x - y = 4 \end{cases} \]解答：首先，我们可以将方程组写成矩阵形式：\[ \begin{bmatrix} 1 & 2 \\ 3 & -1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 5 \\ 4 \end{bmatrix} \]计算矩阵的行列式：\[ \text{det} = 1 \cdot (-1) - 2 \cdot 3 = -1 - 6 = -7 \]由于行列式不为零，方程组有唯一解。

行列式习题及答案行列式是线性代数中的重要概念，它在矩阵运算和方程组求解中起着重要的作用。

本文将介绍一些行列式的习题及其答案，帮助读者更好地理解和掌握这一概念。

1. 习题一：计算行列式的值已知行列式A = |2 3||4 5|求解行列式A的值。

答案：根据行列式的定义，可以得到A的值为：2*5 - 3*4 = 10 - 12 = -2。

2. 习题二：行列式的性质已知行列式B = |a b||c d|如果行列式B的值为0，是否可以得出a、b、c、d中至少有一个为0的结论？答案：是的，如果行列式B的值为0，根据行列式的性质，可以得出至少存在一组a、b、c、d中的一个为0的情况。

这是因为行列式的值为0意味着矩阵的行向量或列向量线性相关，即存在线性关系式使得行向量或列向量之间存在依赖关系。

3. 习题三：行列式的展开已知行列式C = |1 2 3||4 5 6||7 8 9|求解行列式C的值。

答案：根据行列式的展开定理，可以选择第一行或第一列展开计算。

选择第一行展开，可以得到C的值为：1 * (-1)^(1+1) * |5 6| - 2 * (-1)^(1+2) * |4 6| + 3 * (-1)^(1+3) * |4 5||8 9| |7 9| |7 8|= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)= 1 * (-3) - 2 * (-6) + 3 * (-3)= -3 + 12 - 9= 04. 习题四：行列式的性质已知行列式D = |a b||c d|如果行列式D的值为1，是否可以得出a、b、c、d中至少有一个为1的结论？答案：不可以。

行列式的值为1并不能直接得出a、b、c、d中至少有一个为1的结论。

因为行列式的值为1并不代表矩阵的元素本身就是1，行列式的值只是表示了矩阵的行向量和列向量之间的线性关系。

5. 习题五：行列式的性质已知行列式E = |1 2||3 4|如果行列式E的值为k，是否可以得出a、b、c、d中的元素之和等于k的结论？答案：是的。