最新几何作图讲义
- 格式:doc
- 大小:190.50 KB
- 文档页数:7
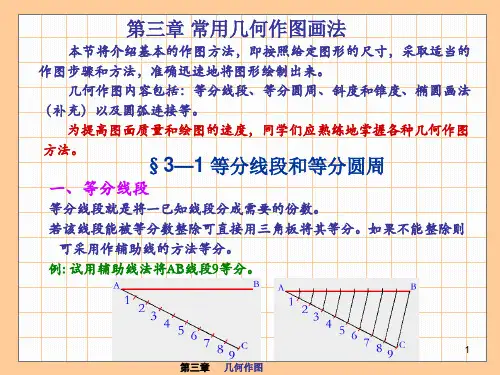




2023年中考复习讲义几何初步与尺规作图第一部分:知识点精准记忆一、直线、射线、线段1.直线的性质:1)两条直线相交,只有一个交点;2)经过两点有且只有一条直线,即两点确定一条直线;3)直线的基本事实:经过两点有且只有一条直线.2.线段的性质:两点确定一条直线,两点之间,线段最短,两点间线段的长度叫两点间的距离.3.线段的中点性质:若C是线段AB中点,则AC=BC=12AB;AB=2AC=2BC.4.两条直线的位置关系:在同一平面内,两条直线只有两种位置关系:平行和相交.5.垂线的性质:1)两条直线相交所构成的四个角中有一个角是直角,则这两条直线互相垂直,其中一条直线叫做另一条直线的垂线;2)①经过一点有且只有一条直线与已知直线垂直;②直线外一点与直线上各点连接的所有线段中,垂线段最短.6.点到直线的距离:从直线外一点向已知直线作垂线,这一点和垂足之间线段的长度叫做点到直线的距离.二、角1.角:有公共端点的两条射线组成的图形.2.角平分线(1)定义:在角的内部,以角的顶点为端点把这个角分成两个相等的角的射线(2)性质:若OC是∠AOB的平分线,则∠AOC=∠BOC =12∠AOB,∠AOB=2∠AOC =2∠BOC.3.度、分、秒的运算方法:1°=60′,1′=60″,1°=3600″.1周角=2平角=4直角=360°.4.余角和补角1)余角:∠1+∠2=90°⇔∠1与∠2互为余角;2)补角:∠1+∠2=180°⇔∠1与∠2互为补角.3)性质:同角(或等角)的余角相等;同角(或等角)的补角相等.5.方向角和方位角:在描述方位角时,一般应先说北或南,再说偏西或偏东多少度,而不说成东偏北(南)多少度或西偏北(南)多少度.当方向角在45°方向上时,又常常说成东南、东北、西南、西北方向.三、相交线1.三线八角1)直线a,b被直线l所截,构成八个角(如图).∠1和∠5,∠4和∠8,∠2和∠6,∠3和∠7是同位角;∠2和∠8,∠3和∠5是内错角;∠5和∠2,∠3和∠8是同旁内角.2)除了基本模型外,我们还经常会遇到稍难一些的平行线加折线模型,主要是下面两类:做这类题型时,一般在折点处作平行线,进而把线的关系转换成角的关系,如上图:2.垂直1)定义:两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直.2)性质:过一点有且只有一条直线垂直于已知直线;垂线段最短.3.点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.4.邻补角1)定义:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角.2)邻补角是补角的一种特殊情况:邻补角既包含位置关系,又包含数量关系,数量上两角的和是180°,位置上有一条公共边.3)邻补角是成对出现的,单独的一个角不能称为邻补角,两条直线相交形成四对邻补角.5.对顶角1)定义:两个角有一个公共的顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种关系的两个角,互为对顶角.2)性质:对顶角相等.但相等的角不一定是对顶角.四、平行线1.定义:在同一平面内,不相交的两条直线叫做平行线.2.平行线的判定1)同位角相等,两直线平行.2)内错角相等,两直线平行.3)同旁内角互补,两直线平行.4)平行于同一直线的两直线互相平行.5)垂直于同一直线的两直线互相平行. 3.平行线的性质1)两直线平行,同位角相等.2)两直线平行,内错角相等.3)两直线平行,同旁内角互补. 4.平行线间的距离1)定义:同时垂直于两条平行线,并且夹在这两条平行线的线段的长度,叫做这两条平行线的距离.2)性质:两平行线间的距离处处相等,夹在两平行线间的平行线段相等.五、五种基本作图:1.作一条线段等于已知线段。






画法几何及工程制图讲稿与教案第一章:画法几何与工程制图概述1.1 画法几何的概念与发展历程1.2 工程制图的重要性与基本要求1.3 画法几何与工程制图的基本原理1.4 学习方法与教学内容安排第二章:点、线、面的基本性质与绘制2.1 点的基本性质与绘制方法2.2 线的基本性质与绘制方法2.3 面的基本性质与绘制方法2.4 点、线、面的综合应用实例第三章:直线与圆的方程3.1 直线方程的推导与应用3.2 圆的方程推导与应用3.3 直线与圆的位置关系及应用3.4 直线与圆的相交、相切问题实例第四章:平面几何图形的解析与绘制4.1 三角形、四边形的解析与绘制4.2 圆形的解析与绘制4.3 平面几何图形的应用实例4.4 平面几何图形的解析与绘制技巧第五章:立体几何图形的解析与绘制5.1 立方体及其表面图形的解析与绘制5.2 球体、圆柱体、圆锥体的解析与绘制5.3 立体几何图形的投影变换5.4 立体几何图形的应用实例第六章:组合体的解析与绘制6.1 组合体的概念与分类6.2 组合体的视图与绘制方法6.3 组合体的尺寸标注与阅读6.4 组合体的应用实例与练习第七章:机件的表达方法7.1 视图的表达与绘制7.2 剖视图与断面图的绘制7.3 斜视图与局部视图的应用7.4 机件表达方法的实践案例第八章:标准件与常用件的绘制8.1 螺纹件的绘制方法8.2 齿轮的绘制方法8.3 键、销、轴承等常用件的绘制8.4 标准件与常用件的综合应用实例第九章:图样的编制与标准9.1 图纸的格式与规格9.2 图样的标注方法与规则9.3 标准尺寸及其应用9.4 图样编制的实践案例与分析第十章:工程制图的软件应用10.1 AutoCAD软件的基本操作10.2 利用AutoCAD绘制简单图形10.3 常见工程图形的AutoCAD绘制技巧10.4 工程制图软件的实践案例与练习第十一章:建筑图形的解析与绘制11.1 建筑平面图的解析与绘制11.2 建筑立面图的解析与绘制11.3 建筑剖面图的解析与绘制11.4 建筑图形应用实例与练习第十二章:水利工程图的解析与绘制12.1 水利工程平面图的解析与绘制12.2 水利工程立面图与剖面图的解析与绘制12.3 水利工程图的尺寸标注与阅读12.4 水利工程图的应用实例与练习第十三章:电气工程图的解析与绘制13.1 电气工程图的基本构成与类型13.2 电气元件的表示方法与绘制13.3 电气线路图的解析与绘制13.4 电气工程图的应用实例与练习第十四章:机械零件图的解析与绘制14.1 机械零件图的概述与内容14.2 机械零件图的尺寸标注与技术要求14.3 机械零件图的绘制方法与技巧14.4 机械零件图的应用实例与练习第十五章:装配图的解析与绘制15.1 装配图的概念与作用15.2 装配图的绘制步骤与方法15.3 装配图的尺寸标注与技术要求15.4 装配图的应用实例与练习重点和难点解析重点:1. 点、线、面的基本性质与绘制方法。
几何作图讲义
几何作图讲义
一、知识点睛
1.几何作图:__________________________________________; 2.多种情况作图:______________________________________.
二、精讲精练
板块一:根据几何语言作图
1. 如图,已知四点A ,B ,C ,D ,按要求作图: ① 作射线AD ,作直线AC ; ② 连接BD 与直线AC 交于点E ; ③
连接BC 并延长交射线AD 于点F .
D
B
C
A
2. 作图:
(1) 如图,已知线段a ,b ,按要求作图:①作射线AM ,在射线AM 上依次
截取AB =a ,BC =b ;②过点C 作直线 CD ⊥AM ,垂足为点C .
a b
(2) 如图,已知四点A ,B ,C ,D ,按要求作图:①连接AB ,CD ;②延长
AB 到点E 使BE =AB ,延长DC 到点F 使CF =AB ;③延长FD 交AB 的延长线于点G .
A
C
B
3. 如图,点M ,P 分别在直线AB 上和直线AB 外,按题意作图、填空. ①
连接PM ;
②过点P作直线AB的垂线PH交AB于点H,那么点P到点M的距离是线段
_____的长度,点P到直线AB的距离是线段_____的长度;
③过点P作直线PQ∥AB.
P
4.已知∠AOB,按要求作图:
(1)①在OA和OB上分别截取OD,OE,使OD=OE;
②分别以D,E为圆心、以OD长为半径作弧,两弧在∠AOB内部
交于点C;
③作射线OC.
(2)用量角器验证∠AOC和∠BOC的数量关系.
A
O
板块二:定理应用
5.说出日常生活现象中的数学原理:
(1)有人和你打招呼,你笔直向他走过去,应用的数学原理是______________________________________________;
(2)要用两个钉子把木条安装在墙上,应用的数学原理是__________________________________________________;
(3)如图1,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是___________________________________;
B
A
P
C
Q
图1 图2
(4)如图2,PC ∥AB ,QC ∥AB ,则点P ,C ,Q 在一条直线上,理由是_______________________________________.
6. 如图,平原上有A ,B ,C ,D 四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你作图确定蓄水池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H 中,怎样开渠最短并说明理由.
D
B
A C
7. 一辆汽车在直线形的公路AB 上由A 向B 行驶,C ,D 是分别位于公路AB 两侧的加油站.
(1)设汽车行驶到公路AB 上点M 的位置时,距离加油站C 最近;行驶到点N 的位置时,距离加油站D 最近,请在图中的公路上分别作出点M ,N 的位置.
(2)当汽车从A 出发向B 行驶时,在公路AB 的哪一段路上距离C ,D 两加油站都越来越近?在哪一段路上距离加油站D 越来越近,而离加油站C 却越来越远?
(3)在公路AB上找一点P,使得汽车行驶到P点时到两个加油站的距离和最小.
C
B
板块三:多种情况作图
8.在直线l上任取一点A,截取AB=8cm,再截取AC=12cm,则线段BC的长
为______________.
A B A B
9.在直线l上任取一点A,截取AB=16cm,再截取AC=40cm,则AB的中点D
与AC的中点E之间的距离为___________.
A
A B
B
10.已知A,B,C三点在同一条直线上,M,N分别为线段AB,BC的中点,且
AB=60,BC=40,则MN的长为___________.
11.已知线段AB=16cm,C点在直线AB上,AC=3BC,则BC的长为
___________.
B B
12.从O点出发的三条射线OA,OB,OC,若∠AOB是直角,
∠AOC为30°,则∠BOC的度数为_____________.
O
A O
A
13. 已知∠AOB =90°,∠BOC =30°,OM 平分∠AOB ,ON 平分∠BOC ,则∠MON 的度数为_____________.
O
A
O
A
14. 已知∠AOB =40°,∠AOD =3∠AOB ,OC 平分∠AOB ,OM 平分∠AOD ,则∠MOC 的度数为_____________.
B
O
40°
A
B
O
40°
A
三、回顾与思考
________________________________________________________________________________________________________________________________________________________________________
【参考答案】
一、知识点睛
1.直尺画线,圆规度量,三角板作垂直. 2.位置不确定时考虑分类讨论. 二、精讲精练
1.作图略;2.作图略3.(1)作图略
(2)PM;PH(3)作图略
4.(1)作图略(2)∠AOC=∠BOC
5.(1)两点之间,线段最短.(2)两点确定一条直线.
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(4)经过直线外一点,有且只有一条直线与这条直线平行.
6.(1)作图略(提示:连接AD,BC,AD与BC的交点即为H点);
(2)作图略(提示:过H点向河边作垂线),理由:直线外一点与直线上各点连接的所有线段中,垂线段最短.
7.(1)作图略;(2)AM,MN;(3)作图略(提示:连接CD,CD与AB的交点就是所求的P点)
8.4cm或20cm 9.28cm或12cm 10.50或10
11.8cm或4cm 12.60°或120°13.30°或60°14.40°或80°。