冲刺中考数学几何压轴题专项复习专题22正方形存在性问题巩固练习(提优)

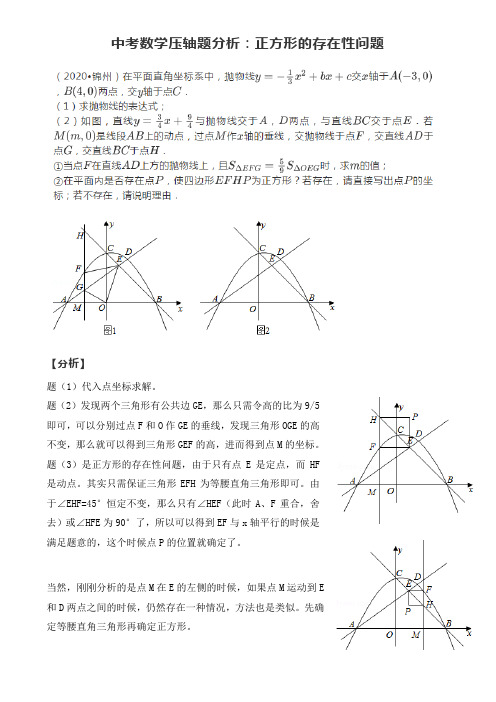
中考数学压轴题分析：正方形的存在性问题
【分析】
题（1）代入点坐标求解。

题（2）发现两个三角形有公共边GE，那么只需令高的比为9/5
即可，可以分别过点F和O作GE的垂线，发现三角形OGE的高
不变，那么就可以得到三角形GEF的高，进而得到点M的坐标。

题（3）是正方形的存在性问题，由于只有点E是定点，而HF
是动点。

其实只需保证三角形EFH为等腰直角三角形即可。

由
于∠EHF=45°恒定不变，那么只有∠HEF（此时A、F重合，舍
去）或∠HFE为90°了，所以可以得到EF与x轴平行的时候是
满足题意的，这个时候点P的位置就确定了。

当然，刚刚分析的是点M在E的左侧的时候，如果点M运动到E
和D两点之间的时候，仍然存在一种情况，方法也是类似。

先确
定等腰直角三角形再确定正方形。

2022年中考数学二次函数压轴题考点大汇总正方形存在性问题知识导航作为特殊四边形中最特殊的一位，正方形拥有更多的性质，因此坐标系中的正方形存在性问题变化更加多样，从判定的角度来说，可以有如下：（1）有一个角为直角的菱形；（2）有一组邻边相等的矩形；（3）对角线互相垂直平分且相等的四边形．依据题目给定的已知条件选择恰当的判定方法，即可确定所求的点坐标．从未知量的角度来说，正方形可以有4个“未知量”，因其点坐标满足4个等量关系，考虑对角线性质，互相平分（2个）垂直（1个）且相等（1个）．比如在平面中若已知两个定点，可以在平面中确定另外两个点使得它们构成正方形，而如果要求在某条线上确定点，则可能会出现不存在的情况，即我们所说的未知量小于方程个数，可能无解．从动点角度来说，关于正方形存在性问题可分为：（1）2个定点+2个全动点；（2）1个定点+2个半动点+1个全动点;甚至可以有：（3）4个半动点．不管是哪一种类型，要明确的是一点，我们肯定不会列一个四元一次方程组求点坐标！常用处理方法：思路1：从判定出发若已知菱形，则加有一个角为直角或对角线相等；若已知矩形，则加有一组邻边相等或对角线互相垂直；若已知对角线互相垂直或平分或相等，则加上其他条件．思路2：构造三垂直全等若条件并未给关于四边形及对角线的特殊性，则考虑在构成正方形的4个顶点中任取3个，必是等腰直角三角形，若已知两定点，则可通过构造三垂直全等来求得第3个点，再求第4个点．总结：构造三垂直全等的思路仅适合已知两定点的情形，若题目给了4个动点，则考虑从矩形的判定出发，观察该四边形是否已为某特殊四边形，考证还需满足的其他关系．正方形的存在性问题在中考中出现得并不多，正方形多以小题压轴为主．方法突破例：在平面直角坐标系中，A （1,1），B （4,3），在平面中求C 、D 使得以A 、B 、C 、D 为顶点的四边形是正方形．如图，一共6个这样的点C 使得以A 、B 、C 为顶点的三角形是等腰直角三角形．至于具体求点坐标，以1C 为例，构造△AMB ≌△1C NA ，即可求得1C 坐标．至于像5C 、6C 这两个点的坐标，不难发现，5C 是3AC 或1BC 的中点，6C 是2BC 或4AC 的中点．题无定法，具体问题还需具体分析，如上仅仅是大致思路．专项训练1.如图，已知抛物线2y x bx c =++的图象经过点A （1，0），B （-3，0），与y 轴交于点C ，抛物线的顶点为D ，对称轴与x 轴相交于点E ，连接BD ．（1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE=PC 时，求点P 的坐标．（3）在（2）的条件下，作PF ⊥x 轴于F ，点M 为x 轴上一动点，点N 为直线PF 上一动点，G 为抛物线上一动点，当以点F 、N 、G 、M 四点为顶点的四边形为正方形时，求点M 的坐标．2．如图，在平面直角坐标系中，抛物线21322y x bx =-++与x 轴正半轴交于点A ，且点A 的坐标为(3,0)，过点A 作垂直于x 轴的直线l ．P 是该抛物线上的任意一点，其横坐标为m ，过点P 作PQ l ⊥于点Q ，M 是直线l 上的一点，其纵坐标为32m -+．以PQ ，QM 为边作矩形PQMN ．（1）求b 的值．（2）当点Q 与点M 重合时，求m 的值．（3）当矩形PQMN 是正方形，且抛物线的顶点在该正方形内部时，求m 的值．（4）当抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小时，直接写出m 的取值范围．3．在平面直角坐标系中，抛物线213y x bx c =-++交x 轴于(3,0)A -，(4,0)B 两点，交y 轴于点C ．（1）求抛物线的表达式；（2）如图，直线3944y x =+与抛物线交于A ，D 两点，与直线BC 交于点E ．若(,0)M m 是线段AB 上的动点，过点M 作x 轴的垂线，交抛物线于点F ，交直线AD 于点G ，交直线BC 于点H ．①当点F 在直线AD 上方的抛物线上，且59EFG OEG S S ∆∆=时，求m 的值；②在平面内是否存在点P ，使四边形EFHP 为正方形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．正方形存在性问题知识导航作为特殊四边形中最特殊的一位，正方形拥有更多的性质，因此坐标系中的正方形存在性问题变化更加多样，从判定的角度来说，可以有如下：（1）有一个角为直角的菱形；（2）有一组邻边相等的矩形；（3）对角线互相垂直平分且相等的四边形．依据题目给定的已知条件选择恰当的判定方法，即可确定所求的点坐标．从未知量的角度来说，正方形可以有4个“未知量”，因其点坐标满足4个等量关系，考虑对角线性质，互相平分（2个）垂直（1个）且相等（1个）．比如在平面中若已知两个定点，可以在平面中确定另外两个点使得它们构成正方形，而如果要求在某条线上确定点，则可能会出现不存在的情况，即我们所说的未知量小于方程个数，可能无解．从动点角度来说，关于正方形存在性问题可分为：（1）2个定点+2个全动点；（2）1个定点+2个半动点+1个全动点;甚至可以有：（3）4个半动点．不管是哪一种类型，要明确的是一点，我们肯定不会列一个四元一次方程组求点坐标！常用处理方法：思路1：从判定出发若已知菱形，则加有一个角为直角或对角线相等；若已知矩形，则加有一组邻边相等或对角线互相垂直；若已知对角线互相垂直或平分或相等，则加上其他条件．思路2：构造三垂直全等若条件并未给关于四边形及对角线的特殊性，则考虑在构成正方形的4个顶点中任取3个，必是等腰直角三角形，若已知两定点，则可通过构造三垂直全等来求得第3个点，再求第4个点．总结：构造三垂直全等的思路仅适合已知两定点的情形，若题目给了4个动点，则考虑从矩形的判定出发，观察该四边形是否已为某特殊四边形，考证还需满足的其他关系．正方形的存在性问题在中考中出现得并不多，正方形多以小题压轴为主．方法突破例：在平面直角坐标系中，A （1,1），B （4,3），在平面中求C 、D 使得以A 、B 、C 、D 为顶点的四边形是正方形．如图，一共6个这样的点C 使得以A 、B 、C 为顶点的三角形是等腰直角三角形．至于具体求点坐标，以1C 为例，构造△AMB ≌△1C NA ，即可求得1C 坐标．至于像5C 、6C 这两个点的坐标，不难发现，5C 是3AC 或1BC 的中点，6C 是2BC 或4AC 的中点．题无定法，具体问题还需具体分析，如上仅仅是大致思路．专项训练1.如图，已知抛物线2y x bx c =++的图象经过点A （1，0），B （-3，0），与y 轴交于点C ，抛物线的顶点为D ，对称轴与x 轴相交于点E ，连接BD ．（1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE=PC 时，求点P 的坐标．（3）在（2）的条件下，作PF ⊥x 轴于F ，点M 为x 轴上一动点，点N 为直线PF 上一动点，G 为抛物线上一动点，当以点F 、N 、G 、M 四点为顶点的四边形为正方形时，求点M 的坐标．【分析】（1）抛物线：223y x x =+-；（2）求CE 的直线解析式或设P 点坐标表示PE=PC ，可得P 点坐标为()2,2--．（3）考虑FN ⊥FM ，故四边形为MFNG ，若要成为正方形，则GN ∥FM ，GM ⊥x 轴，即四边形MFNG 为矩形．设FN 长度为m ，则NG=FN=m ，故G 点横坐标为m-2，代入解析式得：()22,23G m m m ---，故223GM m m m =--=，解得：1m =，2m =（舍），3m =，4m =（舍）．则M 点坐标为12⎛⎫-+ ⎪ ⎪⎝⎭或12⎛⎫-+ ⎪ ⎪⎝⎭．【小结】根据题目描述可知四边形是矩形，考虑四边形的边均与坐标轴平行或垂直，故构造一组邻边相等求得点坐标．2．如图，在平面直角坐标系中，抛物线21322y x bx =-++与x 轴正半轴交于点A ，且点A 的坐标为(3,0)，过点A 作垂直于x 轴的直线l ．P 是该抛物线上的任意一点，其横坐标为m ，过点P 作PQ l ⊥于点Q ，M 是直线l 上的一点，其纵坐标为32m -+．以PQ ，QM 为边作矩形PQMN ．（1）求b 的值．（2）当点Q 与点M 重合时，求m 的值．（3）当矩形PQMN 是正方形，且抛物线的顶点在该正方形内部时，求m 的值．（4）当抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小时，直接写出m 的取值范围．【分析】（1）利用待定系数法求解即可．（2）根据点M 与点P 的纵坐标相等构建方程求解即可．（3）根据PQ MQ =，构建方程求解即可．（3）当点P 在直线l 的左边，点M 在点Q 是下方下方时，抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小，则有2313222m m m -+<-++，解得04m <<，观察图象可知．当03m <<时，抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小，如图41-中．当4m >时，点M 在点Q 的上方，也满足条件，如图42-中．【解答】解：（1）把点(3,0)A 代入21322y x bx =-++，得到930322b =-++，解得1b =．（2） 抛物线的解析式为21322y x x =-++，213(,22P m m m ∴-++，M ，Q 重合，2313222m m m ∴-+=-++，解得0m =或4．（3）22131(1)2222y x x x =-++=--+，∴抛物线的顶点坐标为(1,2)，由题意PQ MQ =，且抛物线的顶点在该正方形内部，23133()222m m m m ∴-=-+--++且322m -+>，得12m <-解得1m =1+（不合题意舍弃），1m ∴=．（4）当点P 在直线l 的左边，点M 在点Q 下方时，抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小，则有2313222m m m -+<-++，240m m ∴-<，解得04m <<，观察图象可知．当03m <<时，抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小，如图41-中，当34m <<时，抛物线不在矩形PQMN 内部，不符合题意，当4m >时，点M 在点Q 的上方，也满足条件，如图42-中，综上所述，满足条件的m 的值为03m <<或4m >．【点评】本题属于二次函数综合题，考查了二次函数的性质，待定系数法，矩形的性质等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于中考压轴题．3．在平面直角坐标系中，抛物线213y x bx c =-++交x 轴于(3,0)A -，(4,0)B 两点，交y 轴于点C ．（1）求抛物线的表达式；（2）如图，直线3944y x =+与抛物线交于A ，D 两点，与直线BC 交于点E ．若(,0)M m 是线段AB 上的动点，过点M 作x 轴的垂线，交抛物线于点F ，交直线AD 于点G ，交直线BC 于点H ．①当点F 在直线AD 上方的抛物线上，且59EFG OEG S S ∆∆=时，求m 的值；②在平面内是否存在点P ，使四边形EFHP 为正方形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．【分析】（1）根据抛物线解析式中13a =-和交x 轴于(3,0)A -，(4,0)B 两点，利用交点式可得抛物线的解析式；（2）①如图1，先利用待定系数法求直线BC 的解析式，联立方程可得交点E 的坐标，根据(,0)M m ，且MH x ⊥轴，表示点39(,44G m m +，211(,4)33F m m m -++，由59EFG OEG S S ∆∆=，列方程可得结论；②存在，根据正方形的性质得：FH EF =，90EFH FHP HPE ∠=∠=∠=︒，同理根据(,0)M m ，得(,4)H m m -+，211(,4)33F m m m -++，分两种情况：F 在EP 的左侧，在EP 的右侧，根据EF FH =，列方程可得结论．【解答】解：（1） 抛物线213y x bx c =-++交x 轴于(3,0)A -，(4,0)B 两点，2111(3)(4)4333y x x x x ∴=-+-=-++；（2）①如图1，(4,0)B ，(0,4)C ，∴设BC 的解析式为：y kx n =+，则404k n n +=⎧⎨=⎩，解得14k n =-⎧⎨=⎩，BC ∴的解析式为：4y x =-+，39444x x ∴-+=+，解得：1x =，(1,3)E ∴，(,0)M m ，且MH x ⊥轴，39(,)44G m m ∴+，211(,4)33F m m m -++，59EFG OEG S S ∆∆=，∴151()()292E F E G FG x x ON x x ⨯-=⨯-，2113959[(4)()](1)(1)334494m m m m m -++-+-=⨯-，解得：134m =，22m =-；②存在，由①知：(1,3)E ，四边形EFHP 是正方形，FH EF ∴=，90EFH FHP HPE ∠=∠=∠=︒，(,0)M m ，且MH x ⊥轴，(,4)H m m ∴-+，211(,4)33F m m m -++，分两种情况：)i 当31m -< 时，如图2，点F 在EP 的左侧，221114(4)(4)3333FH m m m m m ∴=-+--++=-，EF FH = ，∴214133m m m -=-，解得：112m +=（舍)，212m -=，1(2H -∴，72+，P ∴，)ii 当14m <<时，点F 在PE 的右边，如图3，同理得214133m m m -+=-，解得：11132m +=，21132m =（舍)，同理得713(1,2P -；综上，点P 的坐标为：713+或713)-．【点评】本题考查的是二次函数综合运用，涉及到一次函数，正方形的性质，二次函数，两函数的交点，图形的面积计算等，与方程相结合，求解点的坐标，难度适中．相似三角形存在性问题知识导航在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．【相似判定】判定1：三边对应成比例的两个三角形是相似三角形；判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；判定3：有两组角对应相等的三角形是相似三角形．以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题．【题型分析】通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．然后再找：思路1：两相等角的两边对应成比例；思路2：还存在另一组角相等．事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．一、如何得到相等角？二、如何构造两边成比例或者得到第二组角？搞定这两个问题就可以了．方法突破例一、如图，抛物线2y ax bx c =++与x 轴交于点A （-1，0），点B （3，0），与y 轴交于点C ，且过点D （2，-3）．点Q 是抛物线2y ax bx c =++上的动点．（1）求抛物线的解析式；（2）如图2，直线OQ 与线段BC 相交于点E ，当△OBE 与△ABC 相似时，求点Q 的坐标．【分析】（1）抛物线：223y x x =--；（2）思路：考虑到△ABC 和△BOE 有一组公共角，公共角必是对应角．∠ABC 的两边BA 、BC 与∠OBE 的两边BO 、BE 成比例即可，故可得：BE BA BO BC =或BE BC BO BA=．解得：BE =或BE =E 点坐标为()1,2-或39,44⎛⎫- ⎪⎝⎭．当E 点坐标为()1,2-时，直线OE 解析式为2y x =-，联立方程：2223x x x -=--，解得：1x ，2x =，此时Q 点坐标为-或(；当E 点坐标为39,44⎛⎫- ⎪⎝⎭时，直线OE 解析式为3y x =-，联立方程：2323x x x -=--，解得：112x -+=，212x --=，此时Q 点坐标为⎝⎭或⎝⎭．综上所述，Q 点坐标为-或(或⎝⎭或⎝⎭．说明：过程应详细分类讨论两种情况，分别求出结果．例二、如图1，在平面直角坐标系中，直线y =x -1与抛物线2y x bx c =-++交于A 、B 两点，其中A （m ，0）、B （4，n ），该抛物线与y 轴交于点C ，与x 轴交于另一点D ．（1）求m 、n 的值及该抛物线的解析式；（2）如图2，连接BD 、CD ，在线段CD 上是否存在点Q ，使得以A 、D 、Q 为顶点的三角形与△ABD 相似，若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【分析】（1）m =1，n =3，抛物线解析式为265y x x =-+-；（2）思路：平行得相等角，构造两边成比例由题意得D （5，0），故直线CD 解析式为：y =x -5，∴CD ∥AB ，∴∠CDA =∠BAD ，考虑到点Q 在线段CD上，∴DA AB DQ AD =或DA AD DQ AB =，解得：DQ =或DQ =Q 点坐标为78,33⎛⎫- ⎪⎝⎭或()2,3-．专项训练1．已知抛物线2:L y x bx c =-++过点(3,3)-和(1,5)-，与x 轴的交点为A ，B （点A 在点B 的左侧）．（1）求抛物线L 的表达式；（2）若点P 在抛物线L 上，点E 、F 在抛物线L 的对称轴上，D 是抛物线L 的顶点，要使(PEF DAB P ∆∆∽的对应点是)D ，且:1:4PE DA =，求满足条件的点P 的坐标．2．在平面直角坐标系xOy 中，已知抛物线2y ax bx c =++与x 轴交于(1,0)A -，(4,0)B 两点，与y 轴交于点(0,2)C -．（1）求抛物线的函数表达式；（2）如图1，点D 为第四象限抛物线上一点，连接AD ，BC 交于点E ，连接BD ，记BDE ∆的面积为1S ，ABE ∆的面积为2S ，求12S S 的最大值；（3）如图2，连接AC ，BC ，过点O 作直线//l BC ，点P ，Q 分别为直线l 和抛物线上的点．试探究：在第一象限是否存在这样的点P ，Q ，使PQB CAB ∆∆∽．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．3．在平面直角坐标系xOy 中，把与x 轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线2113:222L y x x =--的顶点为D ，交x 轴于点A 、B （点A 在点B 左侧），交y 轴于点C ．抛物线2L 与1L 是“共根抛物线”，其顶点为P ．（1）若抛物线2L 经过点(2,12)-，求2L 对应的函数表达式；（2）当BP CP -的值最大时，求点P 的坐标；（3）设点Q 是抛物线1L 上的一个动点，且位于其对称轴的右侧．若DPQ ∆与ABC ∆相似，求其“共根抛物线”2L 的顶点P 的坐标．4．如图，抛物线2y x bx c =++经过点(3,12)和(2,3)--，与两坐标轴的交点分别为A ，B ，C ，它的对称轴为直线l ．（1）求该抛物线的表达式；（2）P 是该抛物线上的点，过点P 作l 的垂线，垂足为D ，E 是l 上的点．要使以P 、D 、E 为顶点的三角形与AOC ∆全等，求满足条件的点P ，点E 的坐标．5．如图1，抛物线21(2)62y x =-++与抛物线21122y x tx t =-++-相交y 轴于点C ，抛物线1y 与x 轴交于A 、B 两点（点B 在点A 的右侧），直线23y kx =+交x 轴负半轴于点N ，交y 轴于点M ，且OC ON =．（1）求抛物线1y 的解析式与k 的值；（2）抛物线1y 的对称轴交x 轴于点D ，连接AC ，在x 轴上方的对称轴上找一点E ，使以点A ，D ，E 为顶点的三角形与AOC ∆相似，求出DE 的长；（3）如图2，过抛物线1y 上的动点G 作GH x ⊥轴于点H ，交直线23y kx =+于点Q ，若点Q '是点Q 关于直线MG 的对称点，是否存在点G （不与点C 重合），使点Q '落在y 轴上？若存在，请直接写出点G 的横坐标，若不存在，请说明理由．6．如图，抛物线28(0)y ax bx a =++≠与x 轴交于点(2,0)A -和点(8,0)B ，与y 轴交于点C ，顶点为D ，连接AC ，BC ，BC 与抛物线的对称轴l 交于点E ．（1）求抛物线的表达式；（2）点P 是第一象限内抛物线上的动点，连接PB ，PC ，当35PBC ABC S S ∆∆=时，求点P 的坐标；（3）点N 是对称轴l 右侧抛物线上的动点，在射线ED 上是否存在点M ，使得以点M ，N ，E 为顶点的三角形与OBC ∆相似？若存在，求点M 的坐标；若不存在，请说明理由．7．如图，抛物线22y ax bx =++与x 轴交于A ，B 两点，且2OA OB =，与y 轴交于点C ，连接BC ，抛物线对称轴为直线12x =，D 为第一象限内抛物线上一动点，过点D 作DE OA ⊥于点E ，与AC 交于点F ，设点D 的横坐标为m ．（1）求抛物线的表达式；（2）当线段DF 的长度最大时，求D 点的坐标；（3）抛物线上是否存在点D ，使得以点O ，D ，E 为顶点的三角形与BOC ∆相似？若存在，求出m 的值；若不存在，请说明理由．8．如图，抛物线2336y bx c +=++与x 轴交于A ，B 两点，点A ，B 分别位于原点的左、右两侧，33BO AO ==，过点B 的直线与y 轴正半轴和抛物线的交点分别为C ，D ，3BC CD =．（1）求b ，c 的值；（2）求直线BD 的函数解析式；（3）点P 在抛物线的对称轴上且在x 轴下方，点Q 在射线BA 上．当ABD ∆与BPQ ∆相似时，请直接写出所有满足条件的点Q 的坐标．9．如图，抛物线212y x bx c =++与x 轴交于A 、B 两点（点A 在点B 左边），与y 轴交于点C ．直线122y x =-经过B 、C 两点．（1）求抛物线的解析式；（2）点P 是抛物线上的一动点，过点P 且垂直于x 轴的直线与直线BC 及x 轴分别交于点D 、M ．PN BC ⊥，垂足为N ．设(,0)M m ．①点P 在抛物线上运动，若P 、D 、M 三点中恰有一点是其它两点所连线段的中点（三点重合除外）．请直接写出符合条件的m 的值；②当点P 在直线BC 下方的抛物线上运动时，是否存在一点P ，使PNC ∆与AOC ∆相似．若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，在平面直角坐标系中，抛物线21y ax bx =++的对称轴为直线32x =，其图象与x 轴交于点A 和点(4,0)B ，与y 轴交于点C ．（1）直接写出抛物线的解析式和CAO ∠的度数；（2）动点M ，N 同时从A 点出发，点M 以每秒3个单位的速度在线段AB 上运动，点N 个单位的速度在线段AC 上运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动的时间为(0)t t >秒，连接MN ，再将线段MN 绕点M 顺时针旋转90︒，设点N 落在点D 的位置，若点D 恰好落在抛物线上，求t 的值及此时点D 的坐标；（3）在（2）的条件下，设P 为抛物线上一动点，Q 为y 轴上一动点，当以点C ，P ，Q 为顶点的三角形与MDB ∆相似时，请直接写出点P 及其对应的点Q 的坐标．（每写出一组正确的结果得1分，至多得4分）相似三角形存在性问题知识导航在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．【相似判定】判定1：三边对应成比例的两个三角形是相似三角形；判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；判定3：有两组角对应相等的三角形是相似三角形．以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题．【题型分析】通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．然后再找：思路1：两相等角的两边对应成比例；思路2：还存在另一组角相等．事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．一、如何得到相等角？二、如何构造两边成比例或者得到第二组角？搞定这两个问题就可以了．方法突破例一、如图，抛物线2y ax bx c =++与x 轴交于点A （-1，0），点B （3，0），与y 轴交于点C ，且过点D （2，-3）．点Q 是抛物线2y ax bx c =++上的动点．（1）求抛物线的解析式；（2）如图2，直线OQ 与线段BC 相交于点E ，当△OBE 与△ABC 相似时，求点Q 的坐标．【分析】（1）抛物线：223y x x =--；（2）思路：考虑到△ABC 和△BOE 有一组公共角，公共角必是对应角．∠ABC 的两边BA 、BC 与∠OBE 的两边BO 、BE 成比例即可，故可得：BE BA BO BC =或BE BC BO BA=．解得：BE =或BE =故E 点坐标为()1,2-或39,44⎛⎫- ⎪⎝⎭．当E 点坐标为()1,2-时，直线OE 解析式为2y x =-，联立方程：2223x x x -=--，解得：1x ，2x =此时Q 点坐标为-或(；当E 点坐标为39,44⎛⎫- ⎪⎝⎭时，直线OE 解析式为3y x =-，联立方程：2323x x x -=--，解得：1x =2x =此时Q 点坐标为⎝⎭或⎝⎭．综上所述，Q 点坐标为-或(或⎝⎭或⎝⎭．说明：过程应详细分类讨论两种情况，分别求出结果．例二、如图1，在平面直角坐标系中，直线y =x -1与抛物线2y x bx c =-++交于A 、B 两点，其中A （m ，0）、B （4，n ），该抛物线与y 轴交于点C ，与x 轴交于另一点D ．（1）求m 、n 的值及该抛物线的解析式；（2）如图2，连接BD 、CD ，在线段CD 上是否存在点Q ，使得以A 、D 、Q 为顶点的三角形与△ABD 相似，若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【分析】（1）m =1，n =3，抛物线解析式为265y x x =-+-；（2）思路：平行得相等角，构造两边成比例由题意得D （5，0），故直线CD 解析式为：y =x -5，∴CD ∥AB ，∴∠CDA =∠BAD ，考虑到点Q 在线段CD 上，∴DAABDQ AD =或DAADDQ AB =，解得：823DQ =或32DQ =故Q 点坐标为78,33⎛⎫- ⎪⎝⎭或()2,3-．专项训练1．已知抛物线2:L y x bx c =-++过点(3,3)-和(1,5)-，与x 轴的交点为A ，B （点A 在点B 的左侧）．（1）求抛物线L 的表达式；（2）若点P 在抛物线L 上，点E 、F 在抛物线L 的对称轴上，D 是抛物线L 的顶点，要使(PEF DAB P ∆∆∽的对应点是)D ，且:1:4PE DA =，求满足条件的点P 的坐标．【分析】（1）利用待定系数法可求解析式；（2）先求出点A ，点B ，点D 坐标，由相似三角形的性质可求解．【解答】解：（1） 抛物线2y x bx c =-++过点(3,3)-和(1,5)-，∴51393b c b c -=-++⎧⎨=--+⎩，解得：40b c =-⎧⎨=⎩，∴抛物线解析式为24y x x =--；（2）令0y =，则204x x =--，14x ∴=-，20x =，∴点(4,0)A -，点(0,0)B ，∴对称轴为2x =-，∴点(2,4)D -，如图，设对称轴与x 轴的交点为H ，过点P 作PQ DH ⊥于Q ，设点2(,4)P m m m --，PEF DAB ∆∆ ∽，∴14PE PQ AD DH ==，1414PQ ∴=⨯=，|2|1m ∴+=，1m ∴=-或3-，∴点(1,3)P -或(3,3)-．【点评】本题是二次函数综合题，考查了二次函数的性质，相似三角形的判定和性质，灵活运用相似三角形的性质是本题的关键．2．在平面直角坐标系xOy 中，已知抛物线2y ax bx c =++与x 轴交于(1,0)A -，(4,0)B 两点，与y 轴交于点(0,2)C -．（1）求抛物线的函数表达式；（2）如图1，点D 为第四象限抛物线上一点，连接AD ，BC 交于点E ，连接BD ，记BDE ∆的面积为1S ，ABE ∆的面积为2S ，求12S S 的最大值；（3）如图2，连接AC ，BC ，过点O 作直线//l BC ，点P ，Q 分别为直线l 和抛物线上的点．试探究：在第一象限是否存在这样的点P ，Q ，使PQB CAB ∆∆∽．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．【分析】（1）设抛物线的解析式为(1)(4)y a x x =--，将点C 的坐标代入可求得a 的值，从而得到抛物线的解析式；（2）过点D 作DG x ⊥轴于点G ，交BC 于点F ，过点A 作AK x ⊥轴交BC 的延长线于点K ，证明AKE DFE ∆∆∽，得出DF DE AK AE =，则12BDE ABE S S DE DF S S AE AK∆∆===，求出直线BC 的解析式为122y x =-，设213(,2)22D m m m --，则1(,2)2F m m -，可得出12S S 的关系式，由二次函数的性质可得出结论；（3）设1(P a ，12a ，①当点P 在直线BQ 右侧时，如图2，过点P 作PN x ⊥轴于点N ，过点Q 作QM ⊥直线PN 于点M ，得出13(4Q a ，12)a -，将点Q 的坐标代入抛物线的解析式求得a 的值即可，②当点P 在直线BQ 左侧时，由①的方法同理可得点Q 的坐标为15(4a ，2)，代入抛物线的解析可得出答案．【解答】解：（1）设抛物线的解析式为(1)(4)y a x x =+-．将(0,2)C -代入得：42a =，解得12a =，∴抛物线的解析式为1(1)(4)2y x x =+-，即213222y x x =--．（2）过点D 作DG x ⊥轴于点G ，交BC 于点F ，过点A 作AK x ⊥轴交BC 的延长线于点K，//AK DG ∴，AKE DFE ∴∆∆∽，∴DF DE AK AE=，∴12BDE ABE S S DE DF S S AE AK ∆∆===，设直线BC 的解析式为1y kx b =+，∴11402k b b +=⎧⎨=-⎩，解得1122k b ⎧=⎪⎨⎪=-⎩，∴直线BC 的解析式为122y x =-，(1,0)A - ，15222y ∴=--=-，52AK ∴=，设213(,2)22D m m m --，则1(,2)2F m m -，2211312222222DF m m m m m ∴=--++=-+．∴222121214142(2)555552m m S m m m S -+==-+=--+．∴当2m =时，12S S 有最大值，最大值是45．（3）符合条件的点P 的坐标为6834(,99或63()55++．//l BC ，∴直线l 的解析式为12y x =，设1(P a ，1)2a ，①当点P 在直线BQ 右侧时，如图2，过点P 作PN x ⊥轴于点N ，过点Q 作QM ⊥直线PN 于点M ，(1,0)A - ，(0,2)C -，(4,0)B ，5AC ∴=5AB =，5BC =，222AC BC AB += ，90ACB ∴∠=︒，PQB CAB ∆∆ ∽，∴12PQ AC PB BC ==，90QMP BNP ∠=∠=︒ ，90MQP MPQ ∴∠+∠=︒，90MPQ BPN ∠+∠=︒，MQP BPN ∴∠=∠，QPM PBN ∴∆∆∽，∴12QM PM PQ PN BN PB ===，14a QM ∴=，1111(4)222PM a a =-=-，12MN a ∴=-，1134444a BN QM a a -=--=-，13(4Q a ∴，12)a -，将点Q 的坐标代入抛物线的解析式得21111333()222424a a a ⨯-⨯-=-，解得10a =（舍去）或1689a =．6834(,)99P ∴．②当点P 在直线BQ 左侧时，由①的方法同理可得点Q 的坐标为15(4a ，2)．此时点P 的坐标为63()55++．【点评】本题是二次函数综合题，考查了待定系数法求一次函数和二次函数的解析式，相似三角形的性质和判定，勾股定理的应用，二次函数的性质，三角形的面积等知识，熟练掌握相似三角形的判定与性质是解题的关键．3．在平面直角坐标系xOy 中，把与x 轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线2113:222L y x x =--的顶点为D ，交x 轴于点A 、B （点A 在点B 左侧），交y 轴于点C ．抛物线2L 与1L 是“共根抛物线”，其顶点为P ．（1）若抛物线2L 经过点(2,12)-，求2L 对应的函数表达式；（2）当BP CP -的值最大时，求点P 的坐标；（3）设点Q 是抛物线1L 上的一个动点，且位于其对称轴的右侧．若DPQ ∆与ABC ∆相似，求其“共根抛物线”2L 的顶点P 的坐标．【分析】（1）由题意设抛物线2L 的解析式为(1)(4)y a x x =+-，利用待定系数法求出a 即可解决问题．（2）由题意BP AP =，如图1中，当A ，C ，P 共线时，BP PC -的值最大，此时点P 为直线AC 与直线32x =的交点．（3）由题意，顶点3(2D ，258-，PDQ ∠不可能是直角，第一种情形：当90DPQ ∠=︒时，①如图31-中，当QDP ABC ∆∆∽时．②如图32-中，当DQP ABC ∆∆∽时．第二种情形：当90DQP ∠=︒．①如图33-中，。

正方形中的几何综合正向思维：是一类常规性的、传统的思维形式，指的是大家按照自上而下，由近及远、从左到右、从可知到未知等一般而言的线性方向做出探究问题的思维途径。

逆向思维：是指在剖析、破解数学难题进程中，可以灵活转换思维方向，从常规思维的相反方向出发进行探索的思维方式，比如正向思维无法解决问题时可反其道而行采取逆向思维，直接证明有困难时可采用间接证明。

分类讨论思想：当问题所给的对象不能进行统一研究时，我们就需要对研究对象进行分类，然后对每一类分别进行研究，得出每一类的结论，最后综合各类的结果，得到整个问题的解答。

分类讨论的分类并非是随心所欲的，而是要遵循以下基本原则：1. 不重（互斥性）不漏（完备性）；2. 按同一标准划分（同一性）；3. 逐级分类（逐级性）。

一、正方形的定义有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．二、正方形的性质1．正方形的四条边都相等，四个角都是直角；2．正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；3．正方形具有四边形、平行四边形、矩形、菱形的一切性质；4．两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．三、正方形的判定1．先判定四边形是矩形，再判定这个矩形有一组邻边相等；2．先判定四边形是菱形，再判定这个菱形有一个角为直角；3．还可以先判定四边形是平行四边形，再用1或2进行判定．【典例1】问题背景：如图1，在正方形ABCD 中，点E 、F 分别在边BC 、CD 上，∠EAF =45°，（1）求证：EF =BE +DF ；（2）迁移应用：如图2，在正方形ABCD 中，QA 、QB 交CD 于点G 、H ，若∠AQB =45°，CH =3，GH =1，求AG 的长；（3）联系拓展：如图3，在矩形ABCD 中，点E 、F 分别在边BC 、CD 上，∠EAF =45°，若DF:AD:AB =1:2:4，探究BE 与EC 的数量关系，并给出证明．（1）先判断出RtΔABE≅RtΔADP (SAS)，得出AE =AP ，∠BAE =∠DAP ，再判断出△AEF≌△APF (AAS)，即可得出结论；（2）先判断出ΔABM≌ΔBCH (ASA)，得出CH =3=BM ，设DG =a ，则GM =a +3，CM =a +1，再根据勾股定理得出(a +3)2=42+(a +1)2，求出a =1，即可得出结论；（3）先判断出四边形AMND 是正方形，设DF =m ，得出AD =2m =DN ，再设BE =2x ，则FT =x +m ，利用勾股定理得出2x =43m ，即可得出结论．（1）证明：延长FD 到点P 使DP =BE ，连接AP ，∵正方形ABCD ，∴AB =AD ，∠ADP =∠ABE =90°，在Rt △ABE 和Rt △ADP 中，AB =AD ∠ABE =∠ADP BE =DP，∴Rt △ABE≌Rt △ADP (SAS)，∴AE =AP ，∠BAE =∠DAP ，∵∠DAE +∠BAE =90°，∴∠DAE +∠DAP =90°，∵∠EAF =45°，∴∠EAF =∠FAP =45°，在△AEF 和ΔAPF 中，AE =AP ∠EAF =∠FAP AF =AF，∴△AEF≌△APF (SAS)，∴EF =PF ，∵DP =BE ，∴EF =BE +DF ；（2）如图2，过点A 作AM ⊥BH 交BC 于M ，交BH 于I ，连接GM ，∴∠BAM +∠ABI =90°，∵∠ABI +∠CBH =90°，∴∠BAM =∠CBH ，∵∠ABM =∠C =90°，AB =BC，∴△ABM≌△BCH(ASA)，∴CH=3=BM，∵∠Q=45°，∴∠QAM=45°，由（1）知，GM=BM+DG，设DG=a，∴GM=BM+DG=a+3，∵BC=CD=a+4，∴CM=a+4―3=a+1，在Rt△MCG中，GM2=GC2+CM2，∴(a+3)2=42+(a+1)2，∴a=2，∴DG=2，在Rt△ADG中，根据勾股定理得，AG==（3）BE=2EC，证明：如图3，分别取AB，AE的中点M，T，连接MT并延长MT交CD于N，连接TF，BE，∴MT∥BE，MT=12∴∠AMN=90°=∠DAM=∠D，∴四边形AMND是正方形，∵DF:AD:AB=1:2:4，设DF=m，∴AD=2m=DN，∴矩形AMND是正方形，∵∠EAF=45°，∴由（1）知，FT =DF +TM ，∵MT =12BE ，设BE =2x ，∴FT =DF +TM =x +m ，在Rt △FTN 中，FT 2=FN 2+TN 2，∴(x +m )2=m 2+(2m ―x )2，∴2x =43m ，∴BE =43m ， ∴EC =BC ―BE =23m ， ∴BE =2EC ．1．（23-24九年级上·河南郑州·阶段练习）如图，在△ABC 中，AC =6，BC =8，AB =10．分别以AB 、AC 、BC 为边在AB 的同侧作正方形ABEF 、ACPQ 、BCMN ，四块阴影部分的面积分别为S 1、S 2、S 3、S 4．则S 1―2S 2―3S 3+4S 4等于（ ）A ． 66B ． 56C ． 24D ． 122．（23-24九年级下·湖南邵阳·阶段练习）如图，在正方形ABCD 中，E 是对角线BD 上一点，且满足BE =BC ．连接CE ，并延长交AD 于点F ，连接AE ，过B 点作BG ⊥AE 于点G ，延长BG 交AD 于点H ．在下列结论中：①BH 垂直平分AE ；②AH =DF ；③DF =DE ；④∠AEF =45°；⑤S 四边形EFHG =S △DEF +S △AGH ，其中正确的结论有（ ）个．A ．2B ．3C ．4D ．53．（23-24九年级下·江苏无锡·阶段练习）如图，在正方形ABCD中，AB=4，对角线AC上的有一动点P，以DP为边作正方形DPFG．下列结论：①在P点运动过程中，F点始终在射线BC上；②在P点运动过程中，∠CPD可能为135°；③若E是DC的中点，连接EG，则EG④△CDP为等腰三角形时，AP的值为4．其中结论正确的是（）A．①②③B．①③④C．①③D．②④4．（22-23八年级下·辽宁铁岭·阶段练习）如图，E是正方形ABCD外一点，连接AE、BE、DE，AF⊥AE交DE于点F，若AE=AF=2，BF=①△AFD≌△AEB；②BE⊥DE：③四边形AEBF的面积是2+④点B到直线AE⑤AB2=16+）A．4个B．3个C．2个D．1个5．（2023·江苏南通·二模）如图，在边长为4的正方形ABCD中，点E为边BC的中点，点F为边AB上的动点，以EF为一边在EF的右上方作等边三角形FEG，当CG最小时，△ECG的周长为．6．（23-24九年级上·辽宁丹东·期末）如图，正方形ABCD，点E是射线AB上的动点，过点E作EF∥DB，交直线AD于点F，连接DE，取DE中点G，连接FG并延长交直线DB于点H，若AB=4，EB=3，则FH的长为．7．（2024·山东临沂·二模）如图，已知四边形ABCD为正方形，E为对角线AC上一点，连接DE，过点E作EF⊥DE，交BC的延长线于点F，以DE，EF为邻边作矩形DEFG，连接CG．下列结论：①矩形DEFG是正方形；②CE+CG=；③CG平分∠DCF；④CE=CF．其中正确的是（填序号）．8．（2024八年级下·山东·专题练习）如图，现有边长为4的正方形纸片ABCD，点P为AD边上的一点(不与点A点D重合）将正方形纸片沿EF折叠，使点B落在P处，点C落在G处，PG交DC于H，连结BP、BH，下列结论：①BP=EF；②当P为AD中点时，△PAE三边之比为3:4:5；③∠APB=∠BPH；④△PDH周长等于8．其中正确的是（写出所有正确结论的序号）9．（2024·浙江杭州·ABCD中，P是对角线BD所在直线上一点．若P在对角线BD上（如图1），连接PC，过点P作PQ⊥CP交AB于点Q．若PD=AB=6，则BQ的长为；若P在BD的延长线上（如图2），连接AP，过点P作PE⊥AP交BC延长线于点E，连接DE，若CE=8，△DPE 的面积是20，则PE的长为．10．（23-24八年级下·重庆开州·阶段练习）如图，四边形ABCD是正方形，AB=6．（1）如图1，点M在边BC上（不与端点B、C重合），点N在对角线AC上，且MN⊥AC，连接AM，点G是AM 的中点，连接DN、NG．①若BM=2，求NG的长；②求证：DN=；（2）如图2，点E、F分别为AB、BC边上的点，且BE=CF，请直接写出AF+CE的最小值．11．（23-24九年级上·广东广州·期中）已知正方形ABCD，E为平面内任意一点，连接DE，将线段DE绕点D 顺时针旋转90°得到线段DG，连接EC，AG．（1）如图，当点E在正方形ABCD内部时，补全图形，判断AG与CE的关系，并写出证明过程；（2）当点B，D，G在一条直线上时，若AD=4，DG=CE的长．12．（22-23九年级下·广东汕头·期中）如图，Rt△CEF中，∠C=90°，∠CEF，∠CFE外角平分线交于点A，过点A分别作直线CE，CF的垂线，B，D为垂足．（1）∠EAF=______（直接写出结果不写解答过程）；（2）①求证：四边形ABCD是正方形；②试说明EF=BE+DF，若AB=6，求(BE+6)(DF+6)的值．13．（22-23八年级下·浙江台州·期末）如图1，在正方形ABCD中，点E是线段CD上任意一点（不含端点），点F在射线BE上，且CF=CB，连接DF，过点D作DH⊥DF交BE于点H，连接CH．（1）①若∠EBC=20°，求∠DFB的度数；②试判断∠DFB的度数是否变化？请说明理由；若不变，请求出它的度数；（2）若BC=5，当CH∥DF时，求CH的长度；（3）如图2，当CH⊥BF时，求证：DE=CE．14．（23-24九年级上·江苏南京·开学考试）如图，P是正方形ABCD的边CD右侧一点，CP=CD，∠PCD为锐角，连接PB，PD．（1）如图①，若PD=PC，求∠BPD的度数；（2）如图②，作CE平分∠PCD交PB于E．①∠BEC的度数是___°；②探究PD，BE，CE之间的数量关系，并证明．15．（23-24九年级上·湖北武汉·阶段练习）如图1，正方形ABCD中，点E、F分别是边BC、CD上的点，∠BAD=2∠EAF，（1）请你直接写出BE、DF、EF之间的数量关系：___________．（2）如图2，在四边形ABCD中，AB=AD，∠BAD与∠BCD互补，点E、F分别是边BC、CD上的点，∠BAD=2∠EAF，请问：（1）中结论是否成立？若成立，请证明结论；若不成立，请说明理由；（3）在（1）的条件下，若E、F分别在直线BC和直线CD上，若BE=2，AB=5，则EF=___________．16．（2023·辽宁营口·一模）如图1，在正方形ABCD的BC边的延长线上取点G，以CG为边作正方形CGFE，连接AF，取AF的中点M，连接DM，EM．（1）请说明线段DM，EM的关系，不必说理；（2）如图2，把正方形CGFE绕点C顺时针旋转，当点G在BC上时，（1）中结论是否仍然成立？若成立，请说明理由；（3）在旋转过程中，当D，E，F三点在一条直线上时，若AB=13，CE=5，请直接写出MF的长．17．（22-23八年级下·湖北武汉·期中）已知正方形ABCD中，等腰直角△BEG绕着点B旋转．（1）如图1，若E点落在边AD上，BG交DC于H，直接写出AE，CH，EH的数量关系；（2）如图2，连DG，取DG中点F，连EF、CF，试探究EF与CF的关系：（3）若E点落在直线DC上，且CE:DE=1:2，连接CG，AG，直接写出CG:AG=______．18．（22-23八年级下·重庆铜梁·期末）在正方形ABCD中，E为直线AB上一点．（1）如图1，E在AB延长线上，F为对角线BD上一点，连接EF，AF，CF，若EF=CF，求∠EFC度数；（2）如图2，E在AB边上，连接DE，点H在BC边上且BH=2AE，过点H作HQ⊥DE，垂足为Q，延长HQ交AD于点G，连接AQ．求证：EQ+GQ=；（3）如图3，E在AB边上运动，连接DE，取DE中点M．点N在CD边上运动，连接BN，将△BCN沿着BN 翻折到同一平面内得到△BC′N．当点M与点C′重合时，直接写出CN的值．AE19．（23-24八年级下·江苏盐城·阶段练习）正方形ABCD中，点E在边BC、CD上运动（不与正方形顶点重合），作射线AE，将射线AE绕点A逆时针旋转45°，交射线CD于点F．（1）如图，当点E在边BC上时，①若BE=DF，则图中与线段AE相等的线段是________．②过点E作EG⊥AF，垂足为G，连接DG，求∠GDC的度数．③求证：在②的条件下，AB+BE=．（2）当点E在边CD上，点F在边CD延长线上时，仍过点E作EG⊥AF于点G，再过点G作GN⊥EF于点N，连的值．接DG，若DF=DG，求ENGN20．（23-24八年级下·江苏宿迁·期中）问题提出：（1）如图1，在正方形ABCD中，E为边BC上一点（不与点B，C重合），垂直于AE的一条直线MN分别交AB，AE，CD于点M，P，N．判断线段DN，MB，EC之间的数量关系，并说明理由；问题探究：（2）在（1）的基础上，解答下列问题：①如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ并延长，交边AD于点F，求∠AEF的度数；②如图③，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P′处．若正方形ABCD的边长为4，AD的中点为S，求P′S的最小值．。

中考数学复习----《正方形的性质》知识点总结与专项练习题（含答案解析）知识点总结1.正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形2.正方形的性质：①具有平行四边形的一切性质。

②具有矩形与菱形的一切性质。

所以正方形的四条边都相等，四个角都是直角。

对角线相互平分且相等，且垂直，且平分每一组对角，把正方形分成了四个全等的等腰直角三角形。

正方形既是中心对称图形，也是轴对称图形。

对角线交点是对称中心，对角线所在直线是对称轴，过每一组对边中点的直线也是对称轴。

练习题1．（2022•黄石）如图，正方形OABC的边长为，将正方形OABC绕原点O顺时针旋转45°，则点B的对应点B1的坐标为（）A．（﹣2，0）B．（2，0）C．（0，2）D．（0，2）【分析】连接OB，由正方形的性质和勾股定理得OB＝2，再由旋转的性质得B1在y轴正半轴上，且OB1＝OB＝2，即可得出结论．【解答】解：如图，连接OB，∵正方形OABC的边长为，∴OC＝BC＝，∠BCO＝90°，∠BOC＝45°，∴OB＝＝＝2，∵将正方形OABC绕原点O顺时针旋转45°后点B旋转到B1的位置，∴B 1在y 轴正半轴上，且OB 1＝OB ＝2，∴点B 1的坐标为（0，2），故选：D ．2．（2022•广州）如图，正方形ABCD 的面积为3，点E 在边CD 上，且CE ＝1，∠ABE 的平分线交AD 于点F ，点M ，N 分别是BE ，BF 的中点，则MN 的长为（ ）A ．26B ．23C ．2﹣3D ．226− 【分析】连接EF ，由正方形ABCD 的面积为3，CE ＝1，可得DE ＝﹣1，tan ∠EBC ＝＝＝，即得∠EBC ＝30°，又AF 平分∠ABE ，可得∠ABF ＝∠ABE ＝30°，故AF ＝＝1，DF ＝AD ﹣AF ＝﹣1，可知EF ＝DE ＝×（﹣1）＝﹣，而M ，N 分别是BE ，BF 的中点，即得MN ＝EF ＝． 【解答】解：连接EF ，如图：∵正方形ABCD 的面积为3，∴AB ＝BC ＝CD ＝AD ＝，∵CE ＝1，∴DE＝﹣1，tan∠EBC＝＝＝，∴∠EBC＝30°，∴∠ABE＝∠ABC﹣∠EBC＝60°，∵AF平分∠ABE，∴∠ABF＝∠ABE＝30°，在Rt△ABF中，AF＝＝1，∴DF＝AD﹣AF＝﹣1，∴DE＝DF，△DEF是等腰直角三角形，∴EF＝DE＝×（﹣1）＝﹣，∵M，N分别是BE，BF的中点，∴MN是△BEF的中位线，∴MN＝EF＝．故选：D．3．（2022•贵阳）如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形．若图中的直角三角形的两条直角边的长分别为1和3，则中间小正方形的周长是（）A．4B．8C．12D．16【分析】根据题意和题目中的数据，可以计算出小正方形的边长，然后即可得到小正方形的周长．【解答】解：由题意可得，小正方形的边长为3﹣1＝2，∴小正方形的周长为2×4＝8，故选：B．4．（2022•青岛）如图，O为正方形ABCD对角线AC的中点，△ACE为等边三角形．若AB＝2，则OE 的长度为（ ）A ．26B ．6C ．22D ．23【分析】首先利用正方形的性质可以求出AC ，然后利用等边三角形的性质可求出OE ．【解答】解：∵四边形ABCD 为正方形，AB ＝2，∴AC ＝2，∵O 为正方形ABCD 对角线AC 的中点，△ACE 为等边三角形，∴∠AOE ＝90°，∴AC ＝AE ＝2，AO ＝，∴OE ＝×＝． 故选：B ．5．（2022•泰州）如图，正方形ABCD 的边长为2，E 为与点D 不重合的动点，以DE 为一边作正方形DEFG ．设DE ＝d 1，点F 、G 与点C 的距离分别为d 2、d 3，则d 1+d 2+d 3的最小值为（ ）A ．2B ．2C ．22D ．4【分析】连接AE ，那么，AE ＝CG ，所以这三个d 的和就是AE +EF +FC ，所以大于等于AC ，故当AEFC 四点共线有最小值，最后求解，即可求出答案．【解答】解：如图，连接AE ，∵四边形DEFG 是正方形，∴∠EDG ＝90°，EF ＝DE ＝DG ，∵四边形ABCD 是正方形，∴AD ＝CD ，∠ADC ＝90°，∴∠ADE ＝∠CDG ，∴△ADE ≌△CDG （SAS ），∴AE ＝CG ，∴d 1+d 2+d 3＝EF +CF +AE ，∴点A ，E ，F ，C 在同一条线上时，EF +CF +AE 最小，即d 1+d 2+d 3最小，连接AC ，∴d 1+d 2+d 3最小值为AC ，在Rt △ABC 中，AC ＝AB ＝2，∴d 1+d 2+d 3最小＝AC ＝2， 故选：C ．6．（2022•黔东南州）如图，在边长为2的等边三角形ABC 的外侧作正方形ABED ，过点D 作DF ⊥BC ，垂足为F ，则DF 的长为（ ）A ．23+2B ．5﹣33C ．3﹣3D ．3+1【分析】方法一：如图，延长DA 、BC 交于点G ，利用正方形性质和等边三角形性质可得：∠BAG ＝90°，AB ＝2，∠ABC ＝60°，运用解直角三角形可得AG ＝2，DG ＝2+2，再求得∠G ＝30°，根据直角三角形性质得出答案．方法二：过点E 作EG ⊥DF 于点G ，作EH ⊥BC 于点H ，利用解直角三角形可得EH ＝1，BH ＝，再证明△BEH ≌△DEG ，可得DG ＝BH ＝，即可求得答案．【解答】解：方法一：如图，延长DA、BC交于点G，∵四边形ABED是正方形，∴∠BAD＝90°，AD＝AB，∴∠BAG＝180°﹣90°＝90°，∵△ABC是边长为2的等边三角形，∴AB＝2，∠ABC＝60°，∴AG＝AB•tan∠ABC＝2×tan60°＝2，∴DG＝AD+AG＝2+2，∵∠G＝90°﹣60°＝30°，DF⊥BC，∴DF＝DG＝×（2+2）＝1+，故选D．方法二：如图，过点E作EG⊥DF于点G，作EH⊥BC于点H，则∠BHE＝∠DGE＝90°，∵△ABC是边长为2的等边三角形，∴AB＝2，∠ABC＝60°，∵四边形ABED是正方形，∴BE＝DE＝2，∠ABE＝∠BED＝90°，∴∠EBH＝180°﹣∠ABC﹣∠ABE＝180°﹣60°﹣90°＝30°，∴EH＝BE•sin∠EBH＝2•sin30°＝2×＝1，BH＝BE•cos∠EBH＝2cos30°＝，∵EG⊥DF，EH⊥BC，DF⊥BC，∴∠EGF＝∠EHB＝∠DFH＝90°，∴四边形EGFH是矩形，∴FG＝EH＝1，∠BEH+∠BEG＝∠GEH＝90°，∵∠DEG+∠BEG＝90°，∴∠BEH＝∠DEG，在△BEH和△DEG中，，∴△BEH≌△DEG（AAS），∴DG＝BH＝，∴DF＝DG+FG＝+1，故选：D．7．（2022•随州）七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点，AP⊥EF分别交BD，EF于O，P两点，M，N分别为BO，DO的中点，连接MP，NF，沿图中实线剪开即可得到一副七巧板．则在剪开之前，关于该图形，下列说法正确的有（）①图中的三角形都是等腰直角三角形；②四边形MPEB是菱形；③四边形PFDM的面积占正方形ABCD面积的．A．只有①B．①②C．①③D．②③【分析】①利用正方形的性质和中位线的性质可以解决问题；②利用①的结论可以证明OM≠MP解决问题；③如图，过M作MG⊥BC于G，设AB＝BC＝x，利用正方形的性质与中位线的性质分别求出BE和MG即可判定是否正确．【解答】解：①如图，∵E，F分别为BC，CD的中点，∴EF为△CBD的中位线，∴EF∥BD，∵AP⊥EF，∴AP⊥BD，∵四边形ABCD为正方形，∴A、O、P、C在同一条直线上，∴△ABC、△ACD、△ABD、△BCD、△OAB、△OAD、△OBC、△OCD、△EFC都是等腰直角三角形，∵M，N分别为BO，DO的中点，∴MP∥BC，NF∥OC，∴△DNF、△OMP也是等腰直角三角形．故①正确；②根据①得OM＝BM＝PM，∴BM≠PM∴四边形MPEB不可能是菱形．故②错误；③∵E，F分别为BC，CD的中点，∴EF∥BD，EF＝BD，∵四边形ABCD是正方形，且设AB＝BC＝x，∴BD＝x，∵AP⊥EF，∴AP⊥BD，∴BO＝OD，∴点P在AC上，∴PE＝EF，∴PE＝BM，∴四边形BMPE是平行四边形，∴BO＝BD，∵M为BO的中点，∴BM＝BD＝x，∵E为BC的中点，∴BE＝BC＝x，过M作MG⊥BC于G，∴MG＝BM＝x，∴四边形BMPE的面积＝BE•MG＝x2，∴四边形BMPE的面积占正方形ABCD面积的．∵E、F是BC，CD的中点，∴S△CEF＝S△CBD＝S四边形ABCD，∴四边形PFDM的面积占正方形ABCD面积的（1﹣﹣﹣）＝．故③正确．故选：C．8．（2022•宁波）将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内，其中矩形纸片和正方形纸片的周长相等．若知道图中阴影部分的面积，则一定能求出（）A．正方形纸片的面积B．四边形EFGH的面积C．△BEF的面积D．△AEH的面积【分析】根据题意设PD＝x，GH＝y，则PH＝x﹣y，根据矩形纸片和正方形纸片的周长相等，可得AP＝x+y，先用面积差表示图中阴影部分的面积，并化简，再用字母分别表示出图形四个选项的面积，可得出正确的选项．【解答】解：设PD＝x，GH＝y，则PH＝x﹣y，∵矩形纸片和正方形纸片的周长相等，∴2AP+2（x﹣y）＝4x，∴AP＝x+y，∵图中阴影部分的面积＝S矩形ABCD﹣2△ADH﹣2S△AEB＝（2x+y）（2x﹣y）﹣2ו（x﹣y）（2x+y）﹣2ו（2x﹣y）•x＝4x2﹣y2﹣（2x2+xy﹣2xy﹣y2）﹣（2x2﹣xy）＝4x2﹣y2﹣2x2+xy+y2﹣2x2+xy＝2xy，A、正方形纸片的面积＝x2，故A不符合题意；B、四边形EFGH的面积＝y2，故B不符合题意；C、△BEF的面积＝•EF•BQ＝xy，故C符合题意；D、△AEH的面积＝•EH•AM＝y（x﹣y）＝xy﹣y2，故D不符合题意；故选：C．9．（2022•重庆）如图，在正方形ABCD中，AE平分∠BAC交BC于点E，点F是边AB上一点，连接DF，若BE＝AF，则∠CDF的度数为（）A．45°B．60°C．67.5°D．77.5°【分析】根据正方形的性质和全等三角形的判定和性质，可以得到∠ADF的度数，从而可以求得∠CDF的度数．【解答】解：∵四边形ABCD是正方形，∴AD＝BA，∠DAF＝∠ABE＝90°，在△DAF和△ABE中，，△DAF≌△ABE（SAS），∠ADF＝∠BAE，∵AE平分∠BAC，四边形ABCD是正方形，∴∠BAE＝∠BAC＝22.5°，∠ADC＝90°，∴∠ADF＝22.5°，∴∠CDF＝∠ADC﹣∠ADF＝90°﹣22.5°＝67.5°，故选：C．10．（2022•重庆）如图，在正方形ABCD中，对角线AC、BD相交于点O．E、F分别为AC、BD上一点，且OE＝OF，连接AF，BE，EF．若∠AFE＝25°，则∠CBE的度数为（）A．50°B．55°C．65°D．70°【分析】利用正方形的对角线互相垂直平分且相等，等腰直角三角形的性质，三角形的内角和定理和全等三角形的判定与性质解答即可．【解答】解：∵四边形ABCD是正方形，∴∠AOB＝∠AOD＝90°，OA＝OB＝OD＝OC．∵OE＝OF，∴△OEF为等腰直角三角形，∴∠OEF＝∠OFE＝45°，∵∠AFE＝25°，∴∠AFO＝∠AFE+∠OFE＝70°，∴∠F AO＝20°．在△AOF和△BOE中，，∴△AOF ≌△BOE （SAS ）．∴∠F AO ＝∠EBO ＝20°，∵OB ＝OC ，∴△OBC 是等腰直角三角形，∴∠OBC ＝∠OCB ＝45°，∴∠CBE ＝∠EBO +∠OBC ＝65°．故选：C ．11．（2022•益阳）如图，将边长为3的正方形ABCD 沿其对角线AC 平移，使A 的对应点A ′满足AA ′＝31AC ，则所得正方形与原正方形重叠部分的面积是 ．【分析】由正方形边长为3，可求AC ＝3，则AA ′＝AC ＝，由平移可得重叠部分是正方形，根据正方形的面积公式可求重叠部分面积．【解答】解：∵正方形ABCD 的边长为3，∴AC ＝3，∴AA ′＝AC ＝， ∴A ′C ＝2，由题意可得重叠部分是正方形，且边长为2，∴S 重叠部分＝4．故答案为：4．12．（2022•海南）如图，正方形ABCD 中，点E 、F 分别在边BC 、CD 上，AE ＝AF ，∠EAF ＝30°，则∠AEB ＝ °；若△AEF 的面积等于1，则AB 的值是 ．【分析】利用“HL”先说明△ABE与△ADF全等，得结论∠BAE＝∠DAF，再利用角的和差关系及三角形的内角和定理求出∠AEB；先利用三角形的面积求出AE，再利用直角三角形的边角间关系求出AB．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠B＝∠D＝90°．在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL）．∴∠BAE＝∠DAF．∴∠BAE＝（∠BAD﹣∠EAF）＝（90°﹣30°）＝30°．∴∠AEB＝60°．故答案为：60．过点F作FG⊥AE，垂足为G．∵sin∠EAF＝，∴FG＝sin∠EAF×AF．∵S△AEF＝×AE×FG＝×AE×AF×sin∠EAF＝1，∴×AE2×sin30°＝1．即×AE2×＝1．∴AE＝2．在Rt△ABE中，∵cos∠BAE＝，∴AB＝cos30°×AE＝×2＝．故答案为：．13．（2022•广西）如图，在正方形ABCD中，AB＝42，对角线AC，BD相交于点O．点E是对角线AC上一点，连接BE，过点E作EF⊥BE，分别交CD，BD于点F，G，连接BF，交AC于点H，将△EFH沿EF翻折，点H的对应点H′恰好落在BD上，得到△EFH′．若点F为CD的中点，则△EGH′的周长是．【分析】作辅助线，构建全等三角形，先根据翻折的性质得△EGH'≌△EGH，所以△EGH′的周长＝△EGH的周长，接下来计算△EGH的三边即可；证明△BME≌△FNE（ASA）和△BEO≌△EFP（AAS），得OE＝PF＝2，OB＝EP＝4，利用三角函数和勾股定理分别计算EG，GH和EH的长，相加可得结论．【解答】解：如图，过点E作EM⊥BC于M，作EN⊥CD于N，过点F作FP⊥AC于P，连接GH，∵将△EFH沿EF翻折得到△EFH′，∴△EGH'≌△EGH，∵四边形ABCD是正方形，∴AB＝CD＝BC＝4，∠BCD＝90°，∠ACD＝∠ACB＝45°，∴BD＝BC＝8，△CPF是等腰直角三角形，∵F是CD的中点，∴CF＝CD＝2，∴CP＝PF＝2，OB＝BD＝4，∵∠ACD＝∠ACB，EM⊥BC，EN⊥CD，∴EM＝EN，∠EMC＝∠ENC＝∠BCD＝90°，∴∠MEN＝90°，∵EF⊥BE，∴∠BEF＝90°，∴∠BEM＝∠FEN，∵∠BME＝∠FNE，∴△BME≌△FNE（ASA），∴EB＝EF，∵∠BEO+∠PEF＝∠PEF+∠EFP＝90°，∴∠BEO＝∠EFP，∵∠BOE＝∠EPF＝90°，∴△BEO≌△EFP（AAS），∴OE＝PF＝2，OB＝EP＝4，∵tan∠OEG＝＝，即＝，∴OG＝1，∴EG＝＝，∵OB∥FP，∴∠OBH＝∠PFH，∴tan∠OBH＝tan∠PFH，∴＝，∴＝＝2，∴OH＝2PH，∵OP＝OC﹣PC＝4﹣2＝2，∴OH＝×2＝，在Rt△OGH中，由勾股定理得：GH＝＝，∴△EGH′的周长＝△EGH的周长＝EH+EG+GH＝2+++＝5+．故答案为：5+．14．（2022•无锡）如图，正方形ABCD的边长为8，点E是CD的中点，HG垂直平分AE 且分别交AE、BC于点H、G，则BG＝．【分析】设CG＝x，则BG＝8﹣x，根据勾股定理可得AB2+BG2＝CE2+CG2，可求得x 的值，进而求出BG的长．【解答】解：连接AG，EG，∵E是CD的中点，∴DE＝CE＝4，设CG＝x，则BG＝8﹣x，在Rt△ABG和Rt△GCE中，根据勾股定理，得AB2+BG2＝CE2+CG2，即82+（8﹣x）2＝42+x2，解得x＝7，∴BG＝BC﹣CG＝8﹣7＝1．故答案是：1．15．（2022•江西）沐沐用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的对角线长为．【分析】根据图形可得长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，然后利用勾股定理即可解决问题．【解答】解：根据图形可知：长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，则长方形的对角线长＝＝．故答案为：．。

二十二正方形1.正方形具有而菱形不一定有的性质是 (B)A.四边相等B.对角线相等C.对角线平分一组对角D.对角线垂直2.如图,四边形ABCD的对角线AC,BD相交于点O,下列条件中,能判定四边形ABCD是正方形的是(C)A.AC=BC=CD=DAB.AO=CO,BO=DO,AC⊥BDC.AO=BO=CO=DO,AC⊥BDD.AB=BC,CD⊥DA2题图3题图3.如图,直线l上方有三个正方形a,b,c,且正方形a和c的一边在直线l上,正方形b的一个顶点在直线l上,有两个顶点分别与a和c的一个顶点重合.若a,c的面积分别为5和11,则b 的面积为(B)A.6B.16C.41D.554.由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为2的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分),则图中AB的长应是(A)A.2√2-2B.√3-1C.1D.√25.将图1中两个三角形按图2所示的方式摆放,其中四边形ABCD为矩形,连接PQ,甲、乙两人有如下结论:甲:若四边形ABCD是边长为1的正方形,则四边形PQMN必是正方形;乙:若四边形PQMN为正方形,则四边形ABCD必是边长为1的正方形.下列判断正确的是(D)A.甲正确,乙不正确B.甲不正确,乙正确C.甲、乙都不正确D.甲、乙都正确6.如图,正方形ABCD中,点E,F分别在BC,CD上,连接AE,BF,请添加一个条件:BE=CF(答案不唯一),使△ABE≌△BCF.6题图8题图7.我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α-β|,于是|α-β|越小,菱形越接近正方形.①若菱形的一个内角为80°,则该菱形的“接近度”为20;②当菱形的“接近度”等于0时,菱形是正方形.8.现有一张边长等于a(a>16)的正方形纸片,从距离正方形的四个顶点8 cm处,沿45°角画线,将正方形纸片分成5部分,则阴影部分是正方形(填写图形的形状)(如图),它的一边长是8√2 cm.9.如图,三个边长均为√2的正方形重叠在一起,M,N是其中两个正方形对角线的交点,则两个阴影部分面积之和是1.10.如图,△ABC中∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC.求证:四边形CFDE为正方形.【证明】∵∠ACB=90°,DE⊥BC,DF⊥AC,∴四边形CFDE是矩形.又∵CD平分∠ACB,DE⊥BC,DF⊥AC,∴DE=DF.∴四边形CFDE是正方形.11.如图,延长平行四边形ABCD的边DC到E,使CE=CD,连接AE交BC于点F.(1)求证:△ABF≌△ECF;(2)若AE=AD,连接BE,当线段OF与BD满足怎样的数量关系时,四边形ABEC是正方形?请说明理由.【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠ABF=∠ECF,∠BAF=∠CEF,∵CE=DC.∴AB=CE.∴△ABF≌△ECF.(2)当线段OF与BD满足BD=2√5OF时,四边形ABEC是正方形,理由如下:∵AB∥CD,AB=CE,∴四边形ABEC是平行四边形.又AE=AD,DC=CE.∴AC⊥DE.∴∠ACE=90°.∴平行四边形ABEC是矩形.∴∠BED=90°.令OF=x,则BD=2√5x,∵OF是△BCD的中位线,∴CD=2OF=2x,∴DE=4x.∴BE=√BD2-DE2=2x.∴BE=CE.∴四边形ABEC是正方形.∴当线段OF与BD满足BD=2√5OF时,四边形ABEC是正方形.。

2020年中考数学二轮专项冲刺复习——几何综合、压轴题1、（2019河南•中考第22题•10分）在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是1，直线BD与直线CP相交所成的较小角的度数是60°．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．【考点】相似形综合题．【分析】（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．证明△CAP≌△BAD（SAS），即可解决问题．（2）如图2中，设BD交AC于点O，BD交PC于点E．证明△DAB∽△P AC，即可解决问题．（3）分两种情形：①如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．证明AD＝DC即可解决问题．②如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC解决问题．【解答】解：（1）如图1中，延长CP交BD的延长线于E，设AB交EC于点O．∵∠P AD＝∠CAB＝60°，∴∠CAP＝∠BAD，∵CA＝BA，P A＝DA，∴△CAP≌△BAD（SAS），∴PC＝BD，∠ACP＝∠ABD，∵∠AOC＝∠BOE，∴∠BEO＝∠CAO＝60°，∴＝1，线BD与直线CP相交所成的较小角的度数是60°，故答案为1，60°．（2）如图2中，设BD交AC于点O，BD交PC于点E．∵∠P AD＝∠CAB＝45°，∴∠P AC＝∠DAB，∵＝＝，∴△DAB∽△P AC，∴∠PCA＝∠DBA，＝＝，∵∠EOC＝∠AOB，∴∠CEO＝∠OABB＝45°，∴直线BD与直线CP相交所成的小角的度数为45°．（3）如图3﹣1中，当点D在线段PC上时，延长AD交BC的延长线于H．∵CE＝EA，CF＝FB，∴EF∥AB，∴∠EFC＝∠ABC＝45°，∵∠P AO＝45°，∴∠P AO＝∠OFH，∵∠POA＝∠FOH，∴∠H＝∠APO，∵∠APC＝90°，EA＝EC，∴PE＝EA＝EC，∴∠EP A＝∠EAP＝∠BAH，∴∠H＝∠BAH，∴BH＝BA，∵∠ADP＝∠BDC＝45°，∴∠ADB＝90°，∴BD⊥AH，∴∠DBA＝∠DBC＝22.5°，∵∠ADB＝∠ACB＝90°，∴A，D，C，B四点共圆，∠DAC＝∠DBC＝22.5°，∠DCA＝∠ABD＝22.5°，∴∠DAC＝∠DCA＝22.5°，∴DA＝DC，设AD＝a，则DC＝AD＝a，PD＝a，∴＝＝2﹣．如图3﹣2中，当点P在线段CD上时，同法可证：DA＝DC，设AD＝a，则CD＝AD＝a，PD＝a，∴PC＝a﹣a，∴＝＝2+．2、（2019陕西•中考第22题•9分）在图1，2，3中，已知ABCDY，120ABC∠=︒，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且120EAG∠=︒．（1）如图1，当点E与点B重合时，CEF∠=60︒；（2）如图2，连接AF．①填空：FAD∠EAB∠（填“>”，“<“，“=”)；②求证：点F在ABC∠的平分线上；（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求BCAB的值．【考点】相似形综合题【分析】（1）根据菱形的性质计算；（2）①证明60DAB FAE∠=∠=︒，根据角的运算解答；②作FM BC⊥于M，FN BA⊥交BA的延长线于N，证明AFN EFM∆≅∆，根据全等三角形的性质得到FN FM=，根据角平分线的判定定理证明结论；（3）根据直角三角形的性质得到2GH AH=，证明四边形ABEH为菱形，根据菱形的性质计算，得到答案．【解答】解：（1）Q四边形AEFG是菱形，18060AEF EAG∴∠=︒-∠=︒，60CEF AEC AEF∴∠=∠-∠=︒，故答案为：60︒；（2）①Q四边形ABCD是平行四边形，18060DAB ABC ∴∠=︒-∠=︒，Q 四边形AEFG 是菱形，120EAG ∠=︒，60FAE ∴∠=︒，FAD EAB ∴∠=∠，故答案为：=；②作FM BC ⊥于M ，FN BA ⊥交BA 的延长线于N ，则90FNB FMB ∠=∠=︒，60NFM ∴∠=︒，又60AFE ∠=︒，AFN EFM ∴∠=∠，EF EA =Q ，60FAE ∠=︒，AEF ∴∆为等边三角形，FA FE ∴=，在AFN ∆和EFM ∆中，AFN EFM FNA FME FA FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFN EFM AAS ∴∆≅∆，FN FM ∴=，又FM BC ⊥，FN BA ⊥，∴点F 在ABC ∠的平分线上；（3）Q 四边形AEFG 是菱形，120EAG ∠=︒，60AGF ∴∠=︒，30FGE AGE ∴∠=∠=︒，Q 四边形AEGH 为平行四边形，//GE AH ∴，30GAH AGE ∴∠=∠=︒，30H FGE ∠=∠=︒，90GAH ∴∠=︒，又30AGE ∠=︒，2GH AH ∴=，60DAB ∠=︒Q ，30H ∠=︒，30ADH ∴∠=︒，AD AH GE ∴==，Q 四边形ABEH 为平行四边形，BC AD ∴=，BC GE ∴=，Q 四边形ABEH 为平行四边形，30HAE EAB ∠=∠=︒，∴平行四边形ABEH 为菱形，AB AH HE ∴==，3GE AB ∴=， ∴3BC AB=．3、（2019上海•中考 第22题•10分）图1是某小型汽车的侧面示意图，其中矩形ABCD 表示该车的后备箱，在打开后备箱的过程中，箱盖ADE 可以绕点A 逆时针方向旋转，当旋转角为60︒时，箱盖ADE 落在AD E ''的位置（如图2所示）．已知90AD =厘米，30DE =厘米，40EC =厘米．（1）求点D '到BC 的距离；（2）求E 、E '两点的距离．【考点】解直角三角形的应用；矩形的性质【分析】（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，利用旋转的性质可得出90AD AD '==厘米，60DAD ∠'=︒，利用矩形的性质可得出90AFD BHD ∠'=∠'=︒，在Rt △AD F '中，通过解直角三角形可求出D F '的长，结合FH DC DE CE ==+及D H D F FH '='+可求出点D '到BC 的距离；（2）连接AE ，AE '，EE '，利用旋转的性质可得出AE AE '=，60EAE ∠'=︒，进而可得出AEE ∆'是等边三角形，利用等边三角形的性质可得出EE AE '=，在Rt ADE ∆中，利用勾股定理可求出AE 的长度，结合EE AE '=可得出E 、E '两点的距离．【解答】解：（1）过点D '作D H BC '⊥，垂足为点H ，交AD 于点F ，如图3所示．由题意，得：90AD AD '==厘米，60DAD ∠'=︒．Q 四边形ABCD 是矩形，//AD BC ∴，90∴∠'=∠'=︒．AFD BHD在Rt△AD F'中，sin90sin60453g厘米．D F AD DAD'='∠'=⨯︒=又40Q厘米，30DE=厘米，CE=∴==+=厘米，FH DC DE CE70∴'='+=+厘米．D H D F FH(45370)答：点D'到BC的距离为(45370)+厘米．（2）连接AE，AE'，EE'，如图4所示．由题意，得：AE AE'=，60∠'=︒，EAE∴∆'是等边三角形，AEE∴'=．EE AEQ四边形ABCD是矩形，90∴∠=︒．ADE在Rt ADEDE=厘米，AD=厘米，30∆中，90223010∴=+=厘米，AE AD DE∴'=厘米．EE3010答：E、E'两点的距离是3010厘米．4、（2019河南•中考第17题•9分）如图，在△ABC中，BA＝BC，∠ABC＝90°，以AB为直径的半圆O交AC于点D，点E是上不与点B，D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC于点G．（1）求证：△ADF≌△BDG；（2）填空：①若AB＝4，且点E是的中点，则DF的长为4﹣2；②取的中点H，当∠EAB的度数为30°时，四边形OBEH为菱形．【考点】圆的综合题．【分析】（1）利用直径所对的圆周角是直角，可得∠ADB＝∠AEB＝90°，再应用同角的余角相等可得∠DAF＝∠DBG，易得AD＝BD，△ADF≌△BDG得证；（2）作FH⊥AB，应用等弧所对的圆周角相等得∠BAE＝∠DAE，再应用角平分线性质可得结论；由菱形的性质可得BE＝OB，结合三角函数特殊值可得∠EAB＝30°．【解答】解：（1）证明：如图1，∵BA＝BC，∠ABC＝90°，∴∠BAC＝45°∵AB是⊙O的直径，∴∠ADB＝∠AEB＝90°，∴∠DAF+∠BGD＝∠DBG+∠BGD＝90°∴∠DAF＝∠DBG∵∠ABD+∠BAC＝90°∴∠ABD＝∠BAC＝45°∴AD＝BD∴△ADF≌△BDG（ASA）；（2）①如图2，过F作FH⊥AB于H，∵点E是的中点，∴∠BAE＝∠DAE∵FD⊥AD，FH⊥AB∴FH＝FD∵＝sin∠ABD＝sin45°＝，∴，即BF＝FD∵AB＝4，∴BD＝4cos45°＝2，即BF+FD＝2，（+1）FD＝2∴FD＝＝4﹣2故答案为．②连接OE，EH，∵点H是的中点，∴OH⊥AE，∵∠AEB＝90°∴BE⊥AE∴BE∥OH∵四边形OBEH为菱形，∴BE＝OH＝OB＝AB∴sin∠EAB＝＝∴∠EAB＝30°．故答案为：30°5、（2019河北•中考第23题•9分）如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．【考点】圆的综合题．【分析】（1）由条件易证△ABC≌△ADE，得∠BAC＝∠DAE，∴∠BAD＝∠CAE．（2）PD＝AD﹣AP＝6﹣x，∵点P在线段BC上且不与B、C重合，∴AP的最小值即AP⊥BC时AP的长度，此时PD可得最大值．（3）I为△APC的内心，即I为△APC角平分线的交点，应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC，从而得到m，n的值．【解答】解：（1）在△ABC和△ADE中，（如图1）∴△ABC≌△ADE（SAS）∴∠BAC＝∠DAE即∠BAD+∠DAC＝∠DAC+∠CAE∴∠BAD＝∠CAE．（2）∵AD＝6，AP＝x，∴PD＝6﹣x当AD⊥BC时，AP＝AB＝3最小，即PD＝6﹣3＝3为PD的最大值．（3）如图2，设∠BAP＝α，则∠APC＝α+30°，∵AB⊥AC∴∠BAC＝90°，∠PCA＝60°，∠P AC＝90°﹣α，∵I为△APC的内心∴AI、CI分别平分∠P AC，∠PCA，∴∠IAC＝∠P AC，∠ICA＝∠PCA∴∠AIC＝180°﹣（∠IAC+∠ICA）＝180°﹣（∠P AC+∠PCA）＝180°﹣（90°﹣α+60°）＝α+105°∵0＜α＜90°，∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，∴m＝105，n＝150．6、（2019海南•中考第21题•13分）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q．（1）求证：△PDE≌△QCE；（2）过点E作EF∥BC交PB于点F，连结AF，当PB＝PQ时，①求证：四边形AFEP是平行四边形；②请判断四边形AFEP是否为菱形，并说明理由．【考点】四边形综合题．【分析】（1）由四边形ABCD是正方形知∠D＝∠ECQ＝90°，由E是CD的中点知DE＝CE，结合∠DEP＝∠CEQ即可得证；（2）①由PB＝PQ知∠PBQ＝∠Q，结合AD∥BC得∠APB＝∠PBQ＝∠Q＝∠EPD，由△PDE≌△QCE知PE ＝QE，再由EF∥BQ知PF＝BF，根据Rt△P AB中AF＝PF＝BF知∠APF＝∠P AF，从而得∠P AF＝∠EPD，据此即可证得PE∥AF，从而得证；②设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，由PD2+DE2＝PE2得关于x的方程，解之求得x的值，从而得出四边形AFEP为菱形的情况．【解答】解：（1）∵四边形ABCD是正方形，∴∠D＝∠ECQ＝90°，∵E是CD的中点，∴DE＝CE，又∵∠DEP＝∠CEQ，∴△PDE≌△QCE（ASA）；（2）①∵PB＝PQ，∴∠PBQ＝∠Q，∵AD∥BC，∴∠APB＝∠PBQ＝∠Q＝∠EPD，∵△PDE≌△QCE，∴PE＝QE，∵EF∥BQ，∴PF＝BF，∴在Rt△P AB中，AF＝PF＝BF，∴∠APF＝∠P AF，∴∠P AF＝∠EPD，∴PE∥AF，∵EF∥BQ∥AD，∴四边形AFEP是平行四边形；②当AP＝时，四边形AFEP是菱形．设AP＝x，则PD＝1﹣x，若四边形AFEP是菱形，则PE＝P A＝x，∵CD＝1，E是CD中点，∴DE＝，在Rt△PDE中，由PD2+DE2＝PE2得（1﹣x）2+（）2＝x2，解得x＝，即当AP＝时，四边形AFEP是菱形．7、（2019福建•中考第21题•8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．【考点】平行四边形的判定；旋转的性质．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB ＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．8、（2019北京•中考第20题•5分）如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE＝DF，连接EF．（1）求证：AC⊥EF；（2）延长EF交CD的延长线于点G，连接BD交AC于点O．若BD＝4，tan G＝，求AO的长．【考点】全等三角形的判定与性质；菱形的性质；解直角三角形．【分析】（1）由菱形的性质得出AB＝AD，AC⊥BD，OB＝OD，得出AB：BE＝AD：DF，证出EF∥BD即可得出结论；（2）由平行线的性质得出∠G＝∠ADO，由三角函数得出tan G＝tan∠ADO＝＝，得出OA＝OD，由BD ＝4，得出OD＝2，得出OA＝1．【解答】（1）证明：连接BD，如图1所示：∵四边形ABCD是菱形，∴AB＝AD，AC⊥BD，OB＝OD，∵BE＝DF，∴AB：BE＝AD：DF，∴EF∥BD，∴AC⊥EF；（2）解：如图2所示：∵由（1）得：EF∥BD，∴∠G＝∠ADO，∴tan G＝tan∠ADO＝＝，∴OA＝OD，∵BD＝4，∴OD＝2，∴OA＝1．10、（2019北京•中考第27题•7分）已知∠AOB＝30°，H为射线OA上一定点，OH＝+1，P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON．（1）依题意补全图1；（2）求证：∠OMP＝∠OPN；（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON＝QP，并证明．【考点】三角形综合题．【分析】（1）根据题意画出图形．（2）由旋转可得∠MPN＝150°，故∠OPN＝150°﹣∠OPM；由∠AOB＝30°和三角形内角和180°可得∠OMP ＝180°﹣30°﹣∠OPM＝150°﹣∠OPM，得证．（3）根据题意画出图形，以ON＝QP为已知条件反推OP的长度．由（2）的结论∠OMP＝∠OPN联想到其补角相等，又因为旋转有PM＝PN，已具备一边一角相等，过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，即可构造出△PDM≌△NCP，进而得PD＝NC，DM＝CP．此时加上ON＝QP，则易证得△OCN≌△QDP，所以OC＝QD．利用∠AOB＝30°，设PD＝NC＝a，则OP＝2a，OD＝a．再设DM＝CP＝x，所以QD＝OC＝OP+PC ＝2a+x，MQ＝DM+QD＝2a+2x．由于点M、Q关于点H对称，即点H为MQ中点，故MH＝MQ＝a+x，DH ＝MH﹣DM＝a，所以OH＝OD+DH＝a+a＝+1，求得a＝1，故OP＝2．证明过程则把推理过程反过来，以OP＝2为条件，利用构造全等证得ON＝QP．【解答】解：（1）如图1所示为所求．（2）设∠OPM＝α，∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN＝150°，PM＝PN∴∠OPN＝∠MPN﹣∠OPM＝150°﹣α∵∠AOB＝30°∴∠OMP＝180°﹣∠AOB﹣∠OPM＝180°﹣30°﹣α＝150°﹣α∴∠OMP＝∠OPN（3）OP＝2时，总有ON＝QP，证明如下：过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，如图2∴∠NCP＝∠PDM＝∠PDQ＝90°∵∠AOB＝30°，OP＝2∴PD＝OP＝1∴OD＝∵OH＝+1∴DH＝OH﹣OD＝1∵∠OMP＝∠OPN∴180°﹣∠OMP＝180°﹣∠OPN即∠PMD＝∠NPC在△PDM与△NCP中∴△PDM≌△NCP（AAS）∴PD＝NC，DM＝CP设DM＝CP＝x，则OC＝OP+PC＝2+x，MH＝MD+DH＝x+1∵点M关于点H的对称点为Q∴HQ＝MH＝x+1∴DQ＝DH+HQ＝1+x+1＝2+x∴OC＝DQ在△OCN与△QDP中∴△OCN≌△QDP（SAS）∴ON＝QP11、（2019北京•中考第28题•7分）在△ABC中，D，E分别是△ABC两边的中点，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中内弧．例如，图1中是△ABC的一条中内弧．（1）如图2，在Rt△ABC中，AB＝AC＝，D，E分别是AB，AC的中点，画出△ABC的最长的中内弧，并直接写出此时的长；（2）在平面直角坐标系中，已知点A（0，2），B（0，0），C（4t，0）（t＞0），在△ABC中，D，E分别是AB，AC的中点．①若t＝，求△ABC的中内弧所在圆的圆心P的纵坐标的取值范围；②若在△ABC中存在一条中内弧，使得所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．【考点】圆的综合题．【分析】（1）由三角函数值及等腰直角三角形性质可求得DE＝2，最长中内弧即以DE为直径的半圆，的长即以DE为直径的圆周长的一半；（2）根据三角形中内弧定义可知，圆心一定在DE的中垂线上，①当t＝时，要注意圆心P在DE上方的中垂线上均符合要求，在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP＜135°；②根据题意，t的最大值即圆心P在AC上时求得的t值．【解答】解：（1）如图2，以DE为直径的半圆弧，就是△ABC的最长的中内弧，连接DE，∵∠A＝90°，AB＝AC＝，D，E分别是AB，AC的中点，∴BC＝＝＝4，DE＝BC＝×4＝2，∴弧＝×2π＝π；（2）如图3，由垂径定理可知，圆心一定在线段DE的垂直平分线上，连接DE，作DE垂直平分线FP，作EG ⊥AC交FP于G，①当t＝时，C（2，0），∴D（0，1），E（1，1），F（，1），设P（，m）由三角形中内弧定义可知，圆心线段DE上方射线FP上均可，∴m≥1，∵OA＝OC，∠AOC＝90°∴∠ACO＝45°，∵DE∥OC∴∠AED＝∠ACO＝45°作EG⊥AC交直线FP于G，FG＝EF＝根据三角形中内弧的定义可知，圆心在点G的下方（含点G）直线FP上时也符合要求；∴m≤综上所述，m≤或m≥1．②如图4，设圆心P在AC上，∵P在DE中垂线上，∴P为AE中点，作PM⊥OC于M，则PM＝，∴P（t，），∵DE∥BC∴∠ADE＝∠AOB＝90°∴AE＝＝＝，∵PD＝PE，∴∠AED＝∠PDE∵∠AED+∠DAE＝∠PDE+∠ADP＝90°，∴∠DAE＝∠ADP∴AP＝PD＝PE＝AE由三角形中内弧定义知，PD≤PM∴AE≤，AE≤3，即≤3，解得：t≤，∵t＞0∴0＜t≤．12、（2019安徽•中考第20题•10分）如图，点E在ABCDY内部，//AF BE，//DF CE．（1）求证：BCE ADF∆≅∆；（2）设ABCDY的面积为S，四边形AEDF的面积为T，求ST的值．【考点】全等三角形的判定与性质；平行四边形的性质【分析】（1）根据ASA 证明：BCE ADF ∆≅∆；（2）根据点E 在ABCD Y 内部，可知：12BEC AED ABCD S S S ∆∆+=Y ，可得结论． 【解答】解：（1）Q 四边形ABCD 是平行四边形，AD BC ∴=，//AD BC ，180ABC BAD ∴∠+∠=︒，//AF BE Q ，180EAB BAF ∴∠+∠=︒，CBE DAF ∴∠=∠，同理得BCE ADF ∠=∠，在BCE ∆和ADF ∆中，Q CBE DAF BC AD BCE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()BCE ADF ASA ∴∆≅∆；（2）Q 点E 在ABCD Y 内部，12BEC AED ABCD S S S ∆∆∴+=Y ， 由（1）知：BCE ADF ∆≅∆，BCE ADF S S ∆∆∴=，12ADF AED BEC AED ABCD AEDF S S S S S S ∆∆∆∆∴=+=+=Y 四边形， ABCD QY 的面积为S ，四边形AEDF 的面积为T ， ∴212S S T S ==． 13、如图，矩形ABCD 中，点E 在边CD 上，将BCE ∆沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作//FG CD 交BE 于点G ，连接CG ．（1）求证：四边形CEFG 是菱形；（2）若6AB =，10AD =，求四边形CEFG 的面积．【考点】LA：菱形的判定与性质；PB：翻折变换（折叠问题）；LB：矩形的性质【分析】（1）根据题意和翻着的性质，可以得到BCE BFE∆≅∆，再根据全等三角形的性质和菱形的判定方法即可证明结论成立；（2）根据题意和勾股定理，可以求得AF的长，进而求得EF和DF的值，从而可以得到四边形CEFG的面积．【解答】（1）证明：由题意可得，BCE BFE∆≅∆，BEC BEF∴∠=∠，FE CE=，//FG CEQ，FGE CEB∴∠=∠，FGE FEG∴∠=∠，FG FE∴=，FG EC∴=，∴四边形CEFG是平行四边形，又CE FE=Q，∴四边形CEFG是菱形；（2）Q矩形ABCD中，6AB=，10AD=，BC BF=，90BAF∴∠=︒，10AD BC BF===，8AF∴=，2DF∴=，设EF x=，则CE x=，6DE x=-，90FDE=︒Q，2222(6)x x∴+-=，解得，103x=，103CE∴=，∴四边形CEFG的面积是：1020233 CE DF=⨯=g．14、（2019成都•中考第27题•10分）如图1，在ABC∆中，20AB AC==，3tan4B=，点D为BC边上的动点（点D 不与点B ，C 重合）．以D 为顶点作ADE B ∠=∠，射线DE 交AC 边于点E ，过点A 作AF AD ⊥交射线DE 于点F ，连接CF ．（1）求证：ABD DCE ∆∆∽；（2）当//DE AB 时（如图2)，求AE 的长；（3）点D 在BC 边上运动的过程中，是否存在某个位置，使得DF CF =？若存在，求出此时BD 的长；若不存在，请说明理由．【考点】SO ：相似形综合题【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）解直角三角形求出BC ，由ABD CBA ∆∆∽，推出AB DB CB AB =，可得222025322AB DB CB ===，由//DE AB ，推出AE BD AC BC=，求出AE 即可． （3）点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =．作FH BC ⊥于H ，AM BC ⊥于M ，AN FH ⊥于N ．则90NHM AMH ANH ∠=∠=∠=︒，由AFN ADM ∆∆∽，可得3tan tan 4AN AF ADF B AM AD ==∠==，推出3312944AN AM ==⨯=，推出1697CH CM MH CM AN =-=-=-=，再利用等腰三角形的性质，求出CD 即可解决问题．【解答】（1）证明：AB AC =Q ，B ACB ∴∠=∠，ADE CDE B BAD ∠+∠=∠+∠Q ，ADE B ∠=∠，BAD CDE ∴∠=∠，BAD DCE ∴∆∆∽．（2）解：如图2中，作AM BC ⊥于M ．在Rt ABM∆中，设4BM k=，则3tan434AM BM B k k ==⨯=g，由勾股定理，得到222AB AM BM=+，22220(3)(4)k k∴=+，4k∴=或4-（舍弃），AB AC=Q，AM BC⊥，22432BC BM k∴===g，//DE ABQ，BAD ADE∴∠=∠，ADE B∠=∠Q，B ACB∠=∠，BAD ACB∴∠=∠，ABD CBA∠=∠Q，ABD CBA∴∆∆∽，∴AB DBCB AB=，222025322ABDBCB∴===，//DE ABQ，∴AE BDAC BC=，252012523216AC BDAEBC⨯∴===g．（3）点D在BC边上运动的过程中，存在某个位置，使得DF CF=．理由：作FH BC⊥于H，AM BC⊥于M，AN FH⊥于N．则90NHM AMH ANH∠=∠=∠=︒，∴四边形AMHN为矩形，90MAN∴∠=︒，MH AN=，AB AC=Q，AM BC⊥，11321622BM CM BC∴===⨯=，在Rt ABM ∆中，由勾股定理，得12AM ==， AN FH ⊥Q ，AM BC ⊥，90ANF AMD ∴∠=︒=∠，90DAF MAN ∠=︒=∠Q ，NAF MAD ∴∠=∠，AFN ADM ∴∆∆∽， ∴3tan tan 4AN AF ADF B AM AD ==∠==， 3312944AN AM ∴==⨯=， 1697CH CM MH CM AN ∴=-=-=-=， 当DF CF =时，由点D 不与点C 重合，可知DFC ∆为等腰三角形， FH DC ⊥Q ，214CD CH ∴==，321418BD BC CD ∴=-=-=，∴点D 在BC 边上运动的过程中，存在某个位置，使得DF CF =，此时18BD =．。

正方形问题1 如图，在边长为6的正方形ABCD的两侧作正方形BEFG和正方形DMNK，恰好使得N、A、F三点在一直线上，连接MF交线段AD于点P，连接NP，设正方形BEFG的边长为x，正方形DMNK的边长为y．（1）求y关于x的函数关系式及自变量x的取值范围；（2）当△NPF的面积为32时，求x的值；（3）以P为圆心，AP为半径的圆能否与以G为圆心，GF为半径的圆相切？如果能，请求出x的值，如果不能，请说明理由．解析：（1）∵正方形BEFG、正方形DMNK、正方形ABCD∴∠E＝∠F＝90O，AE∥MC，MC∥NK∴AE∥NK，∴∠KNA＝∠EAF∴△KNA∽△EAF，∴NKEA＝KAEF，即yx＋6＝y－6x∴y＝x＋6（0＜x≤6）（2）由（1）知NK＝AE，∴AN＝AF∵正方形DMNK，∴AP∥NM，∴FPPM＝AFAN＝1∴FP＝PM，∴S△MNP ＝S△NPF ＝32∴S正方形DMNK ＝2S△MNP ＝64∴y＝8，∴x＝2（3）连接PG，延长FG交AD于点H，则GH⊥AD易知：AP＝y2，AH＝x，PH＝y2－x，HG＝6；PG＝AP＋GF＝y2＋x①当两圆外切时在Rt△GHP中，PH2＋HG2＝PG2，即(y2－x)2＋62＝(y2＋x)2解得：x＝－3－33（舍去）或x＝－3＋3 3 ②当两圆内切时在Rt△GHP中，PH2＋HG2＝PG2，即(y2－x)2＋62＝(y2－x)2方程无解所以，当x＝33－3时，两圆相切N KGCEDFA BPM2 已知：正方形ABCD的边长为1，射线AE与射线BC交于点E，射线AF与射线CD交于点F，∠EAF ＝45°，连接EF．（1）如图1，当点E在线段BC上时，试猜想线段EF、BE、DF有怎样的数量关系？并证明你的猜想；（2）设BE＝x，DF＝y，当点E在线段BC上运动时（不包括点B、C），求y关于x的函数解析式，并指出x的取值范围；（3）当点E在射线BC上运动时（不含端点B），点F在射线CD上运动．试判断以E为圆心，以BE 为半径的⊙E和以F为圆心，以FD为半径的⊙F之间的位置关系；（4）如图2，当点E在BC的延长线上时，设AE与CD交于点G．问：△EGF与△EFA能否相似？若能相似，求出BE的长，若不可能相似，请说明理由．解析：（1）猜想：EF＝BE＋DF证明：将△ADF绕点A顺时针旋转90°，得△ABF′，易知点F′、B、E在同一直线上（如.图1）∵AF′＝AF∠F′AE＝∠1＋∠3＝∠2＋∠3＝90°－45°＝45°＝∠EAF又AE＝AE，∴△AF′E≌△AFE∴EF＝F′E＝BE＋BF＝BE＋DF（2）在Rt△EFC中，EC2＋FC2＝EF2∵EC＝1－x，FC＝1－y，EF＝x＋y∴(1－x)2＋(1－y)2＝(x＋y)2∴y＝1－x1＋x（0＜x＜1）A BDCEF图1ABDC EFG图2ABDCEF图1F′12（3）①当点E 在点B 、C 之间时，由（1）知EF ＝BE ＋DF ，故此时⊙E 与⊙F 外切； ②当点E 在点C 时，DF ＝0，⊙F 不存在.③当点E 在BC 延长线上时，将△ADF 绕点A 顺时针旋转90°，得△ABF′（如图2） 则AF′＝AF ，∠1＝∠2，B F′＝DF ，∠F ′AF ＝90° ∴∠F ′AE ＝∠EAF ＝45° 又AE ＝AE ，∴△AF ′E ≌△AFE ∴EF ＝EF′＝BE －B F′＝BE －DF ∴此时⊙E 与⊙F 内切综上所述，当点E 在线段BC 上时，⊙E 与⊙F 外切；当点E 在BC 延长线上时，⊙E 与⊙F 内切 （4）△EGF 与△EFA 能够相似，只要当∠EFG ＝∠EAF ＝45° 即可 此时CE ＝CF设BE ＝x ，DF ＝y ，由（3）知EF ＝x －y 在Rt △CFE 中，CE 2＋CF 2＝EF 2∴( x －1 )2＋( 1＋y )2＝( x －y )2∴y ＝ x －1x ＋1 （x ＞1）由CE ＝CF ，得x －1＝1＋y ，即x －1＝1＋ x －1x ＋1化简得x 2－2x －1＝0，解得x 1＝1－ 2（舍去），x 2＝1＋ 2 ∴△EGF 与△EFA 能够相似，此时BE 的长为1＋ 23 已知：如图，在直角梯形ABCD 中，AD ∥BC ，∠B ＝90°，AD ＝2，BC ＝6，AB ＝3．E 为BC 边上一点，以BE 为边作正方形BEFG ，使正方形BEFG 和梯形ABCD 在BC 的同侧． （1）当正方形的顶点F 恰好落在对角线AC 上时，求BE 的长；（2）将（1）问中的正方形BEFG 沿BC 向右平移，记平移中的正方形BEFG 为正方形B′EFG ，当点E 与点C 重合时停止平移．设平移的距离为t ，正方形B′EFG 的边EF 与AC 交于点M ，连接B′D ，B′M ，DM ．是否存在这样的t ，使△B′DM 是直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）在（2）问的平移过程中，设正方形B′EFG 与△ADC 重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式以及自变量t 的取值范围．A D A DABD CEF G图2F ′12解析：（1）如图①，设正方形BEFG的边长为x 则BE＝FG＝BG＝x∵AB＝3，BC＝6，∴AG＝AB－BG＝3－x∵GF∥BE，∴△AGF∽△ABC∴AGAB＝GFBC，即3－x3＝x6解得x＝2，即BE＝2（2）存在满足条件的t，理由如下：如图②，过D作DH⊥BC于点H则BH＝AD＝2，DH＝AB＝3由题意得：BB′＝HE＝t，HB′＝|t－2|，EC＝4－t在Rt△B′ME中，B′M2＝B′E2＋ME2＝22＋(2－12t)2＝14t2－2t＋8∵EF∥AB，∴△MEC∽△ABC∴MEAB＝ECBC，即ME3＝4－t6，∴ME＝2－12t在Rt△DHB′中，B′D2＝DH2＋B′H2＝32＋(t－2)2＝t2－4t＋13 过M作MN⊥DH于点N则MN＝HE＝t，NH＝ME＝2－12t∴DN＝DH－NH＝3－(2－12t)＝12t＋1在Rt△DMN中，DM2＝DN2＋MN2＝54t2＋t＋1（ⅰ）若∠DB′M＝90°，则DM2＝B′M2＋B′D2即54t2＋t＋1＝(14t2－2t＋8)＋(t2－4t＋13)，解得t＝207（ⅱ）若∠B′MD＝90°，则B′D2＝B′M2＋DM2即t2－4t＋13＝(14t2－2t＋8)＋(54t2＋t＋1)，解得t1＝－3＋17，t2＝－3－17∵0≤t≤4，∴t＝－3＋17BACD图①EFGBACD图②EFGH B′MN（ⅲ）若∠B′DM＝90°，则B′M2＝B′D2＋DM2即14t2－2t＋8＝(t2－4t＋13)＋(54t2＋t＋1)，此方程无解综上所述，当t＝207或－3＋17时，△B′DM是直角三角形（3）当0≤t≤43时，S＝14t2当43≤t≤2时，S＝－18t2＋t－23当2≤t≤103时，S＝－38t2＋2t－53当103≤t≤4时，S＝－12t＋52提示：当点F落在CD上时，如图③FE＝2，EC＝4－t，DH＝3，HC＝4由△FEC∽△DHC，得FEEC＝DHHC即24－t＝34，∴t＝43当点G落在AC上时，点G也在DH上（即DH与AC的交点）t＝2当点G落在CD上时，如图④GB′＝2，B′C＝6－t由△GB′C∽△DHC，得G′BB′C＝DHHC即26－t＝34，∴t＝103当点E与点C重合时，t＝4①当0≤t≤43时，如图⑤∵MF＝t，FN＝12t∴S＝S△FMN＝12·t·12t＝14t2②当43≤t≤2时，如图⑥∵PF＝t－43，FQ＝34PF＝34t－1BC图⑤EBC图⑥EBACD图③EFGB′HBACD图④EFGB′H∴S△FPQ＝12(t－43)(34t－1)＝38t2－t＋23∴S＝S△FMN－S△FPQ＝14t2－(38t2－t＋23)＝－18t2＋t－23③当2≤t≤103时，如图⑦∵B′M＝12B′C＝12(6－t)＝3－12t∴GM＝2－(3－12t)＝12t－1∴S梯形GMNF＝12(12t－1＋12t)×2＝t－1∴S＝S梯形GMNF－S△FPQ＝(t－1)－(38t2－t＋23)＝－38t2＋2t－53④当103≤t≤4时，如图⑧∵P B′＝34B′C＝34(6－t)＝92－34t∴GP＝2－(92－34t)＝34t－52∴S梯形GPQF＝12(34t－52＋34t－1)×2＝32t－72∴S＝S梯形GMNF－S梯形GPQF＝(t－1)－(32t－72)＝－12t＋52BC图⑦EB C图⑧EB。

中考数学总复习《正方形》专项提升训练（带答案)学校:___________班级：___________姓名：___________考号：___________ 1. 如图，在四边形ABCD中，对角线AC，BD相交于点O .第1题图(1)若四边形ABCD是平行四边形，请添加条件__________，使四边形ABCD是正方形；【判定依据】__________________________；(2)若四边形ABCD是矩形，请添加一个条件________，使四边形ABCD是正方形；【判定依据】__________________________；(3)若四边形ABCD是菱形，请添加一个条件________，使四边形ABCD是正方形；【判定依据】__________________________．2. 如图，在正方形ABCD中，对角线AC，BD相交于点O.(1)∠ABC＝________，∠BAC＝________，∠COD＝________；(2)若AB＝3，则BC＝________，CD＝________；(3)若OA＝2，则AC＝________，BD＝________，AD＝________；(4)若OA＝4，则正方形ABCD 的面积是________，周长是________．第2题图知识逐点过考点1 正方形的性质及面积边四条边都相等，对边平行角四个角都是直角1.对角线相等且互相①________；对角线2．每一条对角线平分一组对角对称性既是轴对称图形，又是中心对称图形，有4条对称轴，对称中心是两条②________的交点面积公式S＝a2＝12l2【温馨提示】正方形的两条对角线把正方形分成四个全等的等腰直角三角形考点2 正方形的判定边1.有一组邻边相等，并且有一个角是③________的平行四边形是正方形(定义)；2．有一组邻边④________的矩形是正方形角有一个角是⑤________的菱形是正方形对角线1.对角线⑥________的矩形是正方形；2．对角线⑦________的菱形是正方形；3．对角线互相⑧__________的四边形是正方形考点3 平行四边形、矩形、菱形、正方形的关系从边、角的角度看从对角线的角度看考点4 中点四边形概念依次连接任意一个四边形各边中点所得的四边形原图形任意四边形矩形菱形正方形对角线相等的四边形对角线垂直的四边形对角线垂直且相等的四边形中点四边形形状平行四边形菱形矩形正方形菱形矩形正方形【温馨提示】连接特殊四边形中点的四边形面积是原图形的一半教材原题到重难考法与正方形有关的证明与计算例如图，在正方形ABCD中，点F为对角线AC上一点，连接BF，DF.你能找出图中的全等三角形吗？选择其中一对进行证明．例题图变式题1. 结合角度求线段长如图，正方形ABCD的边长为4，点F为对角线AC上一点，连接BF，当∠CBF＝22.5°时求AF的长．第1题图2. 过点F作AB边的垂线如图，在正方形ABCD中，F是对角线AC上一点，作EF⊥AB于点E，连接DF，若BC＝6，BE＝2，求DF的长．第2题图3. 过点F分别作AB，BC边的垂线如图，F是正方形ABCD对角线AC上一点，过点F分别作FE⊥AB，FG⊥BC，垂足分别为点E，G，连接DF，EG.(1)求证：EG＝DF；(2)若正方形的边长为3＋3，∠BGE＝30°，求DF的长．第3题图真题演练命题点正方形性质的相关计算1. 如图，正方形ABCD的边长为4，延长CB至点E使EB＝2，以EB为边在上方作正方形EFGB，延长FG交DC于M，连接AM，AF，H为AD的中点，连接FH分别与AB，AM交于点N，K .则下列结论：①△ANH≌△GNF；②∠AFN＝∠HFG；③FN＝2NK；④S△AFN∶S△ADM ＝1∶4.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个第1题图2. 边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上(如图)，则图中阴影部分的面积为________．第2题图基础过关1. 正方形具有而菱形不具有的性质是()A. 对角线平分一组对角B. 对角线相等C. 对角线互相垂直平分D. 四条边相等2. 若顺次连接四边形ABCD各边的中点所得的四边形是正方形，则四边形ABCD的两条对角线AC，BD一定是()A. 互相平分B. 互相垂直C. 互相平分且相等D. 互相垂直且相等3.如图，边长为3的正方形OBCD两边与坐标轴正半轴重合，点C的坐标是()A. (3，－3)B. (－3，3)C. (3，3)D. (－3，－3)第3题图4. 如图，在正方形ABCD中，点E，F分别在BC，CD上，连接AE，AF，EF，∠EAF＝45°.若∠BAE＝α，则∠FEC一定等于()A. 2αB. 90°－2αC. 45°－αD. 90°－α第4题图5.在矩形ABCD中，对角线AC，BD相交于点O，试添加一个条件_________________________ 使得矩形ABCD为正方形．6. 如图，在边长为2的正方形ABCD中，点E在AD上，连接EB，EC，则图中阴影部分的面积是__________．第6题图7. 七巧板是我国民间广为流传的一种益智玩具，某同学用边长为4 dm的正方形纸板制作了一副七巧板，如图所示，由5个等腰直角三角形，1个正方形和1个平行四边形组成，则图中阴影部分的面积为__________dm2.第7题图8. 如图，点P是正方形ABCD的对角线AC上的一点，PE⊥AD于点E，PE＝3.则点P到直线AB的距离为__________．第8题图9. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝7，点F为DE的中点，若△CEF的周长为32，则OF的长为__________．第9题图10. 如图，在正方形ABCD中，E为AD上一点，连接BE，BE的垂直平分线交AB于点M，交CD于点N，垂足为O，点F在DC上，且MF∥AD.(1)求证：△ABE≌△FMN；(2)若AB＝8，AE＝6，求ON的长．第10题图综合提升11. 如图，点E在正方形ABCD的对角线AC上，EF⊥AB于点F，连接DE并延长，交边BC于点M，交边AB的延长线于点G.若AF＝2，FB＝1，则MG＝()A. 23B. 352 C. 5＋1 D. 10第11题图12. 如图，在正方形ABCD 中，点E 为BD 上一点，DE ＝3BE ，连接AE ，过点E 作AE 的垂线，交CD 于点F ，连接AF 交BD 于点G .下列结论：①sin ∠BAE ＝13 ；②∠EAF ＝45°；③点F 为CD 的中点；④BE ＋DG ＝GE .其中正确的有( ) A. 1个 B. 2个 C. 3个 D. 4个第12题图13. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形(△DAE ，△ABF ，△BCG ，△CDH )和中间一个小正方形EFGH 拼成的大正方形ABCD 中，∠ABF >∠BAF ，连接BE .设∠BAF ＝α，∠BEF ＝β，若正方形EFGH 与正方形ABCD 的面积之比为1∶n ，tan α＝tan 2β，则n ＝( ) A. 5 B. 4 C. 3 D. 2第13题图参考答案1. (1)AC ＝BD ，且AC ⊥BD (答案不唯一)；【判定依据】对角线互相垂直且相等的平行四边形是正方形(答案不唯一)； (2)AC ⊥BD (答案不唯一)；【判定依据】对角线互相垂直的矩形是正方形； (3)∠ABC ＝90°(答案不唯一)【判定依据】有一个角是直角的菱形是正方形．2. (1)90°，45°，90°；(2)3，3；(3)4，4，22 ；(4)32，162 . 教材原题到重难考法例 解：△ABC ≌△ADC ，△ABF ≌△ADF ，△CDF ≌△CBF ，理由如下： ∵四边形ABCD 是正方形∴AB ＝AD ＝BC ＝CD ，∠DAC ＝∠BAC ＝∠DCA ＝∠BCA ＝45° 在△ABC 和△ADC 中 ⎩⎪⎨⎪⎧AB ＝AD ∠BAC ＝∠DAC AC ＝AC∴△ABC ≌△ADC (SAS) 在△ABF 和△ADF 中 ⎩⎪⎨⎪⎧AB ＝AD ∠BAF ＝∠DAF AF ＝AF∴△ABF ≌△ADF (SAS) 在△DCF 和△BCF 中 ⎩⎪⎨⎪⎧DC ＝BC ∠DCF ＝∠BCF CF ＝CF∴△DCF ≌△BCF (SAS).(选择其中任意一对证明即可) 1. 解：在正方形ABCD 中，∠ABC ＝90°，AB ＝BC ∴∠BAC ＝∠BCA ＝45° ∵∠CBF ＝22.5°∴∠ABF ＝∠ABC －∠CBF ＝90°－22.5°＝67.5°∴∠AFB ＝180°－∠BAC －∠ABF ＝180°－45°－67.5°＝67.5° ∴∠ABF ＝∠AFB ∴AF ＝AB ＝4.2. 解：如解图，连接BF第2题解图∵四边形ABCD是正方形∴AB＝BC＝6，∠EAF＝45°∵EF⊥AB∴EF＝AE＝AB－BE＝6－2＝4∴BF＝BE2＋EF2＝25∵正方形ABCD关于AC对称∴DF＝BF＝25.3. (1)证明：如解图，连接FB.∵四边形ABCD为正方形∴DA＝AB，∠DAC＝∠BAC∵AF＝AF∴△DAF≌△BAF∴DF＝BF∵四边形ABCD为正方形∴∠ABC＝90°∵FG⊥BC，FE⊥AB∴∠FGB＝∠FEB＝90°∴∠FGB＝∠FEB＝∠ABC＝90°∴四边形FEBG是矩形∴EG＝FB∴EG＝DF；(2)解：∵正方形的边长为3＋3，∠BGE＝30°∴BC＝3＋3∴BG＝BC－CG＝3＋3－CG∵∠BGE＝30°∴BG＝3BE∵AC为正方形ABCD的对角线∴∠DCF＝∠BCF＝45°∵FG⊥BC∴∠FGC＝∠FGB＝90°∴∠CFG＝45°∴FG＝CG∵四边形FEBG是矩形∴EB＝FG∴FG＝CG＝EB设FG＝CG＝EB＝x∴GE＝2x∴BG＝3BE＝3x∵BG＝BC－CG＝3＋3－x∴3＋3－x＝3x∴x＝3∴GE＝2x＝23∴DF＝BF＝GE＝23.第3题解图知识逐点过①垂直平分②对角线③直角④相等⑤直角⑥互相垂直⑦相等⑧垂直平分且相等真题演练1. C 【解析】∵四边形EFGB 是正方形，EB ＝2，∴FG ＝BE ＝2，∠FGB ＝90°，∵四边形ABCD 是正方形，H 为AD 的中点，∴AD ＝4，AH ＝2，∠BAD ＝90°，∴∠HAN ＝∠FGN ，AH ＝FG ，∵∠ANH ＝∠GNF ，∴△ANH ≌△GNF (AAS)，故①正确；∴∠AHN ＝∠HFG ，∵AG ＝FG ＝2＝AH ，∴AF ＝2 FG ＝2 AH ，∴∠AFH ≠∠AHF ，∵AD ∥FG ，∴∠AHF ＝∠HFG ，∴∠AFN ≠∠HFG ，故②错误；∵△ANH ≌△GNF ，∴AN ＝12 AG ＝1，∵GM＝BC ＝4，∴AH AN ＝GM AG＝2，∵∠HAN ＝∠AGM ＝90°，∴△AHN ∽△GMA ，∴∠AHN ＝∠AMG ，∠MAG ＝∠HNA ，∴AK ＝NK ，∵AD ∥GM ，∴∠HAK ＝∠AMG ，∴∠AHK ＝∠HAK ，∴AK ＝HK ，∴AK ＝HK ＝NK ，∵FN ＝HN ，∴FN ＝2NK ；故③正确；∵延长FG 交DC 于M ，∴四边形ADMG 是矩形，∴DM ＝AG ＝2，∵S △AFN ＝12 AN ·FG ＝12 ×2×1＝1，S △ADM＝12 AD ·DM ＝12×4×2＝4，∴S △AFN ∶S △ADM ＝1∶4，故④正确． 2. 15 【解析】如解图，∵四边形ABCD ，ECGF ，IGHK 均为正方形，∴CD ＝AD ＝10，CE ＝FG ＝CG ＝EF ＝6，∠CEF ＝∠F ＝90°，GH ＝IK ＝4，∴CH ＝CG ＋GH ＝10，∴CH ＝AD ，∵∠D ＝∠DCH ＝90°，∠AJD ＝∠HJC ，∴△ADJ ≌△HCJ (AAS)，∴CJ ＝DJ ＝5，∴EJ ＝1，∵GL ∥CJ ，∴△HGL ∽△HCJ ，∴GL CJ ＝GH CH ＝25，∴GL ＝2，∴FL ＝4，∴S阴影＝S梯形EJLF＝12 (EJ ＋FL )·EF ＝12(1＋4)×6＝15.第2题解图基础过关1. B2. D 【解析】如解图，点E ，F ，G ，H 分别为AB ，BC ，CD ，DA 的中点，则EH ∥DB ∥GF ，HG ∥AC ∥EF ，EF ＝12 AC ，FG ＝12 BD ，∴四边形EFGH 为平行四边形．要使其为正方形，即EF ⊥FG ，FE ＝FG ，则AC ⊥BD ，AC ＝BD ，即对角线一定互相垂直且相等．第2题解图3. C 【解析】 ∵边长为3的正方形OBCD 两边与坐标轴正半轴重合，∴OB ＝BC ＝3，∴C (3，3).4. A 【解析】如解图，将△ADF 绕点A 顺时针旋转90°得到△ABG ，则AF ＝AG ，∠DAF ＝∠BAG .∵∠EAF ＝45°，∴∠BAE ＋∠DAF ＝45°，∴∠GAE ＝∠EAF ＝45°.在△GAE 和△F AE 中，⎩⎪⎨⎪⎧AG ＝AF ∠GAE ＝∠F AE AE ＝AE ，∴△GAE ≌△F AE (SAS)，∴∠AEF ＝∠AEG .∵∠BAE ＝α，∴∠AEB ＝90°－α，∴∠AEF ＝∠AEB ＝90°－α，∴∠FEC ＝180°－∠AEF －∠AEB ＝180°－2(90°－α)＝2α.第4题解图5. AB ＝BC (答案不唯一，符合条件即可，如：AC ⊥BD ) 【解析】∵邻边相等的矩形是正方形，∴可添加条件AB ＝BC ；∵对角线互相垂直的矩形是正方形，∴还可以添加条件AC ⊥BD .6. 2 【解析】如解图，过点E 作EF ⊥BC 于点F .∵四边形ABCD 是正方形，∴AB ＝BC ＝2，AD ∥BC ，∴EF ＝AB ＝2，∴S △BCE ＝12 BC ·EF ＝12×2×2＝2.∵S 正方形ABCD ＝BC 2＝22＝4，∴S阴影＝S 正方形ABCD －S △BCE ＝4－2＝2.第6题解图7. 2 【解析】如解图，依题意得OD ＝22 AD ＝22 ，OE ＝12OD ＝2 ，∴图中阴影部分的面积为OE 2＝(2 )2＝2(dm 2).第7题解图8. 3 【解析】如解图，过点P 作PF ⊥AB 于点F .∵四边形ABCD 是正方形，AC 是对角线，∴∠DAC ＝∠BAC .∵PE ⊥AD ，PF ⊥AB ，∴PE ＝PF .∵PE ＝3，∴点P 到直线AB 的距离为PF ＝3.第8题解图9.172【解析】∵CE ＝7，△CEF 的周长为32，∴CF ＋EF ＝32－7＝25.∵点F 为DE 的中点，∴DF ＝EF .∵四边形ABCD 为正方形，∴∠BCD ＝90°，BC ＝CD ，∴CF ＝EF ＝DF ＝252，∴DE ＝25，∴在Rt △DCE 中，CD ＝DE 2－CE 2 ＝24，∴BC ＝CD ＝24.∵点O 为BD 的中点，∴OF 是△BDE 的中位线，∴OF ＝12 (BC －CE )＝12 (24－7)＝172 .10. (1)证明：∵四边形ABCD 为正方形 ∴AB ＝AD ，∠A ＝∠D ＝90°. ∵MF ∥AD ∴∠DFM ＝90° ∴四边形ADFM 为矩形 ∴MF ＝AD ＝AB . ∵MN 垂直平分BE ∴∠BOM ＝90° ∴∠ABE ＋∠BMO ＝90°. ∵∠FMN ＋∠BMO ＝90° ∴∠ABE ＝∠FMN . 在△ABE 和△FMN 中⎩⎪⎨⎪⎧∠A ＝∠MFN AB ＝FM ∠ABE ＝∠FMN∴△ABE ≌△FMN (ASA)； (2)解：如解图，连接ME . ∵MN 垂直平分BE ∴ME ＝BM .设BM ＝x ，则AM ＝8－x ，ME ＝x .在Rt △AME 中，由勾股定理得ME 2＝AE 2＋AM 2，即x 2＝62＋(8－x )2. 解得x ＝254 ，即BM ＝254.在Rt △ABE 中，由勾股定理得BE ＝62＋82 ＝10. ∵∠MBO ＝∠EBA ，∠MOB ＝∠A ∴△BOM ∽△BAE ∴OM AE ＝BMBE∴OM ＝AE ·BM BE ＝6×25410 ＝154 .由(1)知△ABE ≌△FMN ∴MN ＝BE ＝10∴ON ＝MN －OM ＝10－154 ＝254.第10题解图11. B 【解析】∵四边形ABCD 是正方形，∴BC ⊥AB ，CD ∥AB ，CD ＝AB .∵EF ⊥AB ，∴EF ∥BC ，∴AE EC ＝AF FB .∵AF ＝2，FB ＝1，∴AE EC ＝21 .∵CD ∥AB ，∴CD ∥AG ，∴∠DCE＝∠GAE ，∠CDE ＝∠AGE ，∴△DCE ∽△GAE ，∴AG CD ＝AE CE ＝21，∴AG ＝2CD ，∴CD ＝AB ＝BG .∵∠DCM ＝∠GBM ＝90°，∠DMC ＝∠GMB ，∴△DCM ≌△GBM (AAS)，∴DM＝GM ＝12 DG .∵AF ＝2，FB ＝1，∴AB ＝3.∵AD ＝AB ＝3，∴AG ＝6，∴在Rt △DAG 中，DG ＝32＋62 ＝35 ，∴MG ＝352.12. B 【解析】 如解图，延长AE 交BC 于点H .∵四边形ABCD 是正方形，∴AD ＝AB ，AD ∥BC ，∴△ADE ∽△HBE ，∴AD HB ＝DEBE ，∵DE ＝3BE ，∴AD ＝3HB ，∴AB ＝3HB ，在Rt △ABH 中，由勾股定理得AH ＝AB 2＋HB 2 ＝10 HB ，∴sin ∠BAE ＝HB AH ＝1010 ，①错误；如解图，过点E 分别作AB ，CD 的垂线，交AB ，CD 于点M ，N ，∴∠AME ＝∠ENF ＝90°，∴∠AEM ＋∠MAE ＝90°，∵∠AEF ＝90°，∴∠AEM ＋∠NEF ＝90°，∴∠MAE ＝∠NEF ，∵∠MBE ＝45°，∴MB ＝ME ，∵AB ＝MN ，∴AM ＝EN ，∴△AME ≌△ENF ，∴AE ＝EF ，∵∠AEF ＝90°，∴∠EAF ＝45°，②正确；∵△AME ≌△ENF ，∴ME ＝NF ＝MB ，∵BE ＝2 ME ，∴CF ＝2ME ＝2 BE ，∵DE ＝3BE ，∴BD ＝4BE ，∴CD ＝22BD ＝22 BE ，∴CD ＝2CF ，∴点F 为CD 的中点，③正确；∵点F 为CD 的中点，∴DF ＝12 CD ＝12 AB ，∵AB ∥CD ，∴△FDG ∽△ABG ，∴DG BG ＝DF AB ＝12 ，∴DG ＝13 BD ，GB ＝23 BD ，设BE ＝x ，则DE ＝3x ，BD ＝4x ，∴DG ＝43 x ，GB ＝83 x ，∴GE ＝GB －BE ＝53 x ，∴BE ＋DG ＝73 x ≠GE ，④错误．第12题解图13. C 【解析】设BF ＝a ，AF ＝b ，则AB ＝a 2＋b 2 ，EF ＝b －a ，∴tan α＝tan ∠BAF ＝BFAF＝a b ，tan β＝tan ∠BEF ＝BF EF ＝a b －a .∵正方形EFGH ∽正方形ABCD ，∴S 正方形EFGH S 正方形ABCD ＝(EFAB )2＝EF 2AB 2 ＝（b －a ）2a 2＋b 2 ＝1n .∵tan α＝tan 2β，∴a b ＝a 2（b －a ）2 .∴(b －a )2＝ab ，b 2＋a 2－2ab ＝ab ，∴a 2＋b 2＝3ab ，∴n ＝a 2＋b 2（b －a ）2＝a 2＋b 2ab ＝3abab ＝3.。

正方形存在性问题巩固练习（基础）1．如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24厘米，AB＝8厘米，BC ＝30厘米，动点P从A开始沿AD边向D以每秒1厘米的速度运动，动点Q从点C开始沿CB边向B以每秒3厘米的速度运动，P，Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为t秒．（1）当t在什么时间范围时，CQ＞PD？（2）存在某一时刻t，使四边形APQB是正方形吗？若存在，求出t值；若不存在，请说明理由．2．如图，在矩形ABCD中，AB＝16cm，AD＝6cm，动点P、Q分别从A、C同时出发，点P以每秒3cm的速度向B移动，一直达到B止，点Q以每秒2cm的速度向D移动．（1）P、Q两点出发后多少秒时，四边形PBCQ的面积为36cm2？（2）是否存在某一时刻，使PBCQ为正方形？若存在，求出该时刻；若不存在，说明理由．3．如图，正比例函数y＝ax与反比例函数（x＞0）的图象交于点（1）求这两个函数的表达式；（2）如图1，若∠AMB＝90°，且其两边分别于两坐标轴的正半轴交于点A、B．求四边形OAMB的面积．（3）如图2，点P是反比例函数（x＞0）的图象上一点，过点P作x轴、y轴的垂线，垂足分别为E、F，PF交直线OM于点H，过作x轴的垂线，垂足为G．设点P的横坐标为m，当时，是否存在点P，使得四边形PEGH为正方形？若存在，求出P点的坐标；若不存在，请说明理由．4．如图，在平面直角坐标系中Rt△AOB≌Rt△CDA，且A（﹣1，0），B（0，2）抛物线y ＝ax2+ax﹣2经过点C．（1）求抛物线的解析式；（2）在抛物线（对称轴的右侧）上是否存在两点P、Q，使四边形ABPQ为正方形？若存在，求点P、Q的坐标；若不存在，请说明理由．5．已知：t1，t2是方程t2+2t﹣24＝0的两个实数根，且t1＜t2，抛物线y x2+bx+c的图象经过点A（t1，0），B（0，t2）．（1）求这个抛物线的解析式；（2）设点P（x，y）是抛物线上一动点，且位于第三象限，四边形OP AQ是以OA为对角线的平行四边形，求平行四边形OP AQ的面积S与x之间的函数关系式，并写出自变量x 的取值范围；（3）在（2）的条件下，当平行四边形OP AQ的面积为24时，是否存在这样的点P，使平行四边形OP AQ为正方形？若存在，求出P点坐标；若不存在，说明理由．6．如图，抛物线y＝﹣ax2+bx+5过点（1，2）、（4，5），交y轴于点B，直线AB经过抛物线顶点A，交x轴于点C，请解答下列问题：（1）求抛物线的解析式；（2）点Q在平面内，在第一象限内是否存在点P，使以A，B，P，Q为顶点的四边形是正方形？若存在，直接写出点P的坐标；若不存在，请说明理由．7．如图，在平面直角坐标系中，点A是动点且纵坐标为6，点B是线段OA上一动点，过点B作直线MN∥x轴，设MN分别交射线OA与x轴所成的两个角的平分线于点E、F．（1）求证：EB＝BF；（2为何值时，四边形AEOF是矩形？证明你的结论；（3）是否存在点A、B，使四边形AEOF为正方形？若存在，求点A与B的坐标；若不存在，说明理由．8．如图，已知二次函数y＝ax2+c图象的顶点为点M（0，﹣9），且经过点A（3，0）．（1）求此二次函数的关系式；（2）设点D（x，y）是此二次函数图象上一动点，且位于第三象限，点C的坐标为（﹣5，0），四边形ABCD是以AC为对角线的平行四边形．①求平行四边形ABCD的面积S与x之间的函数关系式，并写出自变量x的取值范围；②当点B在此二次函数图象的对称轴上时，求平行四边形ABCD的面积；③当平行四边形ABCD的面积为64时，请判断平行四边形ABCD是否为菱形？④是否存在点D，使平行四边形ABCD为正方形？若存在，求出点D的坐标；若不存在，请说明理由．9．如图（1），在平面直角坐标系中，直线y＝﹣x+m交y轴于点A，交x轴于点B，点C 为OB的中点，作C关于直线AB的对称点F，连接BF和OF，OF交AC于点E，交AB于点M．（1）直接写出点F的坐标（用m表示）；（2）求证：OF⊥AC；（3）如图（2），若m＝2，点G，0），过G点的直线GP：y＝kx+b（k≠0）与直线AB始终相交于第一象限；①求k的取值范围；②如图（3），若直线GP经过点M，过点M作GM的垂线交FB的延长线于点D，在平面内是否存在点Q，使四边形DMGQ为正方形？如果存在，请求出Q点坐标；如果不存在，请说明理由．正方形存在性问题巩固练习（基础）1．如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24厘米，AB＝8厘米，BC＝30厘米，动点P从A开始沿AD边向D以每秒1厘米的速度运动，动点Q从点C开始沿CB边向B以每秒3厘米的速度运动，P，Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为t秒．（1）当t在什么时间范围时，CQ＞PD？（2）存在某一时刻t，使四边形APQB是正方形吗？若存在，求出t值；若不存在，请说明理由．【解答】（1）当6＜t≤10时，CQ＞PD；（2）不存在【解析】（1）∵CQ＝3t，24﹣t，∴由CQ＞PD有3t＞24﹣t，解得t＞6．又∵P、Q点的运动时间只能是30÷3＝10（s），∴6＜t≤10，即当6＜t≤10时，CQ＞PD．（2）若四边形是正方形，则AP＝AB且BQ＝AB，∴1×t＝8且30﹣3t＝8，显然无解，即不存在t的值使得四边形APQB是正方形．2．如图，在矩形ABCD中，AB＝16cm，AD＝6cm，动点P、Q分别从A、C同时出发，点P以每秒3cm的速度向B移动，一直达到B止，点Q以每秒2cm的速度向D移动．（1）P、Q两点出发后多少秒时，四边形PBCQ的面积为36cm2？（2）是否存在某一时刻，使PBCQ为正方形？若存在，求出该时刻；若不存在，说明理由．【解答】（1）P、Q两点出发后4秒时，四边形PBCQ的面积为36cm2；（2）不存在【解析】（1）设P、Q两点出发t秒时，四边形PBCQ的面积为36cm2．由矩形ABCD得∠B＝∠C＝90°，AB∥CD，所以四边形PBCQ为直角梯形，故S梯形PBCQ CQ+PB）•BC．又S梯形PBCQ＝36，所以2t+16﹣3t）•6＝36，解得t＝4（秒）；（2）不存在．因为要使四边形PBCQ为正方形，则PB＝BC＝CQ＝6，所以P点运动的时间为秒，Q点运动的时间是3秒，P、Q的时间不一样，所以不存在该时刻．3．如图，正比例函数y＝ax与反比例函数（x＞0）的图象交于点（1）求这两个函数的表达式；（2）如图1，若∠AMB＝90°，且其两边分别于两坐标轴的正半轴交于点A、B．求四边形OAMB的面积．（3）如图2，点P是反比例函数（x＞0）的图象上一点，过点P作x轴、y轴的垂线，垂足分别为E、F，PF交直线OM于点H，过作x轴的垂线，垂足为G．设点P的横坐标为m，当时，是否存在点P，使得四边形PEGH为正方形？若存在，求出P点的坐标；若不存在，请说明理由．【解答】（1）y＝x；（2）6；（3）P）【解析】（1y＝ax与得：，解得：a＝1，k＝6．∴这两个函数的表达式分别为：y＝x．（2）如图，过点M分别做x轴、y轴的垂线，垂足分别为C、D．则∠MCA＝∠MDB＝90°，∠AMC＝∠BMD＝90°﹣∠AMD，MC＝MD＝，∴△AMC≌△BMD，∴S四边形OCMD＝S四边形OAMB＝6．（3）设P点坐标为（x，），则PE＝HG＝GE＝，OE＝x，∵∠MOE＝45°，∴OG＝GH＝，∴OE＝OG+GH＝，∴x＝，解得x，∴P，）．4．如图，在平面直角坐标系中Rt△AOB≌Rt△CDA，且A（﹣1，0），B（0，2）抛物线y ＝ax2+ax﹣2经过点C．（1）求抛物线的解析式；（2）在抛物线（对称轴的右侧）上是否存在两点P、Q，使四边形ABPQ为正方形？若存在，求点P、Q的坐标；若不存在，请说明理由．【解答】（1）y＝x2+x﹣2；（2）P（2，1）、Q（1，﹣1）【解析】（1）由Rt△AOB≌Rt△CDA，得OD＝2+1＝3，CD＝1∴C点坐标为（﹣3，1），∴抛物线经过点C，∴1＝a（﹣3）2+a（﹣3）﹣2，∴a＝∴抛物线的解析式为y＝2+x﹣2；（2）在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形．以AB为边在AB的右侧作正方形ABPQ，过P作PE⊥OB于E，QG⊥x轴于G，可证△PBE ≌△AQG≌△BAO，∴PE＝AG＝BO＝2，BE＝QG＝AO＝1，∴P点坐标为（2，1），Q点坐标为（1，﹣1）．由（1）抛物线y x2+﹣2，当x＝2时，y＝1；当x＝1时，y＝﹣1．∴P、Q在抛物线上．故在抛物线（对称轴的右侧）上存在点P（2，1）、Q（1，﹣1），使四边形ABPQ是正方形．5．已知：t1，t2是方程t2+2t﹣24＝0的两个实数根，且t1＜t2，抛物线y x2+bx+c的图象经过点A（t1，0），B（0，t2）．（1）求这个抛物线的解析式；（2）设点P（x，y）是抛物线上一动点，且位于第三象限，四边形OP AQ是以OA为对角线的平行四边形，求平行四边形OP AQ的面积S与x之间的函数关系式，并写出自变量x 的取值范围；（3）在（2）的条件下，当平行四边形OP AQ的面积为24时，是否存在这样的点P，使平行四边形OP AQ为正方形？若存在，求出P点坐标；若不存在，说明理由．【解答】（1）y2+x+4；（2）S＝﹣4（x）2+25（﹣6＜x＜﹣1）；（3）不存在【解析】（1）t2+2t﹣24＝0，（t+6）（t﹣4）＝0，t1＝﹣6，t2＝4∵t1＜t2，∴A（﹣6，0），B（0，4）∵抛物线y＝x2+bx+c经过A，B两点．∴，解得，∴y＝2+x+4．（2）∵点P（x，y）在抛物线上，位于第三象限，∴y＜0，即﹣y＞0．又∵S＝2S△APO＝2×|OA|•|y|＝|OA|•|y|＝6|y|，∴S＝﹣6y＝﹣6x2+x+4）＝﹣4（x2+7x+6）＝﹣4（x）2+25令y＝0时，x2x+4＝0，解得x1＝﹣6，x2＝﹣1．∵抛物线与x轴的交点坐标为（﹣6，0），（﹣1，0），∴x的取值范围为﹣6＜x＜﹣1．（3）当S＝24时，得24＝﹣4（x+2+25，解得：x1＝﹣3，x2＝﹣4代入解析式得：y1＝﹣4，y2＝﹣4．∴点P的坐标为（﹣3，﹣4），（﹣4，﹣4）当点P为（﹣3，﹣4）时，满足PO＝P A，此时，平行四边形OP AQ是菱形．当点P为（﹣4，﹣4）时，不满足PO＝P A，此时，平行四边形OP AQ不是菱形．而要使平行四边形OP AQ为正方形，那么，一定有OA⊥PQ，AO＝PQ，此时，点P的坐标为（﹣3，﹣3），而（﹣3，﹣3）不在抛物线y＝x2x+4上，故不存在这样的点P，使四边形OP AQ为正方形．6．如图，抛物线y＝﹣ax2+bx+5过点（1，2）、（4，5），交y轴于点B，直线AB经过抛物线顶点A，交x轴于点C，请解答下列问题：（1）求抛物线的解析式；（2）点Q在平面内，在第一象限内是否存在点P，使以A，B，P，Q为顶点的四边形是正方形？若存在，直接写出点P的坐标；若不存在，请说明理由．【解答】（1）y＝x2﹣4x+5；（2）P（6，3）或（4，7）【解析】（1）∵抛物线y＝﹣ax2+bx+5过点（1，2）、（4，5），∴，解得，∴抛物线解析式为y＝x2﹣4x+5；（2）在y＝x2﹣4x+5中，令x＝0可得y＝5，∴B（0，5），∵y＝x2﹣4x+5＝（x﹣2）2+1，∴A（2，1），∴，设直线AB解析式为y＝kx+n，则有，解得，∴直线AB解析式为y＝﹣2x+5，①当P A⊥AB时，如图，可设直线P A解析式为y+m，把A（2，1）代入可得1+m＝1，解得m＝0，∴直线P A解析式为y x，∴可设点P坐标为（x，），∴，∵四边形P ABQ为正方形，∴P A＝AB，即，解得x＝﹣2或x＝6∵点P在第一象限内，∴x＝﹣2不符合题意，舍去，故x＝6，此时P点坐标为（6，3）；②当PB⊥AB时，如图2，可设直线PB解析式为y+s，把B（0，5）代入可得s＝5，∴直线PB解析式为y x+5，∴可设P点坐标为（x，+5），∴，解得x＝﹣4（舍去）或x＝4，此时P点坐标为（4，7）；综上可知存在满足条件的点P，其坐标为（6，3）或（4，7）．7．如图，在平面直角坐标系中，点A是动点且纵坐标为6，点B是线段OA上一动点，过点B作直线MN∥x轴，设MN分别交射线OA与x轴所成的两个角的平分线于点E、F．（1）求证：EB＝BF；（2为何值时，四边形AEOF是矩形？证明你的结论；（3）是否存在点A、B，使四边形AEOF为正方形？若存在，求点A与B的坐标；若不存在，说明理由．【解答】（1）见解析；（2）是，见解析；（3）A（0，6），B（0，3）【解析】（1）证明：∵OF平分OA与x轴正方向的夹角，如图所示：∴∠1＝∠3，∵MN∥x轴，∴∠1＝∠2，∴∠2＝∠3，∴BO＝BF，同理可得BE＝BO，∴BE＝BF；（2时，四边形AEOF是矩形．理由如下：∵，即BO＝BA，而BE＝BF，∴四边形AEOF为平行四边形，∵MN分别交射线OA与x轴所成的两个角的平分线于点E、F．∴∠EOF180°＝90°，∴四边形AEOF是矩形；（3）存在．∵四边形AEOF是矩形，∴当OA⊥EF时，四边形AEOF为正方形，而EF∥x轴，∴OA⊥x轴，∴点A在y轴上，∴点A的坐标为（0，6），∵BO＝BA，∴B点坐标为（0，3）．8．如图，已知二次函数y＝ax2+c图象的顶点为点M（0，﹣9），且经过点A（3，0）．（1）求此二次函数的关系式；（2）设点D（x，y）是此二次函数图象上一动点，且位于第三象限，点C的坐标为（﹣5，0），四边形ABCD是以AC为对角线的平行四边形．①求平行四边形ABCD的面积S与x之间的函数关系式，并写出自变量x的取值范围；②当点B在此二次函数图象的对称轴上时，求平行四边形ABCD的面积；③当平行四边形ABCD的面积为64时，请判断平行四边形ABCD是否为菱形？④是否存在点D，使平行四边形ABCD为正方形？若存在，求出点D的坐标；若不存在，请说明理由．【解答】（1）y＝x2﹣9；（2）①（﹣3＜x＜0），②40，③是菱形；（4）不存在【解析】（1）由题意得，解得故二次函数的关系式为y＝x2﹣9，（2）①D（x，y）在二次函数的图象上，且位于第三象限，∴y＜0，即﹣y＞0，﹣y表示点D到AC的距离．∵AC是平行四边形ABCD的对角线，．当y＝0时，x2﹣9＝0，得x＝±3所以二次函数的图象与x轴的另一个交点是（﹣3，0），所以，自变量x的取值范围是﹣3＜x＜0．②如图：当点B在此二次函数图象的对称轴上时，过点D作DE⊥AC，垂足为点E，∵四边形ABCD是平行四边形，∴AB＝CD，∠DCE＝∠BAO，∠CED＝∠AOB＝90°，∴△ABO≌△CDE∵点B在二次函数的图象的对称轴上OA＝3，∴CE＝OA＝3，所以OE＝2，所以当x＝﹣2时，y＝﹣5，S＝40；③根据题意，当S＝64时，即﹣8x2+72＝64．解之，得x1＝1，x2＝﹣1．故所求的点D有两个，分别为D1（1，﹣8）（舍去），D2（﹣1，﹣8），所以平行四边形ABCD不是菱形（或者说明点D不在第三象限）；点D2（﹣1，﹣8）满足DC＝DA，所以平行四边形ABCD是菱形．④当AC⊥BD，且AC＝BD时，平行四边形ABCD是正方形，此时点D的坐标只能是（﹣1，﹣4）．而坐标为（﹣1，﹣4）的点不在二次函数的图象上，故不存在这样的点D，使平行四边形ABCD为正方形．9．如图（1），在平面直角坐标系中，直线y＝﹣x+m交y轴于点A，交x轴于点B，点C 为OB的中点，作C关于直线AB的对称点F，连接BF和OF，OF交AC于点E，交AB于点M．（1）直接写出点F的坐标（用m表示）；（2）求证：OF⊥AC；（3）如图（2），若m＝2，点G，0），过G点的直线GP：y＝kx+b（k≠0）与直线AB始终相交于第一象限；①求k的取值范围；②如图（3），若直线GP经过点M，过点M作GM的垂线交FB的延长线于点D，在平面内是否存在点Q，使四边形DMGQ为正方形？如果存在，请求出Q点坐标；如果不存在，请说明理由．【解答】（1）F（m m）；（2）见解析；（3）①0＜k＜6，②Q（【解析】（1）y＝﹣x+m，令x＝0，则y＝m，令y＝0，则x＝m，则∠ABO＝45°，故点A、B的坐标分别为：（0，m）、（m，0），则点C（，0），如图（1）作点C的对称轴F交AB于点R，则CF⊥AB，CR＝FR，则∠RCB＝45°，则RC＝RB＝RF，∴∠RBF＝45°，即FB⊥x轴，故点F（m m）；（2）∵OC＝BF，OB＝OA，∴△AOC≌△OBF（HL），∴∠OAC＝∠FOB，∵∠OAC+∠AOE＝90°，∴∠OAC+∠AOE＝90°，∴∠AEO＝90°，∴OF⊥AC；（3）①将点（0）代入y＝kx+b得：，解得：，由一次函数图象知：k＞0，∵交点在第一象限，则，解得：0＜k＜6；②存在，理由：直线OF的表达式为：AB的表达式为：y＝﹣x+2，联立上述两个表达式并解得：x＝，故点M（，直线GM所在函数表达式中的k，则直线MD所在直线函数表达式中的k值为，将点M坐标和直线DM表达式中的k值代入一次函数表达式并解得：直线DM的表达式为：y＝x+4，故点D（2，﹣1），过点M作x轴的垂线于点N，作x轴的平行线交过点G于y轴的平行线于点S，过点G作y轴的平行线交过点Q与x轴的平行线于点T，则MN＝MH＝2＝，GN＝＝＝DH＝1）＝∴△MNG≌△MHD（HL），∴MD＝MG，则△GTQ≌△MSG，则GT＝MS＝GN＝，TQ＝SG＝MN，故点Q（，﹣．。

正方形问题1 如图，在边长为6的正方形ABCD 的两侧作正方形BEFG 和正方形DMNK ，恰好使得N 、A 、F 三点在一直线上，连接MF 交线段AD 于点P ，连接NP ，设正方形BEFG 的边长为x ，正方形DMNK 的边长为y ．（1）求y 关于x 的函数关系式及自变量x 的取值X 围； （2）当△NPF 的面积为32时，求x 的值；（3）以P 为圆心，AP 为半径的圆能否与以G 为圆心，GF 为半径的圆相切？如果能，请求出x 的值，如果不能，请说明理由．解析：（1）∵正方形BEFG 、正方形DMNK 、正方形ABCD ∴∠E ＝∠F ＝90O ，AE ∥MC ，MC ∥NK ∴AE ∥NK ，∴∠KNA ＝∠EAF∴△KNA ∽△EAF ，∴NK EA ＝KA EF ，即y x ＋6＝y －6x∴y ＝x ＋6（0＜x ≤6）（2）由（1）知NK ＝AE ，∴AN ＝AF∵正方形DMNK ，∴AP ∥NM ，∴FP PM ＝AFAN ＝1∴FP ＝PM ，∴S △MNP ＝S △NPF ＝32 ∴S 正方形DMNK ＝2S △MNP ＝64 ∴y ＝8，∴x ＝2（3）连接PG ，延长FG 交AD 于点H ，则GH ⊥AD易知：AP ＝y2，AH ＝x ，PH ＝y 2－x ，HG ＝6；PG ＝AP ＋GF ＝y2＋x①当两圆外切时在Rt △GHP 中，PH 2＋HG 2＝PG 2，即(y2－x )2＋62＝(y2＋x )2解得：x ＝－3－33（舍去）或x ＝－3＋3 3 ②当两圆内切时NK G CE DFAB PM在Rt △GHP 中，PH 2＋HG 2＝PG 2，即(y2－x )2＋62＝(y2－x )2方程无解所以，当x ＝33－3时，两圆相切2 已知：正方形ABCD 的边长为1，射线AE 与射线BC 交于点E ，射线AF 与射线CD 交于点F ，∠EAF ＝45°，连接EF ．（1）如图1，当点E 在线段BC 上时，试猜想线段EF 、BE 、DF 有怎样的数量关系？并证明你的猜想； （2）设BE ＝x ，DF ＝y ，当点E 在线段BC 上运动时（不包括点B 、C ），求y 关于x 的函数解析式，并指出x 的取值X 围；（3）当点E 在射线BC 上运动时（不含端点B ），点F 在射线CD 上运动．试判断以E 为圆心，以BE 为半径的⊙E 和以F 为圆心，以FD 为半径的⊙F 之间的位置关系；（4）如图2，当点E 在BC 的延长线上时，设AE 与CD 交于点G ．问：△EGF 与△EFA 能否相似？若能相似，求出BE 的长，若不可能相似，请说明理由．解析：（1）猜想：EF ＝BE ＋DF证明：将△ADF 绕点A 顺时针旋转90°，得△ABF′，易知点F′、B 、E 在同一直线上（如.图1） ∵AF′＝AF∠F′AE ＝∠1＋∠3＝∠2＋∠3＝90°－45°＝45°＝∠EAF 又AE ＝AE ，∴△AF ′E ≌△AFEAB DCEF图1AB D CEFG图2AB DCEF图1F ′12∴EF ＝F′E ＝BE ＋BF ＝BE ＋DF （2）在Rt △EFC 中，EC 2＋FC 2＝EF 2 ∵EC ＝1－x ，FC ＝1－y ，EF ＝x ＋y ∴(1－x )2＋(1－y )2＝(x ＋y )2 ∴y ＝1－x1＋x （0＜x ＜1）（3）①当点E 在点B 、C 之间时，由（1）知EF ＝BE ＋DF ，故此时⊙E 与⊙F 外切； ②当点E 在点C 时，DF ＝0，⊙F 不存在.③当点E 在BC 延长线上时，将△ADF 绕点A 顺时针旋转90°，得△ABF′（如图2） 则AF′＝AF ，∠1＝∠2，B F′＝DF ，∠F ′AF ＝90° ∴∠F ′AE ＝∠EAF ＝45° 又AE ＝AE ，∴△AF ′E ≌△AFE ∴EF ＝EF′＝BE －B F′＝BE －DF ∴此时⊙E 与⊙F 内切综上所述，当点E 在线段BC 上时，⊙E 与⊙F 外切；当点E 在BC 延长线上时，⊙E 与⊙F 内切 （4）△EGF 与△EFA 能够相似，只要当∠EFG ＝∠EAF ＝45°即可 此时CE ＝CF设BE ＝x ，DF ＝y ，由（3）知EF ＝x －y 在Rt △CFE 中，CE 2＋CF 2＝EF 2∴(x －1)2＋(1＋y )2＝(x －y )2∴y ＝x －1x ＋1（x ＞1）由CE ＝CF ，得x －1＝1＋y ，即x －1＝1＋x －1x ＋1化简得x 2－2x －1＝0，解得x 1＝1－2（舍去），x 2＝1＋ 2 ∴△EGF 与△EFA 能够相似，此时BE 的长为1＋ 23已知：如图，在直角梯形ABCD 中，AD ∥BC ，∠B ＝90°，AD ＝2，BC ＝6，AB ＝3．E 为BC 边上一点，ABD CEFG图2F ′12以BE 为边作正方形BEFG ，使正方形BEFG 和梯形ABCD 在BC 的同侧． （1）当正方形的顶点F 恰好落在对角线AC 上时，求BE 的长；（2）将（1）问中的正方形BEFG 沿BC 向右平移，记平移中的正方形BEFG 为正方形B′EFG ，当点E 与点C 重合时停止平移．设平移的距离为t ，正方形B′EFG 的边EF 与AC 交于点M ，连接B′D ，B′M ，DM ．是否存在这样的t ，使△B′DM 是直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）在（2）问的平移过程中，设正方形B′EFG 与△ADC 重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式以及自变量t 的取值X 围．解析：（1）如图①，设正方形BEFG 的边长为x 则BE ＝FG ＝BG ＝x∵AB ＝3，BC ＝6，∴AG ＝AB －BG ＝3－x ∵GF ∥BE ，∴△AGF ∽△ABC∴AG AB ＝GF BC ，即3－x 3＝x 6解得x ＝2，即BE ＝2（2）存在满足条件的t ，理由如下： 如图②，过D 作DH ⊥BC 于点H 则BH ＝AD ＝2，DH ＝AB ＝3由题意得：BB′＝HE ＝t ，HB′＝|t －2|，EC ＝4－t在Rt△B′ME 中，B′M 2＝B′E 2＋ME 2＝22＋(2－12t )2＝14t 2－2t ＋8∵EF ∥AB ，∴△MEC ∽△ABC∴ME AB ＝EC BC ，即ME 3＝4－t 6，∴ME ＝2－12t在Rt△DHB′中，B′D 2＝DH 2＋B′H 2＝32＋(t －2)2＝t 2－4t ＋13BACDBACD备用图B A CD 图①EFGB A CD 图②EFG HB ′ M N过M 作MN ⊥DH 于点N 则MN ＝HE ＝t ，NH ＝ME ＝2－12t ∴DN ＝DH －NH ＝3－(2－12t )＝12t ＋1 在Rt△DMN 中，DM 2＝DN 2＋MN 2＝54t 2＋t ＋1（ⅰ）若∠DB′M ＝90°，则DM 2＝B′M 2＋B′D 2 即54t 2＋t ＋1＝(14t 2－2t ＋8)＋(t 2－4t ＋13)，解得t ＝207 （ⅱ）若∠B′MD ＝90°，则B′D 2＝B′M 2＋DM 2即t 2－4t ＋13＝(14t 2－2t ＋8)＋(54t 2＋t ＋1)，解得t 1＝－3＋17，t 2＝－3－17∵0≤t ≤4，∴t ＝－3＋17（ⅲ）若∠B′DM ＝90°，则B′M 2＝B′D 2＋DM 2即14t 2－2t ＋8＝(t 2－4t ＋13)＋(54t 2＋t ＋1)，此方程无解 综上所述，当t ＝207或－3＋17时，△B′DM 是直角三角形 （3）当0≤t ≤43时，S ＝14t 2当43≤t ≤2时，S ＝－18t 2＋t －23 当2≤t ≤103时，S ＝－38t 2＋2t －53 当103≤t ≤4时，S ＝－12t ＋52 提示：当点F 落在CD 上时，如图③FE ＝2，EC ＝4－t ，DH ＝3，HC ＝4 由△FEC ∽△DHC ，得FE EC ＝DHHC即24－t ＝34，∴t ＝43当点G 落在AC 上时，点G 也在DH 上（即DH 与AC 的交点）t ＝2当点G 落在CD 上时，如图④B ACD图③E FGB ′ HB ACD图④E FGB ′ HGB ′＝2，B ′C ＝6－t由△GB ′C ∽△DHC ，得G ′B B ′C ＝DHHC即26－t ＝34，∴t ＝103 当点E 与点C 重合时，t ＝4 ①当0≤t ≤43时，如图⑤ ∵MF ＝t ，FN ＝12t∴S ＝S △FMN ＝12·t ·12t ＝14t 2②当43≤t ≤2时，如图⑥ ∵PF ＝t －43，FQ ＝34PF ＝34t －1 ∴S △FPQ ＝12(t －43)(34t －1)＝38t 2－t ＋23∴S ＝S △FMN －S △FPQ ＝14t 2－(38t 2－t ＋23)＝－18t 2＋t －23 ③当2≤t ≤103时，如图⑦ ∵B′M ＝12B′C ＝12(6－t )＝3－12t ∴GM ＝2－(3－12t )＝12t －1 ∴S 梯形GMNF ＝12(12t －1＋12t )×2＝t －1∴S ＝S 梯形GMNF －S △FPQ ＝(t －1)－(38t 2－t ＋23)＝－38t 2＋2t －53 ④当103≤t ≤4时，如图⑧ ∵P B′＝34B′C ＝34(6－t )＝92－34t ∴GP ＝2－(92－34t )＝34t －52∴S 梯形GPQF ＝12(34t －52＋34t －1)×2＝32t －72∴S ＝S 梯形GMNF －S 梯形GPQF ＝(t －1)－(32t －72)＝－12t ＋52BC图⑥EB ′BC图⑦EB ′B C 图⑧E B ′。