第六章动态规划解析

第6章 动态规划动态规划（Dynamic Programming ）是解决多阶段决策过程最优化的一种有用的数学方法。

它是由美国学者Richard .Bellman 在1951年提出的，1957年他的专著《动态规划》一书问世，标志着运筹学的一个重要分支－动态规划的诞生.动态规划也是一种将多变量问题转化为单变量问题的一种方法。

在动态规划中，把困难的多阶段决策问题变换成一系列相互联系的比较容易的单阶段问题一个个地求解。

动态规划是考察解决问题的一种途径 ,而不是一种特殊的算法，不像线性规划那样有统一的数学模型和算法（如单纯形法）.事实上，在运用其解决问题的过程中还需要运用其它的优化算法。

因此，动态规划不像其它方法局限于解决某一类问题,它可以解决各类多阶段决策问题。

动态规划在工程技术、经济管理等社会各个领域都有着广泛的应用，并且获得了显著的效果。

在经济管理方面,动态规划可以用来解决最优路径问题、资源分配问题、生产调度问题、库存管理问题、排序问题、设备更新问题以及生产过程最优控制问题等，是经济管理中一种重要的决策技术。

许多规划问题用动态规划的方法来处理,常比线性规划或非线性规划更有效。

特别是对于离散的问题，由于解析数学无法发挥作用，动态规划便成为了一种非常有用的工具。

动态规划可以按照决策过程的演变是否确定分为确定性动态规划和随机性动态规划；也可以按照决策变量的取值是否连续分为连续性动态规划和离散性动态规划。

本教材主要介绍动态规划的基本概念、理论和方法,并通过典型的案例说明这些理论和方法的应用。

6.1动态规划的基本理论6.1.1多阶段决策过程的数学描述有这样一类活动过程,其整个过程可分为若干相互联系的阶段，每一阶段都要作出相应的决策,以使整个过程达到最佳的活动效果。

任何一个阶段(stage ，即决策点)都是由输入(input ）、决策（decision ）、状态转移律（transformation function )和输出(output )构成的，如图6-1（a ）所示.其中输入和输出也称为状态(state ）,输入称为输入状态，输出称为输出状态。

动态规划算法的详细原理及使用案例一、引言动态规划是一种求解最优化问题的算法，它具有广泛的应用领域，如机器学习、图像处理、自然语言处理等。

本文将详细介绍动态规划算法的原理，并提供一些使用案例，以帮助读者理解和应用这一算法的具体过程。

二、动态规划的基本原理动态规划算法通过将问题分解为多个子问题，并利用已解决子问题的解来求解更大规模的问题。

其核心思想是利用存储技术来避免重复计算，从而大大提高计算效率。

具体来说，动态规划算法通常包含以下步骤：1. 定义子问题：将原问题分解为若干个子问题，这些子问题具有相同的结构，但规模更小。

这种分解可以通过递归的方式进行。

2. 定义状态：确定每个子问题的独立变量，即问题的状态。

状态具有明确的定义和可计算的表达式。

3. 确定状态转移方程：根据子问题之间的关系，建立状态之间的转移方程。

这个方程可以是简单的递推关系式、递归方程或其他形式的方程。

4. 解决问题：使用递推或其他方法，根据状态转移方程求解每个子问题，直到获得最终解。

三、动态规划的使用案例1. 背包问题背包问题是动态规划算法的经典案例之一。

假设有一个背包，它能容纳一定重量的物品，每个物品有对应的价值。

目的是在不超过背包总重量的前提下，选取最有价值的物品装入背包。

这个问题可以通过动态规划算法来求解。

具体步骤如下：（1）定义问题：在不超过背包容量的限制下，选取物品使得总价值最大化。

（2）定义状态：令dp[i][j]表示将前i个物品放入容量为j的背包中所能获得的最大价值。

（3）状态转移方程：dp[i][j] = max(dp[i-1][j-w[i]]+v[i], dp[i-1][j])，其中w[i]为第i个物品的重量，v[i]为第i个物品的价值。

（4）解决问题：根据状态转移方程依次计算每个子问题的解，并记录最优解，直到获得最终答案。

2. 最长公共子序列最长公共子序列（Longest Common Subsequence，简称LCS）是一种经典的动态规划问题，它用于确定两个字符串中最长的共同子序列。

动态规划（生产和存储问题）一、动态规划法的发展及其研究内容动态规划是运筹学的一个分支，是求解决策过程最优化的数学方法。

20世纪50年代初美国数学家R.E.BELLMAN等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，把多阶段问题转化为一系列的单阶段问题，逐个求解创立了解决这类过程优化问题的新方法——动态规划。

1957年出版的他的名著《Dynamic Proggramming》，这是该领域的第一本著作。

动态规划问世以来，在经济管理·生产调度·工程技术和最优控制等方面得到了广泛的应用。

例如最短路线·库存管理·资源分配·设备更新·组合·排序·装载等问题，采用动态规划法求解比用其他方法更为简便。

二、动态规划法基本概念一个多阶段决策过程最优化问题的动态规划模型通常包括以下几个要素：1．阶段阶段（stage）是对整个过程的自然划分。

通常根据时间顺序或是空间特征来划分阶段，对于与时间，空间无关的“静态”优化问题，可以根据其自然特征，人为的赋予“时段”概念，将静态问题动态化，以便按阶段的顺序解优化问题。

阶段变量一般用k=1.2….n.表示。

1.状态状态(state)是我们所研究的问题（也叫系统）在过个阶段的初始状态或客观条件。

它应能描述过程的特征并且具有无后效性，即当某阶段的状态给定时，这个阶段以后的过程的演变与该阶段以前各阶段的状态无关。

通常还要求状态是可以直接或者是间接可以观测的。

描述状态的变量称为状态变量（State Virable）用s 表示，状态变量的取值集合称为状态集合，用S表示。

变量允许取值的范围称为允许状态集合(set of admissble states).用x(k)表示第k阶段的状态变量，它可以是一个数或者是一个向量。

用X(k)表示第k阶段的允许状态集合。

n 个阶段的决策过程有n+1个状态变量，x(n+1)是x(n)的演变的结果。

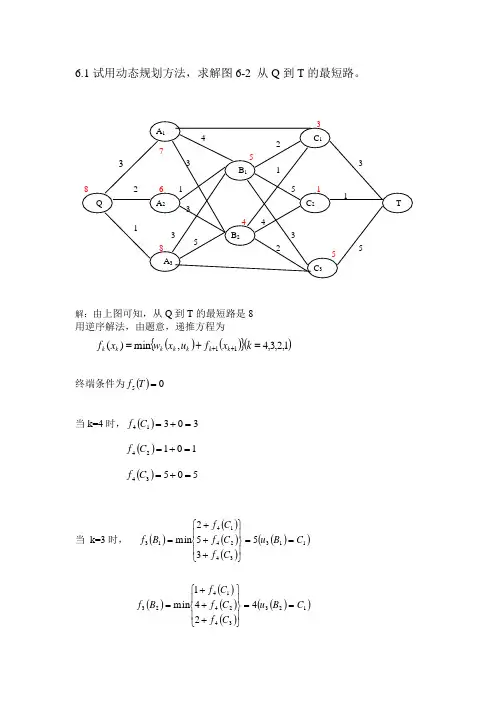
6.1试用动态规划方法，求解图6-2 从Q 到T 的最短路。

解：由上图可知，从Q 到T 的最短路是8用逆序解法，由题意，递推方程为()(){}()1,2,3,4,min )(11=+=++k x f u x w x f k k k k k k k终端条件为()05=T f当k=4时，()30314=+=C f()10124=+=C f()50534=+=C f当 k=3时， ()()()()()()113342414135352min C B u C f C f C f B f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=()()()()()()123342414234241min C B u C f C f C f B f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=当k=2时，()()()()()212231312734min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=()()()()()122231322731min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=()()()()()132231332853min B A u B f B f A f ==⎭⎬⎫⎩⎨⎧++=当k=1 时，()()()()()()2132221218123min A Q u A f A f A f Q f ==⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=最优解策略为()2*1A Q u = ()12*2B A u = ()11*3C B u = ()T C u =1*4最短路长为86.2用动态规划方法求解 （1）3221max x x x F ⋅⋅=⎩⎨⎧=≥=++3,2,1,04..321i x x x x t s i解：3211x x x S ++=322x x S += 33x S = 121x S S +=232x S S += 33x S =()(){}3max 22022222f x s f sx ⋅=≤≤=(){}2220222max x s x sx -⋅≤≤由导数法求得，当3222s S =时，()22x f 有最大值27432s ()(){}22140111max x f x s f x ⋅=≤≤=()⎭⎬⎫⎩⎨⎧⋅=≤≤274max 32140111s x s f x =()()⎭⎬⎫⎩⎨⎧-⋅=≤≤2744max 31140111x x s f x解得：11=x 时，()4max 11=x f∴ ()⎪⎩⎪⎨⎧+==++322323241x x x x x∴⎩⎨⎧==1232x x ∴1,2,1321===x x x （2）321232223222124222min x x x x x x x x F ---+-++=⎩⎨⎧=≥=++3,2,1,03..321i x x x x t s i解： 31=S 112x S S -= 223x S S -=()(){}41min 23333--==x s f x s =(){}4123--s()()(){}4112min 2322222--+-=≤s x s f x x=()(){}411222222---+-x s x=1422224222222222222+-+-+-++-x s x x s s x x()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+-=≤222221413423221min 1s s x s f x =()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛--+-≤1342632321min 21212141x x x x=()()112194219212221211121--+-++-++-x x x x x x =96930915121+-x x =30301-x =011=x6.3 有四台设备分给甲，乙，丙，丁四厂，各厂盈利如表6-6所示。

第六章动态规划法• P137 2 ,3, 4•2.解答:cost[i]表示从顶点i 到终点n-1 的最短路径，path[i]表示从顶点i 到终点n-1 的路径上顶点i 的下一个顶点。

cost[i]=min{cij+cost[j]}3 有5 个物品，其重量分别是{3, 2, 1, 4,5}，价值分别为{25, 20, 15, 40, 50}，背包的容量为6。

V[i][j]表示把前i 个物品装入容量为j 的背包中获得的最大价值。

最优解为（0，0，1，0，1）最优值为65. 4.序列A =(x, z , y , z , z , y,x )，B =(z , x , y , y , z , x , z )，建立两个(m+1)×(n+1)的二 维表L 和表S ，分别存放搜索过程中得到的子序列的长度和状态。

z , x , y , y , z,x , z )path[i]= 使 cij+cost[j] 最小的 j i 012345678 9 10 11 12 13 14 15 Cost[i] 18 13 16 13 10 9 12 7 6875943Path[i]145778911 11 11 13 14 14 15 15 0得到最短路径 0->1->4->7->11->14->15 , 长度为 18(a)长度矩阵L(b)状态矩阵S 。

第七章贪心算法2.背包问题:有7 个物品，背包容量W=15。

将给定物品按单位重量价值从大到小排序，结果如下：个物品，物品重量存放在数组w[n]中，价值存放在数组放在数组x[n]中。

按算法7.6——背包问题1．改变数组w 和v 的排列顺序，使其按单位重量价值v[i]/w[i]降序排列；2．将数组x[n]初始化为0；//初始化解向量3．i=1;4．循环直到( w[i]>C )4.1 x[i]=1; //将第i个物品放入背包4.2 C=C-w[i];4.3 i++;5. x[i]=C/w[i];得出,该背包问题的求解过程为:: x[1]=1;c=15-1=14 v=6 x[2]=1; c=14-2=12V=6+10=10 x[3]=1; c=12-4=8V=16+18=34 x[4]=1; c=8-5=3V=34+15=49 x[5]=1; c=3-1=2 V=49+3=52x[6]=2/3 ; c=0; V=52+5*2/3=156/3 最优值为156/3 最优解为(1,1,1,1,1,2/3,0)) (x[i]按排序后物品的顺序构造)5.可以将该问题抽象为图的着色问题,活动抽象为顶点,不相容的活动用边相连(也可以将该问题理解为最大相容子集问题,重复查找剩余活动的最大相容子集,子集个数为所求).具体参见算法7.3 算法7.3——图着色问题1．color[1]=1; //顶点1着颜色12．for (i=2; i<=n; i++) //其他所有顶点置未着色状态color[i]=0;3．k=0;4．循环直到所有顶点均着色4.1k++; //取下一个颜色4.2for (i=2; i<=n; i++) //用颜色k 为尽量多的顶点着色4.2.1 若顶点i已着色，则转步骤4.2，考虑下一个顶点;4.2.2 若图中与顶点i邻接的顶点着色与顶点i着颜色k 不冲突，则color[i]=k;5．输出k;第八章回溯法4.搜索空间(a) 一个无向图(b) 回溯法搜索空间最优解为（1，2，1，2，3）5.0-1 背包问题n∑w i x i≤c 1• 可行性约束函数：i =1• 上界函数：nr =∑Vi5 = 3A B *CD8 ** * 131 =12 =23 = 14 = 2 34215课后答案网（）i=k+1 1第九章分支限界法5，解：应用贪心法求得近似解：(1,4,2,3)，其路径代价为：3+5+7+6=21，这可以作为该问题的上界。