混合成本分解例题:
- 格式:doc
- 大小:67.00 KB
- 文档页数:2

第二章1、某公司2005年甲产品生产工时和制造费用总额的资料摘录如下:高点低点生产工时(小时)75000 50000制造费用(元)176250 142500制造费用是由变动成本、固定成本与混合成本三部分组成的。
公司对低点制造费用进行了分解:变动成本为50000元,固定成本为60000元,混合成本为32500元。
要求:(1)采用高低点法对混合成本进行分解,并写出混合成本公式。
(2)当生产工时为65000小时时,预测其制造费用总额。
要求:采用高低点法进行成本性态分析第三章1、已知:某公司从事单一产品生产,连续三年销售量均为1000件,而三年的产量分别为1000件、1200件和800件。
单位产品售价为200元,管理费用与销售费用均为固定成本,两项费用各年总额均为50000元,单位产品变动生产成本为90元,固定性制造费用为20000元。
第一年的期初存货量为零。
要求:(1)分别采用变动成本法和完全成本法计算第一年的营业利润。
(2)不用计算,直接判断第二年和第三年按变动成本法确定的营业利润。
(3)按照利润差额简算法分别计算第二年和第三年两种成本法的利润差额。
(4)不用编利润表,计算第二年和第三年完全成本法下的营业利润。
(5)根据本题计算结果,验证两种成本法广义利润差额特殊变动规律的合理性。
2、己知某企业只产销一种产品,其有关资料如下:生产量为2000件,销售量为1800件,期初存货为零;贡献边际率为60%;原材料为6000元,计件工资为4000元,其他变动性制造费用每件0.4元,固定性制造费用总额2000元,变动性销售与管理费用每件0.2元,固定性销售与管理费用总额为300元。
要求:(1)根据给定的贡献边际率确定售价。
(2)按两种方法计算单位产品成本。
(3)按两种成本法编制利润表。
(4)说明两种成本法计算的营业利润不同的原因。
3、已知:某公司按变动成本法核算的20×2年1月产品成本资料如下(该公司采用先进先出法计价):单位产品成本50元,本期固定性制造费用30000元,期初存货数量500件,本期完工产品6000件,本期销售产品5500件,销售价格100元/件,固定性销售与管理费用45000元。

四、混合成本的分解方法混合成本的分解,一般是根据大量的历史成本资料或成本发生的具体过程,进行分析计算,寻找混合成本与业务量之间的规律性的数量关系,最终确定固定成本和变动成本的历史平均值或标准值,他们代表正常的成本水平。
(一)高低点法从中选取业务量最高点和业务量最低点以过去会计期间的总成本和业务量资料为依据, ,将总成本进行分解。
单位变动成本-/-=(最高点业务量成本 最低点业务量成本) (最高点业务量 最低点业务量)固定成本总额-=最高点业务量成本 单位变动成本×最高点业务量或-=最低点业务量成本 单位变动成本×最低点业务量应用举例A20191-12 5.0【教材例题】假设 公司的业务量以直接人工工时为单位, 年 月份的业务量在7.52-5万— 万小时之间变化,维修成本与业务量之间的关系如表 所示。
表 2-5月份123456789101112业务量5.1 5.5 5.66.0 6.17.57.47.27.0 6.8 6.5 5.0(小时)维修成本100104105108109120121118115112111101(万元)单位变动成本-/-=(最高点业务量成本 最低点业务量成本) (最高点业务量 最低点业务量)120-101/7.5-5.0=7.6/=( ) ( ) (元 小时)7.5=63固定成本总额=120-7.6× (万元)=101-7.6 5.0=63或者: × (万元)维修成本的方程式: y=63+7.6x若 年计划的业务量为 万小时,预计的维修成本:2020 6.56.5=112.4Y=63+7.6× (万元)。
【提示】( )单位变动成本的计算公式中,分子是业务量变动时总成本的增加额,分母是业务量的增加1额。
由于业务量增加时总成本的增加是变动成本增加引起的,所以, 单位产品的增量成本就是单位产品的变动成本。
2--( )分子不是(最高成本 最低成本),而是(最高业务量成本 最低业务量成本)。

混合成本分解(两种方法运用比较)
基本案情
K公司某年度之电费及直接人工小时如图表:
分析要点
试用高低点法、回归直线法对混合成本进行分解。
案例分析
1、高低点法
由上表可知,该公司3月份直接人工小时最高,计500小时,电费总额为1500,而以11月份直接人工小时最低,计300小时,电费总额为1080,所以:
直接人工小时电费总额
高点 500 1500
低点 300 1080
差额 200 420
变动电费率:
b=Δy/Δx=420/200=2.1
a=y- b x=1500-2.1×500=450
所以电费成本公式为:y=450+2.1x
2、回归直线法
(1)编制计算表
2)计算固定成本及单位变动成本
(2)混合成本公式为:y=427.21+1.9446x
问题探讨
针对此案例,可深入探讨两种分解混合成本的方法的共性及差异?
从数学观点来看,两种方法均含有估计成分(即都有一定的假设性),所以分解混合成本的结果只是一个近似值。
两种分解方法均要求在一定的相关范围内,即有一个相关系数的问题。
两种分解方法均假定成本与产量之间完全线性联系,因而用直线方程y=a+bx来反映成本性态。
两种分解方法之区别主要体现在计算结果的准确性上。
高低点法由于仅使用两点(高点、低点)的成本数据来推知混合成本公式,如果两点的代表性不是很强,会使得最终结果很不准确;回归直线法因摒弃了两者之缺点而使其计算结果最为准确。
也欠准确性;回归直线法因摒弃了两者之缺点而使其计算结果最为准确。
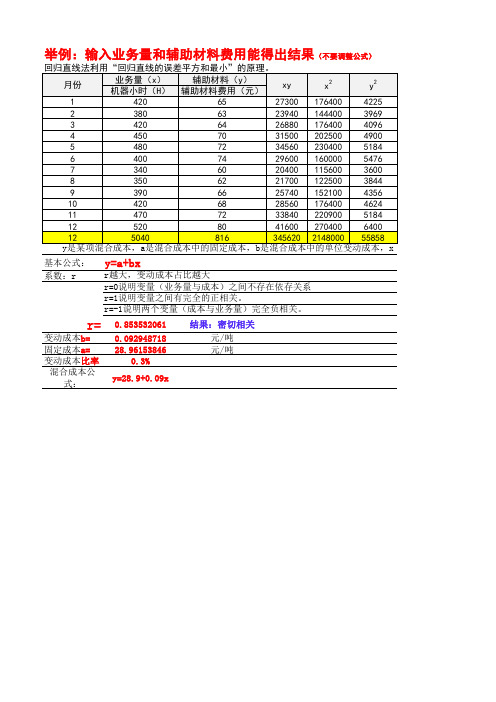

高低点法例题计算混合成本混合成本是指多种产品或服务生成的总成本。
在计算混合成本时,需要考虑到不同产品或服务的产量、成本和混合比例。
以下是一个关于计算混合成本的例题,详细解答如下。
假设公司生产两种产品A和B,产品A和产品B的产量分别为2000个和3000个。
对于产品A,每个单位的原材料成本为10元,每个单位的人工成本为5元,每个单位的制造费用为8元。
对于产品B,每个单位的原材料成本为15元,每个单位的人工成本为4元,每个单位的制造费用为12元。
现在我们需要计算这两种产品的混合成本。
首先,我们需要计算产品A和产品B各自的总成本。
产品A的成本计算如下:总成本=产量×(原材料成本+人工成本+制造费用)=2000×(10+5+8)=2000×23同样地,产品B的成本计算如下:总成本=产量×(原材料成本+人工成本+制造费用)=3000×(15+4+12)=3000×31接下来,我们需要根据产品A和产品B的产量,计算出混合比例。
总产量为2000个产品A和3000个产品B,所以总产量为5000个。
产品A 的混合比例计算如下:产品A的混合比例=产品A的产量/总产量=2000/5000=0.4同样地,产品B的混合比例计算如下:产品B的混合比例=产品B的产量/总产量=3000/5000=0.6最后,我们可以计算出两种产品的混合成本。
将产品A的混合比例和产品B的混合比例分别与其总成本相乘,并相加即可得到混合成本。
计算公式如下:混合成本=产品A的总成本×产品A的混合比例+产品B的总成本×产品B的混合比例。

管理会计习题与案例一、混合成本分解上述表格制造费用中包括变动成本、固定成本和混合成本三类。
该厂会计部门曾对低点业务量为50000机器小时的制造费用总额进行分析,其各类成本的组成情况如下:变动成本总额50000元固定成本总额60000混合成本总额32500制造费用总额142500要求:1、采用高低点法将该厂的混合成本分解为变动成本和固定成本,并写出混合成本公式。
2、若该厂计划期间的生产能力为65000机器小时,则其制造费用总额将为多少?二、变动成本法大方公司2005年只产销一种产品,产量、售价和成本的资料如下:生产量4000件直接材料20000元销售量3500件直接人工32000元期初存货量0件制造费用:单位变动费用6元贡献毛益率50% 固定费用总额28000元推销管理费用:单位变动费用4元固定费用总额21000元要求:1、分别采用两种不同成本法计算2005年的期末存货成本2、分别采用两种成本法编制收益表,并说明产生差异的原因三、本量利分析基本情况:常印曾经是一家乡镇企业的经营策划者,他一直渴望自己能成为一个老板,因此,他随时都寻找自己发展事业的机会。
常印的家位于某城市郊县的一个乡镇,周围方圆几十里没有一个冷饮厂。
每到夏天,百里以外的企业到这里批发或零售雪糕或冰淇淋,他时常看到这些乡村的孩子花着高价吃到劣质的所谓的冰淇淋。
于是,他决定自己创办一个冰淇淋加工厂,让自己的父老乡亲随时吃到价廉可口的冰淇淋,并开始作市场调研。
调查显示:1、需求量:周遍5个乡镇,每个乡镇约有8万人,总计有40万,按现在的生活水平和消费观念估算,在春秋淡季,每日需要40000支冰淇淋,在盛夏旺季,每日约需80000---90000支。
经咨询有关部门测算,若考虑乡村距离的远近,和其他竞争因素,该厂如能保证质量,价格合理,将占60—65%的市场,即淡季的每日需求量约有24000----26000支,旺季的每日需求量约有48000----58500支。
四、混合成本的分解方法混合成本的分解,一般是根据大量的历史成本资料或成本发生的具体过程,进行分析计算,寻找混合成本与业务量之间的规律性的数量关系,最终确定固定成本和变动成本的历史平均值或标准值,他们代表正常的成本水平。
(一)高低点法以过去会计期间的总成本和业务量资料为依据,从中选取业务量最高点和业务量最低点,将总成本进行分解。
单位变动成本=(最高点业务量成本-最低点业务量成本)/(最高点业务量-最低点业务量)固定成本总额=最高点业务量成本-单位变动成本×最高点业务量或=最低点业务量成本-单位变动成本×最低点业务量应用举例【教材例题】假设A公司的业务量以直接人工工时为单位,2019年1-12月份的业务量在5.0万—7.5万小时之间变化,维修成本与业务量之间的关系如表2-5所示。
表2-5月份123456789101112业务量5.1 5.5 5.66.0 6.17.57.47.27.0 6.8 6.5 5.0(小时)维修成100104105108109120121118115112111101本(万元)单位变动成本=(最高点业务量成本-最低点业务量成本)/(最高点业务量-最低点业务量)=(120-101)/(7.5-5.0)=7.6(元/小时)固定成本总额=120-7.6×7.5=63(万元)或者:=101-7.6×5.0=63(万元)维修成本的方程式:y=63+7.6x若2020年计划的业务量为6.5万小时,预计的维修成本:Y=63+7.6×6.5=112.4(万元)。
【提示】(1)单位变动成本的计算公式中,分子是业务量变动时总成本的增加额,分母是业务量的增加额。
由于业务量增加时总成本的增加是变动成本增加引起的,所以,单位产品的增量成本就是单位产品的变动成本。
(2)分子不是(最高成本-最低成本),而是(最高业务量成本-最低业务量成本)。
(3)高低点法计算较简单,但代表性较差。
翰林公司混合成本分解
翰林公司是一家专业的教育培训机构。
课程设置涵盖了幼儿教育、
小学教育、中学教育以及各种留学考试培训等。
针对不同层次的学生
推出了多套课程,是广大学子和家长信赖的品牌。
在运营过程中,把
握成本的分解和核算是非常重要的。
下面是翰林公司的混合成本分解
情况:
1. 直接材料成本
翰林公司的课程设置需要使用大量的教材和学习资料。
这些教材和学
习资料的采购成本是公司直接材料的成本。
同时,还有一些教具和实
验器材等相关物品也属于公司直接材料的成本。
2. 直接人工成本
翰林公司聘请了众多的教师和辅导员,这些人员是课程中不可或缺的
部分。
他们的工资、福利、社保等费用是公司的直接人工成本。
3. 制造费用
翰林公司的制造费用主要包括了房屋租赁费用、水电费、物业管理费、保洁费用等。
这些费用与公司的教学活动密切相关,是公司必要的制
造费用。
4. 营销费用
翰林公司的课程需要在市场上大力宣传和推广。
因此广告费用、促销
费用、推广费用等,都是公司的营销费用。
通过混合成本分解,可以清楚地分析公司各个方面的成本构成,这有
助于公司进行成本控制和优化,提高公司的经济效益。
同时,通过混
合成本分解,也可以更好地理解公司的价格策略,帮助客户认识到公
司产品和服务的价值,提高客户对于公司的信任和满意度。
最后,翰林公司将继续秉承为客户提供优质服务的宗旨,借助混合成
本分解,不断优化自身的经营模式,为广大客户提供更好的教育服务。
1 / 2'.
混合成本分解例题:
例1:某企业1998年1-6月份的设备维修费是混合成本,有关数据如下:
月份 机器工作小时 维修费 1 400 5500 2 420 5600 3 500 6500 4 410 5550 5 390 5400 6 410 5600
确定高低点:项目 最高点(3月份) 最低点(5月份) 机器工作小时(x ) 500 390 维修费(y ) 6500 5400
计算b 和a : b =(6500-5400)÷(500-390)=10 (元)
a = y 高-bx 高=6500-10×500=1500(元)或:a=y 低-bx 低=5400-10×390=1500(元)
例2: 已知:某企业的甲产品1~8月份的产量及总成本资料如下表所示: 月份
指标
1 2 3 4 5 6 7 8
产量(件) 18 5 21 总称本(元) 6 52 200 6800
要求:采用高低点法进行成本性态分析。
注:高低点坐标的选择必须以一定时期内业务量的高低来确定,而不是按成本的高低。
解:选择高低点坐标分别为:
高点 (28 8200) 低点 (16 5200)
b =
16
285200
8200--=250
a =8200-250×28=1200 或a =5200-250×16=1200 成本模型为:y =1200+250x
答:该项混合成本中的固定部分1200元;变动部分250x 。
例3:已知:某企业业务量和总成本资料如下表所示: 月份
指标 1 2 3 4 5 6
7 8 产量(件) 18 5 21 总称本
(元)
6 52
200
6800
要求:用回归直线法进行成本性态分析。
解:①列表计算 n ∑x ∑y ∑xy ∑x2 ∑y2 数据计算表
月份 产量x 总成本y xy x 2 y 2 1 0 324 2 2 00 3 19 65
4 16 5200 83200 256
5 22 7
6 25 79 7
28 82
2 / 2'.
8 21 68
n=8
∑x =169 ∑y =542
00
∑xy =11706
00
∑x2=3675
∑y2=3737400
00
②计算相关系数 R=
)
542003737400008()16936758(54200
169117060082
2
-⨯⨯-⨯⨯-⨯=0.9788 判断:r →+1基体正相关。
③计算a b 值 b=
244391693675854200169117060082
=-⨯⨯-⨯ a=1612268169
2443954200=⨯-
④建立成本性态模型:y=161226+24439x 。
例:某企业2008年上半年有关资料如下表:
该企业采用多步骤分析法,对制造费用进行分解。
会计部门用账户分析法对3月份的制造费用进行分析,结果为:固定成本总额38千元,变动成本总额52千元,混合成本为16千元。
要求: (1) 把各月的制造费用,划分为固定费用总额、变动成本总额和混合成本总额三个部分; (2) 用高低点法对上半年的混合成本进行分解;
(3) 列出制造费用总额的成本模型,并预计8月份产量为580台的制造费用总额; (4) 用回归直线法直线对上半年的制造费用总额进行直接分解(单步骤),列出制造费用总额的成本模
型,预计8月份产品产量为580台的制造费用总额,并与(3)的结果进行比较。