拱桥结构受力分析典型例题
- 格式:docx
- 大小:202.22 KB
- 文档页数:2

目录摘要第一章绪论.................................................1.1拱桥概述............................................拱桥的特点..............................................国内外发展状况 ........................................我国拱桥的发展方向及主要结构型式........................我国拱桥的施工方法......................................1.2论文简述............................................课题介绍 ...........................................建模依据 ...........................................第二章ANSYS软件介绍.....................................2.1 ANSYS 发展........................................2.2主要功能及特点......................................2.3典型的分析过程.....................................2.4负载定义及附表...................................... 第三章有限元分析 ........................................3.1模型参数............................................3.2建模过程............................................3.3加载及后处理........................................简述自重(deadweight) 作用在中跨处施加车辆荷载(load)第四章模型实验简介第五章数据分析比较4.1 .....................第六章结论...........展望 .............致谢 .............参考文献 .........拱桥静载受力分析和模态分析计算摘要:本文对跨度为3米,矢跨比为1/6的系杆拱桥在一定外力作用下的应力、应变、位移和拱桥模态利用an sys软件,进行了有限元建模和分析计算,得到了相应的计算结果,并与实验结果进行了比对,证明了建模是合理的,计算结果是可信的。

某下承式系杆拱桥的结构受力分析叶博【摘要】以某下承式系杆拱桥为研究背景,运用Midas/Civil软件建立全桥有限元模型,分别对该桥吊杆、拱肋和系杆结构的轴力及弯矩进行数值分析,得出以下结论:1)活载引起吊杆、拱肋和系杆的轴力与弯矩值仅为恒载的1/10左右;2)恒载和活载作用下,拱肋、系杆与吊杆固结处产生附加内力随着时间推移会致使吊杆产生损伤.3)系杆拱桥的吊杆、系杆结构在恒载与活载作用下均处于受拉状态,故布置于结构内的预应力钢束能有效改善自身受力状态.【期刊名称】《兰州工业学院学报》【年(卷),期】2017(024)006【总页数】4页(P41-44)【关键词】下承式系杆拱桥;Midas/civil;吊杆;系杆;拱肋【作者】叶博【作者单位】山西省交通科学研究院,山西太原 030006【正文语种】中文【中图分类】U448.22下承式系杆拱桥主要由吊杆、拱肋以及系杆组成,其中吊杆仅承担轴力,拱肋承压为主承弯为辅,而系杆均承担弯矩和轴力,构成一个梁拱组合结构体系共同承受荷载[1-4].20纪中期,系杆拱桥逐渐在我国得到广泛运用,如临清卫运河桥、扬州大运河桥等,均为下承式系杆拱桥结构[5-6].近年来,由于国内部分系杆拱桥的建时过久,使用频率较高,且当时设计和施工阶段技术不成熟,导致目前许多下承式系杆拱桥出现诸多问题[7-8].基于此,笔者以某下承式系杆拱为研究背景,运用Midas/Civil软件建立全桥有限元模型,分别对该桥吊杆、拱肋和系杆结构的轴力及弯矩进行数值分析,研究结果可为同类桥梁设计与后期加固提供参考依据.某下承式系杆拱桥全长168 m,跨径布置为(2×22+72+2×22) m,桥面宽为:2×[1.9 m(人行道)+4.6 m(非机动车道)+2 m(分隔带)]+15 m(行车道)=32 m,设计荷载为:汽车-20级,挂车-100级.桥梁立面布置如图1所示.该桥主跨为下承式钢管混凝土系杆拱,计算跨径为72 m,矢高14.4 m,矢跨比为1/5,拱轴线为二次抛物线.拱肋采用圆形钢管混凝土截面,钢管外径为1.4 m,壁厚14 mm.系杆采用圆形截面,外径为0.8 m,壁厚10 mm,钢管内设有高强度低松弛预应力钢绞线;拱肋和系杆钢管内均使用C40微膨胀混凝土泵送填充.吊杆采用φ0.18 m圆形无缝钢管,壁厚14 mm,管内填充C30细粒式混凝土.运用Midas/Civil有限元软件建立下承式系杆拱桥计算模型,模型中拱肋、横撑、横梁、系杆、吊杆外套管均以空间梁单元进行模拟;桥面板及铺装层以板单元模拟;吊杆内预应力钢束采用初拉力形式进行张拉,并以桁架单元模拟,拱桥计算模型具体如图2所示.模型坐标系中XYZ分别表示拱桥的纵向、横向与竖向,原点O设置于某一拱脚处,将原点处支座进行固定,并分别约束其纵桥向支座的Y方向和横桥向支座的X方向,其余支座则设定为活动支座.另外,模型中拱肋和系杆采用固结连接.拱桥模拟过程中采用简化计算方法,将拱肋、系杆单元模拟成一种各项同性的材料,即将钢材和混凝土视为等效材料,并将其截面换算为等效截面.模拟中基本材料拟定为钢材,运用以下计算公式将混凝土换算成钢材.A=As+,I=Is+,γ=(γcAc+γsAs)/A.式中,s、c分别表示钢和混凝土;A、E、I、γ分别表示材料的面积、杨氏模量、惯性矩和容重.假定模拟材料均为各项同性.钢的弹性模量分别为E1=2.1×105 MPa,μ1=0.3;混凝土的弹性模量为E2=3.31×104 MPa,μ2=0.167;拱肋、系杆结构内钢-混的弹性模量比为6.34,比重为3.07.计算过程中恒载作用仅考虑结构自重,汽车活载根据《公路桥涵设计通用规范(JTG D60—2015)》中相关规定进行计算.吊杆是下承式系杆拱桥中的主要组成部分,其工作状态能反映出桥梁是否安全.通过对系杆拱桥内吊杆结构进行数值分析,获得恒载、活载作用下各吊杆的轴力变化曲线如图3所示.根据图3可知,恒载作用下吊杆左右幅的轴力变化一致,且拱桥两侧吊杆的轴力呈对称分布;而活载作用下吊杆左右幅的轴力变化差异相对较为明显,但两侧吊杆的轴力由于最不利荷载的布置差别较小,整体上仍呈对称分布.在恒载或活载作用下各吊杆均处于受拉状态,其中吊杆轴力主要由恒载作用引起,而活载作用的影响相对较小;各吊杆的轴力分布都比较均匀,且变幅较小.拱肋是系杆拱桥中主要的承重构件,其内力的控制对全桥整体受力和成桥线形起着决定性影响.通过对恒载及活载作用下拱肋结构的内力进行数值分析,获得各节点轴力与弯矩的变化规律如图4~5所示.根据图4可知,恒载作用下拱肋结构产生较大的轴向压力,两侧各节点的轴力呈对称分布,拱顶处轴力值最小,沿跨中向两侧拱脚逐渐递增;拱肋上下侧弯矩分别处于受压、受拉状态,其中拱顶处出现负弯矩,拱肋弯矩沿跨中向拱脚侧逐渐增大.从图5可以看出,活载作用下拱肋结构基本处于受拉状态,其轴力由拱脚往拱顶逐渐递减,两侧轴力分布对称,较于恒载作用,活载对拱肋轴线拉力的影响更小;拱肋全跨弯矩均为正弯矩,其中1/4跨处弯矩达到峰值,并分别向跨中、拱脚处逐渐减小.通过对拱桥系杆结构进行受力分析,分别获得恒载、活载作用下各系杆节点的轴力及弯矩变化规律如图6~7所示.根据图6可知,恒载作用下系杆全跨轴力均处于受拉状态,其中跨中处轴力值最小,且向两侧边跨方向逐渐递增,这是由于系杆与吊杆采用固结连接方式,故半刚性吊杆对系梁的轴力变化产生直接影响;而系杆全跨的弯矩分布较不规则,其原因为系杆在吊杆轴向力影响下产生数个集中力,致使吊杆与系杆固结处的弯矩发生突变.从图7可以看出,活载作用下系杆全跨轴力也均表现为受拉,但轴力变化与恒载作用差距较大,其中两侧1/4跨处轴力值最大,且逐渐向跨中及边跨减小;活载作用下系杆和吊杆固结处弯矩存在较小突变,但系杆全跨仍处于正弯矩,这是由于活载作用引起的吊杆轴力并不明显,而恒载对吊杆轴力影响较大.通过对某下承式系杆拱桥的结构受力进行数值分析,分别得出恒载和活载作用下吊杆、拱肋、系杆的结构内力变化规律,其结果可为同类桥梁设计与后期加固提供参考依据.1) 活载作用下吊杆、拱肋和系杆的内力变化明显要小于恒载作用,活载引起各构件的轴力与弯矩值仅为恒载的1/10左右.2) 恒载和活载作用下,拱肋、系杆与吊杆固结处会产生不同程度的附加内力,当拱桥长期使用时,附加内力能逐渐致使吊杆产生损伤.3) 系杆拱桥的吊杆、系杆结构在恒载与活载作用下均处于受拉状态,故布置于结构内的预应力钢束能有效改善自身受力状态,但桥梁长期使用过程中吊杆结构内钢束的预存力会逐渐减小,故可通过增设吊杆以增强拱桥承载能力.【相关文献】[1] 韩保勤.钢答混凝上拱桥吊杆张拉方案比选[J].桥梁建设,2015,45(1):114-119.[2] 赵铭伟.增大截面法在拱桥加固中的应用[J].山西交通科技,2017(1):57-60.[3] 欧阳辉来,张万华.新开河大桥拱脚设计及局部应力分析[J].世界桥梁,2009(3):33-35.[4] 杨剑,邹团结,汪金胜.梁拱组合拱桥拱脚局部应力分析和试验研究[J].铁道科学与工程学报,2014(6):25-29.[5] 于刚.九堡大桥设计过程复杂节点局部分析[J].城市道桥与防洪,2011(12):30-33.[6] 刘芳.下承式钢管混凝土拱桥空间稳定性与极限承载力研究[D].长沙:中南大学,2008.[7] 曾勇,马如进,谭红梅.大跨上承式钢管混凝土拱桥的动力特性研究[J].中外公路,2014(3):113-117.[8] 陈建兵,熊秉贤,李夏元,等.钢管混凝土拱桥新增吊杆加固设计[J].世界桥梁,2016,44(5):83-88.。

系杆拱桥力学性能分析姓名:翟硕学号:73 专业:机电系杆拱桥作为拱桥家族中的一员,具有拱桥的一般特征,又有自身的独有特点。
它是一种集拱与梁的优点于一身的桥型,它将拱与梁两种基本结构形式组合在一起,共同承受荷载,可以充分发挥梁受弯、拱受压的结构性能和组合作用。
一、拱形形状系杆拱桥通过细杆与桥体相连,减少桥体由于自重而产生的变形,增加桥体承重能力。
通过合理的设计拱形形状可以使每根细杆所受应力相同,达到最大承重的效果。
如图2所示,为系杆拱桥的简图。
L为桥拱的跨度。
图 2图 1由于桥体重力分布均匀,而每根细杆给桥体力相同,因此可以认为桥体受到均匀载荷q。
受力分析如图3所示。
图 3两只支脚所受力F=qq2⁄在桥面上任意一点所受到的弯矩M=qq(q−q)2假设挠度为ω,转角为θ。
q2q qq =q qqθ=qqqq =∫qqqqq+q解得ω=−qq24qq(q3−2qq2+q3)由胡克定律,每根杆所受应力σ=E qq q其中Δy=−ω由此可知,桥拱形状y=qq24qq(q3−2qq2+q3)当x=q2时,q qqq=5qq 4384qq 二、桥拱简单强度计算对桥拱受力分析,如图4所示图 4其中q 1是桥拱受系杆拉力所等效的均匀载荷,F与q q 分别为桥体给桥拱垂直与水平方向的拉力。
由于桥拱垂直方向受力平衡,故 F =q 1q2在A 点列桥拱右部分力矩平衡q q ∗q qqq +∫q 1qqqq 2⁄0=q ∗q /2解得 q q =48q 1qq5qq 在(x,y )点处受到的力矩为Mq q ∗q +∫q 1qqq q=q ∗q +q解得 M =q 1(4q 4−8qq 3+5q 2q 2−q 3q )10q 2当 x=(12±√24)q 时, q qqq=−q 1q 2160假设桥拱截面形状为圆形,直径为d 则桥拱所受最大正应力 q 1qqq=q qqq q=q 1q 25qq3三、桥体简单强度计算对进行桥体受力分析,如图5所示图 5假设桥体截面为宽度为b,厚度为c的正方形。

例析桥梁加固受力分析验算一、石拱桥受力分析任务大井桥桥墩基础上游侧冲空,两侧主拱圈近桥墩1/3跨处均见横向裂缝,开裂深度1/2拱圈厚度,裂缝下宽上窄。
由于项目资金少,现在拟对桥梁进行桥墩基础加深扩大、拱圈灌缝加固处理,需要对该桥梁加固方案进行拟加固后的受力分析验算,以掌握桥梁承载能力,保证桥梁安全运行,如果经复核不能满足使用要求,则采取其它方法处理。
二、桥梁情况简介大井桥位于普洱市镇沅县勐大镇平大公路(路线编码Y010530825)K1+083处,该公路等级四级,公路路基宽度4.5米,是连接镇沅县勐大镇平掌村、大井村、文蒙村的重要干道。
该桥全桥长42.3m,桥高10.24m,跨径1×17.4m+1.8m (桥墩)+1×17.4m两跨空腹式石拱桥,主拱圈的拱板的宽度是5米,厚度是0.9米,主拱圈净矢高4.25 m。
桥面0.4米栏杆+车行道4.2米+0.4米栏杆,腹拱如图,腹拱圈为半圆拱,净跨度是2米,腹拱圈厚度是0.4米,腹拱的边立墙的宽度是1米,其他的立墙的宽度是0.8米。
拱顶桥面铺装砂砾石。
桥梁于1979年动工修建,1981年竣工通车。
设计荷载不明。
桥梁簡图如下:三、调查情况对拱轴线的坐标进行检测,通过拱轴线的坐标得出该桥梁主拱圈为圆弧线。
主拱圈中轴线半径为11.1米,中轴线跨径18.136米,中轴线失高4.7米。
拱圈M10砂浆砌MU50块石,重力密度=24kN/m3。
主拱圈轴心抗压强度设计值3.85MPa,块石砌体抗剪强度设计值为0.073MPa。
拱圈石轴心抗压设计值13.24 MPa,直接抗剪强度1.3×103kPa。
(岩石的抗剪强度约为抗压强度的0.1~0.2倍,取0.1倍)抗剪安全系数γm=2.31,抗压安全系数γn=1.54。
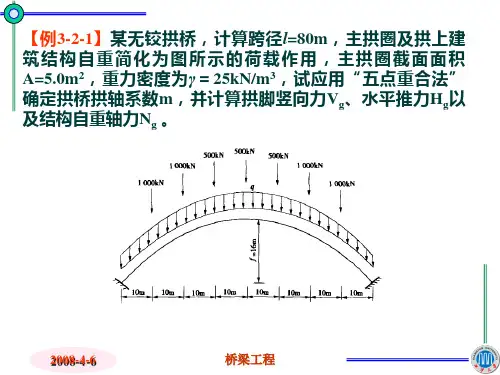
四、受力验算该拱桥构造简单,主要分析计算拱脚、跨中受力情况。
拱桥拱圈由块石砌筑而成,所以设跨中剪力=0。
考虑到桥梁为单行道,活载仅满足当地村民生活生产需要,考虑偏心受压影响,车辆活载取值1400kN(集中荷载),人群荷载3kN/m2。


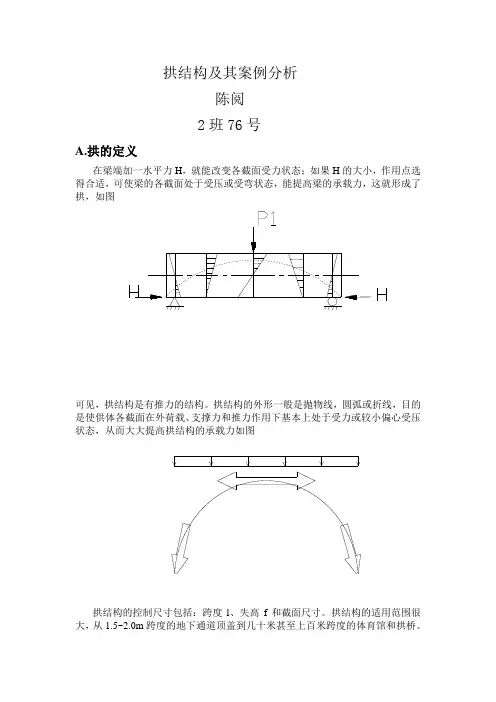
拱结构及其案例分析陈阅2班76号A.拱的定义在梁端加一水平力H,就能改变各截面受力状态;如果H的大小,作用点选得合适,可使梁的各截面处于受压或受弯状态,能提高梁的承载力,这就形成了拱,如图可见,拱结构是有推力的结构。
拱结构的外形一般是抛物线,圆弧或折线,目的是使供体各截面在外荷载、支撑力和推力作用下基本上处于受力或较小偏心受压状态,从而大大提高拱结构的承载力如图拱结构的控制尺寸包括:跨度l、失高f和截面尺寸。
拱结构的适用范围很大,从1.5~2.0m跨度的地下通道顶盖到几十米甚至上百米跨度的体育馆和拱桥。
例如清华大学综合体育中心、东凯尔勃莱德游泳馆等都采用拱结构。
拱结构的支撑形式一般有四种,如下图所示,由图a到图d分别为为:a.拉杆拱,b.落地拱,c.由框架支撑的拱,d.由水平屋盖支撑的拱。
B.拱的受力分析a.如下图所示是拱在集中荷载作用下的受力图简支拱的弯矩M与简支水平梁对应截面的弯矩M0相等。
拱的剪力Q和轴力N 等于简支水平梁对应截面上剪力Q0的两个投影。
即M= M0Q= Q0cosφN=- Q0sinφ式中,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。
b.如下图所示是拱在均布荷载作用设拱的轴线为抛物线,其方程为y=4fx(l-x)/l2求出相应的简支水平梁的弯矩和剪力M0=0.5qx(l-x) Q0=q(0.5l-x)因此,拱的内力为M=0.5qx(l-x)Q= q(0.5l-x)cosφN=- q(0.5l-x)sinφ其M图,Q图,N图分别如下图φ计算Q和N时,先要由轴线方程的一阶导数求出tgφ=dy/dx=4f (l-2x)/l2,再由此式求得截面的倾角φ。
C.三绞拱受力分析拱结构中一种比较合理的方式是三绞拱,如图所示内力计算M= M0-Hy,Q= Q0cosφ-HsinφN= -Q0sinφ-Hcosφ其中H=M0C/f ,M0和Q0分别是简支水平梁的弯矩和剪力,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。

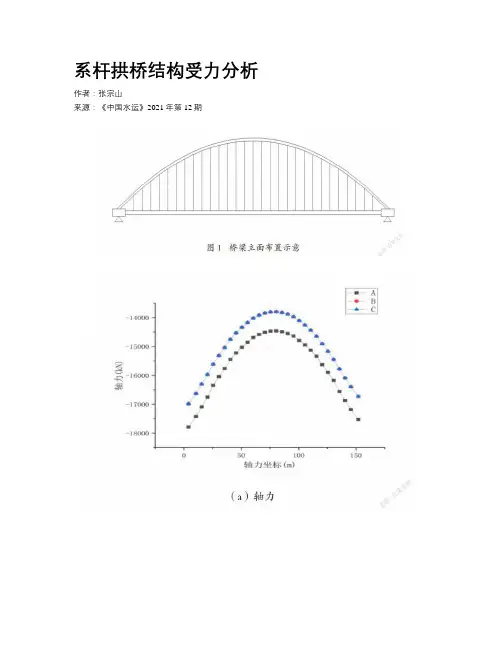
系杆拱桥结构受力分析作者:***来源:《中国水运》2021年第12期摘要:系杆拱桥兼具拱桥的跨越能力和简支梁桥对地质基础的适应能力的优点,故而广泛应用于国内外的桥梁建设。
本文以某系杆拱桥为研究背景,用有限元软件Midas/Civil对桥梁进行模拟,分析其吊杆和拱肋结构受力,得出以下结论:(1)恒载引起吊杆和拱肋的内力比活载较大;(2)在恒载和活载作用下,拱肋在拱脚处弯矩较大;(3)对于有纵坡的系杆拱桥,其纵向的不对称性会对拱肋弯矩产生影响。
研究结果可为同类桥梁设计与后期加固提供参考依据。
关键词:系杆拱桥;Midas/civil;受力分析中图分类号:U448.22+5 文献标识码:A 文章编号:1006—7973(2021)12-0151-03系杆拱桥是主要由拱肋、吊杆和系梁组成的一种复合结构体系,因其内部超静定外部简支的受力特性,故兼具有拱桥的较大跨越能力和简支梁桥对地基适应能力强两大特点。
当桥面高程受到严格限制而桥下又要求有较大的净空,或当墩台基础地质条件不佳但又要保证较大跨径时,系杆拱桥是一种较优越的桥型[1-4]。
由于系杆拱桥设计和施工技术逐渐趋于成熟,在许多城市建设和公路修建上得到大量运用,如广州南沙凤凰三桥、扬州大运河桥等,均为系杆拱桥结构[5-6]。
但随着时间推移,许多系杆拱桥均存在服役过久,使用负荷较大现象,而且当时设计和施工技术不完善,导致目前部分系杆拱桥仍存在许多问题,如出现裂缝,变形等病害,甚至直接发生倒塌,危及人民生命财产安全[7-8]。
为减少此类情况发生,笔者以某系杆拱桥为研究背景,以此桥的受力情况分析其内力作用机理。
具体方法为,使用有限元软件Midas/Civil 对桥梁进行数值模拟,以软件模型模拟桥梁真实受力情况,并读取其各部件在荷载作用下的内力情况,分析其吊杆和拱肋结构受力,本文研究结果可在同类桥梁设计以及后期加固过程中提供一定的参考依据。
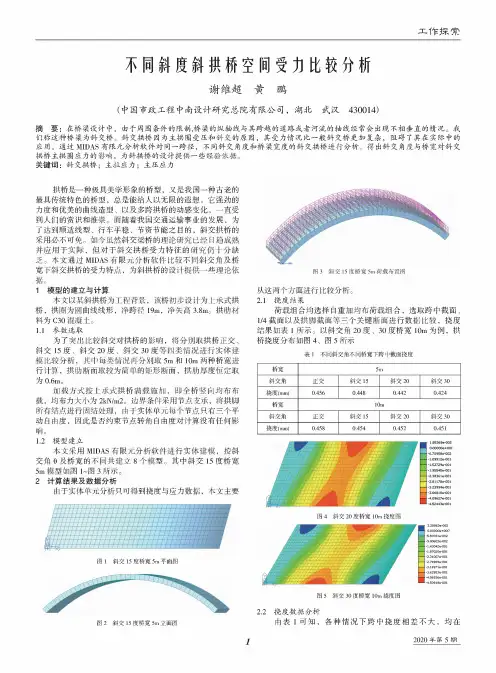
1工程概况桥梁全长179米,全宽40米,按整幅桥设计。
拱券结构是古代人们解决建筑跨度问题的有效方法,比如罗马的万神庙,我国的赵州桥都是拱券结构的典型代表。
拱券结构的特点是利用石块的楔形结构,将重力和压力沿拱向两边分解,最后由拱券两端的基石来承受。
现有六块大小、形状相同,质量相等的楔块组成一个半圆形实验拱券,如图乙所示。
如果每专人楔块的质量m=3kg,g取9.8m/s2,则;
(1)六块楔块组成的拱券对其一边的支撑物的压力是多大?
(2)如果在中间两块楔块3、4上加一个方向向下且大小为50N的压力F,如图乙所示,那么楔块2对楔块3和楔块5对楔块4的弹力F1、F2分别是多大?
(1)六块楔块受到的总重力为:
G=6mg=6×3×9.8=176.4N
由二力平衡条件知拱券对一边支撑物的压力为:
N=G2=176.42N=88.2N;
(2)以中间两楔块3、4为研究对象,其受力如图所示:
由对称性可知F1=F2
由互成120∘的二力合成特点知:
F1=F2=2mg+F=2×3×9.8+50=108.8N,
答:
(1)六块楔块组成的拱券对一边支撑物的压力是88.2N;
(2)楔块2对楔块3和楔块5对楔块4的弹力F1、F2分别是108.8N.
学生问题:第二问为什么是120度?正确答案如下图所示:
或者这样解释
请问为什么F1等于F2?。
桥梁工程-拱桥题库(含解答)预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制第一节概述1.拱桥与梁桥相比在受力性能上有哪三点差异?答:①竖向荷载作用下,支承处存在水平推力H,且全拱均相等②由于水平推力使拱桥截面弯矩比同截面的梁桥小③主拱主要承受弯压内力2.拱桥按拱上结构的形式可分为哪两种类型?答 :分为①实腹式拱桥②空腹式拱桥3.拱桥按结构体系可分为哪两类?各自受力特点就是什么?答 :如下表4.拱桥按主拱圈的横截面形式可分为哪四类?答 :分为①板拱桥②肋拱桥③双曲拱桥④箱形拱桥5.何谓计算矢跨比?何谓净矢跨比?答:计算矢跨比(D):拱圈(或拱肋)的计算矢高(f)与计算跨径(l)的比值净矢跨比(D。
):拱圈(或拱肋)的净矢高(f。
)与净跨径(l。
)的比值拱顶截面第二节拱桥的构造与设计1、何谓板拱?答 :主拱圈为矩形实体截面的拱桥,称为板拱2、何谓肋拱桥?其上部结构由哪几部分组成?答 :肋拱桥就是由两条或多条分离的平行拱肋,以及在拱肋上设置的立柱与横梁支承的形成部分组成的拱桥,其上部结构由横系梁、立柱、横梁、纵梁及桥面板组成。
3、箱形拱的主要特点有哪五点?答:①截面挖空率大,减轻了自重②箱形截面的中性轴大致居中,对于抵抗正负弯矩具有几乎相等的能力,能较好地适应主拱圈各截面的正负弯矩变化的需要③由于就是闭合空心截面,抗弯与抗扭刚度大,拱圈的整体性好,应力分布较均匀④单条肋箱刚度较大,稳定性好,能单箱肋成拱,便于无支架吊装⑤制作要求较高,吊装设备较多,主要用于大跨径拱桥4、箱形截面常用的组成方式有哪四种?各种的优缺点就是什么?答:① U型肋组成的多室箱形截面优点:预制不需要顶模,吊装稳定性好缺点:浇筑顶层砼时需要侧模,安装不方便② I型肋组成的多室箱形截面优点:无需浇筑顶层砼(不需要侧模),施工工序少缺点:吊装稳定性差③箱形肋组成的多室箱形截面优点:吊装稳定性好,抗弯、抗扭刚度大缺点:吊装自重大5、实腹式拱上建筑的特点就是什么?答:①构造简单②施工方便③填料数量较多④恒重大6、拱上侧墙、护拱的作用各就是什么?答:侧墙的作用就是承受拱腹填料及车辆荷载所产生的侧压力(推力)护拱的作用就是加强拱脚段拱圈,同时便于在多孔拱桥中敷设防水层与排出积水7、空腹式拱上建筑的特点就是什么?答:空腹式拱上建筑的最大特点就是除了具有实腹拱上建筑相同构造外,还具有腹孔与腹孔墩,减轻了拱桥恒重,同时增加了美观性8、拱上腹孔的布置原则就是什么?答:①应对称布置在靠拱脚侧的一定区段内②一般为奇数孔③腹孔构造宜统一,以便与施工与有利于腹孔墩的受力④腹拱高度应布置在主拱圈允许的高度内⑤应尽量减轻贡上建筑恒重,不使腹孔墩过分集中或者过分分散9、伸缩缝与变形缝的作用就是什么?答:①符合受力图式②避免不规则开裂10.排除拱桥腹内积水有哪两个重要性?答:①避免含水量的增大,确保路面强度②防止雨水渗到主要结构内,使其发生冻胀破坏11.拱桥中铰按性质可分为哪两种类型?答 :分为①永久性铰②临时性铰12.拱桥的主要设计标高有哪四个?答:①桥面标高(主要有三个:桥梁起点、终点及跨中点的桥面标高)②拱顶底面标高③起拱线标高④基底标高13.为什么说拱桥的主拱的矢跨比就是拱轴设计中的主要参数之一?答:①拱桥的水平推力与垂直反力之比值,随矢跨比的减小而增大②当矢跨比减小时,拱的推力增大,反之则水平推力减小③无铰拱随矢跨比减小其弹性压缩、温度变化、混凝土收缩及墩台位移产生的附加内力越大④拱的矢跨比过大使拱脚段施工困难⑤矢跨比对拱桥的外形及周围景观的协调产生影响14.不等跨拱桥的主要受力特点就是什么?在处理不等跨分孔时应注意控制的实质性问题就是什么?如何作?答 :不等跨拱桥的主要受力特点就是:恒载产生的相邻跨的水平推力不等处理不等跨分孔时应注意控制的实质性问题就是:尽量减小因恒载引起的不平衡推力对桥墩基底的偏心作用处理不等跨分孔的方法:采用不同的矢跨比;采取不同的起拱线标高;15.什么就是拱轴线?什么就是合理拱轴线?拱轴线的种类有哪些?各对应哪种荷载模式?答 :拱轴线就是拱圈横截面形心点的连线将恒载作用下的压力线作为主拱圈的设计拱轴线则称为合理拱轴线圆弧拱轴线:等静水压力;抛物线拱轴线:均布荷载;悬链线:与竖坐标成比例的荷载。
××大桥拱圈浇筑过程中拱圈支架的受力分析××大学应用力学研究所目录1.工程概况 (1)2.有限元分析模型的建立 (1)2.1.结构模型的简化 (1)2.2.材料说明 (3)2.3.按设计说明要求进行整体计算 (3)2.3.1.拱架位移 (4)2.3.2.拱架应力 (5)2.3.3.拱架稳定 (5)3.砼施工过程中拱架受力计算 (6)3.1.荷载的简化 (6)3.2.施工阶段的模拟 (7)4.各施工阶段拱圈支架的受力情况 (7)4.1.第一阶段:拱架自重,拱盔荷、载风荷载作用 (7)4.1.1.拱架位移 (7)4.1.2.拱架应力 (8)4.2.第二阶段:对称浇筑拱脚段22.447m底板 (8)4.2.1.拱架位移 (8)4.2.2.拱架应力 (9)4.3.第三阶段:浇筑拱顶段30.762m底板 (9)4.3.1.拱架位移 (9)4.3.2.拱架应力 (10)4.4.第四阶段:对称浇筑1/4跨段20.073m底板(底板合拢) 104.4.1.拱架位移 (10)4.4.2.拱架应力 (11)4.5.第五阶段:对称浇筑拱脚段22.72m腹板 (11)4.5.1.拱架位移 (11)4.5.2.拱架应力 (12)4.6.第六阶段:浇筑拱顶段31.137m腹板 (12)4.6.1.拱架位移 (12)4.6.2.拱架应力 (13)4.7.第七阶段:对称浇筑1/4跨段20.318m腹板(腹板合拢) 134.7.1.拱架位移 (13)4.7.2.拱架应力 (14)4.8.第八阶段:对称浇筑拱脚段23m顶板 (14)4.8.1.拱架位移 (14)4.8.2.拱架应力 (15)4.9.第九阶段:浇筑拱顶段31.513m顶板 (15)4.9.1.拱架位移 (15)4.9.2.拱架应力 (16)4.10.第十阶段:对称浇筑1/4跨段20.563m顶板(顶板合拢) 164.10.1.拱架位移 (16)4.10.2.拱架应力 (17)5.各施工阶段拱圈支架的稳定情况 (17)5.1.整体稳定计算 (17)5.1.1.浇筑底板时拱架的整体稳定计算 (17)5.1.2.浇筑腹板时拱架的整体稳定计算 (18)5.2.局部稳定计算 (19)5.2.1.上弦杆局部稳定计算 (20)5.2.2.下弦杆局部稳定计算 (20)5.3.抗风倾覆性验算 (22)6.总结 (22)7.结论与建议 (23)1. 工程概况××大桥是××至四级公路项目中的一座大型桥梁,里程桩号K0+177.675~K0+327.325,桥梁全长149.65m ,桥型布置为:2x10m (钢筋混凝土空心板)+1x105(箱型拱)+1x10m (钢筋混凝土空心板),主桥桥宽9.0m 。
第一节概述1.拱桥与梁桥相比在受力性能上有哪三点差异答:①竖向荷载作用下,支承处存在水平推力H,且全拱均相等②由于水平推力使拱桥截面弯矩比同截面的梁桥小③主拱主要承受弯压内力2.拱桥按拱上结构的形式可分为哪两种类型答:分为①实腹式拱桥②空腹式拱桥3.拱桥按结构体系可分为哪两类各自受力特点是什么答:如下表4.拱桥按主拱圈的横截面形式可分为哪四类答:分为①板拱桥②肋拱桥③双曲拱桥④箱形拱桥5.何谓计算矢跨比何谓净矢跨比答:计算矢跨比(D):拱圈(或拱肋)的计算矢高(f)与计算跨径(l)的比值净矢跨比(D。
):拱圈(或拱肋)的净矢高(f。
)与净跨径(l。
)的比值拱顶截面第二节拱桥的构造与设计1.何谓板拱答:主拱圈为矩形实体截面的拱桥,称为板拱2.何谓肋拱桥其上部结构由哪几部分组成答:肋拱桥是由两条或多条分离的平行拱肋,以及在拱肋上设置的立柱和横梁支承的形成部分组成的拱桥,其上部结构由横系梁、立柱、横梁、纵梁及桥面板组成。
3.箱形拱的主要特点有哪五点答:①截面挖空率大,减轻了自重②箱形截面的中性轴大致居中,对于抵抗正负弯矩具有几乎相等的能力,能较好地适应主拱圈各截面的正负弯矩变化的需要③由于是闭合空心截面,抗弯和抗扭刚度大,拱圈的整体性好,应力分布较均匀④单条肋箱刚度较大,稳定性好,能单箱肋成拱,便于无支架吊装⑤制作要求较高,吊装设备较多,主要用于大跨径拱桥4.箱形截面常用的组成方式有哪四种各种的优缺点是什么答:① U型肋组成的多室箱形截面优点:预制不需要顶模,吊装稳定性好缺点:浇筑顶层砼时需要侧模,安装不方便② I型肋组成的多室箱形截面优点:无需浇筑顶层砼(不需要侧模),施工工序少缺点:吊装稳定性差③箱形肋组成的多室箱形截面优点:吊装稳定性好,抗弯、抗扭刚度大缺点:吊装自重大5.实腹式拱上建筑的特点是什么答:①构造简单②施工方便③填料数量较多④恒重大6.拱上侧墙、护拱的作用各是什么答:侧墙的作用是承受拱腹填料及车辆荷载所产生的侧压力(推力)护拱的作用是加强拱脚段拱圈,同时便于在多孔拱桥中敷设防水层和排出积水7.空腹式拱上建筑的特点是什么答:空腹式拱上建筑的最大特点是除了具有实腹拱上建筑相同构造外,还具有腹孔和腹孔墩,减轻了拱桥恒重,同时增加了美观性8.拱上腹孔的布置原则是什么答:①应对称布置在靠拱脚侧的一定区段内②一般为奇数孔③腹孔构造宜统一,以便与施工和有利于腹孔墩的受力④腹拱高度应布置在主拱圈允许的高度内⑤应尽量减轻贡上建筑恒重,不使腹孔墩过分集中或者过分分散9.伸缩缝与变形缝的作用是什么答:①符合受力图式②避免不规则开裂10.排除拱桥腹内积水有哪两个重要性答:①避免含水量的增大,确保路面强度②防止雨水渗到主要结构内,使其发生冻胀破坏11.拱桥中铰按性质可分为哪两种类型答:分为①永久性铰②临时性铰12.拱桥的主要设计标高有哪四个答:①桥面标高(主要有三个:桥梁起点、终点及跨中点的桥面标高)②拱顶底面标高③起拱线标高④基底标高13.为什么说拱桥的主拱的矢跨比是拱轴设计中的主要参数之一答:①拱桥的水平推力与垂直反力之比值,随矢跨比的减小而增大②当矢跨比减小时,拱的推力增大,反之则水平推力减小③无铰拱随矢跨比减小其弹性压缩、温度变化、混凝土收缩及墩台位移产生的附加内力越大④拱的矢跨比过大使拱脚段施工困难⑤矢跨比对拱桥的外形及周围景观的协调产生影响14.不等跨拱桥的主要受力特点是什么在处理不等跨分孔时应注意控制的实质性问题是什么如何作答:不等跨拱桥的主要受力特点是:恒载产生的相邻跨的水平推力不等处理不等跨分孔时应注意控制的实质性问题是:尽量减小因恒载引起的不平衡推力对桥墩基底的偏心作用处理不等跨分孔的方法:采用不同的矢跨比;采取不同的起拱线标高;15.什么是拱轴线什么是合理拱轴线拱轴线的种类有哪些各对应哪种荷载模式答:拱轴线是拱圈横截面形心点的连线将恒载作用下的压力线作为主拱圈的设计拱轴线则称为合理拱轴线圆弧拱轴线:等静水压力;抛物线拱轴线:均布荷载; 悬链线:与竖坐标成比例的荷载。
拱券结构是古代人们解决建筑跨度问题的有效方法,比如罗马的万神庙,我国的赵州桥都是拱券结构的典型代表。
拱券结构的特点是利用石块的楔形结构,将重力和压力沿拱向两边分解,最后由拱券两端的基石来承受。
现有六块大小、形状相同,质量相等的楔块组成一个半圆形实验拱券,如图乙所示。
如果每专人楔块的质量m=3kg,g取9.8m/s2,则;
(1)六块楔块组成的拱券对其一边的支撑物的压力是多大?
(2)如果在中间两块楔块3、4上加一个方向向下且大小为50N的压力F,如图乙所示,那么楔块2对楔块3和楔块5对楔块4的弹力F1、F2分别是多大?
(1)六块楔块受到的总重力为:
G=6mg=6×3×9.8=176.4N
由二力平衡条件知拱券对一边支撑物的压力为:
N=G2=176.42N=88.2N;
(2)以中间两楔块3、4为研究对象,其受力如图所示:
由对称性可知F1=F2
由互成120∘的二力合成特点知:
F1=F2=2mg+F=2×3×9.8+50=108.8N,
答:
(1)六块楔块组成的拱券对一边支撑物的压力是88.2N;
(2)楔块2对楔块3和楔块5对楔块4的弹力F1、F2分别是108.8N.
学生问题:第二问为什么是120度?正确答案如下图所示:
或者这样解释
请问为什么F1等于F2?。