浙江省杭州市2019年中考数学一轮复习第三章函数其图象第四节反比例函数同步测试

专题06 方程及其应用反比例函数1．（2019·浙江温州）验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表，根据表中数据，可得y关于x的函数表达式为近视眼镜的度数y（度）200 250 400 500 1000 镜片焦距x（米）0.50 0.40 0.25 0.20 0.10A．y100x=B．y100x=C．y400x=D．y400x=【答案】A【解析】由表格中数据可得：xy=100，故y关于x的函数表达式为：y100x =．故选A．【名师点睛】此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．2．（2019·浙江台州）已知某函数的图象C与函数y3x=的图象关于直线y=2对称．下列命题①图象C与函数y3x=的图象交于点（32，2）；②点（12，–2）在图象C上；③图象C上的点的纵坐标都小于4；④A（x1，y1），B（x2，y2）是图象C上任意两点，若x1>x2，则y1>y2．其中真命题是A．①②B．①③④C．②③④D．①②③④【答案】A【解析】∵函数y3x=的图象在第一、三象限，函数y3x=的图象关于直线y=2对称，则点（32，2）是图象C与函数y3x=的图象的交点；∴①正确；点（12，–2）关于y=2对称的点为点（12，6），∵（12，6）在函数y3x=上，∴点（12，–2）在图象C上；∴②正确；∵y 3x=中y ≠0，x ≠0， 取y 3x=上任意一点为（x ，3x ），则点（x ，3x ）与y =2对称点的纵坐标为43x-；当x <0时，43x->0，∴③错误；A （x 1，y 1），B （x 2，y 2）关于y =2对称点为（x 1，4–y 1），B （x 2，4–y 2）在函数y 3x=上， ∴4–y 113x =，4–y 223x =，只有当x 1>x 2>0或0>x 1>x 2时，4–y 1<4–y 2，即y 1>y 2， ∴④不正确； 故选A ．【名师点睛】本题考查反比例函数图象及性质；熟练掌握函数关于直线后对称时，对应点关于直线对称是解题的关键．3．（2019·浙江绍兴）如图，矩形ABCD 的顶点A ，C 都在曲线y kx=（常数k >0，x >0）上，若顶点D 的坐标为（5，3），则直线BD 的函数表达式是__________．【答案】y 35=x 【解析】∵D （5，3）， ∴A （3k ，3），C （5，5k）， ∴B （3k ，5k）， 设直线BD 的解析式为y =mx +n ，把D （5，3），B （3k ，5k）代入， 得5335m n k k m n +=⎧⎪⎨+=⎪⎩，解得350m n ⎧=⎪⎨⎪=⎩， ∴直线BD 的解析式为y 35=x ． 故答案为y 35=x ． 【名师点睛】本题考查了反比例函数图象上点的坐标特征：反比例函数y kx=（k 为常数，k ≠0）的图象是双曲线，图象上的点（x ，y ）的横纵坐标的积是定值k ，即xy =k ．也考查了矩形的性质．4．（2019·浙江衢州）如图，在平面直角坐标系中，O 为坐标原点，Y ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，点C 在第一象限，将△AOD 沿y 轴翻折，使点A 落在x 轴上的点E 处，点B 恰好为OE 的中点，DE 与BC 交于点F ．若y kx=（k ≠0）图象经过点C ，且S △BEF =1，则k 的值为__________．【答案】4【解析】如图，连接OC ，BD ，∵将△AOD 沿y 轴翻折，使点A 落在x 轴上的点E 处，∴OA =OE ， ∵点B 恰好为OE 的中点，∴OE =2OB ，∴OA =2OB ， 设OB =BE =x ，则OA =2x ，∴AB =3x ， ∵四边形ABCD 是平行四边形， ∴CD =AB =3x ，∵CD ∥AB ，∴△CDF ∽△BEF ， ∴133BE EF x CD DF x ===， ∵S △BEF =1，∴S △BDF =3，S △CDF =9，∴S△BCD=12，∴S△CDO=S△BDC=12，∴k=2S△CDO=24．【名师点睛】本题考查了反比例函数系数k的几何意义，折叠的性质，平行四边形的性质，相似三角形的判定和性质，正确的作出辅助线是解题的关键．5．（2019·浙江宁波）如图，过原点的直线与反比例函数ykx=（k>0）的图象交于A，B两点，点A在第一象限．点C在x轴正半轴上，连结AC交反比例函数图象于点D．AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连结DE．若AC=3DC，△ADE的面积为8，则k的值为__________．【答案】6【解析】如图，连接OE，CE，过点A作AF⊥x轴，过点D作DH⊥x轴，过点D作DG⊥AF，∵过原点的直线与反比例函数ykx=（k>0）的图象交于A，B两点，∴A与B关于原点对称，∴O 是AB 的中点， ∵BE ⊥AE ， ∴OE =OA ， ∴∠OAE =∠AEO ， ∵AE 为∠BAC 的平分线， ∴∠BAE =∠DAE ， ∴∠DAE =∠AEO ， ∴AD ∥OE ， ∴S △ACE =S △AOC ，∵AC =3DC ，△ADE 的面积为8， ∴S △ACE =S △AOC =12， 设点A （m ，km）， ∵AC =3DC ，DH ∥AF ， ∴3DH =AF ， ∴D （3m ，3km）， ∵CH ∥GD ，AG ∥DH ， ∴△DHC ∽△AGD ， ∴S △HDC 14=S △ADG ， ∵S△AOC =S △AOF +S梯形AFHD +S△HDC1122k =+⨯（DH +AF ）×FH +S △HDC 114223k k m=+⨯⨯2m 112142243236k k km k m +⨯⨯⨯=++=12， ∴2k =12，∴k =6； 故答案为6．【名师点睛】本题考查反比例函数k 的意义；借助直角三角形和角平分线，将△ACE 的面积转化为△AOC 的面积是解题的关键．6．（2019·浙江湖州）如图，已知在平面直角坐标系xOy 中，直线y 12=x ﹣1分别交x 轴，y 轴于点A 和点B ，分别交反比例函数y 1k x =（k >0，x >0），y 22k x=（x ＜0）的图象于点C 和点D ，过点C 作CE ⊥x 轴于点E ，连结OC ，OD ．若△COE 的面积与△DOB 的面积相等，则k 的值是__________．【答案】2【解析】令x =0，得y 12=x ﹣1=﹣1， ∴B （0，﹣1）， ∴OB =1， 把y 12=x ﹣1代入y 22k x =（x ＜0）中得，12x ﹣12k x=（x ＜0），解得x =1∴1D x =，∴1122OBD D S OB x =⋅=V ， ∵CE ⊥x 轴， ∴12OCE S k =V ， ∵△COE 的面积与△DOB 的面积相等，1122k =， ∴k =2，或k =0（舍去）． 故答案为：2．【名师点睛】本题是一次函数与反比例函数的交点问题，主要考查了一次函数和反比例函数的图象与性质，反比例函数“k ”的几何意义，一次函数图象与反比例函数图象的交点问题，关键是根据两个三角形的面积相等列出k 的方程．7．（2019·浙江杭州）方方驾驶小汽车匀速地从A 地行驶到B 地，行驶里程为480千米，设小汽车的行驶时间为t （单位：小时），行驶速度为v （单位：千米/小时），且全程速度限定为不超过120千米/小时． （1）求v 关于t 的函数表达式；（2）方方上午8点驾驶小汽车从A 地出发．①方方需在当天12点48分至14点（含12点48分和14点）间到达B地，求小汽车行驶速度v的范围．②方方能否在当天11点30分前到达B地？说明理由．【答案】（1）v关于t的函数表达式为：v480t=（t≥4）．（2）①可得小汽车行驶速度v的范围为：80≤v≤100．方方不能在当天11点30分前到达B地．【解析】（1）因为vt=480，且全程速度限定为不超过120千米/小时，②所以v关于t的函数表达式为：v480t=（t≥4）．理由见解析.（2）①8点至12点48分，时间长为245小时；8点至14点，时间长为6小时．将t=6代入v480t=，解得v=80；将t245=代入v480t=，解得v=100．综上可得小汽车行驶速度v的范围为：80≤v≤100．②方方不能在当天11点30分前到达B地．理由如下：8点至11点30分，时间长为72小时，将t72=代入v480t=，解得v=9607．因为9607>120，所以超速了．故方方不能在当天11点30分前到达B地．【名师点睛】本题考查反比例函数在行程问题中的应用，根据时间速度和路程的关系可以求解，本题难度不大．8．（2019·浙江金华）如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数yk x =（k>0，x>0）的图象上，边CD在x轴上，点B在y轴上，已知CD=2．（1）点A是否在该反比例函数的图象上？请说明理由；（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标；（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．【答案】（1）点A在该反比例函数的图象上，理由见解析；（2）Q；【解析】（1）点A在该反比例函数的图象上，理由如下：如图，过点P作x轴垂线PG，连接BP，∵P是正六边形ABCDEF的对称中心，CD=2，∴BP=2，G是CD的中点，∴PG=∴P（2），∵P在反比例函数ykx=上，∴k∴y=，由正六边形的性质，A（1，），∴点A在反比例函数图象上；（2）由题易得点D的坐标为（3，0），点E的坐标为（4），设直线DE的解析式为y=ax+b，∴304a b a b +=⎧⎪⎨+=⎪⎩∴a b ⎧=⎪⎨=-⎪⎩， ∴y =﹣，联立方程y y ⎧=⎪⎨⎪=-⎩， 解得x =∴Q点横坐标为32+； （3）A （1，B （0），C （1，0），D （3，0），E （4），F （3，设正六边形向左平移m 个单位，向上平移n 个单位，则平移后点的坐标分别为∴A （1﹣m ，n ），B （﹣mn ），C （1﹣m ，n ），D （3﹣m ，n ），E （4﹣mn ）， F （3﹣m ，n ），①将正六边形向左平移两个单位后，E （2F （1，）； 则点E 与F 都在反比例函数图象上；②将正六边形向左平移–1C （2），B （1，则点B 与C 都在反比例函数图象上；③将正六边形向左平移2个单位，再向上平移–个单位后，B （﹣2，，C （﹣1，﹣； 则点B 与C 都在反比例函数图象上．【名师点睛】本题主要考查反比例函数的图象及性质，正六边形的性质；将正六边形的边角关系与反比例函数上点的坐标结合是解题的关系．9．（2019·浙江舟山）如图，在直角坐标系中，已知点B （4，0），等边三角形OAB 的顶点A 在反比例函数y k x=的图象上． （1）求反比例函数的表达式．（2）把△OAB 向右平移a 个单位长度，对应得到△O 'A 'B '，当这个函数图象经过△O 'A 'B '一边的中点时，求a 的值．【答案】（1）反比例函数的解析式为y =；（2）a 的值为1或3．【解析】（1）如图1，过点A 作AC ⊥OB 于点C ， ∵△OAB 是等边三角形， ∴∠AOB =60°，OC 12=OB ，∵B （4，0）， ∴OB =OA =4， ∴OC =2，AC把点A （2，y k x =，解得k∴反比例函数的解析式为y =；（2）分两种情况讨论：①当点D 是A ′B ′的中点，如图2，过点D 作DE ⊥x 轴于点E ．由题意得A ′B ′=4，∠A ′B ′E =60°，在Rt △DEB ′中，B ′D =2，DE，B ′E =1．∴O′E=3，把y=y=，得x=4，∴OE=4，∴a=OO′=1；②如图3，点F是A′O′的中点，过点F作FH⊥x轴于点H．由题意得A′O′=4，∠A′O′B′=60°，在Rt△FO′H中，FH=O′H=1．把y=y=，得x=4，∴OH=4，∴a=OO′=3，综上所述，a的值为1或3．【名师点睛】本题考查了用待定系数法求反比例函数的解析式，掌握直角三角形、等边三角形的性质以及分类讨论思想是解题的关键．。

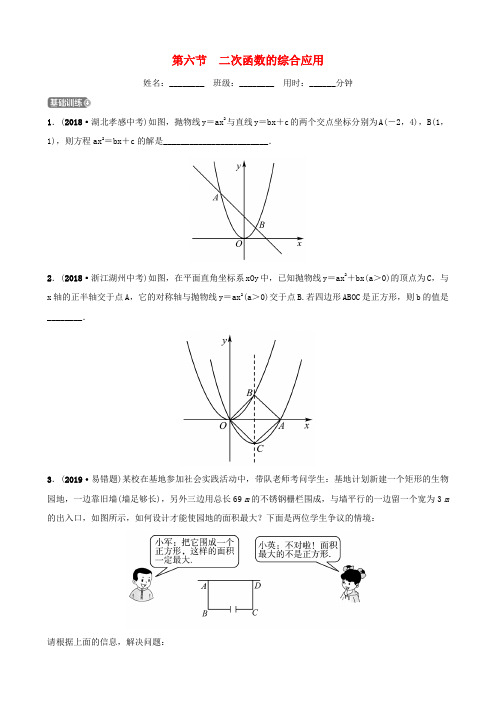
第六节二次函数的综合应用姓名：________ 班级：________ 用时：______分钟1．(2018·湖北孝感中考)如图，抛物线y＝ax2与直线y＝bx＋c的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax2＝bx＋c的解是________________________．2．(2018·浙江湖州中考)如图，在平面直角坐标系xOy中，已知抛物线y＝ax2＋bx(a＞0)的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2(a＞0)交于点B.若四边形ABOC是正方形，则b的值是________．3．(2019·易错题)某校在基地参加社会实践活动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙(墙足够长)，另外三边用总长69 m的不锈钢栅栏围成，与墙平行的一边留一个宽为3 m 的出入口，如图所示，如何设计才能使园地的面积最大？下面是两位学生争议的情境：请根据上面的信息，解决问题：(1)设AB ＝x m (x>0)，试用含x 的代数式表示BC 的长；(2)请你判断谁的说法正确，为什么？4. (2018·湖北襄阳中考)襄阳市精准扶贫工作已进入攻坚阶段．贫困户张大爷在某单位的帮扶下，把一片坡地改造后种植了优质水果蓝莓，今年正式上市销售．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第x 天的售价为y 元/千克，y 关于x 的函数表达式为y ＝⎩⎪⎨⎪⎧mx －76m （1≤x<20，x 为正整数），n （20≤x≤30，x 为正整数），且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售蓝莓的成本是18元/千克，每天的利润是W 元(利润＝销售收入－成本)．(1)m ＝________，n ＝________；(2)求销售蓝莓第几天时，当天的利润最大？最大利润是多少？(3)在销售蓝莓的30天中，当天利润不低于870元的共有多少天？5．(2018·山东泰安中考)一元二次方程(x ＋1)(x －3)＝2x －5根的情况是( )A ．无实数根B ．有一个正根，一个负根C ．有两个正根，且都小于3D ．有两个正根，且有一根大于36．如图，已知直线y ＝－34x ＋3分别交x 轴、y 轴于点A ，B ，P 是抛物线y ＝－12x 2＋2x ＋5上的一个动点，其横坐标为a ，过点P 且平行于y 轴的直线交直线y ＝－34x ＋3于点Q ，则当PQ ＝BQ 时，a 的值是__________________________．7．如图，抛物线y ＝a(x －1)2＋c 与x 轴交于点A(1－3，0)和点B ，将抛物线沿x 轴向上翻折，顶点P 落在点P′(1，3)处．(1)求原抛物线的函数表达式；(2)学校举行班徽设计比赛，九年级(5)班的小明在解答此题时顿生灵感：过点P′作x 轴的平行线交抛物线于C ，D 两点，将翻折后得到的新图象在直线CD 以上的部分去掉，设计成一个“W”型的班徽，“5”的拼音开头字母为W ，“W”图案似大鹏展翅，寓意深远；而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比5－12(约等于0.618)．请你计算这个“W”图案的高与宽的比到底是多少(参考数据：5≈2.236，6≈2.449，结果可保留根号)．8．(2017·湖南邵阳中考)如图所示，顶点为(12，－94)的抛物线y ＝ax 2＋bx ＋c 过点M(2，0)． (1)求抛物线的表达式；(2)点A 是抛物线与x 轴的交点(不与点M 重合)，点B 是抛物线与y 轴的交点，点C 是直线y ＝x ＋1上一点(处于x 轴下方)，点D 是反比例函数y ＝k x(k ＞0)图象上一点，若以点A ，B ，C ，D 为顶点的四边形是菱形，求k 的值．参考答案【基础训练】1．x 1＝－2，x 2＝1 2.－23．解：(1)AB ＝x m ，可得BC ＝69＋3－2x ＝(72－2x)m.(2)小英说法正确，理由如下：矩形面积S ＝x(72－2x)＝－2(x －18)2＋648，∵72－2x>0，∴x<36，∴0<x<36.∴当x ＝18时，S 取最大值，此时x≠72－2x ，∴面积最大的不是正方形．4．解：(1)第12天的售价为32元/千克，代入y ＝mx －76m ，得32＝12m －76m ，解得m ＝－12. 第26天的售价为25元/千克，代入y ＝n ，则n ＝25，故答案为m ＝－12，n ＝25. (2)由题意知，第x 天的销售量为20＋4(x －1)＝4x ＋16，当1≤x＜20时，W ＝(4x ＋16)(－12x ＋38－18)＝－2x 2＋72x ＋320＝－2(x －18)2＋968， ∴当x ＝18时，W 最大＝968元．当20≤x≤30时，W ＝(4x ＋16)(25－18)＝28x ＋112.∵28＞0，∴W 随x 的增大而增大，∴当x ＝30时，W 最大＝952元．∵968＞952，∴当x ＝18时，W 最大＝968元．(3)当1≤x＜20时，令－2x 2＋72x ＋320＝870，解得x 1＝25，x 2＝11.∵抛物线W ＝－2x 2＋72x ＋320的开口向下，∴11≤x≤25时，W≥870.又∵11≤x＜20，x 为正整数，∴有9天利润不低于870元，当20≤x≤30时，令28x ＋112≥870，解得x≥27114. ∴27114≤x≤30.∵x 为正整数，∴有3天利润不低于870元．∴综上所述，当天利润不低于870元的天数共有12天．【拔高训练】5．D 6.－1，4，4＋25，4－2 57．解：(1)∵点P 与点P′(1，3)关于x 轴对称，∴点P 的坐标为(1，－3)．设原抛物线的表达式为y ＝a(x －1)2－3，∵其过点A(1－3，0)，∴0＝a(1－3－1)2－3，解得a ＝1.∴原抛物线的函数表达式为y ＝(x －1)2－3，即y ＝x 2－2x －2.(2)∵CD∥x 轴，P′(1，3)在CD 上，∴C，D 两点纵坐标均为3.由(x －1)2－3＝3，解得x 1＝1－6，x 2＝1＋6，∴C，D 两点的坐标分别为(1－6，3)，(1＋6，3)，∴CD＝2 6.∴“W”图案的高与宽(CD)的比为326＝64(或约等于0.612)． 【培优训练】8．解：(1)依题意可设抛物线的表达式为 y ＝a(x －12)2－94(a≠0)， 将点M(2，0)代入可得a(2－12)2－94＝0， 解得a ＝1.故抛物线的表达式为y ＝(x －12)2－94. (2)由(1)知，抛物线的表达式为y ＝(x －12)2－94， 其对称轴为x ＝12， ∴点A 与点M(2，0)关于直线x ＝12对称，∴A(－1，0)． 令x ＝0，则y ＝－2，∴B (0，－2)．在Rt△OAB 中，OA ＝1，OB ＝2，则AB ＝ 5.设直线y ＝x ＋1与y 轴交于点G ，易求G(0，1)．∴△AOG 是等腰直角三角形，∴∠AGO＝45°.∵点C 是直线y ＝x ＋1上一点(处于x 轴下方)，而k ＞0，∴反比例函数y ＝k x(k ＞0)的图象位于第一、三象限．故点D 只能在第一、三象限，因此符合条件的菱形只能有如下2种情况：①此菱形以AB 为边且AC 也为边，如图1所示，过点D 作DN⊥y 轴于点N ，在Rt△BDN 中，∵∠DBN ＝∠AGO＝45°，∴DN＝BN ＝52＝102， ∴D(－102，－102－2)． ∵点D 在反比例函数y ＝k x(k ＞0)图象上， ∴k＝－102×(－102－2)＝52＋10. ②此菱形以AB 为对角线，如图2，作AB 的垂直平分线CD 交直线y ＝x ＋1于点C ，交反比例函数y ＝k x(k ＞0)的图象于点D. 再分别过点D ，B 作DE⊥x 轴于点F ，BE⊥y 轴，DE 与BE 相交于点E.在Rt△BDE 中，同①可证∠AGO＝∠DBO＝∠BDE＝45°，∴BE＝DE.可设点D 的坐标为(x ，x －2)．∵BE 2＋DE 2＝BD 2， ∴BD＝2BE ＝2x.∵四边形ABCD 是菱形，∴AD＝BD ＝2x.∴在Rt△ADF 中，AD 2＝AF 2＋DF 2，即(2x)＝(x ＋1)2＋(x －2)2， 解得x ＝52， ∴点D 的坐标是(52，12)． ∵点D 在反比例函数y ＝k x(k ＞0)的图象上， ∴k＝52×12＝54，综上所述，k 的值是52＋10或54.。

第三节一次函数的实际应用姓名：________ 班级：________ 用时：______分钟1．(2018·江苏无锡中考)一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2 600 kg的这种水果．已知水果店每售出1 kg该水果可获利润10元，未售出的部分每1 kg将亏损6元，以x(单位：kg，2 000≤x≤3 000)表示A酒店本月对这种水果的需求量，y(元)表示水果店销售这批水果所获得的利润．(1)求y关于x的函数表达式；(2)问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获的利润不少于22 000元？2．某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动，11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家．他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回，同时，爸爸在家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x(小时)后，到达离家y(千米)的地方，图中折线OABCD表示y与x之间的函数关系．(1)活动中心与小宇家相距________千米，小宇在活动中心活动时间为________小时，他从活动中心返家时，步行用了________小时；(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围)；(3)根据上述情况(不考虑其他因素)，请判断小宇是否能在12：00前回到家，并说明理由．3．如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数．(1)设北京时间为x(时)，首尔时间为y(时)，就0≤x≤12，求y关于x的函数表达式，并填写下表(同一时刻的两地时间)．(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间，两地时差为整数．如果现在伦敦时间(夏时制)为7：30，那么此时韩国首尔时间是多少？4. (2017·河北中考)如图，直角坐标系xOy 中，A(0，5)，直线x ＝－5与x 轴交于点D ，直线y ＝－38x －398与x 轴及直线x ＝－5分别交于点C ，E ，点B ，E 关于x 轴对称，连结AB. (1)求点C ，E 的坐标及直线AB 的表达式； (2)设面积的和S ＝S △CDE ＋S 四边形ABDO ，求S 的值；(3)在求(2)中S 时，嘉琪有个想法：“将△CDE 沿x 轴翻折到△CDB 的位置，而△CDB 与四边形ABDO 拼接后可看成△AOC，这样求S 便转化为直接求△AOC 的面积不更快捷吗？”但大家经反复演算，发现S △AOC ≠S，请通过计算解释他的想法错在哪里．5．已知点P(x 0，y 0)和直线y ＝kx ＋b ，则点P 到直线y ＝kx ＋b 的距离d 可用公式d ＝|kx 0－y 0＋b|1＋k 2计算． 例如：求点P(－2，1)到直线y ＝x ＋1的距离．解：因为直线y ＝x ＋1可变形为x －y ＋1＝0，其中k ＝1，b ＝1，所以点P(－2，1)到直线y ＝x ＋1的距离为d ＝|kx 0－y 0＋b|1＋k 2＝|1×（－2）－1＋1|1＋12＝22＝ 2. 根据以上材料，求：(1)点P(1，1)到直线y ＝3x －2的距离，并说明点P 与直线的位置关系； (2)点P(2，－1)到直线y ＝2x －1的距离；(3)已知直线y ＝－x ＋1与y ＝－x ＋3平行，求这两条直线的距离．参考答案1．解：(1)由题意得当2 000≤x≤2 600时，y ＝10x －6(2 600－x)＝16x －15 600， 当2 600＜x≤3 000时，y ＝2 600×10＝26 000. (2)由题意得16x －15 600≥22 000， 解得x≥2 350.∴当A 酒店本月对这种水果的需求量小于等于3 000 kg ，不少于2 350 kg 时，该水果店销售这批水果所获的利润不少于22 000元． 2．解：(1)22 2 25(2)由题意知，点B 的坐标为(3，22)，点C 的坐标为(175，20)，设线段BC 的函数关系式为y ＝kx ＋b ， 把点B 和点C 的坐标代入， 得⎩⎪⎨⎪⎧3k ＋b ＝22，175k ＋b ＝20，解得⎩⎪⎨⎪⎧k ＝－5，b ＝37，所以线段BC 所表示的y(千米)与x(小时)之间的函数关系式是y ＝－5x ＋37.(3)爸爸开车接上小宇前行驶路程为20千米，用时25小时，速度为20÷25＝50(千米/小时)，接上小宇后开车返回的速度是50千米/小时，路程为20千米，需要2050＝25(小时)，到家时间为8＋3＋25＋25＝1145时，即11时48分，所以小宇能在12：00前回到家．3．解：(1)从图1看出，同一时刻，首尔时间比北京时间多1小时， 故y 关于x 的函数表达式是y ＝x ＋1.填表如下：(2)从图2看出，设伦敦时间(夏时制)为t 时，则北京时间为(t ＋7)时， 由第(1)题，知韩国首尔时间为(t ＋8)时，所以，当伦敦时间(夏时制)为7：30时，韩国首尔时间为15：30. 4．解：(1)在直线y ＝－38x －398中，令y ＝0，则有0＝－38x －398，∴x＝－13，∴C(－13，0)．令x ＝－5，则有y ＝－38×(－5)－398＝－3，∴E(－5，－3)．∵点B ，E 关于x 轴对称，∴B(－5，3)． ∵A (0，5)，∴设直线AB 的表达式为y ＝kx ＋5， ∴－5k ＋5＝3，∴k＝25，∴直线AB 的表达式为y ＝25x ＋5.(2)由(1)知，E(－5，－3)，∴DE＝3， ∵C(－13，0)，∴CD＝－5－(－13)＝8， ∴S △CDE ＝12CD·DE＝12.由题意知，OA ＝5，OD ＝5，BD ＝3，∴S 四边形ABDO ＝12(BD ＋OA)·OD＝20，∴S＝S △CDE ＋S 四边形ABDO ＝12＋20＝32. (3)由(2)知，S ＝32， 在△AOC 中，OA ＝5，OC ＝13， ∴S △AOC ＝12OA·OC＝652＝32.5，∴S≠S △AOC .理由：由(1)知，直线AB 的表达式为y ＝25x ＋5，令y ＝0，则0＝25x ＋5，∴x＝－252≠－13.∴点C 不在直线AB 上，即点A ，B ，C 不在同一条直线上， ∴S △AOC ≠S.5．解：(1)∵点P(1，1)，∴点P 到直线y ＝3x －2的距离为d ＝|3×1－1－2|1＋32＝0， ∴点P 在直线y ＝3x －2上． (2)∵y＝2x －1，∴k＝2，b ＝－1. ∵P(2，－1)，∴d＝|2×2－（－1）－1|1＋22＝455. ∴点P(2，－1)到直线y ＝2x －1的距离为455.(3)在直线y ＝－x ＋1任意取一点P ， 当x ＝0时，y ＝1，∴P(0，1)． ∵直线y ＝－x ＋3，∴k＝－1，b ＝3， ∴d＝|－0－1＋3|1＋（－1）2＝2，∴两平行线之间的距离为 2.。

第二节 一次函数的图象与性质姓名：________ 班级：________ 用时：______分钟1．下列y 关于x 的函数中，是正比例函数的为( )A ．y ＝x 2B ．y ＝2xC ．y ＝x 2D ．y ＝x ＋122．若一次函数y ＝3x ＋b 的图象经过点(－1，2)，则b 的值为( )A ．－7B ．－1C ．2D ．53．(2018·陕西中考)若直线l 1经过点(0，4)，l 2经过点(3，2)，且l 1与l 2关于x 轴对称，则l 1与l 2的交点坐标为( )A ．(－2，0)B ．(2，0)C ．(－6，0)D ．(6，0)4．(2019·易错题)已知y 关于x 的函数y ＝(m －2)x ＋m 2－4，当m________时，该函数为一次函数；当m__________时，该函数为正比例函数．5. (2019·易错题)已知一次函数y ＝(1－m)x ＋m －2，当__________时，y 随x 的增大而增大．6．把直线y ＝－x －1沿y 轴向上平移2个单位，所得直线的函数表达式为________________．7．如图，直线y 1＝x ＋b 与y 2＝kx －1相交于点P ，点P 的横坐标为－1，则关于x 的不等式x ＋b>kx －1的解集为____________.8. (2019·易错题)对于一次函数y ＝kx ＋b ，当1≤x≤4时，3≤y≤6，则kb 的值是____________．9．(2018·重庆中考B 卷)如图，在平面直角坐标系中，直线l 1：y ＝12x 与直线l 2交点A 的横坐标为2，将直线l 1沿y 轴向下平移4个单位长度，得到直线l 3，直线l 3与y 轴交于点B ，与直线l 2交于点C ，点C 的纵坐标为－2.直线l 2与y 轴交于点D.(1)求直线l 2的表达式；(2)求△BDC的面积．10．如图，已知直线l1：y＝－2x＋4与直线l2：y＝kx＋b(k≠0)在第一象限交于点M，若直线l2与x轴的交点为A(－2，0)，则k的取值范围为( )A．－2＜k＜2 B．－2＜k＜0C．0＜k＜4 D．0＜k＜211．如图，点A，B的坐标分别为(0，2)，(3，4)，点P为x轴上的一点，若点B关于直线AP的对称点B′恰好落在x轴上，则点P的坐标为____________．12．如图，在平面直角坐标系中，已知直线y＝x上一点P(1，1)，C为y轴上一点，连结PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线y＝x交于点A，且BD ＝2AD，连结CD，直线CD与直线y＝x交于点Q，则点Q的坐标为__________．13．如图，直线l上有一点P1(2，1)，将点P1先向右平移1个单位，再向上平移2个单位得到点P2，点P2恰好在直线l上．(1)写出点P2的坐标；(2)求直线l所表示的一次函数的表达式；(3)若将点P2先向右平移3个单位，再向上平移6个单位得到点P3.请判断点P3是否在直线l上，并说明理由．参考答案【基础训练】1．C 2.D 3.B 4.≠2 ＝－2 5.m<1 6.y ＝－x ＋1 7.x>－1 8.2或－79．解：(1)把x ＝2代入y ＝12x 得y ＝1，∴点A 的坐标为(2，1)．∵将直线l 1沿y 轴向下平移4个单位长度，得到直线l 3，∴直线l 3的表达式为y ＝12x －4，∴x＝0时，y ＝－4，∴B(0，－4)．将y ＝－2代入y ＝12x －4，得x ＝4，∴点C 的坐标为(4，－2)．设直线l 2的表达式为y ＝kx ＋b(k≠0)，∵直线l 2过A(2，1)，C(4，－2)，∴⎩⎪⎨⎪⎧2k ＋b ＝1，4k ＋b ＝－2，解得⎩⎪⎨⎪⎧k ＝－32，b ＝4，∴直线l 2的表达式为y ＝－32x ＋4.(2)∵y＝－32x ＋4，∴x＝0时，y ＝4，∴D(0，4)．∵B(0，－4)，∴BD＝8，∴△BDC 的面积＝12×8×4＝16.【拔高训练】10．D 11.(43，0) 12.(94，94)【培优训练】13．解：(1)P 2(3，3)．(2)设直线l 所表示的一次函数的表达式为y ＝kx ＋b(k≠0)，∵点P 1(2，1)，P 2(3，3)在直线l 上，∴⎩⎪⎨⎪⎧2k ＋b ＝1，3k ＋b ＝3，解得⎩⎪⎨⎪⎧k ＝2，b ＝－3.∴直线l 所表示的一次函数的表达式为y ＝2x －3.(3)点P 3在直线l 上．由题意知点P 3的坐标为(6，9)，∵2×6－3＝9，∴点P 3在直线l 上．。

第三章函数及其图象第一节平面直角坐标系姓名： ________班级：________用时：______分钟1、( 2019·易错题 ) 点(3 ，2) 对于 x 轴的对称点为 ( )A、(3 ，－ 2)B、( －3，2)C、( －3，－ 2)D、(2 ，－ 3)2、( 2018·湖南岳阳中考 ) 函数 y＝x－3中自变量 x 的取值范围是 ( )A、x＞3B、x≠3C、x≥3D、x≥03、( 2017·山东济宁中考 ) 如图， A，B是半径为 1 的⊙O上两点，且 OA⊥OB，点P 从点 A 出发，在⊙O 上以每秒一个单位长度的速度匀速运动，回到点A运动结y，那么以下图象中可能表示y 与束，设运动时间为x(单位： s)，弦BP的长为x 函数关系的是()A、①B、③C、②或④D、①或③x4、( 2019·易错题 ) 函数 y＝x－2中自变量 x 的取值范围是 __________、5、在平面直角坐标系中，点P(3，－ x2－1) 在第 ______象限、6、如，△ ABC 的三个点都在方格的格点上，此中点 A 的坐是 ( －1，0)、将△ABC 点 A旋90°，旋后点 C 的坐是______________、7、 ( 2019·改 ) 如，在平面直角坐系中，已知点A(1， 1) ， B(－ 1，1)，C(－1，－ 2) ，D(1，－ 2) ，把一根 2 019 个位度且没有性的 ( 的粗忽视不 ) 的一端固定在 A，并按 A→B→C→D→A⋯的律在四形 ABCD 的上，的另一端所在位置的点的坐是________________、8、在如所示的方格中，我称每个小正方形的点“格点”，以格点点的三角形叫做“格点三角形”，依据形，回答以下、(1)中格点△ A′B′C′是由格点△ ABC通怎的获得的？(2) 假如以直a，b 坐成立平面直角坐系后，点 A 的坐 ( －3，4)，写出格点△ DEF各点的坐，并求出△ DEF的面、9、定：直l 1与 l 2交于点O，于平面内随意一点M，点 M到直l1，l2的距离分 p，q，称有序数 (p ，q) 是点 M的“距离坐”，依据上述定，“距离坐”是 (1 ，2) 的点的个数是 ( )A、2B、3C、4D、510、在平面直角坐系中，点P( －3， 2) 对于直y＝ x 称的点的坐是( )A、( －3，－ 2)B、(3 ，2)C、(2 ，－ 3)D、(3 ，－ 2)11、( 2019·改 ) 如，在平面直角坐系 xOy 中，已知点M0的坐 (1 ，0)，将段 OM0原点 O 逆方向旋 45°，再将其延到M1，使得M1M0⊥OM0，获得段OM1；又将段OM1原点 O逆方向旋45°，再将其延到M2，使得M2M1⊥OM1，获得段OM2；这样下去，获得段OM3，OM4，OM5，⋯，依据以上律，那么M2 019的坐、12、 ( 2019·新 ) 【】在平面直角坐系中，以随意两点P(x1， y1) ，Q(x2，y2) 端点的段中点坐 (x1＋x2y1＋y2，) 、22【运用】(1)如，矩形 ONEF的角交于点 M，ON，OF分在 x 和 y 上， O坐原点，点 E 的坐 (4 ，3) ，点 M的坐 ________；(2)在平面直角坐系中，有 A(－1，2) ，B(3，1) ，C(1，4) 三点，还有一点 D与点 A，B，C组成平行四形的点，求点D的坐、13、( 2018·浙江台州中考 ) 甲、乙两运在 100 m的直道 AB(A，B 直道两头点 ) 上行匀速来回跑，两人同从 A点起跑，抵达 B 点后，立刻身跑向 A点，抵达 A 点后，又立刻身跑向 B点⋯若甲跑步的速度 5 m/ s，乙跑步的速度 4 m/ s，起跑后 100 s 内，两人相遇的次数 ( )A、5B、4C、3D、2参照答案【基】1、A 2.C 3.D 4.x ≠2 5. 四 6.(2 ，1)7、( －1，1)8、解： (1) 中格点△ A′B′C′是由格点△ ABC 向右平移7 个位度获得的、(2) 如图，过点 F 作 FG ∥直线 a ，交 DE 于点 G.假如以直线 a ，b 为坐标轴成立平面直角坐标系后，点 A 的坐标为 ( －3，4) ，那么格点△ DEF 各极点的坐标分别为 D(0，－ 2) ，E(－4，－ 4) ，F(3 ，－ 3) ， S ＝S ＋ S ＝2 ×5×1＋ 2×5×1△DEF△DGF △GEF 11＝5.【拔高训练】9、C 10.C11、( －21 009 ，21 009 )312、解： (1)(2 ，2)(2) 设点 D 的坐标为 (x ，y) ，若以 AB 为对角线， AC ，BC 为邻边组成平行四边形，则 AB ，CD 的中点重合，1＋x －1＋32 ＝2 ，x ＝1， ∴ 2＋1解得 4＋y ＝ ， y ＝－ 1.2 2若以 BC 为对角线， AB ，AC 为邻边组成平行四边形，则 AD ，BC 的中点重合，－ 1＋x 1＋32 ＝ 2 ，∴2＋y4＋12＝2，x ＝5， 解得y ＝3.若以 AC 为对角线， AB ，BC 为邻边组成平行四边形，则 BD ，AC 的中点重合，3＋x －1＋12 ＝ 2 ，∴1＋y2＋42＝2，x ＝－ 3， 解得y ＝5.综上可知，点 D 的坐标为 (1 ，－1) 或(5 ，3) 或( －3，5) 、【培优训练】13、B。

1．(2018·浙江宁波模拟(3，4) D ．(4，－3)2019·易错题)已知点A(1，y 1)，B(2，y 2)，C(－3，y 3)都在反比例函数y ＝的图象上，则4x y 2，y 3的大小关系是( )3<y 1<y 2B ．y 1<y 2<y 32<y 1<y 3 D ．y 3<y 2<y 1．以正方形ABCD 两条对角线的交点O 为坐标原点，建立如图所示的平面直角坐标系，反比例函数的图象经过点D ，则正方形ABCD 的面积是( )D ．13在平面直角坐标系中，分别过点A(m ，0)，的关系，下列结论中错误的是．如图，一次函数y ＝kx ＋b 与反比例函数y ＝的图象在第一象限交于A ，B 两点，B 点的坐标为ax 2)，连结OA ，OB ，过点B 作BD⊥y 轴，垂足为点D ，交OA 于点C ，若OC ＝CA.求一次函数和反比例函数的表达式；求△AOB 的面积．．如图，点P 1(x 1，y 1)，P 2(x 2，y 2)，…，P n (x n ，y n )在函数y ＝(x>0)的图象上，△P 1OA 1，△1x 2，△P 3A 2A 3，…，△P n A n －1A n 都是等腰直角三角形，斜边OA 1，A 1A 2，A 2A 3，…，A n －1A n 都在x 是大于或等于2的正整数)，则点P 3的坐标是______________；点P n 的坐标是______________(的式子表示)．．如图，已知点A(4，0)，B(0，4)，把一个直角三角尺DEF 放在△OAB 内，使其斜边FD 在线段3上下滑动．其中∠EFD＝30°，ED ＝2，点G 重合时，求经过点G 的反比例函数y ＝(k≠0)的函数表达式；kx 在三角尺滑动的过程中，经过点G 的反比例函数的图象能否同时经过点例函数的表达式；如果不能，说明理由．(2018·江苏泰州中考)平面直角坐标系xOy 中，横坐标为a 的点A 在反比例函数y 1＝(x ＞0)kx 图象上，点A′与点A 关于点O 对称，一次函数y 2＝mx ＋n 的图象经过点A′.设a ＝2，点B(4，2)在函数y 1，y 2的图象上．①分别求函数y 1，y 2的表达式；②直接写出使y 1＞y 2＞0成立的x 的范围；如图1，设函数y 1，y 2的图象相交于点B ，点B 的横坐标为3a ，△AA′B 的面积为16，求k 的值；参考答案2.D3.D4.C5.D6.B7.6．解：(1)∵反比例函数的表达式为y ＝，且反比例函数经过点B(3，2)，∴2＝，即a ＝6.∴反比a x a3例函数的表达式为y ＝.6x 如图，过点A 作AE⊥y 轴于点E ，∵过点B 作BD⊥y 轴，OC ＝CA ，是△AOE 的中位线，即OE ＝2OD ＝4.6，且经过A ，B 两点，根据题意，得解得4k ′＋b ＝0，b ＝43，){k ′＝－3，b ＝43，)∴直线AB 的函数表达式为y ＝－x ＋4.33(2)∵在Rt△DEF 中，∠EFD＝30°，ED ＝2，∴EF＝2，DF ＝4.3D 与点A 重合，∴点D(4，0)，F(2，2)，∴点G(3，)．33∵反比例函数y ＝经过点G ，kx ∴k＝3，3∴反比例函数的表达式为y ＝.33x 经过点G 的反比例函数的图象能同时经过点F ，理由如下：F 在直线AB 上，∴设点F(t ，－t ＋4)．33＝4m ＋n ，＝－2m ＋n ，){m ＝1，n ＝－2.)＝x －2.y 1＞y 2＞0时，y 1＝图象在y 2＝x －2图象上方，且两函数图象在x 轴上方，8x ∴由图象得2＜x ＜4.如图，分别过点A ，B 作AC⊥x 轴于点C ，BD⊥x 轴于点D ，连结BO.k∴AD＝－a.a ∵AD＝AF ，∴点F 和点P 横坐标为a ＋－a ＝.2k a 2ka P 纵坐标为·＋a －＝ a.122k a 12k a 12P 在y 1＝(x ＞0)的图象上．kx。