均匀带电球面和载流柱面上场强的计算

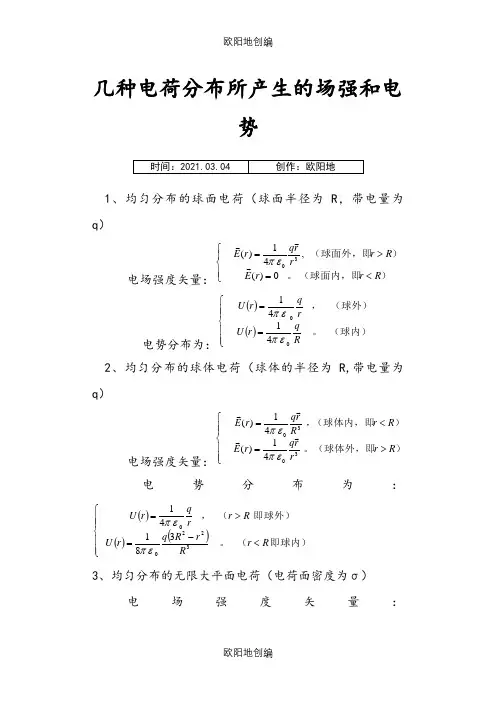
几种电荷分布所产生的场强和电势1、均匀分布的球面电荷（球面半径为R ，带电量为q ）电场强度矢量：⎪⎩⎪⎨⎧<=>=）（球面内，即。

）（球面外，即R r r E R r r r q r E0)( , 41)( 3επ 电势分布为：()()⎪⎪⎩⎪⎪⎨⎧==（球内）。

（球外）， 41 41 00R q r U r q r U επεπ2、均匀分布的球体电荷（球体的半径为R,带电量为q ）电场强度矢量：⎪⎪⎩⎪⎪⎨⎧>=<=）（球体外，即。

）（球体内，即，R r rr q r E R r R r q r E 41)( 41)( 3030επεπ电势分布为：()()()⎪⎪⎩⎪⎪⎨⎧<-=>=即球内）（。

即球外）（， 3 81 41 3220 0 R r R r R q r U R r r q r U επεπ3、均匀分布的无限大平面电荷（电荷面密度为σ）电场强度矢量：离无关。

）（平板两侧的场强与距 ) (2)(0i x E ±=εσ电势分布为：()()r r r U -=002εσ其中假设0r 处为零电势参考点。

若选取原点（即带电平面）为零电势参考点。

即00=U 。

那么其余处的电势表达式为：4、均匀分布的无限长圆柱柱面电荷（圆柱面的半径为R ，单位长度的带电量为λ。

）电场强度矢量 ⎪⎩⎪⎨⎧<=>=，即在柱面内）（。

即在柱面外）（，R r r E R r r r r E 0)( , 2 )( 2επλ电势分布为：()()⎪⎪⎩⎪⎪⎨⎧<=>=即柱体内）（。

即柱体外）（ ln 2 , ln 2 00R r R r r U R r r r r U a a επλεπλ其中假设a r 处为零电势参考点。

且a r 处位于圆柱柱面外部。

（即a r >R ）。

若选取带电圆柱柱面处为零电势参考点。

（即()0=R U ）。

那么，其余各处的电势表达式为： 5、均匀分布的无限长带电圆柱体（体电荷密度为ρ、半径为R 。

关于均匀带电球面上电场强度的求解
蔡莉莉;张晓燕
【期刊名称】《物理与工程》
【年(卷),期】2015(0)1
【摘要】由于均匀带电球面上的电场强度无法用高斯定理求出,现行大部分大学物理基础教材在讨论均匀带电球面产生的场强分布时,只用高斯定理求出了该带电系统内外空间电场的分布,并没有给出球面上场强的计算方法,只是指出在球面上场强值不连续.文章利用叠加原理和电容器能量的变化两种方法分别导出了均匀带电球面上任一点的场强值,验证了均匀带电球面的场强是不连续的,两种方法思路截然不同,但得到的结果完全相同,该结果使得高斯定理求出的均匀带电球面在空间电场分布的结论更加完整.
【总页数】3页(P65-67)
【作者】蔡莉莉;张晓燕
【作者单位】华北科技学院基础部物理教研室,河北廊坊 065201;华北科技学院基础部物理教研室,河北廊坊 065201
【正文语种】中文
【相关文献】
1.均匀带电球面上电场强度的计算 [J], 白俊彪
2.关于均匀带电球面上电场强度的定量计算 [J], 陈正武
3.计算均匀带电球面和柱面面上电场强度的另一方法 [J], 王雪莹
4.均匀带电球面上电场强度之悖及解悖方法 [J], 秦绪玲
5.求解均匀带电球面上场强的三种方法 [J], 孙国标;杨丽芬
因版权原因，仅展示原文概要，查看原文内容请购买。

一、电场的概念电场是指电荷周围空间内的物理场，它描述了电荷对空间内其它电荷的作用力。

在物理学中，电场是一种很重要的概念，它可以帮助我们理解电荷之间相互作用的规律，也是电磁学的重要内容之一。

二、均匀带电球体的电场强度定义均匀带电球体是指球体内每一点的电荷密度都是相同的，而且球体外部没有电荷分布。

对于这样的球体，可以利用高斯定律求出球体内外的电场强度。

三、均匀带电球体内部的电场强度1. 对于均匀带电球体内部的一点P，其到球心的距离记为r，球体的半径记为R。

2. 根据高斯定律，球体内部的电场强度公式为E = k * Q * r / R^3，其中，k为电场常数，Q为球体的总电荷量。

3. 由上式可以看出，均匀带电球体内部的电场强度与点P到球心的距离成正比，与球体的总电荷量成正比，与球体的半径的立方成反比。

这说明球体内部的电场强度分布是均匀的，且与点P到球心的距离成线性关系。

四、均匀带电球体外部的电场强度1. 对于均匀带电球体外部的一点Q，其到球心的距离记为r。

2. 根据高斯定律，球体外部的电场强度公式为E = k * Q / r^2，其中，k为电场常数，Q为球体的总电荷量。

3. 由上式可以看出，均匀带电球体外部的电场强度与点Q到球心的距离成反比，与球体的总电荷量成正比。

随着点Q到球心的距离增大，电场强度逐渐减小。

五、结论通过本文对均匀带电球体内外的电场强度公式的推导和分析，我们可以得出以下结论：1. 均匀带电球体内部的电场强度与点到球心的距离成正比，与球体的总电荷量成正比，与球体的半径的立方成反比。

2. 均匀带电球体外部的电场强度与点到球心的距离成反比，与球体的总电荷量成正比。

均匀带电球体内外的电场强度公式为E = k * Q * r / R^3 (r < R) 和 E = k * Q / r^2 (r > R)。

这些公式在电磁学理论研究和工程实践中具有重要的应用价值。

在物理学中，电场是一种很重要的概念，它可以帮助我们理解电荷之间相互作用的规律，也是电磁学的重要内容之一。

几种典型带电体的场强和电势公式
本文介绍了几种电荷分布所产生的场强和电势。

首先是均匀分布的球面电荷，对于球面外的情况，电场强度矢量为
1/4πεr*q/r^2，对于球面内的情况，电场强度矢量为q/4πεR^3.电势分布方程为q/4πεr（球外）和q/4πεR（球内）。

其次是均匀分布的球体电荷，对于球体内的情况，电场强度矢量为1/4πεR*q/r^2，对于球体外的情况，电场强度矢量为1/4πεr*q/r^2.电势分布方程为q/8πεR（r R）。

第三种情况是均匀分布的无限大平面电荷，电场强度矢量为σ/2ε（±i），电势分布方程为σ(r-r0)/2ε。

如果以带电平面为零电势参考点，则电势表达式为-Ux（x≥0）和Ux（x≤0），其中Ux=σx/2ε。

第四种情况是均匀分布的无限长圆柱柱面电荷，对于柱面外的情况，电场强度矢量为λ/2πεr，对于柱面内的情况，电场强度矢量为λ/2πεR。

电势分布方程为ln(r/a)*λ/2πε（r>a）和
ln(R/a)*λ/2πε（r<a），其中a为零电势参考点。

最后一种情况是均匀分布的无限长带电圆柱体，对于圆柱体内的情况，电场强度矢量为ρr/2ε，对于圆柱体外的情况，电场强度矢量为ρR^2/r/2ε。

电势分布方程为-ρr^2/4ε（r≤R）和-ρR^2/2εln(r/R)（r>R）。

均匀带电球面上的电场强度如何计算
金 仲 辉
北京 100094) ( 中国农业大学应用物理系
对于 电量 q 均匀 分布在半 径 为 R 的球面 上的空 间场 强分布 问 题, 许多大学基础物理教材( 例如北 京大学赵 凯华、 陈熙 谋编 的 电 磁 学 、 陆果编的 基础物理学 和清华 大学张三慧主编的 电磁学 等 ) 中 , 利用高斯定理求出了如下的结果 E= 4 0, q
现代物理知识
0
r< R r
2
, r> R 。
E dV
2
教学中常有学生提问 , 当 r = R 时, 即在带电球面上的电场强 度应 为何值? 现在来求解这个问题。 首先要明确 , 我们不能采用高斯定理求解此问 题。因为将高斯面取在球面上时 , 由于带电模型已 经失效, 无法确定高斯面所包围的电量 , 结果将是不 确定的。我们可以采用功能原理来求解这个问题。 设带电球面在球面上的电场强度为 E R , 由对称 性分析 , 其方向沿矢径方向, 当 q > 0 时 , E R 的方向 沿矢径指向球外。现在设想把带电球面从半径为 R 的学习氛围。把教师和学生的兴奋点、 注意力都吸 引到教学过程中, 让教 学支配考试 , 考试服务 于教 学, 不可本末倒置。 五、 师资水平需不断提高 目前由于多方面的原因, 基础课教师流失严重 , 师资严重不足, 任教的教师将大部分时间和精力都 投入到教学中, 工作相当艰苦 , 在科研方面的投入极 少。致使师资水平的提高受到了一定的限制。知识 经济要求人才要具有创新能力 , 而具有创新能力的 前题是必须拥有广博的知识。作为教育改革的实施 者 ! ! ! 教师, 跟踪世界科技的进步、 不断吸收最新知 识、 提高综合素质、 改善知识结构是当务之急。当然 可以通过培养青年教师攻读硕士、 博士研究生来提 高学历和素质, 但这不是所有教师都能做到的 , 更何

关于均匀带电球面上电场强度的定量计算陈正武 摘　要:用库仑定律定量的计算出了均匀带电球面空间的电场分布,并给出了球面上即电荷所在处的电场强度.关键词:球面;电场强度;计算中图分类号:O 441 文献标识码:A 文章编号:1008-9020(2002)02-028-02 1　引言电荷q 均匀分布在半径为R 的球面上,由高斯定理可以求出球面内外的电场强度分布分别是E =0和e =q/4πε0r 2.但在球面上电荷所在处,r =R 时,电场强度的值是多少,常见的电磁学[1][2]教材均未提及这个问题.本文避开高斯定理,用库仑定律定量地计算出了半径为R 的均匀带电球面空间的电场分布,并定量计算出了球面上即电荷所在处的电场强度的数值.2　均匀带电球面空间的电场分布半径为R 的均匀带电球面,若带有电荷q ,则电荷面密度σ=q/4πR 2.如图所示,在场中任取一点P ,连结OP 并以OP 为轴线在球面上介于θ与θ+dθ之间取一环带,环带所带的电荷dq =σ・2π・Rsin θ・R ・d θ=q 4πR 2・2π・Rsin θ・Rd θ=12・qsin θdθ均匀带电环带在P 点的电场[1]dE =14πε0・(r -Rcos θ)dq [(Rsinθ)2+(r -Rcos θ)2]32=18πε0・q (r -Rcos θ)sin θd θ(R 2+r 2-2Rrcosθ)32在球面上,即r =R 时dE =18πε0・qR (1-cos θ)sin θd θ22R 3(1-cosθ)32=q 162πε0R 2sin θdθ1-cos θE =q 162πε0R 2∫π0sin θd θ1-cos θ=q 82πε0R21-cos θ|π0=q 8πε0R 2在球面外,即r >R 时y 2=R 2+r 2-2Rrcos θ ydy =Rrsin θd θ sin θd θ=ydy Rrcos θ=R 2+r 2-y 22Rr r -Rcos θ=r -R 2+r 2-y 22r =r 2-R 2+y 22r・82・第7卷第2期(2002) 甘肃高师学报 Vol 17No.2(2002)dE =q 8πε0・(r -Rcos θ)sin θd θ(R 2+r 2-2Rrcosθ)32=q8πε0・(r 2-R 2+y 2)・ydy 2r ・y 3・Rr =q (r 2-R 2+y 2)16πε0Rr 2y 2・dy E =q 16πε0Rr 2∫r +R r -R (1+r 2-R 2y )dy =q 16πε0Rr 2(y -r 2-R 2y )(r +R )(r -R )=q16πε0Rr2[(r +R )-r 2-R 2r +R -(r -R )+r 22R 2r -R ]=q 16πε0Rr 2[(r +R )-(r -R )-(r -R )+(r +R )]=q 4πε0r 2在球面内,即r >R 时E =q16πε0Rr 2∫R +r R -r (1+r 2-R 2y 2)dy =q 16πε0Rr2(y -r 2-R 2y )R +r R -r =q 16πε0Rr2[(R +r )-r 2-R 2R +r -(R -r )+r 22R 2R -r ]=q 16πε0Rr2[R +r +R 2-r 2R +r -(R -r )-R 2-r 2R -r ]=q 16πε0Rr2[R +r +(R -r )-(R -r )-(R +r )]=03　结论本文用库仑定律定量的计算出了均匀带电球面空间的电场分布,并定量的计算出了球面上即电荷所在处的电场强度为E =q/8πε0R 2.从而采用面模型表达了整个空间电场的全貌,在宏观领域具有一定的意义.参考文献:[1]赵凯华,陈熙谋.电磁学[M ],第2版.北京:高等教育出版社,1985.[2]梁灿彬等.电磁学[M ].北京:高等教育出版社,1980.作者单位:庆阳师范高等专科学校　745000责任编辑:徐治堂・92・第7卷第2期(2002) 陈正武:关于均匀带电球面上电场强度的定量计算　Vol 17No.2(2002)。

均匀带电平面的场强公式在我们探索物理世界的奇妙之旅中，均匀带电平面的场强公式可是个相当重要的家伙。

想象一下，有一块大大的平板，上面均匀地分布着电荷，就好像在一个大操场上整齐排列的士兵一样。

那这时候，我们怎么来描述这个平面所产生的电场强度呢？这就得请出我们今天的主角——均匀带电平面的场强公式。

这个公式表示为：E = σ / (2ε₀) 。

这里的 E 就是电场强度啦，σ 表示面电荷密度，而ε₀则是一个叫做真空介电常数的常量。

那这个公式到底咋用呢？比如说，有一个边长为 1 米的正方形带电平面，电荷均匀分布在上面，面电荷密度是 5 库仑每平方米。

那我们就可以把σ = 5，ε₀约等于 8.85×10⁻¹²代入公式算算，就能得出这个平面产生的电场强度啦。

我记得之前给学生们讲这部分内容的时候，有个特别调皮的小家伙，怎么都理解不了这个公式。

我就给他打了个比方，我说这均匀带电平面就像是一个会发射力量的大磁场，电荷密度越大，就好像这个磁场的力量越强，而这个公式就是计算这种力量大小的密码。

嘿，这小家伙一下子好像就开窍了，眼睛都亮了起来。

再深入想想，这个公式在实际生活中也有不少应用呢。

比如在电子设备的设计中，工程师们就得考虑各种带电平面产生的电场对电路的影响。

要是不搞清楚这个，说不定你的手机、电脑啥的就会出毛病。

还有啊，在研究高压输电的时候，电线周围的电场也可以用类似的原理来分析。

要是电场强度太大，可能就会出现放电现象，那可就危险啦。

总之，均匀带电平面的场强公式虽然看起来有点复杂，但只要我们用心去理解，就能发现它其实就像一把神奇的钥匙，可以帮助我们打开很多物理现象的神秘大门。

希望大家在学习物理的道路上，都能像勇敢的探险家一样，不怕困难，用这些公式和知识去发现更多的奇妙之处！。

d
l
l
d
i
4 0
1 d
l
1 d
i
。
U
p d
4 0
ln
l
d d
。
（2）在直线的中垂线上，与直线的距离为 d 的 Q 点处：
电场强度矢量为：
EQ
d
4 0
d
l
j
l 2 d 2
4 0 d
2l
j
l 2 4d 2
。
2
电势：
l l 2 d 2
UQ
d
4 0
ln
2 l
2 l 2 d 2
几种电荷分布所产生的场强和电势
1、均匀分布的球面电荷（球面半径为 R，带电量为 q）
电场强度矢量：
E(r)
1
qr ,
（球面外，即r R）
Hale Waihona Puke 4 0 r 3E(r) 0 。 （球面内，即r R）
电势分布为：
U r 1 q ， （球外）
4 0 r
U r 1 q 。 （球内）
4 0 R
2、均匀分布的球体电荷（球体的半径为 R,带电量为 q）
PSin r3
0
其大小为 E P 4 0r 2
3Cos 2 1 ，
方向为 arctg E Er
tg
1
E Er
tg
1
1 2
tg
。其中
为
E
与
r
0
之间的夹角。
电势：U r
1 4 o
P Cos r2
1 4 0
P
r
r3
。
电场强度矢量的另一种表达式为：
E

“均匀带电球⾯上的电场强度如何计算”的再讨论
“均匀带电球⾯上的电场强度如何计算”的再讨论
刘景世
【摘要】摘要：利⽤球形电容器能量的变化求出了均匀带电球⾯上⼀点的电场强度，指出了有关⽂献中的错误，并指出现⾏基础物理教材中对均匀带电球⾯电场强度分布的讨论应遍及空间所有点.
【期刊名称】河南教育学院学报（⾃然科学版）
【年(卷),期】2011(020)004
【总页数】2
【关键词】关键词:均匀带电球⾯;球形电容器;电场能;电场强度;计算
0 引⾔
在现⾏许多⼤学基础物理教材［1－4］中，求电量q均匀分布在半径为R的均匀带电球⾯上的场强分布问题是⼀个典型例题.在做了对称性分析后，⽤⾼斯定理不难求出E).⽽对于球⾯上⼀点(即r=R)的电场强度，上述⽂献未给出确定值.⽂献［5－8］通过理论计算得出r=R时，从⽽解决了这⼀问题.然⽽上述⽂献都采⽤了将均匀带电球⾯切割成⼀个个均匀的带电细圆环的⽅法计算球⾯上的场强，本⽂从另⼀⾓度出发，利⽤球形电容器能量的变化来解决这个问题.
1 均匀带电球⾯上的电场强度
⼀个物理系统在其本⾝各⼒的作⽤下变更它的组态后，各⼒就做了功，倘若外界没有提供能量，该系统只能消耗其本⾝的相互作⽤能.下⾯就⽤这种观点讨论在真空中的球形电容器极板所受的静电场⼒，进⽽求出极板上的场强.设球形电容器极板的电荷各为+q(A极板)和－q(B极板)，球壳的内外半径分别为RA和RB，球壳之间的距离d=RB－RA＜＜RA.。

几种电荷分布所产生的场强和电势1、均匀分布的球面电荷（球面半径为R ，带电量为q ）电场强度矢量：⎪⎩⎪⎨⎧<=>=）（球面内，即。

）（球面外，即R r r E R r rr q r E 0)( , 41)( 3επ电势分布为：()()⎪⎪⎩⎪⎪⎨⎧==（球内）。

（球外）， 41 41 0 0R qr U r q r U επεπ2、均匀分布的球体电荷（球体的半径为R,带电量为q ）电场强度矢量：⎪⎪⎩⎪⎪⎨⎧>=<=）（球体外，即。

）（球体内，即，R r rr q r E R r R r q r E 41)( 41)( 3030επεπ 电势分布为：()()()⎪⎪⎩⎪⎪⎨⎧<-=>=即球内）（。

即球外）（， 3 81 41 3220 0R r R r R q r U R r r q r U επεπ 3、均匀分布的无限大平面电荷（电荷面密度为σ）电场强度矢量：离无关。

）（平板两侧的场强与距 ) (2)(0i x E ±=εσ电势分布为：()()r r r U -=002εσ其中假设0r 处为零电势参考点。

若选取原点（即带电平面）为零电势参考点。

即00=U 。

那么其余处的电势表达式为：()()⎪⎪⎩⎪⎪⎨⎧≤=≥-=0 2 0 2 00x x x U x x x U εσεσ 4、均匀分布的无限长圆柱柱面电荷（圆柱面的半径为R ，单位长度的带电量为λ。

）电场强度矢量 ⎪⎩⎪⎨⎧<=>=，即在柱面内）（。

即在柱面外）（，R r r E R r r r r E 0)( , 2 )( 2επλ 电势分布为：()()⎪⎪⎩⎪⎪⎨⎧<=>=即柱体内）（。

即柱体外）（ ln 2 , ln 2 00R r R r r U R r r r r U a a επλεπλ其中假设a r 处为零电势参考点。

且a r 处位于圆柱柱面外部。

（即a r >R ）。

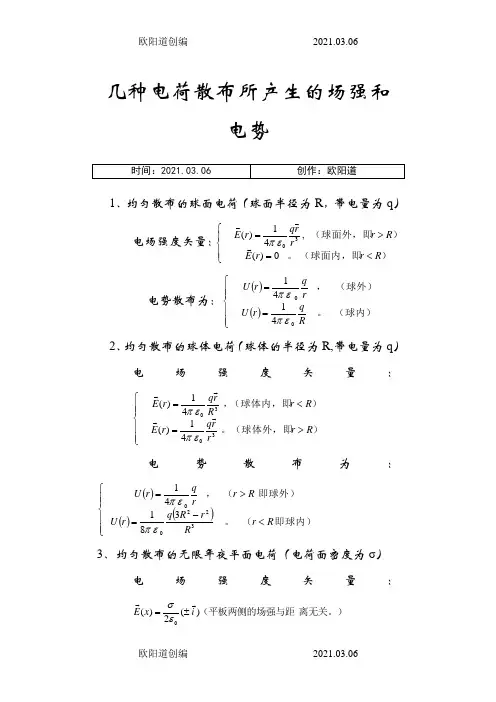
几种电荷散布所产生的场强和电势1、均匀散布的球面电荷（球面半径为R ，带电量为q ）电场强度矢量：⎪⎩⎪⎨⎧<=>=）（球面内，即。

）（球面外，即R r r E R r r r q r E 0)( , 41)( 3επ 电势散布为：()()⎪⎪⎩⎪⎪⎨⎧==（球内）。

（球外）， 41 41 0 0R qr U rq r U επεπ 2、均匀散布的球体电荷（球体的半径为R,带电量为q ）电场强度矢量：⎪⎪⎩⎪⎪⎨⎧>=<=）（球体外，即。

）（球体内，即，R r r r q r E R r R r q r E 41)( 41)( 3030επεπ 电势散布为：()()()⎪⎪⎩⎪⎪⎨⎧<-=>=即球内）（。

即球外）（， 3 81 41 3220 0 R r R r R q r U R r r q r U επεπ 3、均匀散布的无限年夜平面电荷（电荷面密度为σ）电场强度矢量：离无关。

）（平板两侧的场强与距 ) (2)(0i x E ±=εσ电势散布为：()()r r r U -=002εσ其中假设0r 处为零电势参考点。

若选取原点（即带电平面）为零电势参考点。

即00=U 。

那么其余处的电势表达式为：4、均匀散布的无限长圆柱柱面电荷（圆柱面的半径为R ，单位长度的带电量为λ。

）电场强度矢量 ⎪⎩⎪⎨⎧<=>=，即在柱面内）（。

即在柱面外）（，R r r E R r r r r E 0)( , 2 )( 2επλ 电势散布为：()()⎪⎪⎩⎪⎪⎨⎧<=>=即柱体内）（。

即柱体外）（ ln 2 , ln 2 00R r R r r U R r r r r U a a επλεπλ 其中假设a r 处为零电势参考点。

且a r 处位于圆柱柱面外部。

（即a r >R ）。

若选取带电圆柱柱面处为零电势参考点。

（即()0=R U ）。

那么，其余各处的电势表达式为： 5、均匀散布的无限长带电圆柱体（体电荷密度为ρ、半径为R 。

几种电荷散布所产生的场强和电势1、均匀散布的球面电荷（球面半径为R ，带电量为q ）电场强度矢量：⎪⎩⎪⎨⎧<=>=）（球面内，即。

）（球面外，即R r r E R r r r q r E 0)( , 41)( 3επ 电势散布为：()()⎪⎪⎩⎪⎪⎨⎧==（球内）。

（球外）， 41 41 0 0R qr U rq r U επεπ 2、均匀散布的球体电荷（球体的半径为R,带电量为q ）电场强度矢量：⎪⎪⎩⎪⎪⎨⎧>=<=）（球体外，即。

）（球体内，即，R r r r q r E R r R r q r E 41)( 41)( 3030επεπ 电势散布为：()()()⎪⎪⎩⎪⎪⎨⎧<-=>=即球内）（。

即球外）（， 3 81 41 3220 0R r R r R q r U R r r q r U επεπ 3、均匀散布的无限年夜平面电荷（电荷面密度为σ）电场强度矢量：离无关。

）（平板两侧的场强与距 ) (2)(0i x E ±=εσ电势散布为：()()r r r U -=002εσ其中假设0r 处为零电势参考点。

若选取原点（即带电平面）为零电势参考点。

即00=U 。

那么其余处的电势表达式为：4、均匀散布的无限长圆柱柱面电荷（圆柱面的半径为R ，单位长度的带电量为λ。

）电场强度矢量 ⎪⎩⎪⎨⎧<=>=，即在柱面内）（。

即在柱面外）（，R r r E R r r r r E 0)( , 2 )( 2επλ 电势散布为：()()⎪⎪⎩⎪⎪⎨⎧<=>=即柱体内）（。

即柱体外）（ ln 2 , ln 2 00R r R r r U R r r r r U a a επλεπλ其中假设a r 处为零电势参考点。

且a r 处位于圆柱柱面外部。

（即a r >R ）。

若选取带电圆柱柱面处为零电势参考点。

（即()0=R U ）。

那么，其余各处的电势表达式为：5、均匀散布的无限长带电圆柱体（体电荷密度为ρ、半径为R 。

数理科学科技创新导报 Science and Technology Innovation Herald159在求解均匀带电球面上电场强度分布时，一般都是通过静电场的高斯定理求解，但是对于理想的均匀带电球面来讲，这种方法只能求出球面内部和外部的电场强度分布，而对于球面上一点的场强，由于无法确定高斯面内电荷分布而无法利用高斯定理求解，对两边取极限的方法也无法求出，有些教材只指出在球面上场强值不连续或有一突变[1，2]，但并没给出具体值。

同样，在求解无限长均匀载流柱面磁感应强度分布时，一般都是磁场安培环路定理求解，而对柱面上一点的磁感应强度，这种方法也同样由于无法确定环路包围的电流强度大小而无法求解，该文对这两个问题分别采用场叠加原理进行了计算。

1 均匀带电球面上一点的电场强度图1为一半径为R 的均匀带电球面，带电量为q ，根据电场的高斯定理，可求得球面内外的电场强度分布为[3]：该结论并没有给出球面上任一点（即r R ）处的电场强度，原因在于对理想的均匀带电球面，利用高斯定理求解该位置处电场强度时，无法确定高斯面内包围的电荷量。

该问题可通过叠加原理进行求解。

为求球面上任一点P 点的电场强度，建立图示的坐标系，并将球面分割为无数多个半径不同的无限窄的环带，在坐标y 处、取高度为d y 的环带如图1所示，环带面元面积为:所带电量为:根据带电圆环轴线上一点P 的场强公式可得所取环带在P 点的电场强度大小。

由于各环带在P 点产生的电场强度方向均沿y 轴正方向，所以整个球面在P点产生的电场强度为:利用几何关系及可得P 点总场强:与球面内外场强分布比较可知，该处场强发生了一突变。

2 无限长均匀载流柱面上一点的磁感强度图1所示示为一半径为R 、电流沿轴向均匀分布的无限长圆柱面的截面图，总电流强度为I ，根据磁场的安培环路定理，可得柱面内外的磁感强度分布为[3]:为求柱面上任一点P 点的电场强度，建立图1所示的坐标系，且将柱面分割为无数多条截面为圆弧的无限长直线，DOI：10.16660/ k i.1674-098X.2016.06.159均匀带电球面和载流柱面上场强的计算田宝国 宿德志 李慧（海军航空工程学院基础部 山东烟台 264001）摘 要：对于均匀带电球面上一点的电场强度和无限长均匀载流柱面上一点的磁感强度问题，无法采用教材中常用的静电场高斯定理和磁场安培环路定理求解，该文分别用电场和磁场叠加原理进行了求解，得到了该问题的具体表达式。

【均匀带电球体内外各处场强计算例题】1. 概述均匀带电球体内外各处场强计算是电场理论中的经典问题之一，掌握这个问题的解决方法对于深入理解电场的性质和规律具有重要意义。

在本文中，我将根据提供的内容，详细探讨均匀带电球体内外各处场强的计算方法，帮助您全面理解这一问题，并对电场理论有更深入的认识。

2. 均匀带电球体内部场强计算假设半径为R的均匀带电球体带有总电荷量Q，我们要计算球心到球体内某点的电场强度。

根据库仑定律，我们知道电场强度E与电荷量Q和距离r的平方成反比，可表示为E=kQ/r^2，其中k为电场常数。

对于均匀带电球体内部的场强计算，我们可以将球体划分为无数个微小电荷元，然后利用积分的方法对每个微小电荷元的电场强度进行求和，得到总的电场强度。

具体的推导过程略。

3. 均匀带电球体外部场强计算球体外部的场强计算相对而言要简单一些。

根据库仑定律，我们同样可以利用积分的方法将球体划分为无数个微小电荷元，然后对每个微小电荷元的电场强度进行求和，得到球体外某点的电场强度。

在球体外部，可以将球体近似看作点电荷，因此外部的场强计算可以直接使用库仑定律进行求解。

4. 总结与回顾通过上述的详细讨论，我们对均匀带电球体内外各处场强的计算有了更全面的认识。

在计算内部场强时，我们需要将球体划分为无数微小的电荷元，并利用积分方法对每个电荷元的电场强度进行求和；而在计算外部场强时，可以将球体近似看作点电荷，直接使用库仑定律计算。

这些方法和步骤的掌握将对深入理解电场理论起到至关重要的作用。

5. 个人观点和理解对于均匀带电球体内外场强的计算，我个人认为需要在掌握基本原理的基础上进行大量的练习，才能真正掌握解决问题的方法。

通过不断的实践，我们可以更加灵活地运用积分和库仑定律，对各种不同情况进行场强的计算，从而提高自己的理论水平和解决问题的能力。

总结：本文围绕均匀带电球体内外各处场强的计算例题进行了详细的讨论和解释。

通过对内外场强计算方法的探讨，相信读者对这一问题有了更深入和全面的理解。

求解均匀带电球面上场强的三种方法孙国标绍兴县柯桥中学，浙江绍兴，312030问题提出：对于带电量Q 均匀分布在半径为R 的球面上的电场强度分布问题，由于电荷分布的球对称性，由高斯定理很容易求得球面内、外的电场强度，即2r R E Qk r Rr <⎧⎪=⎨>⎪⎩其E-r 曲线如图1：那球面上r=R 处的电场强度究竟是0还是2Qkr呢？下面笔者给出三种解法，供大家参考。

方法一：利用定义式在电场中某点的场强等于检验电荷在该处受到的电场力与其电荷量的比值。

F E q=现在我们要求球面上P 点场强，可以在球面上P 附近取一面元ΔS ，带电量为Δq ，其受到的电场力为球面上除ΔS 外剩余部分在P 处产生电场对其作用力，所以p E q E E q∆==∆剩余剩余其中：E 剩余为球面上除ΔS 外剩余部分在P 处产生的场强。

在P 点两侧分别取点P1和P2，且P1，P2非常接近P ，如图1所示，P1和P2两点的场强为面元ΔS 和剩余部分叠加而成，根据对称性，面元ΔS 在P 1点和P 2产生的场强等大，反向，而剩余部分在P1，P2处产生的场强大小相等，方向相同，如图2所示（该区域已放大）因此有：12S P Q E E E kR ∆+==剩余 20S P E E E ∆-==剩余所以22S Q E E kR ∆==剩余 因此P 点的场强为22R QE k R =方法二：利用微元叠加法如图3所示，对于球面上P 点，其电场强度可以视为许多以P 点和球心连线上某点为圆心，半径不同的带电圆环在P 处产生的场2dS rdl π=带电量为22242Q Qdq rdl rdl R R ππ== 其中sin r R θ=，dl Rd θ=，于是有图1图 1图2sin 2Qdq d θθ=根据对称性，此圆环在P 点产生的场强叠加后仅有x 分量，因此有223/2(cos )[(cos )(sin )]x dq R R dE kR R R θθθ+=++ 223/22c o s2[2(1c o s )]R k d q R θθ=+ 22sin sin 428cos 2Q kQ k d d R R θθθθθ==所以P 点的合场强为20220sin 42sin 2222P x kQ E dE d R kQ kQ d R R ππθθθθ====∑∑∑方法三：利用功能原理现将球面电荷缓慢地压缩到R-ΔR 的球面上，其中ΔR 为一无穷小量，如图4所示，此过程中克服电场力做功为R A E Q R ∆=∆其中R E 为球壳表面的电场强度。

均匀带电球面上场强的计算——也谈高斯定理的应用
高斯定理是物理学中最重要的定律之一，它主要涉及电荷在一个均匀带电球面
上的分布情况。

高斯定理的应用广泛，用于分析复杂的场强情况，是电学方面的重要理论依据。

高斯定理的基本思想是，当静电以均匀分布的方式局限在一定的曲面内部时，
谱线上的静电荷依据某种特定的分布体现其静电场的分布规律。

一颗均匀带电球面上的静电场可以用一维的高斯函数来描述，表示场的梯度的平方与距离的反比。

高斯定理可以帮助我们计算在均匀带电球面上的电场，并可以将计算值与实际测量值比较，以确定球面上是否存在其他影响静电分布的因素。

同时，高斯定理还可以用来计算电子在大量绝缘体中的传播情况，能够有效地
预测和分析不同材料结构中电子传播方向，通过分析跟踪电子在不同结构中传播的路径，从而使发射电流密度更加均匀，有效降低干扰，获得高质量的电子发射图像，这些都有助于我们更准确的理解物理系统状态。

另外，高斯定理还应用于电磁波的传播，用以分析电磁波的振幅随空间的变化，有助于提升现有的通讯技术，实现互联网的快速发展。

总之，高斯定理对我们处理电荷、电子、电磁波等物理现象都具有重要意义。

它为快速准确计算提供了依据，不仅增强了各种物理学研究的可行性，而且在实际应用领域也取得了显著成果，从而推动了现代互联网技术的发展。

均匀带电球体内外各处场强计算过程让我们来了解一下什么是均匀带电球体。

均匀带电球体是指球体上的电荷均匀分布。

电场强度的计算是通过库仑定律来实现的，该定律描述了两个电荷之间的相互作用力。

在这里，我们需要计算球体内外各处的电场强度。

对于球体内部的电场强度计算，我们可以采用高斯定律。

高斯定律表明，如果一个闭合曲面内没有电荷，则曲面上的电场强度积分等于零。

根据球对称性，我们可以选择一个球面作为高斯面，球心与球面上的电荷中心对齐。

在球面上，电场强度的大小是均匀的，并且指向球心。

因此，高斯面上的电场强度积分可以简化为电场强度乘以球面积。

根据高斯定律，这个积分应该等于球体内的总电荷除以电介质常数。

而对于球体外部的电场强度计算，则需要使用库仑定律。

根据库仑定律，两个电荷之间的相互作用力与两个电荷之间的距离的平方成反比。

在这种情况下，球体的电荷可以近似看作位于球心的点电荷。

假设球体上的电荷为Q，半径为R，我们可以使用库仑定律计算球体外部某一点的电场强度。

根据库仑定律的公式，电场强度与球体上电荷的大小和球体与观察点之间的距离有关。

对于球体内部的电场强度计算，首先我们需要确定球体内部的电荷分布情况。

在均匀带电球体中，电荷分布是均匀的，即每个微元上的电荷都相等。

我们可以通过球体内部的电荷总量除以球体内部的体积来得到每个微元上的电荷。

然后，我们选择一个球面作为高斯面，并计算球面上的电场强度积分。

由于球体内部的电荷均匀分布，球面上的电场强度大小是均匀的，并且指向球心。

因此，电场强度积分可以简化为电场强度乘以球面积。

我们将电场强度积分等于球体内部的总电荷除以电介质常数，解出电场强度的大小。

通过高斯定律和库仑定律，我们可以计算均匀带电球体内外各处的电场强度。

在球体内部，我们使用高斯定律，并确保电荷均匀分布。

在球体外部，我们使用库仑定律，并将球体近似为点电荷。

这样，我们就可以准确地计算出均匀带电球体内外各处的电场强度。

这个过程需要注意电荷的均匀分布、选择适当的高斯面和正确应用高斯定律和库仑定律。