第1-4章习题参考答案

第1章 化学热力学参考答案：（一）选择题１.Ａ 2.A 3.C 4.B 5.D 6.C 7.C 8.C 9. A 10. C 11. A 12.C （二）填空题1．40；2．等温、等容、不做非体积功，等温、等压，不做非体积功； 3．＞，＜，＝，＞ 4．增大、不变 5．不变 6．3.990 kJ·mol －1（三）判断题1. ×2. ×3. ×4. ×5. √6. ×7. ×8. ×9. × 10. × （四）计算题1．解：(g)O N (l)H 2N 4242+O(l)4H (g)3N 22+(l)H N 42摩尔燃烧热为2．解：)mol ·(kJ 28.254166.963.502)84.285(401f B r --=-⨯--⨯+=∆=∆∑HH ν)mol ·(kJ 14.627211r-Θ-=∆=H Q pK1077.3109.9824.37333mr r ⨯=⨯--=∆∆=-S T 转)mol ·(kJ 78.34357.86)15.137(36.3941f B r --=---=∆=∆∑G ν)K ·mol ·(J 9.9865.21056.1975.191216.21311B r ---=--⨯+==∆∑νNO(g )CO(g )+(g)N 21(g)CO 22+)mol ·(kJ 24.37325.90)52.110(5.3931f B r --=----=∆=∆∑H ν此反应的 是较大的负值，且)(,)(-∆-∆S H 型反应，从热力学上看，在 T 转的温度以内反应都可自发进行。

3．解：外压kPa 50e =p ，11p nRT V =，22p nRTV =，2e p p = 系统所做功：定温变化，0=∆U0=+=∆W Q U ，所以Q =1 247.1（J ） 定温过程pV =常数 ∆(pV )=0 所以 0)(=∆+∆=∆pV U H 4．解：查表知CaO(s) + SO 3(g) = CaSO 4(s)求得同理求得 因为 所以根据经验推断可知，反应可以自发进行。

计算机网络-清华版_吴功宜(第三版)课后习题解答(第1-4 章)第一章计算机网络概论P421. 请参考本章对现代Internet 结构的描述，解释“三网融合”发展的技术背景。

答：基于Web的电子商务、电子政务、远程医疗、远程教育，以及基于对等结构的P2P网络、3G/4G与移动Internet 的应用，使得Internet 以超常规的速度发展。

“三网融合”实质上是计算机网络、电信通信网与电视传输网技术的融合、业务的融合。

2. 请参考本章对Internet 应用技术发展的描述，解释“物联网”发展技术背景。

答：物联网是在Internet 技术的基础上，利用射频标签、无线传感与光学传感等感知技术自动获取物理世界的各种信息，构建覆盖世界上人与人、人与物、物与物的智能信息系统，促进了物理世界与信息世界的融合。

3. 请参考本章对于城域网技术特点的描述，解释“宽带城域网”发展技术背景。

答：宽带城域网是以IP 为基础，通过计算机网络、广播电视网、电信网的三网融合，形成覆盖城市区域的网络通信平台，以语音、数据、图像、视频传输与大规模的用户接入提供高速与保证质量的服务。

4. 请参考本章对WPAN技术的描述，举出 5 个应用无线个人区域网络技术的例子。

答：家庭网络、安全监控、汽车自动化、消费类家用电器、儿童玩具、医用设备控制、工业控制、无线定位。

5.. 请参考本章对于Internet 核心交换、边缘部分划分方法的描述，举出身边 5 种端系统设备。

答：PDA、智能手机、智能家电、无线传感器节点、RFID 节点、视频监控设备。

7. 长度8B与536B的应用层数据通过传输层时加上了20B的TCP报头, 通过网络层时加上60B 的IP 分组头，通过数据链路层时加上了18B 的Ethernet 帧头和帧尾。

分别计算两种情况下的数据传输效率。

（知识点在：P33）解：长度为8B的应用层数据的数据传输效率：8/(8+20+60+18) ×100%=8/106×100%=7.55%长度为536B的应用层数据的数据传输效率：536/(536+20+60+18) ×100%=536/634×100%=84.54%8. 计算发送延时与传播延时。

第一章习题参考答案1-1多速电风扇的转速控制为开环控制。

家用空调器的温度控制为闭环控制。

1-2 设定温度为参考输入，室内温度为输出。

1-3 室温闭环控制系统由温度控制器、电加热装置、温度传感器等组成，其中温度控制器可设定希望达到的室温，作为闭环控制系统的参考输入，温度传感器测得的室温为反馈信号。

温度控制器比较参考输入和反馈信号，根据两者的偏差产生控制信号，作用于电加热装置。

1-4 当实际液面高度下降而低于给定液面高度h r ，产生一个正的偏差信号，控制器的控制作用使调节阀增加开度，使液面高度逼近给定液面高度。

第二章 习题参考答案2-1 （1）()()1453223++++=s s s s s R s C ； （2）()()1223+++=s s s ss R s C ； （3）()()1223+++=-s s s e s R s C s2-2 （1）单位脉冲响应t t e e t g 32121)(--+=；单位阶跃响应t t e e t h 3612132)(----=； (2)单位脉冲响应t e t g t 27s i n 72)(2-=；单位阶跃响应)21.127sin(7221)(2+-=-t e t h t 。

2-3 （1）极点3,1--，零点2-；(2) 极点11j ±-.2-4)2)(1()32(3)()(+++=s s s s R s C . 2-5 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U ; (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-6 (a)()()RCsRCs s U s U 112+=;(b)()()141112+⋅-=Cs RR R s U s U ; (c)()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U . 2-7 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602. 2-8()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=26023.2-9 ()2.0084.01019.23-=⨯--d d u i .2-10 (2-6) 2-11(2-7)2-12 前向传递函数)(s G 改变、反馈通道传递函数)(s H 改变可引起闭环传递函数)()(s R s C 改变。

光电子技术及应用（第2版）章节习题及自测题参考答案第一章习题参考答案一、单选题1.ABCD2.ABC3.ABC4.D5.B6.C7.B8.B9. A 10.A二、填空题11.500，30012.无线电波，.红外光，可见光和紫外光，X 射线，γ射线13.0.77---1000μm ，近红外，中红外和远红外14.泵浦源，谐振腔和激活介质15.频率，相位，振幅及传播方向16.受激辐射，实现粒子数反转，谐振腔；方向性好，相干性好，亮度高 17.935μm18.919.125103.1--⋅⋅⨯s m kg20.三、计算题21.解：（1）根据距离平方反比定律2/R I E e e =，太阳的辐射强度为sr W R E I e e /10028.3252⨯==。

得到太阳的总功率为W I e e 26108.34⨯==Φπ（2）太阳的辐射亮度为()sr cm W A I L e ./10989.127⨯== 太阳的辐射出射度为27/1025.6m W L M e e ⨯==π 太阳的温度为K M T e 57614==σ22.解：222z r r ='=，22cos cos z r z+'='=θθ，r d r dS '∆'=ϕ 由：2cos cos r BdS S d d dE θθ'='Φ'=2202222022)(2cos 2z R RB z r r d r z B r d r r B E R R+=+'''=''=⎰⎰ππθπ 23.解：设相干时间为τ，则相干长度为光束与相干时间的乘积，即c L c ⋅=τ 根据相干时间和谱线宽度的关系c L c v ==∆τ1 又因为00γλλv ∆=∆，λc v =0，nm 8.6320=λ由以上各关系及数据可以得到如下形式：单色性=101200010328.6108.632-⨯===∆=∆nm nm L v v c λλλ 24.证明：若t=0时刻，单位体积中E 2能级的粒子数为n 20，则单位体积中在t→t+dt 时间内因自发辐射而减少的E2能级的粒子数为：2122122120A t dn A n dt A n e dt --==故这部分粒子的寿命为t ，因此E2能级粒子的平均寿命为212120020211A t tA n e dtn A τ∞-==⎰ 25.解：设两腔镜1M 和2M 的曲率半径分别为1R 和2R ，121m,2m R R =-=工作物质长0.5m l =，折射率 1.52η=根据稳定条件判据：（1） 其中（2） 由（1）解出2m 1m L '>>由（2）得所以得到： 2.17m 1.17m L >>第二章习题参考答案011 1 21L L ''⎛⎫⎛⎫<-+< ⎪⎪⎝⎭⎝⎭() l L L l η'=-+10.5(1)0.171.52L L L ''=+⨯-=+一、选择题1.ABCD2.D3.ABCD4.AC5.ABCD6.A7.A8.A9.A 10. B二、 是非题911.√ 12.× 13.× 14.× 15.√ 16.√三、 填空题17.大气气体分子及气溶胶的吸收和散射；空气折射率不均匀；晶体介质的介电系数与晶体中的电荷分布有关，当晶体被施加电压后，将引起束缚电荷的重新分布，并导致离子晶格的微小形变，从而引起介电系数的变化，并最终导致晶体折射率变化的现象。

习题1.11．证明下列集合等式． (1) ；(2) ()()()C B C A C B A \\\ =；(3) ()()()C A B A C B A \\\=．证明 (1) )()C \B (c C B A A =)()( c c C B A A B A =c C A B A )()( =)(\)(C A B A = .(2) c C B A A )(C \B)(=)()(c c C B C A ==)\()\(C A C A .(3) )(\C)\(B \c C B A A =c c C B A )( =)(C B A c =)()(C A B A c =)()\(C A B A =.2．证明下列命题．(1) ()A B B A = \的充分必要条件是：A B ⊂；(2) ()A B B A =\ 的充分必要条件是：=B A Ø；(3) ()()B B A B B A \\ =的充分必要条件是：=B Ø．证明 (1) A B A B B B A B B A B B A c c ==== )()()()\(的充要[条 是：.A B ⊂(2) c c c c B A B B B A B B A B B A ===)()()(\)(必要性. 设A B B A =\)( 成立，则A B A c = , 于是有c B A ⊂, 可得.∅=B A 反之若,∅≠B A 取B A x ∈, 则B x A x ∈∈且, 那么B x A x ∉∈且与c B A ⊂矛盾.充分性. 假设∅=B A 成立, 则c B A ⊂, 于是有A B A c = , 即.\)(A B B A =(3) 必要性. 假设B B A B B A \)()\( =, 即.\c C A B A B A == 若,∅≠B 取,B x ∈ 则,c B x ∉ 于是,c B A x ∉ 但,B A x ∈ 与c C A B A =矛盾.充分性. 假设∅=B 成立, 显然B A B A \= 成立, 即B B A B B A \)()\( =.3．证明定理1.1.6．定理1.1.6 (1) 如果{}n A 是渐张集列, 即),1(1≥∀⊂+n A A n n 则{}n A 收敛且∞=∞→=1;lim n n n n A A (2) 如果{}n A 是渐缩集列, 即),1(1≥∀⊃+n A A n n 则{}n A 收敛且 ∞=∞→=1.lim n n n n A A 证明 (1) 设),1(1≥∀⊂+n A A n n 则对任意∞=∈1,n n A x 存在N 使得,N A x ∈ 从而),(N n A x N ≥∀∈ 所以,lim n n A x ∞→∈ 则.lim 1n n n n A A ∞→∞=⊂ 又因为∞=∞→∞→⊂⊂1,lim lim n n n n n n A A A 由此可见{}n A 收敛且 ∞=∞→=1;lim n n n n A A(2) 当)1(1≥∀⊃+n A A n n 时, 对于,lim n n A x ∞→∈存在)1(1≥∀<+k n n k k 使得),1(≥∀∈k A x k n 于是对于任意的,1≥n 存在0k 使得n n k >0, 从而,0n n A A x k ⊂∈ 可见.lim 1 ∞=∞→⊂n n n nA A 又因为,lim lim 1n n n n n n A A A ∞→∞→∞=⊂⊂ 所以可知{}n A 收敛且 ∞=∞→=1.lim n n n n A A 4．设f 是定义于集合E 上的实值函数，c 为任意实数，证明： (1) ⎥⎦⎤⎢⎣⎡+≥=>∞=n c f E c f E n 1][1 ； (2) ⎥⎦⎤⎢⎣⎡+<=≤∞=n c f E c f E n 1][1 ； (3) 若))(()(lim E x x f x f n n ∈∀=∞→，则对任意实数c 有 ⎥⎦⎤⎢⎣⎡->=⎥⎦⎤⎢⎣⎡->=≥∞→∞=∞=∞=∞=k c f E k c f E c f E n n k n N n N k 1lim 1][111 ． 证明 (1) 对任意的[],c f E x >∈ 有,)(c x f > 则存在+∈Z n 使得n c x f 1)(+≥成立. 即,1⎥⎦⎤⎢⎣⎡+≥∈n c f E x 那么.11 ∞=⎥⎦⎤⎢⎣⎡+≥∈n n c f E x 故[];11 ∞=⎥⎦⎤⎢⎣⎡+≥⊂>n n c f E c f E 另一方面, 若,11 ∞=⎥⎦⎤⎢⎣⎡+≥∈n n c f E x 则存在+∈Z n 0使得,110 ∞=⎥⎦⎤⎢⎣⎡+≥∈n n c f E x 于是c n c x f >+≥01)(, 故[]c f E x >∈. 则有[].11 ∞=⎥⎦⎤⎢⎣⎡+≥⊃>n n c f E c f E (2) 设[]c f E x ≤∈, 则c x f ≤)(, 从而对任意的+∈Z n , 都有n c x f 1)(+<, 于是 ∞=⎥⎦⎤⎢⎣⎡+<∈11n n c f E x , 故有[];11 ∞=⎥⎦⎤⎢⎣⎡+<⊂≤n n c f E c f E 另一方面, 设 ∞=⎥⎦⎤⎢⎣⎡+<∈11n n c f E x , 则对于任意的+∈Z n , 有n c x f 1)(+<,由n 的任意性, 可知c x f ≤)(, 即[]c f E x ≤∈, 故[] ∞=⎥⎦⎤⎢⎣⎡+<⊃≤11n n c f E c f E . (3) 设[]c f E x ≥∈, 则c x f ≥)(. 由),)(()(lim E x x f x f n n ∈∀=∞→ 可得对于任意的+∈Z k , 存在N 使得)(1|)()(|N n k x f x f n ≥∀<-, 即)1(11)()(≥-≥->k k c k x f x f n , 即k c x f n 1)(->, 故)1(1lim ≥∀⎥⎦⎤⎢⎣⎡->∈∞→k k c f E x n n , 所以 ∞=∞→⎥⎦⎤⎢⎣⎡->∈11lim k n n k c f E x , 故[] ∞=∞→⎥⎦⎤⎢⎣⎡->⊂≥11lim k n n k c f E c f E ； 另一方面, 设 ∞=∞→⎥⎦⎤⎢⎣⎡->∈101lim k n n k c f E x , 则对任意+∈Z k 有⎥⎦⎤⎢⎣⎡->∈∞→k c f E x n n 1lim 0. 由下极限的定义知：存在1N 使得当1N n ≥时, 有)(10+∈∀⎥⎦⎤⎢⎣⎡->∈Z k k c f E x n , 即对任意+∈Z k 有k c x f n 1)(0->; 又由),)(()(lim E x x f x f n n ∈∀=∞→ 知),()(lim 00x f x f n n =∞→ 即对任意的+∈Z k , 存在2N 使得当2N n ≥时, 有k x f x f n 1|)()(|00<-. 取},m ax {21N N N =, 则有k c x f n 1)(0->与k x f x f n 1|)()(|00<-同时成立, 于是有k c x f k x f n 1)(1)(00->>+, 从而k c x f 2)(0->, 由k 的任意性知：c x f ≥)(0, 即[]c f E x ≥∈0, 故有 [] ∞=∞→⎥⎦⎤⎢⎣⎡->⊃≥11lim k n n k c f E c f E ; 综上所述：[].11lim 111 ∞=∞=∞=∞=∞→⎥⎦⎤⎢⎣⎡->=⎥⎦⎤⎢⎣⎡->=≥k N N n n n n n k c f E k c f E c f E 5．证明集列极限的下列性质．(1) c n n cn n A A ∞→∞→=⎪⎭⎫ ⎝⎛lim lim _____； (2) c n n c n n A A _____lim lim ∞→∞→=⎪⎭⎫ ⎝⎛； (3) ()n n n n A E A E ∞→∞→=lim \\lim ； (4) ()n n n n A E A E ∞→∞→=lim \\lim ． 证明 (1) c n n n n m c m n c n m m c n n m m c n n A A A A A ∞→∞=∞=∞=∞=∞=∞=∞→====⎪⎭⎫ ⎝⎛lim )()(lim 111_____ . (2) c n n n n n m c m c n m m c n n m m c n n A A A A A _____111lim )()(lim ∞→∞=∞=∞=∞=∞=∞=∞→====⎪⎭⎫ ⎝⎛ . (3) () ∞=∞=∞=∞=∞=∞=∞→===111))(()()\(\lim n n m n n m c m c m n n m m n n A E A E A E A E c n n m m n c n m m n n m c m A E A E A E )())(()(111 ∞=∞=∞=∞=∞=∞==== ∞=∞=∞→==1lim \\n n m n n m A E A E . (4) () ∞=∞=∞=∞=∞=∞=∞→===111))(()()\(\lim n n m cm n n m n n m c m m n n A E A E A E A E c n nm m n c n m m n n m c m A E A E A E )())(()(111 ∞=∞=∞=∞=∞=∞==== ∞=∞=∞→==1lim \\n n m n n m A E A E .6．如果}{},{n n B A 都收敛，则}\{},{},{n n n n n n B A B A B A 都收敛且(1) ()n n n n n n n B A B A ∞→∞→∞→=lim lim lim ；(2) ()n n n n n n n B A B A ∞→∞→∞→=lim lim lim ；(3) ()n n n n n n n B A B A ∞→∞→∞→=lim \lim \lim ． 习题1.21．建立区间)1,0(与]1,0[之间的一一对应．解 令1111{,,,,}2345E =, 111{0,1,,,}234F =,(0,1)\D E =, 则(0,1)E D =,[0,1]F D =. 定义:(0,1)[0,1]φ→为: ;11();(1,2,)210;2x x D x x n n n x φ⎧⎪∈⎪⎪===⎨+⎪⎪=⎪⎩ 则φ为(0,1)[0,1]→之间的一个一一对应. 2．建立区间],[b a 与],[d c 之间的一一对应，其中d c b a <<,．解 定义: :[,][,]a b c d φ→为:()().([,])d c d c bc ad x x a c x x a b b a b a b a φ---=-+=+∀∈--- 可以验证: :[,][,]a b c d φ→为一个一一对应.3．建立区间),(b a 与],[d c 之间的一一对应，其中d c b a <<,．解 令{,,,}234b a b a b a E a a a ---=+++，{,,,,}23d c d c F c d c c --=++ (,)\D a b E =. 定义:(,)[,]a c d φ→为: ;();(1,2.)d c bc ad x x D b a b a d c b a x c x a n φ--⎧+∈⎪--⎪--⎪=+=+=⎨可以验证: :(,)[,]a b c d φ→为一个一一对应.4．试问：是否存在连续函数，把区间]1,0[一一映射为区间)1,0(?是否存在连续函数，把区间]1,0[一一映射为]4,3[]2,1[ ?答 不存在连续函数把区间[0,1]一一映射为(0,1); 因为连续函数在闭区间[0,1]存在最大、最小值.也不存在连续函数把区间[0,1]一一映射为[1,2][3,4]; 因为连续函数在闭区间[1,2]上存在介值性定理, 而区间[1,2][3,4]不能保证介值性定理永远成立.5．证明：区间2~)1,0()1,0(~)1,0(R ⨯且ℵ=2R ．证明 记(0,1)A =,则(0,1)(0,1)A A ⨯=⨯.任取(,)x y A A ∈⨯, 设1231230.,0.,x a a a y b b b == 为实数,x y 正规无穷十进小数表示, 并令1122(,)0.f x y a b a b =, 则得到单射:f A A A ⨯→. 因此由定理1.2.2知A A A ⨯≤.若令10.5A A =⨯, 则1~A A A A ⊂⨯. 从而由定理1.2.2知: A A A ≤⨯. 最后, 根据Bernstein 定理知: (0,1)~(0,1)(0,1)⨯.对于(,)(0,1)(0,1)x y ∀∈⨯,定义2:(0,1)(0,1)R φ⨯→为:(,)((),())22x y tg x tg y ππφππ=--,则φ为2(0,1)(0,1)R ⨯→的一个一一对应,即2(0,1)(0,1)~R ⨯. 又因为: (0,1)~R , 则由对等的传递性知: 2(0,1)~(0,1)(0,1)~~R R ⨯且2R R ==ℵ. 6．证明：{}1:),(22≤+=y x y x A 与{}1:),(22<+=y x y x B 对等并求它们的基数．证明 令221{(,):(1,2,3,)}E x y x y n n =+==, \D A E =, 221{(,):(1,2,3,)}1F x y x y n n =+==+. 则,A E D B F D ==. 定义: :A B φ→为: 2222(,);(,),(,)11;(1,2,3,),(,).1x y x y D x y x y x y n x y E n n φ∈⎧⎪=⎨+=+==∈⎪+⎩ 可以验证: :A B φ→为一一对应, 即~A B . 又因为2~(0,1)(0,1)~~B R R ⨯, 所以 A B ==ℵ.7．证明：直线上任意两个区间都是对等且具有基数ℵ．证明 对任意的,I J R ⊆， 取有限区间(,)a b I ⊆，则(,)a b I R ℵ=≤≤=ℵ, 则由Bernstern 定理知I =ℵ, 同理J =ℵ. 故I J ==ℵ.习题1.31．证明：平面上顶点坐标为有理点的一切三角形之集M 是可数集． 证明 因为有理数集Q 是可数集，平面上的三角形由三个顶点所确定，而每个顶点由两个数决定，故六个数可确定一个三角形，所以M 中的每个元素由Q 中的六个相互独立的数所确定，即Q},,,,:{621621∈=x x x a M x x x 所以M 为可数集.2．证明：由平面上某些两两不交的闭圆盘之集M 最多是可数集． 证明 对于任意的M O ∈, 使得Q ∈)(O f . 因此可得：Q →M f :. 因为1O 与2O 不相交，所以)()(21O f O f ≠. 故f 为单射，从而a M =≤Q .3．证明：（1）任何可数集都可表示成两个不交的可数集之并；（2）任何无限集都可表成可数个两两不交的无限集之并．证明 (2) 当E 可数时，存在双射Q )1,0(:→E f . 因为∞=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎢⎣⎡+=11,11)1,0(n n n Q Q 所以∞=∞=--=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎢⎣⎡+==11111,11))1,0((n n n A n n f f E Q Q . 其中：)(),3,2,1(1,111j i A A n n n f A j i n ≠Φ==⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎢⎣⎡+=- 且Q . 又因为Q Q ⎪⎭⎫⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎢⎣⎡+-n n n n f 1,11~1,111且Q ⎪⎭⎫⎢⎣⎡+n n 1,11 可数，所以E 可表示成可数个两两不交的无限集之并．当E 不可数时，由于E 无限，所以存在可数集E E ⊂1, 且1\E E 不可数且无限，从而存在可数集12\E E E ⊂，且)(\\)\(2121E E E E E E =无限不可数. 如此下去，可得),3,2,1( =n E n 都可数且不相交，从而1011)()\(E E E E E E i i n i ==∞=∞=. 其中)0(≥i E i 无限且不交. 4．证明：可数个不交的非空有限集之并是可数集．5．证明：有限或可数个互不相交的有限集之并最多是可数集．证明 有限个互不相交的有限集之并是有限集；而可数个互不相交的有限集之并最多是可数集.6．证明：单调函数的不连续点之集至多是可数集．证明 不妨设函数f 在),(b a 单调递增，则f 在0x 间断当且仅当0)(lim )(lim )0()0(_0000>==--+→→+x f x f x f x f x x x x . 于是，每个间断点0x 对应一个开区间))0(),0((00+-x f x f .下面证明：若x x '''<为()f x 的两个不连续点，则有(0)(0)f x f x '''+≤-. 事实上，任取一点1x ，使1x x x '''<<，于是11(0)lim ()inf{()}()sup {()}lim ()x x x x x x x x x f x f x f x f x f x f x +-'>'''→→'''<<'+==≤≤=， 从而x '对应的开区间((0),(0))f x f x ''-+与x ''对应的开区间((0),(0))f x f x ''''-+不相交，即不同的不连续点对应的开区间互不相交，又因为直线上互不相交的开区间所构成的集合至多是可数集，所以可知单调函数的不连续点之集至多是可数集.7．证明：若存在某正数d 使得平面点集E 中任意两点之间的距离都大于d ，则E 至多是可数集．证明 定义映射}:)3,{(:E x d x E f ∈→，即))(3,()(E x d x D x f ∈=，其中)3,(d x D 表示以E x ∈为中心，以3d 为半径的圆盘. 显然当y x ≠时，有∅=)3,()3,(d y D d x D ，即)()(y f x f ≠，于是f 为双射，由第2题知：a E x d x ≤∈}:)3,{(，故a E ≤. 习题1.41．直线上一切闭区之集具有什么基数？区间],[b a 中的全体有理数之集的基数是什么?答 直线上一切闭区间之集的基数是c . 这是因为：2),(],[:R ∈→b a b a f 为单射，而R ∈→a b a f ],[:为满射，所以c M c =≤≤=2R R .区间],[b a 中的全体有理数之集的基数是c ，这是因为：a b a a =≤≤Q Q ],[.2．用],[b a C 表示],[b a 上的一切连续实值函数之集，证明：(1) 设},,,,{],[21 n r r r b a =Q ，],[,b a C g f ∈，则⇔=g f ),2,1)(()( ==k r g r f k k ；(2) 公式)),(,),(),(()(21 n r f r f r f f =π定义了单射)(],[:R S b a C →π；(3) c b a C =],[．证明 (1) 必要性. 显然.充分性. 假设),2,1)(()( ==k r g r f k k 成立. 因为},,,{\],[321 r r r b a x ∈∀，存在有理数列∞=1}{n n x ，使得x x n n =∞→lim ，由],[,b a c g f ∈，可得 )()lim ()(lim x f x f x f n n n ==∞→∞→及)()lim ()(lim x g x g x g n n n ==∞→∞→. 又因为∞=1}{n n x 为有理点列，所以有)()(n n x g x f =，故],[b a x ∈∀，都有)()(x g x f =.(2) ],[,b a c g f ∈∀，设)()(g f ππ=，即 )),(,),(),(()),(,),(),((2121 n n r g r g r g r f r f r f =.由(1)知：g f =. 故π为单射.(3) 由(2)知：c R S b a c =≤)(],[；又由],[b a c ⊂R ，可得],[b a c c ≤=R . 故c b a C =],[.3．设],[b a F 为闭区间]1,0[上的一切实值函数之集，证明：(1) ]},[:))(,{()(b a x x f x f ∈=π定义了一个单射)(],[:2R P b a F →π；(2) ]1,0[⊂∀E ，E E χα=)(定义了单射],[])1,0([:b a F P →α；(3) ],[b a F 的基数是c 2．证明 (1) ],[,b a F g f ∈∀，设)()(g f ππ=，即]},[:))(,{(]},[:))(,{(b a x x g x b a x x f x ∈=∈.从而]),[)(()(b a x x g x f ∈∀=，故π为单射.(2) ]1,0[,⊂∀F E ，设)()(F E αα=，则F E F E χααχ===)()(，故α为单射. (3) 由(1)知：c P b a F 2)(],[2=≤R ；又由(2)知：],[2])1,0([b a F P c ≤=，故c b a F 2],[=.4．证明：c n =C ．证明 因为R R C ⨯~，而c =⨯R R ，故c =C ；又由定理1..4.5知：c n=C . 5．证明：若E 为任一平面点集且至少有一内点，则c E =．证明 显然c E =⨯≤R R . 设00E x ∈，则0>∃δ使得E x B ⊂),(0δ，可知E x B c ≤=),(0δ，故c E =.第一章总练习题.1 证明下列集合等式．(1) ()()F F E F E E F E \\\ ==；(2) ()()()G F G E G F E \\\ =．证明 (1) 因为\()()()()()\c c c c c E E F EE F E E F E E E F E F ====, ()\()()()\c c c E F F E F F E F F F E F ===.所以\\()()\E F E E F E F F ==.(2) 因为()\()()()(\)(\),c c c c E F G E F G E F G E G F G E G F G ==== 所以()()()G F G E G F E \\\ =..2 证明下列集合等式．(1) ()B A B A n n n n \\11∞=∞== ；(2) ()B A B A n n n n \\11∞=∞== ． 证明 (1)1111\()()(\)c c n n n n n n n n A B A B A B A B ∞∞∞∞=======. (2) 1111\()()(\)c c n n n n n n n n A B A B A B A B ∞∞∞∞=======. 3．证明：22[][][]cc E f g c E f E g +≥⊂≥≥，其中g f ,为定义在E 的两个实值函数，c 为任一常数．证明 若()()22c c x E f E g ∉≥≥, 则有()2c f x <且()2c g x <, 于是 ()()()()f x g x f g x c +=+<, 故()x E f g c ∉+≥. 所以()()()22c c E f g c E f E g +≥⊂≥≥. 4．证明：n R 中的一切有理点之集n Q 与全体自然数之集对等． 证明 因为0Q =ℵ,所以0Q Q Q Q n =⨯⨯⨯=ℵ(推论1.3.1). 又因为0N =ℵ, 所以0Q n N ==ℵ, 故Q ~n N .5．有理数的一切可能的序列所成之集)(Q S 具有什么基数？6．证明：一切有理系数的多项式之集][x Q 是可数集．证明 设},Q ,,,,,0,][:][{][Q 1100111∈≠++++==---n n n n n n n n n n a a a a a a x a x a x a x P x P x 于是.][Q ][Q 0 ∞==n n x x 显然,Q~][Q 1n +x n 所以,Q ][Q 1n a x n ==+ 因此由定理1.3.5知：.][Q a x = 7．证明：一切实系数的多项式之集][x R 的基数为c ．证明 记 },R ,,,,,0,][:][{][R 1100111∈≠++++==---n n n n n n n n n n a a a a a a x a x a x a x P x P x 于是.][R ][R 0 ∞==n n x x 显然,R ~][R 1n +x n 所以,R ][R 1n c x n ==+ 因此由定理1.4.3知：.][R c x =8．证明：全体代数数(即可作为有理系数多项式之根的数)之集是可数集，并由此说明超越数(即不是代数数的实数)存在，而且全体超越数之集的基数是c ．证明 由于有理系数多项式的全体是可数集，设其元素为,,,,,,210 n P P P P 记多项式)(x P n 的全体实根之集为,n A 由于n 次多项式根的个数为有限个，故n A 为有限集，从而代数数全体 ∞==0n n A A 为可数个有限集的并，故A 为可数集，即.a A =设超越数全体所成之集为,B 即,\R A B = 则R,=B A 从而B 必为无限集，由于A 为可数集，而任一无限集添加一个可数集其基数不变，故.R c B A B ===9．证明：A B B A \~\，则B A ~．证明 因为),()\(),()\(B A A B B B A B A A ==又因为,)(\)(\,~,\~\∅==B A A B B A B A B A B A A B B A所以由保并性知),()\(~)()\(B A A B B A B A即.~B A10．证明：若,,D B B A <≤则D A <． 证明 (反证法) 假设,D A = 则由已知可得,B D ≤ 这与D B <矛盾. 故有D A <.11．证明：若c B A = ，则c A =或c B =．证明 假设,a B A == 则有,a B A = 这与c B A = 矛盾，故有c A =或c B =.12．证明：若c A k k =+∈Z ，则存在+∈Z k 使得c A k =． 证明同上.。

习题参考答案1章第1章单片机概述1．除了单片机这一名称之外，单片机还可称为和答：微控制器，嵌入式控制器。

2．单片机与普通微型计算机的不同之处在于其将、、和3部分集成于一块芯片上。

答：CPU、存储器、I/O口。

3．8051与8751的区别是A．内部数据存储单元数目不同B．内部数据存储器的类型不同C．内部程序存储器的类型不同D．内部寄存器的数目不同答：C。

4．在家用电器中使用单片机应属于微计算机的A．辅助设计应用；B．测量、控制应用；C．数值计算应用；D．数据处理应用答：B。

5．微处理器、微计算机、微处理机、CPU、单片机它们之间有何区别？答：微处理器、微处理机和CPU都是中央处理器的不同称谓；而微计算机、单片机都是一个完整的计算机系统，单片机特指集成在一个芯片上的用于测控目的的单片微计算机。

6．MCS-51系列单片机的基本型芯片分别为哪几种？它们的差别是什么？答：MCS-51系列单片机的基本型芯片分别是8031、8051和8751。

它们的差别是在片内程序存储器上。

8031无片内程序存储器，8051片内有4KB的程序存储器ROM，而8751片内集成有4KB的程序存储器EPROM。

7．为什么不应当把51系列单片机称为MCS-51系列单片机？答：因为MCS-51系列单片机中的“MCS”是Intel公司生产的单片机的系列符号，而51系列单片机是指世界各个厂家生产的所有与8051的内核结构、指令系统兼容的单片机。

8．AT89C51单片机相当于MCS-51系列单片机中的哪一种型号的产品？答：相当于MCS-51系列中的87C51，只不过是AT89C51芯片内的4KBFlah存储器取代了87C51片内的4KB的EPROM。

第2章AT89C51单片机片内硬件结构1．在AT89C51单片机中，如果采用6MHz晶振，一个机器周期为答：2μ2．AT89C51单片机的机器周期等于个时钟振荡周期。

答：12。

3．内部RAM中，位地址为40H、88H的位，该位所在字节的字节地址分别为和答：28H；88H。

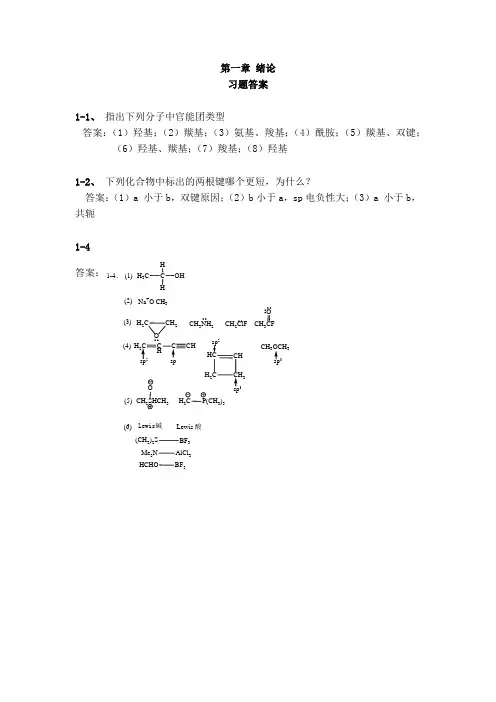
第一章 绪论 习题答案1-1、 指出下列分子中官能团类型答案：（1）羟基；（2）羰基；（3）氨基、羧基；（4）酰胺；（5）羰基、双键；（6）羟基、羰基；（7）羧基；（8）羟基1-2、 下列化合物中标出的两根键哪个更短，为什么？答案：（1）a 小于b ，双键原因；（2）b 小于a ，sp 电负性大；（3）a 小于b ，共轭 1-4 答案：(1)C HHH 3COH(2)Na +O -CH 3(3)H 2C CH 2O(4)CH 3NH 2CH 2ClF3HHC CH H 2CCH2sp 23CH 333(5)CH 2SHCH 3OH 2CP(CH 3)3(6)Lewis 酸Lewis 碱(CH 3)2S BF 3Me 3N AlCl 3HCHOBF 31-4、第2章 烷烃和环烷烃习题及答案2-1 用中文系统命名法命名或写出结构式。

答案： （1）2,6,6-三甲基-3-乙基辛烷 （2）2,6,7-三甲基壬烷（3）1-甲基-1-氯环己烷 (4) 顺-1,2-二溴环己烷 （5（6）（7）CCCC CH 3CH 3CH 3CH 3H 3H 3(8) (CH 3)2CHCH 2CH 2CH 32-2 用不同符号标出下列化合物中伯、仲、叔、季碳原子，并给以命名。

答案： (1) CH 3CH CH 2C C CH 3CH 3CH 2CH 3CH 3CH 3CH 2CH 31o 1o 1o1o1o1oo 2o2o 21o o 3o4o 43,3,4,4,6-五甲基辛烷 (2) CH3CH(CH 3)CH 2C(CH 3)2CH(CH 3)CH 2CH31o1o1o1o1oo2o2o 3o 3o 42,4,4,5-四甲基庚烷2-3 指出下列四个化合物的命名中不正确的地方并给以重新命名。

答案： （1）主链选错。

应为：2,4,6-三甲基-6-乙基辛烷 （2）主链、碳原子编号错。

应为：2-甲基-3乙基己烷 （3）碳原子编号错。

第一章参考答案是非题1.×2. √3.×4.×5.×6.x7.×8.√9.×10.×11.×12.√13.×14.√15.×16.×17.√18.×19.×20.×21.×22.×23.×24.×25.√26.√27.√28.√29.√30.×31.√选择题1.A2.A3.B4.B5.A6.B7.B8.B9.B10.C 11.C 12.A 13.B 14.B 15.C 16.C 17.C 18.A19.A 20.A 21.C 22.A 23.B 24.A 25.A 26.D 27.A28.A 29.B 30.B 31.D填空题1．自由水、束缚水 2．扩散作用、集流和渗透作用3．蒸腾作用、吐水 4．水分子内聚力 5．CO2浓度和湿度 6．变慢 7．越旺盛、越强 8．ψπ+ψp ,ψg9．渗透作用 10．吸涨吸水 11．渗透势、压力势、重力势 12．气孔蒸腾、角质蒸腾 13．呈扇形辐射状，呈径向辐射状14．0.5～2.5g·dm-2·h-1，小于0.1g·dm-2·h-1 15．蒸腾比率 16．5%—10% 17．质外体途径、跨膜途径、共质体途径18．蒸腾速率、蒸腾比率、蒸腾系数 19．质壁分离、质壁分离复原20．光照、温度、二氧化碳21．淀粉-糖转化学说、k+离子吸收学说、苹果酸生成学说 22．吐水作用问答题1．(1)水是细胞质的主要组成分。

(2)水分是重要代谢过程的反应物质和产物。

(3)细胞分裂和伸长都需要水分。

(4)水分是植物对物质吸收和运输及生化反应的溶剂。

(5)水分能使植物保持固有姿态。

(6)可以通过水的理化特性以调节植物周围的大气温度、湿度等。

对维持植物体温稳定和降低体温也有重要作用。

【参考答案】第1节：被动运输一、概念检测1.√××2.D3.B二、拓展应用1.提示:可以配制出一系列浓度梯度的蔗糖溶液,将紫色洋葱鳞片叶表皮细胞置于配好的各种浓度的蔗糖溶液中,适当时间后用显微镜观察细胞质壁分离情况。

记录刚好发生质壁分离的细胞所用的蔗糖溶液度,以及刚好尚未发生质壁分离的细胞所用的蔗糖溶液浓度,据此推算出细胞液溶质浓度应介于这两个浓度之间。

2.假设:温度变化会影响水分通过半透膜的扩散速率设计实验提示:可以借用本节问题探讨中的渗透装置进行实验。

将该渗透装置于不同温度的环境中,通过比较不同温度下漏斗管液面上升速度的快慢,判定温度是否影响⽔分子的扩散速度,实验中要注意排除各种无关变量的干扰,如置于不同温度中的漏斗内的蔗糖溶液的量和浓度必须相等,以确保实验的准确性。

第2节：被动运输一、概念检测1.×××√2.A3.A二、拓展应用1.放入蒸馏水中的草履虫,其伸缩泡的伸缩频率加快,放入海⽔中的则伸缩频率减慢。

2.提示:主动运输和被动运输的区别之一是否需要能量⽔能量来自细胞呼吸,故可通过抑制根细胞呼吸,并观察无机盐离子吸收速率是否受影响来判断其吸收过程属于主动运输还是被动运输,具体步骤:取甲、两组⽔⽔状态基本相同的柽柳幼苗,放入适宜浓度的含有Ca2+、K+的溶液中;甲组给予正常的细胞呼吸条件,乙组抑制细胞呼吸;一段时间后测定两组植株根系对Ca2+、K+的吸收速率,若两组植株对Ca2+、K+的吸收速率相同,说明柽柳从土壤中吸收无机盐为被动运输;若乙组吸收速率明显小于甲组吸收速率,说明柽柳从壤中吸收无机盐是主动运输。

复习与提高一、选择题1.A2.A3.C4.D二、非选择题1.见下图2.(1)K+和Mg2+这两种离子的浓度细胞内大于细胞外,细胞若要吸收这两种离子必须逆着浓度梯度进⽔。

(2)Na+和Cl-这两种离子的浓度细胞内⽔于细胞外,细胞若要排出这两种离子必须逆着浓度梯度进⽔3.(1)渗出增⽔(2)缓慢增大后趋于稳定蔗糖溶液清⽔(3)乙二醇增⽔(4)大液泡1。

《电路分析基础》各章习题参考答案第 1 章习题参考答案1- 1 (1) 50W ; (2) 300 V、25V, 200V、75 V ; (3) 2=12.5 Q R a=100 Q, R4=37.5 Q1- 2 V A=8.5V， V m=6.5V， V B=0.5V， V C=- 12V， V D=-19V， V p=-21.5V， U AB=8V， U BC=12.5，U DA=-27.5V1- 3 电源(产生功率)： A 、 B 元件；负载(吸收功率)： C、 D 元件；电路满足功率平衡条件。

1- 4 (1) V A=1 00V , V B=99V, V C=97V, V D=7V, V E=5V, V F=1V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V；(2) V C=90V, V B=92V , V A=93V, V E=-2V, V F=-6V, V G=- 7V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V1- 5 I 〜0.18A , 6 度，2.7 元1- 6 I=4A， I1=11A，I2=19A1- 7 (a) U=6V, (b) U=24 V, (c) R=5Q, (d) I=23.5A1- 8 (1) i6=-1A ； (2) u4=10V, u6=3 V； (3) P1=-2W 发出, P2 =6W 吸收, P3 =16W 吸收, P4 =-10W 发出, P5 =-7W 发出, P6 =-3W 发出1- 9 I=1A , U s=134V , R~ 7.8Q1- 10 S 断开：U AB=- 4.8V , U AO=- 12V , U BO=-7.2V ;S 闭合：U AB =-12V, U AO =- 12V , U BO=0V1- 11 支路 3，节点 2，网孔 2 ，回路 31- 12 节点电流方程： (A) I1 +I3- I6=0，(B)I6- I5- I7=0，(C)I5 +I 4-I3=0回路电压方程：① I6 R6+ U S5 +I 5 R5- U S3 +1 3 R3=0 ,②-15 R5- U S5+ I 7R7- U S4 =0 ,③-丨3 R3+ U S3 + U S4 + I 1 R2+ I 1 R1=01- 13 U AB=11V , I2=0.5A , l3=4.5A , R3~ 2.4 Q1-14 V A=60V V C=140V V D=90V U AC=- 80V U AD=- 30V U CD=50V1- 15 I1=- 2A I2=3A I3=- 5A I4=7A I5=2A第 2 章习题参考答案2- 1 2.4 Q 5 A2- 2 (1) 4 V 2 V 1 V; (2) 40 mA 20 mA 10 mA2- 3 1.5 Q 2 A 1/3 A2- 4 6 Q 36 Q2- 5 2 A 1 A2- 6 1 A2- 7 2 A2- 8 1 A2- 9 I1 = -1.4 A I2 = 1.6 A I3 = 0.2 A2- 10 I1 = 0 A I2 = -3 A P1 = 0 W P2 = -18 W2- 11 I i = -1 mA , I2 = - 2 mA , E3 = 10 V2- 12 I1 = 6 A , I2 = -3 A , I3 = 3 A2- 13 I1 =2 A , I2 = 1A , I3 = 1 A , I4 =2 A , I5 = 1 A2-14 V a = 12 V , I1 = - 1 A, I2 = 2 A2-15 V a = 6 V , I1= 1.5 A , I2 = - 1 A ,I3 = 0.5 A2-16 V a = 15 V , I1 = - 1 A , I2 =2 A , I3 = 3 A2-17 I1 = -1 A , I2 = 2 A2-18 I1 =1.5 A , I2 = - 1 A , I3 = 0.5 A2-19 I1 =0.8 A , I2 = - 0.75 A , I3 = 2 A , I4 = - 2.75 A , I5 = 1.55 A2-20 I3 = 0.5 A2-21 U o = 2 V , R o = 4 Q, I0 = 0.1 A2-22 I5 = -1 A2-23 (1) I5 = 0 A , U ab = 0 V ; (2) I5 = 1 A , U ab = 11 V2-24 I L = 2 A2-25 I s =11 A , R0 = 2 Q2-26 18 Q, - 2 Q, 12 Q2-27 U = 5 V2-28 I =1 A2-29 U = 5 V2-30 I =1 A2-31 10 V , 180 Q2-32 U0 = 9 V , R0 = 6 Q, U=15 V第3章习题参考答案3- 1 50Hz, 314rad/s, 0.02s, 141V, 100V, 120 °3- 2 200V, 141.4V3- 3 u=14.1si n (314t-60 °V3- 4 (1) ®u1-贏2= 120°(2) ®1 = -90° %= - 210°, %1-屁=120° (不变)3-5 (1) U^50 .^_90 V , U2 =50 .2 -0 V ;(2) U3=100 2 sin (3t+ 45 °)V , U4=100 ■■ 2 sin ( ®t+ 135 °)V3- 6 (1) i 1=14.1 sin ( 72 °)A ; (2) U2=300 sin ( 3—60 °)V3- 7 错误：(1),⑶，(4), (5)3- 8 (1) R； (2) L ； (3) C; (4) R3- 9 i=2.82 sin (10t-30 °)A , Q~ 40 var3- 10 u=44.9sin (3141-135 °V, Q=3.18 var3- 11 (1) I=20A ; (2) P=4.4kW3- 12 (1)I ~ 1.4A , I 1.4 - 30 A ； (3)Q~ 308 var, P=0W ; (4) i~ 0.98 sin (628t-30 °)A3- 13 (1)I=9.67A , I =9.67450 A , i=13.7 sin (314t+150 °) A ; (3)Q=2127.4 var, P=0W;(4) I C=0A3- 14 (1)C=20.3 尸;(2) I L = 0.25A ,l c = 16A第4章习题参考答案4-1 (a) Z =5. 36.87 J, Y =0.2 /36.87 S; (b) Z =2.5 - 2/45 门,Y =0.2.2/45 S4- 2 Y=(0.06-j0.08) S , R~ 16.67 Q, X L=12.5 Q, L~0.04 H4- 3 U R=6 0^0 V U L=80/90 V , U S=100^53.13 V4- 4 卩=2 0 £ 3 6.874-5 Z =100 2^45 ；：■,卩=1^0 A , U R=100^0 V , U L=125/90 V , U C=25/ 90 V4-6 Y =0.25 2^45 S , U =4 “2/0 V ,卩R = .2. 0 A , I L =0.^ 2 / 90 A , I C=1.2.2/90 A4- 7 ll =1 0.「2 4 5，A U S=100 乙90 V4- 8 (a) 30 V ; (b) 2.24 A4- 9 (a) 10 V ; (b) 10 A4- 10 (a) 10 V ; (b) 10 V4- 11 U=14.1 V4- 12 U L1 =15 V , U C2 =8 V , U S=15.65 V4-13 U X1 =100 V, U2 =600 V, X1=10 Q, X2=20 Q, X3=30 Q4- 14 Z =20 .2 45 门，l =2. -45 A , h = 2 0 A , .2/-90 A , U ab=0V 4- 15 (1)1 =£2 A, Z RC=5、2「，Z =5 10 门；(2) R =10 门，X^10'J4- 16 P = 774.4 W , Q = 580.8 var, S = 968 V A-4- 17 l1 = 5 A , l2 = 4 A4-18 I1 = 1 A , I2 =2 A , l =.5. 26.565 A , S =44.72. -26.565 V A4-19 Z=10", I=190A, U R2 =5 2 135 V , P =10 W64-20 a =5X10 rad/s , p= 1000 Q, Q = 100 , l = 2 mA , U R =20 mV , U L = U C = 2 V4-21 30 =104rad/s , p= 100 Q, Q = 100 , U = 10 V, I R = 1 mA , I L = I C = 100 mA4-22 L1 = 1 H , L2 ~ 0.33 H第5章习题参考答案5- 3 M = 35.5 mH5- 4 301 =1000 rad/s ,302 =2236 rad/s5- 5 Z1 = j31.4 Q , Z2 = j6.28 Q 5- 6 Z r = 3+7.5 Q5- 7 M = 130 mH5- 8 “2 二-2/45 A5- 9 U1 = 44.8 V5- 10 M12 = 20 mH , 11 = 4 A5- 11 U2 = 220 V , I1 = 4 A5- 12 n = 1.95- 13 N2 = 254 匝，N3 = 72 匝5- 14 n = 10 , P2 = 31.25 mW章习题参考答案 (1) A 相灯泡电压为零，B 、C 相各位为220V I L = I p = 4.4 A ，U p = 220 V ，U L = 380 V ，P = 2.3 kW (2) I p = 7.62 A ，I L = 13.2 A A 、C 相各为2.2A ，B 相为3.8A U L = 404 V U A N =202/ -47 V cos $ = 0.961 , Q = 5.75 kvar Z =334 28.4 门 (1) I p = 11.26 A , Z = 19.53 / 42.3 °Q; (2) I p = I l = 11.26 A , P = 5.5 kW U l = 391 V i A =22 2sin(・t —53.13 ) A i B =22 .2sin(・t —173.13 ) A i C =22 2 sin(，t 66.87 ) A U V = 160 V (1) 负载以三角形方式接入三相电源 (2) I — =3.8 T 2 -15 A , 1仁 =3.^-2/ 135 A , 仁 =3.8、「2也105 A I A =3.8、. 6/「45 A , I B =3.8I Q 「165 A , I c =3.8.6. 75 A L = 110 mH , C = 91.9 mF 章习题参考答案 P = 240 W, Q = 360 var P = 10.84 W (1) i(t) 4.7sin( t 100 ) - 3sin3 t A (2)I ~ 3.94 A , U ~ 58.84 V , P ~ 93.02 W 0MU m n o L 1 r~2 ------------- 2 u 2(t) m sin(，t —-arctan 1)V , R 2 (丄J 2 z 2 R ' 直流电源中有交流，交流电源中无直流 U 1=54.3 V , R = 1 Q, L = 11.4 mH ;约为 8% , ( L'= 12.33 mH ) 使总阻抗或总导纳为实数(虚部为 0)的条件为 尺二& = Rx = ■ L/C G =9.39 折,C 2 =75.13 M F L 1 = 1 H , L 2 = 66.7 mH C 1 = 10 M F, C 2 = 1.25 M F 章习题参考答案 第66-16-36-46-56-66-76-86-96-106-116-126-136-146- 15第77- 17-27-37-47-57-67-77-87-97- 10第88- 68-78-8i L(0+) = 1.5mA , U L(0+) = - 15Vh(0+) = 4A, i2(0+) = 1A , U L(0+) = 2V, i1(s)= 3A , i2(^)= 0, U L()= 0 i1 (0+) = 75mA , i2(0+) = 75mA , i3(0+) = 0, U L1 (0+) = 0, U L2(0+) = 2.25V6i c (t)二 2訂 A 4tU L (t) =6e _V u C (t) =10(1 _eg 0t )V , i C (t) =56说*人 500t 貝 u C (t) =115e~ sin(866 亠60 ) V10t 10t 山⑴=12e - V , L(t) =2(1 —e — )A 1 t U R (t) =~U s e 下2C V , U R (3 J - -U S e-V (1) T = 0.1s, (2) u c (t) =10e -0t V , (3) t = 0.1s u C (t) =10 _9e 」°t V 10t _ i L (t) =5e 一 A (a)f(t) =1(t —t 。

第1章C语言概述习题（P13）：1.3 写出一个C程序的构成。

答：C程序由一个main函数和0个或多个自定义函数构成，每个函数的构成如下：函数类型函数名（函数参数列表）{说明部分执行部分}1.4 C语言以函数为程序的基本单位，有什么好处？答：一个函数实现一个相对独立的功能，便于实现程序的模块化。

1.5 请参照本章例题，编写一个C程序，输出以下信息：*************************************************Very good!*************************************************答：参照例1.1编程如下# include <stdio.h>void main(){printf("********************************************\n");printf(" Very good!\n");printf("********************************************\n");}1.6 编写一个C程序，输入a、b、c 3个值，输出其中最大者。

答：参照例1.3编程如下法一：修改例1.3的主函数，自定义max函数不变。

# include <stdio.h>void main(){int max(int x,int y); /*函数声明*/int a,b,c,m; /*定义4个变量，m用于存放最大值*/scanf("%d%d%d",&a,&b,&c);/*从键盘上输入3个整数*/m=max(a,b); /*第一次调用max函数求出前两个数的最大值放在m中*/m=max(m,c); /*再调max函数求出m和第三个数的最大数*/printf("max is %d\n",m); /*输出结果*/}int max(int x,int y) /*定义求两个数的最大数的函数max */{int z;if(x>y) z=x;else z=y;return(z);}法二：修改例1.3的主函数和max函数，将max函数改为求3个数的最大数。

关于《通信电子线路》课程的习题安排：第一章习题参考答案：1-11-3解：1-5解：第二章习题解答：2-3解：2-4由一并联回路，其通频带B 过窄，在L 、C 不变的条件下，怎样能使B 增宽？ 答：减小Q 值或减小并联电阻 2-5信号源及负载对谐振回路有何影响，应该如何减弱这种影响？ 答：1、信号源内阻及负载对串联谐振回路的影响：通常把没有接入信号源内阻和负载电阻时回路本身的Q 值叫做无载Q （空载Q 值）如式通常把接有信号源内阻和负载电阻时回路的Q 值叫做有载QL,如式为空载时的品质因数为有载时的品质因数Q Q QQ LL <可见 结论：串联谐振回路通常适用于信号源内阻Rs 很小 (恒压源）和负载电阻RL 也不大的情况。

2、信号源内阻和负载电阻对并联谐振回路的影响oo Q R L Q ==ωLS L R R R LQ ++=0ωLps p p p p p p p 11R R R R Q Q G C LG Q L ++===故ωω同相变化。

与L S L R R Q 、Θ性。

较高而获得较好的选择以使也较大的情况,很大，负载电阻内阻并联谐振适用于信号源L L S Q R R ∴2-8回路的插入损耗是怎样引起的，应该如何减小这一损耗？答：由于回路有谐振电阻R p 存在，它会消耗功率因此信号源送来的功率不能全部送给负载R L ，有一部分功率被回路电导g p 所消耗了。

回路本身引起的损耗称为插入损耗，用K l 表示 无损耗时的功率，若R p = ∞， g p = 0则为无损耗。

有损耗时的功率插入损耗 通常在电路中我们希望Q 0大即损耗小，其中由于回路本身的LgQ 0p 01ω=，而Lg g g Q 0L p s L )(1ω++=。

2-1111P P K l '=率回路有损耗时的输出功率回路无损耗时的输出功L2L s s L 201g g g I g V P ⋅⎪⎪⎭⎫ ⎝⎛+==L 2p L ss L 211g g g g I g V P ⋅⎪⎪⎭⎫ ⎝⎛++=='20L 1111⎪⎪⎪⎪⎭⎫⎝⎛-='=Q Q P P K l2-12解：2-135.5Mhz 时，电路的失调为：66.655.0*23.33f f 2Q p 0==∆=ξ 2-14解：又解：接入系数p=c1/（c1+c2）=0.5，折合后c0’=p2*c0=0.5pf,R0’=R0/ p2=20kΩ,总电容C=Ci+C0’+C1C2/(C1+C2)=15.5pf,回路谐振频率fp=45.2Mhz，谐振阻抗Rp=1/（1/Ri+1/Rp0+1/R0’）,其中Rp0为空载时回路谐振阻抗，Rp0=Q0*2π*fp*L=22.72KΩ，因此，回路的总的谐振阻抗为：Rp=1/（1/Ri+1/Rp0+1/R0’）=5.15 KΩ，有载QL=Rp/（2π*fp*L）=22.67，通频带B=fp/QL=1.994Mhz2-17；第三章习题参考答案：3-3晶体管的跨导gm是什么含义，它与什么参量有关？答：3-4为什么在高频小信号放大器中，要考虑阻抗匹配问题？答：3-7放大器不稳定的原因是什么？通常有几种方法克服？答：不稳定原因：克服方法：3-9解：3-10解：4-1答：答：4-5解：4-64-14 一调谐功率放大器工作于临界状态，已知V CC =24V ，临界线的斜率为0.6A/V ，管子导通角为90︒，输出功率P o =2W ，试计算P =、P c 、ηc 、R p 的大小。

习题一一、单项选择题1.数据管理技术的发展经历了多个理阶段，其中数据独立性最高的是（ A ）阶段。

A)数据库系统 B)文件系统 C)人工管理D)数据项管理2.（ B ）属于信息世界的模型，是现实世界到机器世界的一个中间层次。

A)数据模型 B)概念模型 C)E-R图 D)关系模型3.反映现实世界中实体及实体间联系的信息模型是（ D ）。

A)关系模型 B)层次模型 C)网状模型 D)E-R模型4.下列条目中，（ C ）是数据模型的要素。

Ⅰ.数据管理Ⅱ.数据操作Ⅲ.数据完整性约束Ⅳ.数据结构A)Ⅰ、Ⅱ和Ⅲ B)Ⅰ、Ⅱ和Ⅳ C)Ⅱ、Ⅲ和Ⅳ D)Ⅰ、Ⅲ和Ⅳ5.数据库的概念模型独立于（ B ）。

A)E-R图 B)具体的机器和DBMSC)现实世界 D)用户需求6.按所使用的数据模型来分，数据库可分为哪三种模型（ A ）。

A)层次、关系和网状 B)网状、环状和链状C)大型、中型和小型 D)独享、共享和分时7.层次模型不能直接表示实体间的（ C ）。

A)1﹕1关系 B)1：n关系 C)m﹕n关系 D)1﹕1和1：n关系8.在对层次数据库进行操作时，如果删除双亲节点，则相应的子女节点值也被同时删除。

这是由层次模型的（ B ）决定的。

A)数据结构 B)完整性约束 C)数据操作 D)缺陷9.下列条目中，（ D ）是数据库应用系统的组成成员。

Ⅰ.操作系统Ⅱ.数据库管理系统Ⅲ.用户Ⅳ.数据库管理员Ⅴ.数据库Ⅵ.应用系统A)仅Ⅱ、Ⅳ和Ⅴ B)仅Ⅰ、Ⅱ、Ⅲ、Ⅳ和ⅤC)仅Ⅰ、Ⅱ、Ⅳ和Ⅴ D)都是10.在数据库中，产生数据不一致性的根本原因是（ C ）。

A)数据存储量过大 B)访问数据的用户数太多C)数据冗余 D)数据类型太复杂11.关系模型的完整性规则不包括（ D ）。

A)实体完整性规则 B)参照完整性规则C)用户自定义的完整性规则 D)数据操作性规则12.数据库管理系统中数据操纵语言DML所实现的操作一般包括（ A ）。

A)查询、插入、修改、删除B)排序、授权、删除C)建立、插入、修改、排序D)建立、授权、修改13.关系模型中，一个关键字（ C ）。

vb课后习题参考答案第一章习题参考答案一、填空题1、对象事件驱动2、编译运行模式解释运行模式二、简答题1、简述VB的特点。

答：①可视化的程序设计方法②面向对象的程序设计思想③事件驱动的编程机制④结构化的程序设计语言⑤高度的可扩充性⑥强大的数据库访问能力⑦支持动态数据交换⑧支持对象链接与嵌入2、简述VB的安装过程。

答：①向光驱中放入VB安装光盘；②计算机将运行自动安装程序，若没有，执行VB目录下的Setup.exe；③根据提示逐一回答问题，并点击“下一步”；④点击“完成”；2、如何启动VB。

答：三种方法：①单击“开始”按钮，选择“程序”菜单下的“Microsoft Visual Basic 6.0 中文版”菜单项并单击；②双击桌面上的VB6.0快捷图标；③在“开始”菜单的运行对话框中输入命令来启动VB；第二章习题参考答案一、选择题：1-10、DCACD BCBBC11-20、BADCA BBAAB21-29、AACBB CDDC二、填空题1．窗体、控件2．属性值3．属性窗口设置、代码窗口设置4．事件过程5．对象名、下划线、事件名6．Form_Click第三章习题参考答案一、选择题1、B2、C3、A4、B5、A6、C7、C二、填空题1、11字符型、字节型、整型、长整型、单精度型、双精度型、货币型、逻辑型、日期型、对象型、变体型。

String、Byte、Integer、Long、Single、Double、Currency、Boolean、Date、Object、Variant2、双引号(英文)、#3、ASCII、1、25、&、+、+6、Now()、Time、日期型三、解答题1、(3)2、(1 )3、（1）常量（关键字）（2）字符型常量（3）逻辑型常量（4）变量（5）字符串常量（6）变量（7）字符串常量（8）变量（9）日期型常量（题目应是#11/16/1999#）（10）数值型常量（单精度）4、315、（1）(1+y/x)/(1-y/x) （2）x^3+3*x*y/(2-y)（3）sqr(abs(a*b-c^3)) （4）sqr(s*(s-a)*(s-b)*(s-c))6、7、（1）13 （2）17（3）#1999-11-12# （4）zxy123ABC8、（1）19 （2）8.16666666666667（3）5．25 （4）29、（1）-4 （2）2 . 82842712474619 （3）-3 （4）49 （5）”hello” （6）He7）16 （8）“-459.65” （9）510、（4）11、（2）12、（4）第四章习题参考答案一、选择题：1—7: DAABBCD二、填空题1．500.00%2．将字号扩大为原来的二倍3． B三、编程题（略）1．文本框、标签和命令按钮的名称分别为text1、label1、command1Private Sub Command1_Click()Label1.caption=text1.textCommand1.caption=text1.textEnd Sub2．单价、数量、折扣和应付款对应的文本框的名称分别为：text1、text2、text3和text4，计算和清除命令按钮的名称分别为：command1和command2。