实验二 非线性方程求根实验报告

第七章非线性方程解法⒈二分法考察有根区间[a, b]，取中点x0=(b+a)/2 将它分为两半，假设中点x0不是f(x)的零点，然后进行根的搜索，即查找f(x0)与f(a)是否同号，如果确系同号，说明所求的根x*在x0的右侧，这是令a1= x0，b1=b;否则x*必在x0的左侧，这是令a1=a,b1=x0,不管出现哪一种情况，新的有根区间[a1, b1]的长度仅为[a, b]的一半。

.重复以上做法得新近似根x1,…这样不断将区间分半,得到一系列区间[an , bn],和近似根(区间中点)nx,n=0,1,2,3…,nx误差为(b-a)/2n+1.这样的方法称为二分法。

下面是一个关于二分法的例子。

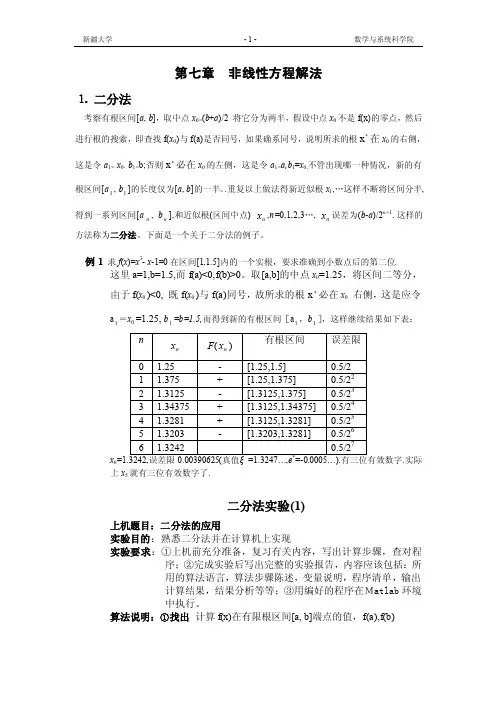
例1求f(x)=x3- x-1=0在区间[1,1.5]内的一个实根，要求准确到小数点后的第二位.这里a=1,b=1.5,而f(a)<0,f(b)>0。

取[a,b]的中点x0=1.25，将区间二等分，由于f(x0 )<0, 既f(x0 )与f(a)同号，故所求的根x*必在x0 右侧，这是应令a1＝x0 =1.25, b1=b=1.5,而得到新的有根区间［a1，b1］，这样继续结果如下表：x6.实际上x5就有三位有效数字了.二分法实验(1)上机题目：二分法的应用实验目的：熟悉二分法并在计算机上实现实验要求：①上机前充分准备，复习有关内容，写出计算步骤，查对程序；②完成实验后写出完整的实验报告，内容应该包括：所用的算法语言，算法步骤陈述，变量说明，程序清单，输出计算结果，结果分析等等；③用编好的程序在Ｍatlab环境中执行。

算法说明：①找出计算f(x)在有限根区间[a, b]端点的值，f(a),f(b)②计算计算f(x)在区间中点（2ba+）处的值f(2ba+) .③判断若f(2ba+)=0，则2ba+即是根，计算过程结束，否则检验若f(2ba+)f(a)<0,则以2ba+代替b,否则以2ba+代替a.反复执行步骤②和步骤③，直到区间[a, b]长度小于允许误差ξ，此时中点2ba+即为所求近似根。

实验报告一：实验题目一、 实验目的掌握求解非线性方程根的二分法、简单迭代法和牛顿迭代法，并通过数值实验比较两种方法的收敛速度。

二、 实验内容1、编写二分法、并使用这两个程序计算02)(=-+=x e x x f 在[0, 1]区间的解，要求误差小于 410- ，比较两种方法收敛速度。

2、在利率问题中，若贷款额为20万元，月还款额为2160元，还期为10年，则年利率为多少？请使用牛顿迭代法求解。

3、由中子迁移理论，燃料棒的临界长度为下面方程的根，用牛顿迭代法求这个方程的最小正根。

4、用牛顿法求方程的根，精确至8位有效数字。

比较牛顿迭代法算单根和重根的收敛速度，并用改进的牛顿迭代法计算重根。

第1题：02)(=-+=x e x x f 区间[0,1] 函数画图可得函数零点约为0.5。

画图函数：function Test1()% f(x) 示意图, f(x) = x + exp(x) - 2; f(x) = 0r = 0:0.01:1;y = r + exp(r) - 2plot(r, y);grid on 二分法程序：计算调用函数：[c,num]=bisect(0,1,1e-4)function [c,num]=bisect(a,b,delta)%Input –a,b 是取值区间范围% -delta 是允许误差%Output -c 牛顿迭代法最后计算所得零点值% -num 是迭代次数ya = a + exp(a) - 2;yb = b + exp(b) - 2;if ya * yb>0return;endfor k=1:100c=(a+b)/2;yc= c + exp(c) - 2;if abs(yc)<=deltaa=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif abs(b-a)<deltanum=k; %num为迭代次数break;endendc=(a+b)/2;err=abs(b-a);yc = c + exp(c) - 2;牛顿迭代法程序：计算调用函数：[c,num]=newton(@func1,0.5,1e-4) 调用函数：function [y] = func1(x)y = x + exp(x) - 2;end迭代算法：function[c,num]=newton(func,p0,delta)%Input -func是运算公式% -p0是零点值% -delta是允许误差%Output -c牛顿迭代法最后计算所得零点值% -num是迭代次数num=-1;for k=1:1000y0=func(p0);dy0=diff(func([p0 p0+1e-8]))/1e-8;p1=p0-y0/dy0;err=abs(p1-p0);p0=p1;if(err<delta)num=k;%num为迭代次数break;endendc=p0;第2题：由题意得到算式：计算调用函数：[c,num]=newton(@func2,0.02,1e-8)程序：先用画图法估计出大概零点位置在0.02附近。

实验 2 解非线性方程实验实验目的：进一步熟练掌握解非线性方程的二分法算法、Steffensen算法、牛顿迭代法，提高编程能力和解算非线性方程问题的实践技能。

实验内容：用二分法算法(取[a,b]=[1,2])、Steffensen算法(取)、牛顿迭代法(取)解算非线性方程的根实验原理二分法算法Steffensen算法牛顿迭代法实验步骤1 要求上机实验前先编写出程序代码2 编辑录入程序3 调试程序并记录调试过程中出现的问题及修改程序的过程4 经反复调试后，运行程序并验证程序运行是否正确。

5 记录运行时的输入和输出。

实验思考试验改变Steffensen算法的迭代初值进行计算，试验改变牛顿迭代算法的迭代初值进行计算，分别对比计算结果并作出分析总结数学建模与应用：请建立数学模型并应用你的程序解决一个物理计算问题--木质球体浸入水中深度问题。

假若球体是由密度为ρ=0.638且半径为r=10cm 的长叶松木质球体构成的，问球体浸入水中深度是多少？又假若球体是由密度为ρ=0.638且三个长半轴分别为a=10cm,b=15cm,c=20cm的长叶松木质椭圆球体构成的，问球体浸入水中深度是多少？（建模可参考课本32页）实验报告书写要求：根据实验情况和结果撰写并递交实验报告。

实验报告应当有算法原理简介，算法流程图，程序代码，运行调试记录，计算结果阐释；对于数学建模的应用问题要有分析建模的过程、求解计算的过程、实际问题解答或阐释的内容。

实验总结(学会了......; 掌握了......; 训练了......; 发现了......; 今后学习中......有待提高。

）参考程序1.二分法1、实验原理：二分法2、实验步骤1建立函数function y=f3(x)y=x.^3-x-12建立函数function[c,err,yc]=bisect(f,a,b,delta)ya=feval(f,a);yb=feval(f,b);if ya*yb>0returnendmax1=1+round((log(b-a)-log(delta))/log(2)); for k=1:max1c=(a+b)/2;yc=feval(f,c)if yc==0a=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif b-a<deltabreakendendc=(a+b)/2;err=abs(b-a);yc=feval(f,c);3调用函数>> [c,err,yc]=bisect('f3',1,2,0.0001)y =-1y =5y =0.8750 yc =0.8750 y =-0.2969 yc =-0.2969 y =0.2246 yc =0.2246 y =-0.0515 yc =-0.0515 y =0.0826 yc =0.0826y =0.0146yc =0.0146y =-0.0187yc =-0.0187y =-0.0021yc =-0.0021y =0.0062yc =0.0062y =0.0020yc =0.0020y =-4.6595e-005yc =-4.6595e-005y =9.9479e-004yc =9.9479e-004y =4.7404e-004yc =4.7404e-004y =2.1371e-004yc =2.1371e-004y =8.3552e-005c =1.3247err =6.1035e-005yc =8.3552e-005 2、牛顿迭代1、实验原理：牛顿迭代法2、实验步骤1.建立函数function y=f(x)y=x.^3-x-12.建立函数function y=f2(x)y=3*x.^2-13.牛顿迭代法函数的程序function [p0,err,k,y]=Newton(f,df,p0,delta,epsilon,max1)for k=1,max1p1=p0-feval(f,p0)/feval(df,p0);err=abs(p1-p0);relerr=2*err/(abs(p1)+delta);p0=p1;y=feval(f,p0);if(err<delta)|(relerr<delta)|(abs(y)<epsilon),break,end end4.函数的调用>> [p0,err,k,y]=Newton('f','f2',1.5,0.001,0.0001,1000)y =0.8750y =5.7500y =0.1007y =0.1007y =4.4499y =0.0021y =0.0021y =4.2685y =9.2438e-07 p0 =1.3247err =4.8222e-04 k =3y =9.2438e-07三、Steffensen算法1、实验原理：Steffensen算法2、实验步骤①function y=f1(x)y=x.^3-x-1②function y=f2(x)y=3*x.^2-1③function [p,Q]=steffensen(f,df,p0,delta,epsilon,max1) R=zeros(max1,3);R(1,1)=p0;for k=1:max1for j=2:3nrdenom=feval(df,R(k,j-1));if nrdenom==0'division by zero in Newton-Raphson method'breakelesR(k,j)=R(k,j-1)-feval(f,R(k,j-1))/nrdenom;endaadenom=R(k,3)-2*R(k,2)+R(k,1);if aadenom==0'division by zero in Aitken’s Acceleration'breakelesR(k+1,1)=R(k,1)-(R(k,2)-R(k,1))^2/aadenom;endendif(nrdenom==0)|(aadenom==0)breakenderr=abs(R(k,1)-R(k+1,1));relerr=err/(abs(R(k+1,1))+delta);y=feval(f,R(k+1,1));if (err<delta)|(relerr<delta)|(y<epsilon)p=R(k+1,1)Q=R(1:k+1,:);breakendend④>> [p,Q]=steffensen('f1','f2',1.5,0.0001,0.001,100)y =5.7500y =-1y =-1p =p =Q =1.5000 0 00 0 0实验总结:学会了用二分法，牛顿迭代法，Steffensen算法来求解线性方程的解; 掌握了一定的解题方法，和建立函数的方法，在调用函数中出现的错误也能及时判断理解并加以改正; 训练了应用MATLAB的技巧和方法，在一定程度上得以提升; 发现了应用此方法的简易方便之处，也认识到自己的很多缺点要继续努力学习掌握好知识技能; 今后学习中不仅要掌握好理论知识理解并记忆，更要多多在实际中操作实验，灵活应用所学知识，来提高自己。

实验报告学院：电子信息工程实验课程：计算方法学生姓名：学号：专业班级：通信工程实验二非线性方程求根1 目的与要求（1）进一步熟练掌握求解非线性方程的二分法与Newton迭代法。

（2）掌握二分法与Newton迭代法的算法，能运用程序设计语言和此方法编制软件求出任意指定一元三次方程在给定点附近的根。

2 实验内容用二分法和Newton迭代法求方程310x x--=在1.5 附近的根，精确到310-，输出每次的迭代结果并统计所用的迭代次数。

3 实验原理（1）二分法实验原理取[a,b]区间二等分的中点x1 =(a+b)/2（1）若f(x1)=0,则x1是f(x)=0的实根。

（2）若f(a)f(x1)<0 成立,则x* 必在区间(a, x1)内，取a1=a,b1= x1；否则x*必在区间(x1,b)内，则取a1= x1,b1=b，这样，得到新区间[a1,b1]，其长度为[a,b]的一半。

（3）如此继续下去，进行n次等分（2）Newton迭代法实验原理4 程序设计（1）流程图二分法程序流程图Newton迭代法程序流程图（2）程序代码①二分法求非线性方程根#include<stdio.h>#include<math.h>double fun1(double x){return x*x*x-x-1;}double fun2(double x1,double x2){return (x1+x2)/2;}main(){int n=1;float a,b,c;printf("二分法求非线性方程的根\n"); scanf("a=%f,b=%f",&a,&b);if (fun1(a)*fun1(b)<0){while(fabs(b-a)>1e-3){c=fun2(a,b);if (fun1(a)*fun1(c)<0){b=c;}else if (fun1(c)*fun1(b)<0){a=c;}else{break;}printf("当前计算次数为%d 计算结果为%lf\n",n,fun2(a,b));n++;}}else{printf("不符合二分法使用条件，请重新输入：\n"); }}②Newton迭代法#include<stdio.h>#include<math.h>double fun1(double x){return x*x*x-x-1;}double fun2(double x){return 3*x*x-1;}double root(double num){double x1,x0;int n=1;x0=num;if (fun2(x0)==0){printf("Algorithm failed. Exit !"); }else{x1=x0-fun1(x0)/fun2(x0);printf("Newton迭代法求根\n");}while (fabs(x1-x0)>1e-3){printf("当前计算次数为%d 计算结果为%lf\n",n,x1); x0=x1;x1=x0-fun1(x0)/fun2(x0);n++;}}main(){root(1.5);}5 实验结果与分析（1）二分法求根结果界面（2）Newton迭代法求根结果界面分析：（1）本次试验两种算法均采用了while循环及if-else判断语句，编程函数并由主函数调用，较简单的实现了二分法与Newton迭代法的编程任务。

数值分析实验报告——非线性方程求根一、实验目的：1.掌握求解非线性方程的常用方法；2.了解非线性方程求根问题的数值解法；3.熟悉使用数值分析软件进行非线性方程求根的实现。

二、实验原理：非线性方程指的是形如f(x)=0的方程，其中f(x)是一个非线性函数。

非线性方程求根的常用方法包括二分法、割线法和牛顿法等。

其中，二分法是通过不断缩小区间范围来逼近方程的解；割线法是通过使用割线来逼近方程的解；牛顿法则是通过使用切线来逼近方程的解。

对于给定的非线性方程，可以根据实际情况选择合适的方法进行求根。

三、实验内容：1.编写求解非线性方程的函数，包括二分法、割线法和牛顿法；2.使用编写的函数求解给定的非线性方程，比较各个方法的收敛速度和精确程度；3.根据实际情况分析和选择合适的方法进行求根。

四、实验步骤：1.针对给定的非线性方程，编写二分法的函数实现：（1）首先确定方程的解存在的区间；（2）根据方程的解存在的区间，使用二分法逐步缩小区间范围；（3）根据设定的精度要求，不断循环迭代，直至满足要求或达到迭代次数限制；2.针对给定的非线性方程，编写割线法的函数实现：（1）首先需要确定方程的解存在的初始点；（2）根据方程的解存在的初始点，根据割线的定义进行迭代；（3）设定迭代的精度要求和限制次数，结束迭代；3.针对给定的非线性方程，编写牛顿法的函数实现：（1）首先需要确定方程的解存在的初始点；（2）根据方程的解存在的初始点，根据牛顿法的定义进行迭代；（3）设定迭代的精度要求和限制次数，结束迭代；4.根据给定的非线性方程，分别使用二分法、割线法和牛顿法进行求解，并比较各个方法的收敛速度和精确程度；5.分析实际情况，选择合适的方法进行求解。

五、实验结果：4.通过比较，发现割线法和牛顿法的收敛速度较快，精确程度较高，因此选择割线法进行求解。

六、实验总结：通过本次实验，我掌握了求解非线性方程的常用方法，并使用数值分析软件实现了二分法、割线法和牛顿法。

【关键字】报告计算机学院上机实践报告一、目的1．通过本实验，帮助加深对非线性方程求根方法的构造过程的理解；2．能将各种方法编写为程序并上机实现；3．比较各种方法在求解同一非线性方程根时，在收敛情况上的差异。

2、内容与设计思想1．用二分法求方程f(x)=x3-2x-5=0在区间[2 , 3]内的根。

2．方程f(x)=2x3-5x2-19x+42=0在x=3.0附近有根，试写出其三种不同的等价形式以构成三种不同的迭代格式，再用简单迭代法求根，观察这三种迭代是否收敛。

三、使用环境1. 硬件环境微型计算机（Intel x86系列CPU）一台2. 软件环境Windows2000/XP操作系统VC++6.0或其它的开发工具。

四、核心代码及调试过程1．用二分法求方程f(x)=x3-2x-5=0在区间[2 , 3]内的根主要代码：void bisect(double a,double b,int max_B){ double root, ya,yb,yroot;int i,actual_B;ya=f(a);yb=f(b);if(ya*yb>0){ printf("method failed!\n");exit(0); }for(i=1;i<=max_B;i++){ root=(a+b)/2;yroot=f(root); //取当前含根区间的中点if(yroot==0){ a=root;b=root;}else if(yb*yroot>0) //取含根区间为[a,(a+b)/2]{ b=root;yb=yroot;}Else //取含根区间为[(a+b)/2,b]{ a=root;ya=yroot;}if(fabs(b-a)<EPS) break;}root=(a+b)/2; yroot=f(root); actual_B=i;printf("root=%10.6lf\tf(root)=%10.6e\tatual_B=%d\n",root,yroot,actual_B); }结果：2．迭代格式分别为：x=2/19*x*x*x-5/19*x*x+42/19x=sqrt(2/5*x*x*x-19/5*x+42/5);x=(5/2*x*x+19/2*x-21)^(1/3)主要代码：double g(double x){return(pow((2.0/19.0*x*x*x-5/19*x*x+42/19),1.0)); /*定义迭代函数*/}void iterate(double a,double b,double x0,int max_D){int k=1;double x1;while(k<=max_D){x1=g(x0); /*迭代计算*/if((x1<a)||(x1>b)){printf("re_select a proper initial value x0!\n");exit(0);}if(fabs(x1-x0)<EPS) /*迭代成功并达到精度要求*/{printf("method succeed!\n");printf("root=%10.6lf\n",x1);break;}x0=x1;k++; /*x0的值被更新，累加迭代次数*/}printf("iteration times=%d\n",k); /*输出实际迭代次数*/if(k>max_D)printf("method failed!\n");}int main(){ double a=2.0,b=3.0,x0=(a+b)/2.0;int max_D=50;iterate(a,b,x0,max_D);}前两种迭代结果：第三种：输入数据时应注意数据的类型，否则程序会报错。

数值分析实验报告——非线性方程求根二分法一、题目用二分法求方程=的所有根x.13要求每个根的误差小于-x+0.001..21二、方法二分法三、程序1、Jiangerfen.M的程序function[c,yc]=jiangerfen(f,a,b,tol1,tol2)if nargin<4 tol1=1e-3;tol2=1e-3;end%nargin<4表示若赋的值个数小于4，则tol1和tol2取默认值。

ya=feval('f',a);%令x=a代入到方程f中，ya即f(a)。

yb=feval('f',b);if ya*yb>0,disp('(a,b)不是有根区间');return,endmax=1+round((log(b -a)-log(tol2))/log(2));%round函数是将数据取整，使数据等于其最接近的整数。

for k=1:maxc=(a+b)/2;yc=feval('f',c);if((b-a)/2<tol2)|(abs(yc)<tol1),break,endif yb*yc<0a=c;ya=yc;elseb=c;yb=yc;endendk,c=(a+b)/2,yc=feval('f',c)2、f.M的程序function y=f(x);y=x^3-2*x-1;四、结果>> format compact>> fplot('[x^3-2*x-1,0]',[-1.5,2]);>> jiangerfen('f',-1.5,-0.8);k =8c =-0.9996yc =3.9017e-004>> jiangerfen('f',-0.8,-0.3);k =8c =-0.6184yc =2.7772e-004>> jiangerfen('f',1.3,2);k =10c =1.6179yc =-9.5348e-004>> jiangerfen('f',2,3);(a,b)不是有根区间方程f(x)=x^3-2*x-1的所有根为-0.9996，-0.6184 ，1.6179 。

实验报告一、实验目的1．迭代函数对收敛性的影响。

2．初值的选择对收敛性的影响。

二、实验题目1．用简单迭代法求方程01)(3=--=x x x f 的根。

分别化方程为如下等价方程： 31+=x x ；13-=x x ；x x 11+=；213-+=x x x 取初值5.10=x ，精度为410-，最大迭代次数为500，观察其计算结果并加以分析。

2．①用牛顿法求方程01)(3=-+=x x x f 在0.5附近的根，分别取初值1000,100,2,1,5.0,5.0,1,2,100,10000-----=x观察并比较计算结果，并加以分析。

②用牛顿法求方程0)(3=-=x x x f 所有根。

三、实验原理简单迭代法程序，牛顿迭代法程序。

四、实验内容及结果fun=inline('x^3-x-1');dfun=inline('3*x^2-1');-1000,x1=manewton(fun,dfun,-1000,1e-4) -100,x2=manewton(fun,dfun,-100,1e-4)-2,x3=manewton(fun,dfun,-2,1e-4)-1,x4=manewton(fun,dfun,-1,1e-4)-0.5,x5=manewton(fun,dfun,-0.5,1e-4) 0.5,x6=manewton(fun,dfun,0.5,1e-4)1,x7=manewton(fun,dfun,1,1e-4)2,x8=manewton(fun,dfun,2,1e-4)100,x9=manewton(fun,dfun,100,1e-4) 1000,x10=manewton(fun,dfun,1000,1e-4)3）在MA TLAB的主程序窗口输出以下结果：ans =-1000k=21x1 =0.682327804075895ans =-100k=16x2 =0.682327803903413ans =-2k=6x3 =0.682327803828020ans =-1k=5x4 =0.682327803828020ans =-0.500000000000000k=4x5 =0.682327803903932ans =0.500000000000000k=3x6 =0.682327803828347五、实验结果分析(1)实验1中用简单迭代法求方程01)(3=--=x x x f 的根：取初始值5.10=x 的时候，等价方程2和4是不收敛的。

2009年——2010年第一学期合肥学院数理系实验报告课程名称：数值分析实验项目：数值积分实验类别：验证性专业班级：08数学与应用数学（2）姓名：卢王菲学号：0807022048 实验地点：7#604实验时间：2009—11－26指导教师：孙梅兰成绩：一．实验目的：理解并掌握二分法、不动点迭代、牛顿切线法及弦截法解非线性方程求根的原理，掌握相应的算法原理，通过计算机解决实验问题二.实验内容：1.求方程01)(3=--=x x x f 在5.1=x 附近的根（精度81021-⨯=），取01x =2. 求方程x x e -=在0.5x =附近的根（精度81021-⨯=），取01x =三 实验方案：利用二分法、不动点迭代、牛顿切线法及弦截法解非线性方程的根，通过计算机解决实验问题。

四. 实验步骤或程序：1. >> f=inline('x^3-x-1');a=1;b=2;dlt=0.5e-5;k=1;while abs(b-a)>dltc=(a+b)/2;if f(c)==0break;elseif f(c)*f(b)<0a=c;else b=c;endfprintf('k=%d,x=%.5f\n',k,c);k=k+1;endk=1,x=1.50000k=2,x=1.25000k=3,x=1.37500k=4,x=1.31250k=5,x=1.34375k=7,x=1.32031k=8,x=1.32422k=9,x=1.32617k=10,x=1.32520k=11,x=1.32471k=12,x=1.32495k=13,x=1.32483k=14,x=1.32477k=15,x=1.32474k=16,x=1.32472k=17,x=1.32471k=18,x=1.324722.>> eps=0.5*10^(-8);dx=1;x0=1;k=0; >> while(dx>eps)k=k+1;x=exp(-x0);dx=abs(x-x0)/(1+abs(x));x0=x;end>> kxk =33x =0.5671五．程序运行结果：1.k=1,x=1.50000k=2,x=1.25000k=3,x=1.37500k=4,x=1.31250k=5,x=1.34375k=6,x=1.32813k=7,x=1.32031k=8,x=1.32422k=9,x=1.32617k=11,x=1.32471k=12,x=1.32495k=13,x=1.32483k=14,x=1.32477k=15,x=1.32474k=16,x=1.32472k=17,x=1.32471k=18,x=1.324722. k =33x =0.5671六．实验总结：通过本次实验本人收获很多。

end 程序输出
n=01,当前有根区间是[0.000000,0.500000],近似根为 0.500000,wucha=0.500000 n=02,当前有根区间是[0.250000,0.500000],近似根为 0.250000,wucha=0.250000 n=03,当前有根区间是[0.250000,0.375000],近似根为 0.375000,wucha=0.125000 n=04,当前有根区间是[0.250000,0.312500],近似根为 0.312500,wucha=0.062500 n=05,当前有根区间是[0.250000,0.281250],近似根为 0.281250,wucha=0.031250 n=06,当前有根区间是[0.265625,0.281250],近似根为 0.265625,wucha=0.015625 n=07,当前有根区间是[0.265625,0.273438],近似根为 0.273438,wucha=0.007813 n=08,当前有根区间是[0.265625,0.269531],近似根为 0.269531,wucha=0.003906 n=09,当前有根区间是[0.265625,0.267578],近似根为 0.267578,wucha=0.001953 n=10,当前有根区间是[0.265625,0.266602],近似根为 0.266602,wucha=0.000977 n=11,当前有根区间是[0.266113,0.266602],近似根为 0.266113,wucha=0.000488 n=12,当前有根区间是[0.266113,0.266357],近似根为 0.266357,wucha=0.000244 n=13,当前有根区间是[0.266235,0.266357],近似根为 0.266235,wucha=0.000122 n=14,当前有根区间是[0.266235,0.266296],近似根为 0.266296,wucha=0.000061 n=15,当前有根区间是[0.266235,0.266266],近似根为 0.266266,wucha=0.000031 n=16,当前有根区间是[0.266235,0.266251],近似根为 0.266251,wucha=0.000015 n=17,当前有根区间是[0.266243,0.266251],近似根为 0.266243,wucha=0.000008 n=18,当前有根区间是[0.266247,0.266251],近似根为 0.266247,wucha=0.000004 n=19,当前有根区间是[0.266247,0.266249],近似根为 0.266249,wucha=0.000002 n=20,当前有根区间是[0.266248,0.266249],近似根为 0.266248,wucha=0.000001

1.用迭代法解方程： f ( x) − ln( x + 2) = 0。 #include "iostream.h" #include "math.h" inline double fun1(double x) { return log(x+2); } inline double fun2(double x) { return exp(x)-2; } double ER(double x,double y,double e,double (*p) (double)) { double xy=p(x),dis=fabs(xy-x); while(dis>e && xy>x && xy<y) { x=xy; xy=p(x); } return xy; } void main() { double a1=1,b1=2,a2=-1.9,b2=-1; double (*p)(double); double m=0.5*pow(10,-6); p=fun1; double f1=ER(a1,b1,m,p); p=fun2; double f2=ER(a2,b2,m,p); cout<<"f1="<<f1<<endl; cout<<"f2="<<f2<<endl; } 2.用牛顿迭代公式计算 26 的近似值。 #include "iostream.h" #include "math.h" void main() {
f (a ) ⋅ f (b) < 0 ；又设 f ( x) 的一个零点 x* ∈ (a, b) 的近似值 (设f ′( x0 ) ≠ 0) 。用过曲

实验2 二分法求解非线性方程的根计机系 041班姓名：刘文杰学号：200410714102【实验内容】1、方法介绍（1）输入区间端点值a、b，步长h，及精度控制量ε1，若|f(a)|< ε1，则a为原方程的一个近似根，若|f(b)|< ε1，则b为原方程的一个近似根。

（2）以h为步长，将区间[a，b]分为两个等距的小区间[a，c]，[c，b]。

如果f(a)<0，f(c)>0，则根在[a，c]中，将区间[a，c]再分半，分点为x i，若|f(x i)|< ε1，则xi是方程的一个根。

（3）精度控制，若|f(x1)|< ε1，则x i是方程的一个根，否则重复（2）。

2、使用说明a：实数型，根之上界。

b：实数型，根之下界。

h：步长，实数型。

E：函数的精度，实数型。

ary：元素的一维数组，存放计算结果。

3、基本原理对于非线性方程，在某个范围内往往有不止一个的根，根的分布情况同时也可很复杂，面对这种情况，通常先将所考察的范围划分成若干子段，然后判断哪些子段内有根，这项手续称作根的隔离。

将所求的根隔离开来以后，再在有根子段内找出满足精度要求的近似根。

为此适当选取有根子段内某一点作为根的初始近似，然后运用迭代方法使之逐步精确化。

程序源代码：#include"stdio.h"#include"math.h"#include"conio.h"#include"iostream.h"double f(double x){return sin(x);}double dichotomy(double a1,double b1,double E){double c,y,y0;y0=f(a1);do{c=((a1+b1)/2.0);y=f(c);if(y*y0>0) a1=c;else b1=c;}while((b1-a1)>=E);return c;}void main(){int i,n=0;double E,a1,b1,R[20],a,b,h,y1,y2;cout<<"***********************二分法求解非线性方程的根*****************"<<endl;cout<<"请输入区间端点值a,b:"<<endl;cout<<"a=";cin>>a;cout<<"b=";cin>>b;cout<<"请输入步长h:"<<endl;cin>>h;cout<<"请输入精度控制量E:"<<endl;cin>>E;a1=a;b1=a1+h;for(;b1<=b;a1=a1+h,b1=b1+h){y1=f(a1);if(fabs(f(a1))<E) {R[n]=a1,n++;}y2=f(b1);if(y1*y2<0) {R[n]=dichotomy(a1,b1,E);n++;}}if(a1<b){b1=b;y1=f(a1);if(fabs(y1)<E) {R[n]=a1;n++;}y2=f(b1);if(y1*y2<0) {R[n]=dichotomy(a1,b1,E);n++;}}if(fabs(f(b))<E) {R[n]=b;n++;}cout<<"二分法求解非线性方程实根为:"<<endl;for(i=0;i<n;i++)cout<<R[i]<<endl;cout<<"***********************二分法求解非线性方程的根*****************"<<endl;getch();}4、实例求超越方程sinx=0在区间[-2，7]内的全部实根。

数值分析实验报告(二)一.实验名称:简单迭代、牛顿迭代求非线性方程的根。

二.实验目的:运用简单迭代、牛顿迭代法求方程根。

三.题目:（1）用简单迭代法求2的近似值，要求误差小于410-。

（2）用牛顿迭代法求x^3-x^2-1=0，要求误差小于0.0000001。

四.程序:（1）简单迭代法#include<iostream.h>#include<math.h>double fun(double); //申明函数int main(){double x0,x,esp;int i=0;cout<<"输入初值x0=";cin>>x0;cout<<"输入迭代精度esp=";cin>>esp;do{x=x0;x0=fun(x0);i++;if(i>1000000){cout<<"迭代失败！！";return 0;}}while(fabs(x-x0)>esp);cout<<"迭代次数为"<<i<<endl;cout<<"迭代结果为"<<x<<endl;}double fun(double x) //定义函数{return 1/(x+2); //x(x+2)=1}（2）牛顿法#include < iostream.h>#include < math.h>#define f(x) (x*x*(x-1.0)-1.0) // 举例函数x^3-x^2-1 #define g(x) (3.0*x*x-2.0*x) // 导函数3x^2-2x#define epsilon 0.0000001 // 精度#define MAXREAPT 100bool RootNewton(double &x)double xk1,xk0;xk0=x;for(int k=0;k< MAXREAPT;k++ ){if(g(xk0)==0.0 ){cout <<"迭代过程中导数为0. " << endl;return false ;}xk1=xk0-f(xk0)/g(xk0);if(fabs(xk1-xk0)<epsilon&&fabs(f(xk1))<epsilon){x=xk1;return true;}else{xk0 = xk1;}}cout << " 迭代次数超过预期. " << endl;return false ;}int main()double x;cout << " 牛顿迭代法求方程根,请输入初始迭代x0值:";cin >> x;if(RootNewton(x)){cout << " 该值附近的根为: " << x << endl;}else{cout << " 迭代失败! " << endl;}return 0 ;}五.运行结果:（1）简单迭代法：（2）牛顿法：六.体会:牛顿法在单根附近有较快的收敛速度。

求解非线性方程实验报告一.实验目的：通过本节实验课的学习，要求我们理解并掌握二分法、不动点迭代、牛顿切线法及弦截法解非线性方程求根的原理，掌握相应的算法原理，通过计算机解决实验问题二.实验内容：1、用对分区间法方程1-x-sinx=0在区间[0,1]上的误差小于10^(-4)的一个根，并记录对方区间的次数。

2、用不动点迭代法求解方程下x-log(x)=2(x>1)要求相对误差容限e=10^(-8)。

3、用Newton法求方程x^3-x-1=0在区间[-3,3]上的误差不大于10^(-5)的根，分别取初值x0=1.5, x0=0, x0=-1进行计算，比较他们的迭代次数。

三. 实验方案（程序设计说明）[包括算法设计思路，必要的流程图，界面设计说明、使用模块及变量的说明等。

]1、二分法是对区间收索法的一种改进，具体做法为：先求一区间的中点，并计算其函数值，若恰好有函数值为0，就是方程的根，若不为0，在判断此点的函数值与两端的函数值乘积的情况，取小于0的那个端点在进行上述对分，直到满足要求为止。

2、迭代法分为两种，一种是从任何可取的初值出发都能保证收敛，称之为大范围收敛的方法。

另一类称之为局部收敛法，即为了保证收敛必须选取初值充分接近于所要求的解。

迭代法的基本思想是一种逐渐逼近的方法，首先给定一个粗造的初值，然后用一个迭代公式，反复矫正这个初值，直到满足预先给出的精确要求为止。

3、双点弦接法与Newton法不同，两者有本质的区别，它分为两步，不属于不动点迭代法。

四. 实验步骤或程序（经调试后正确的源程序）（填写主要步骤与程序代码等，不够可附页）1、f=inline('x+sin(x)-1');a=0;b=1;dlt=1.0e-4;k=1;while abs(b-a)>dltc=(a+b)/2;if f(c)==0break;elseif f(c)*f(b)<0a=c;else b=c;endfprintf('k=%d,x=%.5f\n',k,c); k=k+1;end2、eps=10^(-8);dx=1;x0=3.5;k=0;while(dx>eps)k=k+1;x=log(x0)+2;dx=abs(x-x0)/(1+abs(x));x0=x;endkx3、f=inline('x^3-x-1');df=inline('3*x^2-1');d2f=inline('6*x');a=-3;b=3;dlt=1.0e-5;if f(a)*d2f(a)>0x0=a;elsex0=b;endm=min(abs(df(a)),abs(df(b)));k=0;while abs(f(x0))>m*dltk=k+1;x1=x0-f(x0)/df(x0);x0=x1;fprintf('k=%d x=%.5f\n',k,x0); end for x0=1.5fprintf('k=%d x=%.5f\n',k,x0); end for x0=0fprintf('k=%d x=%.5f\n',k,x0); end for x0=-1fprintf('k=%d x=%.5f\n',k,x0); end 五．程序运行结果：1、k=1,x=0.50000k=2,x=0.75000k=3,x=0.62500k=4,x=0.56250k=5,x=0.53125k=6,x=0.51563k=7,x=0.50781k=8,x=0.51172k=9,x=0.50977k=10,x=0.51074k=11,x=0.51123k=12,x=0.51099k=13,x=0.51086k=14,x=0.51093 2、k =15x =3.14623、k=1 x=-2.03846 k=2 x=-1.39028k=3 x=-0.91161k=4 x=-0.34503k=5 x=-1.42775k=6 x=-0.94242k=7 x=-0.40495k=8 x=-1.70690k=9 x=-1.15576k=10 x=-0.69419 k=11 x=0.74249k=12 x=2.78130k=13 x=1.98273k=14 x=1.53693k=15 x=1.35726k=16 x=1.32566k=17 x=1.32472当x0=1.5时：k=17 x=1.50000当x0=0时：k=17 x=0.00000当x0=-1时：k=17 x=-1.000002、六．实验总结：通过实验学会理解并掌握二分法、不动点迭代、牛顿切线法及弦截法解非线性方程求根的原理，掌握相应的算法原理，通过计算机解决实验问题并通过反复的上机实验操作，解决了在实验过程中遇到的实验问题，并了解了一些函数的特殊用法，学会了用这三种基本方法解决实际遇到的问题，并了解了二分法、不动点迭代、牛顿切线法及弦截法的各种变形算法。

班级： 学号： 姓名： 成绩：实验2 非线性方程的数值解法实验1实验目的1）进一步熟练掌握求解非线性方程的牛顿迭代法和弦截法。

2）根据牛顿迭代法和弦截法的原理，编写程序求解非线性方程，提高编程解决问题的能力。

2 实验内容（1）用牛顿法和割线法求下列方程的根x^2-e^x=0;x*e^x-1=0;（23实验原理（1）牛顿迭代公式：1()/'()k k k k x x f x f x +=- 双点弦法公式：111()()()()k k k k k k k f x x x x x f x f x +--=--- （2）令2()f x x A =-，再用牛顿法求根。

4实验步骤1)根据牛顿迭代法，双点弦法的算法编写相应的求根函数；2)用牛顿迭代法和双点弦法分别对方程进行求解；5 程序设计牛顿迭代法x0=1.0;N=100;k=0;eps=5e-6;delta=1e-6;while(1)x1=x0-fc1(x0)/fc2(x0);k=k+1;if k>Ndisp('Newton method failed')breakendif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endx0=x1;endfprintf('%f',x0)fprintf('%f',abs(fc1(x1)))双点弦法function cutline(x0,x1)N=100;k=0;delta=5e-8;while(1)(abs(x1-x0)>=delta)c=x1;x1=cutnext(x0,x1);x0=c;k=k+1;if k>Ndisp('Cutline method failed')break;endif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endendfprintf('%10f\n',x1);function y=cutnext(a,b)y=b-fc(b)/(fc(b)-fc(a))*(b-a);1）原函数function fc1=fc1(x)fc1=x^2-exp(x);end导函数function fc2=fc2(x)fc2=2*x-exp(x);end2）原函数导函数3）原函数导函数6实验结果及分析注：牛顿迭代法由于设置delta=1e-6，所以算出的误差e<1.0*10^-6;割线法由于设置delta=5e-8，所以误差e<5.0*10^-8.7总结。

实验二 非线性方程求根实验名称：非线性方程求根实验类型: 验证性实验学 时：2.1 实验环境① 操作系统：WindowsXP/Win7② 编程环境：自定2.2 实验目的① 掌握二分法、牛顿迭代法等常用的非线性方程迭代算法；② 了解迭代算法的设计原理及初值对收敛性的影响。

2.3 实验原理和方法2.3.1 二分法的算法描述计算()0f x =的根的二分法如下：① 输入求根取间[,]a b ，根的误差控制量ε和()f x 的容许误差η，并定义函数()f x .计算(),()a b f f a f f b ==如果 ()()0f a f b <，转②；否则，结束② 当b a ε->时，计算中点()/2xa b =+ 以及()f f x = 的值； 分情况处理： 若()f xη< ，则停止计算，输出近似根x ； 若()()0f a f x< ，则,b b x f f == ，转②； 若()()0f xf b < ，则,a a x f f == ，转②； ③ 2a b x += ； ④ 输出近似根x2.3.2 牛顿迭代法的算法描述给定初始值0x ，ε为根的容许误差，η为()f x 的容许误差，N 为最大迭代次数.① 如果'0()0f x =或迭代次数大于N ，则算法失败，结束；否则执行②② 计算010'0()()f x x x f x =- ③ 若10x x ε-<或1()f x η<，则输出近似根1x ，程序结束；否则执行④④ 令01x x =，转向①2.3.3 牛顿迭代法的改进1、单点弦截法牛顿法的突出优点是收敛速度快，但它还有个明显的缺点：每一步迭代都要计算1'()k f x -，增加了计算难度和计算量。

为了避开导数的计算，可以考虑用差商1010()()k k f x f x x x ----替换1'()k f x -，从而得到迭代公式 111010()()()()k k k k k f x x x x x f x f x ----=--- 1,2,3,k = 称为单点弦截法。

实验报告一.MATLAB程序代码（1）function x=agui_bisect(fname,a,b,e)fa=feval(fname,a);fb=feval(fname,b);if fa*fb>0 error('两端函数值为同号');endk=0x=(a+b)/2while(b-a)>(2*e)fx=feval(fname,x);if fa*fx<0b=x;fb=fx;elsea=x;fa=fx;endk=k+1x=(a+b)/2end（2）function x=agui_diedai(fname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<Nk=k+1x0=x;x=feval(fname,x0);disp(x)endif k==N warning('已达到最大迭代次数');end(3)function x=agui_newton(fname,dfname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<Nk=k+1x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);disp(x)endif k==N warning('已达最大迭代次数');end二. 实验结果及分析实验结果（1）x11=0.0903 (2)x5=0.0903 (3)x2=0.0903实验分析由三个结果对比可知，牛顿迭代法的迭代次数较少，且比较简单可靠。

可见牛顿迭代法要比二分法和迭代法的收敛速度快的多。

但是对函数有一定的要求。

牛顿迭代要求函数能求导。