机器人学-欧拉角与RPY角
- 格式:ppt
- 大小:5.96 MB
- 文档页数:21

A3-1.写出齐次变换矩阵 T,它表示相对固定坐标系{A}作以下变换。
B1) 绕Z 퐴轴旋转 90°; 2) 再绕X 퐴轴转-90°;푇3) 最后做移动【3 7 9 】;A3-2.写出齐次变换矩阵 T,它表示相对坐标系{B}做以下变换。
B 푇1) 移动【3 7 9 】;2) 绕X 퐵轴旋转-90°; 3) 绕Z 퐵轴转 90°。
3-3.求下面齐次变换的逆变换푇−1 0 1 0 −10 0 −1 2 −1 0 0 0 T = []13-4.已知 0.25 0.43 0.86 5.0A B T 0.87 −0.50 0 −4.0= [ ] 0.43 0.75 −0.50 3.0 0 0 0 1A求 T的第(2,4)元素.B3-5 已知矩阵? 0 −1 0 ? 0 0 1 ? −10 2 ?1] [代表齐次坐标变换,求其中的未知元素值(第一列元素)。
푈3-6 设工件相对于参考系{U}的描述为T,机器人基座相对于参考系푃푈的描述为T,已知B010−1100100−12−1000푈=[푇푃0105푈]푃=[]퐵001900010001要求机器人手爪坐标系{H}与工件坐标系{P}重合,试求变换퐻퐵푇3-7. 已知坐标变换矩阵푈퐴푇,퐵퐴푇,푈퐶푇.0.866−0.50001110000.5000.8660−100.866−0.50010푈=[]퐵퐴푇=[푇] 퐴001800.5000.866−200001000 10.866−0.5000−30.4330.750−0.5−3퐶=[푇]푈0.2500.4330.86630001画出空间尺寸链图,并求퐵퐶푇.3-8.如图3-17 所示的多面体顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4,5).3-9. 如图3-18 所示的多面体各顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4).3-10. 如图3-19 所正方体的顶点和中心坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3)。

欧拉角名词解释欧拉角(EulerAngles)是旋转空间中最常见的表示姿态变换的数学方法,用它可以表示物体以某种方式从一个姿态旋转到另一个姿态的变换。
它是由普林斯顿大学的数学家兼物理学家Leonhard Euler 发明的一种角度表示法,因此也叫做“尤拉角”。
欧拉角一般被用来描述复杂的三维旋转,可以准确地表示一个空间中的物体的姿态。
【定义】欧拉角定义为三个独立的角度,如α,β,γ,分别表示绕某个坐标轴的顺时针或逆时针旋转角度。
它可以用来指定一个坐标系在另一个坐标系中的方位,以及实现两个坐标系相对旋转的偏转量。
【类型】欧拉角可以分为两种:绕Z-Y-X(顺时针)和绕Z-X-Y(逆时针)。
绕Z-Y-X欧拉角,第一个角度α表示绕Z轴旋转,第二个角度β表示绕Y轴旋转,第三个角度γ表示绕X轴旋转。
而绕Z-X-Y欧拉角中,第一个角度α表示绕Z轴旋转,第二个角度β表示绕X轴旋转,第三个角度γ表示绕Y轴旋转。
【应用】欧拉角在机器人、航空航天、计算机视觉等领域有着广泛的使用。
欧拉角可以用来精确描述物体的旋转变换,进而可以更加精确的描述物体的位置和姿态。
在用欧拉角表示旋转时,需要进行一定的换算,以解决旋转变换的问题,以确保得到的旋转变换的准确性。
另外,欧拉角还可以用来解决其他空间变换问题,例如多维空间的缩放问题,可以用旋转矩阵来进行求解。
由此可见,欧拉角在多维空间变换领域有着广泛的应用。
【特点】欧拉角的一个优点在于它不会受到四元数(Quaternion)的混乱,也不会受到旋转矩阵的低效问题的困扰,它具有较高的准确度和计算效率,从而使得欧拉角成为空间绝对变换的理想表示方法。
此外,欧拉角有着很好的迭代特性,可以容易地模拟空间物体的仿射变换。
当然,欧拉角也有一些缺点,例如它不容易用来表示方位不同,但同时仍未实现旋转差异的情况,这就要求其时刻保持七个自由度,以免发生死区现象。
【总结】从上面可以看出,欧拉角是旋转空间中最常见的表示姿态变换的数学方法,它可以准确地表示一个空间中的物体的姿态。

第一章1.为什么要发展机器人技术()。
答案:精神需求;生产需求;生活需求;探索需求2.下列哪个不是国内的机器人公司()。
答案:柯马3.沃康松发明的机械鸭,能够做扇动翅膀,吃谷物和排便的动作。
()答案:对4.按照机器人的几何结构来分,可分为:()答案:球面坐标;笛卡尔坐标;关节球面坐标;柱面坐标5.按照机器人的控制方式来分,可分为:()答案:非伺服机器人;伺服机器人6.机器人系统中的计算机就相当于人体的什么?()答案:大脑7.机器人的传感器分为内部传感器和外部传感器。
()答案:对8.机器人的精度是指机械零件抵抗变形的能力。
()答案:错9.机器人的控制系统包括()答案:作业控制器;驱动控制器;运动控制器10.搬运机器人属于下列那类机器人()答案:工业机器人第二章1.刚体的位姿表示刚体的位置和姿态,位置用p矩阵表示,姿态用R矩阵表示。
()答案:对2.刚体的位姿一般用什么样的矩阵来表示()。
答案:3×43.以下哪个矩阵表示坐标轴x轴()。
答案:[1 0 0 0]4.旋转变换与变换次序有关。
()答案:对5.以下哪个坐标系表示机器人的基坐标系()。
答案:{B}6.先沿着基坐标系的x轴平移r,再绕基坐标系的z轴旋转α,最后延基坐标系的z轴平移z,形成球面坐标。
()答案:错7.RPY角是绕着当前轴旋转的序列。
()答案:错8.如果已知一个任意的旋转矩阵,可以直接通过公式求得这个旋转变换的等效转角和等效转轴。
()答案:对9.旋转矩阵不是正交矩阵。
()答案:错10.欧拉角是绕着固定轴旋转的序列。
()答案:错第三章1.一个六自由度工业机器人,决定了其末端姿态()。
答案:手腕部分的后三个自由度2.沿着关节的运动轴方向,能确定连杆坐标系的()。
答案:z轴3.D-H参数中ai-1表示()。
答案:zi-1沿着xi-1到zi的距离4.一旦机器人的结构确定了,那么机器人的连杆参数就不变了,只有关节参数会发生变化。
()答案:对5.机器人运动学方程的求解步骤包括()。


姿态的欧拉角表示题目:比较分析,找出一种适合乒乓球机器人的末端姿态的欧拉角方法姿态的欧拉角表示任何旋转矩阵都可以通过三个欧拉角进行参数化,一般来说,绕三个坐标轴的顺次旋转可以达到任意的姿态,由于旋转矩阵的乘法是非交换的,因此旋转的次序是很重要的。
按照旋转所绕轴的次序的不同,共有12 种不同的欧拉角。
六种非对称型欧拉角: XYZ,XZY,YXZ,YZX,ZXY 和ZYX;六种对称型欧拉角: XYX,XZX,YXY,YZY,ZXZ 和ZYZ。
记绕三个坐标轴的基本旋转矩阵为:1、非对称型欧拉角表示当三个旋转所绕的坐标轴相互不同时,称为非对称型欧拉角表示。
以XYZ 欧拉角为例,假定起始时物体坐标系与惯性坐标系重合,首先刚体绕物体坐标系的x-轴旋转α角,接着绕y-轴旋转β角,最后绕z-轴旋转角,则刚体最终的姿态矩阵为:上式给出了XYZ 欧拉角参数的正运动学方程,反解该式可求得其逆运动学方程,给定姿态矩阵R=【r ij】3×3时,可求得其逆运动学方程为:从上式可以看出,当β = π2时,逆运动学存在奇异。
其他五种非对称型欧拉角表示的姿态矩阵计算结果列于表1。
这些表示均在β = π2时存在奇异。
对称型欧拉角表示当三个旋转所绕的坐标轴第一个和第三个相同时,称为对称型欧拉角表示,以ZYZ欧拉角为例,首先绕物体坐标系的z-轴旋转α角,接着绕y-轴旋转β角,最后绕x-轴旋转γ角,则刚体最终的姿态矩阵为:另外还有五种对称型欧拉角表示的姿态矩阵列于表2。
这些表示均在β = 0 时存在奇异。
欧拉角表示与RPY 角表示的对偶性姿态的三参数描述还有一种称为RPY 角参数的方法。
1 和 2 中所描述的欧拉角参数的运动过程都是在物体坐标系中进行的,因此其姿态矩阵是按照矩阵的右乘规则得到的。
而RPY 角参数的运动过程则是在惯性坐标系中完成的,其姿态矩阵是按照矩阵的左乘规则得到。
这样,与12 种欧拉角参数相对应的就有12 种RPY 角参数。

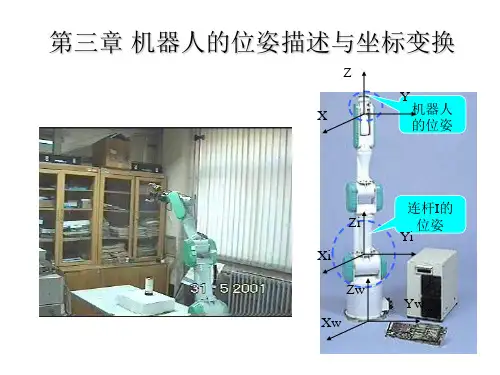


工业机器人技术课程总结任课:班级:学号:姓名:之前在工厂实习见识和操作过很多工业机器人,有焊接机器人,涂装机器人,总装机器人等,但是学习了盖老师教授的工业机器人课程,才真正算是进入了工业机器人的理论世界学习机器人的相关知识。
以下是课程总结。
一、第一章主要是对机器人的概述,从机器人的功能和应用、机器人的机构以及机器人的规格全面呈现学习机器人的框架。
研制机器人的最初目的是为了帮助人们摆脱繁重劳动或简单的重复劳动,以及替代人到有辐射等危险环境中进行作业,因此机器人最早在汽车制造业和核工业领域得以应用。
随着机器人技术的不断发展,工业领域的焊接、喷漆、搬运、装配、铸造等场合,己经开始大量使用机器人。
另外在军事、海洋探测、航天、医疗、农业、林业甚到服务娱乐行业,也都开始使用机器人。
本书主要介绍工业机器人,对譬如军用机器人等涉及不多。
机器人的机构方面,主要介绍了操作臂的工作空间形式、手腕、手爪、和闭链结构操作臂。
工作空间形式常见的有直角坐标式机器人、圆柱坐标式机器人、球(极)坐标式机器人、SCARA机器人以及关节式机器人。
手腕的形式也可分为二自由度球形手腕、三轴垂直相交的手腕以及连续转动手腕。
同时手爪也可分为夹持式手爪、多关节多指手爪、顺应手爪。
机器人的其他规格主要介绍驱动方式、自动插补放大、坐标轴数、工作空间、承载能力、速度和循环时间、定位基准和重复性以及机器人的运行环境。
第一章的内容主要是对机器人各个方面有个简单的介绍使机器人更形象化和具体化。
工业机器人定义为一种拟人手臂、手腕和手功能的机电一体化装置,能将对象或工具按照空间位置姿态的要求移动,从而完成某一生产的作业要求。
工业机械应用:主要代替人从事危险、有害、有毒、低温和高热等恶劣环境中的工作;代替人完成繁重、单调重复劳动。
它带来的好处:减少劳动力费用提高生产率改进产品质量增加制造过程柔性减少材料浪费控制和加快库存的周转消除了危险和恶劣的劳动岗位。
机器人的直角坐标型:结构简单;定位精度高;空间利用率低;操作范围小;实际应用较少。

第一章1机器人组成系统的4大部分: 机构部分、传感器组、控制部分、信息处理部分 2机器人学的主要研究内容:研究机器人的控制与被处理物体间的相互关系 3机器人的驱动方式:液压、气动、电动4机器人行走机构的基本形式:足式、蛇形式、轮式、履带式5机器人的定义:由各种外部传感器引导的、带有一个或多个末端执行器、通过可编程运动,在其工作空间内对真实物体进行操作的软件可控的机械装置6机器人的分类:1工业机器人2极限环境作业机器人3医疗福利机器人7操作臂工作空间形式:1直角坐标式机器人2圆柱坐标式机器人3球坐标式机器人 4 scara 机器人5关节式机器人 8机器人三原则第一条:机器人不得伤害人类.第二条:机器人必须服从人类的命令,除非这条命令与第一条相矛盾。
第三条:机器人必须保护自己,除非这种保护与以上两条相矛盾。
第二章1、什么是位姿:刚体参考点的位置和姿态2、RPY 角与欧拉角的共同点:绕固定轴旋转的顺序与绕运动轴旋转的顺序相反并且旋转角度相同,能得到相同的变换矩阵,都是用三个变量描述。
欧拉角为左乘RPY 角为右乘。
RPY 中绕x 旋转为偏转绕y 旋转为俯仰绕z 旋转为回转3 、矩阵的左乘与右乘:左乘(变换从右向左)—指明运动相对于固定坐标系 右乘(变换从左向右)—指明运动相对于运动坐标系 4、齐次变换TA B:表示同一点相对于不同坐标系{B}和{A}的变换,描述{B}相对于{A}的位姿5、自由矢量:完全由他的维数、大小、方向,三要素所规定的矢量6、线矢量:由维数、大小、方向、作用线,四要素所规定的矢量7、齐次变换矩阵⎥⎦⎤⎢⎣⎡=10000B AA B A BP R T 8、其次坐标变换⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1100010P P RP B B AAB A R AB 为旋转矩阵0B A P 为{B}的原点相对{A}的位置矢量9、旋转矩阵:绕x 轴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-a a a a cos sin 0sin cos 0001y 轴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-a a a a cos 0sin 010sin 0cos z 轴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-1000cos sin 0sin cos a a a a 10、变换矩阵求逆:⎥⎦⎤⎢⎣⎡-=100B A T A B TA B B AP R R T 已知B 相对于A 的描述求A 相对于B 的描述11、⎥⎦⎤⎢⎣⎡+==1000B A C B A BB C A B B CA BA CP P R RR T T T12、运动学方程T T T P Rp p p o o o a a a nn n p o a n n n nn z y x z y x z y x z yx 112010..101001000-=⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡ 第三章1、操作臂运动学研究的是手臂各连杆间的位移、速度、加速度关系 3、运动学反解方法:反变换法、几何法、pieper 解法 4、大多数工业机器人满足封闭解的两个充分条件之一 三个相邻关节轴,1交于一点2相互平行 5、连杆参数:1、()的距离公法线沿(连杆的关节轴)到从111x z z ---=i i i i a2、旋转的角度绕到从111x z z ---=i i i i α3、的距离沿到从i i i i d z x x 1-=4、旋转的角度绕到从i i i iz x x 1-=θ6、连杆变换通式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=----------100001111111111i i i i i i i i i i i i i i i i ii i c d c s c s s s d s c c c s a s c T αααθαθαααθαθθθ 7、灵活空间:机器人手抓能以任意方位到达的目标点的集合 8、可达空间:机器人手抓至少一个方位到达的目标点的集合 工作空间:反解存在的区域就是工作空间9、机器人操作臂运动学反解数决定于:关节数、连杆参数、关节的活动范围 10、操作臂运动学反解方法有1封闭解法(获得封闭解的方法有代数解、几何解) 2数值解法。