中科大电磁学期中考试

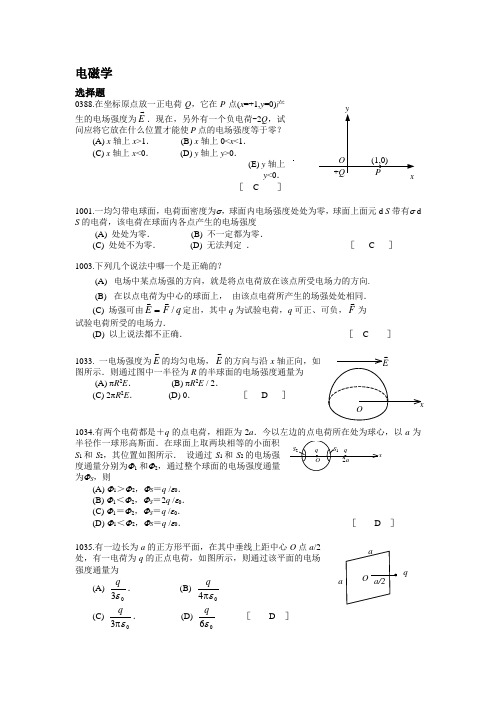
电磁学选择题0388.在坐标原点放一正电荷Q ，它在P 点(x =+1,y =0)产生的电场强度为E ．现在，另外有一个负电荷-2Q ，试问应将它放在什么位置才能使P 点的电场强度等于零？(A) x 轴上x >1． (B) x 轴上0<x <1．(C) x 轴上x <0． (D) y 轴上y >0． (E) y 轴上y <0．［ C ］1001.一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元d S 带有σ dS 的电荷，该电荷在球面内各点产生的电场强度(A) 处处为零． (B) 不一定都为零．(C) 处处不为零． (D) 无法判定 ． ［ C ］1003.下列几个说法中哪一个是正确的？(A) 电场中某点场强的方向，就是将点电荷放在该点所受电场力的方向.(B) 在以点电荷为中心的球面上， 由该点电荷所产生的场强处处相同． (C) 场强可由q F E / =定出，其中q 为试验电荷，q 可正、可负，F 为试验电荷所受的电场力．(D) 以上说法都不正确． ［ C ］1033. 一电场强度为E 的均匀电场，E 的方向与沿x 轴正向，如图所示．则通过图中一半径为R 的半球面的电场强度通量为(A) πR 2E ． (B) πR 2E / 2．(C) 2πR 2E ． (D) 0． ［ D ］1034.有两个电荷都是＋q 的点电荷，相距为2a ．今以左边的点电荷所在处为球心，以a 为半径作一球形高斯面．在球面上取两块相等的小面积S 1和S 2，其位置如图所示． 设通过S 1和S 2的电场强度通量分别为Φ1和Φ2，通过整个球面的电场强度通量为ΦS ，则(A) Φ1＞Φ2，ΦS ＝q /ε0．(B) Φ1＜Φ2，ΦS ＝2q /ε0．(C) Φ1＝Φ2，ΦS ＝q /ε0．(D) Φ1＜Φ2，ΦS ＝q /ε0． ［ D ］1035.有一边长为a 的正方形平面，在其中垂线上距中心O 点a /2处，有一电荷为q 的正点电荷，如图所示，则通过该平面的电场强度通量为 (A) 03εq ． (B) 04επq (C) 03επq ． (D) 06εq ［ D ］ yx O +Q P (1,0) x O E S 1S 2O q q 2a a q a/2 O1054. 已知一高斯面所包围的体积内电荷代数和∑q ＝0，则可肯定：(A) 高斯面上各点场强均为零．(B) 穿过高斯面上每一面元的电场强度通量均为零．(C) 穿过整个高斯面的电场强度通量为零．(D) 以上说法都不对． ［ C ］1055.一点电荷，放在球形高斯面的中心处．下列哪一种情况，通过高斯面的电场强度通量发生变化：(A) 将另一点电荷放在高斯面外．(B) 将另一点电荷放进高斯面内．(C) 将球心处的点电荷移开，但仍在高斯面内．(D) 将高斯面半径缩小． ［ B ］1056.点电荷Q 被曲面S 所包围 ， 从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后：(A) 曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变．(C) 曲面S 的电场强度通量变化，曲面上各点场强变化．(D) 曲面S 的电场强度通量不变，曲面上各点场强变化． ［ D ］1251.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为：［ B ］1252. 半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为：［ B ］E O r (D) E ∝1/r 2 E O r (A) E ∝1/r1253. 半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为： ［ B ］1255. 图示为一具有球对称性分布的静电场的E ～r 关系曲线．请指出该静电场是由下列哪种带电体产生的． (A) 半径为R 的均匀带电球面．(B) 半径为R 的均匀带电球体． (C) 半径为R 的、电荷体密度为ρ＝A r (A 为常数)的非均匀带电球体． (D) 半径为R 的、电荷体密度为ρ＝A/r (A 为常数)的非均匀带电球体．[ B ］1432.高斯定理 ⎰⎰⋅=V S V S E 0/d d ερ(A) 适用于任何静电场．(B) 只适用于真空中的静电场．(C) 只适用于具有球对称性、轴对称性和平面对称性的静电场．(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场．［ A ］1433.根据高斯定理的数学表达式⎰∑⋅=S q S E 0/d ε可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零．(C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电荷． ［ C ］1434.关于高斯定理的理解有下面几种说法，其中正确的是：(A) 如果高斯面上E 处处为零，则该面内必无电荷．(B) 如果高斯面内无电荷，则高斯面上E 处处为零．(C) 如果高斯面上E 处处不为零，则高斯面内必有电荷．(D) 如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零．［ D ］1016.静电场中某点电势的数值等于(A)试验电荷q 0置于该点时具有的电势能．(B)单位试验电荷置于该点时具有的电势能．(C)单位正电荷置于该点时具有的电势能．(D)把单位正电荷从该点移到电势零点外力所作的功． ［ D ］ E1017.半径为R 的均匀带电球面，总电荷为Q ．设无穷远处电势为零，则该带电体所产生的电场的电势U ，随离球心的距离r 变化的分布曲线为 ［ A ］1019. 在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为 (A) a q 04επ． (B) aq 08επ． (C) a q 04επ-． (D) aq 08επ-． ［ D ］1021. 如图，在点电荷q 的电场中，选取以q 为中心、R 为半径的球面上一点P 处作电势零点，则与点电荷q 距离为r 的P'点的电势为 (A)rq 04επ (B) ⎪⎭⎫ ⎝⎛-πR r q 1140ε (C) ()R r q -π04ε (D) ⎪⎭⎫ ⎝⎛-πr R q 1140ε ［ B ］1046.如图所示，边长为l 的正方形，在其四个顶点上各放有等量的点电荷．若正方形中心O 处的场强值和电势值都等于零，则：(A) 顶点a 、b 、c 、d 处都是正电荷．(B) 顶点a 、b 处是正电荷，c 、d 处是负电荷． (C) 顶点a 、c 处是正电荷，b 、d 处是负电荷．(D) 顶点a 、b 、c 、d 处都是负电荷． ［ C ］ 1047.如图所示，边长为 0.3 m 的正三角形abc ，在顶点a 处有一电荷为10-8 C 的正点电荷，顶点b 处有一电荷为-10-8 C 的负点电荷，则顶点c 处的电场强度的大小E 和电势U 为： (041επ=9×10-9 N m /C 2) (A) E ＝0，U ＝0． (B) E ＝1000 V/m ，U ＝0．(C) E ＝1000 V/m ，U ＝600 V ．(D) E ＝2000 V/m ，U ＝600 V ． ［ B ］(A) (B) (C) 2(D)2 (E) b a1172. 有N 个电荷均为q 的点电荷，以两种方式分布在相同半径的圆周上：一种是无规则地分布，另一种是均匀分布．比较这两种情况下在过圆心O 并垂直于圆平面的z 轴上任一点P (如图所示)的场强与电势，则有(A) 场强相等，电势相等．(B) 场强不等，电势不等．(C) 场强分量E z 相等，电势相等．(D) 场强分量Ez 相等，电势不等．［ C ］1267.关于静电场中某点电势值的正负，下列说法中正确的是：(A) 电势值的正负取决于置于该点的试验电荷的正负．(B) 电势值的正负取决于电场力对试验电荷作功的正负．(C) 电势值的正负取决于电势零点的选取．(D) 电势值的正负取决于产生电场的电荷的正负． ［ C ］1516. 如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带电荷Q 2 .设无穷远处为电势零点，则在两个球面之间、距离球心为r 处的P 点的电势U 为：(A) r Q Q 0214επ+ (B)20210144R Q R Q εεπ+π (C)2020144R Q r Q εεπ+π (D) rQ R Q 0210144εεπ+π [ C ]1075.真空中有一点电荷Q ，在与它相距为r 的a 点处有一试验电荷q ．现使试验电荷q 从a 点沿半圆弧轨道运动到b 点，如图所示．则电场力对q 作功为 (A)24220r r Qq π⋅πε． (B) r r Qq 2420επ． (C) r r Qq ππ204ε． (D) 0． ［ D ］1076.点电荷-q 位于圆心O 处，A 、B 、C 、D 为同一圆周上的四点，如图所示．现将一试验电荷从A 点分别移动到B 、C 、D 各点，则 (A) 从A 到B ，电场力作功最大．(B) 从A 到C ，电场力作功最大． (C) 从A 到D ，电场力作功最大．(D) 从A 到各点，电场力作功相等． ［ D ］1199. 如图所示，边长为a 的等边三角形的三个顶点上，分别放置着三个正的点电荷q 、2q 、3q ．若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为：(A) a qQ 023επ ． (B) a qQ 03επ．A q2(C) a qQ 0233επ． (D) aqQ 032επ． ［ C ］1266.在已知静电场分布的条件下，任意两点P 1和P 2之间的电势差决定于(A) P 1和P 2两点的位置．(B) P 1和P 2两点处的电场强度的大小和方向．(C) 试验电荷所带电荷的正负．(D) 试验电荷的电荷大小． ［ A ］1268. 半径为r 的均匀带电球面1，带有电荷q ，其外有一同心的半径为R 的均匀带电球面2，带有电荷Q ，则此两球面之间的电势差U 1-U 2为：(A) ⎪⎭⎫ ⎝⎛-πR r q 1140ε . (B) ⎪⎭⎫ ⎝⎛-πr R Q 1140ε . (C) ⎪⎭⎫ ⎝⎛-πR Q r q 041ε . (D) rq 04επ . [ A ]1085 图中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出： (A) E A ＞E B ＞E C ，U A ＞U B ＞U C ． (B) E A ＜E B ＜E C ，U A ＜U B ＜U C ．(C) E A ＞E B ＞E C ，U A ＜U B ＜U C ． (D) E A ＜E B ＜E C ，U A ＞U B ＞U C ． ［ D ］1069. 面积为S 的空气平行板电容器，极板上分别带电量±q ，若不考虑边缘效应，则两极板间的相互作用力为(A)Sq 02ε． (B) S q 022ε． (C) 2022S q ε． (D) 202Sq ε． ［ B ］1304.质量均为m ，相距为r 1的两个电子，由静止开始在电力作用下(忽略重力作用)运动至相距为r 2，此时每一个电子的速率为(A) ⎪⎪⎭⎫ ⎝⎛-21112r r m ke ． (B) ⎪⎪⎭⎫ ⎝⎛-21112r r m ke ． (C) ⎪⎪⎭⎫ ⎝⎛-21112r r m k e ． (D) ⎪⎪⎭⎫ ⎝⎛-2111r r m k e (式中k =1 / (4πε0) ) ［ D ］1316.相距为r 1的两个电子，在重力可忽略的情况下由静止开始运动到相距为r 2，从相距r 1到相距r 2期间，两电子系统的下列哪一个量是不变的？(A) 动能总和； (B) 电势能总和；(C) 动量总和； (D) 电相互作用力． ［ C ］2014.有一个圆形回路1及一个正方形回路2，圆直径和正方形的边长相等，二者中通有大小相等的电流，它们在各自中心产生的磁感强度的大小之比B 1 / B 2为(A) 0.90． (B) 1.00．(C) 1.11． (D) 1.22． ［ C ］2018. 边长为L 的一个导体方框上通有电流I ，则此框中心的磁感强度(A) 与L 无关． (B) 正比于L 2．(C) 与L 成正比． (D) 与L 成反比．(E) 与I 2有关． ［ D ］2020. 边长为l 的正方形线圈中通有电流I ，此线圈在A 点(见图)产生的磁感强度B 为(A)l I π420μ． (B) l I π220μ． (C) l I π02μ． (D) 以上均不对． ［ A ］2005.图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？(A) Ⅰ区域．(B) Ⅱ区域．(C) Ⅲ区域． (D) Ⅳ区域．(E) 最大不止一个． ［ B ］2046.如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知 (A) 0d =⎰⋅L l B ，且环路上任意一点B = 0．(B) 0d =⎰⋅L l B ，且环路上任意一点B ≠0．(C) 0d ≠⎰⋅L l B ，且环路上任意一点B ≠0．(D) 0d ≠⎰⋅Ll B ，且环路上任意一点B =常量． ［ B ］2016.无限长直导线在P 处弯成半径为R 的圆，当通以电流I 时，则在圆心O 点的磁感强度大小等于(A) R Iπ20μ． (B) RI 40μ． (C) 0． (D) )11(20π-R I μ． (E) )11(40π+R I μ． ［ D ］2019.有一半径为R 的单匝圆线圈，通以电流I ，若将该导线弯成匝数N = 2的平面圆线圈，导线长度不变，并通以同样的电流，则线圈中心的磁感强度和线圈的磁矩分别是原来的(A) 4倍和1/8． (B) 4倍和1/2．ⅠⅡⅢⅣ(C) 2倍和1/4． (D) 2倍和1/2． ［ B ］2042.四条平行的无限长直导线，垂直通过边长为a =20 cm 的正方形顶点，每条导线中的电流都是I =20 A ，这四条导线在正方形中心O 点产生的磁感强度为(μ0 =4π×10-7 N ·A -2) (A) B =0． (B) B = 0.4×10-4 T ．(C) B = 0.8×10-4 T. (D) B =1.6×10-4 T ． ［ C ］ 5664.均匀磁场的磁感强度B 垂直于半径为r 的圆面．今以该圆周为边线，作一半球面S ，则通过S 面的磁通量的大小为(A) 2πr 2B ． (B) πr 2B ．(C) 0． (D) 无法确定的量． ［ B ］5666. 在磁感强度为B 的均匀磁场中作一半径为r 的半球面S ，S 边线所在平面的法线方向单位矢量n 与B的夹角为α ，则通过半球面S 的磁通量(取弯面向外为正)为 (A) πr 2B ．. (B) 2 πr 2B ．(C) -πr 2B sin α． (D) -πr 2B cos α． ［ D ］2354.通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为： (A) B P > B Q > B O . (B) B Q > B P > B O ． (C) B Q > B O > B P ． (D) B O > B Q > B P ．［ D ］2431.在一平面内，有两条垂直交叉但相互绝缘的导线，流过每条导线的电流i 的大小相等，其方向如图所示．问哪些区域中有某些点的磁感强度B 可能为零？ (A) 仅在象限Ⅰ． (B) 仅在象限Ⅱ． (C) 仅在象限Ⅰ，Ⅲ． (D) 仅在象限Ⅰ，Ⅳ．(E) 仅在象限Ⅱ，Ⅳ． ［ E ］2553.在真空中有一根半径为R 的半圆形细导线，流过的电流为I ，则圆心处的磁感强度为(A) R 140πμ． (B) R120πμ．(C) 0． (D) R140μ． ［ D ］2046. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知 a(A) 0d =⎰⋅Ll B ，且环路上任意一点B = 0．(B) 0d =⎰⋅L l B ，且环路上任意一点B ≠0．(C) 0d ≠⎰⋅L l B ，且环路上任意一点B ≠0．(D) 0d ≠⎰⋅Ll B ，且环路上任意一点B =常量． ［ B ］2048.无限长直圆柱体，半径为R ，沿轴向均匀流有电流．设圆柱体内( r < R )的磁感强度为B i ，圆柱体外( r > R )的磁感强度为B e ，则有(A) B i 、B e 均与r 成正比．(B) B i 、B e 均与r 成反比．(C) B i 与r 成反比，B e 与r 成正比．(D) B i 与r 成正比，B e 与r 成反比． ［ D ］2447.取一闭合积分回路L ，使三根载流导线穿过它所围成的面．现改变三根导线之间的相互间隔，但不越出积分回路，则(A) 回路L 内的∑I 不变，L 上各点的B不变． (B) 回路L 内的∑I 不变，L 上各点的B 改变．(C) 回路L 内的∑I 改变，L 上各点的B 不变．(D) 回路L 内的∑I 改变，L 上各点的B改变． ［ B ］2658.若空间存在两根无限长直载流导线，空间的磁场分布就不具有简单的对称性，则该磁场分布(A) 不能用安培环路定理来计算．(B) 可以直接用安培环路定理求出．(C) 只能用毕奥－萨伐尔定律求出．(D) 可以用安培环路定理和磁感强度的叠加原理求出． ［ D ］2717.距一根载有电流为3×104 A 的电线1 m 处的磁感强度的大小为(A) 3×10-5 T ． (B) 6×10-3 T ．(C) 1.9×10-2T ． (D) 0.6 T ．(已知真空的磁导率μ0 =4π×10-7 T ·m/A) ［ B ］2059.一匀强磁场，其磁感强度方向垂直于纸面(指向如图)，两带电粒子在该磁场中的运动轨迹如图所示，则(A) 两粒子的电荷必然同号．(B) 粒子的电荷可以同号也可以异号．(C) 两粒子的动量大小必然不同．(D) 两粒子的运动周期必然不同． ［ B ］2060.一电荷为q 的粒子在均匀磁场中运动，下列哪种说法是正确的？(A) 只要速度大小相同，粒子所受的洛伦兹力就相同．(B) 在速度不变的前提下，若电荷q 变为-q ，则粒子受力反向，数值不变．(C) 粒子进入磁场后，其动能和动量都不变．(D) 洛伦兹力与速度方向垂直，所以带电粒子运动的轨迹必定是圆．［ B ］2373.一运动电荷q ，质量为m ，进入均匀磁场中，(A) 其动能改变，动量不变． (B) 其动能和动量都改变．(C) 其动能不变，动量改变． (D) 其动能、动量都不变． ［ C ］2391.一电子以速度v 垂直地进入磁感强度为B 的均匀磁场中，此电子在磁场中运动轨道所围的面积内的磁通量将(A) 正比于B ，反比于v 2． (B) 反比于B ，正比于v 2． (C) 正比于B ，反比于v ． (D) 反比于B ，反比于v ．［ B ］2083. 如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将 (A) 向着长直导线平移． (B) 离开长直导线平移．(C) 转动． (D) 不动． ［ A ］2085.长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图(但两者间绝缘)，设长直电流不动，则圆形电流将(A) 绕I 2旋转． (B) 向左运动． (C) 向右运动． (D) 向上运动．(E) 不动． ［ C ］2090.在匀强磁场中，有两个平面线圈，其面积A 1 = 2 A 2，通有电流I 1 = 2 I 2，它们所受的最大磁力矩之比M 1 / M 2等于(A) 1． (B) 2．(C) 4． (D) 1/4． ［ C ］2305.如图，匀强磁场中有一矩形通电线圈，它的平面与磁场平行，在磁场作用下，线圈发生转动，其方向是(A) ab 边转入纸内，cd 边转出纸外． (B) ab 边转出纸外，cd 边转入纸内．(C) ad 边转入纸内，bc 边转出纸外．(D) ad 边转出纸外，bc 边转入纸内． ［ A ］I 112460.在一个磁性很强的条形磁铁附近放一条可以自由弯曲的软导线，如图所示．当电流从上向下流经软导线时，软导线将(A) 不动．(B) 被磁铁推至尽可能远．(C) 被磁铁吸引靠近它，但导线平行磁棒． (D) 缠绕在磁铁上，从上向下看，电流是顺时针方向流动的．(E) 缠绕在磁铁上，从上向下看，电流是逆时针方向流动的．［ E ］2464.把通电的直导线放在蹄形磁铁磁极的上方，如图所示．导线可以自由活动，且不计重力．当导线内通以如图所示的电流时，导线将(A) 不动．(B) 顺时针方向转动(从上往下看)．(C) 逆时针方向转动(从上往下看)，然后下降．(D) 顺时针方向转动(从上往下看)，然后下降．(E) 逆时针方向转动(从上往下看)，然后上升． ［ C ］2734.两根平行的金属线载有沿同一方向流动的电流．这两根导线将：(A) 互相吸引． (B) 互相排斥．(C) 先排斥后吸引． (D) 先吸引后排斥． ［ A ］ 2398.关于稳恒电流磁场的磁场强度H ，下列几种说法中哪个是正确的？(A) H 仅与传导电流有关．(B) 若闭合曲线内没有包围传导电流，则曲线上各点的H必为零． (C) 若闭合曲线上各点H 均为零，则该曲线所包围传导电流的代数和为零．(D) 以闭合曲线Ｌ为边缘的任意曲面的H 通量均相等． ［ C ］2400.附图中，M 、P 、O 为由软磁材料制成的棒，三者在同一平面内，当K 闭合后， (A) M 的左端出现N 极． (B) P 的左端出现N 极．(C) O 的右端出现N 极． (D) P 的右端出现N 极．［ B ］2608.磁介质有三种，用相对磁导率μr 表征它们各自的特性时，(A) 顺磁质μr >0，抗磁质μr <0，铁磁质μr >>1．(B) 顺磁质μr >1，抗磁质μr =1，铁磁质μr >>1．(C) 顺磁质μr >1，抗磁质μr <1，铁磁质μr >>1．IM P(D) 顺磁质μr <0，抗磁质μr <1，铁磁质μr >0． ［ C ］2609.用细导线均匀密绕成长为l 、半径为a (l >> a )、总匝数为N 的螺线管，管内充满相对磁导率为μr 的均匀磁介质．若线圈中载有稳恒电流I ，则管中任意一点的(A) 磁感强度大小为B = μ0 μ r NI ．(B) 磁感强度大小为B = μ r NI / l ．(C) 磁场强度大小为H = μ 0NI / l ．(D) 磁场强度大小为H = NI / l ． ［ D ］填空题1005.静电场中某点的电场强度，其大小和方向与__________________________________________________________________相同．答：单位正试验电荷置于该点时所受到的电场力 3分1006.电荷为－5×10-9 C 的试验电荷放在电场中某点时，受到 20×10-9 N 的向下的力，则该点的电场强度大小为_____________________，方向____________．答： 4N / C 2分向上 1分1049.由一根绝缘细线围成的边长为l 的正方形线框，使它均匀带电，其电荷线密度为λ，则在正方形中心处的电场强度的大小E ＝_____________．答：0 3分1050.两根相互平行的“无限长”均匀带正电直线1、2，相距为d ，其电荷线密度分别为λ1和λ2如图所示，则场强等于零的点与直线1的距离a 为_____________ ．答：d 211λλλ+ 3分1188.电荷均为＋q 的两个点电荷分别位于x 轴上的＋a 和－a位置，如图所示．则y 轴上各点电场强度的表示式为E ＝______________________，场强最大值的位置在y ＝__________________________．答： ()j y a qy2/322042+πε， (j 为y 方向单位矢量) 3分 2/a ± 2分12a d +q +q -a +a O x y1258.一半径为R 的带有一缺口的细圆环，缺口长度为d (d<<R)环上均匀带有正电，电荷为q ，如图所示．则圆心O 处的场强大小E ＝____________________________，场强方向为______________________．答： ()30220824R qd d R R qd εεπ≈-ππ 3分 从O 点指向缺口中心点． 2分1408.一半径为R ，长为L 的均匀带电圆柱面，其单位长度带有电荷λ．在带电圆柱的中垂面上有一点P ，它到轴线距离为r (r >R )，则P 点的电场强度的大小：当r <<L 时，E ＝______________________；当r >>L 时，E ＝__________________．答：λ /(2πε0r ) 2分λ L /(4πε0r 2) 2分5087.两块“无限大”的均匀带电平行平板，其电荷面密度分别为σ( σ＞0)及－2 σ，如图所示．试写出各区域的电场强度E ． Ⅰ区E 的大小__________________，方向____________．Ⅱ区E 的大小__________________，方向____________．Ⅲ区E 的大小__________________，方向_____________．答：02εσ 向右 2分 023εσ 向右 2分 02εσ 向左 1分 1037.半径为R 的半球面置于场强为E 的均匀电场中，其对称轴与场强方向一致，如图所示．则通过该半球面的电场强度通量为__________________．答：πR 2E 3分1435.在静电场中,任意作一闭合曲面,通过该闭合曲面的电场强度通量⎰•S E d 的值仅取决于 ,而与 无关.答：包围在曲面内的净电荷 2分 曲面外电荷 1分σⅠⅡⅢ-2σ1498.如图，点电荷q 和－q 被包围在高斯面S 内，则通过该高斯面的电场强度通量⎰⋅S S E d ＝_____________，式中E 为_________________处的场强． 答： 0 2分高斯面上各点 1分1575.图中曲线表示一种轴对称性静电场的场强大小E 的分布，r 表示离对称轴的距离，这是由____________________________________产生的电场．答：半径为R 的无限长均匀带电圆柱面 3分1600.在点电荷＋q 和－q 的静电场中，作出如图所示的三个闭合面S 1、S 2、S 3，则通过这些闭合面的电场强度通量分别是：Φ1＝________，Φ2＝___________，Φ3＝__________． 答： q / ε0 1分0 1分 -q /ε0 1分1604.如图所示，一点电荷q 位于正立方体的A 角上，则通过侧面 abcd 的电场强度通量Φe ＝________________．答： q / (24ε0) 3分 1022.静电场中某点的电势，其数值等于______________________________ 或_______________________________________．答：单位正电荷置于该点所具有的电势能 2分 单位正电荷从该点经任意路径移到电势零点处电场力所作的功 2分1023.一点电荷q ＝10-9 C ，A 、B 、C 三点分别距离该点电荷10 cm 、20 cm 、30 cm ．若选B 点的电势为零，则A 点的电势为______________，C 点的电势为________________．(真空介电常量ε0＝8.85×10-12 C 2·N -1·m -2)答：45 V 2分 －15 V 2分1090.描述静电场性质的两个基本物理量是______________；它们的定义式是________________和__________________________________________．S +q -q O Er E /1∝ r R 1 2 3 +q -q A a b c A B C q答：电场强度和电势 2分 0/q F E =, 1分l E q W U a a ⎰⋅==00d /(U 0=0) 2分1176.真空中，有一均匀带电细圆环，电荷线密度为λ，其圆心处的电场强度E 0＝__________________，电势U 0＝ __________________．(选无穷远处电势为零)答：0 2分 λ / (2ε0) 2分1383.如图所示，一等边三角形边长为a ，三个顶点上分别放置着电荷为q 、2q 、3q 的三个正点电荷，设无穷远处为电势零点，则三角形中心O 处的电势U ＝________________________． 答：()()a q 02/33επ 3分1418.一半径为R 的均匀带电圆环，电荷线密度为λ． 设无穷远处为电势零点，则圆环中心O 点的电势U ＝______________________．答：λ / (2ε0) 3分1041.在点电荷q 的电场中，把一个－1.0×10-9 C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功1.8×10-5 J ，则该点电荷q ＝________________．(真空介电常量ε0＝8.85×10-12 C 2·N -1·m -2 )答：-2×10-7 C 3分1066.静电场的环路定理的数学表示式为：______________________．该式的物理意义是：__________________________________________________________________________________________________________．该定理表明，静电场是____________________________________场． 答：0d =⋅⎰Ll E 2分单位正电荷在静电场中沿任意闭合路径绕行一周，电场力作功等于零 2分有势（或保守力） 1分1077.静电力作功的特点是________________________________________________________________________________，因而静电力属于_________________力．答：功的值与路径的起点和终点的位置有关，与电荷移动的路径无关 2分保守 1分1273.在点电荷q 的静电场中，若选取与点电荷距离为r 0的一点为电势零点，则 Oq2q q a a与点电荷距离为r 处的电势U ＝__________________．⎪⎪⎭⎫ ⎝⎛-π00114r r q ε 3分1313.如图所示，在电荷为q 的点电荷的静电场中，将一电荷为q 0的试验电荷从a 点经任意路径移动到b 点，电场力所作的功A ＝______________． 答：⎪⎪⎭⎫ ⎝⎛-πb a r r q q 1140ε 3分 1178.图中所示为静电场的等势(位)线图，已知U 1＞U 2＞U 3．在图上画出a 、b 两点的电场强度方向，并比较它们的大小．E a __________ E b (填＜、＝、＞)．答：答案见图 2分 ＞ 1分1241.一质量为m 、电荷为q 的小球，在电场力作用下，从电势为U 的a 点，移动到电势为零的b 点．若已知小球在b 点的速率为v b ，则小球在a 点的速率v a= ______________________．答：2/12)/2(m qU b -v 3分1450.一电矩为p 的电偶极子在场强为E 的均匀电场中，p 与E 间的夹角为α，则 它所受的电场力F ＝______________，力矩的大小M ＝__________．答：0 1分pE sin α 2分1145.如图所示，两同心导体球壳，内球壳带电荷+q ，外球壳带电荷-2q ．静电平衡时，外球壳的电荷分布为：内表面___________ ； 外表面___________ ．答：-q 2分-q 2分1153.如图所示，两块很大的导体平板平行放置，面积都是S ，有一定厚度，带电荷分别为Q 1和Q 2．如不计边缘效应，则A 、B 、C 、D 四个表面上的电荷面密度分别为______________ 、______________、_____________、____________．1237.两个电容器1和2，串联以后接上电动势恒定的电源充电．在电源保持联接的情况下，若把电介质充入电容器2中，则电容器1上的电势差______________；电容器1极板上的电荷____________．(填增大、减小、不变)答：增大 1分 增大 2分1331.一个孤立导体，当它带有电荷q 而电势为U 时，则定义该导体的电容为C =______________，它是表征导体的________________的物理量．答： C = q / U 2分储电能力 1分1465.如图所示，电容C 1、C 2、C 3已知，电容C 可调，当调节到A 、B 两点电势相等时，电容C =_________________．答： C 2 C 3 / C 1 3分5287.一个带电的金属球，当其周围是真空时，储存的静电能量为W e 0，使其电荷保持不变，把它浸没在相对介电常量为εr 的无限大各向同性均匀电介质中，这时它的静电能量W e =__________________________．答：W e 0 / εr 3分5681.一个带电的金属球，当其周围是真空时，储存的静电能量为W e 0，使其电荷保持不变，把它浸没在相对介电常量为εr 的无限大各向同性均匀电介质中，这时它的静电能量W e =__________________________．答：3.36×1011 V/m 3分 参考解： 202121E DE w r e εε==r e w E εε02==3.36×1011 V/m2004.磁场中任一点放一个小的载流试验线圈可以确定该点的磁感强度，其大小等于放在该点处试验线圈所受的__________和线圈的________的比值．答：最大磁力矩 2分 磁矩 2分2008.一磁场的磁感强度为k c j b i a B ++= (SI)，则通过一半径为R ，开口向z 轴正方向的半球壳表面的磁通量的大小为____________Wb ．答：πR 2c 3分2255.在匀强磁场B 中，取一半径为R 的圆，圆面的法线n 与B 成60°角，如图所示，则通过以该圆周为边线的如图所示的任意曲面S 的磁通量==⎰⎰⋅S m S B d Φ_______________________．答： 221R B π- 3分2026.一质点带有电荷q =8.0×10-10 C ，以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m的圆周上，作匀速圆周运动．该带电质点在轨道中心所产生的磁感强度B =__________________，该带电质点轨道运动的磁矩p m =___________________．(μ0 =4π×10-7 H ·m -1)答：6.67×10-7 T 3分7.20×10-7 A ·m 2 2分2027.边长为2a 的等边三角形线圈，通有电流I ，则线圈中心 处的磁感强度的大小为________________． 答： )4/(90a I πμ 3分2356.载有一定电流的圆线圈在周围空间产生的磁场与圆线圈半径R 有关，当圆线圈半径增大时，(1) 圆线圈中心点(即圆心)的磁场__________________________．(2) 圆线圈轴线上各点的磁场__________________________________________________________________________________________________．答： 减小 2分 在2/R x <区域减小；在2/R x >区域增大．(x 为离圆心的距离) 3分任意曲面2554.真空中有一电流元l I d ，在由它起始的矢径r 的端点处的磁感强度的数学表达式为_______________． 答：30d 4d r r l I B ⨯⋅π=μ 3分2555.一长直载流导线，沿空间直角坐标Oy 轴放置，电流沿y 正向．在原点O 处取一电流元l I d ，则该电流元在(a ，0，0)点处的磁感强度的大小为________________，方向为__________________．答：20d 4a l I πμ 2分 平行z 轴负向 1分2558.半径为R 的细导线环中的电流为I ，那么离环上所有点的距离皆等于r 的一点处的磁感强度大小为B =____________．(r ≥R )答：3202r IR μ 3分2563. 沿着弯成直角的无限长直导线，流有电流I =10 A ．在直角所决定的平面内，距两段导线的距离都是a =20 cm 处的磁感强度B =____________________．(μ0 =4π×10-7 N/A 2)答： 1.71×10-5 T 3分· 5122.一电流元l I d 在磁场中某处沿正东方向放置时不受力，把此电流元转到沿正北方向放置时受到的安培力竖直向上．该电流元所在处B 的方向为______________．答：正西方向． 3分5123.在如图所示的回路中，两共面半圆的半径分别为a 和b ，且有公共圆心O ，当回路中通有电流I 时，圆心O 处的磁感强度B 0 =________________________，方向______________________． 答：)11(40b a I +μ 2分 垂直纸面向里． 1分 I ab O。

中科大物理试题及答案一、单项选择题（每题3分，共30分）1. 光的波粒二象性中，粒子性表现最明显的是（）。

A. 光的干涉B. 光的衍射C. 光电效应D. 光的偏振答案：C2. 根据能量守恒定律，下列说法正确的是（）。

A. 能量可以在不同形式之间相互转化B. 能量可以在不同物体之间相互转移C. 能量的总量保持不变D. 以上说法都正确答案：D3. 根据热力学第一定律，下列说法正确的是（）。

A. 系统吸收热量，内能一定增加B. 系统对外做功，内能一定减少C. 系统吸收热量且对外做功，内能可能增加也可能减少D. 系统对外做功且吸收热量，内能可能增加也可能减少答案：C4. 根据麦克斯韦方程组，下列说法正确的是（）。

A. 变化的电场产生稳定的磁场B. 变化的磁场产生稳定的电场C. 变化的电场产生变化的磁场D. 变化的磁场产生变化的电场答案：D5. 根据相对论，下列说法正确的是（）。

A. 运动的物体长度会缩短B. 运动的物体质量会增加C. 运动的物体时间会变慢D. 以上说法都正确答案：D6. 根据量子力学，下列说法正确的是（）。

A. 电子在原子核周围以确定的轨道运动B. 电子在原子核周围以概率云的形式出现C. 电子的波动性与粒子性是相互独立的D. 电子的波动性与粒子性是相互联系的答案：B7. 根据电磁感应定律，下列说法正确的是（）。

A. 变化的磁场在导体中产生稳定的电流B. 稳定的磁场在导体中产生变化的电流C. 变化的磁场在导体中产生变化的电流D. 稳定的磁场在导体中产生稳定的电流答案：C8. 根据牛顿第二定律，下列说法正确的是（）。

A. 物体的加速度与作用力成正比B. 物体的加速度与作用力成反比C. 物体的加速度与作用力成正比，与质量成反比D. 物体的加速度与作用力成反比，与质量成正比答案：C9. 根据万有引力定律，下列说法正确的是（）。

A. 两个物体之间的引力与它们的质量成正比B. 两个物体之间的引力与它们的质量成反比C. 两个物体之间的引力与它们的质量的乘积成正比D. 两个物体之间的引力与它们之间的距离成反比答案：C10. 根据热力学第二定律，下列说法正确的是（）。

考试时间：120分钟满分：100分一、选择题（每题5分，共30分）1. 下列各数中，不是有理数的是（）A. 2.5B. √4C. -πD. 02. 已知函数f(x) = x² - 3x + 2，则f(2)的值为（）A. 0B. 2C. 4D. 63. 下列各对数中，成立的是（）A. log₂8 = 3B. log₃27 = 2C. log₄16 = 2D. log₅25 = 24. 若a、b、c是等差数列的连续三项，且a+b+c=0，则公差d为（）A. 0B. 1C. -1D. 无法确定5. 已知向量a=(2, -3)，向量b=(-1, 2)，则向量a与向量b的夹角θ的余弦值为（）A. 1/5B. 2/5C. 3/5D. 4/5二、填空题（每题5分，共25分）6. 已知等差数列的前三项分别为2，5，8，则该数列的公差为______。

7. 若函数f(x) = 2x + 3在区间[1, 4]上单调递增，则f(2)的值为______。

8. 已知log₅(2x + 1) = 3，则x的值为______。

9. 在三角形ABC中，角A、B、C的对边分别为a、b、c，若a² + b² = c²，则三角形ABC是______三角形。

10. 已知复数z = 3 + 4i，则|z|的值为______。

三、解答题（共45分）11. （15分）已知函数f(x) = x³ - 3x² + 2x - 1，求f(x)的导数f'(x)。

12. （15分）已知数列{an}是等比数列，且a₁=2，a₃=32，求该数列的公比q。

13. （15分）已知平面直角坐标系中，点A(2, 3)，点B(4, 5)，点C(x, y)在直线y = 2x + 1上，求点C的坐标。

四、附加题（10分）14. （5分）已知复数z₁ = 1 + i，z₂ = 2 - 3i，求z₁z₂的值。

中科大物理试题及答案一、选择题（每题5分，共20分）1. 光在真空中的传播速度是（）。

A. 300,000 km/sB. 299,792 km/sC. 299,792 km/hD. 300,000 km/h答案：B2. 根据牛顿第三定律，作用力和反作用力的大小（）。

A. 相等B. 不相等C. 相反D. 无法确定答案：A3. 一个物体从静止开始做匀加速直线运动，其加速度为a，经过时间t后的速度为（）。

A. atB. a*t^2C. a*t^(1/2)D. a*t^3答案：A4. 以下哪个选项不是电磁波（）。

A. 无线电波B. 微波C. 光波D. 声波答案：D二、填空题（每题5分，共20分）1. 根据欧姆定律，电流I等于电压V除以电阻R，即I = ________。

答案：V/R2. 物体的动能Ek可以用公式Ek = ________表示。

答案：1/2 * m * v^23. 光的折射定律，即斯涅尔定律，可以用公式n1 * sin(θ1) = n2 * sin(θ2)表示，其中n1和n2分别代表光从介质1到介质2的折射率，θ1和θ2分别代表入射角和折射角。

当光从空气进入水中时，若入射角为30°，则折射角θ2 = ________。

答案：sin^-1(n1/n2 * sin(θ1))4. 根据热力学第一定律，能量守恒，即ΔU = Q + W，其中ΔU代表内能变化，Q代表热量，W代表做功。

如果一个系统吸收了100J的热量，同时对外做了50J的功，则系统的内能变化ΔU = ________。

答案：150J三、计算题（每题10分，共20分）1. 一辆汽车以20m/s的速度行驶，突然刹车，刹车加速度为-5m/s^2，求汽车在刹车后10秒内滑行的距离。

答案：由于汽车在刹车后不会超过5秒就停止，所以10秒内滑行的距离等于5秒内滑行的距离。

使用公式s = ut + 1/2at^2，代入u=20m/s，a=-5m/s^2，t=5s，得到s = 20*5 + 1/2*(-5)*5^2 = 50m。

中科大强基试题物理一、关于量子力学的基本原理，以下说法正确的是？A. 量子力学中，粒子的位置和动量可以同时被精确测量B. 波函数描述了粒子在某一位置出现的概率密度C. 量子力学否定了经典力学的所有观点D. 量子纠缠是一种超自然现象（答案）B。

解析：根据量子力学的不确定性原理，粒子的位置和动量不能同时被精确测量；波函数是描述粒子量子态的数学函数，其绝对值的平方表示粒子在某一位置出现的概率密度；量子力学并不是否定经典力学，而是在微观领域对经典力学进行了补充和修正；量子纠缠是量子力学中的一种现象，并非超自然。

二、在光学实验中，当光从空气射入水中时，以下说法正确的是？A. 光的速度会增加B. 光的频率会改变C. 光的波长会变短D. 光的传播方向一定不变（答案）C。

解析：光从光疏介质（如空气）射入光密介质（如水）时，光的速度会减小；光的频率是由光源决定的，不会因介质改变而改变；由于光速减小，而频率不变，根据波长等于光速除以频率，光的波长会变短；光的传播方向在入射角不等于零时会发生改变，即发生折射。

三、关于牛顿运动定律，以下说法错误的是？A. 牛顿第一定律揭示了力是改变物体运动状态的原因B. 牛顿第二定律表明物体的加速度与所受的合外力成正比C. 牛顿第三定律说明作用力和反作用力总是大小相等、方向相反D. 牛顿运动定律只适用于宏观物体的低速运动（答案）D。

解析：牛顿运动定律是经典力学的基础，其中第一定律揭示了力与运动的关系，第二定律给出了加速度与合外力的关系，第三定律描述了作用力和反作用力的关系。

这些定律在宏观物体的低速运动中得到了广泛的应用，但在微观领域或高速运动中，需要引入量子力学或相对论进行修正。

然而，这并不意味着牛顿运动定律“只”适用于宏观物体的低速运动，而是说在这些条件下，牛顿运动定律的预测与实验结果相符。

四、在电磁学中，关于电场和磁场的说法，以下正确的是？A. 电场和磁场都是客观存在的物质B. 电场线总是从正电荷出发，终止于负电荷C. 磁场线总是闭合的，不会终止于某一点D. 电场和磁场都不能传递能量（答案）A、B、C。

电磁学考试题库及答案详解一、单项选择题1. 真空中两个点电荷之间的相互作用力遵循（）。

A. 牛顿第三定律B. 库仑定律C. 高斯定律D. 欧姆定律答案：B解析：库仑定律描述了真空中两个点电荷之间的相互作用力，其公式为F=k*q1*q2/r^2，其中F是力，k是库仑常数，q1和q2是两个电荷的量值，r是它们之间的距离。

2. 电场强度的方向是（）。

A. 从正电荷指向负电荷B. 从负电荷指向正电荷C. 垂直于电荷分布D. 与电荷分布无关解析：电场强度的方向是从正电荷指向负电荷，这是电场的基本性质之一。

3. 电势能与电势的关系是（）。

A. 电势能等于电势的负值B. 电势能等于电势的正值C. 电势能等于电势的两倍D. 电势能与电势无关答案：A解析：电势能U与电势V的关系是U=-qV，其中q是电荷量，V是电势。

4. 电容器的电容C与板间距离d和板面积A的关系是（）。

A. C与d成正比B. C与d成反比C. C与A成正比D. C与A和d都成反比解析：电容器的电容C与板间距离d成反比，与板面积A成正比，公式为C=εA/d，其中ε是介电常数。

5. 磁场对运动电荷的作用力遵循（）。

A. 洛伦兹力定律B. 库仑定律C. 高斯定律D. 欧姆定律答案：A解析：磁场对运动电荷的作用力遵循洛伦兹力定律，其公式为F=qvBsinθ，其中F是力，q是电荷量，v是电荷的速度，B是磁场强度，θ是速度与磁场的夹角。

二、多项选择题1. 以下哪些是电磁波的特性？（）A. 传播不需要介质B. 具有波粒二象性C. 传播速度等于光速D. 只能在真空中传播答案：ABC解析：电磁波的传播不需要介质，具有波粒二象性，传播速度等于光速，但它们也可以在其他介质中传播，只是速度会因为介质的折射率而改变。

2. 以下哪些是电场线的特点？（）A. 电场线从正电荷出发，终止于负电荷B. 电场线不相交C. 电场线是闭合的D. 电场线的疏密表示电场强度的大小答案：ABD解析：电场线从正电荷出发，终止于负电荷，不相交，且电场线的疏密表示电场强度的大小。

《中山大学授予学士学位工作细则》第六条：“考试作弊不授予学士学位。

”2012 学年 2 学期期中《电磁学》 试卷提前交卷5分钟以上加1分，提前10分钟以上加2分，……一些可能要用到的常数：电子电荷C 1910602.1-⨯-，真空介电常数2212/1085.8m N C ⋅⨯-,69.00.2ln =1. 一个无限大平行板电容器两极板的距离为l ，两极板分别带自由电荷面密度±σf .然后在电容器内插入一块厚度为 d (d < l )的无限大电介质平板，设它的极化强度矢量P 处处相同并与电容器的极板垂直. 求两板间介质内外的电场。

（10分）第一题图第五题图答：自由电荷在两板间产生的电场为00εσfE =（2分） 介质板两面的极化电荷面密度分别为P p ±=σ（2分）这些极化电荷在介质板内产生的附加电场00'εεσPE p -=-=，负号表示方向与E 0方向相反；极化电荷在介质外产和的电场为零。

（2分） 所以在介质内的总电场为000'εσεσpf E E E -=+=（2分） 介质外的电场为00εσfE =（2分） 电场的方向是从正极板指向负极板。

2. 半径为R 的球体内电荷体密度为常数ρ，介电常数与真空相同，求静电能。

（15分）。

答： 解法一：⎪⎪⎩⎪⎪⎨⎧≥==≤=)3(ˆ3ˆ434)3(32032030分分R r r r R r r RE R r r E ερπεπρερ )2(626)(36434)2(34)(020202202020300分分ερερερερερπεπρερπεr R r R R r R R r d r R Q r U R r R r -=-+=+=⋅+=⎰ 示分）分2(15460462642134221)(34)(21052052052402302202επρεπρεπρεπρπερπρRR R drr R R dr r r U W RR e =-=-==⎰⎰解法二：⎪⎪⎩⎪⎪⎨⎧≥==≤=)3(ˆ3ˆ434)3(32032030分分R r r r R r r R E R r r E ερπεπρερ 0520520520625022220300220015492452192592)4(43214321επρεπρεπρεπρεπρπερεπερεR R R r R R dr r r R dr r r W RR Re =+=⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∞∞⎰⎰分3. 空气的介电强度为 3.0×106V/m ，铜的密度为8.9 g/cm 3，铜的原子量为63.75 g/mol ，阿伏伽德罗常量N A =6.022×1023mol -1，金属铜里每个铜原子有一个自由电子。

合肥市普通高中六校联盟2024－2025学年第一学期期中联考高二年级物理试卷（答案在最后）（考试时间：75分钟满分：100分）命题学校：一、选择题（本题共10小题，满分42分。

在每小题给出的四个选项中，第1－8题只有一项符合题目要求，每小题4分；第9－10题有多项符合题目要求，全部选对的得5分，选对但不全的得3分，错选或不选的得0分）1．新一代人造太阳——中国环流三号，创造了我国可控核聚变装置运行新纪录，技术水平居国际前列。

其核心部件示意如图所示，通过一簇线圈（类似于通电螺线管）产生磁场，使高温等离子体（含有带正、负电的粒子）在磁场中发生可控核聚变反应。

取某处线圈截面，其电流方向与线圈内的磁场方向关系正确的是（）A ．B ．C ．D ．2．2024年5月3日我国发射的嫦娥六号在历时53天、38万公里的太空往返之旅后，取回了人类历史上第一抔来自月球背面的古老月壤平安返回地球！嫦娥六号在进入地月转移轨道时，由于卫星姿势的改变，卫星中一边长为50cm 的正方形导线框由水平方向转至竖直方向，若此处磁场磁感应强度5B 810T -=⨯，方向如图所示，则下列说法正确的是（sin 370.6︒=，cos370.8︒=）（）A ．在水平位置时，穿过线框的磁通量的大小为51.610bW -⨯B ．在竖直位置时，穿过线框的磁通量的大小为51.210b W -⨯C ．该过程中穿过线框的磁通量的变化量的大小是6410b W -⨯D ．该过程中穿过线框的磁通量的变化量的大小是52.810bW -⨯3．为了打击酒驾醉驾行为，保障交通安全，交警常用酒精浓度检测仪对驾驶员进行酒精测试，图1是某型号酒精测试仪，其工作原理如图2所示，R 为气敏电阻，其阻值随酒精气体浓度的增大而减小，电源的电动势为E 、内阻为r ，电路中的电表均为理想电表，0R 为定值电阻，且0R r =。

当酒驾驾驶员对着测试仪吹气时，下列说法错误．．的是（）A ．饮酒量越多，电源的输出功率一定越小B ．饮酒量越多，电源的效率越小C ．电压表的示数变小，电流表的示数变大D ．电压表示数变化量与电流表示数变化量的绝对值之比保持不变4．锂离子电池已被广泛地用于智能手机、智能机器人、电动自行车、电动汽车等领域，锂离子电池以碳材料为负极，以含锂的化合物为正极，依靠带正电的Li +在电池内部正极和负极之间移动来工作。

09006 2010~2011第二学期期末考试卷
一、简答题
1、电偶极子和磁偶极子的物理模型和条件是-----------。

2、有人说：截止存在时的静电场能量等于无介质时吧自由电荷和极化电荷（看作自由电荷）从无穷远搬到静电场中原来位置过程中外力所作的功。

这种说法对吗？为什么？
3解释为何在导体中维持一个稳定的电流场必须依靠外电源不断补充能量？ 4证明理想介质中传播的圆极化波瞬时坡阴亭矢量与时间和距离均无关。

5.色散的定义是---------。

若介质特性参数（μεσ）与频率无关，是否存在色散？
6.叙述一般时变场的唯一性定理。

7.说明辐射场分为近区、中中间区、远区的条件-----。

二。

计算题
1、一个矩形区域的边界条件如右图，求区域内的电位分布。

ψ|y=0=0 ψy |y=b =-v 0cos(Π
ψx |x=0=0 ψ|x=a =0
2、求证法拉第圆盘的电阻
R=1/（(2Πσd)*ln(R 2/R 1)）
其中d 为圆柱的高，R1为内径，R2为外径。

3、真空中两个频率均为w 的时谐电流分布。

电流分布分别为Ja 和Jb ， Ja 单独产生Ea 和Ha ，Jb 单独产生Eb 和Hb （粗体表示矢量的复数形式）
（1）写出每一组电磁场所满足的复数形式色麦克斯韦方程组。

（2）证明∮s （Ea ×Hb —Eb ×Ha ）ds=∫（Eb ·Ja —Ea ·Jb ）dv （粗体表示矢量的
复数形式）4.。

电磁学试题库 试题3一、填空题（每小题2分，共20分）1、带电粒子受到加速电压作用后速度增大，把静止状态下的电子加速到光速需要电压是（ ）。

2、一无限长均匀带电直线（线电荷密度为λ）与另一长为L ，线电荷密度为η的均匀带电直线AB 共面，且互相垂直，设A 端到无限长均匀带电线的距离为a ，带电线AB 所受的静电力为（ ）。

3、如图所示，金属球壳内外半径分别为a 和b ，带电量为Q ，球壳腔内距球心O 为r 处置一电量为q 的点电荷，球心O 点的电势（4、两个同心的导体薄球壳，半径分别为b a r r 和,其间充满电阻率为ρ的均匀介质（1）两球壳之间的电阻（ ）。

（2）若两球壳之间的电压是U ，其电流密度（ ）。

5、载流导线形状如图所示，(虚线表示通向无穷远的直导线)O 处的磁感应强度的大小为（ ）6、一矩形闭合导线回路放在均匀磁场中，磁场方向与回路平 面垂直，如图所示，回路的一条边ab 可以在另外的两条边上滑动，在滑动过程中，保持良好的电接触，若可动边的长度为L ，滑动速度为V ，则回路中的感应电动势大小（ ），方向（ ）。

7、一个同轴圆柱形电容器，半径为a 和b ，长度为L ，假定两板间的电压t U u m ω=sin ,且电场随半径的变化与静电的情况相同，则通过半径为r （a<r<b ）的任一圆柱面的总位移电流是（ ）。

8、如图，有一均匀极化的介质球，半径为R ，极 化强度为P ，则极化电荷在球心处产生的场强 是（ ）。

9、对铁磁性介质M B H、、三者的关系是（ ） ）。

10、有一理想变压器，12N N =15，若输出端接一个4Ω的电阻，则输出端的阻抗为（ ）。

一、选择题（每小题2分，共20分） 1、关于场强线有以下几种说法（ ） （A ）电场线是闭合曲线（B ）任意两条电场线可以相交（C ）电场线的疏密程度代表场强的大小（D ）电场线代表点电荷在电场中的运动轨迹R I O a b vPzRLI2、对某一高斯面S ，如果有0=⋅⎰S S d E则有（ ） （A ）高斯面上各点的场强一定为零 （B ）高斯面内必无电荷 （C ）高斯面内必无净电荷 （D ）高斯面外必无电荷3、将一接地的导体B 移近一带正电的孤立导体A 时，A 的电势。

04级电磁学期中考试 （05年10月29日）院系 ______班 学号 姓名______________成绩_____________ 一、填空题: (36分)1. （4分）电磁场的麦克斯韦方程组积分形式：______________________，___________________________， _______________________________________，_______________________________________________。

2. （4分）如图所示，已知电源电动势为ε，内阻为零，在t =0 时,C 1和C 2上都没有电荷, 在 K 接通的瞬间，通过R 1的电流为______________；R 2的电流为______________。

流过电源的稳态电流__________________ _；此时，电容C 1上的电量大小是___________________。

3. （4分）一平面线圈的磁矩大小为p m ＝1×10-8A•m 2，把它放入待测磁场中的A 处。

当p m 与z 轴平行时，所受力矩为最大，且最大值为M ＝5×10-9N•m ，方向沿x 轴负方向；当p m 与y 轴平行时，所受力矩大小为零，则空间A 点处的磁感 应强度B 的大小为______________________，方向为_____________________。

4. （4分）两平行金属板D 、F 间有均匀电场E ，为了使速率为V 的电子 从孔S 1入射，从孔S 2飞出，须在两金属板间加上均匀磁场，该磁 场的方向应该是 ；磁感应强度的大小应等于 ___________________________。

5. （4分）真空中有一均匀带电球体和一均匀带电球面，如果它们的半径和所带的电量相等，则球体的静电能______________（填＜、＞或＝）球面的静电能。

大学电磁学习题1一．选择题（每题3分）1.如图所示，半径为R 的均匀带电球面，总电荷为Q ，设无穷远处的电势为零，则球内距离球心为r 的P 点处的电场强度的大小和电势为：(A) E =0，RQ U 04επ=． (B) E =0，rQ U 04επ=． (C) 2Q E =，Q U = ．2. 3.? ，则(A) (C) 4. (A)(C) (E) 5.流I 2 (A) (C) 6.(A) (C) 0． (D) 11(20π-R I μ． (E) 11(40π+R I μ． ［ ］ 7.如图所示的一细螺绕环，它由表面绝缘的导线在铁环上密绕而成，每厘米绕10匝．当导线中的电流I 为2.0 A 时，测得铁环内的磁感应强度的大小B 为1.0 T ，则可求得铁环的相对磁导率?r 为(真空磁导率??0 =4?×10-7 T ·m ·A -1)(A) 7.96×102 (B) 3.98×102(C) 1.99×102 (D) 63.3 ［ ］ 8.一根长度为L 的铜棒，在均匀磁场 B 中以匀角速度?绕通过其一端??的定轴旋转着，B 的方向垂直铜棒转动的平面，如图所示．设t =0时，铜棒与Ob 成??角(b 为铜棒转动的平面上的一个固定点)，则在任一时刻t 这根铜棒两端之间的感应电动势的大小为：(A) )cos(2θωω+t B L ． (B)t B L ωωcos 212． (C) )cos(22θωω+t B L ． (D) B L 2ω．(E)B L 221ω． ［ ］ 9.面积为S 和2 S 的两圆线圈1、2如图放置，通有相同的电流I ．线圈1的电流所产生的通过线圈2的磁通用?21表示，线圈2的电流所产生的通过线圈1的磁通用?12表示，则?21和?12的大小关系为：(A) ?21 =2?12． (B) ?21 >?12．(C) ?21 =?12． (D) ?21 =21?12． ［ ］ 10.如图，平板电容器(忽略边缘效应)充电时，沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H 的环流两者，必有： (A)(B) (C) (D) 1.2.是3.4.5.6.×108 m/s, 7.z 8.是云室的原理．今在云室中有磁感强度大小为B = 1 T 的均匀磁场，观测到一个质子的径迹是半径r = 20 cm 的圆弧．已知质子的电荷为q = 1.6×10-19 C ，静 止质量m = 1.67×10-27 kg ，则该质子的动能为_____________．9.真空中两只长直螺线管1和2，长度相等，单层密绕匝数相同，直径之比d 1 / d 2 =1/4．当它们通以相同电流时，两螺线管贮存的磁能之比为W 1 / W 2=___________．10.平行板电容器的电容C 为20.0 ?F ，两板上的电压变化率为d U /d t =1.50×105 V ·s -1，则该平行板电容器中的位移电流为____________．三．计算题（共计40分）1. （本题10分）一“无限长”圆柱面，其电荷面密度为：??= ?0cos ???，式中??为半径R 与x 轴所夹的角，试求圆柱轴线上一点的场强．2. （本题5分）厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为? ．试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差．3. （本题10分）一电容器由两个很长的同轴薄圆筒组成，内、外圆筒半径分别为R 1 = 2 cm ，R 2 = 5 cm ，其间充满相对介电常量为?r 的各向同性、均匀电介质．电容器接在电压U = 32 V 的电源上，(如图所示)，试求距离轴线R = 3.5 cm 处的A 点的电场强度和A 点与外筒间的电势差．4. （本题5分）一无限长载有电流I 的直导线在一处折成直角，P 点位于导线所在平面内，距一条折线的延长线和另一条导线的距离都为a ，如图．求P 点的磁感强度B ．5. （本题10分）无限长直导线，通以常定电流I ．有一与之共面的直角三角形线圈ABC ．已知AC 边长为b ，且与长直导线平行，BC 边长为a ．若线圈以垂直于导线方向的速度v 向右平移，当B 点与长直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和感应电动势的方向．基础物理学I 模拟试题参考答案一、选择题(每题3分，共30分) 1．(U 4.C7. 而 8. 9. 10. 1. （本题10分）解：将柱面分成许多与轴线平行的细长条，每条可视为“无限长”均匀带电直线，其电荷线密度为? = ?0cos ? R d ?，它在O 点产生的场强为：φφεσελd s co 22d 000π=π=RE 3分 它沿x 、y 轴上的二个分量为：d E x =－d E cos ? =φφεσd s co 2200π- 1分d E y =－d E sin ? =φφφεσd s co sin 200π 1分 积分： ⎰ππ-=20200d s co 2φφεσx E ＝002εσ 2分 0)d (s i n s i n 22000=π-=⎰πφφεσy E 2分 ∴ i i E E x 002εσ-== 1分 2. （本题5分）解：选坐标如图．由高斯定理，平板内、外的场强分布为：E = 0 (板内))2/(0εσ±=x E (板外) 2分1、223. （本题解得 A4. （本题 )2402πa 方向为⊙ )4/(2021a I B B B π=-=μ 方向为? 各1分5. （本题10分）解：建立坐标系，长直导线为y 轴，BC 边为x 轴，原点在长直导线上，则斜边的方程为 a br a bx y /)/(-=式中r 是t 时刻B 点与长直导线的距离．三角形中磁通量⎰⎰++-π=π=Φr a r ra r x axbr a b I x x y I d )(2d 200μμ)ln (20r r a a br b I +-π=μ 6分 t r r a a r r a a Ib t d d (ln 2d d 0+-+π=Φ-=μ 3分当r =d 时， v (l n 20da a d d a a Ib +-+π=μ 方向：ACBA (即顺时针) 1分。

期中复习一、填空1.经典氢原子模型中，电子与质子相距0.529×10-10m，则电子与质子间的库仑力=8.24×10-8N。

2.半径为a的薄圆板均匀带电，中心区域表面附近电场大小为E，则离平板中心r (r>>a) 处的电场大小=a2E/(2r2)。

3.点电荷q位于边长为a的立方体中心，则q在立方体一个面上的电通量=q/(6ε0)。

4.一球壳由彼此绝缘的两个金属半球壳组成，一半接地，另一半电势为U，则球心处的电势为U/2。

5.四个标称值均为20pF，10V的电容器，其中两个并联后再与另外两个串联，则总电容=8pF，可以耐受的最高电压值=25V。

6.三个点电荷排列在x轴上，q1=q2=-q3，q1位于x=0，q2位于x=1，则当q3位于、、时，该点电荷系的总相互作用能为零。

x=或1/22/3(9(37.点电荷q与接地无穷大导体平板相距a，则q受力=q2/(16πε0a2)，体系互能=-q2/(16πε0a)。

8.四面体的全部棱边所构成的电路中，节点数=4，独立回路数=3。

9.一根长2m，横截面10cm2的铜棒，两端电压为50mV。

已知铜的电导率是5.8×107S/m，则铜棒电阻=3.45×10-5Ω，0.1秒内产生的焦耳热=7.25J。

10.如图所示，U ab=10V，则I=10/27A，R ab=108/55Ω。

二、判断1.(×) 闭合曲面上各点电场均为零时，面内必没有宏观电荷。

2.(×) 等势面间距大的地方电场线较密。

3.(×) 两导体均带正电，则二者不可能相互吸引。

4.(√) 铁电体中电位移与电场强度一般不成正比。

5.(√) 电源的路端电压可以大于其电动势。

6.(√) 如果点电荷之间的库仑力不与其距离平方成反比，则高斯定理不再成立。

7.(×) 一导体空腔中有一正点电荷，则该电荷越靠近内腔表面，导体的电势越高。

一、单选题1、 如果通过闭合面S 的电通量e Φ为零，则可以肯定A 、面S 内没有电荷B 、面S 内没有净电荷C 、面S 上每一点的场强都等于零D 、面S 上每一点的场强都不等于零2、 下列说法中正确的是A 、沿电场线方向电势逐渐降低B 、沿电场线方向电势逐渐升高C 、沿电场线方向场强逐渐减小D 、沿电场线方向场强逐渐增大3、 高压输电线在地面上空m 25处，通有A 1023⨯的电流，则该电流在地面上产生的磁感应强度为A 、T 104.15-⨯B 、T 106.15-⨯C 、T 1025-⨯D 、T 104.25-⨯4、 载流直导线和闭合线圈在同一平面内，如图所示，当导线以速度v 向左匀速运动时，在线圈中A 、有顺时针方向的感应电流B 、有逆时针方向的感应电C 、没有感应电流D 、条件不足，无法判断5、 两个平行的无限大均匀带电平面，其面电荷密度分别为σ+和σ-，则P 点处的场强为A 、02εσB 、0εσ C 、02εσ D 、0 6、 一束α粒子、质子、电子的混合粒子流以同样的速度垂直进入磁场，其运动轨迹如图所示，则其中质子的轨迹是A 、曲线1B 、曲线2C 、曲线3D 、无法判断 7、 一个电偶极子以如图所示的方式放置在匀强电场E 中，则在电场力作用下，该电偶极子将A 、保持静止B 、顺时针转动C 、逆时针转动D 、条件不足，无法判断8、 点电荷q 位于边长为a 的正方体的中心，则通过该正方体一个面的电通量为A 、0B 、0εqC 、04εqD 、06εq 9、 长直导线通有电流A 3=I ，另有一个矩形线圈与其共面，如图所示，则在下列哪种情况下，线圈中会出现逆时针方向的感应电流？A 、线圈向左运动B 、线圈向右运动C 、线圈向上运动D 、线圈向下运动10、 下列说法中正确的是A 、场强越大处，电势也一定越高3B 、电势均匀的空间，电场强度一定为零C 、场强为零处，电势也一定为零D 、电势为零处，场强一定为零11、 关于真空中静电场的高斯定理0εi S q S d E ∑=∙⎰ ，下述说法正确的是：A. 该定理只对有某种对称性的静电场才成立；B. i q ∑是空间所有电荷的代数和；C. 积分式中的E 一定是电荷i q ∑激发的；D. 积分式中的E 是由高斯面内外所有电荷激发的。

11级电磁学期中考试解答2011--2012学年第二学期电磁学期中考试解答一、填空题（30分，2分/空）1. 如图，立方体顶点处的点电荷q 在面ABCD 上的电通量=q /24ε0。

2. 体电荷密度r e 为常数的无限大平板厚度为a ，则平板外的电场大小=a r e /2ε0。

3. 三个标称值均为30pF ，10V 的电容器，其中两个并联后再与第三个串联，则总电容为20pF ，总耐压值为15V 。

4. 中子由1个u 夸克 (荷电2e/3) 和2个d 夸克 (荷电?e/3) 构成，设彼此距离均为10?15m ，则u 夸克所受静电力大小=89N ，三个夸克的相互作用能=7.7×10?14J 。

5. 半径为R 的球形空间内有体密度为常数ρe 的电荷，则球外空间的静电能=2πρe 2R 5/45ε0，全空间的静电能=4πρe 2R 5/15ε0。

6. 如图，两个嵌套的长方体，所有棱边以及相应顶点的连线构成一复杂电路，其节点数=16，独立回路数=17。

7. 一根长2.0m ，横截面10cm 2的金属棒，两端电压为50mV 。

已知铜的电导率是4.0×107S/m ，导电电子数密度为6.0×1028/m 3，则铜棒电阻=5.0×10?5Ω，电子平均漂移速度=1.0×10?4m/s ，0.1秒内产生的焦耳热=5.0J 。

8. 如图，电动势均为U ，电阻均为R ，则I 1=U /7R ，I 3=3U /7R 。

二、判断题（10分，1分/小题）1. ( × ) 一个点电荷与带电体的距离越近，所受到的静电力越大。

2. ( √ ) 仅有静电力时电荷体系不能实现稳定平衡。

3. ( √ ) 如果点电荷之间的库仑力不与其距离平方成反比，则高斯定理不成立。

4. ( × ) 若d 0S=∫∫A S w 对任意闭合曲面S 都成立，则A =0。

5. ( × ) 一区域内电势为零，则场强处处为零；反之亦然。