高中数学21向量的线性运算212向量的加法课后导练新人教B版4

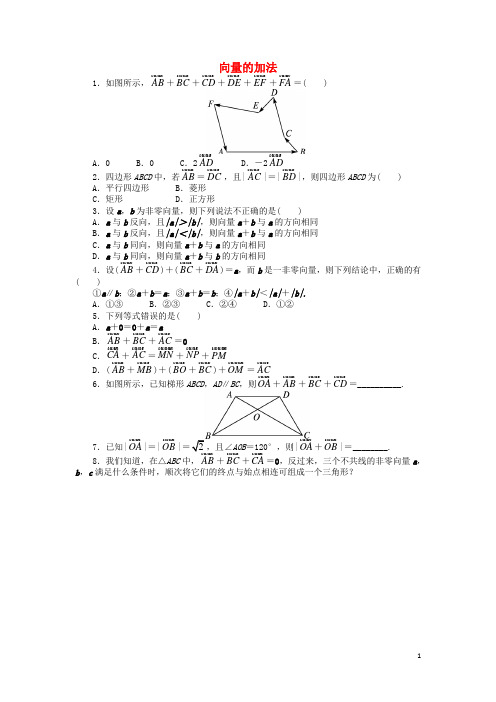
向量的加法1．如图所示，AB＋BC＋CD＋DE＋EF＋FA＝( )A．0 B．0 C．2AD D．－2AD2．四边形ABCD中，若AB＝DC，且|AC|＝|BD|，则四边形ABCD为( )A．平行四边形 B．菱形C．矩形 D．正方形3．设a，b为非零向量，则下列说法不正确的是( )A．a与b反向，且|a|＞|b|，则向量a＋b与a的方向相同B．a与b反向，且|a|＜|b|，则向量a＋b与a的方向相同C．a与b同向，则向量a＋b与a的方向相同D．a与b同向，则向量a＋b与b的方向相同4．设(AB＋CD)＋(BC＋DA)＝a，而b是一非零向量，则下列结论中，正确的有( )①a∥b；②a＋b＝a；③a＋b＝b；④|a＋b|＜|a|＋|b|.A．①③ B．②③ C．②④ D．①②5．下列等式错误的是( )A．a＋0＝0＋a＝aB．AB＋BC＋AC＝0C．CA＋AC＝MN＋NP＋PMD．(AB＋MB)＋(BO＋BC)＋OM＝AC6．如图所示，已知梯形ABCD，AD∥BC，则OA＋AB＋BC＋CD＝__________.7．已知|OA|＝|OB|AOB＝120°，则|OA＋OB|＝________.8．我们知道，在△ABC中，AB＋BC＋CA＝0，反过来，三个不共线的非零向量a，b，c满足什么条件时，顺次将它们的终点与始点相连可组成一个三角形？参考答案1．解析：利用向量加法的多边形法则求解．答案：B2．解析：由AB＝DC，可判断四边形ABCD为平行四边形．由|AC|＝|BD|，可进一步判断四边形ABCD的对角线相等，所以四边形ABCD为矩形．答案：C3．答案：B4．解析：由(AB＋CD)＋(BC＋DA)＝AB＋BC＋CD＋DA＝0，可知a＝0，而零向量与任意向量平行，任意向量与零向量相加仍得原向量，所以①和③正确；②中应为a＋b＝b，④中应为|a＋b|＝|a|＋|b|.答案：A5．解析：对于零向量和任一向量a，有a＋0＝0＋a＝a，故选项A正确；∵AB＋BC＋AC＝AC＋AC＝2AC，∴选项B错误；对于选项C，CA＋AC＝0，MN＋NP＋PM＝MP＋PM＝0，∴CA＋AC＝MN＋NP＋PM，故选项C正确；对于选项D，由向量加法的交换律和结合律，得(AB＋MB)＋(BO＋BC)＋OM＝AB＋BO＋OM＋MB＋BC＝AC，故选项D正确．答案：B6．解析：原式＝(OA＋AB)＋(BC＋CD)＝OB＋BD＝OD.答案：OD7．解析：以OA，OB为邻边作平行四边形OACB，则OC＝OA＋OB.因为|OA|＝|OB|且∠AOB＝120°，所以△OAC是等边三角形．所以|OA＋OB|＝|OC|＝|OA|答案： 28．解：当a＋b＋c＝0时，顺次将它们的终点与始点相连可组成一个三角形．可作AB＝a，BC＝b，CA＝c，则AB＋BC＝AC，∴AC＋c＝0，即c与AC方向相反，大小相同，即c＝CA，∴a，b，c可构成一个三角形．。

2.2 平面向量的线性运算教学目标1.通过物理中的位移合成、力的合成等实例，认识、理解向量加法的意义，体验数学知识发生、发展的过程。

2．理解、掌握向量的加法运算，并理解其几何意义. 会用三角形法则和平行四边形法则作两个向量的和向量，培养数形结合解决问题的能力.3．通过将向量运算与熟悉的数的运算进行类比，使学生掌握向量加法运算的交换律和结合律，并会用它们进行向量计算，渗透类比的数学方法；4.通过由实例到概念，由具体到抽象，使学生学会如何用数学方法描述问题、解决问题。

教学重点、难点教学重点：会用向量加法的三角形法则和平行四边形法则作两个向量的和向量及向量加法的运算律．教学难点：对向量加法意义的理解．教学关键：向量加法的三角形法则和平行四边形法则的探究引导.教学突破方法：由物理中力的合成与分解拓展延伸，引导学生探讨得到结论．教法与学法导航教学方法；启发诱导，讲练结合．学习方法：数能进行运算，向量是否也能进行运算呢？数的加法启发我们，从运算的角度看，位移的合成、力的合成可看作向量的加法．借助于物理中位移的合成、力的合成来理解向量的加法，让学生顺理成章接受向量的加法定义．结合图形掌握向量加法的三角形法则和平行四边形法则．联系数的运算律理解和掌握向量加法运算的交换律和结合律．教学准备教师准备：课件、直尺．学生准备：练习本、直尺.教学过程一、创设情境，导入新课上一节，我们一起学习了向量的有关概念，明确了向量的表示方法，了解了零向量、单位向量、平行向量、相等向量等概念，并接触了这些概念的辨析判断．数能进行运算，向量是否也能进行运算呢？这一节，我们将借助于物理中位移、力的合成来学习向量的加法运算及其几何意义.二、主题探究，合作交流1. 师生互动：教师引导学生回顾物理中位移的概念，如图．某对象从A点经B点到C点，两次位移、的结果，与A点直接到C点的位移结果相同．力也可以合成，老师引导，让学生共同探究如下的问题.图（1）表示橡皮条在两个力的作用下，沿着GC的方向伸长了EO；图（2）表示撤去F1和F2，用一个力F作用在橡皮条上，使橡皮条沿着相同的方向伸长相同的长度．你能发现F与F1、F2之间的关系吗？力F对橡皮条产生的效果与力F1与F2共同作用产生的效果相同，物理学中把力F叫做F1与F2的合力．合力F与力F1、F2有怎样的关系呢？由图（3）发现，力F在以F1、F2为邻边的平行四边形的对角线上，并且大小等于平行四边形对角线的长．数的加法启发我们，从运算的角度看，F可以认为是F1与F2的和，即位移、力的合成看作向量的加法．讨论结果：1. 向量加法的定义：如下图，已知非零向量a、b，在平面内任取一点A，作=a，=b，则向量叫做a与b的和，记作a+b，即a+b= + = ．求两个向量和的运算，叫做向量的加法．2. 向量加法的法则：（1）向量加法的三角形法则在定义中所给出的求向量和的方法就是向量加法的三角形法则．运用这一法则时要特别注意“首尾相接”，即第二个向量要以第一个向量的终点为起点，则由第一个向量的起点指向第二个向量的终点的向量即为和向量．位移的合成可以看作向量加法三角形法则的物理模型．（2）向量加法的平行四边形法则如图，以同一点O为起点的两个已知向量a、b为邻边作平行四边形，则以O为起点的对角线就是a与b的和．我们把这种作两个向量和的方法叫做向量加法的平行四边形则．力的合成可以看作向量加法平行四边形法则的物理模型．3.下面请同学们来体验一下如何用所学的向量加法的两条法则作图师生合作完成例一：例1 如下左图，已知向量a、b，求作向量a+b．活动：教师引导学生，让学生探究分别用向量加法的三角形法则和平行四边形法则作两个向量的和向量．在向量加法的作图中，学生体会作法中在平面内任取一点O的依据——它体现了向量起点的任意性．在向量作图时，一般都需要进行向量的平移，用平行四边形法则作图时应强调向量的起点放在一起，而用三角形法则作图则要求首尾相连．解：作法一：在平面内任取一点O（上中图），作=a，=b，则=a+b．作法二：在平面内任取一点O（上右图），作=a，=b．以OA、OB为邻边作OACB，连接OC，则=a+b．小练习：学生动手完成课本84页练习1（1）和(2)、2，然后展示结果，老师给予点评．（学生通过自己动手作图进一步体验如何区分用两种向量加法法则作图的的方法）．4.观察教材82页图2.2-10，师生互动：观察实际例子，教师启发学生思考，并适时点拨，诱导，探究向量的加法在特殊情况下的运算.提问:当在数轴上表示两个共线向量时，它们的加法与数的加法有什么关系？用哪条法则进行求和？（讨论结果：两个数相加其结果是一个数，对应于数轴上的一个点;在数轴上的两个向量相加，它们的和仍是一个向量，对应于数轴上的一条有向线段．用的是三角形法则来求两个共线向量的和）类比数的加法，数0与任意实数a 的和仍得实数a．对于零向量与任一向量a，我们规定a+0=0+a=a．5.思考|a+b|，|a|，|b|存在着怎样的关系？由例一发现：当a，b不共线时，|a+b|<|a|+|b|（即三角形两边之和大于第三边）;当a，b共线且方向相同时，|a+b|=|a|+|b|;当a，b共线且方向相反时，|a+b|=|a|-|b|（或|b|-|a|）．6 .数的运算和运算律紧密联系，运算律可以有效地简化运算．类似地，向量的加法是否也有运算律呢？数的加法满足交换律与结合律，即对任意a，b∈R，有a+b=b+a，（a+b）+c=a+（b+c）．任意向量a，b的加法是否也满足交换律和结合律？引导学生画图进行探索．如下左图，作=a，=b，以AB、AD为邻边作ABCD，则=b，=a．因为= + =a+b，= + =b+a，所以a+b=b+a．如上右图，因为= + =（+ ）+ =（a+b）+c，= + = +（+ ）=a+（b+c），所以（a+b）+c=a+（b+c）．综上所述，向量的加法满足交换律和结合律。

【2019最新】高中数学2-1向量的线性运算2-1-3向量的减法课后导练新人教B 版必修4 向量的减法课后导练基础达标 1.AC 可以写成①OC AO +；②OC AO -；③OC OA -；④OA OC -.其中正确的是( )A.①②B.②③C.③④D.①④解析:由三角形法则知①④正确.而=--=-+=-,22.答案:D2.化简下列各式,结果为零向量的个数是( ) ①++ ②-+- ③AD OD OA +- ④MP MN QP NQ -++A.1B.2C.3D.4解析:①++=+=0. ②-+-=(+)-(+)=-=0. ③+-=-=0. ④-+++=++==0.答案:D3.若||=8,||=5,则||的取值范围是( )A.［3,8］B.(3,8)C.［3,13］D.(3,13)解析:∵=-,当、同向时,||=8-5=3； 当,反向时,||=8+5=13； 当,AC 不共线或有零向量时3＜|BC |＜13.综上,知3≤|BC |≤13.答案:C4.△ABC 中,D 、E 、F 分别为AB 、BC 、CA 的中点,-等于( )A. B. C. D.解析:==-=-.答案:D5.下列四式中,不能化简为的是( ) A.(+)+ B.(+)+(+CM ) C.+-BM D.+-解析:(+)+(AC +CM )=++=+.答案:B6.已知=a ,=b ,若||=12,||=5,且∠AOB=90°,则|a -b |=__________. 解析:|a -b |=|OA -OB |=||=1351222=+.答案:137.在边长为1的正方形ABCD 中,设=a ,=b ,=c ,则|a +b +c |=________,|a +c -b |=________,|c -a -b |=______.解析:|a +b +c |=2|c |=22,|a +c -b |=|(c -b )+a |=2|a |=2,|c -a-b |=0.答案:22 2 08.在平行四边形ABCD 中,若|+|=|-|,则ABCD 是__________(填正方形或矩形或菱形).解析:由|+|=|-|,即|AC |=||,可得ABCD 的对角线相等且为平行四边形,因此可得ABCD 为矩形.答案:矩形综合运用9.(2004全国高考,文5) 已知向量a ,b 满足:|a |=1,|b |=2,|a -b |=2,则|a +b |等于( ) A.1 B.2 C.5 D.6解析:由|a +b |2+|a -b |2=2(|a |2+|b |2),知|a +b |2+4=2(1+4),故|a +b |=6.答案:D10.平面上有三点A,B,C,设m= +,n=-,若m,n的长度恰好相等,则有( )A.A,B,C三点必在同一直线上B.△ABC必为等腰三角形且∠B为顶角C.△ABC必为直角三角形且∠B=90°D.△ABC必为等腰直角三角形解析:如图,作ABCD,则+=,-BC=-=,∵|m|=|n|,∴||=||.∴ABCD为矩形.∴△ABC为直角三角形,∠B=90°.答案:C11.已知等腰直角△ABC,∠C=90°,M为斜边的中点,设=a,=b,试用向量a,b表示AM、,CB,.解:AM=CM-CA=a-b,=AM=a-b,=+=+AM+=b+a-b+a-b=2a-b,=-=-(+)=-2(a-b )=2(b -a ).拓展探究12.一艘船以35 km/h 的速度向垂直于岸的方向行驶,而船的实际速度是10 km/h,求水流的速度和船行驶的方向(用与水流方向间的夹角表示).解:如图所示,设表示船垂直于对岸行驶的速度,表示水流的速度,以,为边作ABCD,则AC 表示的就是船实际航行的速度.在Rt△ABC 中, |AC |=10 km/h, ||=||=35 km/h,∴|75100-= (km/h). ∵tan∠CAB=3,∴∠CAB=60°.答:水流速度为5 km/h,船行驶方向与水流方向夹角为60°.。

——教学资料参考参考范本——【高中教育】最新高中数学2-1向量的线性运算2-1-3向量的减法课后导练新人教B版必修4______年______月______日____________________部门课后导练基础达标1.可以写成①；②；③；④.其中正确的是( )AC OC AO +OCAO -OC OA -OA OC -A.①②B.②③C.③④D.①④ 解析:由三角形法则知①④正确.而.CA OC OA OC AC OC OC AO OC AO =--=-+=-,22 答案:D2.化简下列各式,结果为零向量的个数是( ) ① ②-+-CA BC AB ++AB AC BD CD ③ ④AD OD OA +-MP MN QP NQ -++A.1B.2C.3D.4 解析:①==0.CA BC AB ++CA AC +②-+-=(+)-(+)=-=0.AB AC BD CD AB BD AC CD AD AD ③==0.AD OD OA +-OD OD -④=0.MP MN QP NQ -++MN NM MN PM NP +=++= 答案:D3.若||=8,||=5,则||的取值范围是( )AB AC BCA.［3,8］B.(3,8)C.［3,13］D.(3,13)解析:∵=-,当、同向时,||=8-5=3；BC AC AB AB AC BC 当,反向时,||=8+5=13；AB AC BC当,不共线或有零向量时3＜||＜13.AB AC BC 综上,知3≤||≤13.BC 答案:C4.△ABC 中,D 、E 、F 分别为AB 、BC 、CA 的中点,等于( )DB AF - A. B. C. D.FD FC FE BE 解析:.BE DF AD AF DB AF ==-=- 答案:D5.下列四式中,不能化简为的是( )ADA.()+B.(+)+(+)CD AB +BC AD MB AC CMC.+-D.MB AD BM CD OA OC +- 解析:(+)+(+)=++=+.AD MB AC CM AD MB AM AD AB 答案:B6.已知=a,=b,若||=12,||=5,且∠AOB=90°,则|a-b|=__________.OAOB OA OB解析:|a-b|=|-|=||=.OA OB BA 1351222=+ 答案:137.在边长为1的正方形ABCD 中,设=a,=b,=c,则|a+b+c|=________,|a+c-b|=________,|c-a-b|=______.AB BC AC 解析:|a+b+c|=2|c|=,|a+c-b|=|(c-b)+a|=2|a|=2,|c-a-b|=0.22 答案: 2 0228.在平行四边形ABCD 中,若|+|=|-|,则ABCD 是__________(填正方形或矩形或菱形).AB AD AB AD 解析:由|+|=|-|,AB AD AB AD即||=||,可得ABCD的对角线相等且为平行四边形,AC DB因此可得ABCD为矩形.答案:矩形综合运用9.(20xx全国高考,文5) 已知向量a,b满足:|a|=1,|b|=2,|a-b|=2,则|a+b|等于( )A.1B.C.D.256解析:由|a+b|2+|a-b|2=2(|a|2+|b|2),知|a+b|2+4=2(1+4),故|a+b|=.6答案:D10.平面上有三点A,B,C,设m=+,n=-,若m,n的长度恰好相等,则有( )AB BC AC AB BCA.A,B,C三点必在同一直线上B.△ABC必为等腰三角形且∠B为顶角C.△ABC必为直角三角形且∠B=90°D.△ABC必为等腰直角三角形解析:如图,作ABCD,则+=,AB BC ACAB-=-=,BC AB AD DB∵|m|=|n|,∴||=||.AC BD∴ABCD为矩形.∴△ABC 为直角三角形,∠B=90°. 答案:C11.已知等腰直角△ABC,∠C=90°,M 为斜边的中点,设=a,=b,试用向量a,b 表示、,,.CM CA AM MB CB BA 解:=-=a-b,AM CM CAMB ==a-b,AMCB =+=++=b+a-b+a-b=2a-b,CA AB CA AM MBBA ==-(+)=-2(a-b)=2(b-a).AB -AM MB拓展探究12.一艘船以 km/h 的速度向垂直于岸的方向行驶,而船的实际速度是10 km/h,求水流的速度和船行驶的方向(用与水流方向间的夹角表示).35解:如图所示,设表示船垂直于对岸行驶的速度,表示水流的速度,以,为边作ABCD,则表示的就是船实际航行的速度.AD AB AD AB AC在Rt△ABC 中, ||=10 km/h,AC||=||= km/h,BC AD 35∴||= (km/h).AB 75100||||22-=-BC AC ∵tan∠CAB=,∴∠CAB=60°.3答:水流速度为5 km/h,船行驶方向与水流方向夹角为60°.。

——教学资料参考参考范本——【高中教育】最新高中数学2-1向量的线性运算2-1-4数乘向量课后训练新人教B版必修4______年______月______日____________________部门1．设a是非零向量，λ是非零实数，下列结论正确的是( ) A．a与－λa的方向相反B．|－λa|≥|a|C．a与λ2a的方向相同D．|－λa|＝|λ|a2．已知AD，BE，CF分别为△ABC的三条中线，G是它们的交点，则下列等式不正确的是( )A．＝ B．＝BG23BE DG12AGC．＝－2 D．＋＝CG FG13DA23FC12BC3．如图所示，在梯形ABCD中，AD∥BC，＝a，＝b，＝c，＝d，且E，F分别为AB，CD的中点，则( )OA OB OC ODA．＝(a＋b＋c＋d)EF12B．＝(a－b＋c－d)EF12C．＝(c＋d－a－b)EF12D．＝(a＋b－c－d)EF124．(20xx·四川雅安期末)设四边形ABCD中，有＝，且||＝||，则这个四边形是( )DC12AB AD BCA．平行四边形 B．矩形C．菱形 D．等腰梯形5．已知四边形ABCD 为菱形，点P 在对角线AC(不包括端点A ，C)上，则等于( )APA ．λ(＋)，λ∈(0,1)AB AD B ．λ(＋)，λ∈AB BC 20,2⎛⎫⎪ ⎪⎝⎭C ．λ(－)，λ∈(0,1)AB ADD ．λ(－)，λ∈AB BC 20,2⎛⎫⎪ ⎪⎝⎭6．O 为平行四边形ABCD 的中心，若＝4e1，＝6e2，则＝__________.AB BC BO7．如图所示，已知＝，若用，表示，则等于__________．AP43AB OA OB OP OP8．给出下面四个结论：①对于实数p 和向量a ，b ，有p(a －b)＝pa －pb ； ②对于实数p ，q 和向量a ，有(p －q)a ＝pa －qa ； ③若pa ＝pb(p ∈R)，则a ＝b ；④若pa ＝qa(p ，q ∈R ，a ≠0)，则p ＝q. 其中正确结论的序号为__________．9．如图所示，L ，M ，N 是△ABC 三边的中点，O 是△ABC 所在平面内的任意一点，求证：＋＋＝＋＋.OA OB OC OL OM ON10．已知，在△ABC 中，＝a ，＝b.对于△ABC 所在平面内的任意一点O ，动点P 满足＝＋λa ＋λb ，λ∈[0，＋∞)．试问，动点P 的轨迹是否过某一个定点？并说明理由．AB AC OP OA参考答案1．解析：如果λ＞0，则a与－λa的方向相反，如果λ≤0，则a与－λa的方向相同，故选项A错误；如果|λ|＜1，则|－λa|＜|a|，故选项B错误；|－λa|是一个大于或等于零的实数，而|λ|a是向量，它们之间不能比较大小，故选项D错误．答案：C2．解析：由图知，选项A，C，D均正确，选项B应该为＝.DG12AG答案：B3．解析：如图，连接OF，OE，则＝－＝(＋)－(＋)＝(c＋d)－(a＋b)＝(c＋d－a－b)．故选C．EF OF OE12OC OD12OA OB121212答案：C4．解析：∵＝，DC12AB∴四边形ABCD是梯形．又∵||＝||，AD BC∴四边形ABCD是等腰梯形．答案：D5．解析：由向量的运算法则，可得＝＋.又点P在对角线AC上，所以与同向，且||＜||，故＝λ＝λ(＋)，λ∈(0,1)．AC AB AD AP AC AP AC AP AC AB AD答案：A6．解析：＝＝(－)＝(－)＝(6e2－4e1)＝3e2－2e1.BO12BD 12AD AB12BC AB 12答案：3e2－2e17．解析：由＝＋OP BP OB ＝＋＝(－＋)＋13AB OB 13OA OB OB ＝＋.13-OA43OB 答案：＋13-OA43OB 8．解析：①②正确；③当p ＝0时不正确；④可化为(p －q)a ＝0， ∵a ≠0，∴p －q ＝0，即p ＝q ，∴④正确． 答案：①②④9．证明：∵＋＋＝＋＋＋＋＋OA OB OC OL LA OM MB ON NC ＝(＋＋)＋(＋＋)OL OM ON LA MB NC ＝(＋＋)＋(＋＋)OL OM ON 12CA AB BC ＝(＋＋)＋0OL OM ON ＝＋＋，OL OM ON ∴原式成立．10．解：是．理由：如图，以，为邻边作ABDC ，设对角线AD ，BC 交于点E ，AB AC则＝＝(a ＋b)．AE12AD 12由＝＋λa ＋λb ，得OP OAOP－＝＝2λ·(a＋b)＝2λ·，λ∈[0，＋∞)．OA AP 12AE∴与共线．AP AE由λ∈[0，＋∞)可知，动点P的轨迹是射线AE，∴动点P的轨迹必过△ABC的重心．。

2.1.3 向量的减法课后导练基础达标 1.可以写成①+；②-；③-；④-.其中正确的是( )A.①②B.②③C.③④D.①④解析:由三角形法则知①④正确.而CA OC OA OC AC OC OC AO OC AO =--=-+=-,22.答案:D2.化简下列各式,结果为零向量的个数是( ) ①++ ②AB -+BD - ③+- ④-++A.1B.2C.3D.4解析:①CA BC AB ++=CA AC +=0. ②AB -AC +BD -CD =(AB +BD )-(AC +CD )=AD -AD =0. ③+-=-=0. ④MP MN QP NQ -++MN NM MN PM NP +=++==0.答案:D3.若||=8,|AC |=5,则|BC |的取值范围是( )A.［3,8］B.(3,8)C.［3,13］D.(3,13)解析:∵BC =AC -AB ,当AB 、AC 同向时,|BC |=8-5=3； 当,AC 反向时,|BC |=8+5=13； 当,不共线或有零向量时3＜||＜13.综上,知3≤||≤13.答案:C4.△ABC 中,D 、E 、F 分别为AB 、BC 、CA 的中点,-等于( ) A. B. C. D.解析:BE DF AD AF DB AF ==-=-.5.下列四式中,不能化简为的是( ) A.(+)+ B.(AD +MB )+(+) C.MB +AD -BM D.CD OA OC +-解析:(+)+(AC +CM )=++=+.答案:B6.已知OA =a ,OB =b ,若|OA |=12,|OB |=5,且∠AOB=90°,则|a -b |=__________. 解析:|a -b |=|OA -OB |=||=1351222=+.答案:137.在边长为1的正方形ABCD 中,设AB =a ,BC =b ,AC =c ,则|a +b +c |=________,|a +c -b |=________,|c -a -b |=______.解析:|a +b +c |=2|c |=22,|a +c -b |=|(c -b )+a |=2|a |=2,|c -a-b |=0.答案:22 2 08.在平行四边形ABCD 中,若|+|=|-|,则ABCD 是__________(填正方形或矩形或菱形).解析:由|AB +AD |=|AB -AD |,即|AC |=||,可得ABCD 的对角线相等且为平行四边形,因此可得ABCD 为矩形.答案:矩形综合运用9.(2004全国高考,文5) 已知向量a ,b 满足:|a |=1,|b |=2,|a -b |=2,则|a +b |等于( ) A.1 B.2 C.5 D.6解析:由|a +b |2+|a -b |2=2(|a |2+|b |2),知|a +b |2+4=2(1+4),故|a +b |=6.10.平面上有三点A,B,C,设m=++,n=-,若m,n的长度恰好相等,则有( )A.A,B,C三点必在同一直线上B.△ABC必为等腰三角形且∠B为顶角C.△ABC必为直角三角形且∠B=90°D.△ABC必为等腰直角三角形解析:如图,作ABCD,则AB+=,AB-BC=AB-AD=DB,∵|m|=|n|,∴||=|BD|.∴ABCD为矩形.∴△ABC为直角三角形,∠B=90°.答案:C11.已知等腰直角△ABC,∠C=90°,M为斜边的中点,设CM=a,CA=b,试用向量a,b表示AM、MB,CB,BA.解:=CM-CA=a-b,==a-b,=+=++=b+a-b+a-b=2a-b,-=-(AM+MB)=-2(a-b)=2(b-a).BA=AB拓展探究5 km/h的速度向垂直于岸的方向行驶,而船的实际速度是10 km/h,求水流12.一艘船以3的速度和船行驶的方向(用与水流方向间的夹角表示).解:如图所示,设AD 表示船垂直于对岸行驶的速度,AB 表示水流的速度,以AD ,AB 为边作ABCD,则表示的就是船实际航行的速度.在Rt△ABC 中, |AC |=10 km/h, |BC |=|AD |=35 km/h,∴|75100-= (km/h). ∵tan∠CAB=3,∴∠CAB=60°.答:水流速度为5 km/h,船行驶方向与水流方向夹角为60°.。

高中数学2-1向量的线性运算2-1-4向量数乘课后导练新人教B 版必修4课后导练基础达标1.［(2a+4b)-(4a-4b)］等于( )3121A.2a-bB.2b-aC.b-aD.a-b 解析:原式=(a+2b-4a+4b)=(6b-3a)=2b-a.3131答案:B2.下列各组中的向量a,b 共线的有( )①a=2e,b=-2e ②a=e1-e2,b=-2e1+2e2 ③a=4e1-e2,b=e1-e2 ④a =e1+e2,b=2e1-2e252101A.①②③B.②③④C.①③④D.①②③④解析:对于①②③中的向量a 与b,都存在一个相应的实数λ,使a=λb.而④中的两个向量不存在实数λ,使b=λa 成立. 答案:A3.若O 是△ABC 内一点,=0,则O 是△ABC 的( )OC OB OA ++ A.垂心 B.重心 C.内心 D.外心 解析:∵=0,OCOB OA ++ ∴=-(+).如图,+==-,OB OC OE OA- ∴A、O 、E 三点共线,点D 为BC 中点. ∴O 为三角形三条中线的交点. ∴O 是△ABC 的重心. 答案:B4.设e1,e2是两个不共线的向量,则向量a=2e1-e2与向量b=e1+λe2(λ∈R)共线,当且仅当λ的值为…( )A.0B.-1C.-2D.-21解析:设a=μb(μ∈R),则2e1-e2=μ(e1+λe2),即.⎪⎩⎪⎨⎧-==⎩⎨⎧-==.21,2.1,2λμλμμ解得答案:D5.设=(a+5b),=-2a+8b,=3(a-b),则共线的三点是( )AB 22BC CDA.A 、B 、CB.B 、C 、DC.A 、B 、DD.A 、C 、D解析:∵+==(-2a+8b)+3(a-b)=a+5b, ∴=,又与有公共点B,AB 22BD AB BD∴A、B 、D 三点共线. 答案:C6.在平行四边形ABCD 中,++等于( ) A. B. C. D. 解析:++=++=-==.可知D 选项正确.AB CA BD AB BD CA AD AC CD BA 答案:D7.设a 是非零向量,λ是非零实数,下列结论正确的是( ) A.a 与-λa 的方向相反 B.|-λa|≥|a|C.a 与λ2a 的方向相同D.|-λa|=|λ|a解析:如果λ>0,则a 与-λa 的方向相反,如果λ<0,则a 与-λa 的方向相同,A 错;如果|λ|<1,则|-λa|<|a|,B 错;|-λa|是一个大于或等于零的实数,而|λ|a 是向量,它们之间不能比较大小,D 错. 答案:C8.已知向量a 、b 不共线,实数x,y 满足向量等式5xa+(8-y)b=4x b+3(y+9)a,则x=____,y=______.解析:∵a 与b 不共线,根据向量相等,得,解得⎩⎨⎧=-+=.48,2735x y y x ⎩⎨⎧-==.4,3y x 答案:3 -4 综合运用9.(2005南京第二十七中) 设a,b 为不共线的非零向量,=2a+3b,=-8a-2b,=-6a-4b,那么( )AB BC CD A.与同向,且||>|| B.AD 与同向,且||<|| C.与反向,且||>|| D.∥ 解析:由=(2a+3b)+(-8a-2b),BC AB AC += 则=-6a+b. 又有=+=-12a-3b=(-8a-2b),AD AC CD 23 即=.AD 23∴与同向,||>||.AD BC AD BC 故选A. 答案:A10.(2006武汉一中) 如图所示,已知=,用,表示,则等于( )AP 34 A.-+ B.+31OA 34OB 31OA 34OB C.- D.--31OA 34OB 31OA 34解析:由=+ =+=(-+)+31OB 31=+.故选A.31-OA 34OB答案:A11.已知四边形ABCD 中,=a-2c,=5a+6b-8c,对角线AC,BD 的中点为E,F,则向量=___________.AB CDEF 解析:在四边形ABCD 中取AD 的中点M,连结ME,MF. 所以ME 为△ACD 的中位线,MF 为△DAB 的中位线, 故=-=-=(+)=［(a-2c)+(5a+6b-8c)］=3a+3b-5c.E 21AB 21DC 21CD 21 答案:3a+3b-5c 拓展探究12.已知△ABC 中,=a,=b.对于平面ABC 上任意一点O,动点P 满足=+λa+λb,λ∈［0,+∞).试问动点P 的轨迹是否过某一个定点?说明理由. 思路分析:按向量的运算法则作出图形分析求解. 解:以,为邻边作ABDC,设对角线,交于点E,AD BC则==(a+b).AE 21AD 21由=+λa+λb 得OP OA-==2λ(a+b)=2λ·,λ∈［0,+∞).AP 21∴与共线.AP AE由λ∈［0,+∞)可知动点P 的轨迹是射线AE,所以必过△ABC 的重心.。

2.1.2 向量的加法预习导航1．向量加法的三角形法则已知向量a ，b(如图)，在平面上任取一点A ，作=a ，=b ，再作向量，则向量AC叫做a 与b 的和(或和向量)，记作a ＋b ，即a ＋b ＝AB ＋BC＝AC ．上述求两个向量和的作图法则，叫做向量求和的三角形法则． 名师点拨 (1)向量的和仍然是一个向量．(2)用三角形法则求和必须使两个向量“首尾相接”(即前一个向量的终点与后一个向量的起点重合)，其和是第一个向量的起点指向第二个向量的终点，简述为“加向量，首尾连；和向量，起点到终点”．(3)当a 与b 同向共线时，a ＋b 与a ，b 同向，且|a ＋b |＝|a |＋|b |．(4)当a 与b 反向共线时，若|a |>|b |，则a ＋b 与a 的方向相同，且|a ＋b |＝|a |－|b |；若|a |<|b |，则a ＋b 的方向与b 相同，且|a ＋b |＝|b |－|a |．(5)当两个非零向量a 与b 不共线时，则a ＋b 的方向与a ，b 的方向都不相同，且|a ＋b |<|a |＋|b |，这是三角形两边之和大于第三边的向量表示．2．向量求和的平行四边形法则已知两个不共线向量a ，b(如图)，作AB =a ，AD =b ，则A ，B ，D 三点不共线，以AB，AD为邻边作平行四边形ABCD ，则对角线上向量AC =a+b ，这个法则叫做两个向量求和的平行四边形法则．名师点拨 (1)利用平行四边形法则的条件是这两个向量必须是从同一点出发的不共线的向量．(2)向量求和的三角形法则与平行四边形法则的区别与联系：当两个向量不共线时，它们是一致的，但当两个向量共线时，三角形法则仍然适用，而平行四边形法则就不适用了．(3)向量加法的三角形法则和平行四边形法则实际上就是向量加法的几何意义． 3．向量求和的多边形法则已知n 个向量，依次把这n 个向量首尾相连，以第一个向量的始点为始点，第n 个向量的终点为终点的向量叫做这n 个向量的和向量．这个法则叫做向量求和的多边形法则．名师点拨 (1)向量求和的多边形法则是向量求和的三角形法则的推广，是由求两个向量的和推广到求多个向量的和，强调的也是“首尾相接”．(2)当首尾顺次相接的向量构成封闭的向量链时，那么各向量的和就是0． 自主思考1 如何用向量证明A ，B ，C 三点共线？提示：(1)若AB ∥BC，则A ，B ，C 三点共线．(2)若AC ＝AB ＋BC，则A ，B ，C 三点共线．自主思考2 在△ABC 中，若D 是BC 的中点，则AD 用AB ，AC可以怎样表示？提示：在△ABC 中，若D 为BC 的中点，则AD ＝12(AB ＋AC)．证明如下：如图所示，以AB ，AC 为邻边构造平行四边形ABD ′C ． 因为D 为BC 的中点，所以D 为平行四边形ABD ′C 对角线的交点．所以AD=1211,133,11.33x x x yy λλ⎧-=-⎪⎪=⎨⎪=⎪⎩AD ′． 又AD =AB +AC，所以AD =12AD '=12()AB AC + ．自主思考3 在△ABC 中，若G 为△ABC 的重心，则GA ＋GB 与GC有何关系？提示：在△ABC 中，若G 为△ABC 的重心，则GA ＋GB ＋GC＝0．证明如下：如图，延长GD 至点H ，使DH=DG ，显然四边形GBHC 是平行四边形，则有GB +GC =GH ．又G 为△ABC 的重心， 所以GA=2GD=GH ．因为GA 与GH的大小相等，方向相反，所以GA +GH=0．所以GA ＋GB ＋GC＝0．4．向量加法的运算律 (1)交换律：a ＋b ＝b ＋a ；(2)结合律：(a ＋b )＋c ＝a ＋(b ＋c )．自主思考4 向量加法与实数加法从运算法则、运算结果、运算律和运算意义上来比较，有何异同？提示：(1)运算法则：向量的加法法则是三角形法则或平行四边形法则，可以用有向线段的连接来表示；实数的加法法则是数的运算．(2)运算结果：向量的和还是向量；实数的和还是实数．(3)运算律：向量的加法与实数的加法都满足交换律与结合律；向量加法的交换律可以用平行四边形法则来验证；向量加法的结合律可以用三角形法则来验证：如图，作AB=a ，BC =b ，CD =c ，连接AC ，BD ，AD ， 则AC =a+b ，BD=b+c ．因为AD =AB +BD=a+(b+c)，AD =AC+CD =(a+b)+c ，所以(a+b)+c=a+(b+c)．(4)运算的几何意义：向量加法的几何意义是向量加法的三角形法则和平行四边形法则；实数加法的意义是实数的加法法则．。

2.1.3 向量的减法课后导练基础达标 1.可以写成①+；②-；③-；④-.其中正确的是( )A.①②B.②③C.③④D.①④解析:由三角形法则知①④正确.而CA OC OA OC AC OC OC AO OC AO =--=-+=-,22.答案:D2.化简下列各式,结果为零向量的个数是( ) ①CA BC AB ++ ②AB -AC +BD -CD ③AD OD OA +- ④-++A.1B.2C.3D.4解析:①CA BC AB ++=CA AC +=0. ②-+-=(+)-(+)=-=0. ③+-=-=0. ④MP MN QP NQ -+++=++==0.答案:D3.若||=8,||=5,则||的取值范围是( )A.［3,8］B.(3,8)C.［3,13］D.(3,13)解析:∵=-,当、同向时,||=8-5=3； 当,反向时,||=8+5=13； 当,不共线或有零向量时3＜||＜13.综上,知3≤|BC |≤13.答案:C4.△ABC 中,D 、E 、F 分别为AB 、BC 、CA 的中点,-等于( ) A. B.FC C. D.解析:BE DF AD AF DB AF ==-=-.5.下列四式中,不能化简为的是( ) A.(CD AB +)+BC B.(AD +MB )+(AC +CM ) C.+-BM D.+-解析:(+)+(+CM )=++=+.答案:B6.已知=a ,=b ,若||=12,||=5,且∠AOB=90°,则|a -b |=__________. 解析:|a -b |=|-|=||=1351222=+.答案:137.在边长为1的正方形ABCD 中,设=a ,=b ,=c ,则|a +b +c |=________,|a +c -b |=________,|c -a -b |=______.解析:|a +b +c |=2|c |=22,|a +c -b |=|(c -b )+a |=2|a |=2,|c -a-b |=0.答案:22 2 08.在平行四边形ABCD 中,若|+|=|-|,则ABCD 是__________(填正方形或矩形或菱形).解析:由|+|=|-|,即||=||,可得ABCD 的对角线相等且为平行四边形,因此可得ABCD 为矩形.答案:矩形综合运用9.(2004全国高考,文5) 已知向量a ,b 满足:|a |=1,|b |=2,|a -b |=2,则|a +b |等于( ) A.1 B.2 C.5 D.6解析:由|a +b |2+|a -b |2=2(|a |2+|b |2),知|a +b |2+4=2(1+4),故|a +b |=6.10.平面上有三点A,B,C,设m=+BC+AC,n=-BC,若m,n的长度恰好相等,则有( )A.A,B,C三点必在同一直线上B.△ABC必为等腰三角形且∠B为顶角C.△ABC必为直角三角形且∠B=90°D.△ABC必为等腰直角三角形解析:如图,作ABCD,则AB+BC=AC,-=-=,∵|m|=|n|,∴|AC|=|BD|.∴ABCD为矩形.∴△ABC为直角三角形,∠B=90°.答案:C11.已知等腰直角△ABC,∠C=90°,M为斜边的中点,设CM=a,CA=b,试用向量a,b表示AM、,,.解:=CM-=a-b,=AM=a-b,CB=CA+=CA+AM+=b+a-b+a-b=2a-b,-=-(AM+MB)=-2(a-b)=2(b-a).BA=AB拓展探究5 km/h的速度向垂直于岸的方向行驶,而船的实际速度是10 km/h,求水流12.一艘船以3的速度和船行驶的方向(用与水流方向间的夹角表示).解:如图所示,设表示船垂直于对岸行驶的速度,表示水流的速度,以,为边作ABCD,则表示的就是船实际航行的速度.在Rt△ABC 中, ||=10 km/h, ||=|AD |=35 km/h,∴|75100-= (km/h). ∵tan∠CAB=3,∴∠CAB=60°.答:水流速度为5 km/h,船行驶方向与水流方向夹角为60°.。