统计学：两变量关联性分析

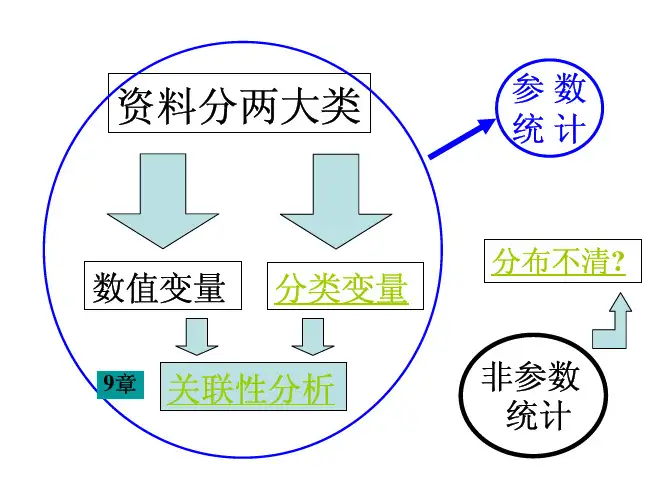
第十章 两变量关联性分析三、两个分类变量的关联分析n对分类变量间的联系，可作关联（association）分析n对两个分类变量交叉分类计数所得的频数资料（列联表） 作关于两种属性独立性的c 2 检验交叉分类2×2列联表n对样本量为n的一份随机样本同时按照两个二项分类的特 征（属性）进行交叉分类形成一个2×2交叉分类资料表, 也称为2×2列联表（contingency table）。

n 例10­3：为观察行为类型与冠心病的关系，某研究组收集 了一份包含3154个个体的样本，研究者将观察对象按行 为类型分为A型（较具野心、进取心和有竞争性），B型 （较沉着、轻松、和做事不慌忙）。

对每个个体分别观 察是否为冠心病患者和行为类型两种属性，2×2种结果 分类记数如下表所示。

试分析两种属性的关联性。

表 10­3 行为类型与冠心病的关系行为类型（属性 A） 冠心病（属性 B）合计 有(1) 无(2)类型 A(1) 178 **** **** 类型 B(2) 79 1486 1565 合计 257 2897 3154表 10­42×2 交叉分类频数表的一般形式及概率表达属性 A属性 B合计121 11 A ( 11 p ) 12 A ( 12 p ) 1 n ( 1 r p ) 2 21 A ( 21 p ) 22 A ( 22 p ) 2 n ( 2 r p )合计1 m ( 1 c p )2 m ( 2 c p )n （1.0）0 H ：属性 A 与 B 互相独立，1 H ：属性 A 与 B 互相关联。

独立性检验就是考察 cj ri ij p p p = 成立与否。

å- = ji i i i T T A , j2j j 2)( c0 H ：行为类型与冠心病之间互相独立1 H ：行为类型与冠心病之间有关联a =0.05将表中各数据代入公式（9­9），22(1781486791411)3154 39.90158915652572897c ´-´´ == ´´´ 20.05,13.84 c= ， 220.05,1c c> P <0.05，说明行为类型与冠心病之间存在着关联性。

偏相关和双变量相关
偏相关和双变量相关都是统计学中用来衡量变量之间关系的概念，但它们有着不同的特点和应用场景。

偏相关：
偏相关衡量的是两个变量之间的线性相关性，当控制其他变量的影响时，两个变量之间的相关程度。

它可以在多元线性回归中用来衡量某两个变量之间的关系，排除了其他变量的影响。

举个例子，假设有三个变量A、B、C，偏相关分析可以帮助确定在保持C 不变的情况下，A 和B 之间的相关性。

这种分析可以消除其他变量对A 和B 之间关系的干扰，帮助更准确地理解A 和B 之间的独立关联。

双变量相关：
双变量相关是指两个变量之间的直接关系，通常通过相关系数来衡量。

这种关系不考虑其他变量的影响，仅仅是衡量两个变量之间的线性关系程度。

常见的相关系数包括皮尔逊相关系数，它测量了两个变量之间的线性关系的强度和方向（正相关或负相关）。

例如，如果有两个变量X 和Y，皮尔逊相关系数可以告诉我们它们之间的相关性有多强，以及是正相关还是负相关。

总体来说，偏相关主要用于探究两个变量之间的关系，在考虑其他变量因素的情况下进行分析；而双变量相关更侧重于衡量两个变量之间的直接关系，不考虑其他变量的影响。

这两种方法在统计学和数据分析中都是重要的工具，可用于不同类型的研究和分析。

两个变量间相关关系的举例相关关系是指两个变量之间的变化是否存在某种联系或者依赖。

在统计学中，我们可以通过计算相关系数来度量两个变量之间的相关程度。

下面，我将为你举例说明两个变量间的相关关系。

举例一：首先，我们来看身高和体重之间的相关关系。

身高和体重是人体的两个重要指标，一般来说，身高越高，体重也会相应增加。

我们可以通过一个调查统计来验证这种关系。

在调查中，我们随机选择了1000名男性被试，记录了他们的身高和体重。

通过运用统计学方法，我们计算得到了身高和体重之间的相关系数为0.8，这说明身高和体重之间存在着强正相关关系。

也就是说，身高增加会促使体重的增加。

举例二：其次，让我们来考察学习时间和考试成绩之间的相关关系。

有一种常见的观点是，学习时间越多，考试成绩也会越好。

我们可以通过一个实验证明这种关系。

我们在一所学校中随机选取了500名学生，将他们分为两组：一组进行了加强学习时间的训练，每天学习4个小时；另一组保持正常学习时间，每天学习2个小时。

在经过一段时间的训练后，我们进行了一次考试，记录了两组学生的考试成绩。

通过对比两组学生的考试成绩，我们发现加强学习时间组的平均分高于正常学习时间组，这说明学习时间和考试成绩之间存在着正相关关系。

举例三：再次，让我们来研究睡眠时间和工作效率之间的相关关系。

一般来说，充足的睡眠对于提高工作效率很重要。

为了验证这个假设，我们进行了一项睡眠实验。

我们让20名被试者进行七天的实验，在前三天，他们每晚只睡4个小时；在后四天，他们每晚睡眠时间恢复到正常的8个小时。

在每天的工作结束后，我们记录了被试者当天的工作成绩。

通过实验数据的分析，我们发现在睡眠时间缺乏的前三天，被试者的工作效率明显降低；而在恢复充足睡眠的后四天，工作效率也得到了明显的提高。

这表明睡眠时间和工作效率之间存在着正相关关系。

以上三个例子表明，两个变量之间的相关关系可以通过实验证明或者调查统计来证实。

将变量之间的相关关系研究清楚，对我们了解事物的本质以及提高效率具有重要意义。

皮尔逊相关性分析相关性分析是统计学中的重要方法之一，用于衡量两个变量之间的关联程度。

皮尔逊相关性分析是最常用的相关性分析方法之一，可以计算出两个连续变量之间的线性相关性。

本文将介绍皮尔逊相关性分析的原理、应用场景以及计算方法。

1. 皮尔逊相关性分析原理皮尔逊相关系数（Pearson correlation coefficient）是用来衡量两个连续变量之间的线性关系强度和方向的统计量。

相关系数的取值范围为-1到1，当相关系数为1时，表示变量之间存在完全正相关；当相关系数为-1时，表示变量之间存在完全负相关；当相关系数为0时，表示变量之间不存在线性关系。

2. 皮尔逊相关性分析的应用场景皮尔逊相关性分析可以用于许多领域的研究和分析，例如：(1) 经济学：分析收入和消费之间的相关性；(2) 市场营销：分析广告投入和销售额之间的相关性；(3) 医学研究：分析药物剂量和疗效之间的相关性；(4) 社会科学：分析教育水平和收入之间的相关性。

3. 皮尔逊相关性分析的计算方法计算皮尔逊相关系数的公式为：r = (Σ(xy) - (Σx)(Σy) / n) / sqrt((Σx^2 - (Σx)^2 / n) * (Σy^2 - (Σy)^2 / n))其中，r为皮尔逊相关系数，Σ表示求和符号，Σxy表示两个变量的乘积之和，Σx和Σy分别表示两个变量的总和，n表示样本数量。

4. 皮尔逊相关性分析的示例为了更好地理解皮尔逊相关性分析的应用，我们举个例子来进行说明。

假设我们有一组数据，其中X表示产品的销售额，Y表示产品的广告投入。

我们希望分析产品的销售额和广告投入之间的相关性。

首先，我们计算X和Y的总和，然后计算X和Y的乘积之和。

接下来，我们使用上述公式计算皮尔逊相关系数。

假设我们有以下数据：X = [10, 20, 30, 40, 50]Y = [5, 10, 15, 20, 25]X和Y的总和为：Σx = 150Σy = 75X和Y的乘积之和为：Σxy = 2750根据公式，我们可以计算皮尔逊相关系数：r = (2750 - (150*75) / 5) / sqrt((550 - (150^2) / 5) * (275 - (75^2) / 5))经过计算，我们得到皮尔逊相关系数r的值为0.981，接近于1，表示产品的销售额和广告投入之间存在较强的正相关。

相关性分析原理相关性分析是指在数据挖掘和统计学中，用来衡量两个变量之间关系的一种方法。

它可以帮助我们理解变量之间的相互作用，找出它们之间的关联程度，从而为后续的决策和预测提供依据。

在实际应用中，相关性分析被广泛应用于市场营销、金融分析、医学研究等领域，为决策提供重要参考。

相关性分析的原理是基于变量之间的协变性来衡量它们之间的关系。

在统计学中，常用的相关性分析方法包括皮尔逊相关系数、斯皮尔曼相关系数和肯德尔相关系数等。

其中，皮尔逊相关系数是最常用的方法之一，它衡量的是两个连续变量之间的线性关系强度和方向。

斯皮尔曼相关系数则是一种非参数的方法，适用于不满足正态分布假设的情况。

而肯德尔相关系数则可以衡量变量之间的等级关系，适用于等级数据的相关性分析。

在进行相关性分析时，我们需要注意一些问题。

首先，相关性不代表因果关系，即使两个变量之间存在高度相关，也不能说明其中一个变量的变化引起另一个变量的变化。

其次，相关性分析只能发现线性关系，对于非线性关系的发现需要使用其他方法。

此外，在进行相关性分析时，还需要考虑样本的大小和数据的分布情况，以避免由于样本偏差和数据异常导致的误判。

除了单变量之间的相关性分析，我们还可以进行多变量之间的相关性分析。

多变量相关性分析可以帮助我们理解多个变量之间的复杂关系，识别出主要影响因素，为多变量建模提供依据。

在实际应用中，多变量相关性分析常常用于金融风险管理、医学诊断、市场预测等领域。

总之，相关性分析是数据分析中的重要工具，它可以帮助我们理解变量之间的关系，为决策提供依据。

在进行相关性分析时，我们需要选择合适的方法，并注意相关性不代表因果关系，还需要考虑样本的大小和数据的分布情况。

同时，多变量相关性分析也是一个重要的研究方向，可以帮助我们理解多个变量之间的复杂关系。

希望本文能够对相关性分析的原理有所帮助，谢谢阅读。