大学物理刚体的转动惯量的研究实验报告

刚体转动惯量的测定实验报告一、实验目的1、学习用三线摆法测定刚体的转动惯量。

2、加深对转动惯量概念的理解。

3、掌握用游标卡尺和秒表等仪器的使用方法。

二、实验原理三线摆是由三根等长的悬线将一水平圆盘悬挂在一个固定的支架上构成的。

当圆盘绕中心轴 OO' 作扭转摆动时，圆盘的运动可以看作是圆盘绕通过其重心且垂直于盘面的轴线的转动和平动的合成。

设圆盘的质量为 m，半径为 R，对于通过其重心且垂直于盘面的轴线的转动惯量为Ic。

当圆盘扭转一个小角度θ 时，圆盘的势能变化为：ΔEp ＝ mgh其中，h 为圆盘重心上升的高度。

由于θ 很小，所以可以近似认为：h ≈ Rθ²根据能量守恒定律，圆盘的势能变化等于其动能的变化，即：ΔEp ＝1/2 Iω²其中，ω 为圆盘的角速度。

又因为圆盘的摆动周期为 T，所以ω ＝2π/T。

联立上述式子可得：Ic ＝（mgR²T²) ／（4π²h)实验中通过测量圆盘的质量 m、半径 R、摆动周期 T 以及圆盘扭转角度θ 对应的重心上升高度 h，即可计算出圆盘对于通过其重心且垂直于盘面的轴线的转动惯量 Ic。

三、实验仪器三线摆、游标卡尺、米尺、秒表、待测刚体（圆环、圆柱等）、托盘天平。

四、实验步骤1、用托盘天平测量圆盘和待测刚体的质量。

2、用游标卡尺测量圆盘和待测刚体的直径，分别测量多次，取平均值。

3、调整三线摆的悬线长度，使上下圆盘之间的距离约为 50cm 左右。

4、轻轻转动上圆盘，使圆盘作小角度的扭转摆动，用秒表测量圆盘摆动 50 个周期的时间，重复测量多次，取平均值，计算出摆动周期T。

5、将待测刚体放在圆盘上，使两者的中心轴线重合，按照上述方法测量系统（圆盘和待测刚体）的摆动周期 T'。

五、实验数据记录与处理1、圆盘质量 m ＝＿_____ g，直径 D ＝＿_____ cm，半径 R ＝D/2 ＝＿_____ cm。

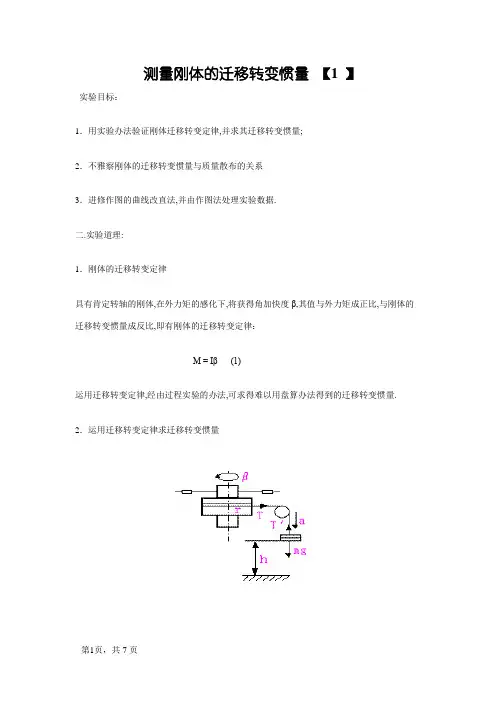
测量刚体的迁移转变惯量【1 】实验目标：1．用实验办法验证刚体迁移转变定律,并求其迁移转变惯量;2．不雅察刚体的迁移转变惯量与质量散布的关系3．进修作图的曲线改直法,并由作图法处理实验数据.二.实验道理:1．刚体的迁移转变定律具有肯定转轴的刚体,在外力矩的感化下,将获得角加快度β,其值与外力矩成正比,与刚体的迁移转变惯量成反比,即有刚体的迁移转变定律：M = Iβ (1)运用迁移转变定律,经由过程实验的办法,可求得难以用盘算办法得到的迁移转变惯量. 2．运用迁移转变定律求迁移转变惯量如图所示,待测刚体由塔轮,伸杆及杆上的配重物构成.刚体将在砝码的拖动下绕竖直轴迁移转变.设细线不成伸长,砝码受到重力和细线的张力感化,从静止开端以加快度a下落,其活动方程为mg – t=ma,在t时光内下落的高度为h=at2/2.刚体受到张力的力矩为Tr和轴摩擦力力矩Mf.由迁移转变定律可得到刚体的迁移转变活动方程：Tr - Mf = Iβ.绳与塔轮间无相对滑动时有a = rβ,上述四个方程得到：m(g - a)r - Mf = 2hI/rt2 (2)Mf与张力矩比拟可以疏忽,砝码质量m比刚体的质量小的多时有a<<g,所以可得到近似表达式：mgr = 2hI/ rt2 (3)式中r.h.t可直接测量到,m是实验中随意率性选定的.是以可依据（3）用实验的办法求得迁移转变惯量I.3．验证迁移转变定律,求迁移转变惯量从（3）动身,斟酌用以下两种办法：A．作m – 1/t2图法：伸杆上配重物地位不变,即选定一个刚体,取固定力臂r和砝码下落高度h,（3）式变成：M = K1/ t2 (4)式中K1 = 2hI/ gr2为常量.上式标明：所用砝码的质量与下落时光t的平方成反比.实验中选用一系列的砝码质量,可测得一组m与1/t2的数据,将其在直角坐标系上作图,应是直线.即若所作的图是直线,便验证了迁移转变定律.从m – 1/t2图中测得斜率K1,并用已知的h.r.g值,由K1 = 2hI/ gr2求得刚体的I.B．作r – 1/t图法：配重物的地位不变,即选定一个刚体,取砝码m和下落高度h为固定值.将式（3）写为：r = K2/ t （5）式中K2 = (2hI/ mg)1/2是常量.上式标明r与1/t成正比关系.实验中换用不合的塔轮半径r,测得统一质量的砝码下落时光t,用所得一组数据作r－1/t图,应是直线.即若所作图是直线,便验证了迁移转变定律.从r－1/t图上测得斜率,并用已知的m.h.g值,由K2 = (2hI/ mg)1/2求出刚体的I.刚体迁移转变仪,滑轮,秒表,砝码.1.调节实验装配：调节转轴垂直于程度面调节滑轮高度,使拉线与塔轮轴垂直,并与滑轮面共面.选定砝码下落起点到地面的高度h,并保持不变.取塔轮半径为,砝码质量为20g,保持高度h不变,将配重物逐次取三种不合的地位,分离测量砝码下落的时光,剖析下落时光与迁移转变惯量的关系.本项实验只作定性解释,不当准据盘算.3.测量质量与下落时光关系：测量的根本内容是：改换不合质量的砝码,测量其下落时光t.用游标卡尺测量塔轮半径,用钢尺测量高度,砝码质量按已给定命为每个;用秒表记载下落时光.将两个配重物放在横杆上固定地位,选用塔轮半径为某一固定值.将拉线平行围绕纠缠在轮上.逐次选用不合质量的砝码,用秒表分离测量砝码从静止状况开端下落到达地面的时光.对每种质量的砝码,测量三次下落时光,取平均值.砝码质量从5g开端,每次增长5g,直到35g止.用所测数据作图,从图中求出直线的斜率,从而盘算迁移转变惯量.测量的根本内容是：对统一质量的砝码,改换不合的塔轮半径,测量不合的下落时光.将两个配重物选在横杆上固定地位,用固定质量砝码施力,逐次选用不合的塔轮半径,测砝码落地所用时光.对每一塔轮半径,测三次砝码落地之间,取其平均值.留意,在改换半径是要响应的调节滑轮高度,并使绕过滑轮的拉线与塔轮平面共面.由测得的数据作图,从图上求出斜率,并盘算迁移转变惯量.五.实验数据及数据处理：r-1/t的关系：⨯103-kg 2m ⋅m-(1/t)2的关系：由此关系得到的迁移转变惯量I=231087.1m kg ⋅⨯-六.实验成果：⨯103-kg 2m ⋅;由m-1/t 2的关系得到迁移转变惯量I=231087.1m kg ⋅⨯-.七.实验留意事项：1．细心调节实验装配,保持转轴铅直.使轴尖与轴槽尽量为点接触,使轴迁移转变自如,且不克不及扭捏,以削减摩擦力矩.2．拉线要围绕纠缠平行而不重叠,切忌乱绕,以防各匝线之间挤压而增大阻力.3．掌控好启动砝码的动作.计时与启动一致,力图防止计时的误差.4．砝码质量不宜太大,以使下落的加快度a不致太大,包管a<<g前提的知足.八.实验思虑题：1.定性剖析实验中的随机误差和可能的体系误差.答：随机误差重要出如今计时与启动的一致性上面还有,拉线的平行情形.体系误差主如果轴的摩擦及空气阻力.。

测量刚体的转动惯量实验目的：1．用实验方法验证刚体转动定律，并求其转动惯量；2．观察刚体的转动惯量与质量分布的关系3．学习作图的曲线改直法，并由作图法处理实验数据。

二.实验原理:1．刚体的转动定律具有确定转轴的刚体，在外力矩的作用下，将获得角加速度β，其值与外力矩成正比，与刚体的转动惯量成反比，即有刚体的转动定律：M = Iβ(1)利用转动定律，通过实验的方法，可求得难以用计算方法得到的转动惯量。

2．应用转动定律求转动惯量如图所示，待测刚体由塔轮，伸杆及杆上的配重物组成。

刚体将在砝码的拖动下绕竖直轴转动。

设细线不可伸长，砝码受到重力和细线的张力作用，从静止开始以加速度a下落，其运动方程为mg –t=ma，在t时间内下落的高度为h=at2/2。

刚体受到张力的力矩为T r和轴摩擦力力矩M f。

由转动定律可得到刚体的转动运动方程：T r- M f= Iβ。

绳与塔轮间无相对滑动时有a = rβ，上述四个方程得到：m(g - a)r - M f = 2hI/rt2 (2)M f与张力矩相比可以忽略，砝码质量m比刚体的质量小的多时有a<<g，所以可得到近似表达式：mgr = 2hI/ rt2 (3)式中r、h、t可直接测量到，m是试验中任意选定的。

因此可根据（3）用实验的方法求得转动惯量I。

3．验证转动定律，求转动惯量从（3）出发，考虑用以下两种方法：A．作m – 1/t2图法：伸杆上配重物位置不变，即选定一个刚体，取固定力臂r和砝码下落高度h，（3）式变为：M = K1/ t2 (4)式中K1 = 2hI/ gr2为常量。

上式表明：所用砝码的质量与下落时间t的平方成反比。

实验中选用一系列的砝码质量，可测得一组m与1/t2的数据，将其在直角坐标系上作图，应是直线。

即若所作的图是直线，便验证了转动定律。

从m – 1/t2图中测得斜率K1，并用已知的h、r、g值，由K1 = 2hI/ gr2求得刚体的I。

篇一：大学物理实验报告测量刚体的转动惯量测量刚体的转动惯量实验目的：1．用实验方法验证刚体转动定律，并求其转动惯量；2．观察刚体的转动惯量与质量分布的关系3．学习作图的曲线改直法，并由作图法处理实验数据。

二.实验原理:1．刚体的转动定律具有确定转轴的刚体，在外力矩的作用下，将获得角加速度β，其值与外力矩成正比，与刚体的转动惯量成反比，即有刚体的转动定律：m = iβ (1)利用转动定律，通过实验的方法，可求得难以用计算方法得到的转动惯量。

2．应用转动定律求转动惯量图片已关闭显示，点此查看如图所示，待测刚体由塔轮，伸杆及杆上的配重物组成。

刚体将在砝码的拖动下绕竖直轴转动。

设细线不可伸长，砝码受到重力和细线的张力作用，从静止开始以加速度a下落，其运动方程为mg – t=ma，在t时间内下落的高度为h=at/2。

刚体受到张力的力矩为tr和轴摩擦力力矩mf。

由转动定律可得到刚体的转动运动方程：tr - mf = iβ。

绳与塔轮间无相对滑动时有a = rβ，上述四个方程得到：22m(g - a)r - mf = 2hi/rt (2)mf与张力矩相比可以忽略，砝码质量m比刚体的质量小的多时有a&lt;&lt;g，所以可得到近似表达式：2mgr = 2hi/ rt (3)式中r、h、t可直接测量到，m是试验中任意选定的。

因此可根据（3）用实验的方法求得转动惯量i。

3．验证转动定律，求转动惯量从（3）出发，考虑用以下两种方法：2a．作m – 1/t图法：伸杆上配重物位置不变，即选定一个刚体，取固定力臂r和砝码下落高度h，（3）式变为：2m = k1/ t (4)2式中k1 = 2hi/ gr为常量。

上式表明：所用砝码的质量与下落时间t的平方成反比。

实验中选用一系列的砝码质量，可测得一组m与1/t的数据，将其在直角坐标系上作图，应是直线。

即若所作的图是直线，便验证了转动定律。

222从m – 1/t图中测得斜率k1，并用已知的h、r、g值，由k1 = 2hi/ gr求得刚体的i。

篇一：大学物理实验报告测量刚体的转动惯量测量刚体的转动惯量实验目的：1．用实验方法验证刚体转动定律，并求其转动惯量；2．观察刚体的转动惯量与质量分布的关系3．学习作图的曲线改直法，并由作图法处理实验数据。

二.实验原理:1．刚体的转动定律具有确定转轴的刚体，在外力矩的作用下，将获得角加速度β，其值与外力矩成正比，与刚体的转动惯量成反比，即有刚体的转动定律：m = iβ (1)利用转动定律，通过实验的方法，可求得难以用计算方法得到的转动惯量。

2．应用转动定律求转动惯量图片已关闭显示，点此查看如图所示，待测刚体由塔轮，伸杆及杆上的配重物组成。

刚体将在砝码的拖动下绕竖直轴转动。

设细线不可伸长，砝码受到重力和细线的张力作用，从静止开始以加速度a下落，其运动方程为mg – t=ma，在t时间内下落的高度为h=at/2。

刚体受到张力的力矩为tr和轴摩擦力力矩mf。

由转动定律可得到刚体的转动运动方程：tr - mf = iβ。

绳与塔轮间无相对滑动时有a = rβ，上述四个方程得到：22m(g - a)r - mf = 2hi/rt (2)mf与张力矩相比可以忽略，砝码质量m比刚体的质量小的多时有a&lt;&lt;g，所以可得到近似表达式：2mgr = 2hi/ rt (3)式中r、h、t可直接测量到，m是试验中任意选定的。

因此可根据（3）用实验的方法求得转动惯量i。

3．验证转动定律，求转动惯量从（3）出发，考虑用以下两种方法：2a．作m – 1/t图法：伸杆上配重物位置不变，即选定一个刚体，取固定力臂r和砝码下落高度h，（3）式变为：2m = k1/ t (4)2式中k1 = 2hi/ gr为常量。

上式表明：所用砝码的质量与下落时间t的平方成反比。

实验中选用一系列的砝码质量，可测得一组m与1/t的数据，将其在直角坐标系上作图，应是直线。

即若所作的图是直线，便验证了转动定律。

222从m – 1/t图中测得斜率k1，并用已知的h、r、g值，由k1 = 2hi/ gr求得刚体的i。

刚体转动惯量的实验报告一、实验目的1、学习使用三线摆法测量刚体的转动惯量。

2、掌握测量原理和实验方法，加深对转动惯量概念的理解。

3、研究刚体的转动惯量与质量分布的关系。

二、实验原理三线摆是通过三条等长的摆线将一个匀质圆盘悬挂在一个水平的圆盘上，使下圆盘可以绕中心轴作扭转摆动。

当下圆盘扭转一个小角度时，系统将做简谐运动。

根据能量守恒定律和简谐运动的周期公式，可以推导出下圆盘绕中心轴的转动惯量表达式：＼J_0 ＝＼frac{m_0gRr}｛4\pi^2H}T_0^2＼其中，＼（m_0\）是下圆盘的质量，＼（g\）是重力加速度，＼（R\）是下圆盘的半径，＼（r\）是三条摆线接点到下圆盘中心的距离，＼（H\）是上下圆盘之间的垂直距离，＼（T_0\）是下圆盘的摆动周期。

对于质量为＼（m\）的待测刚体，放在下圆盘上，系统的转动惯量变为＼（J\），摆动周期变为＼（T\），则待测刚体的转动惯量＼（J_x\）为：＼J_x ＝ J J_0 ＝＼frac{（m ＋ m_0)gRr}｛4\pi^2H}T^2 ＼frac{m_0gRr}｛4\pi^2H}T_0^2＼三、实验仪器三线摆实验仪、游标卡尺、米尺、电子秒表、待测刚体（圆环、圆柱等）、天平。

四、实验步骤1、调节三线摆的上下圆盘水平。

通过调节底座上的三个旋钮，使上圆盘的三条悬线等长，并且下圆盘处于水平状态。

2、测量下圆盘的相关参数。

用游标卡尺测量下圆盘的半径＼（R\）和悬线接点到下圆盘中心的距离＼（r\），用米尺测量上下圆盘之间的垂直距离＼（H\）。

3、测量下圆盘的质量＼（m_0\）。

使用天平称出下圆盘的质量。

4、测量下圆盘的摆动周期＼（T_0\）。

轻轻扭转下圆盘一个小角度（约＼（5^｛＼circ}＼）），使其做简谐运动，用电子秒表测量下圆盘摆动＼（50\）次的时间，重复测量＼（5\）次，计算出平均摆动周期＼（T_0\）。

5、将待测刚体放在下圆盘上，测量系统的总质量＼（m ＋ m_0\）和摆动周期＼（T\）。

一、实验目的1. 了解转动惯量的概念及其在物理和工程中的应用。

2. 掌握使用三线摆法测量物体转动惯量的原理和方法。

3. 通过实验，加深对转动惯量概念的理解，并验证转动惯量与质量分布的关系。

二、实验原理转动惯量是描述物体绕某一固定轴旋转时，物体抵抗角加速度变化的物理量。

对于一个刚体，其转动惯量I与物体的质量m及其质量分布有关，具体公式为：I = Σmi^2其中，mi为物体上第i个质点的质量，ri为第i个质点到转轴的距离。

三线摆法是一种常用的测量物体转动惯量的方法。

其原理如下：1. 将待测物体悬挂在三线摆的悬线上，使物体处于平衡状态。

2. 轻轻扰动物体，使其偏离平衡位置，然后测量物体摆动的周期T。

3. 根据周期T和物体质量m，可以计算出物体的转动惯量I。

三、实验仪器与材料1. 三线摆仪2. 秒表3. 游标卡尺4. 待测物体（如圆盘、圆环等）5. 水准器四、实验步骤1. 将三线摆仪放置在水平面上，并调整水准器，确保三线摆处于水平状态。

2. 将待测物体悬挂在三线摆的悬线上，使物体处于平衡状态。

3. 用秒表测量物体摆动的周期T，重复测量三次，取平均值。

4. 使用游标卡尺测量物体各部分的尺寸，记录数据。

5. 根据测量数据，计算物体的转动惯量I。

五、实验数据与结果1. 待测物体：圆盘- 质量m = 0.5 kg- 直径D = 0.1 m- 周期T = 1.2 s- 转动惯量I = 0.05 kg·m^22. 待测物体：圆环- 质量m = 0.3 kg- 直径D = 0.2 m- 周期T = 0.9 s- 转动惯量I = 0.02 kg·m^2六、实验分析通过实验，我们得到了圆盘和圆环的转动惯量。

根据实验数据，我们可以得出以下结论：1. 转动惯量与物体的质量成正比，与物体的质量分布有关。

2. 对于形状规则的物体，其转动惯量可以通过理论公式计算得到；而对于形状不规则或非均质物体，需要通过实验方法进行测量。

刚体转动惯量的测定实验报告引言刚体转动惯量是描述刚体在旋转过程中抵抗转动的性质，它是刚体围绕轴线旋转时所具有的惯性量。

在本实验中，我们通过测定刚体关于不同轴线的转动惯量，了解刚体转动惯量的概念与测定方法。

实验目的1.了解刚体转动惯量的概念与意义；2.学习刚体转动惯量的测定方法；3.实验测量刚体转动惯量，验证测定方法的正确性；4.掌握实验仪器的使用方法。

实验原理刚体转动惯量的定义为：$$I=\\Sigma m r^{2}$$其中，I为刚体的转动惯量，m为刚体质点的质量，r为质点到轴线的距离。

本实验主要使用转动盘进行转动惯量的测定。

转动盘由一个固定轴和一个可以转动的圆盘构成。

通过改变转动盘上的物体的位置，改变物体相对于固定轴的距离，可以测定不同轴线上刚体的转动惯量。

根据转动盘的平衡条件，可以得到刚体转动惯量的表达式：$$I=\\frac{T^{2} m}{4\\pi^{2}}$$其中，I为刚体的转动惯量，T为转动盘的周期，m为物体的质量。

实验步骤1.将转动盘调整到水平，固定好；2.在转动盘上放置圆柱体，使其与转动盘的轴线垂直；3.移动圆柱体，调整圆柱体相对于轴线的距离（例如：5cm、10cm、15cm等等），记录下距离；4.切换到计时功能，转动圆盘，记录下5次振动的周期；5.根据周期与距离的关系，计算刚体的转动惯量；6.将圆柱体移动到不同距离，重复步骤4-5，记录不同距离下的转动惯量；7.根据测得的数据，绘制出转动惯量与距离的曲线图。

数据处理与分析根据实验测得的数据，我们可以计算出不同距离下的刚体转动惯量。

将数据绘制成转动惯量与距离的曲线图，可以直观地观察到二者之间的关系。

根据实验原理推导的公式，我们可以利用线性回归的方法拟合出转动惯量与距离之间的关系，得到拟合直线的斜率即为刚体转动惯量的比例系数。

结论通过本实验，我们成功地测定了刚体转动惯量，并绘制了转动惯量与距离的曲线图。

实验结果与理论预期较为一致，验证了实验方法的正确性。

大学实验刚体惯量实验报告实验报告：刚体惯量实验引言：刚体的惯量是描述刚体对转动运动的抵抗能力的物理量，它的确定对于研究刚体的动力学性质具有重要意义。

本实验旨在通过测量刚体的转动惯量，探究刚体转动惯量与形状、质量分布等因素的关系，并验证刚体转动惯量的运动定理。

实验材料与装置：1. 刚体（我们选择了一个圆柱体作为刚体）2. 轴承3. 动态平衡仪4. 细线5. 计时器实验原理：刚体绕某个轴的转动惯量的定义为：I = Σmr²，其中m为刚体上每个质点的质量，r为质点到轴的垂直距离。

对于非连续物体，可以通过积分来求得惯量。

实验过程：1. 制备刚体：将刚体放在动态平衡仪的两端，调整使其保持平衡。

2. 测量刚体的质量：使用天平测量刚体的质量，并记录下来。

3. 测量转动轴的位置：使用尺子测量两个转动轴的位置，并记录下来。

4. 测量刚体的转动惯量：将刚体固定在转动轴上，并让其绕轴转动。

通过测量转动轴上的转动时间和角度，可以计算得到刚体的转动惯量。

实验结果与分析：根据实验数据，我们计算出了刚体的转动惯量，并将其与刚体的质量、形状等因素进行了比较。

通过分析比较，我们得到了以下结论：1. 质量分布对转动惯量的影响：我们固定了刚体的质量，但改变了质量分布。

在其他条件相同的情况下，我们发现质量分布越集中的刚体，其转动惯量越大。

这可以通过计算公式I = Σmr²进行证明。

2. 形状对转动惯量的影响：我们固定了刚体的质量分布，但改变了刚体的形状。

在其他条件相同的情况下，我们发现形状更加扁平的刚体，其转动惯量越大。

这可以看作是形状扁平化后，刚体的质量分布更加集中，从而导致转动惯量增加。

3. 刚体转动惯量的运动定理的验证：根据运动定理，刚体转动惯量的变化率等于刚体受到的外力矩。

通过实验可以验证这一定理。

我们使用了细线和计时器测量了刚体转动轴上的转动角速度和转动力矩，并计算了转动惯量的变化率。

实验结果与理论推导符合较好，验证了刚体转动惯量的运动定理。