下载文档原格式
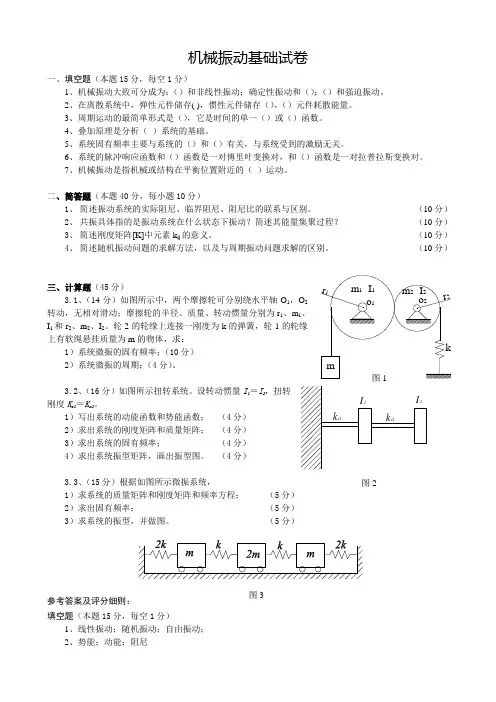
机械振动基础试卷一、填空题（本题15分，每空1分）1、机械振动大致可分成为：（）和非线性振动；确定性振动和（）；（）和强迫振动。
2、在离散系统中，弹性元件储存( )，惯性元件储存（），（）元件耗散能量。
3、周期运动的最简单形式是（），它是时间的单一（）或（）函数。
4、叠加原理是分析（ ）系统的基础。
5、系统固有频率主要与系统的（）和（）有关，与系统受到的激励无关。
6、系统的脉冲响应函数和（）函数是一对傅里叶变换对，和（）函数是一对拉普拉斯变换对。
7、机械振动是指机械或结构在平衡位置附近的（ ）运动。
二、简答题（本题40分，每小题10分）1、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
（10分）2、 共振具体指的是振动系统在什么状态下振动？简述其能量集聚过程？ （10分）3、 简述刚度矩阵[K]中元素k ij 的意义。
（10分）4、 简述随机振动问题的求解方法，以及与周期振动问题求解的区别。
（10分）三、计算题（45分） 3.1、（14分）如图所示中，两个摩擦轮可分别绕水平轴O 1，转动，无相对滑动；摩擦轮的半径、质量、转动惯量分别为r 1、m I 1和r 2、m 2、I 2。
轮2的轮缘上连接一刚度为k 的弹簧，轮1上有软绳悬挂质量为m 的物体，求： 1）系统微振的固有频率；（10分）2）系统微振的周期；（4分）。
3.2、（16分）如图所示扭转系统。
设转动惯量I 1＝I 2，扭转刚度K r1＝K r2。
1）写出系统的动能函数和势能函数； （4分） 2）求出系统的刚度矩阵和质量矩阵； （4分）3）求出系统的固有频率； （4分）4）求出系统振型矩阵，画出振型图。
（4分）3.3、（15分）根据如图所示微振系统， 1）求系统的质量矩阵和刚度矩阵和频率方程； （5分）2）求出固有频率； （5分）3）求系统的振型，并做图。
（5分）参考答案及评分细则：填空题（本题15分，每空1分）1、线性振动；随机振动；自由振动；2、势能；动能；阻尼图2图33、简谐运动；正弦；余弦4、线性5、刚度；质量6、频响函数；传递函数7、往复弹性简答题（本题40分，每小题10分）5、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
机械振动试题(含答案)一、机械振动选择题1．沿某一电场方向建立x轴，电场仅分布在-d≤x≤d的区间内，其电场场强与坐标x的关系如图所示。
规定沿+x轴方向为电场强度的正方向，x=0处电势为零。
一质量为m、电荷量为+q的带点粒子只在电场力作用下，沿x轴做周期性运动。
以下说法正确的是（）A．粒子沿x轴做简谐运动B．粒子在x=-d处的电势能为12-qE0dC．动能与电势能之和的最大值是qE0dD．一个周期内，在x>0区域的运动时间t≤2mdqE2．如图所示的单摆，摆球a向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b发生碰撞，并粘在一起，且摆动平面不便．已知碰撞前a球摆动的最高点与最低点的高度差为h，摆动的周期为T，a球质量是b球质量的5倍，碰撞前a球在最低点的速度是b球速度的一半．则碰撞后A56TB65TC．摆球最高点与最低点的高度差为0.3hD．摆球最高点与最低点的高度差为0.25h3．下列说法中不正确的是( )A．将单摆从地球赤道移到南(北)极,振动频率将变大B．将单摆从地面移至距地面高度为地球半径的高度时,则其振动周期将变到原来的2倍C ．将单摆移至绕地球运转的人造卫星中,其振动频率将不变D ．在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变4．如图为某简谐运动图象，若t ＝0时，质点正经过O 点向b 运动，则下列说法正确的是( )A ．质点在0.7 s 时的位移方向向左，且正在远离平衡位置运动B ．质点在1.5 s 时的位移最大，方向向左，在1.75 s 时，位移为1 cmC ．质点在1.2 s 到1.4 s 过程中，质点的位移在增加，方向向左D ．质点从1.6 s 到1.8 s 时间内，质点的位移正在增大，方向向右5．甲、乙两单摆的振动图像如图所示，由图像可知A ．甲、乙两单摆的周期之比是3:2B ．甲、乙两单摆的摆长之比是2:3C ．t b 时刻甲、乙两摆球的速度相同D ．t a 时刻甲、乙两单摆的摆角不等 6．如图所示，质量为m 的物块放置在质量为M 的木板上，木板与弹簧相连，它们一起在光滑水平面上做简谐振动，周期为T ，振动过程中m 、M 之间无相对运动，设弹簧的劲度系数为k 、物块和木板之间滑动摩擦因数为μ，A ．若t 时刻和()t t +∆时刻物块受到的摩擦力大小相等，方向相反，则t ∆一定等于2T 的整数倍 B ．若2T t ∆=，则在t 时刻和()t t +∆时刻弹簧的长度一定相同 C ．研究木板的运动，弹簧弹力充当了木板做简谐运动的回复力 D ．当整体离开平衡位置的位移为x 时，物块与木板间的摩擦力大小等于m kx m M+ 7．如图所示，将小球甲、乙、丙（都可视为质点）分别从A 、B 、C 三点由静止同时释放，最后都到达竖直面内圆弧的最低点D ，其中甲是从圆心A 出发做自由落体运动，乙沿弦轨道从一端B 到达最低点D ，丙沿圆弧轨道从C 点运动到D ，且C 点很靠近D 点，如果忽略一切摩擦阻力，那么下列判断正确的是（ ）A ．丙球最先到达D 点，乙球最后到达D 点B ．甲球最先到达D 点，乙球最后到达D 点C ．甲球最先到达D 点，丙球最后到达D 点D ．甲球最先到达D 点，无法判断哪个球最后到达D 点8．如图所示的弹簧振子在A 、B 之间做简谐运动，O 为平衡位置，则下列说法不正确的是（ ）A ．振子的位移增大的过程中，弹力做负功B ．振子的速度增大的过程中，弹力做正功C ．振子的加速度增大的过程中，弹力做正功D ．振子从O 点出发到再次回到O 点的过程中，弹力做的总功为零9．如图所示，在一条张紧的绳子上悬挂A 、B 、C 三个单摆，摆长分别为L 1、L 2、L 3，且L 1＜L 2＜L 3，现将A 拉起一较小角度后释放，已知当地重力加速度为g ，对释放A 之后较短时间内的运动，以下说法正确的是（ ）A ．C 的振幅比B 的大B ．B 和C 的振幅相等 C ．B 的周期为2L gD ．C 的周期为1L g10．如图所示，PQ 为—竖直弹簧振子振动路径上的两点，振子经过P 点时的加速度大小为6m/s 2，方向指向Q 点；当振子经过Q 点时，加速度的大小为8m/s 2，方向指向P 点，若PQ 之间的距离为14cm ，已知振子的质量为lkg ，则以下说法正确的是（ ）A．振子经过P点时所受的合力比经过Q点时所受的合力大B．该弹簧振子的平衡位置在P点正下方7cm处C．振子经过P点时的速度比经过Q点时的速度大D．该弹簧振子的振幅一定为8cm11．如图所示，在水平地面上，有两个用轻质弹簧相连的物块A和B，它们的质量均为m，弹簧的劲度系数为k，现将一个质量也为m的物体C从A的正上方一定高度处由静止释放，C和A相碰后立即粘在一起，之后在竖直方向做简谐运动。
机械振动试题(含答案)(2)一、机械振动 选择题1．下列说法中正确的有（ ）A ．简谐运动的回复力是按效果命名的力B ．振动图像描述的是振动质点的轨迹C ．当驱动力的频率等于受迫振动系统的固有频率时，受迫振动的振幅最大D ．两个简谐运动：x 1＝4sin (100πt ＋3π) cm 和x 2＝5sin (100πt ＋6π) cm ，它们的相位差恒定2．如图所示，质量为A m 的物块A 用不可伸长的细绳吊着，在A 的下方用弹簧连着质量为B m 的物块B ，开始时静止不动。
现在B 上施加一个竖直向下的力F ，缓慢拉动B 使之向下运动一段距离后静止，弹簧始终在弹性限度内，希望撤去力F 后，B 向上运动并能顶起A ，则力F 的最小值是（ ）A ．(A m +B m )gB ．(A m +2B m )gC ．2(A m +B m )gD ．(2A m +B m )g3．如图所示的单摆，摆球a 向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b 发生碰撞，并粘在一起，且摆动平面不便．已知碰撞前a 球摆动的最高点与最低点的高度差为h ，摆动的周期为T ，a 球质量是b 球质量的5倍，碰撞前a 球在最低点的速度是b 球速度的一半．则碰撞后A 56T B 65T C ．摆球最高点与最低点的高度差为0.3hD ．摆球最高点与最低点的高度差为0.25h4．如图所示，固定的光滑圆弧形轨道半径R ＝0.2m ，B 是轨道的最低点，在轨道上的A 点（弧AB 所对的圆心角小于10°）和轨道的圆心O 处各有一可视为质点的静止小球，若将它们同时由静止开始释放，则（ ）A ．两小球同时到达B 点B ．A 点释放的小球先到达B 点C ．O 点释放的小球先到达B 点D ．不能确定5．如图甲所示，一个单摆做小角度摆动，从某次摆球由左向右通过平衡位置时开始计时，相对平衡位置的位移x 随时间t 变化的图象如图乙所示．不计空气阻力，g 取10m/s 2．对于这个单摆的振动过程，下列说法中不正确的是（ ）A ．单摆的位移x 随时间t 变化的关系式为8sin(π)cm x t =B ．单摆的摆长约为1.0mC ．从 2.5s t =到 3.0s t =的过程中，摆球的重力势能逐渐增大D ．从 2.5s t =到 3.0s t =的过程中，摆球所受回复力逐渐减小6．图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子，图(乙)为这个弹簧振子的振动图象，由图可知下列说法中正确的是( )A ．在t =0.2s 时，弹簧振子可能运动到B 位置B ．在t =0.1s 与t =0.3s 两个时刻，弹簧振子的速度相同C ．从t =0到t =0.2s 的时间内，弹簧振子的动能持续地增加D ．在t =0.2s 与t =0.6s 两个时刻，弹簧振子的加速度相同7．如图所示，物块M 与m 叠放在一起，以O 为平衡位置，在ab 之间做简谐振动，两者始终保持相对静止，取向右为正方向，其振动的位移x 随时间t 的变化图像如图，则下列说法正确的是（ ）A ．在1~2T t 时间内，物块m 的速度和所受摩擦力都沿负方向，且都在增大 B ．从1t 时刻开始计时，接下来4T 内，两物块通过的路程为A C ．在某段时间内，两物块速度增大时，加速度可能增大，也可能减小D ．两物块运动到最大位移处时，若轻轻取走m ，则M 的振幅不变 8．装有一定量液体的玻璃管竖直漂浮在水中，水面足够大，如图甲所示。
机械振动考试题和答案一、单项选择题（每题2分，共20分）1. 简谐运动的振动周期与振幅无关，与（）有关。
A. 质量B. 频率C. 弹簧常数D. 初始条件答案：C2. 阻尼振动中，振幅逐渐减小的原因是（）。
A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：C3. 两个简谐运动合成时，合成运动的频率等于（）。
A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：D4. 受迫振动的频率与（）有关。
A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：A5. 阻尼振动中，阻尼系数越大，振动周期（）。
A. 越大B. 越小C. 不变D. 无法确定答案：B6. 受迫振动中，当驱动力频率接近系统固有频率时，会发生（）。
A. 共振B. 反共振C. 振动增强D. 振动减弱答案：A7. 简谐运动的振动周期与（）成正比。
B. 频率C. 弹簧常数D. 质量的平方根答案：D8. 阻尼振动中，阻尼系数越小，振动周期（）。
A. 越大B. 越小C. 不变D. 无法确定答案：C9. 受迫振动中，当驱动力频率等于系统固有频率时，振动的振幅（）。
A. 最小C. 不变D. 无法确定答案：B10. 简谐运动的振动周期与（）无关。
A. 质量B. 频率C. 弹簧常数D. 初始条件答案：D二、多项选择题（每题3分，共15分）11. 简谐运动的振动周期与以下哪些因素有关？（）A. 质量C. 弹簧常数D. 初始条件答案：AC12. 阻尼振动中，振幅逐渐减小的原因包括（）。
A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：CD13. 两个简谐运动合成时，合成运动的频率等于以下哪些选项？（）A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：BD14. 受迫振动的频率与以下哪些因素有关？（）A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：AB15. 阻尼振动中，阻尼系数越大，振动周期的变化情况是（）。
机械振动期末考试题及答案一、选择题（每题2分，共20分）1. 简谐振动的周期与振幅无关，这是由哪个定律决定的？A. 牛顿第二定律B. 牛顿第三定律C. 胡克定律D. 能量守恒定律答案：C2. 下列哪个不是阻尼振动的特点？A. 振幅逐渐减小B. 频率逐渐增大C. 能量逐渐减少D. 振幅随时间呈指数衰减答案：B3. 一个物体做自由振动，若其振幅逐渐减小，这表明振动受到了：A. 阻尼B. 共振C. 强迫振动D. 非线性振动答案：A4. 质点的振动方程为 \( y = A \sin(\omega t + \phi) \)，其中\( \omega \) 表示：A. 振幅B. 频率C. 角频率D. 相位答案：C5. 弹簧振子的振动周期与下列哪个参数无关？A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始相位答案：C6. 阻尼振动的振幅随时间呈指数衰减，其衰减速率与什么有关？A. 振幅大小B. 阻尼系数C. 振动频率D. 振动周期答案：B7. 以下哪个不是振动系统的自由度？A. 1B. 2C. 3D. 无穷大答案：D8. 共振现象发生在以下哪种情况下？A. 系统固有频率等于外部激励频率B. 系统阻尼系数最大C. 系统振幅最小D. 系统能量最大答案：A9. 以下哪个是简谐振动的特有现象？A. 振幅不变B. 频率不变C. 能量不变D. 周期不变答案：A10. 一个物体在水平面上做简谐振动，其振动能量主要由以下哪两个因素决定？A. 振幅和频率B. 振幅和阻尼系数C. 阻尼系数和频率D. 振幅和劲度系数答案：A二、填空题（每空2分，共20分）11. 简谐振动的周期公式为 \( T = \frac{2\pi}{\omega} \)，其中\( \omega \) 为________。
答案：角频率12. 当外部激励频率接近系统的________时，系统将产生共振现象。
答案：固有频率13. 阻尼振动的振幅随时间的变化规律可表示为 \( A(t) = A_0 e^{-\beta t} \)，其中 \( \beta \) 为________。
机械振动试题(含答案)(1)一、机械振动 选择题1．沿某一电场方向建立x 轴，电场仅分布在-d ≤x ≤d 的区间内，其电场场强与坐标x 的关系如图所示。
规定沿+x 轴方向为电场强度的正方向，x =0处电势为零。
一质量为m 、电荷量为+q 的带点粒子只在电场力作用下，沿x 轴做周期性运动。
以下说法正确的是（ ）A ．粒子沿x 轴做简谐运动B ．粒子在x =-d 处的电势能为12-qE 0d C ．动能与电势能之和的最大值是qE 0d D ．一个周期内，在x >0区域的运动时间t ≤20md qE 2．如图所示,甲、乙两物块在两根相同的弹簧和一根张紧的细线作用下静止在光滑水平面上,已知甲的质量小于乙的质量．当细线突然断开斤两物块都开始做简谐运动,在运动过程中（ ）A ．甲的最大速度大于乙的最大速度B ．甲的最大速度小于乙的最大速度C ．甲的振幅大于乙的振幅D ．甲的振幅小于乙的振幅3．如图所示，弹簧的一端固定，另一端与质量为2m 的物体B 相连，质量为1m 的物体A 放在B 上，212m m =．A 、B 两物体一起在光滑水平面上的N 、N '之间做简谐运动，运动过程中A 、B 之间无相对运动，O 是平衡位置．已知当两物体运动到N '时，弹簧的弹性势能为p E ，则它们由N '运动到O 的过程中，摩擦力对A 所做的功等于（ ）A ．p EB ．12p EC ．13p E D ．14p E 4．如图所示是扬声器纸盆中心做简谐运动的振动图象，下列判断正确的是A ．t =2×10-3s 时刻纸盆中心的速度最大B ．t =3×10-3s 时刻纸盆中心的加速度最大C ．在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D ．纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt （m ）5．如图1所示，轻弹簧上端固定，下端悬吊一个钢球，把钢球从平衡位置向下拉下一段距离A ，由静止释放。
大学机械振动考试题目及答案一、选择题（每题2分，共10分）1. 在简谐振动中，振幅与振动的能量关系是（）。
A. 无关B. 成正比C. 成反比D. 振幅越大，能量越小答案：B2. 下列哪个不是机械振动系统的自由度？（）。
A. 转动B. 平动C. 振动D. 形变答案：C3. 一个单自由度系统在受到初始条件激励后，其振动形式是（）。
A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案：D4. 在阻尼振动中，如果阻尼系数增加，振动的振幅将（）。
A. 增加B. 不变C. 减小D. 先增加后减小答案：C5. 对于一个二自由度振动系统，其振动模态数量是（）。
A. 1B. 2C. 3D. 4答案：B二、填空题（每题2分，共10分）6. 一个物体做自由振动时，其频率称为______。
答案：固有频率7. 当外力的频率与系统的固有频率相等时，系统发生的振动称为______。
答案：共振8. 阻尼力与速度成正比的阻尼称为______阻尼。
答案：线性9. 振动系统的动态响应可以通过______分析法求解。
答案：傅里叶10. 在转子动力学中，临界转速是指转子发生______振动的转速。
答案：自激三、简答题（每题5分，共20分）11. 简述什么是简谐振动，并说明其运动方程的形式。
答案：简谐振动是一种周期性的振动，其加速度与位移成正比，且方向相反。
在数学上，简谐振动的运动方程可以表示为：x(t) = A * cos(ωt + φ)其中，A 是振幅，ω 是角频率，t 是时间，φ 是初相位。
12. 解释什么是阻尼振动，并说明其特点。
答案：阻尼振动是指在振动系统中存在能量耗散，导致振幅随时间逐渐减小的振动。
其特点包括振幅逐渐衰减，振动频率可能会随着振幅的减小而发生变化，且阻尼力通常与振动速度成正比。
13. 描述什么是受迫振动，并给出其稳态响应的条件。
答案：受迫振动是指系统在周期性外力作用下的振动。
当外力的频率接近系统的固有频率时，系统将发生共振，此时振幅会显著增大。
机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体，在弹簧下端受到一个向下的力2 sin(10t) N，其中t为时间（秒）。
求物体的振动方程。
根据牛顿第二定律，可以得到物体的振动方程为：m * x'' + k * x = F(t)其中，m是物体的质量，x是物体的位移，x''是位移对时间的二阶导数，k是弹簧的常数，F(t)是作用在物体上的外力。
根据题目中给出的数据，代入上述公式，我们可以得到：0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。
2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动，已知质点的质量为0.5 kg。
求质点的角频率和振动周期。
根据振动方程的形式，我们可以知道物体的振动频率和周期与力的形式有关。
在这个题目中，我们可以看出力的形式为cos(3t)，它是一个正弦函数。
如果将cos(3t)函数展开，我们可以得到下面的表达式：F(t) = a cos(wt)其中，a是振幅，w是角频率。
根据题目中给出的数据，我们可以得到：a = 0.1 N，w = 3 rad/s由于振动的频率与角频率之间是有关联的，振动的周期T可以表示为：T = 2π/w代入上述数据，我们可以得到：T = 2π/3 s这就是质点的振动周期。
3. 一个质点质量为0.3 kg，在一竖直方向上的弹簧中振动，弹簧的劲度系数为2000 N/m。
当质点受到一个外力F(t) = 0.5 cos(5t) N时，求质点的振动方程。
根据题目中给出的数据，我们可以得到：m = 0.3 kg，k = 2000 N/m，F(t) = 0.5 cos(5t)代入振动方程的一般形式，我们可以得到：0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。
机械振动试题及答案⼀、填空题1、机械振动按不同情况进⾏分类⼤致可分成（线性振动）和⾮线性振动；确定性振动和（随机振动）；（⾃由振动）和强迫振动，连续振动和离散系统。
2、（弹性元件）元件、（惯性元件）元件、（阻尼元件）元件是离散振动系统的三个最基本元素。
3、在振动系统中，弹性元件存储（势能）、惯性元件存储（动能）、（阻尼元件）元件耗散能量。
4、系统固有频率主要与系统的（质量）和（刚度）有关，与系统受到的激励⽆关。
5、研究随机振动的⽅法是（数理统计），⼯程上常见的随机过程的数字特征有：（均值）（⽅差）（⾃相关函数）和（互相关函数）。
6、周期运动的最简单形式是（简谐运动），它是时间的单⼀（正弦）或（余弦）函数。
7、单⾃由度系统⽆阻尼⾃由振动的频率只与（质量）和（刚度）有关，与系统受到的激励⽆关。
8、简谐激励下单⾃由度系统的响应由（瞬态响应）和（稳态响应）组成。
9、⼯程上分析随机振动⽤（数学统计）⽅法，描述随机过程的最基本的数字特征包括均值、⽅差、（⾃相关函数）和（互相关函数）。
10、机械振动是指机械或结构在（静平衡）附近的（弹性往复）运动。
11、单位脉冲⼒激励下，系统的脉冲响应函数和系统的（频响函数）函数是⼀对傅⾥叶变换对，和系统的（传递函数）函数是⼀对拉普拉斯变换对。
12、叠加原理是分析（线性振动系统）和（振动性质）的基础。
⼆、简答题1、什么是机械振动？振动发⽣的内在原因是什么？外在原因是什么？答：机械振动是指机械或结构在它的静平衡位置附近的往复弹性运动。
振动发⽣的内在原因是机械或结构具有在振动时储存动能和势能，⽽且释放动能和势能并能使动能和势能相互转换的能⼒。
外在原因是由于外界对系统的激励或者作⽤。
2、机械振动系统的固有频率与哪些因素有关？关系如何？答：机械振动系统的固有频率与系统的质量矩阵、刚度矩阵和阻尼有关。
质量越⼤，固有频率越低；刚度越⼤，固有频率越⾼；阻尼越⼤，固有频率越低。
3、从能量、运动、共振等⾓度简述阻尼对单⾃由度系统振动的影响。
机械振动期末试题及答案1. 选择题1.1 哪种情况下，系统的振动是简谐振动？A. 有耗尽能量的情况B. 存在非线性的力恢复系统中C. 无外部干扰D. 系统的振幅随时间而增长答案：C1.2 振动系统达到稳态的条件是：A. 初始位移为零B. 扰动力为零C. 初始速度为零D. 振幅随时间减小答案：B1.3 一个简谐振动的周期与振幅的关系是：A. 周期与振幅无关B. 周期与振幅成正比C. 周期与振幅成反比D. 周期与振幅正弦相关答案：A2. 判断题2.1 简谐振动的周期和角频率之间满足正比关系。
A. 对B. 错答案：B2.2 简谐振动的中心力是恒力。
A. 对B. 错答案：A2.3 当振动系统有阻尼情况时，振幅会随时间增大。
A. 对B. 错答案：B3. 简答题3.1 什么是简谐振动？它的特点是什么？答案：简谐振动是指振动系统在没有外力干扰的情况下，其平衡位置附近以某一频率固定幅度上下振动的现象。
它的特点包括振动周期与振幅无关，且系统的振动可由正弦或余弦函数进行描述。
3.2 请简要说明受迫振动的原理。
答案：受迫振动是指振动系统在外力作用下的振动。
外力的频率与系统的固有频率相近或相等时，会发生共振现象。
在共振时，外力的能量会以最大幅度传递给振动系统，导致振动幅度增大。
4. 计算题4.1 一个弹簧振子平衡位置附近的势能函数为U(x) = 4x^2 + 3，求振子的振动周期。
答案：根据简谐振动的势能函数表达式，势能函数为U(x) =1/2kx^2，其中k为弹簧的劲度系数。
将已知的势能函数与标准表达式进行比较，可得4x^2 = 1/2kx^2，解得k = 8。
由振动周期公式T =2π√(m/k)，代入m和k的值，可计算出振子的振动周期。
5. 算法题设计一个程序，计算一个简谐振动系统的振动频率和振幅，并将结果打印输出。
// 输入参数float k; // 弹簧的劲度系数float m; // 系统的质量// 计算振动频率float omega = sqrt(k / m);// 计算振幅float A = 1; // 假设振幅为1// 打印输出结果print("振动频率：", omega);print("振幅：", A);经过以上计算，我们可以得到一个简谐振动系统的振动频率和振幅。
动力机械强度与振动复习题（2013-05-30）1 对于叶片较长、径高比<10的级，为什么要采用变截面扭叶片？ 采用变截面是为了降低叶型截面上的离心应力。
2 常见的汽轮机叶片的叶根有哪些型式？各有什么特点？T 型叶根: 结构简单，加工方便，增大受力面积，提高承载能力，多用于短叶片，加有 凸肩的可用于中长叶片。
凸肩T 型叶根枞树型叶根: 承载截面按等强度分布，适应性好。
但加工复杂，精度要求高。
叉型叶根：强度高，适应性好。
同时加工简单，更换方便。
3 围带、拉金有几种形式，各有什么作用？围带的型式：整体围带结构型式，铆接围带结构形式 （采用围带或拉金可增加叶片刚性，）围带：增加叶片刚性，减少级内漏气损失。
降低叶片蒸汽力引起的弯应力，调整叶片频率。
拉金：增加叶片刚性，改善振动性能。
4 等截面叶片的横截面积是由哪些强度因素确定的？等截面叶片的离心拉应力与那些因素有关？等截面叶片的截面积是根据许用弯曲应力确定的，与拉伸应力无关。
等截面叶片的离心应力（材料密度，截面积，叶高，转速）5 离心力在什么情况下引起弯应力？什么是叶片的最佳安装值？等截面叶片，各截面形心的连线是一条直线。
该直线如果与离心力辐射线重合，则离心力引起的弯曲应力等于零；如果不重合，就产生弯曲应力2m C FlR ρω=变截面叶片，各截面的形心连线通常是一条空间曲线，不可能使其与离心力辐射线完全重合，因此离心力必然引起弯应力。
最佳安装值：叶片应力最大的截面中，其合成应力为最小时的安装值。
6 什么是蠕变，什么叫蠕变极限？请解释 的意义。
零件在高温和应力作用下长期工作时，虽然应力没有超过屈服极限，也会产生塑性变形，而且这种变形随时间不断增长，这种现象称为蠕变。
蠕变极限：通常把一定温度下、在一定时间间隔内引起一定数量的相对蠕变变形量的应力称为蠕变极限。
指当温度为550℃ 、蠕变速度为1X10-5%/h 对应的应力为90MPa 。
7 蠕变分哪几个阶段？什么叫持久强度极限？请解释 的意义。
蠕变分成三个阶段：1 初始阶段（AB 段）：蠕变速度由大到小，金属变形强化。
2 恒定阶段（BC 段）：蠕变速度保持不变，材料的变形强化与再结晶软化趋势达到平衡。
3 破断阶段（CD 段）：应力值由颈缩现象而增加，蠕变速度加快，直到发生断裂持久强度极限：在一定温度下，经过一定时间间隔后引起试件断裂的应力叫持久强度极限。
05550211090MN/m σ-⨯=05550210160MN/m σ=05550211090MN/m σ-⨯=05550210160MN/m σ=指当温度为550℃ 、经过105小时造成断裂的应力为160MPa 。
8 对安装带凸肩的T 型叶根的轮缘，简述其应力计算所依据的原理和计算主要步骤。
卡氏定理：构件或结构在若干外部载荷Fp1，Fp2，…，Fpn 作用下，其内部贮藏的应变能V 是载荷Fp1，Fp2，…，Fpn 的函数构件或结构的应变能对于某一个载荷的一阶偏导数，等于这一载荷的作用点处、沿着这一载荷作用方向上的位移。
其数学表达式为：9 写出气流引起的叶片周向力和轴向力的表达式，并说明影响其大小的因素。
12(,,......,)p p pn V V F F F =1212,,......,n p p pn V V V F F F ∂∂∂∆=∆=∆=∂∂∂10 叶片截面的几何特性是指哪些量？叶片截面的几何特性是指叶片的截面积、形心坐标、惯性矩、截面系数等一些和叶型几何形状和尺寸有关的数据。
11 请分别写出计算单个叶片的A型弯曲振动和B型弯曲振动的叶根和叶顶边界条件。
A型振动（叶根固定、叶顶自由）的边界条件：B型振动（叶根固定而叶顶为铰支）的边界条件：12 汽轮机中能够引起叶片振动的激振力有哪些？一、由于结构上的因素产生的激振力：1 喷嘴叶栅出口气流不均匀引起的激振力2 喷嘴组部分进气引起的激振力3 抽汽管、排气管引起的激振力4 气流通道中加强筋和肋引起的激振力二、制造安装偏差引起的激振力：1 喷嘴和叶片槽道偏差引起的激振力2 隔板中分面处喷嘴偏差引起的激振力13 等截面单个叶片弯曲振动的频率与哪些因素有关？A型振动:叶根固定、叶顶自由B型振动: 叶根固定，叶顶铰支叶片的自振频率与下列因素有关：(1)叶片的抗弯刚度(EI)。
EI越大，频率越高；(2)叶片的质量[)(Almρ=]。
越大，频率越低；(3)叶片的高度()。
增加时，叶片的质量增大，刚度减小，频率降低。
(4)叶片频率方程的根()。
14 等截面单个叶片扭转振动的频率与哪些因素有关？A 顶部自由:B 顶部有围带:15 叶片弯曲振动自振频率需要做哪些修正？一、叶根联结刚性、切力和转动惯量的影响1 叶根联结刚性影响2 切力的影响3 转动惯量的影响4 根部牢固修正系数二、温度对叶片自振频率的影响（温度升高时，弹性模量降低，刚度也就降低。
叶片自振频率减小。
）三、离心力对自振频率的影响（离心力的存在，相当于增加了叶片的刚度，因此使叶片自振频率增加。
）16 什么是调频叶片和不调频叶片？将叶片自振频率与激振力频率调开，以避免在运行中发生共振的叶片称为调频叶片；在保证安全运行的前提下，按叶片可能处于共振条件下工作来设计的叶片称作不调频叶片17 改变叶片自振频率的方法有哪些？调整叶片(叶栅)的自振频率主要是通过改变叶片的质量和刚性来实现的，常用的调频方法有：(1) 重新安装叶片，改善安装质量。
(2) 增加叶片与围带或拉金的连接牢固度。
(3) 加大拉金直径或改用空心拉金。
可以增加拉金对叶片的反弯矩。
(4) 改变成组叶片数目。
(5) 叶顶钻孔。
18 转动惯量和温度对叶片弯曲振动频率有何影响？1.惯性力矩的存在，使叶片振动系统总的惯量增加，因而使叶片的自振频率降低。
当叶片柔度小时，转动惯量影响较大。
转动惯量对高阶振动频率影响较大。
2.温度升高时，弹性模量降低，刚度也就降低。
叶片自振频率减小。
对高中压级叶片，温度较高必须修正。
19 说明能量法计算单个叶片振动固有频率所依据的原理和计算主要步骤。
原理：能量守恒定律。
若不计能量损失（忽略一切阻尼），则叶片振动过程中的总能量不变，即在某一瞬间动能T和位能U之和为常数。
计算步骤：叶片振动时最大变形曲线为Y(ξ)，ξ=x/l。
叶片作简谐振动，有运动速度：最大速度：叶片的最大动能：在分布载荷q的作用，变形功为：根据能量守恒，可得到：由此可求出自振频率。
20 叙述初参数法计算单个叶片固有频率的主要步骤。
1 分段，分配质量。
假定振动圆频率。
2 确定起始端边界条件，建立包含起始端未知数的的递推公式。
3 确定递推公式的未知数的系数（二次计算法）。
4 根据末端边界条件，判断假定圆频率是否满足---计算残值。
5 根据残值曲线，确定各阶振动圆频率。
21 转子和叶轮的结构形式有哪几种，各有何特点？1.转子按照制造工艺，分为整锻式、套装式、组合式和焊接式四种形式。
套装转子：叶轮、轴封套、联轴器等部件是分别加工后，热套在阶梯形主轴上的。
各部件与主轴之间采用过盈配合，金属的蠕变产生松动。
不宜作为高温高压汽轮机的高压转子。
整锻转子：叶轮、轴封套和联轴节等部件与主轴是由一整锻件车削而成，无热套部件，解决了高温下叶轮与主轴连接可能松动的问题，结构紧凑，强度和刚度较高。
因此整缎转子常用作大型汽轮机的高、中压转子。
组合转子：高压部分采用整锻结构，中、低压部分采用套装结构。
焊接转子：由若干实心轮盘和端轴焊接而成。
焊接转子重量轻，锻件小。
强度高，结构紧凑，转子刚性较大2.按照轮面的型线可将叶轮分成等厚度叶轮、锥形叶轮、双曲线形叶轮和等强度叶轮等。
等厚度叶轮：加工方便，轴向尺寸小，但强度较低。
锥形叶轮：不但加工方便，而且强度高，套装式叶轮几乎全是采用的这种结构形式。
双曲线形叶轮：它的重量轻，但强度不一定高，且加工较复杂，故仅用在某些汽轮机的调节级中。
等强度叶轮：这种叶轮没有中心孔，强度最高。
此种叶轮多用在盘式焊接转子或高速单级汽轮机中。
22 空心等厚度叶轮的应力与哪些因素有关，应力分布有何特点？ 222222222222222222222222(3)()8(1)(1)(316)(3)13()a i r a i a i a ara ri a i a i a ia iR R R R R R R R R R R R R R R R R R R R R θρωμσσσρωμμσ+=+--+-+----++=++-+径向应力：切向应力：在空心等厚叶轮中，径向和切向应力都有三部分组成：离心力部分、外载荷部分和内孔载荷部分。
空心等厚叶轮径向最大应力在叶轮中部，切向应力随半径减小而增大，最大载中心孔处。
23 实心等厚度叶轮的应力与哪些因素有关，应力分布有何特点？ 径向应力： 切向应力：在实心等厚叶轮中，径向和切向应力都有两部分组成：离心力部分和外载荷部分。
外载荷产生的径向应力和切向应力各处均相等，且都为 ；切向应力不小于径向应力；在叶轮中心处应力最大，而且径向、切向应力相等。
（ ：叶轮外径上的径向应力）24 什么是松动转速？与工作转速的关系是多少？松动转速n0：叶轮与轴之间产生松动现象(σri=0)的最低转速。
通常取工作转速nr 的1.2倍。
25 请推导旋转薄圆环的应力计算公式。
2222223()8313()83r a raa raR R R R θμσρωσμμσρωσμ+=-+++=-++raσraσ微元段离心力：微元段切向力：微元体径向分力平衡：代入dT 、dC 表达式： 求得圆环的应力：(薄圆环的应力只与材料密度、旋转线速度的平方有关。
对常用材料，线速度限制在400m/s 左右。
旋转圆环强度低，不适宜作高速、大直径的透平转子。
优点是重量轻、抗弯刚度大。
)26 套装叶轮的过盈量由哪些因素决定？(过盈量：在套装前，轴的半径R is 与叶轮内孔半径R id 之差∆R = R is –R id 。
)按松动转速计算过盈量:∆R = R is –R id ：过盈量，安装前轴与孔的半径差。
Vs:轴外半径相比安装前的变形量。
Vd:孔半径相比安装前的变形量。
在松动转速时，叶轮和轴的半径与径向变形之间满足： 过盈值可以用叶轮和轴的径向变形表示：1.如果不考虑叶轮和轴的温度变形，根据虎克定律，有如下关系：叶轮内孔的径向应力与轴表面的径向应力相等，即因此有22dC R dm R b Rd ωωρδθ==dT b θσδ=2sin 2d dC dT dTd θθ==2R b Rd b d θωρδθσδθ=id d is sR v R v +=+(337)R is id d sR R v v ∆=-=--()(338)()(339)id i ri i s s rs R v E Rv E θθσμσσμσ=--=--ri rs σσ=()(340)iR i s R Eθθσσ∆=--2222200220{[(1)(3)]}4(342)i i R i ri i i R R R R R E R R θρωσσμμ+∆=---++--进一步求出：2.当松动转速时ω=ω0，叶轮内孔径向应力 ，切向应力 ，此时公式可以写成：若过盈用直径表示，可写成：27 叶轮上为什么要开平衡孔？平衡孔的数目为什么一般是奇数？写出平衡孔处的最大应力的表达式。
