下载文档原格式
第一章船舶操纵基础理论通过本章的学习，要求学员概念理解正确，定义描述准确，对船舶操纵性能够正确评估，并具有测定船舶操纵性能的知识。
根据船舶操纵理论，操纵性能包括：1）机动性（旋回性能和变速运动性能）2）稳定性（航向稳定性）第一节船舶操纵运动方程为了定量地描述船舶的操纵运动，我们引入船舶操纵运动方程，用数学方法来讨论船舶的运动问题。
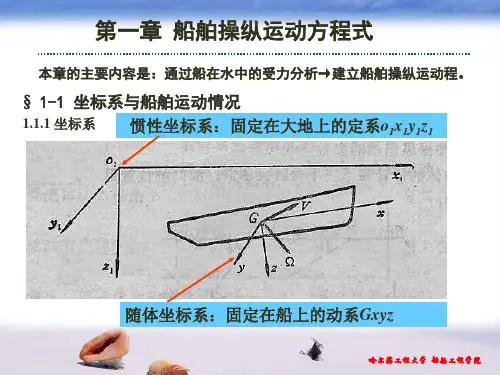
一、船舶操纵运动坐标系1．固定坐标系Ox0y0z0其原点为O，坐标分别为x0，y0，z0，由于我们仅讨论水面上的船舶运动，因此，该坐标系固定于地球表面。
作用于船舶重心的合外力在x0，y0轴上的投影分别为X0和Y0对z0轴的合外力矩为N2． 运动坐标系Gxyz其原点为点G （船舶重心），坐标分别为x ，y ，z ，该坐标系固定于船上。
这主要是为了研究船舶操纵性的方便而建立的坐标系。
x ，y ，两个坐标方向的运动速度分别为u 和v ，所受的外力分别为X 和Y ，对z 轴的转动角速度为r ，z 轴的外力矩为N 。
二、 运动方程的建立根据牛顿关于质心运动的动量定理和动量矩定理，船舶在水面的平面运动可由下列方程描述：y 0⎪⎩⎪⎨⎧===ϕZ og o og o I N y m Y x m X该式一般很难直接解出。
为了方便，将其转化为运动坐标系表示，这样可以使问题大为简化。
经过转换，得：⎪⎩⎪⎨⎧=+=-=r I N ur vm Y vr u m X Z )()( 该方程看似复杂，但各函数和变量都与固定坐标系没有关系，因此，可以使问题大为简化。
三、 水动力和水动力矩的求解对于上述方程中的水动力和水动力矩可表示为：⎪⎩⎪⎨⎧===),,,,,,(),,,,,,(),,,,,,(δδδr v u r v u f N r v ur v u f Y r v u r v u f X N Y X经过台劳级数展开，可得X ，Y ，N 对各自变量的偏导数，称为水动力导数和水动力矩导数，它们可以通过船模试验求得。
第一章船舶操纵基础理论通过本章的学习，要求学员概念理解正确，定义描述准确，对船舶操纵性能够正确评估，并具有测定船舶操纵性能的知识。
根据船舶操纵理论，操纵性能包括：1）机动性（旋回性能和变速运动性能）2）稳定性（航向稳定性）第一节船舶操纵运动方程为了定量地描述船舶的操纵运动，我们引入船舶操纵运动方程，用数学方法来讨论船舶的运动问题。
一、船舶操纵运动坐标系1．固定坐标系Ox0y0z0其原点为O，坐标分别为x0，y0，z0，由于我们仅讨论水面上的船舶运动，因此，该坐标系固定于地球表面。
作用于船舶重心的合外力在x0，y0轴上的投影分别为X0和Y0对z0轴的合外力矩为N2． 运动坐标系Gxyz其原点为点G （船舶重心），坐标分别为x ，y ，z ，该坐标系固定于船上。
这主要是为了研究船舶操纵性的方便而建立的坐标系。
x ，y ，两个坐标方向的运动速度分别为u 和v ，所受的外力分别为X 和Y ，对z 轴的转动角速度为r ，z 轴的外力矩为N 。
二、 运动方程的建立根据牛顿关于质心运动的动量定理和动量矩定理，船舶在水面的平面运动可由下列方程描述：y 0⎪⎩⎪⎨⎧===ϕZ og o og o I N y m Y x m X该式一般很难直接解出。
为了方便，将其转化为运动坐标系表示，这样可以使问题大为简化。
经过转换，得：⎪⎩⎪⎨⎧=+=-=r I N ur vm Y vr u m X Z )()( 该方程看似复杂，但各函数和变量都与固定坐标系没有关系，因此，可以使问题大为简化。
三、 水动力和水动力矩的求解对于上述方程中的水动力和水动力矩可表示为：⎪⎩⎪⎨⎧===),,,,,,(),,,,,,(),,,,,,(δδδr v u r v u f N r v ur v u f Y r v u r v u f X N Y X经过台劳级数展开，可得X ，Y ，N 对各自变量的偏导数，称为水动力导数和水动力矩导数，它们可以通过船模试验求得。
第一章船舶操纵基础理论通过本章的学习，要求学员概念理解正确，定义描述准确，对船舶操纵性能够正确评估，并具有测定船舶操纵性能的知识。
根据船舶操纵理论，操纵性能包括：1）机动性（旋回性能和变速运动性能）2）稳定性（航向稳定性）第一节船舶操纵运动方程为了定量地描述船舶的操纵运动，我们引入船舶操纵运动方程，用数学方法来讨论船舶的运动问题。
一、船舶操纵运动坐标系1．固定坐标系Ox0y0z0其原点为O，坐标分别为x0，y0，z0，由于我们仅讨论水面上的船舶运动，因此，该坐标系固定于地球表面。
作用于船舶重心的合外力在x0，y0轴上的投影分别为X0和Y0对z0轴的合外力矩为N2． 运动坐标系Gxyz其原点为点G （船舶重心），坐标分别为x ，y ，z ，该坐标系固定于船上。
这主要是为了研究船舶操纵性的方便而建立的坐标系。
x ，y ，两个坐标方向的运动速度分别为u 和v ，所受的外力分别为X 和Y ，对z 轴的转动角速度为r ，z 轴的外力矩为N 。
二、 运动方程的建立根据牛顿关于质心运动的动量定理和动量矩定理，船舶在水面的平面运动可由下列方程描述：y 0⎪⎩⎪⎨⎧===ϕ&&&&&&Z ogo ogo I N y m Y x m X该式一般很难直接解出。
为了方便，将其转化为运动坐标系表示，这样可以使问题大为简化。
经过转换，得：⎪⎩⎪⎨⎧=+=-=r I N ur vm Y vr u m X Z &&&)()( 该方程看似复杂，但各函数和变量都与固定坐标系没有关系，因此，可以使问题大为简化。
三、 水动力和水动力矩的求解对于上述方程中的水动力和水动力矩可表示为：⎪⎩⎪⎨⎧===),,,,,,(),,,,,,(),,,,,,(δδδr v u r v u f N r v ur v u f Y r v u r v u f X N Y X &&&&&&&&&经过台劳级数展开，可得X ，Y ，N 对各自变量的偏导数，称为水动力导数和水动力矩导数，它们可以通过船模试验求得。
四、 一阶船舶操纵运动方程任何一种模型都是只是对真实物理现象的近似描述，不能准确代表真实物理过程。
为了简化研究，往往需要引入一定的假设，才能使方程易解。
将上述方程忽略二阶以上的水动力导数和水动力矩导数，得到的方程称为线性方程。
它适用于小扰动的情况。
对于船舶的旋回性，我们关心的是航向角和转向角速度随时间的变化，较少考虑x 方向的情况。
因此，仅取Y 和N 两方程式联立，并进行无因次化处理，得到船舶操纵运动的线性方程:)()(32121δδ&&&&T K r r T T r T T +=+++T 1、T 2、T 3为船舶追随性指数 K 为船舶旋回性指数设T= T 1+T 2-T 3，经过求解，得:δK r r T =+&即得一阶船舶操纵运动方程。
第二节船舶的旋回性能一、船舶的旋回性的定义、旋回运动的过程1．船舶的旋回性的定义船舶定速度直航中操某一舵角并保持之，船舶进入旋回运动的性能称为船舶的旋回性能。
2．旋回运动的过程—参考《船舶操纵性与耐波性》p241）转舵阶段—横移内倾阶段δ从0增加到δC随着舵角的增加，产生YR和NR，由此产生横向加速度和旋转角加速度，由于船舶的质量和转动惯量很大，横移速度v和转动角速度r还不明显。
β较小，降速不明显，重心外移L/100，船尾外移(1/5～1/10)L，内倾。
内倾的原因是舵力作用中心较水动力作用中心低。
旋转角速度r 旋转角加速度横移速度v 横移加速度r&舵角δT图1-1 船舶旋回运动过程中运动要素的变化2）过渡阶段—加速旋回阶段δ维持在δC，横向加速度、旋转角加速度、横移速度v和转动角速度r都存在，并不断变化，只有舵角为常量。
β增加，Vs降低较快，出现外倾。
外倾的原因是离心力产生的外倾力矩大于内倾力矩。
3）定常旋回阶段横向加速度、旋转角加速度均为0。
δ，v，r均为常量。
航向角变化约120○之后，船舶开始进入定常旋回阶段。
β为定值，Vs降速不变，稳定外倾。
二、旋回圈1．旋回圈的概念船舶定速直航中操某一舵角并保持之，船舶重心所描绘的轨迹称为旋回圈。
旋回圈是表示船舶旋回性能的重要指标。
旋回圈越小，旋回性能越好。
2．旋回圈的要素1）旋回圈的几何要素⑴进距Ad—advance从开始转舵到航向变化为任意值时的船舶重心纵向移动的距离，通常用航向角变化为90○时，为最大进距称为进距Ad。
一般Ad=0.6D T ~ 1.2D T⑵横距Tr—transfer从开始转舵到航向变化为90○时的船舶重心横向移动的距离。
一般Tr≈0.5D T⑶旋回初径D T — tactical diameter从开始转舵到航向变化为180○时的船舶重心横向移动的距离。
一般D T =3L ~ 6L⑷ 旋回直径D — final diameter 船舶进入定常旋回时的旋回圈直径。
一般D=0.9D T ~ 1.2D T ⑸ 反移量L K — kick在旋回过渡阶段，由于船舶转动惯量很大还来不及产生较大的旋转角速度，则在Y R 的作用下，产生横向移动加速度，进而产生横向移动速度v ，使船舶重心产生向转舵相反方向的横移量，其称为反移量L K 。
一般船舶满载时其L K ≈L ·1%，而船尾可能要偏出(1/5~1/10)L 。
2）旋回圈的运动要素 ⑴ 漂角β— drift angle⎪⎩⎪⎨⎧-==ββsin cos V v V u船首尾线与船舶重心运动轨迹切线的夹角。
它在转舵阶段和过渡阶段是不断变化的，当船舶进入定常旋回时，漂角为常量。
一般β≈3~15○⑵转心P —pivoting point船舶回转曲率中心到船舶首尾线所作垂线的垂足P 。
由刚体的平面运动可知：船舶在水平面的运动可以分解为转心的平动和绕转心的转动。
因此在该点处v=β=0。
一般船舶转心在船舶首柱之后约1/3~1/5L 处。
β越大越靠近船首。
⑶旋回过程中的船速u船舶在旋回过程中，会产生纵向速度降低的现象。
这是因为：船舶斜航阻力要远大于直航阻力； 船舶斜航时推进器效率降低； 舵阻力增加。
旋回圈越小，旋回过程中速度降低越大。
一般旋回速降为原船速的1/2~1/4。
⑷旋回时间O指旋回过程中船舶航向改变360所需要的时间。
其与船舶排水量有关。
一般万吨级船舶满载时，其快速旋回时间约为6分钟，VLCC 要增加一倍。
⑸旋回横倾角旋回过程中的横倾与作用在正横方向的力有关。
这些力包括：)1(2tan 2-=GMBMgD V t c θ —《操船论》 • 舵的横向力Y δ； • 水阻力的横向力Y W ；和 • 离心力Y F 。
上述三个横向力构成的横倾力矩为 M θ= Y F z F ＋ Y W z W － Y δz R在旋回初始阶段，因重心轨迹的曲率半径很大，因此，离心力Y F 可以忽略不计，而Y W 和Y δ大小基本一致，但由于z W 大于z R ，因此，旋回初始阶段船舶向转舵方向横倾。
内倾的原因是舵力作用中心较水动力作用中心低。
Y船舶开始旋回之后，随着重心轨迹的曲率半径的减小，由于Y F的增大，合力矩也向外增大，因此，船舶开始向转舵相反方向横倾。
外倾的原因是离心力产生的外倾力矩大于内倾力矩。
船速越高，旋回直径越小，GM越小则稳定外倾角越大。
三、影响旋回圈大小的因素影响旋回圈大小的因素包括：方形系数，水下侧面积形状，舵角，舵面积，船速，吃水等因素。
1．方形系数C B—block coefficient从试验可知，方形系数C B越小的船舶，即比较瘦削的船舶的旋回性能比方形系数C B大的船舶的旋回性能差，即旋回圈越大。
C B越大旋回直径越小，旋回性能越好。
2．水下侧面积形状就整体而言，船首部分分布面积较大如有球鼻首者，或船尾比较瘦削的船舶，旋回中的阻尼力矩小，旋回性较好，旋回圈较小，但航向稳定性较差；而船尾部分分布面积较大者如船尾有钝材，或船首比较削进（cut up）的船舶，旋回中的阻尼力矩比较大，旋回性较差，旋回圈较大，但航向稳定性较好。
首侧面积大D T小，如球鼻首；尾侧面积大D T大，如尾钝材；3．舵角舵角越大，旋回圈越小。
4．舵面积舵面积比是指舵面积与船体浸水侧面积（L PP×d）的比值。
舵力与舵面积成正比，一般来说，舵面积增大会提高船舶的旋回性能。
但舵面积增大也会增加旋回阻尼力矩，因此，舵面积要适当。
各类船舶的最佳舵面积比:拖轮为1/20～1/25，渔船为1/30～1/40；高速货船1/35～1/40；大型油轮1/65～1/75；一般货船为1/45～1/60。
5．船速船速越大，旋回时间越短，但船速对旋回圈影响不大。
当船速低至某一程度，船舶旋回初径将有逐渐增大的趋势；6．吃水（排水量）排水量的增大可使旋回进距增大，但对旋回圈的影响不是很大。
7．吃水差尾倾越大，旋回圈越大。
四、旋回圈要素在实际操船中的应用1．旋回圈要素在操纵中的应用（1）港内掉头（A d，D T）；（2）进入锚地旋回；（3）人员落水救助本船航行中发现有人落水时，应立即向落水者一舷操舵，使船尾迅速摆离落水者，以免使之卷进船尾螺旋桨流之内。
2．旋回圈要素在避碰中的应用近距离避让时的最晚施舵点，紧急避让时的进距。
第三节航向稳定性一、稳定性的一般概念运动物体的稳定性定义：是指处于运动状态的物体（或系统）受到干扰作用而使某些运动参数偏离原来状态值，干扰过后能否恢复原来值的性能。
若能恢复原来状态值，则物体运动状态对参数是稳定的，否则就是不稳定的。
船舶运动稳定性分为两种：无控稳定性：不用控制（δ=0）而自动稳定的性能。
控制稳定性：用控制器来控制的运动稳定性能。
在此，我们讨论的是船舶的无控稳定性。
二、船舶运动稳定性正舵直航中的船舶受到外界干扰而偏离原航向，当干扰消除后，分三种情况来讨论：1．直线稳定当t→∞时，r→0，△ψ≠0，由于干扰，航向改变，干扰消除后，船舶最终恢复新的直线运动。
这种情况称为船舶具有直线稳定性。
2．方向稳定当t→∞时，r→0，△ψ→0，△y0G≠0，由于干扰，航向改变，干扰消除后，船舶最终恢复与原航向平行的直线运动。
这种情况称为船舶具有方向稳定性。
3．位置稳定当t→∞时，r→0，△ψ→0，△y0G→0，由于干扰，航向改变，干扰消除后，船舶最终恢复原航向延长线上的直线运动。
这种情况称为船舶具有位置稳定性。
上述三种情况之间的关系：具有位置稳定性也一定具有方向稳定性；具有方向稳定性也一定具有直线稳定性。
反之，不具有直线稳定性也不具有方向稳定性和位置稳定性。
三、 航向稳定性根据上面的讨论，对于水面上的船舶，一般不具有方向稳定性和位置稳定性，因此，一般所说的航向稳定性就是指直线稳定性。
