第二讲 宏观经济指标的季节性分析
- 格式:pdf
- 大小:546.64 KB
- 文档页数:40
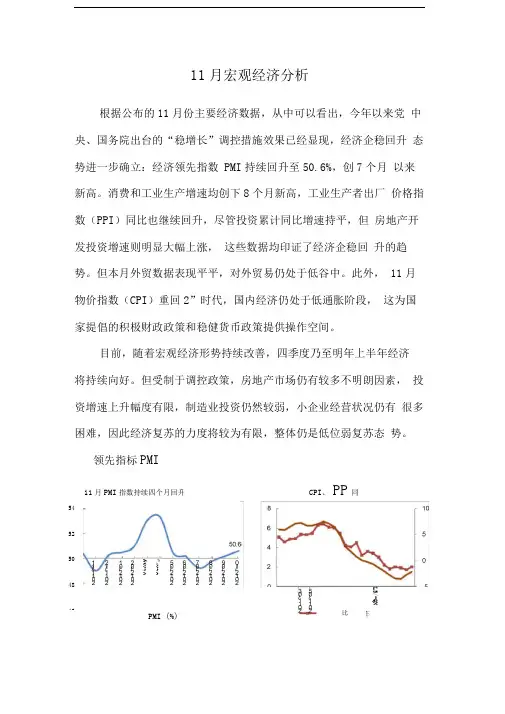
11月宏观经济分析根据公布的11月份主要经济数据,从中可以看出,今年以来党 中央、国务院出台的“稳增长”调控措施效果已经显现,经济企稳回升 态势进一步确立:经济领先指数 PMI 持续回升至50.6%,创7个月 以来新高。
消费和工业生产增速均创下8个月新高,工业生产者出厂 价格指数(PPI )同比也继续回升,尽管投资累计同比增速持平,但 房地产开发投资增速则明显大幅上涨, 这些数据均印证了经济企稳回 升的趋势。
但本月外贸数据表现平平,对外贸易仍处于低谷中。
此外, 11月物价指数(CPI )重回2”时代,国内经济仍处于低通胀阶段, 这为国家提倡的积极财政政策和稳健货币政策提供操作空间。
目前,随着宏观经济形势持续改善,四季度乃至明年上半年经济 将持续向好。
但受制于调控政策,房地产市场仍有较多不明朗因素, 投资增速上升幅度有限,制造业投资仍然较弱,小企业经营状况仍有 很多困难,因此经济复苏的力度将较为有限,整体仍是低位弱复苏态 势。
领先指标PMIL5/-QN车PMI (%)11月PMI 指数持续四个月回升CPI 、PP 同545250484603X20'4X20比月11月,中国制造业采购经理指数(PMI)为50.6%,比上月回升0.4个百分点。
该指数最近三个月的稳步小幅回升,显示经济运行企稳态势进一步巩固,呈现温和回升基本走势。
价格指数11月,全国居民消费价格指数(CPI)同比上涨2%比10月回升0.3个百分点,上升主要来自于食品价格的上扬,12月食品更是进入季节性涨价阶段,预计持续至明年春节CPI仍将温和上升;全国工业生产者出厂价格指数(PPI)同比下降2.2%,比10月回升0.6 个百分点,由于经济复苏的延续,预计未来几个月PPI回升的趋势将不变。
工业增加值11月,规模以上工业增加值同比实际增长10.1%,比10月回升0.5个百分点,处于8个月以来最高点,终于回升至10%以上。
分产品看,11月钢材和发电量同比增速增加明显。

浅谈国民经济数据的季节性影响与调整关于国民经济数据的季节性影响与调整1. 季节性核算在国民经济数据分析中的意义2. 季节性变动对国民经济数据的影响3. 季节性调整方法的分类与实践4. 分析季节性调整方法的优缺点5. 经验案例:季节性调整对国民经济数据的影响与解读1. 季节性核算在国民经济数据分析中的意义季节性指随着自然和社会活动的变化,某些经济指标会呈现出周期性的波动,导致对季节性因素敏感性的统计指标难以得到真实准确的结果。
季节性核算是研究季节性因素对经济变量统计结果的影响过程,以及可采用的技术方法与评价标准。
季节性核算在国民经济数据分析中的意义体现在以下三个方面:第一方面,季节性核算可帮助准确分析经济发展状况。
国民经济数据往往基于季度或年度发布,但在一年中的不同季节,各个行业、企业和产业部门都会经历不同的生产和销售状况。
季节性核算能帮助经济分析和决策人员预测和评估市场和经济行业在特定的季度发展状况。
第二方面,季节性核算可帮助持续建立可靠的经济模型。
经济模型是用来模拟影响宏观经济发展的因素,季节性变动是其中一个重要因素。
季节性核算可确保季节效应被合理地纳入宏观经济模型中,从而提高模型预测的准确性。
第三方面,季节性核算可帮助改进经济指标的制宪与修订。
在民生服务、生产效率等方面,需衡量不同季节的变化,以便更好地反映发展趋势和准确让政策制定人员作出正确决策。
2. 季节性变动对国民经济数据的影响季节性变动对国民经济数据的影响包括以下几个方面:第一方面,季节性变动影响了经济数据的长、短期变化趋势。
采用统计方法对不同的季节进行拆卸,可以更准确地对经济变化进行分析。
第二方面,季节性变动导致季节缩小指标的波动。
季节缩小是统计分析工具,指为排除或减少季节性因素而采取的一种数据处理方法。
季节性缩小有助于更明确,更准确识别经济活动的剪切点,如大停止止工业生产的年休息日。
第三方面,季节性变动可导致偏差及误差。
国民经济数据中,例如季节性因素及调整偏差很容易产生。

宏观经济指标的解读与分析宏观经济指标是评估国家经济运行状况和预测未来经济发展趋势的重要工具。
它们是衡量国民经济总体状况的数据指标,包括国内生产总值(GDP)、通货膨胀率、失业率、消费者物价指数(CPI)等。
本文将从这些主要宏观经济指标的角度出发,对其进行解读与分析。
一、国内生产总值(GDP)国内生产总值是一个国家或地区一定时期内产生的全部最终产品和服务的市场价值总和。
它是衡量一个国家经济规模和增长速度的重要指标。
GDP增长率代表了经济的增长速度。
当GDP增长率高时,通常意味着经济繁荣,投资和消费增加;当GDP增长率低时,可能意味着经济衰退或增长放缓。
在解读GDP时,除了关注总量的增长率外,还需要分析其构成部分。
投资、消费和出口是推动经济增长的主要因素。
如果投资增长率高于消费增长率,可能意味着经济正处于投资驱动型增长阶段;如果消费增长率高于投资增长率,可能意味着经济正处于消费驱动型增长阶段。
二、通货膨胀率通货膨胀率是衡量物价水平总体上持续上涨的速度。
通货膨胀率的提高意味着货币购买力下降,人民币每单位所能购买的商品和服务减少。
通货膨胀率过高可能导致恶性通货膨胀,影响经济稳定。
解读通货膨胀率时可以从物价变动的原因和影响因素入手。
物价上涨可能与需求过旺盛、供应不足、成本上升等因素有关。
理解通货膨胀的结构性特点和所处阶段有助于分析其对经济的影响。
三、失业率失业率是指劳动力市场上正在寻找工作但找不到工作的人数与总劳动力人口(就业者和失业者)的比率。
失业率是衡量就业问题的重要指标,对于表征经济的闲置资源和劳动力市场状况有着重要的意义。
解读失业率要考虑结构性和季节性因素对失业率的影响。
结构性失业可能与产业结构调整、技术进步等因素有关;季节性失业则与一年中某些行业的劳动力需求存在关联。
四、消费者物价指数(CPI)消费者物价指数是衡量消费品价格总体持续上涨的速度。
CPI的涨跌直接影响着人们购买力的变化,对于居民生活有着重要的指导意义。


有关GDP时间序列季节调整的一些说明GDP(国内生产总值)是一个非常重要的经济指标,用于衡量一个国家或地区一定时期内所生产的所有最终商品和服务的总价值。
然而,由于季节因素的影响,GDP数据可能会出现季节性的波动。
为了更准确地反映经济的发展趋势,需要对GDP进行季节调整。
本文将对GDP时间序列季节调整的一些说明进行探讨。
1. 季节调整的背景季节调整指的是对经济数据进行去除季节性成分的处理,以便更好地捕捉出经济的长期趋势。
季节性因素包括一年中某个特定季节的自然事件、传统节假日和周期性的销售促销活动等。
忽略这些季节性因素,可以让我们更好地理解经济数据的趋势和变动。
2. 季节调整方法在季节调整中,有两种常见的方法:移动平均法和X-12-ARIMA法。
移动平均法是一种简单而常用的方法,通过计算每一特定季节的平均值,然后将该季节的值调整为其平均值,从而去除季节性波动。
而X-12-ARIMA法则是一种基于时间序列分析的复杂模型,可以更准确地确定季节性成分的波动。
3. 季节调整的意义季节调整可以帮助我们更好地识别经济趋势。
通过去除季节性影响,我们可以更准确地判断经济的长期表现,从而有效地进行政策制定和经济决策。
季节调整后的GDP数据更具有可比性和稳定性,能够提供更准确的经济分析和预测。
4. 季节调整与其他调整方式的区别除了季节调整,还有一些其他常见的调整方式,如通胀调整和实际GDP调整。
通胀调整是为了排除价格上涨对GDP数据的影响,计算出真实的购买力。
实际GDP调整则是针对GDP中包含的价格变动进行调整,以反映产出的真实增长。
这些调整方式与季节调整不同,但它们共同的目标都是更准确地反映经济的实际情况。
5. 季节调整的局限性尽管季节调整在经济数据分析中很有用,但它也存在一些局限性。
首先,季节调整无法完全消除季节性变动的影响,因为某些季节性因素一直存在,如圣诞节和春节等。
其次,季节调整可能会导致数据失真,特别是在数据样本较小或长期趋势发生变化的情况下。

经济统计数据的季节性调整方法随着经济的不断发展和变化,统计数据的准确性对于政府决策和企业经营至关重要。
然而,由于季节性因素的影响,原始统计数据可能存在波动和不稳定的现象。
因此,进行季节性调整是保证数据准确性的重要步骤之一。
本文将介绍几种常见的经济统计数据的季节性调整方法。
首先,我们来了解一下什么是季节性调整。
简而言之,季节性调整是一种通过消除季节性变动对数据的影响,以便更好地观察长期趋势和周期性变化的方法。
季节性因素是指经济数据在特定季节内出现的周期性变化,例如节假日购物季节、农业季节等。
这些季节性因素会导致原始数据的波动,使得我们很难观察到真实的经济趋势。
一种常见的季节性调整方法是移动平均法。
这种方法通过计算一定时间范围内的平均值来消除季节性变动。
具体来说,移动平均法将每个季节性周期内的数据加总,然后除以季节性周期的长度,得到一个平均值。
这样一来,我们就能够得到消除季节性影响的数据,更好地观察长期趋势。
另一种常见的季节性调整方法是季节性指数法。
这种方法通过计算每个季节性周期内的相对指数来消除季节性变动。
具体来说,季节性指数法将每个季节性周期内的数据除以整个数据集的平均值,得到一个相对指数。
然后,将所有的相对指数进行加权平均,得到一个季节性指数。
最后,将原始数据除以季节性指数,即可得到消除季节性影响的数据。
除了以上两种方法,还有一种常见的季节性调整方法是回归模型法。
这种方法通过建立一个回归模型来消除季节性变动。
具体来说,回归模型法将季节性因素作为一个变量引入回归方程中,通过拟合回归模型来估计季节性因素对原始数据的影响。
然后,将估计得到的季节性因素从原始数据中减去,即可得到消除季节性影响的数据。
需要注意的是,不同的季节性调整方法适用于不同的数据类型和情况。
在选择合适的方法时,我们需要考虑数据的特点和目标,以及方法的适用性和可行性。
此外,季节性调整并不是完美无缺的,它可能会引入一些误差和不确定性。
因此,在使用季节性调整数据时,我们需要谨慎分析和解读,结合其他指标和数据进行综合判断。

季度分析宏观经济经济研究报告近几个季度以来,全球宏观经济形势发生了较大变化。
本文将对最近三个季度的宏观经济数据进行分析和研究,以了解经济趋势,预测未来发展方向,为相关部门和企业提供参考。
第一季度分析第一季度,全球宏观经济呈现出较为疲弱的态势,主要原因是新冠疫情的爆发和全球经济衰退。
各国政府采取了各种措施来应对疫情,包括封锁措施、限制交通和关闭非关键行业。
这些措施导致供应链中断、企业倒闭和失业率上升。
据统计数据显示,第一季度全球经济增长率下滑,投资和消费需求受到明显冲击。
尤其是在旅游、零售和航空等行业,受疫情限制导致营业额大幅下降。
此外,国际贸易也受到负面影响。
很多国家出口大幅减少,特别是对疫情重点地区的贸易额下降较为明显。
这导致了全球贸易格局的重构,国家之间的经济合作受到了冲击。
第二季度分析第二季度,全球经济逐渐从疫情的冲击中恢复,各国经济逐渐开放。
随着疫苗的研发和分发,疫情得到了一定程度的控制,减少了限制和封锁措施。
在这一季度,全球经济开始出现回升的迹象。
已有的经济数据显示,国内生产总值开始增长,投资需求有所回升,不少企业纷纷复工复产。
然而,第二季度依然充满不确定性,这主要是因为疫苗接种进度和疫情变异的风险。
全球各国在疫苗分发和接种上存在差异,而新的病毒变种增加了进一步控制疫情的难度。
第三季度展望虽然第二季度有所恢复,但第三季度的宏观经济发展仍然存在挑战。
疫情在一些地区出现反复,限制和封锁措施的重新实施可能对经济造成冲击。
此外,全球通胀压力也是一个需要关注的问题。
由于各国政府对疫情提供了大量的财政刺激,通胀压力可能随之而来。
这可能导致货币政策的调整,进一步影响全球经济的走势。
不过,全球经济也存在一些积极的因素。
首先,疫苗接种进度的加快可以有效控制疫情的蔓延,推动经济的复苏。
其次,各国采取的财政刺激措施和货币政策的宽松仍将继续支持经济的增长。
综上所述,2021年上半年的宏观经济形势总体上呈现出逐渐恢复的趋势,但仍面临挑战。

季度宏观经济分析报告1. 引言本文是针对当前季度的宏观经济情况进行分析的报告。
我们将从国内生产总值(GDP)、就业状况、通货膨胀率、货币政策和国际贸易等多个方面深入剖析当前宏观经济的表现和趋势,以此为基础给出未来的预测和建议。
2. 国内生产总值(GDP)本季度,我国国内生产总值达到XXX万亿元,同比增长X.X%。
我国经济增速仍然保持在合理区间内,显示出韧性和稳定性。
受全球经济放缓和贸易摩擦冲击的影响,我国出口增速略有放缓,但消费和投资对经济增长的贡献明显增加。
其中,消费者信心指数上升,个人消费支出稳步增长,拉动了内需的增长。
此外,国家加大基础设施建设力度,投资增速较上季度有所提升,为经济提供了有力支撑。
3. 就业状况在就业方面,本季度我国就业形势总体平稳。
全国城镇新增就业人数达到X.X万人,就业率稳定在较高水平。
尽管外部不确定因素增加,企业招聘意愿略有下降,但随着国内市场需求的增加,新兴产业的发展为就业创造了新的机会。
4. 通货膨胀率本季度,我国通货膨胀率保持在合理区间内。
CPI(居民消费价格指数)同比增长X.X%,处于温和增长水平,并未出现明显上升的趋势。
通货膨胀主要受到食品价格和能源价格等因素的影响。
本季度,食品价格上涨压力相对较小,原油价格相对稳定,因此通货膨胀率整体仍然保持较低的水平。
然而,我们也需要密切关注可能对通胀产生压力的因素,比如劳动力成本的上升和国际油价的变化等。
5. 货币政策货币政策是宏观经济调控的重要手段之一。
本季度,央行继续实施稳健的货币政策,保持流动性合理稳定。
同时,央行通过定向降准和公开市场操作等手段,维护市场利率在合理水平,促进金融资源的有效配置。
未来,我们预计货币政策将继续保持稳健,同时注重结构性调控。
央行将注重疏导资金流向实体经济,推动支持新兴产业发展,提高金融服务实体经济的能力。
6. 国际贸易国际贸易对于我国经济的影响依然显著。
本季度,由于全球经济增长放缓和贸易保护主义抬头,我国出口面临一定的压力。

国民经济数据的季节性影响与调整国民经济数据的季节性影响与调整本文首先探讨了国民经济数据的季节性影响,指出季节调整后的序列所具有的优点,然后分析了国际上流行的几种季节调整方法,并在此基础上,指出我国一方面要进行季节调整方法的研究,另一方面也要开展国民经济数据的季节调整。
关键词:国民经济数据季节成分季节调整方法目前,我国公布的宏观经济时间序列都是实际数据,没有经过季节调整,在讨论、分析和研究时使用同比法,这与国际主流统计方法不一致。
因此,我国有必要应用季节调整方法对经济序列进行调整,以更好地反映经济发展趋势,同时也跟国际数据具有可比性。
经济数据的季节性影响可以把经济时间序列看成一些成分的组合。
一般地,经济时间序列包括趋势循环成分、季节性成分、不规则成分和历法效应四个部分。
季节性成分是指时间序列围绕趋势循环年复一年地重复出现的一种有规律的波动,这种波动称为季节性波动。
产生季节性波动的主要原因是气候变化,如寒冷的冬季使建筑业和农业生产减少、取暖燃油消费增加、外出旅游人数减少,这种影响会产生连锁反应。
此外,一些固定的节假日,如国际劳动节、圣诞节、各个国家的国庆节,对商品零售额有一定影响,包含这些节假日的月份其商品零售额往往会高于其它月份。
经济时间序列月度(季度)数据是由每日的经济活动构成的,因此,其值可能受月份的星期结构、月份长度、移动假日等的影响,这些影响有时难以被季节成分吸收,被称为历法效应。
月份的星期结构是指本月所含星期一至星期日的天数,一般地,这些天数对不同月份是不同的。
不同月份长度对月度国民生产总值影响较大。
由于月份长度的影响主要由每月中的工作天数决定,因此把这种影响归为交易日效应。
同时二月份长度随年变化,可以单独考虑其影响,即闰年效应。
移动假日主要指美国的复活节、感恩节和劳动节,还可以包括其它不固定日子的节日。
移动假日前夕、期间和过后,人们的经济活动会发生较大变化,这种变化称为假日效应。
不固定日子节日为了提高不同月度或季度之间数据的可比性,进行季节调整。

经济学中的宏观经济学分析方法宏观经济学是研究国家整体经济运行规律及其影响因素的学科,其分析方法旨在解读和预测经济增长、通货膨胀、国际贸易、就业状况以及其他宏观经济指标。
本文将介绍宏观经济学中常用的一些分析方法,包括经济周期分析、总量分析、比较静态分析和动态分析等。
一、经济周期分析经济周期是指经济活动的波动性,它经历着扩张期、峰值期、衰退期和底部期。
经济周期分析旨在研究和预测这些周期性波动,了解经济何时进入或退出不同阶段。
在经济周期分析中,常用的方法包括趋势分析、周期分析和季节性分析。
趋势分析用来识别长期的增长或下降趋势,周期分析则关注经济活动在短期内的波动性,而季节性分析则用来检测经济活动在每年的不同季节是否存在规律性波动。
二、总量分析总量分析是对经济整体进行分析的方法,关注国家经济的总体规模和总体性质,以宏观经济指标为主要研究对象。
该方法通过分析国民生产总值(GDP)、总人口、就业率、失业率、通货膨胀率等指标来评估国家经济的状况和发展趋势。
总量分析的目的是了解和预测国家经济的总体运行状况,为制定宏观经济政策提供依据。
三、比较静态分析比较静态分析是通过对不同时间点或不同国家的经济指标进行比较,以揭示宏观经济学中的问题和现象。
比较静态分析用来比较不同国家、地区或时间点之间的经济差异,例如比较不同国家的经济增长率、通货膨胀率、失业率等指标,以了解不同经济体之间的差异和相似性。
通过比较静态分析,我们可以了解不同经济体之间的相对优势和劣势,为国际贸易和合作提供参考依据。
四、动态分析动态分析是研究经济变量之间的关联性和变化趋势的方法。
这种分析方法通过考察经济变量之间的时间序列数据,例如GDP增长率、通货膨胀率变化等,来分析宏观经济学中的问题。
动态分析旨在揭示经济变量之间的长期关系和短期波动性,并对未来的发展趋势进行预测。
该方法常用的工具包括VAR模型、协整分析和动态方程等。
总结:宏观经济学分析方法是经济学家用来研究宏观经济现象和问题的重要工具。

季节性趋势季节性趋势是指经济或其他统计数据在不同季节中表现出的一种变化规律。
这种趋势对于许多行业和经济活动都有重要影响,对于制定计划和预测市场走势都具有重要意义。
季节性趋势可以在不同层面上观察到。
在宏观层面上,季节性趋势可以表现为整个经济活动的波动。
例如,农业生产在春季和夏季往往较为繁忙,而冬季则相对较为冷清。
这种季节性变化可以影响农业生产的供应和需求,进而对物价和市场产生影响。
在微观层面上,不同行业和企业也面临着季节性趋势的挑战和机遇。
例如,服装行业往往在春季和秋季销售较为火爆,而冬季和夏季则相对较为冷清。
餐饮业也会在节假日和特定季节如暑假、寒假等期间经历客流高峰。
这种季节性的变化需要企业合理规划产能和库存,以及调整市场推广和销售策略。
季节性趋势的原因可以是多种多样的。
首先,自然因素往往是季节性波动的主要原因。
例如,不同季节的气温、降水量、光照等环境因素都会对农业、旅游和其他户外活动产生影响,进而引起经济和市场的季节性波动。
其次,节假日和学期等文化因素也会对季节性趋势产生影响。
例如,春节、国庆节等节假日会引发大规模的人口流动和消费需求,导致相关行业的季节性变化。
对于企业和决策者来说,了解和应对季节性趋势具有重要意义。
首先,可以帮助企业合理规划生产和销售策略,以充分利用季节性需求的高峰期。
其次,可以帮助企业减轻季节性变化带来的冲击。
例如,农业企业可以通过温室种植等措施,减少季节性变化对生产的影响。
此外,还可以通过市场调查和数据分析等手段,预测和预测季节性趋势,为决策提供参考。
然而,季节性趋势也会给企业带来一定的挑战。
例如,季节性波动可能导致生产和销售压力的不均衡。
企业需要合理调整生产能力和库存,以应对不同季节的需求变化,以避免资源浪费和经济损失。
此外,季节性波动可能还会导致行业竞争加剧,企业需要制定有效的市场策略来争取市场份额。
总之,季节性趋势是经济和市场中的一种重要现象,对企业和决策者都具有重要意义。
季节性波动规律是大宗商品特别是农产品价格运动的特有属性,虽然期货市场产生的初始动机是为了缓解现货价格的季节性波动,但是季节性波动的规律并不是完全可以消除的,而且在期货与现货的联系越来越密切的今天,商品期货价格的季节性波动越来越明显,并普遍表现为:在供应淡季或者消费旺季时,价格高启;而在供应旺季或消费淡季价格低落。
例如,在正常情况下,每年的七八月份属于全球大豆的供应淡季,大豆”青黄不接”,消费需求旺盛,因此价格高企。
而每年的11月份左右是全球大豆的供应旺季,现货供应充足,价格属年内低谷。
再比如,早春季节里,住房和汽车业为晚春和夏季的生产高峰大量购买铜原料,铜价在2月至4月达到年内季节性高点。
晚春需求高峰过去后,夏季的到来使得需求趋于疲软,铜价低点也一般在秋初出现,等等。
季节性分析法就是根据商品价格的季节性变化规律对商品期货走势进行分析的方法。
它力图勾画出在某一年份中,可能发生价格上升或下降的某些特殊时期,或者力图指出最可能出现全年价格最高点和最低点的一些特殊月份。
在实践中,我们可以把价格的季节性波动作为影响市场走势的一个基本因素。
例如,在供应淡季末期,价格的上涨将受到供应旺季即将到来的影响,季节性压力就成为市场中的一个利空因素。
如果季节性利空因素对市场的作用超过市场中的其他利多因素,那么价格的上涨通常就会趋于结束。
在一般意义上,期货商品总供求面的变化决定着商品期货的长期走向,而季节性因素和其它阶段性因素决定着商品期货的中短期走势。
因此,在阶段性因素没有突出表现的情况下,商品期货(特别是农产品期货)的走势轮廓就是由长期大趋势和季节性价格周期变化叠加而成的。
但是特别值得注意的是,在商品总供求关系处于基本平衡的时候,季节性规律表现的最为明显,但是在供求失衡的状态下,这种规律的表现非常不明显。
特别是在供求刚刚开始逆转的时候,季节性规律常常会被市场汹猛的涨跌趋势所冲淡。
以2002年的大豆市场为例,由于国内外大豆供应处于紧张状态,大豆价格在新豆上市后依然保持强势周期之分析(Cycle Analysis)周期分析与波浪理论具有相似的野心,企图找出价格变化之不变模式,以能进行长期之预测,与波浪理论不同处在於,周期分析只著眼於价格重复出现所经过的时间.若某一商品期货价格经常在一段时间回到原来之价位区,则可算是周期之现象.对商品价格之周期分析,最有名的是S.Benner,早在十九世纪末期,他即发现有些农产品和肉类价格,如玉米与猪肉等之上下波动,显示出相当的规律.目前期货交易界最具权威的周期分析家当推J.Bernstein.根据他对各类商品之研究,发现肉类价格之周期最有规律,1877至1985一百多年期间者,牛肉价格(以公牛肉现货价计算)显示出大约十年左右的长期周期,即每隔十年,牛肉价格陷於低潮.除了长期之周期,肉类也显示出稳定的短期周期,根据1974年至1985年期间之研究,发现活猪期货的周期约为20个月.另外,若以五年期研究,则从肉牛价格中可找出大约11个月之周期.周期之分析若能找出可靠的规律,则可预测未来价格之顶点或底点,交易时将有很大的利润.在实际交易时,由於只能知道周期之大约时间,因此进场时最好能做为长期投资,并须配合其它之技术指标.就期货交易者而言,明显地,较短期的周期比较具有实用价值.季节性的研究,是另一种周期之分析,此种研究之重点在於一年之中每月或每周价格涨跌之变化.若经过长期之统计,发现价格通常在一年中之某一期间会上涨或下跌,则表示价格具有季节的周期.有关季节周期之研究,贡献最大者仍推J.Bernstein,他对许多期货项目价格在一年中之变化,进行长期之季节性分析,并统计出一年中每月与每周价格涨跌之概然率,此研究可做为实际交易时的重要参考.利用季节性来分析市场,目的是为了预测未来的价格运动方向,而不被滔滔不绝的经常相互矛盾的新闻所困。
研究生经济学教案:宏观经济指标的分析与解读1. 引言•经济学的背景和重要性•宏观经济学的基本概念和原理2. 宏观经济指标简介•GDP(国内生产总值):定义、计算方法和意义•CPI(消费者物价指数):定义、计算方法和作用•PPI(生产者物价指数):定义、计算方法和应用•其他重要的宏观经济指标(失业率、贸易平衡等)3. GDP分析及解读3.1. GDP构成•GDP核算方法:支出法、收入法和产出法•消费支出、投资支出、政府支出和净出口对GDP的影响解读3.2. GDP增长率及其解读•平均年增长率和季度增长率的计算及其意义•增长率与经济发展的关系3.3. GDP与其他宏观经济指标之间的关联性分析•就业水平对GDP的影响解读•物价水平对GDP的影响解读4. CPI与PPI分析及解读4.1. CPI指数的分析•CPI计算方法及其局限性•物价上涨和通货膨胀对经济的影响4.2. PPI指数的分析•PPI计算方法及其应用领域•PPI对企业利润和价格变动的影响解读5. 其他宏观经济指标分析与解读5.1. 失业率的分析•失业率计算方法及解读•失业率对经济状况和社会稳定性的影响5.2. 贸易平衡与国际收支状况的分析•贸易平衡计算方法及其意义•贸易逆差或顺差对经济发展的影响6. 总结与展望•宏观经济指标在政策制定和经济预测中的重要性总结回顾•对未来宏观经济指标研究和应用的展望以上是关于研究生经济学教案:宏观经济指标的分析与解读的一个概括。
具体内容可以根据需要进行进一步扩展,包括相关理论、案例分析等,以满足2500个中文字的需求。
第二讲宏观经济指标的季节性分析对外经济贸易大学金融学院金融工程系黄晓薇xwhuang@本讲参考教材《时间序列X12-ARIMA季节调整——原理与方法》《时间序列X12ARIMA季节调整原理与方法》¾中国人民银行调查统计司,中国金融出版社,2006《计量经济分析方法与建模——Eviews应用及实例》高铁梅(主编)清华大学出版社2006¾高铁梅(主编),清华大学出版社,2006《时间序列分析及应用R语言》《时间序列分析及应用——R语言》¾Jonathan D. Cryer Kung-Sik Chan,机械工业出版社,2011时间序列的构成(Long term trend),长期趋势(Long term trend),T。
¾描述序列中长期运动趋势(Cyclical component)循环分量(Cyclical component),C。
¾描述序列中不同幅度的扩张与收缩,且时间间隔不同的循环变动。
经济问题中常指一年以上的起伏变化。
经济问题中常指一年以上的起伏变化¾实际测算难度较大,因此将循环和趋势放在一起不加区分。
(S l t)季节分量(Seasonal component),S。
¾描述序列中一定周期的重复变动,周期常为一年,一季,一周等。
不规则分量(Irregular component),I。
¾描述随机因素引起的变动,常带有偶然性由于各种因素引起变化相互抑制抵消,变动幅度常较小。
1800TREND Y 1.10时间序列的构成时间序列的构成趋势X t循环或者季节性随机time经典的确定性时间序列模型这四种因素对时间序列变化的影响有二种模型加法模型Y = T + S + C + I T *S*C*I乘法模型Y = T *S* C* I 对于一个时间序列,采用哪种模型分析,取决于各成分之对于个时间序列,采用哪种模型分析,取决于各成分之间关系。
一般来讲,若4种成分是相互独立的用加法模型,若相互有关联用乘法模型,对于社会经济问题主要使用乘法模型。
季节调整的特点为了克服季节性的传统方法是采用“同比”来反映经济增 为了克服季节性的传统方法是采用同比来反映经济增长变化。
缺点在于无法及时反映经济变化转折点,可能产生错误的结论。
经验表明,采用同比增长反映经济拐点平均滞后6个月。
季节调整的数据可以更及时地反映经济的瞬间变化季节调整的数据可以更及时地反映经济的瞬间变化。
季节调整的数据可以进行年化率的测算。
¾调整后的绝对数(季度)*4=年度数据季节调整后数据不是实际的统计数据,不同的方法可能产生不同的季节调整数据。
第二讲宏观经济指标的季节性分析时间序列的平滑方法2.1 时间序列的平滑方法2.1时间序列的平滑方法平滑(Smoothing)是研究时间序列的一个基本方法,用它g 来平抑或削弱时间序列中的波动变化,从而获得序列变化趋势的信息。
平滑技术是消除或者至少减少时间序列短期波动的一个手段的个手段。
在实际情况下,某经济数据不具有明显的季节波动和趋势波动。
我们可以刻采用指数平滑方法进行拟合及预测。
主要的平滑方法移动平均方法¾简单移动平均¾中心化移动平均¾加权移动平均指数平滑方法¾单指数平滑¾双指数平滑¾Holt-Winters乘法模型Holt Winters加法模型¾Holt-Winters加法模型¾Holt-Winters无季节性模型移动平均法移动平均是使未调整的序列在t时刻被一个加权平均值替代 移动平均是使未调整的序列在t时刻被个加权平均值替代。
q+mt pm m t y y M +−=∑=θ)(记k=p+q+1,上式亦称为k期移动平均。
当p=f,并且对于任意的m都有θ-m =θ-m, 我们称为中心化的移动平均。
∑+q 为了保留趋势项,我们要求1=−=p m m θ移动平均法k的选择:从上图可以看出,k值越大平滑的效果越好。
但损失的项数(k-1)¾从上图可以看出,k值越大平滑的效果越好。
但损失的项数(k也越大,所以要在保持足够的数据与消除波动之间做出选择,一般取k与循环波动周期相一致,这样可有效地抑制循环变化。
复合移动平均法复合移动平均是连续使用两次移动平均,其中P×Q移动平复合移动平均假设考虑加法模型Y t=(T t+C t)+S t+I t=TC t+S t+I t消除季节项保留趋势项循环项可以采用 为了消除季节项、保留趋势项-循环项,可以采用对季度数据采用2 ×4移动平均:M2×4={1,2,2,2,1}/8对月度数据采用2 12移动平均对月度数据采用2×12移动平均M2×12={1,2,2,2,2,2,2,2,2,2,2,2,1}/24复合移动平均复合移动平均可以从季节-不规则成分中提取季节成分复合移动平均可以从季节不规则成分中提取季节成分¾季节-不规则成分为SI t=Yt-(T t+C t)=¾提取季节成分为SI t S t+I t这里仅仅是平滑的问题,经常采用的是={1221}/9¾3×3移动平均:M3×3={1,2,3,2,1}/9¾3×5移动平均:M3×5= {1,2,3,3,3,2,1}/15={12333333321}/27¾3×9移动平均:M3×9= {1,2,3,3,3,3,3,3,3,2,1}/27这几种移动平均可以很好保留年度季节性特征,具体分析见《时间序列X12-ARIMA》71页。
见《时间序列X12ARIMA》71页Henderson移动平均由于上述提到的k期移动平均的系数曲线都是非平滑的,因单指数平滑法我们通常认为的近期值比早期值更重要,近期值在移动平均时应有更大的权重。
实现这一思想的一个简单的方法是指数加权移动平均法(单指数平滑法)。
注意到权数和为1注意到权数和为1平滑系数的选择确定指数平滑系数a:¾a较大则最近的数据赋予的权重大,相当于选择较小的k;¾a较小,权重逐渐减小,过去很久的数据仍然对未来有影响,相当于选择较大的k;¾简单滑动平均期数k和指数平滑系数的关系¾a=2/(k+1)双指数平滑法时间序列}的双指数平滑以递归形式定义为{ytHolt-Winters 乘法模型ˆt t yy 为的平滑序列节性变化。
有线性趋势性和乘法季这种方法适用于序列具Holt-Winters 加法模型t t yy ˆ为的平滑序列节性变化。
有线性趋势性和加法季这种方法适用于序列具k t t t k t Ts s t S k b a y ++++=++=,...,2,1,)(ˆk t t t s S k b a ++的递推公式如下数斜率的初值,这三个系节因子、趋势项截距和另外,需要事先给定季表示季节周期长度。
,为乘法模型的季节因子表示趋势项,其中t t s t t t b a S y a −−−+−+−=))(1()(11ααst t t t t t t t S a y S b a a b −−−−+−=−+−=)1()()1()(11γγββs k T T T k T S k b a y−++++=)(ˆ预测值为第二讲宏观经济指标的季节性分析2.2 X11季节季节调整法调整法2.2 X1122X11季节X11移动平均法————移动平均法X11方法的演变过程1954年,美国普查局Shiskin研发了普查局模型I普查局模型II,X0,X1,X2,X31965年,美国普查局Shiskin,Young和Musgrave研发X111975年1988年,加拿大统计局Dagum研发X11ARIMA1975年-1988年,加拿大统计局Dagum研发X11-ARIMA1998年美国普查局Fi dl M ll B ll Ott Ch共同 1998年美国普查局Findley,Monsell,Bell,Otto,Chen共同研发了X12-ARIMAX11季节调整的原理X11季节调整法本质是使用移动平均法(非参数方法)分理出序列的趋势-循环项和季节项。
假设考虑加法模型Y t=(T t+C t)+S t+I t=TC t+S t+I t这里假设考虑月度数据X11——第一阶段季节调整法第阶段)1(−)1()1(t 122.2)(122.1TC Y SI Y M TC tt t t −==××估计季节不规则成分:循环成分:移动平均估计趋势使用33.3×成分:移动平均估计预备季节对每个月份应用()1(t 33)1(ˆˆ)(ˆSI M S t =×)1(122)1()1t .4)(S M S S t t −=×估计季节调整后序列然后标准化)1(t)1()1()(S Y I TC A t t t −=+=估计季节序X11——第二阶段季节调整法第阶段)1()2(-)2()2(13-)(.5TC Y SI A H TC Henderson t t t t t −==不规则成分估计季节循环成分移动平均估计趋势使用53.6×成分移动平均估计最终季节对每个月份应用()2(53)2(t ˆˆ)(ˆSI M S t =×)2(t 122)2(t )2t .7)(-S M S S =×然后标准化)2(t )2()2()(S Y I TC A t t t −=+=估计季节调整后序列X11——第三阶段季节调整法第阶段)2(t 12)3(t )()12(.8A H TC H Henderson H =++:移动平均估计最终趋势使用.9估计最终不规则成分:)3(t)2(t )3(t -TC A I =第二讲宏观经济指标的季节性分析X11季节季节调整法调整法2.3 X112.323X11移动平均法和趋势性模型————移动平均法和趋势性模型X11季节调整法X11方法就是一种把一个时间序列分解为趋势分量、循环分 X11方法就是种把个时间序列分解为趋势分量、循环分量、不规则分量的连续计算方法。
目的:通过求时间序列的各个分量,达到对时间序列短期预测的目的。
预测的目的时间序列的分解:求其各个分量¾趋势分量¾循环分量¾季节分量¾不规则分量趋势分量()趋势分量(T)求出移动平均序列,即TC,下一步确定趋势分量T(trend)。
求出移动平均序列,即TC,下步确定趋势分量T(trend)。
¾在求趋势T之前,首先要观察趋势特征。