勾股定理

第1讲勾股定理第一部分知识梳理1．勾股定理：直角三角形的两直角边的平方和等于斜边的平方。

若直角三角形的两条直角边为a、b，斜边为c，则a²+b²=c²。

2．勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a²+b²=c²，那么这个三角形是直角三角形。

3．满足a²+b²=c²的三个正整数，称为勾股数。

若a，b，c是一组勾股数，则ak，bk，ck（k为正整数）也必然是一组勾股数。

常用的几组勾股数有3,4,5；5,12,13；6,8,10；7,24,25；8,15,17；9,40,41等。

4．勾股定理的应用:①圆柱形物体表面上的两点间的最短距离；②长方体或正方体表面上两点间的最短距离问题。

5．直角三角形的判别：①定义，判断一个三角形中有一个角是直角；②根据勾股定理的逆定理，三角形一边的平方等于另外两边的平方和，则该三角形是直角三角形。

6．勾股定理中的方程思想：勾股定理三角形有一个直角的“形”的特征，转化为三边“数”的关系，因此它是数形结合的一个典范．对于一些几何问题，往往借助于勾股定理，利用代数方法来解决．把一条边的长设为未知数，根据勾股定理列出方程，解方程求出未知数的值，即使有时出现了二次方程，大多可通过抵消而去掉二次项。

7．勾股定理中的转化思想：在利用勾股定理计算时，常先利用转化的数学思想构造出直角三角形，比如立体图形上两点之间的最短距离的求解，解答时先把立体图形转化为平面图形，在平面图形中构造直角三角形求解。

8．拓展：特殊角的直角三角形相关性质定理。

第二部分精讲点拨考点1. 勾股定理【例1】在Rt△ABC中，已知两边长为3、4，则第三边的长为变式1 等腰三角形的两边长为10和12，则周长为______，底边上的高是________，面积是_________。

变式2 等边三角形的边长为6，则它的高是________变式3 在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C所对的边，（1）已知c＝4，b＝3，求a；（2）若a:b=3:4，c=10cm，求a、b。

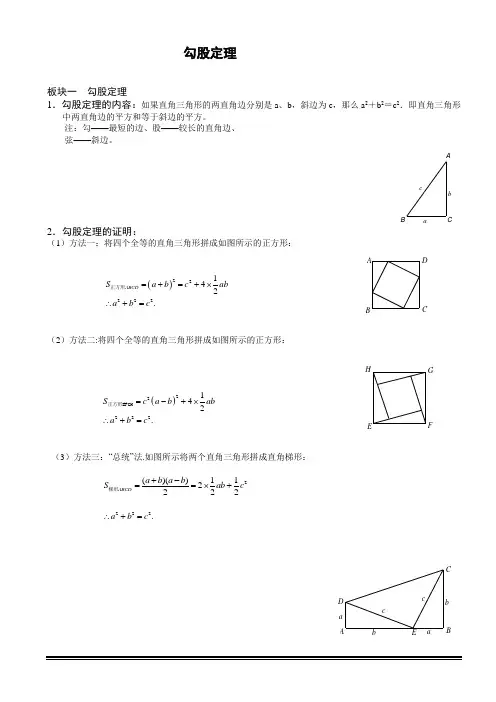
板块一 勾股定理1．勾股定理的内容：如果直角三角形的两直角边分别是a 、b ，斜边为c ，那么a 2＋b 2＝c 2．即直角三角形中两直角边的平方和等于斜边的平方。

注：勾——最短的边、股——较长的直角边、 弦——斜边。

CAB cba勾股定理3．勾股定理的逆定理：如果三角形中两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

即 222,,ABC AC BC AB ABC ∆+=∆在中如果那么是直角三角形。

4．勾股数：满足a 2 +b 2=c 2的三个正整数，称为勾股数．勾股数扩大相同倍数后，仍为勾股数．常用勾股数：3、4、5； 5、12、13；7、24、25；8、15、17。

板块一、勾股定理【例1】 下列说法正确的是（ ）A. 若a b c ，，是ABC ∆的三边，则222a b c +=B. 若a b c ，，是Rt ABC ∆的三边，则222a b c +=C. 若 a b c ，，是Rt ABC ∆的三边，90A ∠=︒，则222a b c +=D. 若 a b c ，，是Rt ABC ∆的三边，90C ∠=︒，则222a b c +=【例2】 在Rt ABC ∆中， 90C ∠=︒，（1）如果34a b ==，，则c = ； （2）如果68a b ==，，则c = ； （3）如果512a b ==，，则c = ； （4）如果1520a b ==，，则c = .【例3】 若一个直角三角形三边的长分别是三个连续的自然数，则这个三角形的周长为【例4】 一个直角三角形的三边为三个连续偶数，则它的三边长分别为 ．【例5】 已知直角三角形的两边长分别为3、4，求第三边长.【例6】 已知直角三角形两边x ，y 的长满足240x -，则第三边长为______________．【例7】 一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（ ）A ．斜边长为25B ．三角形周长为25C ．斜边长为5D ．三角形面积为20【例8】 如果梯子的底端距离墙根的水平距离是9m ，那么15m 长的梯子可以达到的高度为【例9】 如图，梯子AB 斜靠在墙面上，AC BC AC BC ⊥=，，当梯子的顶端A 沿AC 方向下滑x 米时，梯足B 沿CB 方向滑动y 米，则x 与y 的大小关系是（ ） A ．x y = B ．x y > C ．x y < D ．不确定CA【例10】 如图，一个长为10米的梯子，斜靠在墙上，梯子的顶端距离地面的垂直距离为8米，如果梯子的顶端下滑1米，那么，梯子底端的滑动距离 米（填“大于”、“等于”、“小于”）68【例11】 三角形的三边长分别为6,8,10，它的最短边上的高为( )A. 6B. 4.5C. 2.4D.8【例12】 若ABC ∆的三边a b c ，，满足条件：222338102426a b c a b c +++=++，则这个三角形最长边上的高为【例13】 如果把直角三角形的两条直角边同时扩大到原来的2倍，那么斜边扩大到原来的( )A. 1倍B. 2倍C. 3倍D. 4倍【例14】 如图，一根高8米的旗杆被风吹断倒地，旗杆顶端A 触地处到旗杆底部B 的距离为6米，则折断点C到旗杆底部B 的距离为CBA【例15】 已知，如图所示，折叠长方形的一边AD ，使点D 落在BC 边的点F 处，•如果8cm AB =，10cm BC =，求EC 的长．【例16】 如图，有一个直角三角形纸片，两直角边6cm 8cm AC BC ==，，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，那么CD 的长为多少？EDCBA【例17】 如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC 中，边长为无理数的边数是（ ）A. 0B. 1C. 2D. 3CBA【例18】 如图所示，在ABC ∆中，三边a b c ，，的大小关系是（ ）cbaCBAA. a b c <<B. c a b <<C. c b a <<D. b a c <<【例19】 设,,,a b c d 都是正数。

几种简单证明勾股定理的方法勾股定理是一个著名的数学定理，它描述了直角三角形三条边的长度之间的关系。

下面是几种简单证明勾股定理的方法：方法一：特例验证法对于任意一个直角三角形，我们可以列出它的两条直角边的长度的平方和，以及斜边的长度的平方，验证它们是否相等。

例如，对于一个直角边分别为3和4的直角三角形，我们可以计算出它的斜边的长度为5，然后验证3²+4²=5²。

这种方法虽然简单，但是只适用于特例，不能推广到一般情况。

方法二：几何构造法将两个大小相同的直角三角形放在同一直线上，使得它们的斜边成为一条直线。

这时，我们可以证明两个三角形的面积之和等于底边长度之和的两倍。

由于两个三角形面积相等，因此可以得出底边长度之和等于斜边长度。

例如，对于两个直角边分别为a和b的直角三角形，它们的斜边长度分别为c，将它们放在同一直线上，使得它们的斜边成为一条直线。

可以证明两个三角形的面积之和等于底边长度之和的两倍，即ab/2+ab/2=c²/2。

因此，可以得出a²+b²=c²。

方法三：代数推导法通过代入特殊值的方式，可以得到勾股定理的公式。

例如，当直角三角形的两条直角边分别为3和4时，可以得出斜边的长度为5，然后代入公式3²+4²=5²得到验证。

这种方法虽然简单，但是只适用于已知直角三角形两条直角边长度的特殊情况。

方法四：平方法通过平方法证明勾股定理的思路是：将直角三角形的一条直角边平移到斜边所在的直线上方，与斜边重合。

这时，可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差，因此可以得出斜边的平方等于两条直角边的平方和。

例如，对于一个直角边分别为a和b的直角三角形，可以将其一条直角边平移到斜边所在的直线上方，与斜边重合。

这时，可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差，即a²+b²=c²。

勾股定理勾股定理，又称商高定理，西方称毕达哥拉斯定理或毕氏定理（英文：Pythagorean theorem或Pythagoras's theorem）是一个基本的几何定理，相传由古希腊的毕达哥拉斯首先证明。

据说毕达哥拉斯证明了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”。

在中国，相传于商代就由商高发现，记载在一本名为《周髀算经》的古书中。

而三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释。

法国和比利时称为驴桥定理，埃及称为埃及三角形。

直角边的平方和等于斜边的平方勾股定理指出：直角三角形两直角边(即“勾”，“股”)边长平方和等于斜边(即“弦”)边长的平方。

也就是说，设直角三角形两直角边为a和b，斜边为c，那么A2+ b2= c2勾股定理现发现约有400种证明方法，是数学定理中证明方法最多的定理之一。

一种证明方法的图示：左右两正方形面积相等，各扣除四块蓝色三角形后面积仍相等勾股定理勾股定理的美妙证明证明[广西梁卷明的证法]：如图1,分别以AC、CB、BA为边长作正方形ACNM、正方形CBSQ、正方形BAPR，则易知⊿ABC≌⊿RBS,从而点Q 必在SR上，又把梯形ABNM沿BR方向平移，使点B与点R重合,则梯形ABNM平移至梯形PRQT的位置；显然⊿RSB≌⊿PTA, 如图2，再把⊿RSB沿BA方向平移，使点B与点A重合，则⊿RSB必与⊿PTA重合！故有：正方形ACNM的面积+正方形CBSQ的面积=正方形BAPR的面积，即得： a的平方 + b的平方 = c的平方.勾股定理【梁卷明证法】勾股定理 - 勾股数组勾股数组是满足勾股定理a2+ b2= c2的正整数组(a,b,c)，其中的a,b,c称为勾股数。

例如(3,4,5)就是一组勾股数组。

任意一组勾股数(a,b,c)可以表示为如下形式：a = m−n,b = 2mn,c = m + n，其中勾股定理。

勾股定理公元前500-200年，《周髀算经》的图解《勾股圆方图》勾股定理 - 参考资料勾股定理 - 历史上的勾股定理定理：如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2；即直角三角形两直角边的平方和等于斜边的平方。

十种方法证明勾股定理勾股定理是中学数学中最基本的定理之一，解决了数学中的许多问题。

它是一个既基础且实用的定理，有许多方法可以证明它，下面介绍十种方法：1.欧拉定理证明法：构造出一个直角三角形，把它的两条直角边对应的两个正方形放在直角三角形外面，另一条边对应的正方形放在直角三角形内部，再利用欧拉定理计算出三个正方形的面积，可以证明勾股定理。

2.代数证明法：利用代数的平方公式，把直角三角形的两条直角边平方相加，再把斜边平方，然后再将两者相减，得到一个等式，即可证明勾股定理。

3.数学归纳法证明：用数学归纳法证明勾股定理，证明当n为正整数时，定理成立。

4.相似三角形证明法：构造出相似的三角形，利用相似三角形的性质，可以推导出勾股定理。

5.向量证明法：用向量的几何意义证明勾股定理，首先利用向量的长度和夹角的公式计算出向量的长度和夹角，再利用向量的点积公式计算出勾股定理中的各个变量，最后推导出勾股定理。

6.割圆术证明法：利用割圆术将直角三角形对角线作为半径画圆，利用圆上弧角定理，可以得到勾股定理。

7.平面几何证明法：用平面几何证明勾股定理，利用平面几何图形的形状和大小关系，推导出勾股定理。

8.解析几何证明法：用解析几何证明勾股定理，利用平面直角坐标系，将三角形的三个点用坐标表示出来，推导出勾股定理。

9.三角函数证明法：用三角函数证明勾股定理，利用三角函数的性质，将三角形分离出直角三角形和非直角三角形，再用三角函数计算出各个变量，推导出勾股定理。

10.古希腊证明法：古希腊人对勾股定理有自己的证明方法，即利用几何图形的形状和大小，通过构造几何图形推导出勾股定理。

这些证明方法都可以证明勾股定理的正确性，它们有不同的适用范围和难度级别，可以根据自己的水平和兴趣选择合适的证明方法。

第三讲 勾股定理一、基础知识点： 1．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c += 勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方 2.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下： 方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a a b b =+=++ 所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证 3.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边。

勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形； 4.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）．、 5.勾股定理及其逆定理的应用c b a HGFEDCBAbacbac cabcab a bcc baED CBA勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：ABC30°D C BA ADB C二、经典例题：题型一：直接考查勾股定理 例１.在ABC ∆中，90C ∠=︒． ⑵ 知6AC =，8BC =．求AB 的长 ⑵已知17AB =，15AC =，求BC 的长题型二：应用勾股定理建立方程例1.在ABC ∆中，90ACB ∠=︒，5AB =cm ，3BC =cm ，CD AB ⊥于D ，CD ＝ 2.已知直角三角形的两直角边长之比为3:4，斜边长为15，则这个三角形的面积为 3. 如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2。

证明勾股定理的多种方法勾股定理是数学中一条重要的几何定理，它是数学中的基础知识之一。

勾股定理的形式可以简洁地表达为：直角三角形的斜边的平方等于两直角边的平方和。

本文将探索并介绍证明勾股定理的多种方法。

方法一：几何证明最常见的证明勾股定理的方法之一是几何证明。

该方法利用了直角三角形的特性，根据三角形的几何关系和平行线的性质，从而得出勾股定理的结论。

以直角三角形ABC为例，其中∠C为直角，假设∠A=α，∠B=β，边长分别为a, b, c。

根据正弦定理和余弦定理，可以推导出以下关系式：sinα = a / c，sinβ = b / c，cosα = b / c，cosβ = a / c由此可得：sin²α + cos²α = a² / c² + b² / c² = (a² + b²) / c²根据三角恒等式sin²α + cos²α = 1，可得：(a² + b²) / c² = 1即 a² + b² = c²，从而证明了勾股定理。

方法二：代数证明除了几何证明外，勾股定理还可以通过代数方法进行证明。

假设直角三角形的边长分别为a, b, c，且∠C为直角。

根据勾股定理，我们有：a² + b² = c²我们可以将其转化为代数方程组，从而进行证明。

构造方程组如下：x² + y² = 1²(x+c)² + y² = a²x² + (y+c)² = b²解方程组可得：x = (a² - b² + c²) / (2c)y = ±√(a² - x²)因此，可得到：a² + b² = (a² - b² + c²)² / (4c²) + (a² - (a² - b² + c²)² / (4c²) = c² · [(a² + b²) / (4c²) + (a² + b² - 2ab)/(4c²)]将a² + b² = c²带入上式，得到：c² = (c² · [(c² + 2ab) / (4c²)])化简后可得：c² = (c² + 2ab) / 4即 a² + b² = c²，从而证明了勾股定理。

勾股定理、一、勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。

2. 勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）*附：常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,133. 判断直角三角形：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c2＝a2＋b2，则△ABC是以∠C为直角的三角形；若a2＋b2＜c2，则此三角形为钝角三角形（其中c为最大边）；若a2＋b2＞c2，则此三角形为锐角三角形（其中c为最大边）4.注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

5. 勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n的线段（一）结合三角形：1.已知∆ABC 的三边a 、b 、c 满足0)()(22=-+-c b b a ，则∆ABC 为 三角形2.在∆ABC 中，若2a =（b +c ）（b -c ），则∆ABC 是 三角形，且∠ ︒90 3.在∆ABC 中，AB=13，AC=15，高AD=12，则BC 的长为1.已知2512-++-y x x 与25102+-z z 互为相反数，试判断以x 、y 、z 为三边的三角形的形状。

勾股定理定义
勾股定理是一种数学定理，通常用来计算三角形的边、角和面积等问题。

它的定义如下：
在一个直角三角形中，直角对边所对的角度为90度，另外两条边分别
为a和b，则有a²+b²=c²（c为斜边）。

这个定理是由公元前6世纪中国数学家毕达哥拉斯所发现的。

勾股定理的应用非常广泛，我们可以用它来解决各种问题。

下面我们
来一步步了解勾股定理的应用。

第一步，首先我们要确定一个三角形是否为直角三角形，这个很简单，只需要看这个三角形的两个边是否垂直即可。

第二步，我们要分别测量三角形的三个边的长度，这个也比较容易，
使用尺子或者测量仪器即可。

第三步，我们要根据勾股定理的公式进行计算：a²+b²=c²。

将值代入
即可得出斜边的长度。

除了计算斜边长度之外，我们还可以利用勾股定理计算角度。

如何计
算呢？我们可以使用反正切函数，即tan-1（b/a）来计算相应的角度。

此外，勾股定理还有一个重要的应用，就是解决三角形的面积问题。

如何计算三角形的面积呢？我们可以利用斜边长、底边长来计算。

设
三角形的底边为a，斜边为c，高为h，则三角形面积为S=1/2ah，而h 则为：h=c*sinB，其中B为底边a和斜边c所夹的角度。

以上就是勾股定理的一些应用方法。

这个定理虽然简单，但却非常实用，可以帮助我们解决很多实际问题。

我们要好好学习和应用这个定理，让它发挥更大的作用。

第四讲 勾股定理知识梳理一、勾股定理定义：如果直角三角形的两直角边长分别为a ，b ，斜边长为c ，那么 a 2＋b 2＝c 2. 即直角三角形两直角边的平方和等于斜边的平方二、勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a 2＋b 2＝c 2，那么这个三角形是直角三角形。

三、常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,13四、勾股定理的作用（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n 的线段。

例题讲解1、在ABC ∆中，o90=∠C（1）若25c 20b ==，，则=a （2）若4:3:=b a ，20=c ，则=a （3）若b a 3=，10=c ，则=∆ABC S2、已知一个Rt △的两直角边长分别为3和4，则第三边长的平方是（ ） A ．25 B ．7 C ．7或25 D ．无法确定3、已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ） A ．25 B ．7 C ．7或25 D ．无法确定4、已知一个△的两边长分别为3和4，则第三边长的平方是（ ） A ．25 B ．7C ．7或25D ．无法确定5、Rt △ABC 中，斜边BC ＝2，则AB 2＋AC 2＋BC 2的值为( ) A ．8 B ．4C ．6D ．无法计算6、如图，△ABC 中，AB ＝AC ＝10，BD 是AC 边上的高线，DC ＝2，则BD 等于( ) A ．4B ．6C ．8D ．102勾股数树1、如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中正方形A ，B ，C ，D 的边和长分别为2cm 、1cm 、2cm 、4cm ，则最大的正方形的面积之和为___________cm 2.2、如图，所有的四边形都是正方形，所有的三角形都 是直角三角形，其中最大的正方形的边长为6cm,则正方形A ，B ，C ，D 的面积之和为__________cm 2。

勾股定理勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。

中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。

勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

在中国，商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。

在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。

[1]中文名勾股定理外文名Pythagoras theorem 别称商高定理、毕达哥拉斯定理、百牛定理表达式a²+b²=c²提出者毕达哥拉斯赵爽商高提出时间公元前551年应用学科几何学适用领域范围数学，几何学适用领域范围数学，几何学中国记载著作《周髀算经》《九章算术》外国记载著作《几何原本》限制条件直角三角形在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

如果设直角三角形的两条直角边长度分别是和，斜边长度是，那么可以用数学语言表达：勾股定理是余弦定理中的一个特例。

推导赵爽弦图《九章算术》中，赵爽描述此图：“勾股各自乘，并之为玄实。

开方除之，即玄。

案玄图有可以勾股相乘为朱实二，倍之为朱实四。

以勾股之差自相乘为中黄实。

加差实亦成玄实。

以差实减玄实，半其余。

以差为从法，开方除之，复得勾矣。

加差于勾即股。

凡并勾股之实，即成玄实。

或矩于内，或方于外。

形诡而量均，体殊而数齐。

勾实之矩以股玄差为广，股玄并为袤。

而股实方其里。

减矩勾之实于玄实，开其余即股。

倍股在两边为从法，开矩勾之角即股玄差。

加股为玄。

以差除勾实得股玄并。

以并除勾实亦得股玄差。

令并自乘与勾实为实。

倍并为法。

所得亦玄。

勾实减并自乘，如法为股。

勾股定理简单算法1. 什么是勾股定理？勾股定理是指在直角三角形中，直角边的平方和等于斜边的平方。

即a²+b²=c²，其中a、b为直角边，c为斜边。

2. 勾股定理的应用勾股定理在几何学和物理学中都有广泛的应用。

在几何学中，勾股定理可以用来计算三角形的边长和角度。

在物理学中，勾股定理可以用来计算物体的速度、加速度和力等。

3. 勾股定理的简单算法勾股定理的简单算法是通过枚举直角边的长度来计算斜边的长度。

具体步骤如下：（1）输入直角边a和b的长度；（2）计算a²和b²的和；（3）对和开平方，得到斜边c的长度。

4. 勾股定理的优化算法勾股定理的优化算法是通过减少计算量来提高计算效率。

具体步骤如下：（1）判断a和b哪个较大，将较大的值作为斜边c的长度；（2）计算斜边c的平方，即c²=a²+b²；（3）对c²开平方，得到斜边c的长度。

5. 勾股定理的应用举例（1）计算三角形的面积已知直角三角形的两条直角边a和b，求其面积S。

解：根据勾股定理可知，斜边c的长度为c=√(a²+b²)。

因此，三角形的面积为S=1/2ab=1/2ab/2=ab/4。

（2）计算物体的速度已知物体在平面上的运动速度v和加速度a，求物体在t秒后的速度v'。

解：根据物理学中的公式v'=v+at可知，物体在t秒后的速度为v'=v+at。

（3）计算物体的力已知物体的质量m和加速度a，求物体所受的力F。

解：根据牛顿第二定律F=ma可知，物体所受的力为F=ma。

6. 总结勾股定理是一种非常重要的数学定理，其应用广泛。

通过简单算法和优化算法，可以快速计算直角三角形的斜边长度。

在实际应用中，勾股定理可以用来计算三角形的面积、物体的速度和力等。

勾股定理的详细解释
嘿，你知道勾股定理不？那可是数学世界里超级厉害的家伙！咱就说啊，直角三角形知道不？就那个有个直角的三角形。

勾股定理说的就是在直角三角形里，两条直角边的平方和等于斜边的平方。

比如说有个直角三角形，一条直角边是 3 厘米，另一条直角边是 4 厘米，那斜边得是多长呢？用勾股定理一算就知道啦！3 的平方是 9，4 的平方是 16，9 加 16 等于 25，那斜边就是 5 厘米呀！这不就神奇了嘛！
你想想，这勾股定理就像一把神奇的钥匙，能打开好多数学难题的大门呢！咱上学的时候，做几何题可全靠它呀！老师在讲台上讲得眉飞色舞的，“同学们，注意啦，这就是勾股定理的厉害之处！”咱就在下面听得津津有味。

再类比一下哈，勾股定理就像是一个指引方向的灯塔，在茫茫的数学海洋中给我们指明道路。

没有它，那我们不就像没头苍蝇一样乱撞嘛！它多重要啊！
而且勾股定理的应用可广泛了呢！建筑工人盖房子的时候得用吧，工程师设计桥梁的时候得用吧，就连咱平时生活中量个桌子椅子的尺寸都可能用到呢！你说它牛不牛？
我觉得啊，勾股定理就是数学世界里的一颗璀璨明珠，永远闪闪发光，让我们在探索数学的道路上充满惊喜和乐趣！。

勾股定理知识点勾股定理是数学中的一条基本定理，也是三角学中最为著名的一条定理。

它揭示了直角三角形中三条边之间的关系，对于解决实际问题和计算几何等学科都有着广泛的应用。

勾股定理的历史可以追溯到古希腊，但它的应用与证明在不同的文化和时代中有着各种不同的呈现方式。

勾股定理得名于古希腊数学家毕达哥拉斯。

毕达哥拉斯定理，即勾股定理的最原始形态，是指在一个直角三角形中，斜边的平方等于两直角边平方的和。

以a、b、c表示直角三角形的三条边，其中c为斜边，a、b为直角边。

勾股定理的数学表达式为c²=a²+b²。

在实际的应用中，勾股定理有着广泛的运用。

例如，我们经常用勾股定理来测量一个直角三角形中某一边的长度。

在测量工程中，通过测量两条已知边的长度，可以使用勾股定理求得第三条边的长度。

这在建筑、地理测量等领域都有着重要的应用。

此外，勾股定理还可以帮助我们解决一些几何问题。

例如，在解决平行四边形的问题时，我们经常会利用勾股定理来计算对角线的长度。

在分析几何和计算几何中，勾股定理也是解决问题的基础，使我们能够更好地理解和应用于实际。

在古希腊时期，勾股定理的证明主要以几何方法为主。

例如，毕达哥拉斯定理的几何证明是其中最为著名的。

它基于了一个三角形的几何构造，即在直角边所在直线上取一个点，将斜边分为几段，形成一系列的相似三角形。

通过几何相似的关系，可以得到勾股定理的证明。

随着数学的发展，勾股定理也有了不同的证明方式，其中包括代数方法、向量方法和三角函数方法等。

这些不同的证明方式使勾股定理更加丰富和多样化。

例如，使用代数方法证明勾股定理时，我们可以通过平方差或配方法将方程简化，从而得到直观的结果。

总之，勾股定理是数学中的一条重要定理，它揭示了直角三角形中三条边之间的关系，并在实际问题的解决和几何计算中有着广泛的应用。

勾股定理的证明方法多样化，既有几何方法，也有代数方法、向量方法和三角函数方法等。

有关“数学”的勾股定理
有关“数学”的勾股定理如下：
勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。

中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。

在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派。

勾股定理的公式为a²+b²=c²，其中a、b代表两条直角边，c代表斜边。

这个定理的证明方法有很多种，其中最有代表性的是几何证明。

此外，还有代数证明、三角函数证明等多种证明方法。

勾股定理不仅在数学中有着广泛的应用，它在日常生活中也有着很多用途。

比如，可以用勾股定理测量房屋的面积、修建水平线等等。

此外，勾股定理也是其他学科的基础，比如实验物理中的力学、声学等等。

勾股定理知识点勾股定理是数学中的一条重要定理，也被称为直角三角形中的基本定理。

它可以用来计算直角三角形的边长以及判断三角形是否为直角三角形。

勾股定理的数学表达式是a^2 + b^2 = c^2，其中a、b为直角三角形的两条直角边的长度，c为直角三角形的斜边（也称为斜边或斜边）的长度。

勾股定理的名字来自于古希腊的数学家毕达哥拉斯，他是最早发现并证明这个定理的人。

根据古希腊的记录，毕达哥拉斯是在公元前6世纪左右发现这个定理的。

他的证明方法是基于几何学，但现在我们通常使用代数方法来证明勾股定理。

勾股定理的应用非常广泛。

首先，它可以用来计算直角三角形的边长。

如果我们已知一个直角三角形的两条直角边的长度，我们可以通过勾股定理计算出斜边的长度。

例如，如果一个直角三角形的直角边的长度分别为3和4，我们可以用勾股定理计算出斜边的长度为5。

其次，勾股定理还可以用来判断三角形是否为直角三角形。

如果一个三角形的三条边符合勾股定理的条件，那么这个三角形就是直角三角形。

这在实际应用中非常有用，例如建筑工程中，我们可以通过勾股定理来判断一个墙角是否为直角。

除了上述应用外，勾股定理还有一些有趣的性质。

例如，如果a、b、c是勾股定理中的三个数字，且a和b互质（即它们没有公因数），那么a、b、c就被称为无关系勾股三元组。

无关系勾股三元组有很多有趣的性质，例如它们符合数学上的等差数列性质。

勾股定理的证明方法有很多种，其中最有名的是毕达哥拉斯的几何证明。

他的证明基于一个特殊的直角三角形，称为毕达哥拉斯三角形。

这个三角形的两条直角边的长度分别为3和4，斜边的长度为5。

通过几何方法，毕达哥拉斯证明了勾股定理对于任意直角三角形都成立。

总结来说，勾股定理是数学中的一条重要定理，它可以用来计算直角三角形的边长以及判断三角形是否为直角三角形。

勾股定理具有广泛的应用，并且有很多有趣的性质和证明方法。

它不仅在数学中有重要作用，在实际生活中也经常被使用。