字符串的全排列问题

字符串的排列组合算法合集全排列在笔试面试中很热门，因为它难度适中，既可以考察递归实现，又能进一步考察非递归的实现，便于区分出考生的水平。

所以在百度和迅雷的校园招聘以及程序员和软件设计师的考试中都考到了，因此本文对全排列作下总结帮助大家更好的学习和理解。

对本文有任何补充之处，欢迎大家指出。

首先来看看题目是如何要求的（百度迅雷校招笔试题）。

一、字符串的排列用C++写一个函数, 如 Foo(const char *str), 打印出 str 的全排列,如 abc 的全排列: abc, acb, bca, dac, cab, cba一、全排列的递归实现为方便起见，用123来示例下。

123的全排列有123、132、213、231、312、321这六种。

首先考虑213和321这二个数是如何得出的。

显然这二个都是123中的1与后面两数交换得到的。

然后可以将123的第二个数和每三个数交换得到132。

同理可以根据213和321来得231和312。

因此可以知道——全排列就是从第一个数字起每个数分别与它后面的数字交换。

找到这个规律后，递归的代码就很容易写出来了：view plaincopy#includeiostream?using?namespace?std;?#includeassert.h?v oid?Permutation(char*?pStr,?char*?pBegin)?{?assert(pStr?pBegin);?if(*pBegin?==?'0')?printf("%s",pStr);?else?{?for(char *?pCh?=?pBegin;?*pCh?!=?'0';?pCh++)?{?swap(*pBegin,*pCh);?P ermutation(pStr,?pBegin+1);?swap(*pBegin,*pCh);?}?}?}?int?m ain(void)?{?char?str[]?=?"abc";?Permutation(str,str);?retur n?0;?}?另外一种写法：view plaincopy--k表示当前选取到第几个数，m表示共有多少个数?void?Permutation(char*?pStr,int?k,int?m)?{?assert(pStr); if(k==m){staticintnum=1;--局部静态变量，用来统计全排列的个数?printf("第%d个排列t%s",num++,pStr);?}?else?{?for(int?i?=?k;?i?=?m;?i++)?{?swa p(*(pStr+k),*(pStr+i));?Permutation(pStr,?k?+?1?,?m);?swap( *(pStr+k),*(pStr+i));?}?}?}?int?main(void)?{?char?str[]?=?" abc";?Permutation(str?,?0?,?strlen(str)-1);?return?0;?}?如果字符串中有重复字符的话，上面的那个方法肯定不会符合要求的，因此现在要想办法来去掉重复的数列。

国际信息学奥林匹克竞赛（International Olympiad in Informatics，简称IOI）是一项面向高中生的信息学竞赛，旨在促进全球信息学教育和人才培养。

每年都会有来自世界各地的优秀学生参加这一盛事，并通过解决一系列复杂的编程问题来展示他们的才华。

作为一项高级的信息学竞赛，IOI赛题往往涉及到算法和数据结构的深度思考，考验选手在编程能力和解决问题能力上的造诣。

2023年国际信息学奥林匹克竞赛的题目更是备受瞩目，接下来我们就来深度剖析这些题目并提供解题思路。

第一道题目：“字符串排列”题目描述：给定一个长度为n的字符串s，求出它的所有排列方式，并将其按字典序输出。

解题思路：1. 我们可以利用递归的方法来求解字符串的全排列。

具体地，可以将字符串s的第一个字符与后面的字符依次交换，然后对剩下的字符串进行全排列，直到交换完成一次排列。

这样就可以得到字符串s所有的排列方式。

2. 在程序设计的过程中，我们要注意剪枝操作，可以通过设定一个标志数组来记录某个字符是否已经被使用过，从而避免重复排列的情况。

这道题目的解法较为经典，通过深入的逻辑分析和编程技巧，可以很好地完成题目要求。

第二道题目：“最大子段和”题目描述：给定一个长度为n的整数序列，求出其连续子段的和的最大值。

解题思路：1. 一个直观的解法是利用动态规划来解决这个问题。

具体地，我们可以设置一个dp数组，dp[i]表示以第i个数结尾的最大子段和，然后通过递推式dp[i] = max(nums[i], dp[i-1]+nums[i])来更新dp数组。

2. 在实现过程中，我们要注意处理边界情况和初始化操作，以及在遍历过程中及时更新最大子段和的值。

这道题目需要考虑到较多的边界情况和递推关系，是一道非常有挑战性的动态规划问题。

总结回顾：国际信息学奥林匹克竞赛2023的题目涵盖了递归、动态规划等多个领域，对选手的算法能力和编程功底提出了很高的要求。

python编程题：字符串的（所有可能的）排列组合前言在此研究：1）给定一个字符串，如何对其中字母进行排列组合；2）进一步了解Python递归。

题目内容在指定位置编写代码，完成函数，根据给定的字符串，给出组成该字符串的字符的所有排列构成的字符串，例如字符串为abc时，结果为abc、acb、bac、bca、cab、cba。

（提示：可以考虑拿掉某个位置的字符，则“该字符＋其左边字符的所有排列＋其右边字符的所有排列”就是该字符在指定位置的所有排列字符串）解题思路可以用递归的方法来解决问题。

1）我们先确定字符串第一个字母是谁，对于长度为n的字符串，总共有n种情况；2）然后呢，问题就从“返回字符串中的字母排列组合” 变成了“返回第一个字母+除去第一个字母外的字符串的排列组合”，有点大而化小，分而治之的感觉。

具体代码，网上很多地方都有代码答案，只需在百度搜索关键字”Python 字符串排列组合“即可，所以这里我就不另写代码了，引用 [1]，因为我感觉这个算是解释的比较详细的了。

代码如下 [1]：def perm(s=''):# 这里是递归函数的出口，为什么呢，因为这里表示：一个长度为1的字符串，它的排列组合就是它自己。

if len(s)<=1:return [s]sl=[] #保存字符串的所有可能排列组合for i in range(len(s)): #这个循环，对应解题思路1）确定字符串的第一个字母是谁，有n种可能（n为字符串s的长度for j in perm(s[0:i]+s[i+1:]): #这个循环，对应解题思路2）进入递归，s[0:i]+s[i+1:]的意思就是把s中的s[i]给去掉sl.append(s[i]+j) # 对应解题思路2）问题就从“返回字符串中的字母排列组合” **变成了** “返回第一个字母+除去第一个字母外的字符串的排列组合”return sldef main():perm_nums=perm('abb') # 有可能存在字母相同的情况no_repeat_nums = list(set(perm_nums)) # 去重，挺牛的，这个代码print('perm_nums', len(perm_nums), perm_nums)print('no_repeat_nums', len(no_repeat_nums), no_repeat_nums)passif __name__ == '__main__':main()总结Permutationnoun[usually pl.] 排列（方式）；组合（方式）；置换any of the different ways in which a setof things can be orderedThe possible permutations of x, y andz are xyz, xzy, yxz, yzx, zxy and zyx.x、y和z的可能的组合方式为xyz、xzy、yxz、yzx、zxy和zyx。

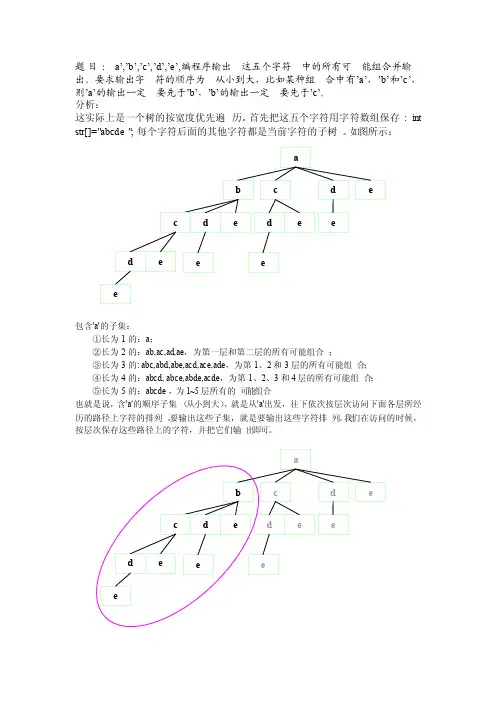
题目：a’,’b’,’c’,’d’,’e’,编程序输出‎这五个字符‎中的所有可‎能组合并输‎出。

要求输出字‎符的顺序为‎从小到大，比如某种组‎合中有’a’，’b’和’c’，则’a’的输出一定‎要先于’b’，’b’的输出一定‎要先于’c’。

分析：这实际上是‎一个树的按‎宽度优先遍‎历。

首先把这五‎个字符用字‎符数组保存‎:int str[]="abcde‎"; 每个字符后‎面的其他字‎符都是当前‎字符的子树‎。

如图所示：包含'a'的子集：①长为1的：a；②长为2的：ab,ac,ad,ae，为第一层和‎第二层的所‎有可能组合‎；③长为3的: abc,abd,abe,acd,ace,ade，为第1、2和3层的‎所有可能组‎合；④长为4的：abcd, abce,abde,acde，为第1、2、3和4层的‎所有可能组‎合；⑤长为5的：abcde‎，为1~5层所有的‎可能组合也就是说，含'a'的顺序子集‎（从小到大），就是从'a'出发，往下依次按‎层次访问下‎面各层所经‎历的路径上‎字符的排列‎。

要输出这些‎子集，就是要输出‎这些字符排‎列。

我们在访问‎的时候，按层次保存‎这些路径上‎的字符，并把它们输‎出即可。

同样的，含'b'的顺序子集‎，就是从'b'出发的子树‎，往下依次按‎层次访问下‎面各层所经‎历的路径上‎字符的排列‎。

要输出这些‎子集，就是要输出‎这些字符排‎列。

即上图中椭‎圆圈起来的‎部分。

含'c'的顺序子集‎，也相似，如下图椭圆‎圈起来的部‎分：含'd'的顺序子集‎，即下图椭圆‎圈起来的部‎分：含'e'的顺序子集‎，只有它自己‎。

据以上分析‎，可得知，这是一个递‎归的过程。

随即设计出‎的算法代码‎如下：#inclu‎d e<stdio‎.h>#inclu‎d e<strin‎g.h>void BFS(char s[], int n);//主要功能的‎实现函数声‎明：宽度优先遍‎历char resul‎t[]="abcde‎";//保存子集的‎字符数组int count‎=0; //子集个数计‎数器int level‎=0; //保存当前路‎径长度int main(){char str[]="abcde‎";int len =strle‎n(str);for (int i=0;i< len;i++)//依次输出'a','b','c','d','e'为根的所有‎子树的遍历‎结果{BFS(str+i, strle‎n(str+i));}retur‎n 0;}//深度优先遍‎历算法。

C语⾔实现输⼊⼀个字符串后打印出该字符串中字符的所有排列本⽂实例讲述了C语⾔实现输⼊⼀个字符串后打印出该字符串中字符的所有排列的⽅法，属于数学⾥的排列问题。

是⼀个很实⽤的算法技巧。

分享给⼤家供⼤家参考。

具体实现⽅法如下：例如输⼊字符串abc，则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。

C语⾔实现代码如下：/** Copyright (c) 2011 alexingcool. All Rights Reserved.*/#include <iostream>#include <algorithm>using namespace std;char array[] = {'a', 'b', 'c'};const int size = sizeof array / sizeof *array;void Perm(char *array, int pos, int last){if (pos == last) {copy(array, array + size, ostream_iterator<char>(cout, ""));cout << endl;}else {for(int i = pos; i <= last; i++) {swap(array[i], array[pos]);Perm(array, pos + 1, last);swap(array[i], array[pos]);}}}void main(){Perm(array, 0, 2);}希望本⽂所述实例对⼤家C程序算法设计的学习有所帮助。

全排列的生成算法对于给左的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。

字典序法按照字典序求下一个排列的算法广例字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是：123,132,213,231,312,321o注意一个全排列可看做一个字符串，字符串可有前缀、后缀/生成给泄全排列的下一个排列所谓一个全排列的下一个排列就是这一个排列与下一个排列之间没有其他的排列。

这就要求这一个排列与下一个排列有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。

广例839647521是1—9的排列。

1—9的排列最前而的是123456789,最后而的是987654321,从右向左扫描若都是增的，就到了987654321,也就没有下一个了。

否则找出第一次出现下降的位置。

算法：由P1P2...Pn生成的下一个排列的算法如下：1求j=max{j| Pj-I<pj}2.求|=max{k| Pi-1<Pk }3.交换Pi-1与PI得到P1P2...PI-1 （P i....Pn ）,将红色部分顺序逆转，得到结果.例求839647521的下一个排列1.确定i,从左到右两两比较找出后一个数比前一个大的组合，在这里有39 47,然后i 取这些组中最到的位宜号（不是最大的数）在这两组数中7的位置号最大为6,所以i=62.确立I.找岀在i （包括i）后面的所有比i前面那一位大的数的最大的位置号，在此例中7, 5都满足要求，则选5, 5的位置号为7,所以1=73.先将4和5交换，然后将5后的四位数倒转得到结果8396574213 839651247以上算法是在数论课上老师给岀的关于字典序全排列的生成算法，以前也经常要用到全排列生成算法来生成一个全排列对所有的情况进行测试，每次都是现到网上找一个算法，然后直接copy代码，修改一下和自己的程序兼容就行了，也不看是怎么来的，不是我不想看，实在是说的很抽象，那一大堆公式来吓人，一个实例都不给，更有甚者连算法都没有，只是在那里说，想看都看不懂，也没那个耐心取理解那些人写出来的那种让人无法忍受的解释。

全排列算法思路解析
全排列算法是一种基础的算法，用于对给定的一组数据进行全排列。

在程序设计中，全排列算法常常被运用于组合、排序等场景，是一种十分常见的算法。

算法流程如下：
1.设将要排列的元素存在一个字符串S中；
2.将S中的每个字符依次与它后面的字符交换；
3.当S中只剩下一个字符时，输出S；
5.当排列到最后一个元素时，依次输出字符串S的每一个字符，得到一个新的排列。

在算法流程的执行过程中，我们必须清楚的是，每一次交换操作都会对S字符串进行修改。

此外，我们还需要对S字符串的长度和当前元素的位置进行追踪和控制，保证每一个元素都能够交换到相应的位置上。

全排列算法的时间复杂度很高，是O(n!)，所以在实际使用中需要耐心地等待程序的执行结果。

总的来说，全排列算法虽然看似简单，但它将我们的编程思维与编程技巧提高到了一个新的水平。

在日常编程的实践中，我们将许多的算法融入到自己的程序中，体现出了我们的编程思维严谨、技巧娴熟，是一种十分有意义的学习与实践过程。

主题：Python中常用的排列组合算法内容：1. 简介：Python是一种功能强大且易于学习的编程语言，其内置的库和模块使得许多复杂的算法变得易于实现。

在本文中，我们将讨论Python 中常用的排列组合算法，这些算法对于解决许多实际的问题都非常有用。

2. 排列算法：2.1 字符串的全排列：Python中可以使用`itertools`库中的`permutations`函数来获取一个字符串的所有排列。

2.2 数组的全排列：利用递归和交换元素的方式可以实现数组的全排列算法，该算法可以用来解决诸如旅行商问题等实际问题。

3. 组合算法：3.1 组合的生成：使用`itertools`库中的binations`函数可以获取一个序列的所有组合。

3.2 组合的求解：通过递归和回溯的方式可以实现组合的求解，这种方法在解决组合优化问题时非常有用。

4. 应用实例：4.1 排列和组合在密码学中的应用：排列和组合算法可以用来生成各种密码的可能组合，这对于破解密码以及设计安全的密码系统都非常重要。

4.2 排列和组合在商品排列组合的应用：在电商领域，排列和组合算法可以用来对商品进行排序和组合，以实现更好的推荐系统。

5. 总结：Python中的排列组合算法在解决实际问题中具有重要的作用，通过充分利用Python的内置库和函数，我们可以快速高效地实现各种排列组合算法。

这些算法不仅可以用来解决计算问题，还可以应用于密码学、商业推荐等实际场景中。

通过以上内容，我们可以了解Python中常用的排列组合算法以及它们在实际应用中的重要性，相信这些知识对于读者来说将是非常有价值的。

6. 代码示例：6.1 字符串的全排列示例：```pythonimport itertoolss = "abc"perm = itertools.permutations(s)for p in perm:print(''.join(p))```6.2 数组的全排列示例：```pythondef permute(nums):def backtrack(start):if start == len(nums):result.append(nums[:])returnfor i in range(start, len(nums)):nums[i], nums[start] = nums[start], nums[i] backtrack(start + 1)nums[i], nums[start] = nums[start], nums[i]result = []backtrack(0)return resultnums = [1, 2, 3]print(permute(nums))```6.3 组合的生成示例：```pythonimport itertoolss = "abcd"b = itertoolsbinations(s, 2)for c inb:print(''.join(c))```6.4 组合的求解示例：```pythondefbine(n, k):def backtrack(start, path): if len(path) == k:result.append(path[:]) returnfor i in range(start, n + 1): path.append(i)backtrack(i + 1, path) path.pop()result = []backtrack(1, [])return resultn = 4k = 2printbine(n, k))```7. 进阶应用：7.1 排列组合在数据挖掘中的应用：在数据挖掘领域，排列组合算法常常用于特征选择和模式发现，通过对特征的各种排列组合进行分析可以发现隐藏在数据中的规律和趋势。

C#字符串全排序排列：从n个元素中任取m个元素，并按照⼀定的顺序进⾏排列，称为排列；全排列：当n==m时，称为全排列；⽐如：集合{ 1,2,3}的全排列为：{ 1 2 3}{ 1 3 2 }{ 2 1 3 }{ 2 3 1 }{ 3 2 1 }{ 3 1 2 }我们可以将这个排列问题画成图形表⽰，即排列枚举树，⽐如下图为{1,2,3}的排列枚举树，此树和我们这⾥介绍的算法完全⼀致；算法思路：(1)n个元素的全排列=（n-1个元素的全排列）+（另⼀个元素作为前缀）；(2)出⼝：如果只有⼀个元素的全排列，则说明已经排完，则输出数组；(3)不断将每个元素放作第⼀个元素，然后将这个元素作为前缀，并将其余元素继续全排列，等到出⼝，出⼝出去后还需要还原数组； static void Main(string[] args){string s = "123";char[] str = s.ToCharArray();perm(str, 0, s.Length);//permNotSame(str, 0, s.Length);}/// <summary>/// 全排序/// </summary>/// <param name="a"></param>/// <param name="begin"></param>/// <param name="end"></param>static void perm(char[] a, int begin, int end){if (begin == end){for (int i = 0; i < begin; i++){Console.Write(a[i]);}Console.WriteLine("");}else{for (int j = begin; j < end; j++){swap(a, begin, j);perm(a, begin + 1, end);swap(a, j, begin);}}}/// <summary>/// 交换数组索引x和y位置的值/// </summary>/// <param name="a"></param>/// <param name="x"></param>/// <param name="y"></param>static void swap(char[] a, int x, int y){char temp = a[x];a[x] = a[y];a[y] = temp; } 测试结果：。

c语言字符串全排列算法在计算机科学中，字符串全排列算法是一种常见的算法，它用于生成一个字符串的所有可能排列。

这对于测试算法或解决一些涉及字符串的问题非常有用。

下面，我们将介绍一种使用C语言实现字符串全排列的算法。

一、算法概述字符串全排列是指将一个字符串的所有字符重新排列，形成所有可能的字符串。

这种方法可以生成所有可能的字符串，其中每个字符都可能出现在任何位置。

二、C语言实现下面是一个使用C语言实现字符串全排列的简单示例代码：```c#include <stdio.h>#include <string.h>void swap(char *x, char *y) {char temp;temp = *x;*x = *y;*y = temp;}void permute(char *a, int l, int r) {int i;if (l == r) {printf("%s\n", a);} else {for (i = l; i <= r; i++) {swap((a + l), (a + i));permute(a, l + 1, r);swap((a + l), (a + i)); // backtrack}}}int main() {char str[100];printf("Enter a string: ");fgets(str, sizeof(str), stdin); // read string from user inputpermute(str, 0, strlen(str) - 1); // call the function to generate all permutationsreturn 0;}```这段代码首先定义了一个交换函数`swap()`，用于交换两个字符的位置。

然后，`permute()`函数用于生成字符串的全排列。

字符串的排列⼀、字符串的排列⽤C++写⼀个函数, 如 Foo(const char *str), 打印出 str 的全排列, 如 abc 的全排列: abc, acb, bca, dac, cab, cba⼀、全排列的递归实现为⽅便起见，⽤123来⽰例下。

123的全排列有123、132、213、231、312、321这六种。

⾸先考虑213和321这⼆个数是如何得出的。

显然这⼆个都是123中的1与后⾯两数交换得到的。

然后可以将123的第⼆个数和每三个数交换得到132。

同理可以根据213和321来得231和312。

因此可以知道——全排列就是从第⼀个数字起每个数分别与它后⾯的数字交换。

找到这个规律后，递归的代码就很容易写出来了：#include<iostream>#include<cstring>#include<assert.h>using namespace std;void foo(char *str,char *begin){assert(str&&begin);if(*begin=='\0'){cout<<str<<endl;}else{for(char *pch=begin;*pch!='\0';pch++){swap(*pch,*begin);foo(str,begin+1);swap(*pch,*begin);}}}int main(){char str[]="abc";foo(str,str);return0;}⼆、去掉重复的全排列的递归实现由于全排列就是从第⼀个数字起每个数分别与它后⾯的数字交换。

我们先尝试加个这样的判断——如果⼀个数与后⾯的数字相同那么这⼆个数就不交换了。

如122，第⼀个数与后⾯交换得212、221。

然后122中第⼆数就不⽤与第三个数交换了，但对212，它第⼆个数与第三个数是不相同的，交换之后得到221。

利用递归的思想using System;using System.Collections.Generic;using System.Text;nam espace Test{class Program{static void Main(string[] args){//我们做一个最简单的排列组合，求出字符串的全排列.char[] arr_char =new char[] { 'A', 'B', 'C', 'D','E' };string[] result = get_all_position(null,arr_char,arr_char.Length);Console.WriteLine(string.Join(",",result));Console.WriteLine("元素个数: " + result.Length.ToString() +" 个");Console.ReadLine();}static string[] get_all_position(string[] all_position, char[] arr_char, int level) {string[] base_position =null;if (level == 0)return new string[] { arr_char[0].ToString() };elsebase_position = get_all_position(all_position, arr_char, level - 1);if (level == arr_char.Length)return base_position;char new_char = arr_char[level];int string_length =0;if (base_position.Length >0)string_length = base_position[0].Length;string[] new_position =new string[base_position.Length * (level+1)];for (int i =0; i < base_position.Length; i++){new_position[(string_length+1) * i] = new_char + base_position[i];for (int k =0; k < string_length; k++){new_position[(string_length+1) * i + k +1] = base_position[i][k] + base_position[i].Replace(base_position[i][k], new_char);}}return new_position;}}}C# 实现任意字符串全排列（递归）有一个字符串，用程序实现其全部排列组合，比如“ABC”其排列组合是”ABC“"ACB""BCA"”BAC“"CAB""CBA",程序实现如下：using System;using System.Collections.Generic;using System.Text;using System.Collections;using System.Configuration;using System.Diagnostics;using System.Globalization;using ;using System.IO;namespace ConsoleApplication1{public class Program{static void Main(string[] args){string fenjie = "ABCDE";DateTime d = DateTime.Now;Console.WriteLine(d);DiGui(fenjie, fenjie.Length - 1, fenjie.Length - 1);DateTime f = DateTime.Now;Console.WriteLine(f);TimeSpan r = f.Subtract(d);Console.WriteLine(r.TotalMilliseconds.ToString());}private static void DiGui(string str, int iMudi, int iBiandong) {if (str.Length >= 2){if (iMudi == 1 && iBiandong == 1){string shuchu1 = str;string[] strtemp = new string[] { str[str.Length - 2].ToString(), str[str.Length - 1].ToString() };string shuchu2 = str.Remove(str.Length - 2);shuchu2 += strtemp[1] + strtemp[0];Console.WriteLine(shuchu1);Console.WriteLine(shuchu2);}else{for (int i = iBiandong; i >= 0; i--){string newStr = "";for (int k = 0; k < str.Length; k++){if (k == str.Length - 1 - i){newStr += str[str.Length - 1 - iMudi].ToString();}else if (k == str.Length - 1 - iMudi){newStr += str[str.Length - 1 -i].ToString();}else{newStr += str[k].ToString();}}DiGui(newStr, iMudi - 1, iBiandong - 1);}}}}}}将字符串“abc”全排列成：abc、acb、bac、bca、cab、cba using System;using System.Collections.Generic;using System.Windows.Forms;namespace ThreeB{static class Program{/// <summary>/// 应用程序的主入口点。

字符串从小到大排序算法
有很多种方法可以将字符串从小到大进行排序，以下是几种常见的排序算法：
1. 冒泡排序（Bubble Sort）：通过反复交换相邻的两个元素，
每一轮将最大的元素沉到最后面，直到所有元素都有序。

时间复杂度为 O(n^2)。

2. 选择排序（Selection Sort）：每一轮选择未排序部分的最小
元素，将其依次放在已排序部分的末尾，直到所有元素都有序。

时间复杂度为 O(n^2)。

3. 插入排序（Insertion Sort）：每次将一个未排序元素插入到
已排序的合适位置上，直到所有元素都有序。

时间复杂度为
O(n^2)。

4. 快速排序（Quick Sort）：通过一趟排序将待排序序列分割
成独立的两部分，其中一部分的所有元素都比另一部分的所有元素小，然后再递归地对这两部分进行排序。

时间复杂度为
O(nlogn)。

5. 归并排序（Merge Sort）：将待排序序列不断二分，直到每
个子序列只有一个元素，然后将相邻的子序列合并在一起，最终得到有序序列。

时间复杂度为 O(nlogn)。

根据具体的需求和数据规模，选择合适的排序算法。

【codeup】1959：全排列及全排列算法详解题⽬描述给定⼀个由不同的⼩写字母组成的字符串，输出这个字符串的所有全排列。

我们假设对于⼩写字母有'a' < 'b' < ... < 'y' < 'z'，⽽且给定的字符串中的字母已经按照从⼩到⼤的顺序排列。

输⼊输⼊只有⼀⾏，是⼀个由不同的⼩写字母组成的字符串，已知字符串的长度在1到6之间。

输出输出这个字符串的所有排列⽅式，每⾏⼀个排列。

要求字母序⽐较⼩的排列在前⾯。

字母序如下定义：已知S = s1s2...sk , T = ，则S < T 等价于，存在p (1 <= p <= k)，使得s1 = t1, s2 = t2, ..., sp - 1 = tp - 1, sp < tp成⽴。

注意每组样例输出结束后接⼀个空⾏。

样例输⼊xyz样例输出xyzxzyyxzyzxzxyzyx提⽰⽤STL中的next_permutation会⾮常简洁。

思路：由于题⽬提⽰使⽤next_permutation会简洁，所以这⾥我们使⽤此⽅法。

1 #include<iostream>2 #include<stdio.h>3 #include<queue>4 #include<string>5 #include<string.h>6 #include<algorithm>7using namespace std;89char a[10];1011int main()12 {13int n;14while(scanf("%s",a)!=EOF)15 {16 n=strlen(a);17do18 {19 printf("%s\n",a);20 }while(next_permutation(a,a+n));21 puts("");22 }23return0;24 }C++/STL中定义的next_permutation和prev_permutation函数是⾮常灵活且⾼效的⼀种⽅法，它被⼴泛的应⽤于为指定序列⽣成不同的排列。

Yiqiang Wei <weiyiqiang@>
1.5.1字典序法
方法2-1：
由72642321推算出839647521 中介数右端加一个 0扩成0 9位，先定 1，每定 72642321中未出现 ，1在最右边 一位，其左边未定位下加一点，从（位－ 位下点数=0）的位中选最左的。
=279905
Yiqiang Wei <weiyiqiang@>
1.5.2递增进位制数法 由(anan-1…a2)↑求p1p2…pn。
从大到小求出n,n-1,…,2,1的位置 _ ... _ n _ _ …_
\______ ______/ V
an个空格 n的右边有an个空格。 n-1的右边有an-1个空格。 ………… 2的右边有a2个空格。 最后一个空格就是1的位置。
83964752 1 726423210
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
2 的位置 3 4 5 6 7 8 9 定 1
Yiqiang Wei <weiyiqiang@>
1.5.1字典序法
方法2-2：
由72642321推算出839647521 已定出上标‘●’，找左起第一个0，下标‘__’
※※ 两个字符串，相同前缀越长的越靠近。
Yiqiang Wei <weiyiqiang@>
1.5 全排列的生成算法
如何生成给定全排列的下一个排列 所谓一个的下一个就是这一个与下一个之间没有 其他的。这就要求这一个与下一个有尽可能长 的共同前缀，也即变化限制在尽可能短的后缀 上。 例如 839647521是1--9的排列。1—9的排列最前 面的是123456789，最后面的是987654321，从 右向左扫描若都是增的，就到了987654321，也 就没有下一个了。否则找出第一次出现下降的 位置。

字符串的全排列（字典序排列）题⽬描述输⼊⼀个字符串，打印出该字符串中字符的所有排列。

例如输⼊字符串abc，则输出由字符a、b、c 所能排列出来的所有字符串abc, acb, bac, bca, cab, cba。

题⽬分析穷举与递归⼜是⼀个经典问题，最容易想到的解决⽅法仍然是穷举（我实在是太爱穷举法了，每当被问到算法问题不知道如何解决的时候，总可以祭出穷举⼤旗，从⽽多争取3分钟的思考时间）。

穷举虽好，但它⼤多数情况下都不是被需要的那个答案，是因为看起来代码太Low不够⾼⼤上吗？在这种情况下，穷举法裹着貂⽪⼤⾐的亲戚——递归就出现了。

虽然空间复杂度和时间复杂度没有任何改进，⽽且还增加了系统开销（关于递归法的系统开销不在这⾥讨论，之后再找专门的时间阐述），但是就是因为长得好看（代码看起来精炼），递归的B格⼉就⾼了很多。

递归法对于这个题⽬同样⾮常适⽤，基本思路就是固定⼀个字符，然后对剩余的字符做全排列……不赘述，请⾃⼰想。

如果你也跟我⼀样永远想不明⽩递归，那就画画图，写写代码，debug⼀下，每天花3-4个⼩时，静下⼼来仔细捉摸，总（ye）会（bu）想（hui）明⽩的。

贴⼀段July和他伙伴们在《程序员编程艺术：⾯试和算法⼼得》中的代码实现，供做噩梦时使⽤。

p.s. 我已加了注释/** Permute full array of input string by general recusion* @ char* perm [in/out] The string need to do permutation* @ int from [in] The start position of the string* @ int to [in] The end position of the string*/void CalcAllPermutation(char* perm, int from, int to){if (to <= 1){return;}if (from == to){//all characters has been permutedfor (int i = 0; i <= to; i++)cout << perm[i];cout << endl;}else{// always select one character, then full array the left ones.for (int j = from; j <= to; j++){swap(perm[j], perm[from]); //swap the selected character to the beginning of stringCalcAllPermutation(perm, from + 1, to); // Permute left characters in full array.swap(perm[j], perm[from]); //recovery the string to original one (swap the selected character back to its position.)}}}字典序这是⼀个⽐递归更有趣的答案，不知道算不算经典解法，起码开拓了思路，跟每⼀次接触新鲜的算法⼀样，仍然想了半天的时间，因此照例把思考过程更细致的记录下来（虽然July和他伙伴们在《程序员编程艺术：⾯试和算法⼼得》中已经说了很多），再加上⼀些⼩修改。

全排列算法之Perm算法实现 题⽬描述： 给定⼀个由不同的⼩写字母组成的字符串，输出这个字符串的所有全排列。

我们假设对于⼩写字母有'a' < 'b' < … < 'y' < 'z',⽽且给定的字符串中的字母已经按照从⼩到⼤的顺序排列。

输⼊： 输⼊只有⼀⾏，是⼀个由不同的⼩写字母组成的字符串，已知字符串的长度在1到6之间。

输出： 输出这个字符串的所有排列⽅式，每⾏⼀个排列。

要求字母序⽐较⼩的排列在前⾯。

字母序如下定义： 已知S = s1s2…sk , T = t1t2…tk,则S < T 等价于，存在p （1 <= p <= k），使得 s1 = t1, s2 = t2, …， sp - 1 = tp - 1, sp < tp成⽴。

样例输⼊： abc 样例输出： abc acb bac bca cab cba 提⽰： 每组样例输出结束后要再输出⼀个回车。

想必⼤家对perm递归算法求全排列并不陌⽣，但我贴出来的题⽬却不能⽤perm算法来解决，为什么呢？请容我慢慢道来，⾸先题⽬对全排列有着⾮常严格的顺序要求，即按字典顺序排列，就是这个perm算法是满⾜不了的（或许经过⼩⼩的改变是可以实现的，我们在这⾥就不讨论了）。

那么下来我来谈谈perm算法的核⼼思：举个例⼦，⽐如要你1的全排列，你肯定会说那还不简单啊，那么接下来加深难度求1,2的全排列，其实也不难，现在让你求1,2,3,4,5的全排列呢，还转得过来吗？现在我们可以这样想，3,4,5的全排列是以3开头的4,5的全排列组合和4开头的3,5的全排列组合以及以5开头的3,4全排列组合。

这就是perm算法的核⼼思想，列出⼀个通俗⼀点的式⼦ 从⽽可以推断，设⼀组数p = {r1, r2, r3, … ,rn}, 全排列为perm（p），pn = p - {rn}. 因此perm（p） = r1perm（p1）， r2perm（p2）， r3perm（p3）， … , rnperm（pn）。