圆曲线坐标计算(坐标正算法)

一、坐标正算与坐标反算 1、坐标正算 已知 点的坐标、 边的方位角、 两点间的水平距离，计算待 定点 的坐标，称为坐标正算。

如图 6-6 所示，点的坐标可由下式计 算：式中 、 为两导线点坐标之差，称为坐标增量，即：【例题 6-1】已知点 A 坐标， =1000 、 =1000 、方位角 =35°17＇36.5"， 两点水平距离 =200.416 ，计算 点的坐标？35o17＇36.5"=1163.580 35o17＇36.5"=1115.793 2、坐标反算 已知 两点的坐标，计算 两点的水平距离与坐标方位角， 称为坐标反算。

如图 6-6 可知，由下式计算水平距离与坐标方位角。

（6-3） （6-4） 式中反正切函数的值域是-90°～+90°，而坐标方位角为 0°～ 360°，因此坐标方位角的值，可根据 、 的正负号所在象限，将反 正切角值换算为坐标方位角。

【例题 6-2】 =3712232.528 、 =523620.436 、 =3712227.860 、 =523611.598 ，计算坐标方位角计算坐标方位角、水平距离 。

=62°09＇29.4"+180°=242°09＇29.4"注意：一直线有两个方向，存在两个方位角，式中：、的计算是过 A 点坐标纵轴至直线 的坐标方位角，若所求坐标方位角为，则应是 A 点坐标减 点坐标。

坐标正算与反算，可以利用普通科学电子计算器的极坐标和直角坐标相互转换功能计算，普通科学电子计算器的类型比较多，操作方法不相同，下面介绍一种方法。

【例题 6-3】坐标反算，已知 =2365.16 、 =1181.77 、=1771.03 、 =1719.24 ，试计算坐标方位角 、水平距离 。

键入 1771.03-2365.16 按等号键［=］等于纵坐标增量，按储存键［ ］，键入 1719.24-1181.77 按等号键［=］等于横坐标增量，按［ ］键输入，按［ ］显示横坐标增量，按［ ］键输入，按第二功能键［2ndF］，再按［ ］键，屏显为距离，再按［ ］键，屏显为方位角。

坐标正算的公式是什么在地图制图和定位导航系统中，坐标正算是一种重要的计算方法，用于计算出给定地理位置的坐标值。

坐标正算通常基于已知的参考点或者经纬度等信息，计算出目标点的坐标。

本文将介绍坐标正算的公式和计算过程。

坐标正算的基本原理坐标正算基于几何学和数学原理，通过一些特定的计算公式，将地理位置的描述转换为具体的坐标值。

在进行坐标正算之前，需要明确一些基本信息，例如已知参考点的坐标、目标点与参考点的距离和方位角等。

计算目标点坐标的步骤下面是一个常见的坐标正算的步骤：1.确定参考点坐标：首先需要确定至少一个已知坐标的参考点，可以是已知的地理位置或者其他参考点的坐标。

2.测量目标点与参考点之间的距离和方位角：使用合适的测量方法，测量目标点与参考点之间的水平距离和方位角。

这些信息可以由仪器测量，也可以通过其他方法估算得出。

3.计算目标点的坐标：根据已知的参考点坐标、目标点与参考点的距离和方位角，应用特定的计算公式进行坐标计算。

不同的计算方法可能有不同的公式，但基本原理是一致的。

常用的坐标正算公式在不同的坐标系统和进行坐标正算的方法中，可能会使用不同的公式和算法。

以下是一些常见的坐标正算的公式：•平面坐标正算公式：对于平面坐标系统，常见的方法是使用平面直角坐标系或UTM坐标系统。

在这种情况下，可以使用已知参考点的坐标、目标点与参考点的距离和方位角来计算目标点的坐标。

具体的公式可以根据不同的坐标系统而有所不同。

•大地坐标正算公式：对于大地坐标系统，常用的方法是使用经纬度来表示坐标。

在这种情况下，可以通过已知参考点的经纬度以及目标点与参考点的距离和方位角，应用大地测量学中的公式计算目标点的经纬度。

•三角形法：坐标正算中常用的计算方法是三角形法。

通过已知点的坐标和目标点与已知点之间的距离和方位角，可以构建一个三角形模型，然后使用三角函数和三角关系来计算目标点的坐标。

这种方法在平面坐标和大地坐标系统中都可以使用。

坐标正反算定义及公式坐标正算和反算是地图投影中的重要概念，用于将地球表面上的经纬度坐标转换为平面坐标（正算），或将平面坐标转换为经纬度坐标（反算）。

这种转换是为了方便地图上的测量和计算。

坐标正算是指根据地球表面上的经纬度坐标，计算出对应的平面坐标。

在这个过程中，需要考虑地球的形状、椭球体模型以及地图投影方法等因素。

不同的投影方法会导致不同的坐标正算公式，下面简单介绍两种常用的投影方法及其公式。

1.经纬度-平面直角坐标投影（简称平面直角投影）平面直角投影是将地球表面上的经纬度坐标转换为平面直角坐标的一种常用方法。

在平面直角投影中，地球被近似为一个大椭球体，通过将经纬度坐标映射到一个平面上完成转换。

公式如下：X = N * (L - L0) * cosφ0Y=N*(φ-φ0)其中，X和Y为平面直角坐标，L和φ分别为经纬度坐标，L0和φ0分别为中央经线和标准纬线，N为椭球的半径。

2.地心正投影（简称球面正投影或者高斯正算）地心正投影是一种在地心球面上进行的坐标正算方法，适用于小范围的地图投影。

在地心正投影中，将地球看作一个球体，并通过一个中央经线来进行投影。

公式如下：X = A * (L - L0) * cosφY=A*(φ-φ0)其中，X和Y为平面直角坐标，L和φ分别为经纬度坐标，L0和φ0分别为中央经线和标准纬线，A为一个与椭球参数相关的常数。

坐标反算是指根据平面坐标计算出对应的经纬度坐标。

在坐标反算中，需要将平面坐标反映射回地球表面，恢复为经纬度坐标。

与坐标正算类似，不同的投影方法会导致不同的坐标反算公式，下面介绍两种常用的投影方法及其公式。

1.平面直角坐标-经纬度投影（平面直角反算）平面直角反算是将平面直角坐标转换为地球表面上的经纬度坐标的一种方法。

利用与坐标正算相反的操作，将平面直角坐标通过逆转换还原为经纬度坐标。

公式如下：φ=φ0+Y/NL = L0 + X / (N * cosφ0)其中，φ和L分别为经纬度坐标，φ0和L0分别为标准纬线和中央经线，X和Y为平面直角坐标，N为椭球的半径。

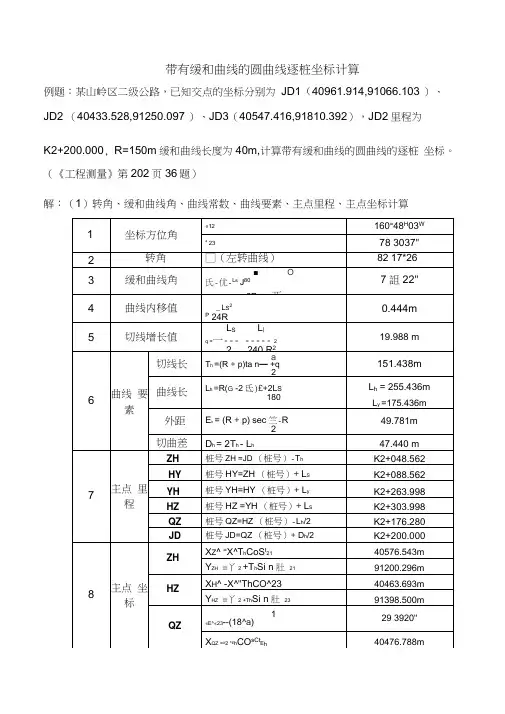
带有缓和曲线的圆曲线逐桩坐标计算
例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103 ）、JD2 （40433.528,91250.097 ）、JD3（40547.416,91810.392），JD2里程为
K2+200.000, R=150m缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）
解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算
方法一：偏角法（坐标正算）
（2）第一缓和段坐标计算-0=7 3822 5 = 160 48 03
X Y
(4)第二缓和段坐标计算.0 = 7 38 22
方法二：切线支距法（坐标系转换）
（2）第一缓和段坐标计算
：-12 =160 48 03
X j =X Z H+ xcosot12+ y si n%2X=X ZH+ xs in a12 - yco^t12（本题为左转曲线）
(3) 圆曲线段坐标计算
0=73822 p = 0.444m q = 19.988m
12 =160 48 03 ZH( 40576.543 , 91200.296)
X i = X ZH xcos：12 ysin：12 Y =Y ZH xsin：12一ycos：12
:12=78 30 37
X i =X HZ—xcosc(23 +ysin o(23 Y =Y HZ— xsin53 _yco^t23 (本题为左转曲线)。

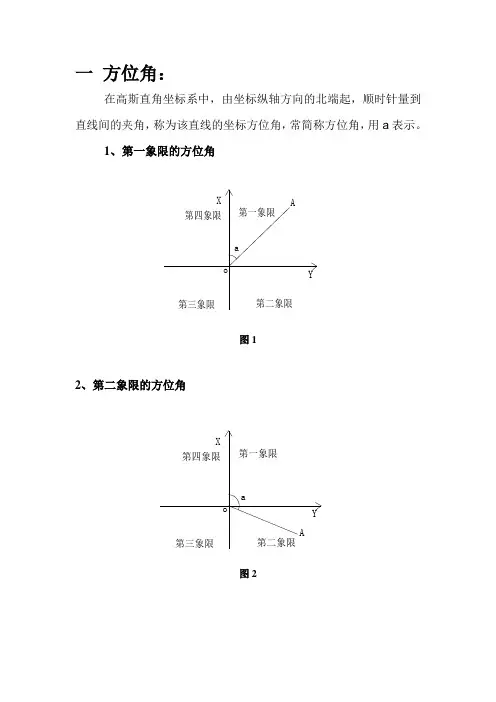
一 方位角：在高斯直角坐标系中，由坐标纵轴方向的北端起，顺时针量到直线间的夹角，称为该直线的坐标方位角，常简称方位角，用a 表示。

1、第一象限的方位角YX第一象限第二象限第三象限第四象限oAa图12、第二象限的方位角Y X第一象限第二象限第三象限第四象限oAa图23、第三象限的方位角YX第一象限第二象限第三象限第四象限o Aa图34、第四象限的方位角YX第一象限第二象限第三象限第四象限oAa图4方位角计算公式：x=a -1tanA Y O Y -AX OX-方位角的计算器计算程序：Pol(X A -X O ,Y A -Y O )直线OA 方位角度值赋予给计算器的字母J ，0≤J ＜360。

直线段OA 的距离值赋予给计算器的字母I,I ＞0 直线OA 与直线AO 的方位角关系： 1、当直线OA 的方位角≤180°时，其反方位角等于a+180°。

2、 当直线OA 的方位角＞180°时，其反方位角等于a-180°。

二 方位角的推算 （一）几个基本公式 1、坐标方位角的推算或：注意：若计算出的方位角>360°，则减去360°；若为负值，则加上360°。

例题:方位角的推算已知：α12=30°，各观测角β如图，求各边坐标方位角α23、α34、α45、α51。

13图5解： α23= α12-β2+180°=30°-130°+180°=80°α34= α23-β3+180°=80°-65°+180°=195°α45=α34-β4+180°=195°-128°+180°=247°α51=α45-β5+180°=247°-122°+180°=305°α12=α51-β1+180°=305°-95°+180°=30°（检查）三坐标正算一、直线段的坐标计算oB DACEaap图6设起点O的坐标（X O,Y O）,直线OP的方位角为F op，求A、C、E点的坐标1、设直线段OA长度为L,则A点坐标为X A=X O+L×Cos(F op)Y A=Y O+L×Sin(F op)2、设直线段OB长度为L OB,直线段BC长度为L BC,则C点坐标为X B=X O+L OB×Cos(F op)Y B=Y O+L OB×Sin(F op)直线BC的方位角F BC=F op+aIF F B C＞360°:Then F BC-360°→F BC:IfEndX C=X B+L BC×Cos(F BC)Y C=Y B+L BC×Sin(F BC)3、设直线段OD长度为L,直线段DE长度为L DE,则E点坐标为ODX D=X O+L OD×Cos(F op)Y D=Y O+L OD×Sin(F op)直线DE的方位角F DE=F op-aIF F DE＜0°:Then F DE+360°→F DE:IfEndX E=X D+L DE×Cos(F DE)Y E=Y D+L DE×Sin(F DE)二、缓和曲线段的坐标计算x Y 00=L- +=L 40R L 52s 2L3456R L 94s 4L 6R L 3s L 336R L 7s 33-90 L πRL sO2切线角=设完整缓和曲线起点O 的坐标为O （XO,YO ）,方位角为F ，曲线长度为L S ,曲线上任一点的曲线长度为L,当线路右转时直线CP 的方位角Fcp=F+90°IF F cp ＞360°:Then F cp-360°→F cp :IfEnd当线路左转时直线CP 的方位角Fcp=F-90°IF F cp＜0°:Then F cp+360°→F cp:IfEndX P=X O+Abs(x O)×Cos(F)+Abs(y O)×COS(F CP)Y P=Y O+Abs(x O)×Sin(F)+Abs(y O)×Sin(F CP)三、圆曲线段的坐标计算圆曲线的已知点数据为起点S的桩号K s、走向方位角αs、起点S 坐标为（X o,Y o）、圆曲线半径为R与曲线长为L。

坐标正反算一、坐标正算与坐标反算1、坐标正算已知点的坐标、边的方位角、两点间的水平距离，计算待定点的坐标，称为坐标正算。

如图6-6所示，点的坐标可由下式计算：式中、为两导线点坐标之差，称为坐标增量，即：=1000、=1000、方位角【例题6-1】已知点A坐标，=35°17＇36.5\，2、坐标反算已知两点的坐标，计算两点水平距离=200.416，计算点的坐标？35o17＇36.5\35o17＇36.5\两点的水平距离与坐标方位角，称为坐标反算。

如图6-6可知，由下式计算水平距离与坐标方位角。

（6-3）（6-4）式中反正切函数的值域是-90°～+90°，而坐标方位角为0°～360°，因此坐标方位角的值，可根据正切角值换算为坐标方位角。

、的正负号所在象限，将反【例题6-2】=3712227.860、、水平距离=3712232.528、=523620.436、=523611.598，计算坐标方位角计算坐标方位角。

=62°09＇29.4\29.4\注意：一直线有两个方向，存在两个方位角，式中：、的计算是过A点坐标纵轴至直线的坐标方位角，若所求坐标方位角为，则应是A点坐标减点坐标。

坐标正算与反算，可以利用普通科学电子计算器的极坐标和直角坐标相互转换功能计算，普通科学电子计算器的类型比较多，操作方法不相同，下面介绍一种方法。

【例题6-3】坐标反算，已知=1771.03、=2365.16、=1181.77、、水平距离。

=1719.24，试计算坐标方位角键入1771.03-2365.16按等号键［=］等于纵坐标增量，按储存键［］，键入1719.24-1181.77按等号键［=］等于横坐标增量，按［］键输入，按［］显示横坐标增量，按［］键输入，按第二功能键［2ndF］，再按［］键，屏显为距离，再按［］键，屏显为方位角。

【例题6-4】坐标正算，已知坐标方位角=200.40，试计算纵坐标增量横坐标增量=294°42＇51\，。

圆曲线的测设由一定半径的圆弧构成的曲线，称为圆曲线。

在路线中线由一直线方向转变为另一直线方向时，或由一坡度转变为另一坡度时，为保证运行安全，一般在水平方向和竖直方向均设置一定半径的圆曲线。

下面介绍水平方向上圆曲线的测设方法。

（一） 圆曲线的要素及其计算如图10-63所示，A 为某道路中线的起点，其里程为0+000，道路中线由AJ D 1方向转变为另一直线方向J D 1 －JD 2,为了行车安全，需在其间设置平面圆曲线“ZY －QZ －YZ ”，其名称和常用符号结合图10-63介绍如下：R ——圆曲线半径，在测设中根据路线等级及地形条件选定；α——转向角，由设计图纸提供，或在路线定测时实测；JD ——转向点，或称交点，根据工程的设计条件测设；ZY ——直圆点，圆曲线的起点；QZ ——曲中点，圆曲线的中点；YZ ——圆直点，圆曲线的终点；T ——切线长，JD 至ZY(YZ)的直线距离；L ——曲线长，ZY 至YZ 的弧长；E ——外矢距，JD 至QZ 的直线距离；q ——切曲差，两倍切线长与曲线长之差。

通常，把T 、L 、E 、q 四元素称为圆曲线要素。

把ZY 、QZ 、YZ 三点称为圆曲线主点。

由图10-64可知，各要素的计算公式如下：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-=⎪⎭⎫ ⎝⎛-⋅=⋅⋅⋅=⋅=︒L T q R E R L tg R T 212sec 1802απαα （10-25）（二） 圆曲线主点桩号的计算在线路测量中，曲线段的桩号是按曲线传递的，若已求出圆曲线要素及交点JD 的桩号，则计算圆曲线主点桩号的一般公式如下：⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=-=22L QZ YZ L ZY QZ T JD ZY 桩号桩号桩号桩号桩号桩号 （10-26） 主点桩号的检核，可用切曲差q 来验算，其公式为：q T JD YZ -+=桩号桩号（三） 圆曲线主点的放样方法求出圆曲线要素之后，可按下述步骤测设圆曲线主点：1. 将经纬仪安置于交点J D 1上（见图10-63），分别瞄准起点A 和交点J D 2，从J D 1起沿切线方向用钢尺测设切线长T ，在地面上分别标定出曲线起点ZY 和曲线终点YZ 。

圆曲线中边桩坐标计算公式： L=F-H；注：L---所求点曲线长；F---所求点里程；H---圆曲线起点（ZY点桩号里程）X=XZY+2×R×SIN（L÷2R）×COS｛α±(L÷2R)｝+S×COS｛α±(L÷R)+M｝; Y =YZY+2×R×SIN（L÷2R）×SIN｛α±(L÷2R)｝+S×SIN｛α±(L÷R)+M｝. 注：α---线路方位角；M---所求边桩与路线的夹角；S---所求边桩至中桩的距离；"±"---曲线左偏取“-”右偏取“+”；当S=0时为中桩坐标。

经高速公路施工一线使用效果很好。

记住在公式中加入Excel的Radians（）函数将度转为弧度即可轻松方便地使用，从ZY点坐标准确快速推算地计算出整条圆曲线。

注意要分清左偏右偏两种情况。

高速公路线路坐标计算公式:高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K③曲线终点桩号：K1④曲线起点坐标：x0，y⑤曲线起点切线方位角：α⑥曲线起点处曲率：P(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

曲线坐标计算程序关键词：曲线坐标计算EXCEL编程坐标曲线坐标实例摘要：利用EXCEL强大的函数功能通过曲线坐标计算的知识编制成曲线计算坐标的计算程序。

简单的输入曲线的里程桩号，通过坐标旋转、平移结合可以快速的计算完成与线路成任意角度的曲线上各中桩、边桩以及任意点坐标的计算。

1、概述一般计算圆曲线可用坐标正算直接进行计算，具体思路和求解步骤，这里不再阐述。

若计算带有缓和曲线的圆曲线时，将测量中所学的支距法与坐标旋转、平移结合在一起，利用EXCEL表中强大的函数自动计算功能，准确快速的完成对缓和曲线的坐标计算。

比一般的手工计算快10～20倍，比CAD绘图计算快5～10倍。

并可以应用来指导工程施工、施工放样、审核图纸等工作。

2、计算过程分段在计算带有缓和曲线的圆曲线或圆曲线时，只要输入待求点的里程，程序将会自动会计算线路中桩的坐标、与中桩有一定夹角、距离的边桩坐标，与边桩中心线任意夹角的垂直桩基坐标。

若要计算其他的距离和夹角的坐标，相应的修改待求点里程、夹角和距离。

2.1、程序初始化:输入每个曲线所对应交点的半径、缓和曲线长、线路转角、连续三交点的里程和坐标、交点连线的坐标方位角，顺便计算出各个曲线要素以及曲线各主点的里程。

2。

2、初直线H Z i—1～ZH i段:(1)X ZHi—1和Y ZHi-1的计算X ZHi—1= X JDi—1+T i-1×cos(A i-1，i）Y ZHi—1= Y JDi—1+ T i-1×sin（A i-1,i）其中：T iJD i-1曲线的切线长；—1-—A i-1，i——JD i—1与JD i直线的坐标方位角；X JDi-1、Y JDi—1—-JD i-1的坐标；X ZHi—1、Y ZHi—1—-JD i-1对应的ZH点坐标。

(2)中桩计算公式：X中=L A×cos（A i—1,i)+ X ZHi—1Y中= L A×sin(A i-1,i)+ Y ZHi-1其中:L A—-待求点与ZH i的里程差;A i—1，i—-JD i-1与JD i直线的坐标方位角;X中、Y中——待求点里程的中桩坐标；其余符号同上。

圆曲线任意点坐标计算简易方法
周旭
【期刊名称】《矿山测量》
【年(卷),期】2010(000)005
【摘要】文中利用平面几何学"同弧上的弦切角等于所对圆心角的一半"定理,解决圆曲线上任意点坐标计算中方位角推算方法,此方法可直接得到圆曲线上任意点的坐标方位角和边长,省略了标准计算方法通过切点为中间过渡的计算办法,最重要的在计算坐标前就得到放线参数而无需通过坐标反算再得到放线数据.此法在计算和施工中极为便利,能迅速得到圆曲线上任意点坐标和放线参数.对测量施测和工程设计中有较好的应用价值.
【总页数】2页(P43-44)
【作者】周旭
【作者单位】陕西煎茶岭镍业有限公司,陕西,略阳,724207
【正文语种】中文
【中图分类】P212+.2
【相关文献】
1.公路曲线任意点中边桩坐标计算编程及放样 [J], 张智杰
2.关于连接两圆曲线的缓和曲线任意点坐标计算方法 [J], 朱志全
3.圆曲线间缓和曲线任意点坐标计算 [J], 朱峻宏
4.关于连接两圆曲线的曲线任意点坐标计算方法 [J], 朱志全
5.缓圆曲线上任意点的测量坐标计算 [J], 成有杰;刘玉玲
因版权原因，仅展示原文概要，查看原文内容请购买。