《基本平面图形》复习

北师大版数学七年级上册第四章《基本平面图形》复习课教学设计E C A D BE C A D B 教 学 过 程 教 学 过 程 样,在接下来的复习总结中能更系统、更全面。

第二环节：知识回顾，形成体系通过提问课本基本内容并板书知识结构的形式复习本章知识。

设计意图:通过板书整章知识结构,让学生对本章知识之间的联系有更具体的认识,同时在课上对重点的内容进行提问,并着重板书,加深学生的记忆。

第三环节：小组交流， 释疑解惑本环节按知识点组织学生交流解惑、变式总结： 知识点一：线段、直线、射线出示以下两题的几何书写并变式提升:5、如图，在直线上顺次取A ，B ，C 三点，且线段AB=10cm, BC=4cm,O 是线段AC 的中点,求线段AO 的长.变式：在直线上取A ，B ，C 三点，且线段AB=10cm, BC=4cm,O 是线段AC 的中点,求线段AO 的长.6、如图,线段AC=14cm, BC=6cm,C 是线段AB 上一点，D 是线段AC 的中点,E 是线段BC 的中点,求线段DE 的长.变式：如图,线段AB=20cm,C 是线段AB 上一点，D 是线段AC 的中点,E 是线段BC 的中点,求线段DE 的长.设计意图:引导学生独立思考变式的题目，能根据已知条件画图并解决问题，初步体会分类讨论、整体的数学思想。

知识点二：角教学过程出示以下两题的几何书写并变式提升:5、如图，已知：∠AOB＝70°，∠BOC＝30°，OM平分∠AOC，求∠BOM的度数.变式：已知：∠AOB＝70°，∠BOC＝30°，OM平分∠AOC，求∠BOM的度数.6、如图，已知OM平分∠AOC,ON平分∠BOC, ∠AOC=40°，∠COB=60°，求∠MON的度数.变式：如图，已知OM平分∠AOC,ON平分∠BOC,∠AOB=100°，求∠MON的度数.设计意图:引导学生类比线段中解决问题的方法独立思考并解决变式的题目，再次体会分类讨论、整体的数学思想并感受数学中的类比思想。

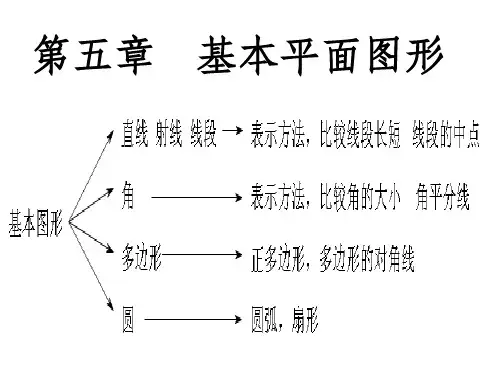
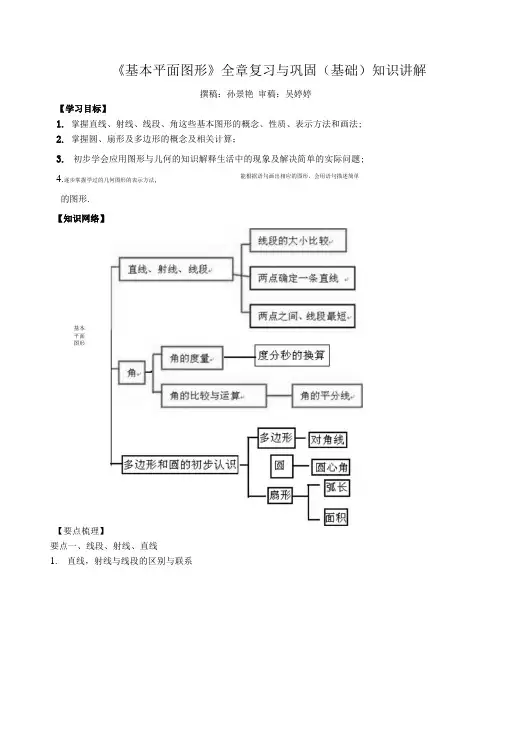
《基本平面图形》全章复习与巩固（基础）知识讲解撰稿：孙景艳审稿：吴婷婷【学习目标】1.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;2.掌握圆、扇形及多边形的概念及相关计算；3.初步学会应用图形与儿何的知识解释生活中的现象及解决简单的实际问题;4.逐步掌握学过的几何图形的表示方法, 能根据语句画出相应的图形，会用语句描述简单的图形.【知识网络】基本平面图形【要点梳理】要点一、线段、射线、直线1.直线，射线与线段的区别与联系类别、直线射线VW，图形 A B ' A B 1 A B1表示方法%1两个大写字母；%1一个小写字母%1再个大写字母(表示端点的字母在筑)；%1一个小写字母①表示两端点的两个大写字号;②一个小写字母端点个数无I个2个延伸性向两方无限延伸向一方无限延伸不可延伸性质两点确定一条宜或两点之间，线段最短SB不可以不可以可以过4、8作直线48以4为端点作射或48连粮48作图叙述2.基本性质(1)直线的性质：两点确定一条直线.(2)线段的性质：两点之间，线段最短.要点诠释：%1本知识点可用来解释很多生活中的现象.如：要在墙上固定一个木条，只要两个钉子就可以了，因为如果把木条看作一条直线，那么两点可确定一条直线.%1连接两点间的线段的长度，叫做两点的距离.3 .画一条线段等于已知线段(1)度量法：可用直尺先量出线段的长度，再画一条等于这个长度的线段.(2)用尺规作图法：用圆规在射线AC上截取AB=a ,如下图：4.线段的比较与运算(1)线段的比较：比较两条线段的长短，常用两种方法，一种是度量法；一种是叠合法.(2)线段的和与差：如下图，有AB+BOAC,或AC二a+b； AD=AB-BD«a A a Bb cb A D B(3)线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点.如下图，有：AM=MB = -AB2 要点诠释:%1线段中点的等价表述：如上图，点M在线段AB上，且有AM=-AB,则点M为线段2AB的中点.%1除线段的中点（即二等分点）夕卜，类似的还有线段的三等分点、四等分点等.如下图，点M, N, P均为线段AB的四等分点.A M N P BAM =MN = NP=PB =、AB4要点二、角1.角的度量（1）角的定义：有公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边；此外，角也可以看作由-•条射线绕着它的端点旋转而形成的图形.（2）角的表示方法：角通常有三种表示方法：一是用三个大写英文字母表示，二是用角的顶点的一个大写英文字母表示，三是用一个小写希腊字母或一个数字表示.例如下图：要点诠释：%1角的两种定义是从不同角度对角进行的定义；%1当一个角的顶点有多个角的时候，不能用顶点的一个大写字母来表示.（3）角度制及角度的换算1周角二360° , 1平角二180° , 1° =60' , 1' =60",以度、分、秒为单位的角的度量制，叫做角度制.要点诠释：%1度、分、秒的换算是60进制，与时间中的小时分钟秒的换算相同.%1度分秒之间的转化方法：由度化为度分秒的形式（即从高级单位向低级单位转化）时用乘法逐级进行；由度分秒的形式化成度（即低级单位向高级单位转化）时用除法逐级进行.%1同种形式相加减：度加（减）度，分加（减）分，秒加（减）秒；超60进一，减一成60.（4）角的分类：五边形（1）n 边形有n 个顶点、n 条边, （5）画一个角等于己知角（1） 借助三角尺能画出15°的倍数的角，在0〜180。

让三亿中国孩子学会学习，学生姓名：学生年级：六年级 任课老师： 讲授科目：数学 时间：教学目标状态激发目标：使学生能够熟练基本图形的意义以及运用。

1. 知识目标：使学生了解基本平面图形。

授课重点难点 教学重点：基本平面图形意义和表示方法。

教学难点：基本平面图形的意义和表示方法以及简单的计算。

教 学 过 程 导学过程：一、知识点回顾：(一)、直线、射线和线段基本概念:1. 线段的定义和表示方法:2. 射线的定义和表示方法3. 直线的定义和表示方法4.直线公理:____________________________________5 线段公理——————————————————————————6、——————————————————————叫两点之间的距离.7、线段的中点: ————————————————————几何语言：（二）、角1．角的定义（两种）2、角的三种表示方法：3、角的度量: 1°= 60′, 1′= 60″4、角平分线意义:————————————几何语言：（三）、多边形多边形是由若干条不在 上的线段首尾顺次相连组成的封闭平面图形。

我们平常所说的多边形都是指凸多边形，即多边形总在任何一条边所在直线的同一侧。

二、自主学习 小组交流1、下列各直线的表示法中，正确的是（ ）A：直线A， B：直线AB， C：直线ab， D：.直线Ab2、一个钝角与一个锐角的差是（） A.锐角 B.直角 C.钝角 D.不能确定3、手电筒射出去的光线,给我们的形象是( ) A.直线 B.射线 C.线段D.折线5已知线段AB=6cm,C是AB的中点，D是AC的中点，则DB等于—6、5点40分点钟时,时针与分针所成的角度是7要把木条固定在墙上至少需要钉__颗钉子,根据——三、自主学习，合作探究：1、计算：48°39′+67°41′= ，41.2°= °2、过八边形的一个顶点可作条对角线，可将八边形分成个三角形。

基本平面图形专题复习一．选择题1．已知数轴上的三点A、B、C所对应的数a、b、c满足a＜b＜c、abc＜O和a+b+c=O．那么线段AB与BC的大小关系是（）A．AB＞BC B．AB=BC C．AB＜BC D．不确定的2．如右图所示，B、C是线段AD上任意两点，M是AB的中点，N是CD中点，若MN=a，BC=b，则线段AD的长是（）A．2（a﹣b）B．2a﹣b C．a+b D．a﹣b3．点P在线段EF上，现有四个等式①PE=PF；②PE=EF；③EF=2PE；④2PE=EF；其中能表示点P是EF中点的有（）A．4个B．3个C．2个D．1个4．点P在∠MON内部，则四个等式：①∠POM=∠NOP；②∠PON+∠POM=∠MON；③∠MOP=∠MON，④∠MON=2∠NOP，其中能表示OP是角平分线的式子有（）A．1个B．2个C．3个D．4个5．如图所示，将一张长方形纸的一角斜折过去，使顶点A落在A′处，BC为折痕，如果BD为∠A′BE的平分线，则∠CBD=（）A．80°B．90°C．100°D．70°第5题图第7题图第8题图二．填空题6．四边形ABCD中，AB=8，AD=6，BC=7.5，CD=10，AC=11，BD=13．在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和最小，则其最小和为．7．如图，C、D是线段AB上的两个点，CD=8cm，M是AC的中点，N是DB 的中点，MN=12cm，那么线段AB的长等于cm．8．将一张长方形纸片折叠成如图所示的形状，则∠ABC的度数．9．如图，∠AOC=∠BOD=110°，若∠AOB=150°，∠COD=m°，则m=．10．如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°46′，OD平分∠COE，则∠COB的度数为．11．如图，射线OC、OD、OE是∠AOB四等分线，图中所有的角的度数之和为360°，则∠AOB的度数等于．第9题图第10题图第11题图12．把两个三角尺ABC与DEF按如图所示那样拼在一起，其中点D在BC上，DM为∠CDE的平分线，DN为∠BDF的平分线，则∠MDN的度数是．13．如图，OM平分∠AOB，ON平分∠COD，若∠MON=60°，∠BOC=10°，则∠AOD=．第12题图第13题图14．已知点A、B、C都是直线l上的点，且AB=5cm，BC=3cm，那么点A与点C之间的距离是．15．已知∠AOB=50°，∠BOC=30°，OD平分∠AOC，则∠AOD的度数为．16．已知线段AB=8cm，在直线AB上有一点C，且BC=4cm，M是线段AC的中点，则线段AM的长为．17．有两根长分别为20cm和50cm的木条，将它们的一端重合，放在同一条直线上，此时两根木条的中点间的距离是．18．在同一平面内，若∠AOB=90°，∠BOC=40°，则∠AOB的平分线与∠BOC 的平分线的夹角等于．三．解答题（共6小题）19．（1）如图，点C在线段AB上，线段AC=6cm，BC=4cm，点M、N分别是AC、BC的中点，求线段MN的长？（2）根据（1）的计算过程和结果，设AC+BC=a，其他条件不变，你能猜出MN的长度吗？用一句话表述你发现的规律？（3）对于（1），如果叙述为：“已知线段AC=6cm，BC=4cm，点C在直线AB上，点M、N分别是AC、BC的中点，求线段MN的长？”结果会有变化吗？如果有，求出结果．20．如图，OM是∠AOC的平分线，ON是∠BOC的平分线．（1）如图1，当∠AOB是直角，∠BOC=60°时，∠MON的度数是多少？（2）如图2，当∠AOB=α，∠BOC=60°时，猜想∠MON与α的数量关系；（3）如图3，当∠AOB=α，∠BOC=β时，猜想∠MON与α、β有数量关系吗？如果有，指出结论并说明理由．21．如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：此时直线ON是否平分∠AOC？请说明理由．（2）将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为（直接写出结果）．（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，求∠AOM﹣∠NOC的度数．22．已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE．（1）如图①，当∠BOC=70°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化若变化，说明理由；若不变，求∠DOE的度数；（3）如图③，当射线OC在∠AOB外绕O点旋转时，画出图形，判断∠DOE 的大小是否发生变化若变化，说明理由；若不变，求∠DOE的度数．。

基本平面图形复习教案以下是查字典数学网为您推荐的基本平面图形复习教案，希望本篇文章对您学习有所帮助。

基本平面图形复习教案一、线段、射线、直线1.直线:表示为:直线AB ,(或)直线BA.表示为:直线c2.射线:表示为:射线OM,注意端点字母一定要写在前边.表示为: 射线m3.线段:表示为:线段AB ,(或)线段BA.表示为: 线段m4.直线的性质:经过两点只有一条直线.5.线段的性质: 在两点的所有连接的线中,线段最段.两点之间线段的长度叫两点间的距离.6.线段的中点: 把一条线段分成两条相等的两条线段的点叫作线段的中点.例如: M是线段AB的中点,则AM = MB =二、角7.角的定义：具有公共端点的两条射线所组成的图形叫做角.8.角的表示：(1). 三个大写字母表示：AOB, ABD, ABC, DBC(2). 一个大写字母表示:A, B, C(3).希腊字母表示:(4). 数字表示:2 39.角也可以看做是一条射线绕端点旋转得到的.10、锐角、直角、钝角、平角、周角的概念和大小(1)平角：角的两边成一条直线时，这个角叫平角。

(2)周角：角的一边旋转一周，与另一边重合时，这个角叫周角。

(3)0锐角，直角=90，90钝角，平角=180，周角=360。

11.角的度量: 1= 60, 1= 6012. 角平分线意义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角平分线∵AOC=BOC= AOB13.点方位:1.北偏东602.北偏西303.西偏南604.南偏东455.东偏南45三、平行线和垂线14.同一平面内两直线的位置：相交或平行.15. 平行线的表示:直线a∥b或直线AB∥CD直线m与直线相n交于O.16.平行线的性质:(1).经过直线外一点,有且只有一条直线与这条直线平行.(2).如果两条直线都与第三条直线平行,那么这两条直线互相平行.∵ l1∥l2, l2∥l3 l1∥l317.垂直的定义:如果两条直线相交成直角,那么这两条直线互相垂直.18.垂直的表示:直线AB垂直于直线CD表示为:ABCD或ab19.垂线的性质:(1).平面内经过一点有且只有一条直线和已知直线垂直.(2).直线外一点与直线上各点的连线中,垂线段最短.垂线段的长度叫做点到直线的距离.如图:PAPCPD, 线段PD的长度就是P点到直线AB的距离.四、七巧板七巧板的制作：七巧板由5块三角形，1块正方形，一块平行四边形组成。