四旋翼无人机编队问题方案

多旋翼无人机协同编队飞行控制研究方案摘要：无人机协同编队飞行控制已经成为时代热题。

本文主要是对MMR之间、MMR与GCS之间的通信模式进行穷尽，并对CFF组织架构，3架MMR编队的几何结构进行总结概括，重点分析了CFF队形与所执行任务之间的内在关系。

在对CFF控制问题上主要总结了主-僚机控制方式及其常规问题和整体式飞行控制方案的研究。

并最终对MMR故障、GCS故障、编队阵型故障、其它应急情况下的容错机制、队形重构机制的研究MMR编队内部避障、整体避障问题研究进行了总结概括。

关键字：通信模式多旋翼无人机协同编队控制方式故障诊断与应急措施一、序言无人机（Unmanned Aerial Vehicle, UAV）是现代战争中重要的作战武器，能够代替有人机执行多种复杂危险的任务。

尽管如此,单架的UAV 执行任务时仍存在相应的问题,如执行侦察任务时,单架UAV可能会受到传感器的角度限制,不能从多个不同方位对目标区域进行观测,当面临大范围搜索任务时，不能有效地覆盖整个侦察区域;而如果是执行攻击任务,同样,单架UAV在作战范围、杀伤半径、摧毁能力以及攻击精度等方面受到的限制,会影响整个作战任务的成功率。

另外,一旦单架UAV中途出现故障，必须立即中断任务返回,在战争中有可能贻误战机而破坏整个战计划。

针对以上现状,多年来人们通过分析生物群体的社会性现象,如模仿群鸟迁徙过程中,其队形保持、节省能量以及协同对抗天敌等能力,来解决目所关注的问题,其目的是为了尽可能地发挥单架UAV的作用,实现多UAV协同编队飞行的控制、决策和管理,从而提高UAV完成任务的效率,拓宽UAV 使用范围,达到安全、高可靠性地执行多种任务的目的。

无人机技术经过几十年的发展已经相对成熟,在军事和民用中发挥了独特的作用。

为了适应未来的挑战,除了提高单机的功能和效用外,还需要考虑如何以现在的技术为基础,发展更加有效的无人机管理和组织模式。

无人机编队飞行是近年来提出的无人机合作化发展方向中的一个核心概念。

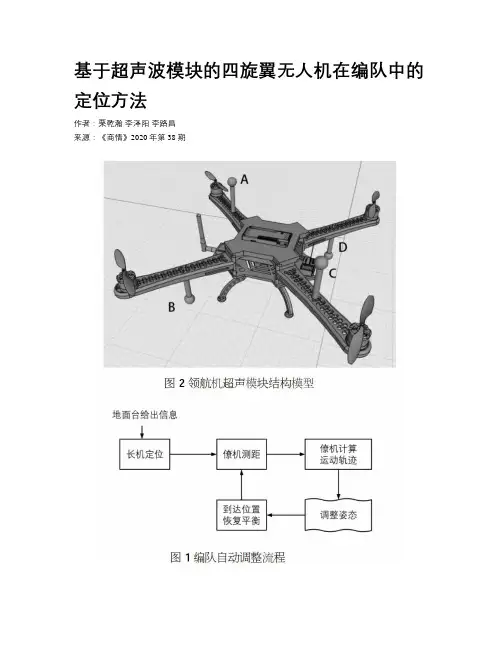
基于超声波模块的四旋翼无人机在编队中的定位方法作者：栗乾瀚李泽阳李路昌来源：《商情》2020年第38期【摘要】在无人机进行编队飞行时，在领航-跟随的编队策略下，针对如何进行长机僚机之间的定位问题提出了超声波定位的解决方案。

在建立的模型当中，进行了定位计算。

可以使无人机在编队飞行当中以固定队形飞行。

【关键词】无人机;编队飞行;超声波定位引言：四旋翼无人机是一种新型飞行器，从结构上来说，它是一种四轴给旋翼提供动力的飞行器。

四旋翼飞行器的工作原理是飞行时调节电机旋转速度，带动桨叶转动，产生竖直向上的升力，使飞行器能够在空中处于一个平稳的飞行状态。

相比于固定翼无人机来讲，四旋翼无人机有机械结构简单，飞行灵活，适合空中悬停和体积小等特点。

相比单架无人机，多无人机编队更易于完成复杂任务，提高了容错率，使得编队飞行控制成为现下研究热门课题。

使用超声波模块进行定位获得的数据精度较高，可达到厘米级，且结构简单。

无论是在容错率高还是在续航，检修，控制等方面都有较大的优势。

1、编队策略1.1 编队形式。

飞行器的编队飞行就是两架及以上的四轴飞行器从任意的初始位置按照事先预定好的队形进行飞行，并且在飞行的过程中在各个飞行器之间的距离和高度保持初始的飞行状态。

无人机的编队控制有多种方法，主要的控制方法有领航-跟随法，虚拟结果法，基于行为的方法。

现在存在多种编队形式，但由于无人机搭载芯片的性能限制和无人机在空中飞行时所实时采集的姿态、位置等多种数据，为防止运算速度低下，实时运动改变不及时。

采用地面基站—长机—僚机编队策略。

即地面基站为机队提供飞行数据，目标坐标。

长机为机队中的参照物，僚机检测自身位置，核对目标点，并进行自身的姿态调整。

1.2 长机僚机结构模型。

在编队过程中，长机根据预先预定的航迹飞行，僚机的编队则是主要控制距离的控制过程。

在水平面上，输出的指令信号都是关于速度和方向上的，通过反馈水平面双机的距离信息来实现跟踪距离控制的功能，在垂直面上，僚机根据高度的测量值来实现高度的控制。

四旋翼无人机一致性编队飞行控制方法作者：陈杰敏吴发林耿澄浩徐珊来源：《航空兵器》2017年第06期摘要：四旋翼无人机在民用及军用领域都发挥着越来越重要的作用。

为了完成某些特定任务，需要由多架四旋翼组成的编队保持适当队形飞行。

与单架四旋翼执行任务相比，四旋翼编队具有能增加任务成功率、提高整体抗干扰性能、扩大监控范围等优点。

本文基于主从式编队结构，结合信息拓扑理论，把四旋翼编队描述为二阶一致性系统，设计编队控制器来实现四旋翼编队的稳定飞行。

主机和从机均采用PID控制，主机跟踪预设轨迹，从机跟踪编队控制器计算出的轨迹跟踪指令。

最后通过仿真分析了控制算法对四旋翼编队队形生成及队形保持的控制效果。

关键词：四旋翼无人机；编队飞行；信息拓扑理论；一致性理论；主从式编队中图分类号： V249.1 文献标识码： A 文章编号： 1673-5048（2017）06-0025-07[SQ0]0 引言四旋翼无人机（以下简称四旋翼）是一种有四个螺旋桨且螺旋桨分别呈十字交叉型的飞行器。

在过去的数十年中，传感器及电子元器件的微型化、低廉化推动了四旋翼的快速发展。

四旋翼在军事领域可用于巡逻侦察、定点攻击等方面，在民用领域可用于遥感测绘、农业植保、通信中继、航拍航测、短途运输等方面，具有广泛的应用前景和实际用途，成为商业公司和科研单位的研究热点[1]。

随着无线传感网络等技术的创新应用，由多架无人机组成的编队在民用及军事等方面都展现出越来越广泛的用途，如能进行空中集群表演、组建军事通信网络、构建网络化军事打击编队等。

无人机编队飞行，是指在三维空间中，多架无人机按照一定的队形进行排列，使其在飞行过程中保持队形不变或者相对位置在一定范围内变动，并能根据外部情况和任务需求进行动态调整，以保持编队的协同一致性。

无人机编队飞行控制方式主要有主从法[2]、虚拟结构法[3-4]、行为控制法[5-6]等。

主从法结构中，其中一个飞行器被指定为主机，其余飞行器则被指定为从机。

基于Pixhawk飞控的四轴飞行器编队控制分析Pixhawk飞控是一种广泛应用于无人机领域的控制器，通过与传感器和执行器的配合，能够控制飞行器的姿态、位置等飞行参数。

同时，利用该控制器的通信功能，可以进行多个飞行器之间的互相通信与协作，实现编队控制。

四轴飞行器编队控制是指多个四轴飞行器在同一空间内通过互相通信与协作，完成一系列复杂的任务，如避障、搜救等。

编队控制的关键在于协调多个飞行器的位置、速度等参数，以便实现整体的协同运动。

下面将分析基于Pixhawk飞控的四轴飞行器编队控制的关键技术。

1.多机协作控制基于Pixhawk飞控的四轴飞行器编队控制需要实现多个飞行器之间的实时通讯，以便共同协作完成任务。

因此，要采用一种高效的通讯协议，如MAVLink协议。

MAVLink协议是一种基于无线通讯的数据传输协议，能够实现实时的数据交换和协作控制。

在编队控制中，多台飞行器都需要使用相同的MAVLink协议进行通讯，以达到协同运动的目的。

2.集群控制集群控制是指一组具有相同控制目标的飞行器协同工作的过程。

在集群控制下，多台飞行器通过协同工作，在不同领域内完成不同的任务，如区域探测、救援等。

集群控制需要通过分布式控制算法实现智能化决策，以提高编队控制的效率和精度。

3.位置控制位置控制是编队控制中最基本的控制方式。

基于Pixhawk飞控的四轴飞行器编队控制需要实现对每一台飞行器的位置控制，以便协同工作。

关键在于通过传感器获取每个飞行器的位置信息，并使用反馈控制算法进行调整。

需要注意的是，位置控制需要考虑到飞行器自身的动力学特性，以提高控制效果。

4.速度控制综上所述，基于Pixhawk飞控的四轴飞行器编队控制需要实现多机协作控制、集群控制、位置控制以及速度控制等多项关键技术。

只有通过高效的编队控制方式，才能实现更加复杂的无人机应用场景，如智能运输、灾害应急等。

无人车辆编队控制方案前言无人驾驶技术是近年来备受关注的领域，能够提高交通效率、降低交通事故率。

无人车辆编队控制是其中一个重要应用场景，实现车辆之间的协同操作，提高交通效率和安全性。

本文介绍一种基于GPS、视觉和通信技术的无人车辆编队控制方案，包括编队形成、运动控制和异常处理等方面。

编队形成编队形成是无人车辆编队控制的第一步，其目的是使车辆在一定的空间范围内快速地对目标车辆进行跟踪和构建编队。

可以采用以下方式进行编队形成：GPS定位算法在GPS定位系统中，通过车辆的GPS坐标信息，计算车辆之间的相对距离和角度，实现编队形成。

GPS定位算法常用的是差分GPS算法（Differential Global Positioning System，DGPS)，它可以提供高精度的定位信息。

当编队移动时，GPS定位算法可以在很大程度上保持编队的稳定性和可靠性。

视觉算法视觉算法可以在车辆间通信的情况下，通过车载摄像头实时捕捉周围车辆的图像信息，对目标车辆进行跟踪和监测，快速形成编队。

视觉算法可以通过基于光流法、特征点法等方法，计算车辆运动轨迹和相对距离。

运动控制在车辆编队形成之后，需要进行运动控制，保持车辆之间的距离和速度，在编队过程中保持稳定。

本文介绍以下两种运动控制方式：PID控制器PID控制器是一种经典的运动控制方法，通过不断地调节车辆的速度和方向，保持车辆之间的距离和时间间隔。

具体步骤如下：1.设置期望的时间间隔和距离。

2.通过车载传感器获取编队中其他车辆的位置和速度信息。

3.计算编队中其他车辆的速度和时间间隔，与期望值进行比较。

4.根据误差调整车辆的速度和方向，保持车辆与其他车辆的距离和时间间隔。

MPC控制器MPC控制器是一种基于模型预测控制的方法，通过预测当前车辆和编队中其他车辆的状态变化，实时调整车辆的运动。

MPC控制器可以通过数学模型计算出车辆与其他车辆的期望运动轨迹，通过实时反馈调整车辆的运动轨迹。

第29卷第11期V ol.29No.11控制与决策Control and Decision2014年11月Nov.2014基于一致性的小型四旋翼机群自主编队分布式运动规划文章编号:1001-0920(2014)11-2081-04DOI:10.13195/j.kzyjc.2013.1002邢关生1,2,杜春燕3,宗群3,陈海永1,孙鹤旭1(1.河北工业大学控制科学与工程学院，天津300130；2.系统控制与信息处理教育部重点实验室，上海200240；3.天津大学电气与自动化工程学院，天津300072)摘要:设计一种小型四旋翼无人机群起飞后自主形成正多边形编队的分布式运动规划方法.在四旋翼无人机的串级控制系统框架下,分布式编队控制器以简化agent模型为基础,同时采用平均一致性算法和有领导一致性算法,共同产生各无人机位置与偏航角的期望轨迹.讨论了达成最终协调目标队形的拓扑条件,并给出一种基于有向Hamilton环的通信拓扑设计方案.最后通过数值仿真验证了所提出算法的有效性.关键词:无人机群；编队生成；一致性算法；四旋翼无人机；分布式运动规划中图分类号:TP242.6文献标志码:AConsensus-based distributed motion planning for autonomous formation of miniature quadrotor groupsXING Guan-sheng1,2,DU Chun-yan3,ZONG Qun3,CHEN Hai-yong1,SUN He-xu1(1.School of Control Science and Engineering，Hebei University of Technology，Tianjin300130，China；2.Key Laboratory of System Control and Information Processing，Ministry of Education，Shanghai200240，China；3.School of Electrical and Automation Engineering，Tianjin University，Tianjin300072，China．Correspondent：XING Guan-sheng，E-mail：xinggs@)Abstract:A distributed motion planning method is designed for a group of miniature quadrotors to attain a formation in regular polygons autonomously after takeoff.In the framework of cascade control systems of quadrotors,based on simplified agent models,formation controllers distributed over communication graph use two average consensus and leader-based consensus algorithms to collaboratively generate the desired position and yaw angle trajectory of quadrotors.The topology conditions of reaching goal formation are discussed and a design scheme of communication topology is designed on the basis of the directed Hamilton circle.Finally,the result of a simulated experiment shows the effectiveness of the proposed algorithm.Key words:unmanned aerial vehicle group；formation generation；consensus algorithm；quadrotors；distributed motion planning0引言由多个尺寸在0.1∼0.5m的微型无人机或人可携带的小尺寸无人机组成的群体系统,在军事监控、安全保卫等领域应用广泛,队形控制问题是其中的关键共性难题.小型四旋翼无人机作为一种较新的飞行机器人,其队形控制问题的研究工作较少.文献[1]研究了微小型四旋翼无人机大规模群体的无领导编队保持任务;文献[2]研究了三维空间中小型四旋翼无人机的紧密队形保持问题;文献[3]采用领导者/跟随者框架,在飞行器镇定控制器的基础上融入了一致性算法,解决了编队轨迹跟踪控制问题.本文主要研究目前研究较少的小型四旋翼无人机群的初始队形产生问题,目标是令各无人机从地面起飞后同时到达指定高度悬停、形成期望队形并保持朝向相同.受文献[4]中的车辆编队控制方法的启发,提出了由不同类型一致性算法混合构成分布式编队控制器的基本思路.所得编队控制器位于无人机运动规划层,为底层自驾仪提供期望位姿轨迹,不同于很收稿日期:2013-07-20；修回日期:2013-11-12.基金项目:国家自然科学基金项目(61203275)；河北省自然科学基金项目(F2013202101)；天津市自然科学基金项目(12JCZDJC30300)；系统控制与信息处理教育部重点实验室开放基金项目(SCIP201204).作者简介:邢关生(1980−),男,讲师,博士,从事机器人网络协调控制、分布式估计的研究；杜春燕(1980−),女,博士,讲师,从事非线性控制、旋翼无人机控制的研究.2082控制与决策第29卷多工作中直接面对底层执行器设计编队控制律(例如文献[3]).优势在于使得单机自主飞行和多机协同工作的软件系统更易切换,便于单机的入队和离队.在编队控制器设计中,使用简化的对象模型作为产生期望轨迹的动态系统.在仅有一个无人机知道群体的期望飞行高度和最终朝向的情况下,通过平均一致性算法规划无人机水平方向的运动,自主协商水平方向的中心点;由有领导一致性算法规划垂直方向、偏航姿态的轨迹.另外,考虑到一致性算法能否达成一致以及最终平衡态的值均与通信拓扑有关,从而基于有向Hamilton 环提出了一种同时保证两种一致性算法均可达到期望目标的无人机群通信拓扑设计方案.1问题描述无人机群由N 个同样的小型四旋翼无人机组成.坐标系和无人机i 的位姿变量定义如图1所示.设全局坐标系为ℐ={e x ,e y ,e z },固定在无人机i 重心Q i上的本体坐标系为ℬi ={b i x ,b i y ,b i z },b ix 的方向为无人机i 的前方.令ξi =[x i ,y i ,z i ]T 为无人机重心Q i 在坐标系ℐ中的位置,ηi =[ϕi ,θi ,ψi ]T 为无人机i 在坐标系ℐ中的姿态,其中ϕi 、θi 、ψi 分别表示横滚角、俯仰角和偏航角.ψ图1四旋翼无人机的位姿定义从本体坐标系ℬi 到全局坐标系ℐ的ZYX 旋转矩阵为ℐℬi R=⎡⎢⎣c θi c ψi s ϕi s θi c ψi −c ϕi s ψi c ϕi s θi c ψi +s ϕi s ψic θi s ψi s ϕi s θi s ψi +c ϕi c ψi c ϕi s θi s ψi −s ϕi c ψi −s θis ϕi c θic ϕi c θi⎤⎥⎦.其中:s =sin(⋅),c =cos(⋅).设无人机i 的质量为m i ,转动惯量矩阵J i =diag(J 1i ,J 2i ,J 3i ),另设驱动无人机位姿变化的控制输入为4个螺旋桨产生的总升力F i 和力矩τi .由刚体动力学可知无人机平动的动力学为m i ¨ξi =ℐℬiRF i −m i g e z .(1)其中:F i =[0,0,F i ]T,e z =[0,0,1]T.设无人机i 在其本体坐标系ℬi 中的旋转角速度为ωi ∈R 3,则根据ℐ与ℬi中的旋转运动量之间的变换关系式˙ηi =Φ(ηi )ωi 以及刚体旋转运动动力学方程J i ˙ωi +ωi ×J i ωi =τi ,τi =[τi 1,τi 2,τi 3]T,可得描述无人机i 姿态变化过程的动力学方程M i (ηi )¨ηi +C i (ηi ,˙ηi )˙ηi =Ψ(ηi )T τi .(2)其中Ψ(ηi )=Φ−1(ηi )=⎡⎢⎣10−s θi0c ϕis ϕi c θi 0−s ϕi c ϕi c θi⎤⎥⎦,M i (ηi )=ΨT (ηi )J i Ψ(ηi ),C i (ηi ,˙ηi )=−M i (ηi )+ΨT (ηi )sk [Ψ(ηi )ηi ]J i Ψ(ηi ),sk [⋅]是反对称矩阵.推导过程可参考文献[5].由式(1)和(2)共同构成无人机动力学模型,两者依靠旋转矩阵ℐℬi R 耦合在一起.无人机群体系统内部存在单机相互之间的信息交互,用通信图G c =(I,E c ,A c )表示.G c 为加权有向图,索引集I ={1,2,⋅⋅⋅,N }为G c 的顶点集,单机间的通信链接的集合E c ⊂I ×I 为G c 的边集.(i,j )c ∈E c 表示无人机i 可获得j 的状态数据,(i,j )c ∈E c ⇎(j,i )c ∈E c ,A c =(a c ij )是N 维加权邻接矩阵,a c ij 表示边(i,j )c 上的权重.对于∀i,j ∈I ,若(i,j )c ∈E c ,则a c ij >0,否则a cij =0.令N c +i={j ∣(i,j )c ∈E c }和N c −i ={j ∣(j,i )c ∈E c }分别表示i 在G c 上的出邻域和入邻域,∣N c +i ∣和∣N c −i ∣分别表示i 的出邻和入邻的数量.定义{(x,y,z )∣z =0}为地面,设z i (0)=0,ϕi (0)=0,θi (0)=0,˙ξi (0)=0,˙ηi (0)=0,∀i ∈I .令z r 表示期望飞行高度,ψr 表示期望朝向.为描述期望队形,令p i =[x i ,y i ]T 表示无人机i 在X -Y 平面内的坐标,则无人机群在X -Y 平面内的几何中心为p c =1NN ∑i =1p i ,初始时刻的几何中心用p c (0)表示.无人机编队采用虚拟领导者/跟随者的方法框架,以ξc =[p T c (0),z r ,ψr ]T 为虚拟领导,令ℱr ={d r 1,d r 2,⋅⋅⋅,d rN }表示期望的无人机编队构型,d r i ∈R 2,i ∈I .此处,d r i 代表无人机i 在水平面内相对于虚拟领导的期望位置偏差.令d i =p i −p c (0)表示无人机与群体几何中心间的实时偏差量.由此,可给出所关注的无人机编队生成问题的定义:各无人机在初始时刻静止于地面且无队形,给定期望的编队构型ℱr ,只有个别无人机被告知虚拟领导的部分信息(z r 和ψr ),在无人机i 仅知d r i 而不知p c (0)的条件下,设计一个通信图G c 和分布在G c 上的控制器,i 根据j ∈N c +i 的信息驱动自身位姿变化,使得∀i ∈I ,∥d i −d r i ∥→0,∣z i −z r ∣→0,∣ψi −ψr ∣→0,˙ξi →0,˙ηi →0.本文的目标队形是正多边形,即每个无人机位于圆环的N 等分点上,则第11期邢关生等:基于一致性的小型四旋翼机群自主编队分布式运动规划2083d r i=[−d rcos 2π(i −1)N ,−d rsin 2π(i −1)N],(3)其中d r 是正多边形外接圆的半径.2四旋翼无人机编队控制系统设计编队控制采用多闭环串级控制系统结构,如图2所示.外环为用于编队控制的轨迹规划算法,运行于无人机本地,根据任务目标和实时同伴状态,输出各自的期望位置与姿态,由内部的位置控制器和姿态控制器实现具体控制任务.此处重点关注最外层的分布式编队控制算法,内部的位姿控制参见文献[5].图2编队控制系统结构图考虑到四旋翼无人机为欠驱动系统,因而选择一种可行的方案,仅令无人机跟踪位置和偏航角,不必跟踪任意位姿.针对无人机的编队生成任务,编队控制器内部将无人机模型抽象为两组一阶积分器,分别为˙pi =u i 1,i ∈I ;(4)˙qi =u i 2,i ∈I.(5)其中q i =[z i ,ψi ]T .将这两组模型用于产生无人机i 的期望轨迹,u i 1和u i 2为虚拟控制输入量.根据编队生成任务的定义,群体几何中心在X -Y 平面上的投影p c 是事先未知的,与群体期望高度和朝向有关的q c 是事先已知的,因而对子系统(4)和(5)分别采用平均一致性算法和有领导一致性算法设计u i 1和u i 2的算式.对于子系统(4),设r i =p i −d r i ,则式(4)变为˙ri =u i 1,设计一致性算法u i 1=N ∑j =1a c ij (r j −r i ),得到˙ri =N ∑j =1a c ij (r j −r i ).(6)由于a c ij 依赖于无人机群的通信图G c 的边,可见G c 的结构可影响a c ij 的动态变化.由文献[6]可知:如果G c 强连通,当且仅当G c 平衡(即∣N c +i ∣=∣N c −i ∣,∀i∈I )时,系统(6)可全局渐近达成平均一致,即对于∀i ∈I ,有r i →1N N∑j =1r i (0)=1N∑N j =1(p i (0)−d r i ).由于式(3)定义的d r i 具有对称性,使得r i →1N∑Nj =1p i (0)=p c (0).可见,在目标位置事先未知的情况下,无人机i 在全局坐标系X -Y 平面上的投影位置最终收敛到与初始时刻群体几何中心的位置p c (0)相差d r i 的位置上,即群体达到期望的正多边形构型.对于子系统(5),设计有领导一致性算法.定义q 0=[z c ,ψc ]T 为虚拟领导,将q 0与所有q i 集成为一个增广系统⎧⎨⎩˙q i =0,i =0;˙q i =u i 2,i =1,2,⋅⋅⋅,N.(7)此增广系统的通信图˜Gc =(˜I c ,˜E c ,˜A c )可在G c 基础上扩展得到,其中˜I c ={0}∪I ,˜E c =E ∪{(i,j )∣j =0,i ∈I },˜A c =(˜a c ij )是(N +1)×(N +1)维加权邻接矩阵,定义为˜Ac =[00T N a A c],a =[˜a 10,˜a 20,⋅⋅⋅,˜a N 0]T .若(i,0)c ∈˜E c ,则˜a i 0>0,否则˜a i 0=0.针对系统(7)设计一致性算法u i 2=N ∑j =0,j =i˜a c ij (q j −q i ),i ∈˜I ,得到闭环系统⎧⎨ ⎩˙q i=0,i =0;˙qi =N ∑j =0,j =i˜a c ij (q j −q i ),i ∈I.(8)由文献[7]可知:当且仅当˜Gc 存在有向生成树时,系统(8)可全局渐近达成一致.有向生成树是指在图˜Gc 存在一个全局可达节点,所有其余节点到全局可达节点均存在一条有向路径.若虚拟领导q 0为唯一全局可达节点,且˙q0=0表示其不参考其他个体状态,则对于∀i ∈I ,q i →q 0.由此可见,各无人机规划的纵向和朝向轨迹可达成一致,保证了具有同一高度和偏航角.由上述分析可见,在给定一致性算法的情况下,G c 和˜Gc 的连通性可决定子系统(6)和子系统(8)的终态.考虑到G c 与˜Gc 之间的关系,采用有向Hamilton 环作为G c ,在Hamilton 环上选择任一节点,在该节点与虚拟领导之间定义一条有向边,得到扩展的通信图˜Gc ,如图3所示,则可同时保证系统(6)达成平均一致、有领导一致所需的拓扑条件.此处的G c 和˜Gc 是时不变的.2084控制与决策第29卷图3基于有向Hamilton 环的通信图设计3仿真实验3.1仿真参数设置在Matlab 中模拟6个四旋翼无人机,工作空间内未设置障碍物.无人机动态模型中的参数均相同(省略下角标i ),具体配置为:m =1.2kg,J 1=J 2=0.015kg/m 2,J 3=0.026kg/m 2.在无人机串级控制系统中,内环使用PID 控制调节位置和姿态,参数设置参见文献[5].无人机之间的通信图设定如图3所示.期望队形的参数设置为:d r =2m,z r =8m,ψr =0rad,仿真时间为40s,仿真步长为0.001s.3.2仿真结果与分析无人机群编队生成的仿真飞行数据曲线如图4所示.由图4可以看出,各无人机从地面起飞后,在飞行过程中经过一段时间的周期式运动,最终收敛到稳定状态,在水平面上形成正六边形编队,验证了基于无领导一致性算法的运动轨迹规划的有效性,说明各无人机在事先未知群体几何中心的前提下利用局部通信获知群体中心信息.图5绘制的是各无人机飞行高度和偏航角曲线,为突出显示数据变化过程,-505-4-2-602024681012345261X /m Y /mZ /m图4无人机群编队生成的仿真飞行数据曲线--44Z /m005101520t /st /sy a w a n g l e /r a d()a ()b 图5各无人机纵向位置和偏航角的变化曲线显示了前20s 的数据.由图5可见,在有领导一致性算法引导下,最终所有无人机的飞行高度为8m 、偏航角保持在0rad,这与设定的z r =8m 、ψr =0rad 一致.各无人机初始高度相同,因而在有领导一致性算法作用下,同步效果较好.各无人机之所以有较长时间的往返运动,是由于在串级控制框架下设计的编队控制的内环PID 控制器对编队控制算法计算所得期望位姿的跟踪效果不完美而造成的.4结论面向小型四旋翼无人机群起飞后的编队生成任务,本文设计了一种自主形成正多边形编队的分布式控制方法.在给出较精确的四旋翼无人机动力学模型的基础上,设计了小型四旋翼无人机的串级编队控制系统框架.重点针对外环的分布式编队控制器的设计问题,以简化agent 模型为基础,同时采用了平均一致性算法和有领导一致性算法,共同产生各无人机位置与偏航角的期望轨迹.讨论了达成最终协调目标队形的拓扑条件,并通过Matlab 数值仿真结果验证了协调控制算法的有效性.需要注意的是,当前工作是为了验证编队轨迹规划中一致性算法应用的有效性,因而尚未考虑碰撞问题,这将成为未来的工作重点之一.参考文献(References )[1]Michael N,Kumar V .Control of ensembles of aerial robots[J].Proc of the IEEE,2011,99(9):1587-1602.[2]Turpin M,Michael N,Kumar V ,et al.Trajectory design and control for aggressive formation flight with quadrotors[J].Autonomous Robots,2012,33(1/2):143-156.[3]Guerrero J A,Castillo P,Salazar S,et al.Mini rotorcraft flight formation control using bounded inputs[J].J of Intelligent and Robotic Systems:Theory and Applications,2012,65(1/2/3/4):175-186.[4]Ren W.Consensus strategies for cooperative control of vehicle formations[J].IET Control Theory and Applications,2007,1(2):505-512.[5]Kendoul F,Yu Z Y ,Nonami K.Guidance and nonlinear control system for autonomous flight of minirotorcraft unmanned aerial vehicles[J].J of Field Robotics,2010,27(3):311-334.[6]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-robot systems[J].Proc of the IEEE,2007,95(1):215-233.[7]Ren W,Beard R W,Atkins rmation consensus in multivehicle cooperative control:Collective groupbehavior through local interaction[J].IEEE ControlSystems Magazine,2007,27(2):71-82.(责任编辑：孙艺红)。