同步奥数培优六年级上第五讲比(比在实际的应用)

第5课时比的应用(1)教材第74～76页相关内容。

1．在解决实际问题的过程中，进一步体会比的意义。

n加油2．能应用比的意义解决有关按比分配的实际问题，提高解决问题的能力。

按一定的比进行分配问题的解法。

找出各部分量与总量之间的关系。

一、创设情境1．出示课本主题图：1班有30人，2班有20人，把这些橘子分给1班和2班，怎么分合理？2．请同学们想一想：你认为怎么分合理？说一说你的分法。

3．揭示课题。

师：在实际的工农业生产和日常生活中，常常需要把一个数量按照一定的比来分配。

这种分配方法通常叫作按比例分配。

板书课题：比的应用(1)二、探究新知学生自主学习并解决教材第74页例题，如果有140个橘子，按照3∶2的比例又应该怎样分？尝试用不同的方法，并记录下分配的过程。

小组交流：1．怎么分更合理？能不能平均分？2．我们可以按照什么标准来分更合理？3．比较不同的方法，找找它们的共同点。

师：今天遇到的问题不是平均分的问题，而是按一定的比进行分配的问题。

先根据已知的比得到每部分的份数及总份数，然后根据具体数量与对应的份数关系解题，可以转化为整份数思考，也可以由份数进一步转化为分数思考。

三、巩固练习完成教材第75页的练习。

(1)独立完成第75页的“试一试”，仔细读题，认真分析。

列式计算，集体订正。

(2)独立试做“练一练”的1、2、3题，抢答并说明理由。

四、课堂小结提出自己还有些疑惑的问题。

比的应用(1)家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，孩子一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。

我把幼儿在园里的阅读活动及阅读情况及时传递给家长，要求孩子回家向家长朗诵儿歌，表演故事。

我和家长共同配合，一道训练，幼儿的阅读能力提高很快。

3＋2＝5140×35＝84(个)140×25＝56(个)观察内容的选择，我本着先静后动，由近及远的原则，有目的、有计划的先安排与幼儿生活接近的，能理解的观察内容。

六年级上数学比的应用培优题类型一：比用于图形中1. 两个正方体棱长的比是2:3 ，这两个正方体底面积的比是（）:（），体积比是（）: （）, 棱长总和比是（）：（），表面积比是（）：（）。

2.一个直角三角形的两个锐角度数的比是 2 ： 1，这两个锐角分别是多少度？3 一个直角三角形的周长为36 厘米，三条边的长度比是 3 ：4 ： 5，这个三角形的面积是多少平方厘米？4、甲、乙、丙三个平行四边形的底之比是 4:5:6 ，高之比是 3:2:1 ，已知三个平行四边形的面积和是 140 平方分米，那么甲、乙、丙三个平行四边形的面积各是多少？类型二：已知相差数和比15. 建筑工地计划运进一批水泥，第一次运来总数的，第二次运来180吨，这时运来的与没有4运来的吨数比是4:3 ，工地计划运进水泥多少吨？6.丁丁、王伟、宁洋共有贴画 150 张，已知丁丁、宁洋的贴画张数的比是 5:4 ，王伟比宁洋多20张，那么王伟有贴画多少张呢？7.. 甲、乙、丙三位同学共有图书 108 本，乙比甲多 18 本，乙与丙的图书数之比是 5 ： 4，求甲、乙、丙三人各有图书多少本？18. 某筑路队计划四月份修完一条路，上旬修了这条路的，中旬比上旬多修7 米，这时，已修5与未修的比是 3:1 ，这条路全长多少米？9.光明小学有三个年级 , 一年级学生占全校学生人数的 1/4, 二年级与三年级学生人数的比是 3:4,已知一年级比三年级学生少 40 人 , 一年级有学生多少人？类型三：已知比和取出或转入10.有袋米，第一袋与第二袋重量的比是 8:9 ，如果从第二袋中取出 10 千克放入第一袋中，两袋米的重量就相等。

两袋米共有多少千克？11.甲乙两个图书架所放图书册数的比是 2:3 ，现从乙书架拿出 42 册图书放到甲书架，甲、乙两个书架图书的比是 5:4 ，甲书架原有图书多少册？12.六⑵班上学期男女生人数比为 5:7 ，这学期转入 2 名男生，转出 2 名女生后，男女生人数比为11:13 。

比的应用（一）一、知识要点我们已经学过比的知识，都知道比和分数、除法其实是一回事，所有比与分数能互相转化。

运用这种方法解决一些实际问题可以化难为易，化繁为简。

二、精讲精练【例题1】甲数是乙数的2/3，乙数是丙数的4/5，甲、乙、丙三数的比是（）：（）：（）。

【思路导航】甲、乙两数的比 2：3乙、丙两数的比 4：5甲、乙、丙三数的比 8：12：15答：甲、乙、丙三数的比是 8：12：15。

练习1：1．甲数是乙数的4/5，乙数是丙数的5/8，甲、乙、丙三数的比是（）：（）：（）。

2．甲数是乙数的4/5，甲数是丙数的4/9，甲、乙、丙三数的比是（）：（）：（）。

3．甲数是丙数的3/7，乙数是丙数的2又1/2，甲、乙、丙三数的比是（）：（）：（）。

【例题2】光明小学将五年级的140名学生，分成三个小组进行植树活动，已知第一小组和第二小组人数的比是2：3，第二小组和第三小组人数的比是4：5。

这三个小组各有多少人？【思路导航】先求出三个小组人数的连比，再按求出的连比进行分配。

①一、二两组人数的比 2：3 二、三两组人数的比 4：5一、二、三组人数的比 8：12：15②总份数：8+12+15＝35③第一组：140×8/35＝32（人）④第二组：140×12/35＝48（人）⑤第三组：140×15/35＝60（人）答：第一小组有32人，第二小组有48人，第三小组有60人。

练习2：1．某农场把61600公亩耕地划归为粮田与棉田，它们之间的比是7：2，棉田与其他作物面积的比6：1。

每种作物各是多少公亩？2．黄山小学六年级的同学分三组参加植树。

第一组与第二组的人数的比是5：4，第二组与第三组人数的比是3：2。

已知第一组的人数比二、三组人数的总和少15人。

六年级参加植树的共有多少人？3．科技组与作文组人数的比是9：10，作文组与数学组人数的比是5：7。

已知数学组与科技组共有69人。

数学组比作文组多多少人？【例题3】甲、乙两校原有图书本数的比是7：5，如果甲校给乙校650本，甲、乙两校图书本数的比就是3：4。

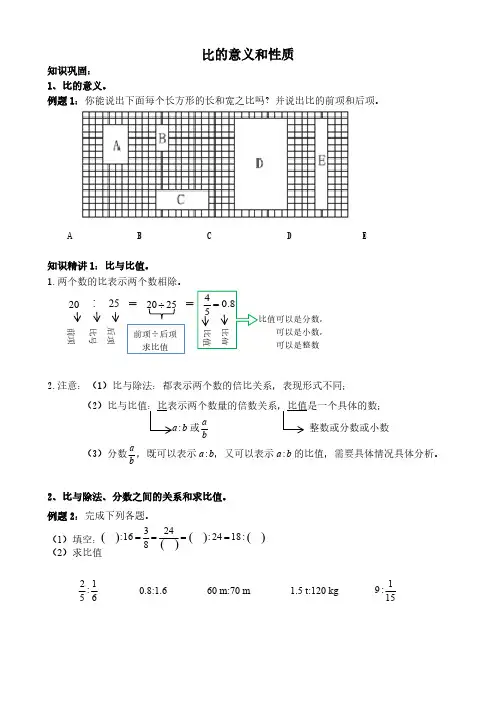
六年级 第5讲、比在实际中的应用、知识方法“比”在实际生活中的应用十分广泛，解答关于“比”的问题时要及时沟通“比”和“分数”之间的联系，已知两个量的比，就是已知一个量是另一个量的几分之几，同时也知道了其中一个量是两个量之和的几分之几，从而把这类应用题转化为分数应用来进行解答。

一，填空1、六（1）班男生人数与女生人数的比是14：13，女生人数是男生人数的（ ），男生人数与全班人数的比是（ ），女生人数占全班人数的（ ）。

2、男生人数比女生人数多61，女生和男生人数的比是（ ）。

男生占全班人数的（ ）。

3、修一段公路，已修的和未修的比为5：4，已修了这段公路的（ ）。

4、甲走的路程是乙的54，甲、乙速度比是（ ）。

5、一个平行四边形和一个三角形，它们底的比是1：2，高的比也是1：2，那么它们的面积比是（ ）。

6、已知一个三角形的三个内角度数比是1：1：2，这是一个（ ）三角形，又是（ ）三角形。

二、例题探究【例1】一块长方形地的周长是20米，长与宽的比是3：2，它的面积是多少？五（1）班男、女生人数比是12：11，又转来4名女生后，全班共有50人。

求现在男、女生的人数比。

商店运来一批电视机，卖出18台，剩下的与卖出的比为4：3，共运来多少台电视机？一个长方体的棱长总和是144厘米，长，宽，高的比是5：4:3，这个长方体的体积是多少？例题2，一个分数和分母的和是18，如果将分子加上8，分母加上9，新的分数约分后是43，原来的分数是多少？一个分数的分子和分母之和是25，如果将分子加上8，分母加上7，新的分数约分后是31，原来的分数是多少？芳芳和圆圆各有一只盒子，里面都放着棋子，两只盒子里的棋子一共是360粒，芳芳从自己的盒子里拿出41的棋子放入圆圆的盒子里，圆圆盒子里的棋子数恰好比原来增加51，原来芳芳有棋子多少粒？圆圆有棋子多少粒？甲乙两人共同录入一份15400字的文稿，当甲完成录入任务的65，乙完成录入任务的54时，两人尚未录入的字数相等，问：甲的录入任务是多少个字？例题3，小风和小玲步行的速度比是2:3，小玲与小红的步行速度比是4:5，三人1分钟步行的路程和是175米三个小伙伴每分钟各行了多少米？某学校学生阅览室里有236本童话故事书，分三层摆放，第一层与第二层的本数比是3:4.第二层与第三层的本数比是5:6，三层各有多少本童话故事书？三位同学去商场购物，小明花去钱数的21等于小林花去钱数的31，小林花去钱数的43等于军军花去钱数的74，结果军军比小明多花钱93元，他们三人共花了多少钱？例题4 ，水果批发商购进了1420箱苹果，香蕉和梨，苹果和香蕉的比是4:3，梨比香蕉少180箱，苹果，香蕉和梨各购进了多少箱？培育花圃的李阿姨培育了850株菊花，玫瑰花和月季花，菊花，玫瑰花的株数比是5:2，月季花比玫瑰花多40株。