机械振动基础课后习题答案
- 格式:ppt
- 大小:1.39 MB
- 文档页数:25

机械振动答案(1)选择题1解析:选D.如图所示,设质点在A 、B 之间振动,O 点是它的平衡位置,并设向右为正.在质点由O 向A 运动过程中其位移为负值;而质点向左运动,速度也为负值.质点在通过平衡位置时,位移为零,回复力为零,加速度为零,但速度最大.振子通过平衡位置时,速度方向可正可负,由F =-kx 知,x 相同时F 相同,再由F =ma 知,a 相同,但振子在该点的速度方向可能向左也可能向右.2.解析:选B.据简谐运动的特点可知,振动的物体在平衡位置时速度最大,振动物体的位移为零,此时对应题图中的t 2时刻,B 对.3.解析:选BD.质点做简谐运动时加速度方向与回复力方向相同,与位移方向相反,总是指向平衡位置;位移增加时速度与位移方向相同,位移减小时速度与位移方向相反.4解析:选C.因为弹簧振子固有周期和频率与振幅大小无关,只由系统本身决定,所以f 1∶f 2=1∶1,选C.5解析:选B.对于阻尼振动来说,机械能不断转化为内能,但总能量是守恒的.6.解析:选B.因质点通过A 、B 两点时速度相同,说明A 、B 两点关于平衡位置对称,由时间的对称性可知,质点由B 到最大位移,与由A 到最大位移时间相等;即t 1=0.5 s ,则T2=t AB +2t 1=2 s ,即T =4 s ,由过程的对称性可知:质点在这2 s 内通过的路程恰为2 A ,即2A =12 cm ,A =6 cm ,故B 正确.7.解析:选A.两球释放后到槽最低点前的运动为简谐运动且为单摆模型.其周期T =2πR g,两球周期相同,从释放到最低点O 的时间t =T4相同,所以相遇在O 点,选项A 正确.8.解析:选C.从t =0时经过t =3π2L g 时间,这段时间为34T ,经过34T 摆球具有最大速度,说明此时摆球在平衡位置,在给出的四个图象中,经过34T 具有负向最大速度的只有C 图,选项C 正确.9.解析:选CD.单摆做简谐运动的周期T =2πlg,与摆球的质量无关,因此两单摆周期相同.碰后经过12T 都将回到最低点再次发生碰撞,下一次碰撞一定发生在平衡位置,不可能在平衡位置左侧或右侧.故C 、D 正确.10.解析:选D.通过调整发生器发出的声波就能使酒杯碎掉,是利用共振的原理,因此操作人员一定是将声波发生器发出的声波频率调到500 Hz ,故D 选项正确. 二、填空题(本题共2小题,每小题8分,共16分.把答案填在题中横线上)11答案:(1)B (2)摆长的测量、漏斗重心的变化、液体痕迹偏粗、阻力变化……12答案:(1)ABC (2)①98.50 ②B ③4π2k计算题13.(10分)解析:由题意知弹簧振子的周期T =0.5 s ,振幅A =4×10-2m. (1)a max =kx max m =kA m=40 m/s 2. (2)3 s 为6个周期,所以总路程为s =6×4×4×10-2m =0.96 m.答案:(1)40 m/s 2(2)0.96 m14.(10分)解析:设单摆的摆长为L ,地球的质量为M ,则据万有引力定律可得地面的重力加速度和高山上的重力加速度分别为:g =G M R 2,g h =G M R +h2据单摆的周期公式可知T 0=2πLg ,T =2πL g h由以上各式可求得h =(T T 0-1)R . 答案:(T T 0-1)R15.(12分解析:球A 运动的周期T A =2πl g, 球B 运动的周期T B =2π l /4g =πl g. 则该振动系统的周期T =12T A +12T B =12(T A +T B )=3π2l g. 在每个周期T 内两球会发生两次碰撞,球A 从最大位移处由静止开始释放后,经6T =9πlg,发生12次碰 撞,且第12次碰撞后A 球又回到最大位置处所用时间为t ′=T A /4. 所以从释放A 到发生第12次碰撞所用时间为t =6T -t ′=9πl g -2T 2l g =17π2lg. 答案:17π2l g16.(12分解析:在力F 作用下,玻璃板向上加速,图示OC 间曲线所反映出的是振动的音叉振动位移随时间变化的规律,其中直线OC 代表音叉振动1.5个周期内玻璃板运动的位移,而OA 、AB 、BC 间对应的时间均为0.5个周期,即t =T 2=12f=0.1 s .故可利用匀加速直线运动的规律——连续相等时间内的位移差等于恒量来求加速度.设板竖直向上的加速度为a ,则有:s BA -s AO =aT 2①s CB -s BA =aT 2,其中T =152 s =0.1 s ②由牛顿第二定律得F -mg =ma ③ 解①②③可求得F =24 N. 答案:24 N机械振动(2)机械振动(3)1【解析】 如图所示,图线中a 、b 两处,物体处于同一位置,位移为负值,加速度一定相同,但速度方向分别为负、正,A 错误,C 正确.物体的位移增大时,动能减少,势能增加,D 错误.单摆摆球在最低点时,处于平衡位置,回复力为零,但合外力不为零,B 错误.【答案】 C2【解析】 质量是惯性大小的量度,脱水桶转动过程中质量近似不变,惯性不变,脱水桶的转动频率与转速成正比,随着转动变慢,脱水桶的转动频率减小,因此,t 时刻的转动频率不是最大的,在t 时刻脱水桶的转动频率与机身的固有频率相等发生共振,故C 项正确.【答案】 C3【解析】 摆球从A 运动到B 的过程中绳拉力不为零,时间也不为零,故冲量不为零,所以选项A 错;由动能定理知选项B 对;摆球运动到B 时重力的瞬时功率是mg v cos90°=0,所以选项C 错;摆球从A 运动到B 的过程中,用时T /4,所以重力的平均功率为P =m v 2/2T /4=2m v 2T ,所以选项D 错.【答案】 B4【解析】 由振动图象可看出,在(T 2-Δt )和(T2+Δt )两时刻,振子的速度相同,加速度大小相等方向相反,相对平衡位置的位移大小相等方向相反,振动的能量相同,正确选项是D.【答案】 D5【解析】 据受迫振动发生共振的条件可知甲的振幅较大,因为甲的固有频率接近驱动力的频率.做受迫振动物体的频率等于驱动力的频率,所以B 选项正确.【答案】 B6【解析】 由题意知,在细线未断之前两个弹簧所受到的弹力是相等的,所以当细线断开后,甲、乙两个物体做简谐运动时的振幅是相等的,A 、B 错;两物体在平衡位置时的速度最大,此时的动能等于弹簧刚释放时的弹性势能,所以甲、乙两个物体的最大动能是相等的,则质量大的速度小,所以C 正确,D 错误.【答案】 C题号 1 2 3 4 5 6 7 8 9 10答案 ACBADACBDACADD(T 2-T 1)R/T 17【答案】 C8【解析】 根据题意,由能量守恒可知12kx 2=mg (h +x ),其中k 为弹簧劲度系数,h 为物块下落处距O 点的高度,x 为弹簧压缩量.当x =x 0时,物块速度为0,则kx 0-mg =ma ,a =kx 0-mg m =kx 0m -g =2mg (h +x 0)mx 0-g =2g (h +x 0)x 0-g >g ,故正确答案为D.【答案】 D9【解析】 由题中条件可得单摆的周期为T =0.30.2s =1.5s ,由周期公式T =2πlg可得l=0.56m.【答案】 A10【解析】 当摆球释放后,动能增大,势能减小,当运动至B 点时动能最大,势能最小,然后继续摆动,动能减小,势能增大,到达C 点后动能为零,势能最大,整个过程中摆球只有重力做功,摆球的机械能守恒,综上可知只有D 项正确.【答案】 D机械振动(4)1解析:选A.周期与振幅无关,故A 正确.2解析:选C.由单摆周期公式T =2π lg知周期只与l 、g 有关,与m 和v 无关,周期不变频率不变.又因为没改变质量前,设单摆最低点与最高点高度差为h ,最低点速度为v ,mgh =12m v 2.质量改变后:4mgh ′=12·4m ·(v 2)2,可知h ′≠h ,振幅改变.故选C.3解析:选D.此摆为复合摆,周期等于摆长为L 的半个周期与摆长为L2的半个周期之和,故D 正确.4解析:选B.由简谐运动的对称性可知,t Ob =0.1 s ,t bc =0.1 s ,故T4=0.2 s ,解得T =0.8s ,f =1T=1.25 Hz ,选项B 正确.5解析:选D.当单摆A 振动起来后,单摆B 、C 做受迫振动,做受迫振动的物体的周期(或频率)等于驱动力的周期(或频率),选项A 错误而D 正确;当物体的固有频率等于驱动力的频率时,发生共振现象,选项C 正确而B 错误.6解析:选BD.速度越来越大,说明振子正在向平衡位置运动,位移变小,A 错B 对;速度与位移反向,C 错D 对.7解析:选AD.P 、N 两点表示摆球的位移大小相等,所以重力势能相等,A 对;P 点的速度大,所以动能大,故B 、C 错D 对.8解析:选BD.受迫振动的频率总等于驱动力的频率,D 正确;驱动力频率越接近固有频率,受迫振动的振幅越大,B 正确.9解析:选B.读图可知,该简谐运动的周期为4 s ,频率为0.25 Hz ,在10 s 内质点经过的路程是2.5×4A =20 cm.第4 s 末的速度最大.在t =1 s 和t =3 s 两时刻,质点位移大小相等、方向相反.。
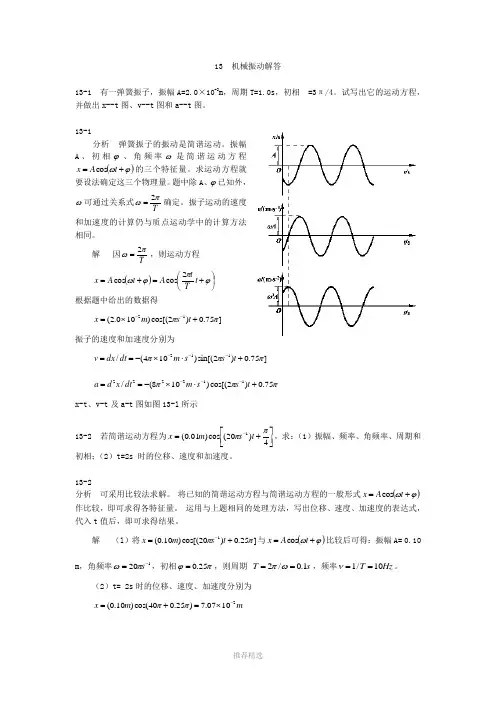
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。

机械振动测验填空题1、所谓振动,广义地讲,指一个物理量在它的①平均值附近不停地经过②极大值和③极小值而往复变化。
2、一般来说,任何具有④弹性和⑤惯性的力学系统均可能产生机械振动。
3、XXXX在机械振动中,把外界对振动系统的激励或作用,①激励或输入;而系统对外界影响的反应,称为振动系统的⑦响应或输出。
4、常见的振动问题可以分成下面几种基本课题:1、振动设计2、系统识别3、环境预测5、按激励情况分类,振动分为:①自由振动和②强迫振动;按响应情况分类,振动分为:③简谐振动、④周期振动和⑤瞬态振动。
6、①惯性元件、②弹性元件和③阻尼元件是离散振动系统三个最基本的元件。
7、在系统振动过程中惯性元件储存和释放①动能,弹性元件储存和释放②势能,阻尼元件③耗散振动能量。
8如果振动时系统的物理量随时间的变化为简谐函数,称此振动为①简谐振动。
9、常用的度量振动幅值的参数有:1、峰值2、平均值3、均方值4、均方根值。
10、系统的固有频率只与系统的①质量和②刚度有关,与系统受到的激励无关。
试证明:对数衰减率也可以用下式表示,式中x n是经过n个循环后的振幅。
利用前面给山的解A = Ae~^,f sing, Jl -鬥 + 0)可得到哀减率为A."=1 =无十1_心4■ m识(“厂对数哀减率为1血〃=“d = In —-3.有阻尼自山振动•画衰薜•测定阻尼口山振动的扳皿衰减率是计算系统阻尼比的一个常用的易行方法自•在振动试验中,可以测出系统阻尼自山振动时的响应,求出对数衰减率*进而得到系统的阻尼比’W 2.5-2证明对裁恁械率也町用F式表示匚—2比丄式中耳是经过岸牛循环后的并画出不同C值下撮輛诫小时50%的循环数耶。
frl任意苗相邻撮恻tt是*0 M 和%、」"■ J J °-^― * ** * 1* = 1 ——™ P如利驹%比值外/牝可以写成:d二」S旦n和求图示振动系统的固有频率和振型。

机械振动基础课后答案机械振动课件【--文秘基础】引导语:振动物体受回复力等于零的位置;也是振动停止后,振动物体所在位置;平衡位置通常在振动轨迹的中点。
下面是为你带来的机械振动课件,希望对你有所帮助。
1、什么是简谐运动?什么是回复力?2、掌握简谐运动的特点和各量的变化规律1、机械振动:物体在平衡位置所做的往复运动叫机械振动2、回复力:总是指向平衡位置,并使物体回到平衡位置的力叫回复力注意:回复力是效果力,是物体所受力的合力或合力的分力 3、简谐运动(1)定义:物体在与偏离平衡位置的位移大小成正比,总是指向平衡位置的力作用下的振动叫简谐运动(2)简谐运动的特征:回复力F:总是指向平衡位置,其大小与偏离平衡位置的位移大小成正比。
公式:F??kx加速度a:总是指向平衡位置,其大小与偏离平衡位置的位移大小成正比。
公式:a??kxm(3)各量的方向特点:位移x:方向偏离平衡位置回复力F:总是指向平衡位置加速度a:总是指向平衡位置,速度v:除两个端点外的任何位置,速度有两个可能的方向(4)各量的大小变化规律请同学们思考:动量和动能的大小变化规律所以:简谐运动是加速度变化的变速运动。
(5)简谐运动的对称性:在简谐运动中对称的两个点有如下的几个关系:位移大小相等方向相反;回复力大小相等方向相反;加速度的大小相等方向相反;速度的大小相等,方向可能相同可能相反;动量的大小相等,方向可能相同可能相反;动能的大小相等;弹簧振子:理想化的物理模型音叉叉股的上各点的振动,弹簧片上各点的振动,钟摆摆锤的振动等简谐运动是最简单的振动形式,要研究振动只有从简谐运动开始例1:下列哪些物体的运动属于机械振动() A、在水面上随波运动的小舟 B、在地面上拍打的篮球 C、摩托车行驶时的颠簸 D、秋千的运动例2、关于振动的平衡位置,下列说法正确的是() A、位移为零 B、回复力为零 C、加速度为零 D、合力为零 E、速度最大例3、弹簧振子在光滑的水平地面上做简谐振动,在振子向平衡位置运动的过程中() A、振子受回复力逐渐增大 B、振子的位移逐渐增大 C、振子的速度逐渐减小 D、振子的加速度逐渐减小例4、一个弹簧振子沿水平方向的x轴做简谐运动,原点O为平衡位置,在震动中某个时刻可能出现的情况是()A、位移与速度均为正,加速的度为负B、位移为负值,加速度为正值C、位移与加速度均为正值,速度为负值D、位移、速度、加速度均为负值例5:证明竖直弹簧振子的振动是简谐运动。
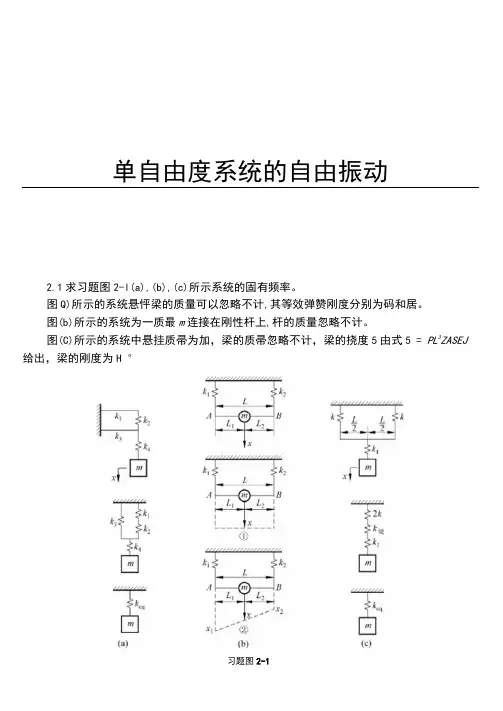
单自由度系统的自由振动2.1求习题图2-l(a),(b),(c)所示系统的固有频率。
图Q)所示的系统悬怦梁的质量可以忽略不计,其等效弹赞刚度分别为码和居。
图(b)所示的系统为一质最m连接在刚性杆上,杆的质量忽略不计。
图(C)所示的系统中悬挂质帚为加,梁的质帚忽略不计,梁的挠度5由式5 = PL3ZASEJ 给出,梁的刚度为H °习题图2-1机械根动习題鮮答解:(a〉系统简化过程如习题图2-l(a)所示。
4和息串联MZ=H⅛;也和b并联:Z= ^eql + &3^«)2 和上4 串联:Hl =即■r _ (焦层+以3 +心3低)加S = d层十(怡1十层)(爲=G所以固有频率为(B)习题图2-1 (B)所示系统可能有下面两种运动帖况:①在机垂i⅛振动的整个过稈中•杆被约束保持水平位置(见图(b)■①);②在悬挂的铅垂面内,杆可以自由转动(见图(b"②)。
①在杆保持水平的情况下,弹簧d和屜并联,有怎q =血+缸所以固有频率为②当杆可以自由转动时•杆和质虽m的运动会出现非水平的一般状态。
设A点的位移为点的位移为H2,加的位移为工,则静力方程利静力矩方程为ZIlXl + k2X3 = Aa l HQJrILl = k2x z L2几何关系又LI 十L2 = L 由以匕方程解得=kλk z∖}eq ki L↑±k z Ll所以固有频率为ω,17 m第2幸单自由度糸统的自由振动(C)系统简化过程如习题图2-1(C)所示。
等效弹簧刚度为其中所以固有频率为2.2如习题图2・2所示的系统中均质刚杆AB的质帚为加,A端弹簧的刚度为仁求()点铃链支座放在何处时系统的固有频率最高。
解:设&坐标如习题图2-2所示。
系统的动能为=-ym(nZ)2^l — + + 右片=-I-^eq(WZ^)2 (I)等效质量加“可以表示为山于固有频率与质量的平方根成反比,即3严厲、欲得最高的固有频率,必须使〃G为最小,即d叫 _ 3”_2 _ dn 3n3得2n = T代入二阶导数•得d'/Meq _ 2(1 —”)、∩~ln r _ ~^√>是极小值•故饺链应放在距A端彳L处。

第一章概述1.一简谐振动,振幅为0.20cm,周期为0.15s,求最大速度和加速度。
解:• 1Xrnax = w * X x =2*^*/* = 2 * * A = 8.31cm/ s11 Id A / IDdA1Xnm = w2 * X niax= (2 * ” * /)2 * X niax = (2 * 7F * —)2 * A = 350.56c〃? / s22.一加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅o(g=10m/s2)解:Xmax =心工皿=(2*4*/)f皿X nux =Xmax/(2*/r*/)2 =(50*10)/(2*3.14* 80)2 = 1.98〃〃〃3.一简谐振动,频率为10Hz,最大速度为4.57m/s,求谐振动的振幅、周期、最大加速度。
解:乂皿=Xnux/(2*^*/) = 4.57 / (2*3.14*10)= 72.77mm7 = —= —= 0.15f 10Xmax = W * Xmax = 2 * * Xmax =2*3.14*10*4.57 = 287.00/?/ / s'4.机械振动按激励输入类型分为哪几类?按自由度分为哪几类?答:按激励输入类型分为自由振动、强迫振动、自激振动按自由度分为单自由度系统、多自由度系统、连续系统振动5.什么是线性振动?什么是非线性振动?其中哪种振动满足叠加原理?答:描述系统的方程为线性微分方程的为线性振动系统,如I()0 + m S a0 = O描述系统的方程为非线性微分方程的为非线性振动系统+ 〃?即sin。
= 0线性系统满足线性叠加原理6.清画出同一方向的两个运动:X]Q) = 2sin(4/〃),x2(f) = 4sin(4^r)合成的的振动波形7.请画出互相垂直的两个运动:%。
)= 2sin(4^r), x2(t) = 2sin(4/zV)合成的结果。
如果是珀。
)=2sin(4^r+ ^/2),x2(t) = 2sin(4/z?)第二章单自由度系统一物体作简谐振动,当它通过距平衡位置为0.05m, 0.1m处时的速度分别为0.2姑和0.08】桃。

机械振动基础课后习题答案1. 简谐振动的特点是什么?简述简谐振动的基本方程。
答:简谐振动是指振动系统在无外力作用下,自身受到弹性力作用而产生的振动。
其特点有以下几点:振动周期固定、振幅不变、振动轨迹为正弦曲线。
简谐振动的基本方程为x = A*cos(ωt + φ),其中x为振动的位移,A为振幅,ω为角频率,t为时间,φ为初相位。
2. 简述自由振动、受迫振动和阻尼振动的区别。
答:自由振动是指振动系统在无外力作用下,自身受到弹性力作用而产生的振动。
受迫振动是指振动系统在外力作用下,产生与外力频率相同的振动。
阻尼振动是指振动系统在有阻尼力作用下,产生的振动。
三者的区别在于外力的有无和阻尼力的存在与否。
3. 什么是振动的自由度?简述单自由度振动和多自由度振动的特点。
答:振动的自由度是指描述振动系统所需的独立坐标的个数。
单自由度振动是指振动系统所需的独立坐标只有一个,可以用一个坐标来描述整个振动系统。
多自由度振动是指振动系统所需的独立坐标大于一个,需要多个坐标来描述整个振动系统。
单自由度振动的特点是简单、容易分析,而多自由度振动具有更复杂的动力学特性。
4. 简述振动系统的自然频率和强迫频率。
答:振动系统的自然频率是指系统在无外力作用下自由振动时的频率。
自然频率只与系统的质量、刚度和几何形状有关。
强迫频率是指系统在受到外力作用下振动的频率。
强迫频率可以是任意频率,与外力的频率相同或不同。
5. 什么是共振?简述共振现象的发生条件。
答:共振是指振动系统在受到外力作用下,当外力的频率接近系统的自然频率时,振动幅度达到最大的现象。
共振现象发生的条件包括:外力的频率接近系统的自然频率,外力的幅度足够大,系统的阻尼较小。
6. 简述振动系统的阻尼对振动的影响。
答:阻尼对振动有以下几种影响:阻尼可以减小振幅,使振动逐渐衰减;阻尼可以改变振动的频率,使其偏离自然频率;阻尼可以引起相位差,使振动的相位发生变化。
7. 什么是振幅衰减?简述振幅衰减的特点。

2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-= 所以:9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩ (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===-因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有: 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知:12()0m m x kx ++= 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。

秦时明月经典语录整理by NeXT_V oyager | NeXT_Voyager 《机械振动基础》秦时明月经典语录整理作者:NeXT_Voyager 来源:网络时间:2017-07-11 20:30 —————————————————————————1、痛苦,是保持清醒的最好方式。
2、你既然已经做出了选择,又何必去问为什么选择。
3、要想成为强者,就不要回避心里的恐惧,恐惧并不是弱点。
强者,是要让你的敌人比你更恐惧。
——盖聂4、有些梦想虽然遥不可及,但不是不可能实现。
只要我足够的强。
——少年盖聂5、我是一只雁,你是南方云烟。
但愿山河宽,相隔只一瞬间。
6、如果提出的问题本身就有问题,那么答案又有什么用呢?——盖聂7、他在走一个圆圈,弧线是他的决心,没有终点。
——荆轲8、若今生执罔虚幻,已成落花。
便许你来世雪扫眉发,执手天涯。
你可愿青丝绾正,笑靥如花,借我一世年华。
——卫庄9、若今生碎如烟花,不为他嫁。
来世,你可愿等飞雪染白头发,娶我回家。
许我一世年华。
——雪女10、失败的人只有一种。
就是在抵达成功之前放弃的人——盖聂11、若今生逆旅天涯,四海为家。
便许你来世雪舞霓裳,步步莲华。
你可愿化身为枷,度我年华,细数山室茶花。
——高渐离12、若今生轻放年华,化身流沙,只为追寻你浪迹的天涯。
来世,你可愿为我折枝白梅花,看一场雪落下。
——赤炼13、你什么也不肯放弃,又得到了什么?——盖聂-1 -秦时明月经典语录整理by NeXT_Voyager | NeXT_Voyager14、奇怪的人往往做一些奇怪的事,这一点也不奇怪。
——墨家巨子(燕太子丹)15、这个世上,胜者生,而败者亡,在世事的胜负面前,生与死不过是必然的因果。
——鬼谷子16、很多人都是被时代改变的,只有极少数的人是可以改变时代的。
17、勇敢,不是靠别人为他担心而证明的,强者,要能够使亲人和朋友感觉到安全和放心。
——盖聂18、从来没有想过这个背影我会用一辈子去眺望——赤练19、天下皆白,唯我独黑;非攻墨门,兼爱平生——墨家巨子20、无论命运把我带到何方,我的心都是自由的。
机械振动基础(李晓雷等)课后习题答案第一章1.3设*两个刚度分别为A. AWtt 性*»如fflT —1.3所示,试证明*由力的平 J 上=k\fS刃对》统施加力P, M 两个弹ff 的变为*F弓=7 1 1■,»«的总变形为「.2百+不=円2+2)D 它们井联W 的总《度*呷为,片呷=心+右2)它们串联时的总刚度/ «£*= +心 A X<5?-\AA/W»i D 对系统施加力P,粥两个弹賛的变3»相同为口 但受力 不同*分别**,>? = <» * =心丫俎0IL $>^«II <V 5X 10故《效刚度为*r -*故W效刚度为’亠=£=芋务=±+±1.4求S所示扭转斥统的总M度•两个串联的納的扭转M度分别为斤八K I対系统n加扭矩T.则两納的转角为,l-fT系统的总转角为,0 = ft +仇=ZY^— + )丄亠丄+丄)心T仏V故《效刚度为* — = —+ —Q Al仏1.5两只性》尼廉ft分别为©• 3 试计«总粘性》尼1)an只MDia并联时.2)衽两只联时•M. 1)对系统tt加力P, M两个績HB的速度m为•讥受力分别为*P yr = G + G故«效刚度为,X2}对«统《加力P, M两个MUM的速度为>.P 叫=—G . »«的总速度为,丘=占+尢=円丄十丄)・ P• q a-r, =—I .G故《效刚度为,r^ = - = - + - 才G A1.6 一简运动,UM为0. 5cm>周期为0.158.求量大速度和加速度•*筒谐运动叽吟二益心® 1•■为3_r= 5x 1()7 cos(—— zX/v)0J52/r 2/1Kb i x= -5x10'^ X— zsin(— /X刃/,) 0J50・15x= -5x10'^ X(-^2-z)" cos(-^^/X/w/.r)0J5 “0J5= 5 X10 X (/W /s) 0.15所以」;r^ =5xl0'x(—)'(/zz<r) z 0・151.7 一加速度计指示出结构援动頻車为82Hz・并具«*大加速度50欽求提动的Ml由町可«b斗二竺竺厶斗3: {In fY (2jr X 25)* I/j' 5(hr'te iiWt两个同频率但不同相角的ffi«运动的舍成仍是同《*»»«运动.SP I 彳cos f0/+ J?COS(W/-^)= t'cOii(ft?Z-0)t 井讨论卩“皿心・兀三种特例.证明tJcosr9Z+ 眉tusU府一vO=./cos w/ + ^cos a>/cos g? + 殍!iin tsj/iintp =(J+ -^cos^)cosfo/+ ^sinflisinfty=J(.J+ ScQs^py +(^sin <p)^ cos(d>/- 0)=q才+用 CM(咖=0)=c询血=0)柚F尿jk=J/+2」尿朋孚+gD当即=0时(9=0-,C= ^+^1刃当卩吆时' 0 = afr/^{SL4YC= J/' + 矿i 3)当甲二托时T円=0;「=彳=占11.9 把Stt4林i«^ 为式.lit 4+5i=A&",其中t 卄J护+5’ ° 9 s 叭垢<2)4第二章24弹*下悬挂一物体,弹*静伸长为<5 -设将输体向下拉・使弹*有静伸长 35 •怫盾无初速厦地释敖,求此«的运动方8.Mt 设«体««为刃.弹«刚度为Mtmg = kS t SPi 3" = Jkf m = Jg/ 6取果统静平術位■为原点T=0,系统运动方《为<mx + k\ = 0A, =25 (♦考« 材 W4)為=012弹賛不受力时长度为65cm >下《挂上Ikgtt 体JB 弹ff 长蚣m.设用手托 住《休便回》原长后无初速度地释放.《求・体的运动方程、jqffi 及弹1(力的量大值•Wt 由H 可知,WK 的静伸长A= 0.85-0.65 =0.2(/w)取祭统的平《位■为廉点,ffSt. »统的运动«分方S 为t ;r+<r=0 其中,初始条件计需::卫e 栅和⑷所以系统的 M 应为《•"/)= -0.2cosroy(zz/)WII 力为(片=^/) =-r(Z) = - cos w^z(A»此* «■为OJm.周期为年($)、弹11力*大值为1N ・= 7(/V7”/$)所以I 3 =2J〃人*挂左MS 为^的上并处于»平會位另一■愉化从*度为力处«由«»加I 上而无弹M,如S 所示•求其«的运动•«>取系统的上下运动・r 为坐标,向上为正・静平«位・为凍点T=0>則当加 «『位移时,系统«.£「= 1( zn, + nh)i"U =二加2由 d (爲 +U) = 0 可知》(m, +zn,)x +fcx = 0RPi w… = jR/(m +nj2)黑统的初绐*件为,V -以a- k/H] +m.(US 守HWi m 妙=-(njj +mj 讦)69ttSft 的Bft 应为》x(t)=人 cosft)/ + A siiuu 」RPi Mf) = ^^(cosq/ - I 2艷 sin 叫0 k Yu +m. M 一质■为"八转动«|为/的n 柱体作a 由純滾《h n 心受w-wuztt «>如ffl 所示.求«统的 Mt 取D 柱休的转角0为坐様.逆时针为正• 转角时,系统 £, =-10- +im(0r)- =i(/ + mr 府「2 2 2U =~k{0ry由 d(Er+U) = 0 可«» (/ +mr)0+kr'e■平會位S 时0 = 0・则当加«0=00h 叫=ylkr^/{I +nir') (nd/t)16求如S所示«统的周期.三个弹««成輪鑿,且A=2£M3=£・JWt取加的上下运动"为堂橄向上为正.静平«位・为康点,r=0.則当刿有•,位»W> MttWi由diEy +(/) =0 可知8 mx +—k,x = 0 …遵5 2摄<.)zIttX"-VAA-'Mr£^JWW' --17如S所示,半&为r的均JRBie可左半&为A的n轨面内无滑动地.以DD 轨S*低位SO为平«位■左右微《•试导出柱体的》动方8,求其S«««・H.设《体・;«角堂様0如9所示.逆时为正.当系统«0«角时• M.0*U = W{R -r)(l -COS0) ^W(R -r)—设©为IB柱体转角速度,«心的»肘速4 = = /XP * Wi 0 =(斤")0r记DD柱体規«时»融点A的转动惯■为/" MloREg 0"「g 2g g爲巴宀g歼今Xrf莎2 2 2 g r 4 g(或#理解为,& =丄/0+丄一(R-rF丼》动和平动的动能)2 2 g由d(£y +U) = 0 可ft* -—(/?-r)-0+W(/? -r)0=02 g2g…船Z)静止农比■为7的液体中.设从平«m ・s 距«期见9),魅后无初速度地Ktt ,若不计 尼,求浮子其后的运动.»> »立如S 所示峑極«统平«Wx=o.*初始*件为.gZo所以浮子的«应为..,v )=-rsin (A/^ + -)V zff 2X9求如图所示系统微《扭撮的周期.S 中M 个可分别規水平納G. 4 转动,它们相互《會,不IB 相対滑劲・左图示位■(半径4*与04左間一水平 tt 上)•不受力.«擦轮可以看《t««均ftUft, *■分别为■“ f Hr 两轮的AS 分别为巾屮比・B 此絵的半径比为*1=區Y 叫由干两轮无相对滑动,因此其转角比为, 色=殳=1 Q 「1 d取《统静平《时q =0,则«,E 『=MCm 斤刈 2 +1(7 叫 f 冷2 =7(^ +叫)/;%/2 2 2 2 4 U =押吋+押©)2 =知+ £)(砂由 WEy +1/) = 0可知《 扌(zn*+;nj/■苗:+(人 + £)/■;% = 0加F+y (乂r )g=0・ Hh3.=X8横徽面面积为■为■的r _•TxX■——:£R .即'"储召"如八+ m 、子 由牛 «*-«»{«.低fi讥)⑺XI0如m 所示.轮子可绕水平軸转劝・对转報的 功《S 为/;轮《绕《软《・下M 握科■*为Q 的 体・《与轮缘之的无滑动•住S 示位由水平 ««ft 持平«・半径*与・均巳》•求ffm 动的罔 Wt 取轮的«tAo 为峑标.WSrttt 为正• JRi«^PW 0 = 0.則峑轮子转A 时.MStWiEr = - to- +- — ((?/?)" = -(/ + — R')^ 2 2 & 2 g(~~T7T —— )/ + —Kli e. ■ I—— <»<l/s)t 故 T = — = 2;rJ ——电— (• J/+£»Q 3. V 3XU 弹ff«堆一js«为■的笹体.A 由攝动的jQM 为7;W 上附加一个JRSwo MS»ff 的静1长増加"•求出地的・力加速度-•・• n.g =彳△/Z A / A7z~m dZ ・・■£= --- =---------- -----"h丁 “h弹«•由&£> +£7)=0可灿P(Z + — R-X)- + lafe = 0 g112 个・的VMttMBKM*. «■■" 中•个为也-a)«m ■■均m 忖入杆■•~r^Ar| \' J iu>Ml n»«Mtl«0Alk«> ■孚《时o ・o(•)若不计杆賣.系统作微提动,M 有.比J 上丄'妙2 gU ■ PgL( \ ■ eosO) * Jp由Mr wo 可Bb 二/?© "“■ 0 gBP t a. ■ ( md/t )如果考虑杆賣,系统作《»1衲,M 有*I PU « PgL( \ - COS0) +\ - COS0) * (― + —2 g 22由d^Ef 4(7)«0可知J (旦 + + (— +■ 0g 3g 2rp mR_r)g01 叫■ i-§—=— (p»d/»)Cb)如果考虫杆C,系线作IMK 动.M 有.Ep ■£(—丄‘妙 W/nJ 诫'■«—+ 牛)L'P'2 g2 32 g 3U 珂F 守tef 分撐)(吟:X 2Ul £宀自沁m 診艸Tf 哼疋■ — M»1-JHh q = H-5-^ ------ - (nd/t)(<r>(c)如«考AffS. »统作《t«l 动.M«tE 七自沁挣旳弓e 哼疋沪1 <r>236求««面"jiHr 内液体《动的n 期・《力不计,ffi 定液柱总长度为厶Mr 假设UJEHF 内液柱长几ft 面积为A. 9度为p ・取*统静平崙时势K 为0.左边液面下降N 时,«.E, = jpAZx- U = pA XX xg XX由(/(坊 +U) =0可知》pAlx +2gpAx =0IPt 誓 (nd/t), T =江总 <*)X13 求如n 所示系统的辱效Pwj*.井把它9咸与Z 的美JK 敦:•*«的《劭*分方《 ”“伴4“•x2U …上+吗或兰+丄g 2 2 222. 17水ai 与2的水平徽面面积分别 八A «部用«面为4的细*连接• 港面上下嫌动的S«频率. «i 设液体密度为取杀统静平K 时势tt 为(h 当左边液面下降・5时・右边液 C 上升液体在水与2和细■中的速度分别为xpx^xp 则倂=jP A" •人)卅 +-[pA^K^ +-[pA (/i + x )tt^(由于》h ~ x^ h; /j + Xy 力;= 4呂;AX] = AXj )由gEf +U )= 0可知,[/j (i+殳)+L (殳)X + 型1 + 殳兀=0126某单・由度廉统左液体中《动,它所受》的澈》为尸=50COSM (N ), 9统 左畀期时共«■为aooscm,求fi 尼IMS-Ml 由Z'=0.20y 时共《可知,系统B 有频率为> 叫 上=伽n当wTqW, S»W 应《«,才=血,(♦«材P30〉CO )所以t r= -=匹-(AXsVzw )X (o JtWh 叫=I ---Mh (I (rad /t )Al* y[A^ +AX19 试i£W. 对 ttX* 車也可用下式*示5=lln&» (式中斗 S 经过"个備〃 工环肩的拥■)• 井绐出左》尼比0为0.01. 0.1. oa »tWNIM 小94 so%以下所需H 的《1环数•Ml 设承统》尼■由拥劝的响应为MC*厶时W 的位移为竝M 厶=厶+//7时«的位移为儿.Mt•E = _________ 才cos(% _y) ____________________ = /■•略-4^ Ff 5"“'COS[3“aQ + zz7^> — <p]AFrl^^V > In = U"、”7]^ = ZA S = /rin • BO i ?> = — In当和《"J5O% 时—r KI —=和 2=ln2 吗IF< = 0.01 mt. //= 111 ■■•个低环*=0,1 mt , ZZ= 13 I 9 2 个fit 环.歹=0・3时・ zz = o.34 I K 1 个«£FtH ■■为—挂住*■的下*. 产生■ 在上下运动时所iB 刮 的■力f A BraiZ ■悖平准隹■劭. 班■・ 体在■FWCft ■以初屋度 性开给运动. 我■!:后的运动IRd. W >逛糸统上下运动为"生标系・系MS •平伽位■为原点・El 糸聂g 运动■ 分方■%«P P—* ♦ “ ♦ —X ■ O&A糸see ■尼比 « r -—■—2v^r f i尸 p7乔H糸统不《R 动条件为. G N 1 ■ RPx UN"; 爭gjc. u O 斤.—U△二■ 土 w叫 _y/iN 》m $ ■ l»t< Mt) ■人& ~F •M<**a{; ~ 二A<Z> ■i3> m 0 V 1 ・t«*<"■<? '^<<7, eoscd^r 十 €7, sin w^r>■ O ©2 ■ 5 * 3.»3. ■叫 S - S2)当.K(r > = usun 叫*2M 若嫌动徇体受》的》力与X 运动速度平方咸正比• K巧="• x<0/> = ~ax x>0求其等效S 尼系(ft 和共摄时的嫌《■•Ml 实际上,这是一种低帖度流体》尼・设礙统的运动为t -»■(/)= A^co^co/ — <p} 叫=J a"a 龙泊(A I H(w) I iv)(w7 —0)=I a[a I H(w) I M< wf — 9?)J [— | H(w) | wA sin(wt — <p)}Jx "一兮匸 M/Vsin'(fuf —g>}dt w*3乙=^ax^ ayzrV/ = <3r<aF'_ —5< 2-29x=才 cos( ftV —初-r = —co^si n( coz — «>).jT/a今.S A */® *";=I a .>^zZr+ f —or ,i^zZrJ O Jjr Fa=丄 才'sin* (foz — </>)(—ft>*^cos(foZ — + I —sin*(ct>z — 9)(—a*才cos(3/— <p))zZ^ J 疔da“;="2 = Ca"—I —aw^X^ sin'(3f —<pyJt =:zXW[2(0>p -i(Of <p]■统■的•數来*示IM ■片的•Mt iftM 舛的转系饺的磁分方《为・IO + [出 + (Jt, + Jt, )21" ff = k^Ly sin ro/Bittu Jt,=八阮-(Jt, +Jkjz?233如图所示由《架支承的车《沿*低 不平的illfttr 进・试求炉的嫌・与行进速 度的关系.并确定S 不利的行进速度-2,33r= Feos 气匚/-z»vT = —Kl -r- r)H 才=KY cos 宁/ “・才+ A :r = A Z cos 书3“/那册+ QS)=人匕彝7皿宀滋5 3:二北=器血°+兰ysin 叫/2-32 —飞机升的片0接于升阵曲的O*上(BB ^=—2-32>,井由一联动 发■检«!• 0芸■相出于一 mdc 为外的扭<«弹*. iflst 片转动m ■为 /» Binr 系 19^00有頻率3宿=K* / /»IB Bic 丁不te 常w»计興•必烦 朋 试工 测农『%•为此m 定升降舵・利用《• « 4^对*■片做筒iwatJttu 井用弹 賛俎乗MPM. 改蛮激勵噸率e ■至 达到其共拥頻事〜• 试l^ov 和 K 升吟舵 O“ 《正峠 $*■ I 乙 .I I 冬i 7^2.32系统的共1«頻車为.3:工+(K + 出)25J ■ 1«»片的00列«車为,=屁-g + 匕)£?I2.33zv 丄■+ ASl = A r七+2才=3: r>vJv ■_七=x= h / k*oIsTk — T “'呼k —r7V= Z3才=140求单罪抵就藏对畸就鮒絶,设鵬統为亀/0)nta制七丹si 叫//Ml )七产叫恥(/呵他-2)=±si 輒(I)](/rX[i}- "co 叫(/-r)专(co 纠/)< 0=£]±si 叫(/讪1)flflrrX[l}- /;(/)^/-r)z/r+ -你/M(/-M*[co 叫(/-/])卜刽l-co 叫(/-/J]X[t}- 7j(/)Z(/-r)z/r+J-A(/)^/-ryA + 0%-/J0 彳 I.|«旷I II ( *hi■糾=#[co 糾(/-/]) 一cos©/]占[co 叫(/-/J-CO 叫(/一/])]b用冲仞申讨)fl(f r妙抑泊)一册皿/删/.伞■翌 川I 帥J皿寸侧/训+仲/"・M当跑何)卜吶血八i0»/|C用冲弘呻1)f!r加)卡加)吋1咖」/咿訥附W flp腓 如炉M+ 0%/■炸治叫严宀叫I*0J/,"»71fl142 -鞭债“维从-脚角为W 光洲®下為如田癇•求輸与帼 娜rnsmn 躺繃亂Uo = 5/5^in3^ =侮 以劇蝴marni 为原恵 轿方为正,畑艄分方程力 mx + kx = mg sin 30°心丄咖+哩泄(|・叫()肿q 事0 kV/nB蚩话IH 脱前的砒)=0故由I .v (f,) = —sinwj, + 詈(l ・cos (叮|)二0fl可卿心匸呦防輕)V/n y/ng也就翳li§i»开赠細牖艄牺飢考翱羅删林他亿二侮 X = 0。
第10章机械振动答案第十章 机械振动一. 选择题:【 C 】1、(基础训练3)一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图13-16所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为 (A)gl π2. (B)gl 22π. (C)gl 322π. (D)gl 3π.提示:均匀的细棒一段悬挂,构成一个复摆,可根据复摆的振动方程求解办法,求出复摆的振动周期。
【 C 】2(基础训练4) 一质点作简谐振动,周期为T .当它由平衡位置向x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12. (B) T /8. (C) T /6. (D) T /4.提示:从从二分之一最大位移处到最大位移处这段路程在旋转矢量图上,矢量转过的角位移为π31,对应的时间为T/6.[ B ] 3(基础训练8) 图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为(A) π23. (B) π. (C) π21. (D) 0. 提示:使用谐振动的矢量图示法,合振动的初始状态为2A-,初相位为π【 B 】 4、(自测提高5)一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s . (C)2.20 s . (D) 2.00 s .提示:使用谐振动的矢量图示法,初始状态旋转矢量位于第四象限,初始相位为3π-,到第一次回x tOA/2 -Ax 1x图13-23x (cm) t (s)O4 2 1T ,以余弦函数表达振动时,初相为零.在0≤t≤T 41范围内,系统在t =_T/8_时刻动能和势能相等.提示:动能和势能相等,为总能量的一半,此时物体偏离平衡位置的位移应为最大位移的22,相位为4π,因为初始相位为零,t=T/83、(基础训练16) 两个同方向同频率的简谐振动,其振动表达式分别为:)215cos(10621π+⨯=-t x (SI) , )5cos(10222t x -π⨯=- (SI)它们的合振动的振辐为210102-⨯(SI),初相为3121-+tg π=108.40提示:用旋转矢量图示法求解4、 (自测提高 8) 在静止的升降机中,长度为l的单摆的振动周期为T 0.当升降机以加速度g a 21=竖直下降时,摆的振动周期2T .提示:当升降机以加速度加速下降时,对于单摆,等效加速度为g-a=0.5g;单摆的周期变为:022T ag lT =-=π5、(自测提高 11) 一单摆的悬线长l = 1.5 m ,在顶端固定点的竖直下方0.45 m 处有一小钉,如图13-26所示.设摆动很小,则单摆的左右两方振幅之比A 1/A 2的近似值为_0.837_.提示:当单摆在最低位置时,对左右两边有:222211)(21)(21A m A m ωω=,对于单摆lg =ω,2211A l g A l g =837.0:2121==l l A A6 (自测提高 14)、两个互相垂直的不同频率谐振动合成后的图形如图13-27所示.由图可知x 方向和y 方向两振动的频率之比νx :νy =___4:3___.提示:在同样的时间间隔内,X 方向的振动为2T x ,而y 方向的振动为1.5T y ,周期之比为3:4,频率之比相反为4:3图13-26l0.45 m小钉图13-27x y三 计算题1. (基础训练23)有两个同方向的简谐振动,它们的方程(SI 单位)如下:⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=ππ4110cos 06.04310cos 05.021t x t x ,(1) 求它们合成振动的振幅和初位相。
胡海岩主编---机械振动基础课后习题解答_第2章习题第2章习题含答案习题2-1 定常力作用下的单自由度系统1. 一个单自由度系统的质量m=2kg,刚度k=1000N/m,阻尼系数c=10N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解:根据公式,该系统的固有频率可计算为:ωn = √(k/m) = √(1000/2) ≈ 22.36 rad/s阻尼比可计算为:ξ = c/(2√(mk)) = 10/(2√(2×1000)) ≈ 0.158振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时,系统为欠阻尼;当ξ=1时,系统为临界阻尼;当ξ>1时,系统为过阻尼。
2. 一个单自由度系统的质量m=5kg,刚度k=500N/m,阻尼系数c=20N·s/m。
试求该系统的固有频率、阻尼比和振动的稳定性。
解:根据公式,该系统的固有频率可计算为:ωn = √(k/m) = √(500/5) = 10 rad/s阻尼比可计算为:ξ = c/(2√(mk)) = 20/(2√(5×500)) ≈ 0.141振动的稳定性取决于阻尼比ξ的大小。
当ξ<1时,系统为欠阻尼;当ξ=1时,系统为临界阻尼;当ξ>1时,系统为过阻尼。
习题2-2 强迫振动的幅值和相位1. 一个单自由度系统的质量m=3kg,刚度k=2000N/m,阻尼系数c=30N·s/m。
给定的外力F(t) = 10sin(5t)N。
试求该系统在稳态时的振动幅值和相位。
解:首先求解系统的强迫响应,即对外力F(t)进行拉氏变换:F(s) = L{F(t)} = L{10sin(5t)} = 10L{sin(5t)} = 10×(5/(s^2+25))根据公式,系统的强迫响应可计算为:X(s) = F(s)/((s^2+ωn^2)+2ξωns)其中,ωn=√(k/m)为系统的固有频率,ξ=c/(2√(mk))为系统的阻尼比。
机械振动习题及答案⼀、选择题1、⼀质点作简谐振动,其运动速度与时间的曲线如图所⽰,若质点的振动按余弦函数描述,则其初相为 [ D ] (A )6π (B) 56π (C) 56π- (D) 6π- (E) 23π-2、已知⼀质点沿y 轴作简谐振动,如图所⽰。
其振动⽅程为3cos()4y A t πω=+,与之对应的振动曲线为 [ B ]3、⼀质点作简谐振动,振幅为A ,周期为T ,则质点从平衡位置运动到离最⼤振幅2A处需最短时间为 [ B ] (A );4T (B) ;6T (C) ;8T (D) .12T4、如图所⽰,在⼀竖直悬挂的弹簧下系⼀质量为m 的物体,再⽤此弹簧改系⼀质量为m 4的物体,最后将此弹簧截断为两个弹簧后并联悬挂质量为m 的物体,此三个系统振动周期之⽐为 (A);21:2:1 (B) ;2:21:1 [ C ] (C) ;21:2:1 (D) .41:2:15、⼀质点在x 轴上作简谐振动,振幅cm A 4=,周期s T 2=,其平衡位置取坐标原点。
若0=t 时刻质点第⼀次通过cm x 2-=处,且向x 轴负⽅向运动,则质点第⼆次通过cm x 2-=处的时刻为 (A);1s (B);32s (C) ;34s (D) .2s [ B ] 6、⼀长度为l ,劲度系数为k 的均匀轻弹簧分割成长度分别为21,l l 的两部分,且21nl l =,则相应的劲度系数1k ,2k 为 [ C ](A );)1(,121k n k k n n k +=+=(B );11,121k n k k n n k +=+= (C) ;)1(,121k n k k n n k +=+= (D) .11,121k n k k n n k +=+=7、对⼀个作简谐振动的物体,下⾯哪种说法是正确的? [ C ] (A )物体处在运动正⽅向的端点时,速度和加速度都达到最⼤值;(B )物体位于平衡位置且向负⽅向运动时,速度和加速度都为零;(C )物体位于平衡位置且向正⽅向运动时,速度最⼤,加速度为零;(D )物体处于负⽅向的端点时,速度最⼤,加速度为零。