(完整word版)单因素重复测量设计
- 格式：doc
- 大小：92.51 KB
- 文档页数：3
下载文档原格式
合集下载
单因素重复实验设计方差分析GLM
/PRINT=CELLINFO(MEANS)
/DESIGN.
混合实验设计方差分析的主要结果
通过对话框定义被试内变量、被试间变量，然后 点击“options”打开对话框，选择描述性统计命令、 方差齐性检验命令和多重比较命令。
选用的结果主要包括：(1)被试内变量的方差分析 表，给出所有含被试内变量的主效应和交互效应，该 表有四种不同检验法得到的结果 ，无所谓哪个更好 ； (2)被试间变量的方差分析表，只包括被试间变量主效 应和交互效应 ;（3）描述性统计结果、方差齐性检验 结果、多重比较结果。
A2B1C1 A2B1C2 A2B2C1 A2B2C2 /Wsfactors=A(2) B(2)C(2) /Print=Cellinfo(means) /Design.
程序运行演示
该程序运行输 出的结果包括 各单元的平均 数和标准差、 各自变量的主 效应、自变量 的二阶交互作 用、三阶交互 作用
五、多因素混合实验设计的方差分析（GLM）
50
5. 用2×3重复实验设计方法，设计一个研究方案以研究任务难度和 动机强度对工作效率的影响，并考察二者是否存在交互作用。然后 根据研究设计构造一个数据表，再对数据进行分析。
6. 用2×2×3混合实验设计方法 ，设计一个研究方案以研究 ：认知 风格（场依存性）、专业训练背景对不同记忆材料（抽象名词、动 植物名称、职业名称）记忆效果的影响。构造一个数据表并进行分 析，同时考察有无交互效应。
例6 某心理学工作者为研究汉字优势字体结构，选取10名被试，要
求每一被试在实验控制条件，对电脑屏幕上呈现的四种不同结构的汉 字作出快速识别反应，记录其正确率和反应时间。其中反应时间的实 验数据如下表所示。试分析不同字体结构下，被试的识别速度是否存 在显著性差异。
单因素重复实验设计方差分析(GLM
实验设计步骤
1. 确定实验目的和假设。
3. 设定实验处理和测量指标。
5. 进行统计分析，包括数据清 洗、方差齐性检验等。
2. 选择样本和分组。
4. 实施实验并记录数据。
6. 解读和分析结果，得出结论 。
实验设计注意事项
样本代表性
确保样本具有足够的代表性，能够反映总体 的情况。
数据处理规范
遵循数据处理规范，确保数据的准确性和可 靠性。
05
结论
研究成果总结
01
验证了单因素重复实验设计方差分析(GLM)在处理重复测量数 据时的有效性。
02
揭示了不同处理组之间的显著差异，为进一步研究提供了依 据。
03
证明了GLM在处理具有重复测量特点的数据时具有优越性， 能够更准确地估计实验处理效应。
研究不足与展望
需要更多的研究来验证GLM在处理不同类型重复测量数据时的适用性和稳 健性。
背景
在科学实验、社会科学调查和工 业生产等领域中，经常需要进行 单因素重复实验设计，以评估不 同处理或条件下的结果差异。
GLM简介
GLM全称General Linear Model，即一般线性模型，是一种广泛使用的统计分析方 法。
它通过构建线性模型来描述因变量和自变量之间的关系，并使用适当的统计技术来 估计模型参数和检验假设。
对数据进行整理，计算出每个 组的均值和观测值的总数。
5. 检验假设
通过比较组间变异和组内变异 的比例，判断处理方式是否对 实验结果验是方差分析中重要的一步，它通过比较组间变异和组内变异的比例来检验多个总体均值是否 相等。
在进行假设检验时，需要选择合适的统计量来描述组间变异和组内变异的比例，并确定显著性水平。
15.1.115.1重复测量单因素实验设计
重复测量设计举例
• 给被试呈现如图所示的照片制成的幻灯片，要求被试利用7点量 表评价每一张幻灯片的情绪的强度。每次呈现一张幻灯片，每张 呈现10秒钟，然后给被试35秒钟进行评定。实验中的自变量为照 片的形式（左侧构成，原始照片，和右侧构成），每位被试评价 54张幻灯片：18张左侧构成照片，18张原始照片和18张右侧构 成照片。
被试在接受实验处 理时，可能由于所 有处理水平对被试 施测的顺序不同， 而产生不同的影响。
重复测量设计的要求（2）
• 在实验设计中的自变量，按照其是否能被研究者所操纵，可以分 为可操纵的变量，和不可操纵的变量。
• 在不可操纵的变量中，有的是能够进行重复测量实验的，如年龄。 • 但是有的不可操纵变量是不能成为重复测量实验中的自变量的，
重复的接受不同的处理水平，因此大大的 减少了实验的被试数量，只需要较少的被
1
试就能获取大量的实验数据。
2
这在被试为特殊群体，或者被试 取样较困难的情况下，具有极大 的优势。
它也有一定的前提要求。
3
重复测量设计的要求（1）
被试先后接受不同 的处理水平时，相 互之间无长期影响。
当被试接受前面的 如在一些学习，记 处理对接受后面的 忆的研究中，就不 处理有长期影响时， 能使用重复测量设 就会将这种影响带 计。 入到下一个处理水 平中，从而混淆实 验处理的效应。
L
31
R
40 O 49
O
5
O 14
L 23 R 32
L
41 R 50 R
6
L
15
R
24
O
33
O
42
L
51
L
7
R 16 R 25 R 34 O 43 R 52 R
单因素和重复测量方差分析
一、陈述虚无假设和备择假设，并确定显著性水平
二、确定检验方向是单尾还是双尾
四、查表得出统计量临界值，并计算实际统计量
若结果具有显著性差异，需要做事后检验（两两比较）
统计量
*
*
THANK YOU WATCH!
03
04
05
01
02
假设2组数据。
两两比较？
分组三
分组四
分组一
分组二
答案是不可以
检验的两类错误
Ⅰ类错误 虚无假设正确，拒绝了虚无假设 或者我们检测到的显著性差异是由数据本身的误导性引起。其概率为0.05或者0.01 实验数据有显著性差异，处理结果显示没有差异 两类错误 Ⅰ类错误 Ⅱ类错误 显著性水平
N组数据，两两比较，求不出现Ⅰ类错误的概率？ 即使只有三组数据进行两两比较，不发生I类错误的最低概率为 1-0.953=0.14，0.14>0.05，分组越多，出现I型错误的概率越大。
方差分析 单因素、重复测量方差分析
方差分析的前提条件
1、观测间彼此独立
方差分析
3、各处理组间方差同质性
2、两个总体均正态分布
假设检验的步骤
统计量=均值之差/标准误
各种检验的统计量
*
z检验 统计量=
独立样本t检验 统计量=
t检验 统计量=
比较临界值和实际值，如|实际值|>临界值，则拒绝H0，认为有显著差异
根据样本容量确定自由度
陈述虚无假设和备择假设，并确定显著性水平
确定检验方向是单尾还是双尾
查表得出统计量临界值，并计算实际统计量
若结果具有显著性差异，需要做事后检验（两两比较）
单因素重复测量统计量
方差分析的前提条件
重复测量设计
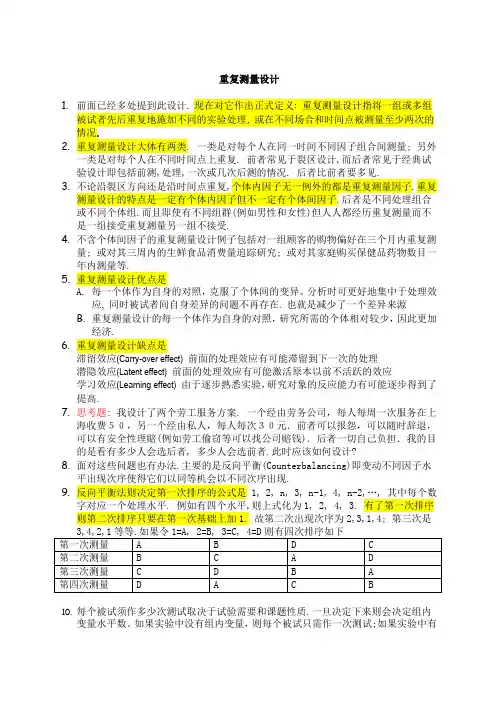
重复测量设计1.前面已经多处提到此设计. 现在对它作出正式定义: 重复测量设计指将一组或多组被试者先后重复地施加不同的实验处理, 或在不同场合和时间点被测量至少两次的情况.2.重复测量设计大体有两类. 一类是对每个人在同一时间不同因子组合间测量; 另外一类是对每个人在不同时间点上重复. 前者常见于裂区设计,而后者常见于经典试验设计即包括前测,处理,一次或几次后测的情况. 后者比前者要多见.3.不论沿裂区方向还是沿时间点重复,个体内因子无一例外的都是重复测量因子.重复测量设计的特点是一定有个体内因子但不一定有个体间因子.后者是不同处理组合或不同个体组.而且即使有不同组群(例如男性和女性)但人人都经历重复测量而不是一组接受重复测量另一组不接受.4.不含个体间因子的重复测量设计例子包括对一组顾客的购物偏好在三个月内重复测量; 或对其三周内的生鲜食品消费量追踪研究; 或对其家庭购买保健品药物数目一年内测量等.5.重复测量设计优点是A.每一个体作为自身的对照，克服了个体间的变异。
分析时可更好地集中于处理效应, 同时被试者间自身差异的问题不再存在. 也就是减少了一个差异来源B.重复测量设计的每一个体作为自身的对照，研究所需的个体相对较少，因此更加经济.6.重复测量设计缺点是滞留效应(Carry-over effect) 前面的处理效应有可能滞留到下一次的处理潜隐效应(Latent effect) 前面的处理效应有可能激活原本以前不活跃的效应学习效应(Learning effect) 由于逐步熟悉实验，研究对象的反应能力有可能逐步得到了提高.7.思考题: 我设计了两个劳工服务方案. 一个经由劳务公司，每人每周一次服务在上海收费５０，另一个经由私人，每人每次３０元．前者可以报怨，可以随时辞退，可以有安全性理赔(例如劳工偷窃等可以找公司赔钱)．后者一切自己负担．我的目的是看有多少人会选后者, 多少人会选前者.此时应该如何设计?8.面对这些问题也有办法.主要的是反向平衡(Counterbalancing)即变动不同因子水平出现次序使得它们以同等机会以不同次序出现.9.反向平衡法则决定第一次排序的公式是 1, 2, n, 3, n-1, 4, n-2,…, 其中每个数字对应一个处理水平. 例如有四个水平,则上式化为1, 2, 4, 3. 有了第一次排序则第二次排序只要在第一次基础上加1. 故第二次出现次序为2,3,1,4; 第三次是10.每个被试须作多少次测试取决于试验需要和课题性质.一旦决定下来则会决定组内变量水平数。
因素重复实验设计方差分析GL
40
36
4
27
22
24
27
3. 为研究四种不同教学方案在不同辅导时间下的效果，取三种不同的辅导时间分别进行四种教学方案的实验，从而得到12 个处理。随机抽取36名样本，每3名被试接受一种处理。实验结果如下表，请完成数据处理。
教 学 方 案
B1
B2
B3
B4
辅 导 时 间
A1
61，49，52
72，65，69
用2×2×3混合实验设计方法 ，设计一个研究方案以研究 ：认知风格（场依存性）、专业训练背景对不同记忆材料（抽象名词、动植物名称、职业名称）记忆效果的影响。构造一个数据表并进行分析，同时考察有无交互效应。
1
2
被试
生字密度1/15
生字密度1/30
说明文
叙事文
说明文
叙事文
语文
实验测试
语文
实验测试
语文
实验测试
语文
实验测试
1
85
20
70
30
80
35
90
45
2
70
15
80
35
65
30
75
43
3
76
23
68
28
85
45
80
55
4
90
24
88
32
80
43
69
46
5
85
22
75
33
75
41
78
50
用2×3重复实验设计方法，设计一个研究方案以研究任务难度和动机强度对工作效率的影响，并考察二者是否存在交互作用。然后根据研究设计构造一个数据表，再对数据进行分析。
36
4
27
22
24
27
3. 为研究四种不同教学方案在不同辅导时间下的效果，取三种不同的辅导时间分别进行四种教学方案的实验，从而得到12 个处理。随机抽取36名样本，每3名被试接受一种处理。实验结果如下表，请完成数据处理。
教 学 方 案
B1
B2
B3
B4
辅 导 时 间
A1
61，49，52
72，65，69
用2×2×3混合实验设计方法 ，设计一个研究方案以研究 ：认知风格（场依存性）、专业训练背景对不同记忆材料（抽象名词、动植物名称、职业名称）记忆效果的影响。构造一个数据表并进行分析，同时考察有无交互效应。
1
2
被试
生字密度1/15
生字密度1/30
说明文
叙事文
说明文
叙事文
语文
实验测试
语文
实验测试
语文
实验测试
语文
实验测试
1
85
20
70
30
80
35
90
45
2
70
15
80
35
65
30
75
43
3
76
23
68
28
85
45
80
55
4
90
24
88
32
80
43
69
46
5
85
22
75
33
75
41
78
50
用2×3重复实验设计方法，设计一个研究方案以研究任务难度和动机强度对工作效率的影响，并考察二者是否存在交互作用。然后根据研究设计构造一个数据表，再对数据进行分析。
重复测量设计
( 2 ) SS对象间 及 对象间
26652
36
2023.72 ； 对象间 9 1 8
( 3 ) SS对象内 及 对象内
相 当 于 第 8 章 的 组 内 变 异 ； 等 于 SS 总 −SS 对 象 间
或 各对象的离均差平方和之和，即
(n 1)
s
2 12
(y 1i
y1 )( y 2i
y2)
y 1i y 2 i
y 1i
y 2i
rij
s
2 ij
s
2 ii
s
2 jj
(n 1) n
s2 yi yj
sy2i
sy2j
2sy2iyj
如：sy21y2 s121s222 2s122
球形对称的实际意义举例
s2 yi yj
sy2i
sy2j
2sy2i yj
如：sy21y2 s121 s222 2s122
协方差阵 A1 A2 A3 A4
A1
10 5 10 15
A2
5 20 15 20
A3
10 15 30 25
A4
15 20 25 40
s1-22 = 10 + 20 - 2(5) = 20 s1-32 = 10 + 30 - 2(10) = 2 s1-42 = 10 + 40 - 2(15) = 2 s2-32 = 20 + 30 - 2(15) = 2 s2-42 = 20 + 40 - 2(20) = 2 s3-42 = 30 + 40 - 2(25) = 2
(a
ng (a 1) ˆ 2
1)n g (a 1)
ˆ
(12-2)
26652
36
2023.72 ； 对象间 9 1 8
( 3 ) SS对象内 及 对象内
相 当 于 第 8 章 的 组 内 变 异 ； 等 于 SS 总 −SS 对 象 间
或 各对象的离均差平方和之和，即
(n 1)
s
2 12
(y 1i
y1 )( y 2i
y2)
y 1i y 2 i
y 1i
y 2i
rij
s
2 ij
s
2 ii
s
2 jj
(n 1) n
s2 yi yj
sy2i
sy2j
2sy2iyj
如：sy21y2 s121s222 2s122
球形对称的实际意义举例
s2 yi yj
sy2i
sy2j
2sy2i yj
如：sy21y2 s121 s222 2s122
协方差阵 A1 A2 A3 A4
A1
10 5 10 15
A2
5 20 15 20
A3
10 15 30 25
A4
15 20 25 40
s1-22 = 10 + 20 - 2(5) = 20 s1-32 = 10 + 30 - 2(10) = 2 s1-42 = 10 + 40 - 2(15) = 2 s2-32 = 20 + 30 - 2(15) = 2 s2-42 = 20 + 40 - 2(20) = 2 s3-42 = 30 + 40 - 2(25) = 2
(a
ng (a 1) ˆ 2
1)n g (a 1)
ˆ
(12-2)
统计-单因素和重复测量方差分析共35页
统计-单因素和重复测量方差分析
51、没有哪个社会可以制订一部永远 适用的 宪法， 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
51、没有哪个社会可以制订一部永远 适用的 宪法， 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
ch15方差分析——单因素重复测量的情况
SS subject n j ( x i xgrand ) 2 210.44
• 这个被试内的平方和提供了对个别差异的一个量度，接下来，将个别 差异的变异从处理内变异中减去，就得到F比率分母部分的误差（残 差）平方和。 =36.67-31.44=5.23
各个平方和对应的自由度
• 第一步：dft=N-1=18-1=17 – dfbg=k-1=3-1=2
单因素重复测量ANOVA的条件
• 测量水平和样本容量 • 正态性假设
– 其偏态和峰度，如果两者都落在-1.0和1.0的范围内，我们就认为
满足这个假定。如果样本容量足够大的话，“正态性假定”即使 没有得到满足，对检验的结果也没有太大的影响。
• 球形分布假设
– 简单来说，指的是每个被试在每个处理条件下的相对位置应该是 一致的。如果处理效应对不同的被试产生不一致的效果，
公式2
=31.44
SSE ( x i x j ) 2
SSwg=SST-SSBG
公式3
=215.67
第二步：移除个别差异导致的变异
• 我们需要计算被试间的平方和。在计算过程中，我们将数据中每个被
试当做是一个处理，那么每个“处理”（被试）下面有三个分数，然 后同样使用的公式跟单因素ANOVA中计算处理间变异的公式（在这里 k=6，而每组内n=3）
（评估治疗的长期效应）分别进行测量3次，研究的目的在于评估反
映疗效的各个抑郁程度之间的均值差异。
单因素重复测量ANOVA
• 单因素重复测量ANOVA在下列几种情况下尤其有用 – 1)一些研究的假说要求重复测量。
– 2)当取样成员之间存在很大的变异时，按标准方法得到的误差变
异很大。对每个取样成员的重复测量可以减小改误差变异。 – 3）当取样成员不宜获取时，重复测量的设计显得经济实惠。
单因素重复测量结果报告
单因素重复测量结果报告一、单因素重复测量结果报告嘿，宝子们！今天咱们来唠唠单因素重复测量结果报告这事儿哈。
单因素重复测量呢，就像是你反复去看同一个东西，但是每次看可能都有不同的结果。
比如说你每天早上看自己的体重（当然这有点扎心啦，哈哈），这就是一种单因素（体重这个因素）的重复测量。
那这个结果报告呢，首先要讲清楚我们到底测量的是什么单因素。
就像刚刚说的体重，那在正经的研究里，可能是某个药物对病人某个症状的影响，这个症状就是我们的单因素啦。
我们得把这个因素描述得特别清楚，让看报告的人一下子就明白。
然后呢，测量的对象是谁呀？是一群大学生，还是特定的病人群体呢？这也得好好说。
如果是大学生，是哪个专业的，男生还是女生多，年龄大概是多少范围。
这些信息就像是给这个报告打基础的砖头，缺了可不行。
接下来就是具体的测量过程啦。
用了啥仪器，或者啥方法去测量的呢？要是用仪器，仪器的精度咋样，是不是很先进的那种，还是比较常规的。
方法呢，是问卷调查，还是实际的测试，比如说测量人的反应速度，是用那种按按钮的反应测试仪器，还是靠人工观察记录。
再说说测量的时间间隔。
是每天测一次，还是每周，甚至每个月呢？这个时间间隔可重要了。
比如说你研究植物的生长，每天测量和每周测量可能得到的结果趋势就不太一样呢。
结果部分那可就是重头戏啦。
我们得把每次测量得到的数据都列出来，可不能偷懒哦。
要是数据太多，做个表格多好呀，清晰又明了。
而且不能光列数据，还要分析这些数据的变化趋势。
是逐渐上升，还是下降，或者是波动很大呢？如果波动大，那为啥呢？是因为测量过程中有啥干扰因素，还是这个单因素本身就很不稳定呢？还有误差分析也不能少。
毕竟测量不可能是完美无缺的，总会有一些误差。
误差是怎么产生的呢？是测量仪器本身的问题，还是人为操作不当呢？比如说测量长度的时候，尺子刻度有点模糊，那这就可能造成误差啦。
最后呢，根据这个结果我们能得出啥结论呀？这个结论得跟我们最开始的研究目的挂钩。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单因素重复测量实验设计
一、单因素重复测量实验设计的基本特点
在单因素完全随机实验中，组内变异实际上是由两部分组成的：实验中测量误差引起的变异和未控制的无关变量带来变异，其中订是被试个体差异带来的变异。
减少误差变异的一个方法是控制个体差异引起的无关变量，达到这个目标的途径之一是使用随机区组设计，而控制个体差异的一个更有效的方法是重复测量实验设计，也叫被试内设计。
在一个非重复测量实验设计，或被试间设计中，例如我们在前面介绍的完全随机设计、随机区组设计和拉丁方设计中，一个共同的特点是实验中每个被试仅接受一个处理水平，被试的个体差异带来的变异混杂在误差变异中。
重复测量实验设计的基本方法是：实验中每个被试接受所有的处理水平。
这种实验设计的目的是利用被试自己做控制，使被试各方面特点在所有的处理中保持恒定，以最大限度地控制由被试的个体差异带来的变异。
使用重复测量设计的前提是研究者必须事先假设，当若干处理水平连续实施给同一被试时，被试接受前面的处理对接受后面的处理没有长期影响。
重复测量设计在有些情况下是不合适的，当处理的实施对被试有长期影响时，如学习、记忆效应，不能使用重复测设计。
例如，在一个教学研究中，要比较两种教学方法对学生学习成绩的影响。
我们不可能使用同一班学生先后接受两种教学方法，然后比较它们对学生学习成绩的影响，因为前一种教法的教学不可避免地对学生接受后一种教法的教学产生影响。
在心理与教育研究中，许多实验处理会对被试产生学习、记忆效应，因此使用重复测量设计要特别谨慎。
另外，顺序效应也是重复设计中应特别注意的问题。
被度连续接受处理时，练习、疲劳等效应是难免的，因此重复测量设计中需要考虑平衡顺序效应的问题。
与完全随机和随机区组设计非常不同的是，重复测量实验设计使用少量的被试，它们的图解比较如下：
（a
（b
（c
图2-4-1 单因素完全随机、随机区组、复重
测量实验设计中分配被试的比较
从三个图的比较中可以看出，在同样的有一个自变量、自变量有4个水平的实验中，完全随机设计使用16个随机选择的被试，随机区组设计使用4组、每组4个同质被试，因此也是16个被试，而重复测量设计仅用4个被试，每个被试接受所有的实验处理。
二、单因素重复测量实验设计与计算举例
（一）研究的问题与实验设计
我们继续以4种文章的生字密度对学生阅读理解的影响的研究为例。
为了更好地控制被试变量，研究者仅用8名被试，每个被试阅读4篇生字密度不同的文章，并测他们各篇文章的阅读理解分数。
选择使用重复测量实验设计是由于研究者假设，当实验安排合适时，被试阅读一篇文章举对阅读另一篇文章产生影响。
但是，在这种实验设计中，疲劳效应和顺序效应是必须考虑的。
为了减少疲劳效应，研究者决定将4篇文章在下午分4次施测。
平衡顺序效应的方式有两种：以随机顺序实施4种生字密度的文章，或以拉丁方实施4 区组区组区组区组被试1 被试2 被试3 被试4
（二）实验数据及其计算
单因素重复测量实验数据的列表，计算与单因素随机区组实验的完全相同，只是在平方和的分解释上有所不同。
单因素重复测量实验中，总平方和首先被分为被试间平方和与被试内平方和，然后再分解被试内平方和为处理效应和误差变异。
1.计算表
表2-4-1 单因素重复测量实验的计算表
2.11
36202.000p
n ij
i j Y
===++⋅⋅⋅⋅⋅⋅=∑∑
2
2
11
()(202)[]1275.125(8)(4)
p
n ij j j Y Y np
=====∑∑
()
21
2211
(
)
22
1
2
[](3)(6)1544.000(35)(31)[]1465.250
8(8)n
ij i p
n i j Y p
j Y
AS ij
A n
======++⋅⋅⋅⋅⋅=∑==++=∑∑∑
L L
()
21(
)
22
1(24)(29)[]1301.0004(4)n
ij j
Y p
j
s P
==∑==++=∑
L L
3．平方和的分解与计算
（1）平方和分解模式：
()(2)[][]268.875[][]25.875243.000[][]190.125
52.875
SS SS SS SS SSA SS AS Y S Y SS SS SSA A Y SS SS SS SSA =+=++=-==-==-==-==--=总变异被试间被试内被试间残差总变异被试间被试内总变异被试间残差总变异被试间平方和计算:
SS SS SS
4.方差分析表及结果的解释
方差分析表中可以看出，实验中的自变量——生字密度的效应是统计显著的（F（3,21）=25.17，P＜.01＝，自变量的F检验的误差项是Mse=2.518。
方差分析表中还有一项“被试间变异”（SS被试间=25.875），这部分变异带有所有被试之间个体差异引起的变异。
由于从总变异中分离出了被试间变异，因此与完全随机实验相比，重复测量实验中提高了实验处理的F检验的敏感性。
5.
图2-4-3 单因素重复测量实验设计的平方和与自由度的分解
6.对平方和分解与计算的一些解释
SS总变异——在重复测量实验中，总变异应首先分解为被试间的平方和和被试内平方和。
SS被试间——被试间平方和，即总变异中所有由被试的个体差异引起的变异。
SS被试内——被试内平方和包括同一被试在接受不同实验处理时产生的变异(被试内因素的处理效应)，以及偶然因素引起的实验误差。
在单因素重复测量实验设计中，被试内平方和被分解为两部分：A因素的处理效应和误差变异。
SS残差——重复测量实验中的残差变异与随机区组实验中的残差性质相同，重复测量实验方差分析中残差的计算是先从总变异中减去被试间平方和，然后再减去处理效应。
由于事先从总变异中分离出了所有的由被试个体差异带来的变异，重复测量实验中的SS残差一般很小。