船舶结构力学复习

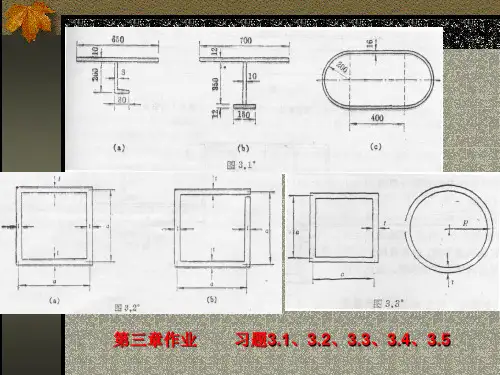
船舶结构⼒学复习题2014.4船舶结构⼒学复习题1、⽤初参数法求图中所⽰受均布载荷作⽤的单跨梁挠曲线⽅程，其中柔性系数为3A l48EI=。

x2、如图所⽰单跨梁的抗弯刚度为EI，跨长为l，跨中受集中⼒P的作⽤，右端弹性固定端EI l3/=α，请⽤初参数法求解图⽰单跨梁的挠曲线⽅程。

3、⽤⼒法求解图中所⽰结构在⽀座0处的转⾓和⽀座1处的⽀反⼒，已知，lll==1201，各杆的抗弯刚度均为EI，集中弯矩M2ql=，弹性⽀座的柔性系数为/3A l24EI=。

（15分）q1A2M4、采⽤位移法求图⽰结构节点2和4的转⾓。

各杆的长度及断⾯惯性矩均为l及I，已知2/2ql=M。

5、如图中所⽰结构，列出求解梁0-1-2的位移法⽅程式组。

已知，lll==1201，断⾯惯性矩均为I。

26、如图所⽰双跨梁，在3处受到⼀弯矩m ，⽤⼒法求2处弯矩2M 。

37、如图所⽰的结构，杆1-2长为l ，刚度为EI ，在右端受有集中⼒P 的作⽤。

试⽤应⼒能原理求右端在集中⼒P 作⽤下的挠度。

P8、设图⽰梁的挠曲线⽅程)(x l ax v -=，⽤李兹法求解此梁的挠曲线。

qx9、⽤矩阵法求解图中的结构，单元和节点编号如图所⽰，采⽤平⾯弯曲杆单元，试解答下列问题：（1）计算各单元的刚度矩阵；（2）写出结构总刚度矩阵；（3）写出以矩阵形式表⽰的节点平衡⽅程式；（4）对节点平衡⽅程式进⾏约束处理，写出约束处理后的⽅程式。

已知：平⾯弯曲杆单元刚度矩阵公式为[]=4 6/- 12/ 2 6/- 4 6/ 12/- 6/ 12222 对称 l l l l l l l EI K eq123,EI l,EI l10、⽤矩阵法求解图中的结构，单元和节点编号如图所⽰，采⽤平⾯弯曲杆单元，试解答下列问题：（1）计算各单元的刚度矩阵；（2）写出结构总刚度矩阵；（3）写出以矩阵形式表⽰的节点平衡⽅程式；（4）对节点平衡⽅程式进⾏约束处理，写出约束处理后的⽅程式。

船体结构力学试题答案一、选择题1. 船体结构中，最常见的骨架类型是（）。

A. 纵向骨架B. 横向骨架C. 混合骨架D. 桁架结构答案：B2. 船体钢板的厚度选择主要取决于（）。

A. 船体尺寸B. 船只用途C. 载荷大小D. 所有上述因素答案：D3. 船体结构设计中，以下哪项不是考虑的因素？（）。

A. 船体的稳定性B. 船体的强度C. 船体的美观性D. 船体的耐腐蚀性答案：C4. 在船体结构力学中，剪力和弯矩的计算是为了确保（）。

A. 船体的刚性B. 船体的强度C. 船体的稳定性D. 船体的安全性答案：B5. 船体结构中，横梁的主要作用是（）。

A. 连接船首和船尾B. 支撑船体的横向结构C. 增加船体的纵向强度D. 减少船体的重量答案：B二、填空题1. 船体结构设计的基本目标是确保船体具有足够的________和________，以适应各种海洋环境和操作条件。

答案：强度、稳定性2. 在船体结构中，船底板的主要功能是提供________和________。

答案：刚性、防水性3. 船体结构的强度计算需要考虑船体在________、________和________状态下的应力分布。

答案：静水、波浪、风载4. 船体结构设计中，通常采用________方法来优化船体的重量和性能。

答案：有限元分析5. 船体结构的耐腐蚀性设计中，常用的方法是应用________和________技术。

答案：防腐涂层、阳极保护三、简答题1. 简述船体结构中的纵向骨架和横向骨架的作用。

答：纵向骨架是船体结构的主体，它沿船长方向布置，主要作用是承受船体的纵向弯曲和扭曲载荷，保持船体的形状和刚性。

横向骨架则沿船宽方向布置，包括横梁、隔板等，其主要作用是支撑船体的横向载荷，增强船体的横向强度和整体稳定性。

2. 阐述船体结构设计中载荷的分类及其影响。

答：船体结构设计中考虑的载荷通常分为静态载荷和动态载荷。

静态载荷包括船体自重、固定设备的重量、货物重量等，它们对船体结构产生持续的、稳定的应力。

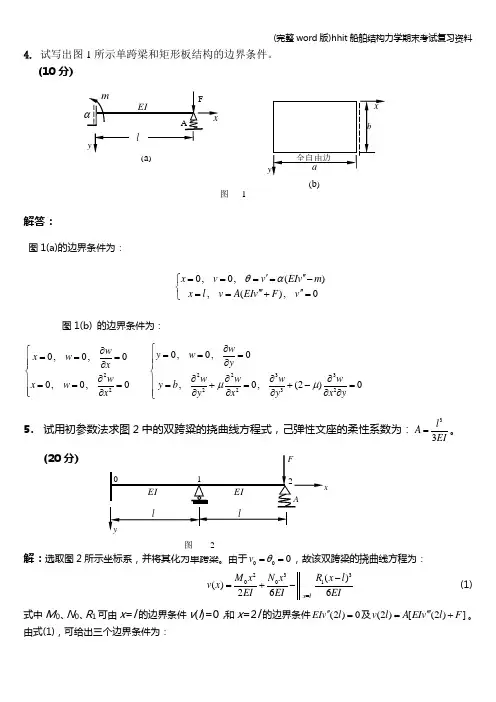
4. 试写出图1所示单跨梁和矩形板结构的边界条件。

(10分)解答：图1(a)的边界条件为：0,0,(),(),0x v v EIv m x l v A EIv F v θα'''====-⎧⎨'''''==+=⎩图1(b) 的边界条件为：22233222320,0,00,0,00,0,0,0,(2)0w w y w x w y x w w w w w x w y b x y x y x y μμ∂⎧∂⎧======⎪⎪∂⎪⎪∂⎨⎨∂∂∂∂∂⎪⎪====+=+-=⎪⎪∂∂∂∂∂∂⎩⎩5. 试用初参数法求图2中的双跨粱的挠曲线方程式，己弹性文座的柔性系数为：33l A EI =。

(20分)解：选取图200233001()()266x lM x N x R x l v x EI EIEI=-=+-(1)式中M 0、N 0、R 1可由x =l 的边界条件v (l )=0，和x =2l 的边界条件(2)0EIv l ''=及(2)[(2)]v l A EIv l F '''=+。

由式(1)，可给出三个边界条件为：0000110010262042()363M N lM N l R l R l l M Nl N R F ⎫+=⎪⎪+-=⎬⎪⎪+-=-+⎭(2) 解方程组式(2)，得0012610,,111111M Fl N F R F =-==将以上初参数及支反力代入式(1)，得挠曲线方程式为：2335()()111133x lFl F Fv x x x x l EI EIEI==-+-- 一． （15分）用初参数法求图示梁的挠曲线方程，已知3l EI α=，36lA EI=，q 均布。

αAqEI ,L解：梁的挠曲线方程为：处的边界条件为： ;处的边界条件：故有：及有二式可解得：；于是梁的挠曲线方程为：三、(20分）用能量法求解如图所示梁的静不定性。

hhit-船舶结构力学-期末考试复习资料处的边界条件：故有：及有二式可解得：；于是梁的挠曲线方程为：三、(20分）用能量法求解如图所示梁的静不定性。

已知图中E 为常数，柔性系数，端部受集中弯矩m 作用，悬臂端的惯性矩是其余部分的2倍。

解：取挠曲线函数为 ，满足梁两端的位移边界条件，即x=0时，3/(12)A l EI LLmx=3L/2时,说明此挠曲线函数满足李兹法的要求，下面进行计算。

(1) 计算应变能。

此梁的应变能包括两部分，一是梁本身的弯曲应变能，二是弹性支座的应变能。

注意到梁是变断面的，故有总的应变能为(2)计算力函数。

此梁的力函数为(3) 计算总位能故梁的挠曲线方程为弹性支座处的挠度为四、（20）用位移法求解下图连续梁的静不定问题。

已知：， ， ， ，画出弯矩图。

解：设节点1、2、3的转角为，由题意可知。

根据平衡条件有节点1：节点2：其中：将其代入整理，联立求解得：P ql =1223l l l ==1223I I I ==/(6)l EI α=;故：；；；弯矩图：四、（20分）用力法求解下图连续梁的静不定问题。

已知：其中杆件EI为常数，分布力q2P/L,集中弯矩m=PL，画出弯矩图。

解: 本例的刚架为一次静不定结构，现将支座1处切开，加上未知弯矩M1，原来作用于节点1上的外力矩m可考虑在杆0-1上亦可考虑在杆1-2上，今考虑在杆1-2上。

于是得到两根单跨梁如上图所示。

变形连续条件为节点1转角连续，利用单跨梁的弯曲要素表，这个条件给出:解得：弯矩图：6、用位移法计算下面刚架结构的杆端弯矩为了书写方便，将钢架的各节点分别命名为0、1、2和3，如上面右图所示。

解：1、确定未知转角的数目本题0、1、2三个节点都可能发生转动，故有三个未知转角 。

解题时将以上三个节点作刚性固定。

2、计算各杆的固端弯矩M 01 = -qL212M 10 =qL212M 12 =M 13 =M 21 =M 31 =003、计算因转角引起的杆端弯矩M 01 =′4EI 01L θ0+2EI 01Lθ1M 10 =′4EI 01L θ1+2EI 01L θ0M 12 =′4EI 12L θ1+2EI 12L θ2M 21 =′4EI 12L θ2+2EI 12Lθ1θ0θ1θ2、、M 13 =′4EI 13Lθ1M 31 =′2EI 13θ14、对节点0、1、2列出弯矩平衡方程式对“0”节点：M 01M 01′+= -qL24EI 01θ0+2EI 01θ1+= 0= -qL28E L θ0+4E Lθ1+= 0对“1”节点：M 10M 10′+12M 12′+13M 13′+++=qL24EI 01θ1+2EI 01θ0+4EI 12L θ1+2EI 12L θ2+4EI 13L θ1+= 0=0=qL2124Eθ0++32E θ1+6E θ2= 021M21′+对“2”节点：4EI21θ2+2EI21θ1=12Eθ2+6Eθ1== 0 = 0即： -qL28Eθ0+4Eθ1+= 0qL2 124Eθ0++32ELθ1+6ELθ2= 012E L θ2+6ELθ1= 0θ1θ2θ0===11qL3864EqL3216EqL3432E-解得未知转角：5、计算各杆的杆端弯矩M01 = M10 =M01 +M01′M10M10 =′+= -qL24EI01θ0+2EI01θ1 += -qL28ELθ0+4ELθ1 += -qL28EL+4EL+11qL3864EqL3216E-（ ）=-0.083+0.102-0.0185=0qL2 124EI01θ1+2EI01θ0+=qL2 8Eθ1+4Eθ0 +=qL2 8E+4E+11qL3864EqL3216E-（ ）=0.083+0.051-0.037 =0.097qL2LM 13 =M 21M 3113M 13 =′ +M 21M 21′+4EI 21L θ2+2EI 21L θ1=12E L +6E ==M 31 =′2EI 13θ1 =M 12 =12M 12 =′ +12E + 6E qL3216E -（ ）qL3432E= -0.056+0.0139= - 0.042qL2qL3432E qL3216E -（ ）= 0qL3216E -（ ）= - 0.056qL2 = 6E qL3216E -（ ）= - 0.028qL2二、(16分)图1所示结构，已知作用在杆中点的弯矩M , 和EI ,l 用初参数法求单跨梁的挠曲线方程。

xy 船舶海洋结构力学复习1、请用初参数法确定图示单跨梁0-1的挠曲线方程，其中单跨梁的刚度为EI ，跨长为l ，均布载荷q 如图所示。

左端刚性固定，右端弹性支座的柔性系数EIl A 4831=。

2、请用初参数法确定图示单跨梁0-1的挠曲线方程，其中单跨梁的刚度为EI ，跨长为l ，均布载荷q 如图所示。

左右端均为刚性固定。

3、用力法计算图示结构1点的弯矩1M ，已知杆1-2及杆2-3的刚度均为EI ，l l l ==2312。

4、用力法计算图示结构2点的弯矩2M ，已知杆1-2及杆2-3的刚度均为EI ，l l l ==2312，ql P =，且P 作用于杆1-2的跨中。

qx5、请用位移法解如图所示结构，只写出正则方程即可，不必求解。

各杆的长度及刚度均为l 及EI 。

6、请用位移法解如图所示结构，只写出正则方程即可，不必求解。

各杆的长度及刚度均为l 及EI ，P 分别作用于杆1-2及2-3的跨中。

7、如图所示的结构，杆1-2长为l ，刚度为EI ，在右端受有集中力P 的作用。

试用应力能原理求右端在集中力P 作用下的挠度。

8、请用应力能原理计算图示简单钢架的端点1在外力 P 作用下的垂向位移。

已知112l l =，223l l =，各杆的刚度均为EI 。

9、设有一纵骨架式船，船底肋板间距为1.2m,纵骨间距为0.7m ，如要保证船底板的临界应力达到2/240mm N cr =σ，求所需板厚为多少？10、设有一纵骨架式船，船底纵桁为T 型材，断面尺寸为：翼板100⨯102m m ，腹板180⨯82m m 。

请分别计算纵桁翼板和腹板的临界应力cr σ。

11、四周自由支持的矩形板长边cm a 400=, 短边cm b 100=，板受垂直于板面的均布载荷2/05.0mm N q =作用，板厚cm t 8.0=，材料弹性模量为25101.2mm N E ⨯=。

(1)请写出板筒形弯曲的条件。

(2)按筒形弯曲画出本题矩形板的计算模型，并计算板中心的挠度及弯矩。

船舶结构力学课后题答案船舶结构力学课后题答案1.什么是船舶结构力学？船舶结构力学是研究船舶结构受到的力学作用及其力学性能的学科。

它主要涉及到船舶结构的强度、刚度、稳定性、疲劳、振动、冲击等方面的问题。

船舶结构力学的研究对于船舶的设计、建造、维修和运营具有重要意义。

2.船舶结构的强度是指什么？船舶结构的强度是指船舶结构在外界力作用下所能承受的最大应力或变形程度。

船舶结构的强度对于船舶的安全性和使用寿命具有重要影响，因此在设计和建造船舶时需要进行强度计算和强度验证。

3.船舶结构的刚度是指什么？船舶结构的刚度是指船舶结构对外界力作用的抵抗能力。

刚度主要包括纵向刚度、横向刚度和扭转刚度。

船舶结构的刚度对于船舶的航行性能和稳定性具有重要影响，因此在设计和建造船舶时需要进行刚度计算和刚度验证。

4.船舶结构的稳定性是指什么？船舶结构的稳定性是指船舶在受到外界力作用时保持平衡的能力。

船舶结构的稳定性对于船舶的航行安全和运载能力具有重要影响，因此在设计和建造船舶时需要进行稳定性计算和稳定性验证。

5.船舶结构的疲劳是指什么？船舶结构的疲劳是指船舶结构在循环荷载作用下产生的疲劳损伤和疲劳破坏。

船舶结构的疲劳对于船舶的使用寿命和安全性具有重要影响，因此在设计和建造船舶时需要进行疲劳计算和疲劳验证。

6.船舶结构的振动是指什么？船舶结构的振动是指船舶结构在受到外界激励作用下产生的振动现象。

船舶结构的振动对于船舶的航行舒适性和结构安全具有重要影响，因此在设计和建造船舶时需要进行振动计算和振动验证。

7.船舶结构的冲击是指什么？船舶结构的冲击是指船舶结构在受到外界冲击力作用下产生的应力和变形。

船舶结构的冲击对于船舶的抗冲击能力和结构安全具有重要影响，因此在设计和建造船舶时需要进行冲击计算和冲击验证。

8.船舶结构力学的研究对船舶设计和建造有什么意义？船舶结构力学的研究对船舶设计和建造具有以下几方面的意义：•提高船舶的强度和刚度，保证船舶的安全性和使用寿命；•提高船舶的稳定性，保证船舶的航行安全和运载能力；•预测和控制船舶结构的疲劳、振动和冲击，保证船舶的航行舒适性和结构安全；•优化船舶结构设计，提高船舶的性能和经济效益。

船舶力学知识点总结船舶力学是研究船舶在水中运动的力学分支，包括了船舶在航行、漂浮、操纵和受力等方面的物理过程。

船舶力学的研究对于设计、建造和运用船舶都有着重要意义，下面将对船舶力学的知识点进行总结。

一、船舶的基本概念和性能指标1. 船舶的基本概念船舶是指用于在水中航行的交通工具，一般包括水面船舶和潜水船舶两种类型。

水面船舶按用途可分为客货船、军舰、渔船等，潜水船舶主要包括潜水艇、潜水器等。

2. 船舶的性能指标船舶的性能指标包括了船速、载重能力、推进力、舵角、操纵性等，这些指标反映了船舶在水中运动时所具备的性能。

船舶的性能指标对于船舶的设计和运用有着重要的参考价值。

二、船舶的漂浮和稳性1. 船舶的漂浮原理船舶的漂浮是指船舶在水中浮力等于船舶的重力，这是由阿基米德原理所决定的。

根据阿基米德原理，浮体在液体中受到的浮力等于它所排挤的液体的重量。

2. 船舶的稳性船舶的稳性是指船舶在水中保持平衡的能力，主要由纵向稳性和横向稳性两部分组成。

纵向稳性是指船舶在航行中不会因为前倾或后倾而失去平衡，而横向稳性是指船舶在航行中不会发生侧翻。

三、船舶的阻力和推进1. 船舶的阻力船舶在水中航行时会受到来自水的阻力，这是由于水对船体的阻碍所产生的力。

船舶的阻力主要可以分为摩擦阻力和波浪阻力两种，其中摩擦阻力是指水对船体表面的摩擦力，而波浪阻力是指船舶在航行中产生的波浪所带来的阻力。

2. 船舶的推进船舶的推进是指船舶在水中航行时所受到的推进力，这是通过船舶的推进装置所产生的。

船舶的推进装置可以分为螺旋桨、水道推进器、水喷射推进器等多种形式，而推进力的大小则取决于推进装置的功率和效率。

四、船舶的操纵和控制1. 船舶的操纵性船舶的操纵性是指船舶在水中航行时所具备的操纵能力，这包括了船舶的转向、加速和减速等动作。

船舶的操纵性对于船舶的航行安全和效率有着重要的影响。

2. 船舶的控制船舶的控制是指船舶在航行中通过操纵装置对船舶的速度、方向等进行控制，这通常通过舵、推进装置等来实现。

天津市考研船舶与海洋工程复习资料船舶结构与船舶动力学知识点梳理船舶结构与船舶动力学是天津市考研船舶与海洋工程专业中的重要知识领域，下面将对相关知识点进行梳理和总结，帮助考生更好地复习和准备考试。

一、船舶结构知识点梳理1. 船体结构船体结构是船舶的骨架，包括船体形状、船体布置、船体材料等方面。

在考研中，需要了解不同船型的特点和设计原则，如平底船、单体船、双体船等。

此外，还需掌握船体结构的强度计算方法、船体防腐、船体修理等相关知识。

2. 船舶钢材船舶结构中广泛使用的材料之一是钢材，考生需了解常用钢材的分类、牌号说明、强度性能等。

同时，还需要掌握钢材的防腐方式和相关术语，如防锈、喷砂、涂装等。

3. 船舶连接件船舶结构中的连接件对船体强度和稳定性有重要影响，考生应该熟悉各种连接件的类型、规格和使用要求，如螺栓、钉、焊接接头等。

4. 船舶设计原则船舶结构设计需要遵循一定的原则和标准，考生需了解常见的船舶设计准则和相关规范，如船舶结构设计规范、船舶建造法规等。

二、船舶动力学知识点梳理1. 船舶运动学船舶运动学是研究船舶在水中运动规律的学科，包括航行速度、航向变化、姿态变化等。

考生需要了解船舶运动学的基本概念和运动方程，以及在船舶设计和控制中的应用。

2. 船舶阻力船舶在水中航行会受到各种阻力的影响，考生需要了解船舶阻力的分类、计算方法和影响因素。

此外，还需熟悉减阻技术，如船体形状优化、润滑剂应用等。

3. 船舶推进系统船舶推进系统是船舶动力学中的重要部分，包括主机系统、推进器系统和传动系统等。

考生需了解不同类型的主机和推进器，以及其工作原理和特点。

4. 船舶操纵性能船舶操纵性能是船舶动力学中的关键指标，涉及到舵效率、操纵装置和操纵性能评价等方面。

考生需要了解不同船型的操纵性能特点和评价方法。

5. 船舶动力系统船舶动力系统包括主机系统、辅助机械和电气设备等，考生需了解不同类型的主机和辅助机械的工作原理、性能参数和调整方法。

重庆市考研船舶与海洋工程复习资料船舶结构力学重难点梳理船舶结构力学是船舶与海洋工程领域中的一门重要课程，它研究船舶结构的受力、变形和破坏等问题。

对于考研学子来说，船舶结构力学是一个重要的复习科目。

本文将梳理重庆市考研船舶与海洋工程复习资料中船舶结构力学的重难点，帮助考生更好地备考。

一、船体受力分析船体受力分析是船舶结构力学的基础，也是考研中经常涉及的一个重点。

在船体受力分析中，需要了解船体的静力特性和动力特性，以及船体在浮动状态下所承受的静荷载和动荷载。

在备考过程中，可以结合相关习题进行练习，提高对船体受力分析的理解。

二、寿命分析与结构设计船舶的寿命分析与结构设计是船舶结构力学的重点和难点之一。

它涉及船舶结构的疲劳分析、强度计算和结构优化设计等内容。

在备考过程中，可以通过学习相关理论知识，掌握船舶结构的疲劳损伤机理和疲劳寿命计算方法，以及结构的强度计算和结构的疲劳寿命提高方法。

三、塑性力学与结构失稳塑性力学与结构失稳是船舶结构力学的另一个重要内容。

它研究船舶结构在超过弹性限度时的变形和破坏行为。

在备考中，可以通过学习相关理论和分析方法，了解船舶结构在受到大荷载作用时的塑性变形和失稳现象，并能够进行相应的分析和计算。

四、船舶振动与噪声分析船舶振动与噪声是船舶结构力学的另一个重要内容，也是船舶与海洋工程中的一个热点问题。

它涉及船舶的结构振动分析、噪声控制和船体的舒适性设计等方面。

在备考过程中，可以通过学习相关理论和分析方法，理解船舶的振动特性和噪声产生机理，以及相应的控制方法和设计要求。

五、船舶结构检测与修理船舶结构检测与修理是船舶结构力学的实际应用部分。

它涉及到船舶结构的定期检测、维修和修复等工作。

在备考中，可以通过学习相关理论和实际案例，了解船舶结构的检测方法和修理技术，以及相应的船级社规定和修船工艺。

在复习船舶结构力学的过程中，需要掌握相关理论知识，并能够灵活运用到解决实际问题中。

同时，还要通过大量的习题练习和真题模拟，巩固和加深对知识点的理解。

大船设计原理知识点总结大船设计是一门综合性的学科，涉及到机械工程、船舶工程、海洋工程等多个领域的知识。

大船的设计原理是大船设计领域的核心内容，它包括了许多复杂的技术和理论知识。

在这篇文章中，我们将对大船设计原理的一些重要知识点进行总结和介绍。

1. 液体力学原理液体力学是大船设计中的重要知识点，它主要研究液体在外力作用下的运动规律。

在大船设计中，液体力学的原理可以帮助设计师预测船舶在不同条件下的水动力性能，如阻力、推进力和操纵性能等。

这对于提高船舶性能、降低燃油消耗、增加航行效率都具有重要意义。

2. 结构力学原理结构力学是大船设计中的另一个重要知识点，它主要研究材料在外力作用下的应力、应变以及变形规律。

在大船设计中，结构力学的原理可以帮助设计师确定船舶的结构设计参数，如材料选型、结构强度、刚度等。

这对于确保船舶的结构安全性和可靠性具有重要意义。

3. 流体力学原理流体力学是大船设计中的又一个重要知识点，它主要研究流体在外力作用下的流动规律。

在大船设计中，流体力学的原理可以帮助设计师分析船舶的流体动力性能，如流体阻力、涡波积聚、波浪干扰等。

这对于提高船舶的航行性能和减少能源消耗具有重要意义。

4. 船舶动力学原理船舶动力学是大船设计中的另一个重要知识点，它主要研究船舶在外部力作用下的运动规律。

在大船设计中，船舶动力学的原理可以帮助设计师确定船舶的推进系统和操纵系统参数，如主机选型、推进器设计、操纵装置等。

这对于提高船舶的航行性能和操纵性能具有重要意义。

5. 船舶设计理论船舶设计理论是大船设计中的又一个重要知识点，它主要研究船舶的总体设计原理和方法。

在大船设计中，船舶设计理论可以帮助设计师确定船舶的总体设计参数，如长度、宽度、高度、吃水线等。

这对于确保船舶的性能和稳定性具有重要意义。

在大船设计中，以上知识点都是十分重要的，设计师需要结合这些知识点，才能够设计出性能优越、结构安全的船舶。

同时，在实际设计过程中，设计师还需要不断地对这些知识点进行研究和应用，以不断提升船舶设计的水平和质量。

船舶结构力学习题答案【篇一：船舶结构力学各章思考题】>（摘自习题）（一）绪论1 什么叫做船体总纵弯曲？船体的总纵强度与局部强度有什么区别与联系？2.船体结构中有哪些受压构件？为什么说船在总弯曲时船体受压的构件（主要是中垂状态时的上层甲板）因受压过度而丧生稳定性后，会大大减低船体抵抗总弯曲的能力？3.何谓骨架的带板？带板的宽度（或面积）与什么因素有关，如何确定？试分析带板宽度对骨架断面几何要素的影响。

4.什么叫做船体结构的计算图形，它是用什么原则来确定的?它与真实结构有什么差别？5.一个完整的船体结构计算图形应包含哪些具体内容？为什么对同一船体结构构件，计算图形不是固定的、一成不变的？（二）单跨梁的弯曲理论1 梁弯曲微分方程式是根据什么基本假定导出的，有什么物理意义，适用范围怎样？2 单跨梁初参数法中的四个参数指什么参数？它们与坐标系统的选择有没有关系？3 为什么当单跨梁两端为自由支持与单跨梁两端为弹性支座支持时，在同样外荷重作用下梁梁断面的弯矩和剪力都相等；而当梁两端是刚性固定与梁两端为弹性固定时，在同样外荷重作用下两梁断面的弯矩和剪力都不同？4 梁的边界条件与梁本身的计算长度、剖面几何要素、跨间荷重有没有关系？为什么？ 5 当梁的边界点上作用有集中外力p或几种外弯矩m时，一种处理是把该项外力放在梁端，写进边界条件中去。

另一种处理时把该项外力放在梁上，不写进边界条件。

在求解梁的弯曲要素时，两种处理方法的具体过程有哪些不同？最后结果有没有差别？6 梁的弹性支座与弹性固定端各有什么特点？它们与梁本身所受的外荷重（包括大小、方向及分布范围）有没有关系？为什么梁在横弯曲时，横荷重引起的弯曲要素可以用叠加法求出？（三）力法1 什么叫力法？如何建立力法方程式？2 什么是力法的基本结构和基本未知量？基本结构与原结构有什么异同？力法正则方程式的物理意义是什么？3 当连续梁两端为弹性固定时，如何按变形连续条件建立该处的方程？4 力法可否用来计算不可动节点的复杂钢架？如可以，应如何做？5 用力法计算某些支座有限位移的连续梁或平面刚架时应注意什么问题？6 刚架与板架的受力特征和变形特征有何区别？7 何谓梁的固定系数？它与梁端弹性固定端的柔性系数有何不同？（四）位移法1 试举例说明位移法的基本原理。

船舶结构力学习题及答案船舶结构力学习题及答案船舶结构力学是船舶工程中的重要学科，它研究船舶结构在不同载荷作用下的力学特性。

在船舶设计和维修中，船舶结构力学的知识是必不可少的。

下面将介绍几个船舶结构力学的学习题及答案，帮助读者更好地理解和掌握这一学科。

1. 问题：什么是船舶结构的静力学特性？答案：船舶结构的静力学特性是指结构在静力平衡状态下的性能，包括刚度、强度和稳定性等。

刚度是指结构对外力的抵抗能力，强度是指结构承受外力时不发生破坏的能力，稳定性是指结构在受到外力作用时不发生失稳的能力。

2. 问题：船舶结构的刚度和强度有何区别？答案：船舶结构的刚度和强度是两个不同的概念。

刚度是指结构在受到外力作用时变形的抵抗能力，通常用刚度系数来表示。

强度是指结构在受到外力作用时不发生破坏的能力，通常用强度参数来表示。

刚度和强度是船舶结构力学中两个重要的性能指标，设计和维修船舶结构时需要考虑它们的平衡。

3. 问题：什么是船舶结构的疲劳强度？答案：船舶结构的疲劳强度是指结构在长期循环载荷作用下不发生破坏的能力。

船舶在航行中会受到多种载荷的作用，如波浪载荷、船舶自重和货物重量等。

这些载荷的反复作用会导致结构的疲劳破坏，因此需要对船舶结构进行疲劳强度分析和设计。

4. 问题：船舶结构的稳定性有哪些因素影响？答案：船舶结构的稳定性受到多种因素的影响。

其中最重要的因素是船舶的重心和浮心位置。

当船舶的重心和浮心位置不在同一垂直线上时，会产生偏倾力矩，导致船舶发生倾覆。

此外，船舶的形状、船体的稳定性曲线和外部环境等因素也会对船舶结构的稳定性产生影响。

5. 问题：如何计算船舶结构的荷载？答案：计算船舶结构的荷载需要考虑多个因素，包括船舶自重、货物重量、燃油重量、波浪载荷等。

其中，船舶自重可以通过船舶的设计参数和结构重量来计算；货物重量可以通过货物的数量和单位重量来计算；燃油重量可以通过燃油的密度和船舶的燃油消耗量来计算；波浪载荷可以通过波浪的特性和船舶的运行状态来计算。