2012_2013学年第一学期末数值分析考试试题A参考答案与评分标准
- 格式:doc
- 大小:433.50 KB
- 文档页数:10

2012-13-1高等数学(A )期末考试参考答案及评分标准一、填空题 (本大题分5小题,每小题4分,共20分)1、()2,3--2、()0f x '-3、04、()()x x f e e f x ----5、8π 二、选择题 (本大题共5小题,每小题4分,共20分)1、C2、A3、C4、D5、B三、解答下列各题(本大题共3小题,每小题6分,共18分) 1、解:原式=tan 2tan 00011sec 1lim lim lim sin cos sin x x xx x x x x e x e e x x x x x --→→→=--⋅=⋅-……………每步2分 2、解:令sin x t =,则cos dx tdt =, 原式2sin cos cos t tdt t=⎰………………………………………………………………………2分 21cos 211sin sin 2222t tdt dt t t c -⎡⎤===-+⎢⎥⎣⎦⎰⎰………………………………………4分 [].1arcsin 212c x x x +--=…………………………………………………………6分 3、解:1(),P x x =sin (),x Q x x =于是所求通解为: 11sin dx dx x x x y e e dx C x -⎛⎫ ⎪ ⎪⎝⎭⎰⎰=⋅+⎰ln ln sin x x x e e dx C x -⎛⎫ ⎪⎝⎭=⋅+⎰1(cos ).x C x =-+……每步2分 四、解答下列各题(本大题共3小题,每小题7分,总计21分)1、解:当000x t y ===,,,()1(0)2t x t e x ''=+= ………………………………3分cos sin 0,(0)0y y e y t e t y y '''-+==…………………………………………6分 故,00x dy dx ==……………………………………………………………………7分 2、证明:()()()a TT a T a aT f x dx f x dx f x dx ++=+⎰⎰⎰………………………………………2分 00()()()a Ta a T x t T f x dx f t T dt f t dt +=+=+=⎰⎰⎰对后者,令,=⎰f x dx a ()0…………5分 所以,f x dx f x dx f x dx a a T a T a ()()()+⎰⎰⎰=+0=⎰f x dx T()0。


金牛区2012-2013学年度七年级上期末检测数学试题答案及评分标准(仅供参考)A 卷(100分)一.选择题1—5:BABDC ;6—10:DCBDA二.填空题 11、6;12、4.98×104;13、12;14、0144三、解答题15、(1)计算:()531()246812-+-⨯- (2)计算: ()24212332-÷---+- 解:原式=531(24)(24)(24)6812-⨯-+⨯--⨯- ----2分 解:原式=-9+2+2 ----1+1+1分=20-9+2 ----2分 =-5 ----2分 =13 ----1分16、17、解:原式= 22223172222ab a b ab a b -+-++-=22551ab a b +- ----4分∵2(2)30a b ++-=,且2(2)0a +≥,30b -≥∴20a +=且30b -=,即2,3a b =-= ----2分∴原式=225(2)35(2)31⨯-⨯+⨯-⨯-=-31 ----2分18、解:∵DB =1.5cm ,AD =6.5cm ,点D 在线段CB 上∴AB=8 ----3分∵点C 是线段AB 的中点,∴CB=142AB =, ----2分∴CD= 2.5C B BD -= ----3分19、解:(1)第4幅图有18把椅子 ----2分(2)4n+2 ----2分(3)将n=10代入4n+2得42把椅子。
----2分若4n+2=120,计算得n=259,不是整数,不符题意,所以椅子数不可能为120把。
----2分())(200%35701名:=÷----2分())(40306070200)(60%302002名名:=---==⨯=m n ----2+2分()0072360200403=⨯心角:艺术类读物所在扇形圆:----2分B 卷(共50分)一、填空题21、-2;22、23-;23、-8;24、b 2-;25、23 二、解答题26.解:解:设专业观众门票x 万张,则普通观众门票为(20)x -万张. ----1分 由题意,得:1510(20)275x x +-= ----4分解得:15x =,所以2020155x -=-= ----2分答:专业观众门票15万张,普通观众门票为5万张. ----1分27. 解:(1)∵∠CPD 是直角,∠APC=40︒,∴∠BPD=50︒,∠BPC=140︒,∵PE 平分∠BPC ,∴∠BPE=70︒,∴∠DPE=∠BPE- ∠BPD= 020; ----4分(2) ∠DPE =2a; ----2分(3) ∠DPE =21∠A PC ,理由如下:设∠A PC=a ,则∠A PC=a -0180,∵OE 平分∠BPC ,∴∠CPE= ()2901802100aa -=- ----2分∵∠CPD 是直角,∴∠DPE= ∠CPD-∠CPE= 22909000a a =⎪⎭⎫ ⎝⎛--∴∠DPE=21∠APC ----2分(1)数轴上点C 表示的数为4-,线段CP 的长度为56t -或65t -(写成|56|t -也是正确的);----2分(2)线段MN 的长度不变,理由如下:①当点P 在C 点右侧时,AP+CP=8,∵M 、N 分别为AP 、CP 的中点, ∴12PM AP =,12PN BP =, ∴MN=()142PM PN AP PC +=+=;----3分②当点P 在C 点左侧时,8AP C P AC -==,∵M 、N 分别为AP 、CP 的中点, ∴12PM AP =,12PN BP =, ∴MN=()142PM PN AP PC -=-=;----3分综上所得,线段MN 的长度始终为4。
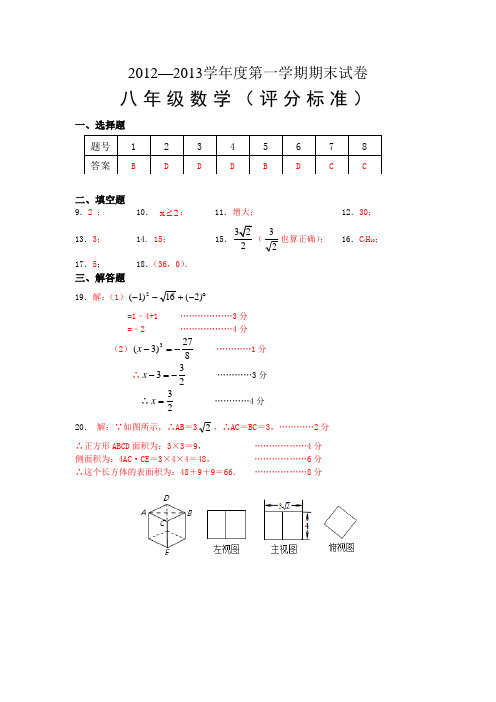
2012—2013学年度第一学期期末试卷八年级数学(评分标准)一、选择题二、填空题9.2 ; 10. x 2≥; 11.增大; 12.30; 13.3; 14. 15; 15.32(23也算正确); 16.C 4H 10; 17.5; 18.(36,0).三、解答题19.解:(1)︒-+--)2(16)1(2=1﹣4+1 ………………3分=﹣2 ………………4分(2)827)3(3-=-x …………1分 ∴233-=-x …………3分∴23=x …………4分20. 解:∵如图所示,∴AB =32,∴AC =BC =3,…………2分 ∴正方形ABCD 面积为:3×3=9, ………………4分 侧面积为:4AC ·CE =3×4×4=48, ………………6分 ∴这个长方体的表面积为:48+9+9=66. ………………8分题号 12345678答案 BDDDBDCC21. 解(1)如图所示:……………… 4分(2)四边形ABCD 的面积=1222122ABD S ∆=⨯⨯⨯=.………………8分 22.解答:(1)证明:∵ABCD 是正方形∴AD=BC,∠ADC=∠BCD=90° …………1分 又∵三角形CDE 是等边三角形∴CE=CD,∠EDC=∠ECD=60°………………2分 ∴∠ADE=∠ECB ………………3分 ∴△ADE≌△BCE.………………4分(2)解:∵△CDE 是等边三角形,∴CE=CD=BC ………………5分∴△CBE 为等腰三角形,且顶角∠ECB=90°﹣60°=30° ∴∠EBC=21(180°﹣30°)=75°…………6分 ∵AD∥BC ………………7分∴∠AFB=∠EBC=75°. ……………………8分23. 解: y=223x -+与x 轴、y 轴的交点坐标为(3,0),(0,2)。

一、单项选择题(每小题3分,共15分) 1、用Simpson 公式求积分1401x dx +⎰的近似值为 ( ).A.2924 B.2429C.65D. 562、已知(1)0.401f =,且用梯形公式计算积分2()f x dx ⎰的近似值10.864T =,若将区间[0,2]二等分,则用递推公式计算近似值2T 等于( ). A.0.824 B.0.401 C.0.864 D. 0.8333、设3()32=+f x x ,则差商0123[,,,]f x x x x 等于( ).A.0B.9C.3D. 64的近似值的绝对误差小于0.01%,要取多少位有效数字( ). A.3 B.4 C.5 D. 25、用二分法求方程()0=f x 在区间[1,2]上的一个实根,若要求准确到小数 点后第四位,则至少二分区间多少次( ).A.12B.13C.14D. 15二、填空题(每小题4分,共40分)1、对于迭代函数2()=(3)ϕ+-x x a x ,要使迭代公式1=()ϕ+k k x x则a 的取值范围为 .2、假设按四舍五入的近似值为2.312,则该近似值的绝对误差限为 .3、迭代公式212(3)=,03++>+k k k k x x a x a x a收敛于α= (0)α>. 4、解方程4()530f x x x =+-=的牛顿迭代公式为 . 5、设()f x 在[1,1]-上具有2阶连续导数,[1,1]x ∀∈-,有1()2f x ''≤,则()f x 在[1,1]-上的线性插值函数1()L x 在点0处的误差限1(0)R ≤______.6、求解微分方程初值问题2(0)1'=-⎧⎨=⎩y xy yy ,0x 1≤≤的向前Euler 格式为 .7、设310131013A -⎛⎫⎪=-- ⎪ ⎪-⎝⎭,则A ∞= .8、用梯形公式计算积分112-⎰dx x 的近似值为 . 9、设12A 21+⎡⎤=⎢⎥⎣⎦a 可作Cholesky 分解,则a 的取值范围为 . 10、设(0)1,(0.5) 1.5,(1)2,(1.5) 2.5,(2) 3.4f f f f f =====,若1=h ,则用三点公式计算(1)'≈f .三、解答题(共45分) 1、给定数据用复化Simpson 公式计算1.381.30()f x dx ⎰的近似值,并估计误差,小数点后保留3位. (8分)2、用直接三角分解法求线性代数方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡432631531321321x x x 的解. (8分) 3、求()λx ,使得迭代公式1()()λ+=+k k k k f x x x x 求方程2()31=+-f x x x 的根的相应迭代序列{}k x 具有平方收敛. (5分)4、已知数据试对数据用最小二乘法求出形如=+y x b的拟合曲线. (8分) 5、已知(2)8f -=,(0)4f =,(2)8=f ,试求二次拉格朗日插值多项式. (8分) 6、设矩阵A 如下,根据谱半径判断用Jacobi 迭代法求解方程组Ax b =的敛散性.(8分)1102111221012A ⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦一、单项选择题(每小题3分,合计15分) 1、A 2、D 3、C 4、C 5、D 二、填空题(每小题3分,合计30分) 1、0<<a ; 2、31102-⨯; 3;4、4135345++-=-+k k k k k x x x x x ; 5、14; 6、1(2)+=+-n n n n n y y h x y y ; 7、5;8、34-; 9、3>a ;10、1.2;三、计算题(合计55分) 1、给定数据用复化Simpson 公式计算 1.381.30()f x dx ⎰的近似值,并估计误差,小数点后保留3位. (8分)解: 401024S [()4()()]6-=++x x f x f x f x ………… 1分 1.38 1.30(3.624 4.20 5.19)6-=+⨯+ 0.341= ………… 2分20422012234S [()4()()][()4()()]66--=+++++x x x xf x f x f x f x f x f x =0.342 ………… 6分2211[]15-≈-I S S S =-⨯40.6710 ………… 8分 2、用直接三角分解法求线性代数方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡432631531321321x x x 的解. (8分) 解:设111213212223313233u u u 123100135l 100u u 136l l 100u ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=*⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦………… 1分 111=u ,212=u ,313=u ,121=l ,131=l 122=u ,223=u ,132=l133=u ,133=l …………6分所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111011001L ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100210321U …………7分 由b Ly =得Ty )1,1,2(=;由y Ux =得Tx )1,1,1(-=. ………… 8分3、求()λx ,使得迭代公式1()()λ+=+k k k k f x x x x 求方程2()31=+-f x x x 的根的相应迭代序列{}k x 具有平方收敛.(6分)解:要使迭代序列具有平方收敛,则()0ϕ'*=x ………… 2分 而()()()ϕλ=+f x x x x ,即 ………… 3分 2()()()()10()λλλ''**-**+=*f x x x f x x …………4分 而()0*=f x 则有()1()λ'*=-*f x x ………… 5分所以()()23λ'=-=--x f x x ………… 6分4、已知数据试对数据用最小二乘法求出形如=+ay x b的拟合曲线. (8分) 解:因为11=+b x y a a ,令0111,,,====b a a y x x a a y……2分 则有法方程01461061410⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭a a ……5分解出014,1==-a a ,则1,4=-=-a b ……7分 所以1=4-y x……8分5、已知(2)8f -=,(0)4f =,(2)8=f ,试求二次拉格朗日插值多项式. (7分)解:01()(2)8l x x x =- …………2分 211()(4)4l x x =-- …………4分21()(2)8l x x x =+ …………6分 2012()()(2)()(0)()(2)L x l x f l x f l x f =-++24=+x …………7分6、设矩阵A 如下,根据谱半径判断用Jacobi 迭代法求解方程组Ax b =的敛散性.(8分)1102111221012A ⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦解:100010001D ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,00010021002L ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,10021002000U ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦…………3分1100211()0221002J B D L U -⎡⎤⎢⎥⎢⎥⎢⎥=+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦…………5分 2102111()0222102J E B λλλλλλ⎡⎤-⎢⎥⎢⎥⎢⎥-=--=-=⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦…………6分()2J B ρ=…………7分 所以用Jacobi 迭代法求解方程组Ax b =收敛 …………8分。

期末考试试卷(A 卷)2007学年第二学期考试科目: 数值分析考试时间:120分钟学号 姓名 年级专业、判断题(每小题 分,共分)100011.用计算机求z —100■时,应按照n 从小到大的顺序相加。
n 3n3 .用数值微分公式中求导数值时,步长越小计算就越精确。
()4 .采用龙格-库塔法求解常微分方程的初值问题时,公式阶数越高,数值解越精确。
()5 .用迭代法解线性方程组时,迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。
()二、填空题(每空 2分,共36分)1 .已知数a 的有效数为0.01 ,则它的绝对误差限为 ,相对误差限为 .10 -11 一0]2 .设 A= 0-2 1 ,x= -5,则| A 1 =, ||^|2 =Ax L =.-1 3 0J3 .已知 f (x) =2x 5 +4x 3—5x,则 f[—1,1,0] =, f[-3,-2,-1,1,2,3] =.13 34 .为使求积公式 f f (x)dx 定A f (———)+ A 2 f (0) + A 3 f (」一)的代数精度尽量局,应使t 3 3A =, A =, A =,此时公式具有 次的代数精度。
5 . n 阶方阵A 的谱半径P (A)与它的任意一种范数| A 的关系是.6 .用迭代法解线性方程组以=8时,使迭代公式 X(k41)=MX (k) + N (k=0,1,2,|||)产生的向量序列{X(k)}收敛的充分必要条件是 .7 .使用消元法解线性方程组 AX =8时,系数矩阵A 可以分解为下三角矩阵 L 和上三角矩2. 为了减少误差 ,应将表达式 J2001 - J1999改写为22001 ,1999进行计算。
4 -2阵U的乘积,即A = LU .若米用图斯消兀法解AX = B,其中A= 1 ,则一1 2 3 4 1 L = , U = ;若使用克劳特消元法解AX = B ,则u11 =;若使用平方根方法解AX = B,则111与u11的大小关系为 (选填:>, <,=,不一'定)。
一、判断题(每题2分,共20分) 1.||ln )(x x f =与2ln 21)(xx g =不相同.2.arctan y x = 是一个基本初等函数.3.在同一变化趋势下,两个无穷大量的和一定是无穷大量. 4.当∞→n 时,n 2ln 的极限是零. 5.若数列{n x }无界,则数列{n x }发散.6.函数在点0x 处有极限,则函数在这点处必连续. 7.可导函数的极值点一定是稳定点. 8.可导的周期函数的导函数是周期函数.9.若0)(,0)(00<'>'-+x f x f ,则()f x 在0x 点有局部极小值.10.在定义区间中,函数的极大值比极小值要大.二、填空题(每题2分,共20分)1. 设函数2()[0,1]()y f x f x =的定义域为,则的定义域为 .2. tan 0()0=20axx f x x a xx ⎧≠⎪==⎨⎪=⎩若函数在点连续,则 .3. ()sgn(cos )f x x =函数的间断点为 .4. ()(1)(2)(100),(0)f x x x x x f '=---= 函数则 .5. 2x e 函数的麦克劳林公式为 2()n o x +.6. (2012)()sin ,(0)f x x f ==设函数则 .7. lim ()x f x →∞=+∞极限的定义为 .8. 2()(ln )f x x =函数的拐点为 . 9. 2(3)()4(1)x f x x -=-曲线的斜渐近线为 .10. 设函数ln y x x x =-,则dy = .三、计算题(每题5分,共20分)1.求极限22212lim ()12n n n n n n→∞++++++ .得 分评卷人2.求极限sin 0limxx x+→.3.求极限3tan sin limsin x x x x→-.4.设232,3,x t t y t t ⎧=-⎨=-⎩ 求二阶导数22d ydx .5.设2arcsinx y a a=(0)a >,求y '.四、证明题(每题10分,共20分)1.若lim n n a a →∞=, 则 lim n →∞=.0()[0,2](0)(2)[0,],f x a f f a x a =∈2.设函数在上连续,且,证明:存在点00()()f x f x a =+使得.五、证明题(每题10分,共20分)1.证明:函数2()[,](,)f x x a b =-∞+∞在上一致连续,在上非一致连续.2.证明:若函数()[0,1](0,1)()2[(1)(0)]f x f f f ξξξ'∃∈=-在可导,则使得.得 分评卷人。
中北大学试题答案及评分标准数值分析课程(课程名称须与教学任务书相同)2012/2013 学年第1 学期试题类别 A拟题日期2012.12.25 拟题教师课程编号教师编号1120048使用班级2012级研究生备注:试题答案要求按指定规格计算机打印,并将电子稿上传至考务管理系统。
2012/2013 学年第 1 学期期末考试试题答案及评分标准(A 卷)数值分析使用班级: 2012级研究生班 一、填空题(每空2分,共30分)1. 设44.754923,44.732534a b ==作为x 与y 的近似值都有5位有效数字,则a 的绝对误差限可取为 0.0005 ,用2a b u -= 作为2x yu -=的近似值具有 2 位有效数字,用1va b =+ 作为1v x y=+的近似值有 5 位有效数字; 2. 设52312,0261037A ⎛⎫⎛⎫⎪ ⎪==-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭x ,则∞=x 5 ,1A = 14 ,A 的谱半径()ρA= 4 ;3. 设20()35,,0,0,1,2,,k f x x x x kh h k =+=+>= ,则12[,,]k k k f x x x ++= 3 ,123[,,,]k k k k f x x x x +++= 0 ;4. 设函数()f x 在区间[0,3]上具有连续的4阶导数,若次数不超过3的多项式()3H x 满足()()3,0,1,2H k f k k ==和()()311H f ''=,则用()3H x 近似计算()()()0,3f x x ∈的截断误差可表示为()()()33R x f x H x =-=()()()()()4212,0,34!f xx x ξξ--∈;5. 为使两点数值求积公式()()()()111d f x x f x f x λ-=+⎰具有最高的代数精度。
则求积节点0x=,1x=,求积系数λ=59;(0x 、1x 的值可以互换) 6. 用Newton 迭代法求解方程310x =的迭代公式为312210,0,1,2,3k k kx x k x ++== ;该公式具有 2阶的收敛速度;若取初始值03x =,则迭代一次后的近似解1x = 2.370。
二、(每小题12分,共24分)1. 用LU 分解法求解线性方程组1234323389512102234141695181832x x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪⎪ ⎪= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;解:()3233832338313129512102212234|34141631312951818321112LU A b ⎛⎫⎛⎫ ⎪-- ⎪ ⎪⎪ ⎪-=−−→ ⎪ ⎪--- ⎪ ⎪⎝⎭ ⎪-⎝⎭10003233813100013121,,,1210002341313100122L U y x ⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪--⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭............................................................................ L U 矩阵(或对应元素每算对两个给1分)2. 用Romberg 方法计算积分1401d 1I x x =+⎰的近似值,要求计算到第一个Romberg 值(3)0T ,说明共计算了多少个求积节点处的函数值,并将计算结果与准确值ln πI ⎫=+⎪⎪⎝⎭进行比较,说明计算的精度; 解:取()410,1,1a b f x x ===+进行计算()()01,10.5f f ==,(0)01((0)(1))0.752T f f =+= ............................................................................................... 1分()0.5,0.50.9411765h f ==;(0)(0)101(0.5)0.84558822T T hf =+=,....................... 2分 (0)(0)(1)10040.87745103T T T -== .......................................................................................... 3分()()0.25,0.250.9961089, 0.750.7596439h f f ===()()(0)(0)211(0.25)0.750.86173232T T h f f =++=, .................................................... 4分(0)(0)(1)21140.86711373T T T -== .......................................................................................... 5分(1)(1)(2)100160.866424515T T T -==......................................................................................... 6分()()0.125,0.1250.9997559, 0.3750.9806081h f f ===()0.6250.8676128f =()0.8750.6304448f =,()3(0)(0)32010.1250.250.86566892k TT h f k =⎛⎫=++= ⎪⎝⎭∑ ..... 7分 (0)(0)(1)3224=0.86698103T T T -=, ....................................................................................... 8分(1)(1)(2)21116=0.866972215T T T -=, ...................................................................................... 9分(2)(2)(3)10064=0.866980963T T T -= ....................................................................................... 10分计算到(3)0T ,共计算了9个求积节点处的函数值; ...........................................................11分与准确值π 0.8669729887...I ⎫=+=⎪⎪⎝⎭进行比较,以(3)00.8669809T =作为I 的近似值,至少有4位有效数字。
......................................................................... 12分三、(每小题10分,共40分) 1. 设有非齐次线性方程组12112222x x b x x b ρρ-=⎧⎨+=⎩,其中ρ为实数。
(1) 写出求解此方程组的Gauss-Seidel 迭代法的迭代公式,并讨论其收敛性; (2) 设2ρ=,给定松驰因子12ω=,写出求解此方程组的SOR(逐次超松驰)迭代方法的迭代公式,并讨论其收敛性。
解:(1) Gauss-Seidel 方法的迭代公式为()()()()()()()110210120112212,12k k k k x x b x x R x x x b ρρ+++⎧=+⎛⎫⎪=∈ ⎪⎨⎪=-+⎪⎝⎭⎩任取.......................................................... 3分 迭代矩阵200GS G ρρ⎛⎫= ⎪-⎝⎭,谱半径为()2GS G ρρ=,所以,上述迭代公式收敛的充分必要条件是1ρ< ......................................................................................................... 5分(2) 当2,ρ=取12ω=时,SOR 方法的迭代公式为 ()()()()()()()()()110121012011221221122,1124k k k k k k x x x b x x R x x x x b +++⎧=++⎛⎫⎪⎪=∈ ⎪⎨ ⎪⎪⎝⎭=-++⎪⎩任取............................................... 8分 迭代矩阵SOR 0.510.50.5G ⎛⎫=⎪--⎝⎭,特征值i 2λ=±,谱半径为()SOR 12G ρ=,所以,上述迭代公式收敛。
........................................................................................................... 10分2. 利用函数011y c c x =+拟合下表所列数据(),i i x y解:记1u y=,则有01u c c x =+ ............................................................................................ 1分 把原数据(),i i x y 变换成(),i i x u 如下:分令01c c c ⎛⎫= ⎪⎝⎭,1 1.001 1.2511.501 1.7512.00A ⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭, .................................................................................................. 4分对应的正规方程组TTA Ac A y =为015.00007.50000.77447.500011.8750 1.1130c c ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ................................................ 6分 解此方程得010.27140.0777c c ⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭ ................................................................................. 8分即最终的拟合函数 10.27140.0777y x=- .......................................................................... 9分()11.6 6.79800.27140.0777 1.6y ≈≈-⨯ ....................................... 10分3. 写出用Newton 迭代法求解非线性方程组232390340x xy x y y ⎧+-=⎨--=⎩的步骤,并取初值00(,)(1.34,1.75)x y =计算近似解11(,)x y (只进行一次迭代)。