1D10-1二重积分概念

二重积分的定义求极限摘要：1.二重积分的定义概述2.二重积分与定积分的关系3.二重积分的计算方法4.二重积分的应用5.求极限的方法正文：一、二重积分的定义概述二重积分是一种在空间中对二元函数进行积分的方法，它是对定积分的扩展。

二重积分的定义与定积分类似，都是求解某种特定形式的和的极限。

在二重积分中，我们需要对一个有界闭区域上的有界函数进行积分。

具体来说，设zf(x,y) 为有界闭区域() 上的有界函数，我们将区域() 任意划分成n 个子域(k)，其面积记作k(k1,2,3,,n)，然后在每一个子域上对函数zf(x,y) 进行积分，最后求得所有子域积分的和的极限。

二、二重积分与定积分的关系二重积分与定积分在形式上有所不同，但在本质上是类似的。

定积分是求解一个函数在某一区间上的累积和，而二重积分则是求解一个函数在某一区域内的累积和。

在求解二重积分时，我们需要将区域划分成更小的子域，并在每个子域上计算函数的积分。

这与定积分的计算方法是相似的，只是在二重积分中，我们需要对更多的子域进行积分。

三、二重积分的计算方法求解二重积分的方法可以分为以下几个步骤：1.确定被积函数zf(x,y) 以及积分区域();2.将积分区域() 任意划分成n 个子域(k)，其面积记作k(k1,2,3,,n);3.在每一个子域(k) 上对函数zf(x,y) 进行积分，得到子域(k) 上的积分值;4.求得所有子域(k) 上的积分值的和;5.求得和的极限，即为所求的二重积分值。

四、二重积分的应用二重积分在实际应用中具有广泛的应用价值，例如计算曲面的面积、平面薄片的重心等。

此外，平面区域的二重积分可以推广为在高维空间中的有向曲面上进行积分，称为曲面积分。

五、求极限的方法在求解二重积分时，我们需要求得所有子域(k) 上的积分值的和的极限。

为了求得这个极限，我们可以采用以下方法：1.采用分割法，将积分区域() 划分成越来越小的子域，然后在每个子域上计算函数的积分;2.采用近似法，将函数在某一子域上近似为一个简单的函数，如多项式函数，然后在该子域上计算近似函数的积分;3.采用求和法，将所有子域上的积分值相加，得到一个总和;4.采用取极限法，当子域划分得越来越小，或者近似函数越来越接近原函数时，求得总和的极限，即为所求的二重积分值。

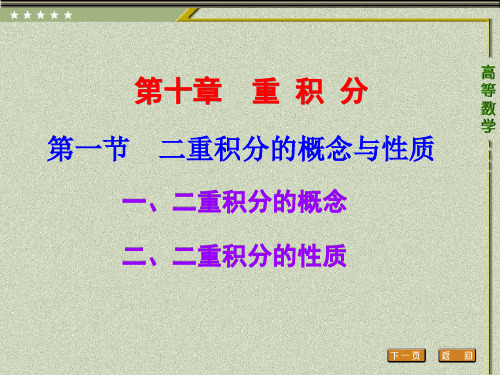
第九章 重积分Chapter 9 Multiple Integrals9.1 二重积分的概念与性质 (The Concept of Double Integrals and Its Properties) 一、二重积分的概念 (Double Integrals)定义 ( 二重积分的定义 ) 设 D 是xy 平面的有界闭区域 ,f 是定义在 D 上的函数。

将 D 任意分成 n 个小区域i σ,它们的面 积用(1,2,)i i n σ∆= 表示。

在每个(1,2,)i i n σ= 上任取一点(,)i i ξη，并作和1(,)ni i i i f ξησ=∆∑。

假设存在一个确定的数I 满足：任给0ε>，存在0δ>，使得当各小区域i σ的直径中的最大值λ小于δ时，就有1(,)niiii f I ξησε=∆-<∑不管区域D 的分法如何，(,)i i ξη的取法如何。

这样就称f 在D 上可积，I 称为f 在D 上的二重积分，记作(,)Df x y d I σ=⎰⎰或01(,)lim (,)λσξησ→==∆∑⎰⎰niiii Df x y d fDefinition (The Double Integral) Let D be a bounded closed region in the 巧1 plane and f a function defined on D. Partition D arbitrarily into ｎsubregionsi σ，whose area is denoted by (1,2,)i i n σ∆= Choose arbitrarily a point (,)i i ξη in (1,2,)i i n σ= and then form the sum 1(,)ni i i i f ξησ=∆∑。

Supposethat there exists a fixed number I such that for any 0ε>, there exists a0δ>such that if the length λ of the longest diameter of those subregions i σin a partition of D is less than δ, then 1(,)ni i i i f I ξησε=∆-<∑，no matter how the partition is and how those points (,)i i ξηare chosen from(1,2,)i i n σ= Then f is said to be integrable over Dand I is the double integral of f over D ,written (,)Df x y d I σ=⎰⎰,or1(,)lim (,)λσξησ→==∆∑⎰⎰ni i i i Df x y d f二、二重积分的性质 (Properties of Double Integrals)性质 1 两个函数和 ( 或差 ) 的二重积分等于它们二重积分的和 ( 或差 ), 即((,)(,))(,)(,)D D D f x y g x y d f x y d g x y d σσσ±=±⎰⎰⎰⎰⎰⎰. Property 1 The double integral of the sum(or difference) of two functions is equal to the sum( or difference) of their double integrals, that is((,)(,))(,)(,)D D D f x y g x y d f x y d g x y d σσσ±=±⎰⎰⎰⎰⎰⎰ 性质 2 被积函数前面的常数因子可以提到积分号前面 , 即(,)(,)D D kf x y d k f x y d σσ=⎰⎰⎰⎰,若k 为常数。

二重积分的概念及性质前面我们已经知道了，定积分与曲边梯形的面积有关。

下面我们通过曲顶柱体的体积来引出二重积分的概念，在此我们不作详述，请大家参考有关书籍。

二重积分的定义设z=f(x,y)为有界闭区域(σ)上的有界函数：(1)把区域(σ)任意划分成n个子域(△σk)(k=1,2,3,…,n）,其面积记作△σk(k=1,2,3,…,n）；(2)在每一个子域(△σk)上任取一点，作乘积；(3)把所有这些乘积相加,即作出和数(4)记子域的最大直径d.如果不论子域怎样划分以及怎样选取,上述和数当n→＋∞且d→0时的极限存在,那末称此极限为函数f(x,y)在区域(σ)上的二重积分.记作:即：=其中x与y称为积分变量，函数f(x,y)称为被积函数,f(x,y)dσ称为被积表达式,(σ)称为积分区域.关于二重积分的问题对于二重积分的定义,我们并没有f(x,y)≥0的限.容易看出,当f(x,y)≥0时,二重积分在几何上就是以z=f(x,y)为曲顶，以(σ)为底且母线平行于z轴的曲顶柱体的体积。

上述就是二重积分的几何意义。

如果被积函数f(x,y)在积分区域(σ)上连续，那末二重积分必定存在。

二重积分的性质(1).被积函数中的常数因子可以提到二重积分符号外面去.(2).有限个函数代数和的二重积分等于各函数二重积分的代数和.(3).如果把积分区域(σ)分成两个子域(σ1)与(σ2),即(σ)=(σ1)+(σ2),那末:(4).如果在(σ)上有f(x,y)≤g(x,y),那末:≤(5).设f(x,y)在闭域(σ)上连续,则在(σ)上至少存在一点(ξ,η),使其中σ是区域(σ)的面积.二重积分的计算法直角坐标系中的计算方法这里我们采取的方法是累次积分法。

也就是先把x看成常量，对y进行积分，然后在对x进行积分，或者是先把y看成常量，对x进行积分，然后在对y进行积分。

为此我们有积分公式，如下：或在这里我们可能会有这个问题：累次积分的上下限是怎么确定的呢？累次积分上下限的确定方法我们先来对区域作些补充说明：如果经过区域(σ)内任意一点(即不是区域边界上的点)作平行于y轴(或x 轴)的直线,且此直线交(σ)的边界不超过两点，那末称(σ)为沿y轴(x轴)方向的正规区域.如果(σ)即是沿y轴方向也是沿x轴方向的正规区域,那末(σ)就称为正规区域.下图所示的即为正规区域:关于累次积分上下限的取法如下所述:(1).如果(σ)为沿y轴方向的正规区域，那末二重积分可化为先对y再对x的累次积分.其中对y的积分下限是(σ)的下部边界曲线所对应的函数y1(x)，积分上限是上部边界曲线所对应的函数y2(x).对x的积分下限与上限分别是(σ)的最左与最右点的横坐标a与b.(2).如果(σ)为沿x轴方向的正规区域,那末二重积分可化为先对x再对y的累次积分.其中对x的积分下限是(σ)的左部边界曲线所对应的函数x1(y)，积分上限是右部边界曲线所对应的函数x2(y).对y的积分下限与上限分别是(σ)的最低与最高点的横坐标c与d.(3).如果(σ)为正规区域，那末累次积分可以交换积分次序。

二重积分通俗理解
二重积分通俗理解
二重积分的概念十分抽象，在没有接触相关课程的情况下，很容易就会感到困惑和不理解。

其实，这个概念在我们日常生活中也不断地出现，只是我们没有意识到而已。

二重积分可以用来计算一个物体在一段时间内所移动的总距离，以及一定面积内降雨量的总量，亦或是在一片土地上植物叶片籽粒的总数。

这些都是不同现实中的例子，但是形式上它们却有着一个共同之处：所有的运算都是按照一个累积的方式进行的，也就是积分。

在积分的时候通常会用到两个维度的变量，比如计算车在一段时间内的总里程就需要时间和速度两个维度变量。

这也就是二重积分的由来，它的数学形式是I=∫∫f(x,y)dA，其中，f(x,y)表示某一个变量在不同时间、不同空间中的变化值，dA表示面积，I则表示累计的值。

所有这些变量都必须要被一一累计，才能得到最终的结果。

这就是二重积分的基本含义，当我们把这个概念应用到每一个具体的问题，都要根据实际情况来进行具体的计算，本质上来说，就是计算某一变量在不同的地方不同时间的累积值。

- 1 -。

2015考研数学:二重积分的基本知识点来源：文都教育二重积分是考研数学中的大题常考点，主要考查的是同学们的计算能力。

下面文都考研数学老师对二重积分的基本知识点进行一些讲解，以帮助广大考生备考。

１．二重积分的概念设二元函数(,)f x y 在有界闭区域D 上有界．（1）将区域D 划分成若干小区域12,,,n σσσ∆∆∆；（2）(,)(1)i i i i n ξησ∀∈∆≤≤，作1(,)n i iii f ξησ=∆∑； （3）令1max{}i i n d λ≤≤=，i d 为i σ∆的直径，01(,)lim (,)n i ii i D f x y d f λσξησ→==∆∑⎰⎰．注：①二重积分与区域的划分及点的取法无关；②若(,)f x y 在有界闭区域D 上连续，则(,)f x y 在D 上的二重积分一定存在； ③(,)D f x y d σ⎰⎰的几何意义是以D 为底，以(,)z f x y =为顶的曲顶柱体的体积； ④(,)Df x y d σ⎰⎰的物理意义是以(,)f x y ρ=为面密度的平面区域D 的质量． 2．二重积分的性质（1）[(,)(,)](,)g(,)D D D f x y g x y d f x y d x y d σσσ±=±⎰⎰⎰⎰⎰⎰． （2）(,)(,)D D kf x y d k f x y d σσ=⎰⎰⎰⎰． （3）1212(,)(,)(,)D D D D f x y d f x y d f x y d σσσ+=+⎰⎰⎰⎰⎰⎰． （4）D d A σ=⎰⎰．（5）（比较定理）若在D 上恒有(,)(,)f x y g x y ≤，则(,)(,)D Df x y dg x y d σσ≤⎰⎰⎰⎰．（6）（估值定理）设,M m 分别为(,)f x y 在区域D 上的最大与最小值，A 为D 的面积，则(,)DmA f x y d MA σ≤≤⎰⎰．（7）（中值定理）若(,)f x y 在闭域D 上连续，A 为D 的面积，则在D 上至少存在一点(,)ξη，使(,)(,)Df x y d f A σξη=⎰⎰．（8）二重积分的对称性质①若积分区域D 关于x 轴对称，则二重积分10,(,)(,)(,)2(,),(,)(,)D D f y f x y f x y f x y d f x y d f y f x y f x y σσ-=-⎧⎪=⎨-=⎪⎩⎰⎰⎰⎰关于为奇函数，即关于为偶函数，即，其中1D 为D 在上半平面部分．②若积分区域D 关于y 轴对称，则二重积分20,(,)(,)(,)2(,),(,)(,)D D x x f f x y f x y f x y d f x y d f f x y f x y σσ-=-⎧⎪=⎨-=-⎪⎩⎰⎰⎰⎰关于为奇函数，即关于为偶函数，即，其中2D 为D 在右半平面部分．③设区域D 关于y x =对称，则(,)(,)D Df x y d f y x d σσ=⎰⎰⎰⎰．④设积分区域D 关于原点对称，(,)f x y 同时为,x y 的奇函数或偶函数，则 1,,0,(,)(,)(,)2(,),(,)(,)D D x y x y f f x y f x y f x y d f x y d f f x y f x y σσ--=-⎧⎪=⎨--=⎪⎩⎰⎰⎰⎰关于的奇函数，即关于为偶函数，即，其中1D 为D 的右半平面部分．3．积分法（1）直角坐标法①（X -型区域）设12{(,)|,()()}D x y a x b x y x ϕϕ=≤≤≤≤，则21()()(,)(,)b x a x D f x y d dx f x y dy ϕϕσ=⎰⎰⎰⎰．②（Y -型区域）设12{(,)|()(),}D x y y x y c y d ϕϕ=≤≤≤≤，则21()(y)(,)(,)d y c D f x y d dy f x y dx ϕϕσ=⎰⎰⎰⎰．（2）极坐标变换令00cos cos ()sin sin x x r x r y r y y r θθθθ-==⎧⎧⎨⎨=-=⎩⎩或，其中12{(,)|,()()}D r r r r θαθβθθ=≤≤≤≤，则 21()()(,)(cos ,sin )r r D f x y d d rf r r dr βθαθσθθθ=⎰⎰⎰⎰．4．应用（1）几何应用设:(,)((,))z x y x y D ϕ∑=∈为空间曲面，则该曲面段的面积为221()()D z z A d x yσ∂∂=++∂∂⎰⎰．（2）物理应用①质量(,)Dm x y d ρσ=⎰⎰． ②形心坐标(,)(,),(,)(,)DD D D x x y d y x y d x y x y d x y d ρσρσρσρσ==⎰⎰⎰⎰⎰⎰⎰⎰，特别地，若薄片密度均为，则形心坐标,DD D D xd yd x y d d σσσσ==⎰⎰⎰⎰⎰⎰⎰⎰．（3）转动惯量设l 为平面xoy 上的直线，区域D 上任意一点(,)P x y 到直线l 的距离为d ，则区域D 绕直线l 的转动惯量为2(,)l D I dx y d ρσ=⎰⎰，特别地，2222(,),(,),()(,)x y o D D DI y x y d I x x y d I x y x y d ρσρσρσ===+⎰⎰⎰⎰⎰⎰．。