2017-2018学年北师大版数学九年级下册同步训练：3.9 弧长及扇形的面积

3.9 弧长及扇形的面积同步测试一、选择题1.如图，半径为1cm 、圆心角为90°的扇形OAB 中，分别以OA 、OB 为直径作半圆，则图中阴影部分的面积为( )A.πcm2B.32πcm2C.21cm2D.32cm22.一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（ ）A.．5π B ．4π C ．3π D ．2π3.如图，在△ABC 中，∠A=90°，AB=AC=2，以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ，则图中阴影部分的面积是（ ）A. B. C. D.4.如图，小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为( )A ．4π－2B ．2π－2C ．4π－4D ．2π－45.如图，直径AB 为6的半圆，绕A 点逆时针旋转60°，此时 点B 到了点B ’，则图中阴影部分的面积是（ ）A. B. C. D.6.如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽(接缝忽略不计)，圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（）A．40cm B．50cm C．60cm D．80cm7.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，点B，A，C′在同一条直线上，则线段BC扫过的区域面积为（）A. B. C. D.8.如图，Rt△ABC中，∠ACB=90°∠A=30°,BC=2,O、H分别为AB、AC的中点，将△ABC顺时针旋转120°到△A1BC1的位置，则整个旋转过程中线段OH所扫过的面积为（）A. B．C. D.9.如图所示，扇形AOB的圆心角120°，半径为2，则图中阴影部分的面积为（）A. B. C. D.10.如图,在Rt △ABC 中,∠ABC ＝90°,AB ＝＝2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π 2π C.π- D.2π-二、填空题11.已知扇形的圆心角为60°，半径为1，则扇形的弧长为 ．12．一个扇形的半径为8cm ，弧长为 cm ，则扇形的圆心角为 ．13.如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为4，∠B=135°，则弧AC 的长为_________.14.)如图,在边长为4的正方形ABCD 中,以点B 为圆心,AB 为半径画弧,交对角线BD与点E,则图中阴影部分的面积是 (结果保留π)15.如图，在边长为4的正方形ABCD 中，先以点A 为圆心，AD 的长为半径画弧，再以AB 边的中点为圆心，AB 长的一半为半径画弧，则阴影部分面积是________(结果保留π)．16.如图，在△ABC 中，CA ＝CB ，∠ACB ＝90°，AB ＝2，点D 为AB 的中点，以点D 为圆心作圆心角为90°的扇形DEF ，点C 恰在弧EF 上，则图中阴影部分的面积为________．三、综合题17.如图，⊙O的半径为6cm，直线AB是⊙O的切线，切点为点B，弦BC∥AO.若∠A ＝30°，求劣弧BC的长。

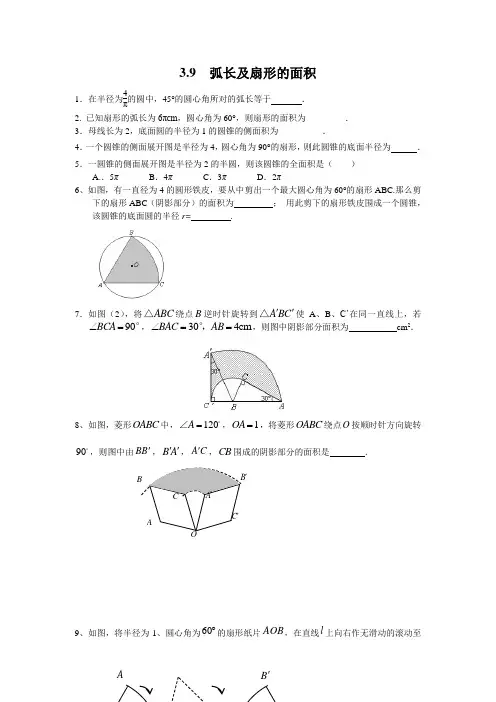
ABC OA 'B 'C '3.9 弧长及扇形的面积1．在半径为4π的圆中，45°的圆心角所对的弧长等于 ．2. 已知扇形的弧长为6πcm ，圆心角为60°，则扇形的面积为_________． 3．母线长为2，底面圆的半径为1的圆锥的侧面积为__________．4．一个圆锥的侧面展开图是半径为4，圆心角为90°的扇形，则此圆锥的底面半径为 ． 5．一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（ ）A.．5π B ．4π C ．3π D ．2π6、如图，有一直径为4的圆形铁皮，要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC （阴影部分）的面积为 ； 用此剪下的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径r= .7．如图（2），将ABC △绕点B 逆时针旋转到A BC ''△使A 、B 、C’在同一直线上，若90BCA ∠=°，304cm BAC AB ∠==°，，则图中阴影部分面积为 cm 2．8、如图，菱形OABC 中，120A =∠，1OA =，将菱形OABC 绕点O 按顺时针方向旋转90，则图中由BB '，B A ''，A C '，CB 围成的阴影部分的面积是 ．9、如图，将半径为1、圆心角为︒60的扇形纸片AOB ，在直线l 上向右作无滑动的滚动至′扇形B O A '''处，则顶点O 经过的路线总长为10、如图，半圆的直径AB=10，P 为AB 上一点，点C\D 为半圆的三等分点，求得阴影部分的面积为11、如图，AC 是汽车挡风玻璃前的刮雨刷．如果AO=65，CO=15，当AC 绕点O 旋转90°时，则刮雨刷AC 扫过的面积为 cm 2.12、如图，王虎使一长为4cm ，宽为3cm 的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A 位置变化为12A A A →→，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A 翻滚到A 2位置时共走过的路径长为_________cm.13．图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一 部分，其展开图是矩形．图2是车棚顶部截面的示意图，AB 所在圆的圆心为O ．车棚顶部是A O′C A ′ABE BDCA O用一种帆布覆盖的，求覆盖棚顶的帆布的面积14、一位小朋友在粗糙不打滑的“Z ”字形平面轨道上滚动一个半径为10cm 的圆盘，如图所示，AB 与C D 是水平的，BC 与水平面的夹角为600，其中AB=60cm ，CD=40cm ，BC=40cm ，请你作出该小朋友将园盘从A 点滚动到D 点其圆心所经过的路线的示意图，并求出此路线的长度。

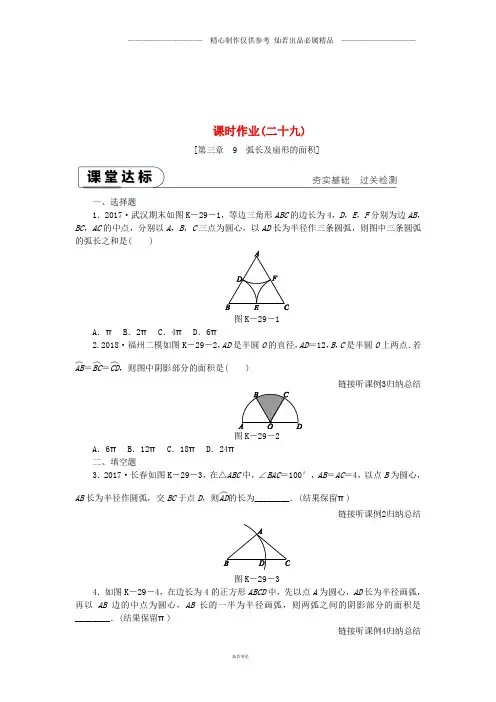
课时作业(二十九)[第三章 9 弧长及扇形的面积]一、选择题1．2017·武汉期末如图K －29－1，等边三角形ABC 的边长为4，D ，E ，F 分别为边AB ，BC ，AC 的中点，分别以A ，B ，C 三点为圆心，以AD 长为半径作三条圆弧，则图中三条圆弧的弧长之和是( )图K －29－1A ．πB ．2πC ．4πD ．6π 2.2018·福州二模如图K －29－2，AD 是半圆O 的直径，AD ＝12，B ，C 是半圆O 上两点．若AB ︵＝BC ︵＝CD ︵，则图中阴影部分的面积是( )链接听课例3归纳总结图K －29－2A ．6πB ．12πC ．18πD ．24π 二、填空题3．2017·长春如图K －29－3，在△ABC 中，∠BAC ＝100°，AB ＝AC ＝4，以点B 为圆心，AB 长为半径作圆弧，交BC 于点D ，则AD ︵的长为________．(结果保留π)链接听课例2归纳总结图K －29－34．如图K －29－4，在边长为4的正方形ABCD 中，先以点A 为圆心，AD 长为半径画弧，再以AB 边的中点为圆心，AB 长的一半为半径画弧，则两弧之间的阴影部分的面积是________．(结果保留π)链接听课例4归纳总结图K －29－45．如图K －29－5，△ABC 是正三角形，曲线CDEF 叫正三角形的渐开线，其中CD ︵，DE ︵，EF ︵的圆心依次是A ，B ，C ，如果AB ＝1，那么曲线CDEF 的长是________．图K －29－56．如图K －29－6，在Rt △ABC 中，∠ACB ＝90°，AC ＝2 3，以点C 为圆心，CB 长为半径画弧，与AB 边交于点D ，将BD ︵绕点D 旋转180°后点B 与点A 恰好重合，则图中阴影部分的面积为________．图K －29－6三、解答题7．如图K －29－7，在扇形OAB 中，∠AOB ＝90°，半径OA ＝6.将扇形OAB 沿过点B 的直线折叠，点O 恰好落在扇形上的点D 处，折痕交OA 于点C ，求整个阴影部分的周长和面积．图K －29－78．2018·椒江区模拟如图K －29－8，AB 是⊙O 的直径，C 是圆上一点，连接CA ，CB ，过点O 作弦BC 的垂线，交BC ︵于点D ，连接AD .(1)求证：∠CAD ＝∠BAD ；(2)若⊙O 的半径为1，∠B ＝50°，求AC ︵的长．图K －29－89．2017·如东县一模如图K －29－9，在△ABC 中，∠ACB ＝130°，∠BAC ＝20°，BC ＝4，以点C 为圆心，BC 长为半径的圆交AB 于点D ，交AC 于点E .(1)求BD 的长；(2)求阴影部分的面积．图K －29－910．2017·贵阳如图K－29－10，C，D是半圆O上的三等分点，直径AB＝4，连接AD，AC，DE⊥AB，垂足为E，DE交AC于点F.(1)求∠AFE的度数；(3)求阴影部分的面积(结果保留π和根号).链接听课例4归纳总结图K－29－1011．如图K－29－11，把Rt△ABC的斜边AB放在直线l上，按顺时针方向将△ABC在l 上转动两次，使它转到△A″B″C″的位置，设BC＝1，AC＝3，则顶点A运动到点A″的位置时，(1)求点A所经过的路线长；(2)点A所经过的路线与l围成的图形的面积是多少？图K－29－11研究型在学习扇形的面积公式时，同学们推得S 扇形＝n πR 2360，并通过比较扇形面积公式与弧长公式l ＝n πR180，得出扇形面积的另一种计算方法S 扇形＝12lR .接着老师让同学们解决两个问题：问题 Ⅰ：求弧长为4π，圆心角为120°的扇形面积． 问题Ⅱ：某小区设计的花坛形状如图K －29－12中的阴影部分，已知弧AB 和弧CD 所在圆的圆心都是点O ，弧AB 的长为l 1，弧CD 的长为l 2，AC ＝BD ＝d ，求花坛的面积．(1)请你解答问题Ⅰ.(2)在解完问题 Ⅱ 后的全班交流中，有名同学发现扇形面积公式S扇形＝12lR 类似于三角形面积公式；类比梯形面积公式，他猜想花坛的面积S ＝12(l 1＋l 2)d .他的猜想正确吗？如果正确，写出推导过程；如果不正确，请说明理由．图K －29－12详解详析【课时作业】 [课堂达标]1．[解析] B 依题意知：图中三条圆弧的弧长之和＝60π×12×4180×3＝2π.故选B.2．[解析] A ∵AB ︵＝BC ︵＝CD ︵， ∴∠AOB ＝∠BOC ＝∠COD ＝60°，∴阴影部分的面积＝60π×62360＝6π.故选A.3．[答案] 8π9[解析] ∵在△ABC 中，∠BAC ＝100°，AB ＝AC ， ∴∠B ＝∠C ＝12(180°－100°)＝40°.∵AB ＝4，∴AD ︵的长为40π×4180＝8π9.4．[答案] 2π5．[答案] 4π[解析] CD ︵的长是120π×1180＝2π3，DE ︵的长是120π×2180＝4π3，EF ︵的长是120π×3180＝2π， 则曲线CDEF 的长是2π3＋4π3＋2π＝4π.故答案为4π. 6．[答案] 2 3－2π3[解析] 依题意，有AD ＝BD .又∠ACB ＝90°，所以CB ＝CD ＝BD ，即△BCD 为等边三角形，∴∠BCD ＝∠B ＝60°，∠A ＝∠ACD ＝30°.由AC ＝2 3，求得BC ＝2，AB ＝4，S 弓形BD ＝S 扇形BCD －S △BCD ＝60π×22360－3＝23π－3，故阴影部分的面积为S △ACD －S 弓形AD ＝3－(2π3－3)＝2 3－2π3.7．解：如图，连接OD .根据折叠的性质，得CD ＝CO ，BD ＝BO ，∠DBC ＝∠OBC ， ∴OB ＝OD ＝BD ，即△OBD 是等边三角形，∴∠DBO ＝60°，∴∠CBO ＝12∠DBO ＝30°.∵∠AOB ＝90°， ∴OC ＝OB ·tan∠CBO ＝6×33＝2 3， ∴S △BDC ＝S △OBC ＝12·OB ·OC ＝12×6×2 3＝6 3.∵S 扇形OAB ＝90360π×62＝9π，lAB ︵＝90180π×6＝3π，∴整个阴影部分的周长为AC ＋CD ＋BD ＋lAB ︵＝AC ＋OC ＋OB ＋lAB ︵＝OA ＋OB ＋lAB ︵＝6＋6＋3π＝12＋3π，整个阴影部分的面积为S 扇形OAB －S △BDC －S △OBC ＝9π－6 3－6 3＝9π－12 3. 8．解：(1)证明：∵点O 是圆心，OD ⊥BC ， ∴CD ︵＝BD ︵，∴∠CAD ＝∠BAD .(2)连接CO ，∵∠B ＝50°，OB ＝OC ， ∴∠OCB ＝∠B ＝50°， ∴∠AOC ＝100°， ∴AC ︵的长为100π×1180＝5π9.9．解：(1)如图，过点C 作CH ⊥AB 于点H .在△ABC 中，∠B ＝180°－∠A －∠ACB ＝180°－20°－130°＝30°. 在Rt △BCH 中，∵∠CHB ＝90°，∠B ＝30°，BC ＝4， ∴CH ＝12BC ＝2，BH ＝3CH ＝2 3.∵CH ⊥BD ，∴DH ＝BH ，∴BD ＝2BH ＝4 3. (2)连接CD .∵BC ＝DC ，∴∠CDB ＝∠B ＝30°，∴∠BCD ＝120°，∴阴影部分的面积＝扇形CBD 的面积－△CBD 的面积＝120π×42360－12×4 3×2＝163π－4 3.10．解：(1)连接OD ，OC ，∵C ，D 是半圆O 上的三等分点，∴AD ︵＝CD ︵＝BC ︵， ∴∠AOD ＝∠DOC ＝∠COB ＝60°，∴∠CAB ＝30°. ∵DE ⊥AB ，∴∠AEF ＝90°， ∴∠AFE ＝90°－30°＝60°. (2)由(1)知∠AOD ＝60°.又∵OA ＝OD ，∴△AOD 是等边三角形． ∵AB ＝4，∴OA ＝AD ＝2.∵DE ⊥AO ，∴DE ＝3，∴S 阴影＝S 扇形AOD －S △AOD ＝60·π×22360－12×2×3＝23π－ 3.11．解：(1)在Rt △ABC 中，BC ＝1，AC ＝3， ∴AB ＝2，∴cos ∠ABC ＝12，∴∠ABC ＝60°，则∠ABA ′＝120°，∠A ′C ″A ″＝90°，∴lAA ′︵＝120π×2180＝4π3，lA ′A ″︵＝90π×3180＝32π，∴点A 所经过的路线长为4π3＋32π.(2)S 扇形BAA ′＝12lAA ′︵·AB ＝12×4π3×2＝4π3，S 扇形C ″A ′A ″＝12lA ′A ″︵·C ″A ′＝12×3π2×3＝34π，S △A ′B ′C ′＝12×1×3＝32， ∴点A 所经过的路线与l 围成的图形的面积是43π＋34π＋32＝2512π＋32.[素养提升][解析] 根据扇形面积公式、弧长公式之间的关系，结合已知条件推出结果． 解：(1)根据弧长公式l ＝n πR180，弧长为4π，圆心角为120°，可得R ＝6，∴S 扇形＝12lR ＝12×4π×6＝12π. (2)他的猜想正确．设大扇形的半径为R ，小扇形的半径为r ，圆心角的度数为n °，则由l ＝n πR180，得R ＝180l 1n π，r ＝180l 2n π， ∴花坛的面积为 12l 1R －12l 2r ＝12·l 1·180l 1n π－12·l 2·180l 2n π ＝90n π()l 12－l 22 ＝90n π(l 1＋l 2)(l 1－l 2) ＝12·180n π(l 1＋l 2)(n π180R －n π180r ) ＝12(l 1＋l 2)(R －r )＝12(l 1＋l 2)d . 故他的猜想正确．。

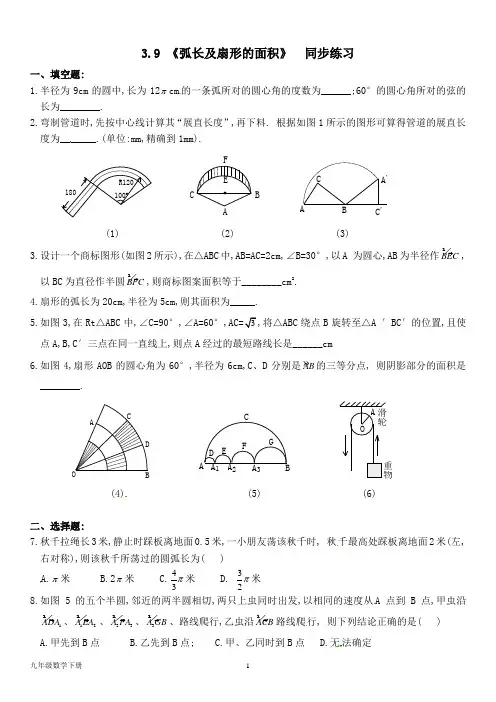
北师大版九年级数学下册《3.9弧长及扇形的面积》同步测试题带答案学校:___________班级：___________姓名：___________考号：___________【基础达标】1.在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形OAB的面积是()A.6π cm2B.8π cm2C.12π cm2D.24π cm2π cm,则扇形的圆心角为() 2.一个扇形的半径为8 cm,弧长为163A.60°B.120°C.150°D.180°3.如图,一块呈三角形的草坪上,一小孩将绳子一端拴住山羊,另一端套在木桩处.若∠BAC=120°,绳子长3米(不包括两个拴处用的绳子),则山羊在草坪上活动的最大面积是()A.π m2B.2π m2C.3π m2D.9π m24.如图,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q,则点P所经过的弧长为(结果保留π).5.一弯形管道如图所示,其中心线为一段圆弧AB.已知半径OA=60 cm,∠AOB=108°,则管道的长⏜的长)为cm.(结果保留π)度(即AB6.如图,AB是☉O的直径,弦CD⊥AB于点E,连接AC,BC.(1)求证:∠A=∠BCD.(2)若CD=4√3,∠B=60°,求扇形OAC(阴影部分)的面积.【能力巩固】7.如图,某厂生产横截面直径为7 cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头的侧面.为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()A.π4cm B.7π4cmC.7π2cm D.7π cm9.图1中特种自行车的轮子形状为“勒洛三角形”,图2是其一个轮子的示意图,“勒洛三角形”是分别以等边三角形ABC三个顶点A,B,C为圆心,以边长为半径的三段弧围成的图形.若这个等边三角形ABC的边长为30 cm,则这种自行车一个轮子的周长为cm.图1图29.如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在的直线l与AB⏜交于点C,连接AC.若OA=2,则图中阴影部分的面积是.10如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以点A,B,C为圆心,12AC的长为半径画弧,三条弧与边AB所围成的阴影部分的面积是.【素养拓展】11.如图,△ABC内接于☉O,AD∥BC交☉O于点D,DF∥AB交BC于点E,交☉O于点F,连接AF,CF.(1)求证:AC=AF.(2)若☉O的半径为3,∠CAF=30°,求AC⏜的长(结果保留π).参考答案【基础达标】1.C2.B3.C4.√102π5.36π6.解:(1)证明:∵AB是☉O的直径,弦CD⊥AB∴BC⏜=BD⏜∴∠A=∠BCD.(2)∵OC=OB,∠B=60°,∴△BOC为等边三角形,∴∠BOC=60°∴∠AOC=120°.∵AB是☉O的直径,弦CD⊥AB,∴CE=12CD=2√3.在Rt△COE中,OC=CEsin∠COB=4∴扇形OAC(阴影部分)的面积=120π×42360=163π.【能力巩固】7.B 8.30π 9.2π3-√3 10.8-2π 【素养拓展】11.解:(1)证明:∵AD ∥BC ,DF ∥AB∴四边形ABED 为平行四边形 ∴∠B=∠D.∵∠AFC=∠B ,∠ACF=∠D ∴∠AFC=∠ACF ,∴AC=AF.(2)如图,连接AO ,CO 由(1)得∠AFC=∠ACF∴∠AFC=180°−30°2=75°∴∠AOC=2∠AFC=150° ∴AC⏜的长=150×π×3180=5π2.。

北师大版九年级数学下册第三章 3.9：弧长及扇形的面积 同步练习题一、选择题1、已知扇形的圆心角为 60°，半径为 1，则扇形的弧长为（） A ．2π B ．π C ．6π D ．3π 2、如图，四边形 ABCD 是⊙O 的内接四边形，⊙O 的半径为 2，∠B=135°，则的长（ ）A ．2πB ．πC ．2πD ．3π3、如图，AB 是⊙O 的直径，弦 CD ⊥AB ，∠CDB=30°， 积为（ ）A ．4πB ．2πC ．ΠD ．23π 4、如图，⊙O 的半径为 2，AB 、CD 是互相垂直的两条直径，点 P 是⊙O 上任意一点（P 与A 、B 、C 、D 不重合），经过 P 作 PM ⊥AB 于点 M ，PN ⊥CD 于点 N ，点 Q 是 MN 的中 点，当点 P 沿着圆周转过 45°时，点 Q 走过的路径长为（ ）A ．4πB ．2πC ．6πD ．3π5、如图，AB 是⊙O 的直径，弦 CD 交 AB 于点 E ，且 E 为 OB 的中点，∠CDB=30°， 则阴影部分的面积为（ ）A．πB．4πC．43πD．163π6、如图，4 个正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（）A．38πB．34π C．74π D．43π7、一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此圆锥的底面半径为（）A．83cm B．163cm C．3cm D．43cm8、如图，在半径为2，圆心角为90°的扇形内，以BC 为直径作半圆，交弦AB 于点D，连接CD，则阴影部分的面积为（）A．π﹣1 B．2π﹣1 C．12π﹣1 D．12π﹣29、如图，AB 是⊙O 的直径，弦CO⊥AB，∠C=30°，CD=24，则阴影部分的面积是（）10、如图，在矩形ABCD 中，CD=1，∠DBC=30°．若将BD 绕点B 旋转后，点D 落在DC 延长线上的点E 处，点D 经过的路径，则图中阴影部分的面积是（）A ．3πB ．3π-C ．2π．2π 11、如图，某厂生产横截面直径为 7cm 的圆柱形罐头盒，需将“蘑菇罐头”字样贴在罐头侧面． 为了获得较佳视觉效果，字样在罐头盒侧面所形成的弧的度数为 90°，则“蘑菇罐头”字样的 长度为（ ）A ．4πcmB ．74πcm C ．72πcm D ．7πcm12、如图，在边长为 6 的正方形 ABCD 中，E 是 AB 的中点，以 E 为圆心，ED 为半径作半 圆，交 A 、B 所在的直线于 M 、N 两点，分别以直径 MD 、ND 为直径作半圆，则阴影部分 面积为（ ）A ．B ．． D ．二、填空题13、如果一个扇形的弧长是43π，半径是 6，那么此扇形的圆心角为 .14、如图，已知扇形的圆心角为 60°，则图中弓形的面积为 .15、如图，两个小正方形的边长都是 1，以 A 为圆心，AD 为半径作弧交 BC 于点 G ，则图 中阴影部分的面积为 .16、如图，AC⊥BC，AC=BC=4，以BC 为直径作半圆，圆心为点O；以点C 为圆心，BC为半径作，过点O 作AC 的平行线交两弧于点D、E，则阴影部分的面积是.17、如图，AB 是⊙O 的直径，弦CD⊥AB，∠C=30°，CD=2．则S 阴影= .18、如图，张三同学把一个直角边长分别为3cm，4cm 的直角三角形硬纸板，在桌面上翻滚（顺时针方向），顶点A 的位置变化为A1⇒A2⇒A3，其中第二次翻滚时被桌面上一小木块挡住，使纸板一边A2C1 与桌面所成的角恰好等于∠BAC，则A 翻滚到A2 位置时共走过的路程为.三、解答题19、如图，三角形ABC 是边长为1 的正三角形，与所对的圆心角均为120°，求图中阴影部分的面积．20、如图，AB 切⊙O 于点B，OA=2，AB=3，弦BC∥OA，求劣弧BC 的弧长？21、如图，以BC 为直径的⊙O 与△ABC 的另两边分别相交于点D、E．若∠A=60°，BC=2，计算图中阴影部分的面积．22、如图，以BC 为直径，在半径为2、圆心角为90°的扇形内作半圆，交弦AB 于点D，连接CD，求阴影部分的面积．23、现有30%圆周的一个扇形彩纸片，该扇形的半径为40cm，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm 的圆锥形纸帽（接缝处不重叠），求剪去的扇形纸片的圆心角的度数？24、如图1，是用边长为2cm 的正方形和边长为2cm 正三角形硬纸片拼成的五边形ABCDE．在桌面上由图1 起始位置将图片沿直线l 不滑行地翻滚，翻滚一周后到图2 的位置．求由点A 到点A4 所走路径的长度？25、如图，Rt△ABC 中，∠ACB=90°，∠B=30°，AB=12cm，以AC 为直径的半圆O 交AB 于点D，点E 是AB 的中点，CE 交半圆O 于点F，求CD 长和图中阴影部分的面积．。

9 弧长及扇形的面积知识点 1 弧长公式及其应用1．若扇形的半径为6，圆心角为120°，则此扇形的弧长是( ) A ．3π B ．4π C ．5π D ．6π2．一个扇形的圆心角为60°，它的弧长为2π cm ，则这个扇形的半径为( ) A ．6 cm B ．12 cm C ．2 3 cm D . 6 cm3．如图3－9－1，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长为( )A .π3B .π2C ．πD ．2π 图3－9－13－9－24．2021·毕节模拟如图3－9－2，在△ABC 中，∠ACB ＝90°，AC ＝1，AB ＝2，以点A 为圆心、AC 的长为半径画弧，交AB 边于点D ，则弧CD 的长为________．(结果保留π)5．如图3－9－3所示，正六边形ABCDEF 内接于半径为3的圆，则劣弧AB 的长为________．图3－9－3知识点 2 扇形的面积公式及其应用6．如图3－9－4，某数学兴趣小组将边长为3的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形(忽略铁丝的粗细)，则所得扇形BAD 的面积为( )A ．6B ．7C ．8D ．9图3－9－43－9－57．如图3－9－5，一扇形纸扇完全打开后，外侧两竹条AB 和AC 的夹角为120°，AB 长为25 cm ，贴纸部分的宽BD 为15 cm .若纸扇两面贴纸，则贴纸的面积为( )A ．175π cm 2B ．350π cm 2C .8003π cm 2 D ．150π cm 2 8．[2021·淄博] 如图3－9－6，半圆的直径BC 恰与等腰直角三角形ABC 的一条直角边完全重合，若BC ＝4，则图中阴影部分的面积是( )A ．2＋πB ．2＋2πC ．4＋πD ．2＋4π图3－9－63－9－79．2021·遵义模拟如图3－9－7，正三角形ABC 的边长为4，D ，E ，F 分别为BC ，CA ，AB 的中点，以A ，B ，C 三点为圆心，2为半径作圆，则图中阴影部分的面积为__________．10．[2021·咸宁] 如图3－9－8，⊙O 的半径为3，四边形ABCD 内接于⊙O ，连接OB ，OD ，若∠BOD ＝∠BCD ，则弧BD 的长为( )A ．πB .32π C ．2π D ．3π3－9－8图3－9－911．[2021·乐山] 如图3－9－9，在Rt △ABC 中，∠ACB ＝90°，AC ＝2 3，以点C 为圆心，CB 的长为半径画弧，与AB 边交于点D ，将BD ︵绕点D 旋转180°后点B 与点A 恰好重合，则图中阴影部分的面积为____________．12．2021·舟山如图3－9－10，小明自制一块乒乓球拍，正面是半径为8 cm 的⊙O ，AB ︵＝90°，弓形ACB(阴影部分)部分粘贴胶皮，则胶皮面积为________．图3－9－103－9－1113．如图3－9－11，一块等边三角形的木板ABC ，边长为1.现将木板沿水平线向右做无滑动的翻滚，那么点B 从开始至结束(点B 翻滚至点B 2)所走过的路径长度为________．14．如图3－9－12所示，AB 是半圆的直径，AB ＝2R ，C ，D 为半圆的三等分点，求阴影部分的面积．图3－9－1215．已知：如图3－9－13，△ABC 内接于⊙O ，OH ⊥AC 于点H ，过点A 的切线与OC 的延长线交于点D ，∠B ＝30°，OH ＝2 3.求：(1)∠AOC 的度数；(2)线段AD 的长(结果保留根号)； (3)图中阴影部分的面积．图3－9－1316．如图3－9－14，在矩形ABCD 中，AB ＝2DA ，以点A 为圆心，AB 长为半径的圆弧交DC 于点E ，交AD 的延长线于点F ，且DA ＝2.(1)求线段EC 的长； (2)求图中阴影部分的面积．图3－9－1417．如图3－9－15所示，等腰直角三角形ABC 的直角边长为4，以A 为圆心，直角边AB 为半径作弧BC 1，交斜边AC 于点C 1，C 1B 1⊥AB 于点B 1，设弧BC 1，C 1B 1，B 1B 围成的阴影部分的面积为S 1，然后以A 为圆心，AB 1为半径作弧B 1C 2，交斜边AC 于点C 2，C 2B 2⊥AB 于点B 2，设弧B 1C 2，C 2B 2，B 2B 1围成的阴影部分的面积为S 2，按此规律继续作下去，求得到的阴影部分的面积S 3.图3－9－15详解1．B [解析] 弧长为n πr 180＝120×π×6180＝4π.故选B.2．A [解析] 根据弧长公式，60180πr ＝2π，解得r ＝6.3．C 4.π3[解析] ∵∠ACB ＝90°，AC ＝1，AB ＝2， ∴∠ABC ＝30°，∴∠A ＝60°.又∵AC ＝1，∴弧CD 的长为60×π×1180＝π3.故答案为：π3. 5．π6．D [解析] ∵正方形的边长为3，∴弧BD 的长为6，∴S 扇形ABD ＝12lr ＝12×6×3＝9.故选D.7．B8．A [解析] 设半圆的圆心为O ，如图，连接CD ，OD ， ∵BC ＝4，∴OB ＝2.∵∠B ＝45°，∴∠COD ＝90°，∴图中阴影部分的面积＝S △BOD ＋S 扇形COD ＝12×2×2＋90·π×22360＝2＋π，故选A.9．4 3－2π [解析] 如图，连接AD ，∵正三角形ABC 的边长为4，D ，E ，F 分别为BC ，CA ，AB 的中点， ∴AD ⊥BC ，∠BAC ＝∠B ＝∠C ＝60°. ∵AB ＝4，∴AD ＝AB ·sin60°＝4×32＝2 3， ∴S 阴影＝S △ABC －3S 扇形AEF ＝12×4×2 3－3×60π×22360＝4 3－2π.故答案为：4 3－2π.10．C [解析] ∵四边形ABCD 内接于⊙O ， ∴∠BCD ＋∠A ＝180°.∵∠BOD ＝2∠A ，∠BOD ＝∠BCD ， ∴2∠A ＋∠A ＝180°，∴∠A ＝60°， ∴∠BOD ＝120°，∴弧BD 的长＝120π×3180＝2π.故选C.11．2 3－2π3[解析] 依题意，有AD ＝BD .又∠ACB ＝90°，所以CB ＝CD ＝BD ，即△BCD 为等边三角形，∠BCD ＝∠B ＝60°，∠A ＝∠ACD ＝30°.由AC ＝2 3，求得BC ＝2，AB ＝4，S 弓形BD ＝S 扇形BCD －S △BCD ＝60π×22360－3＝23π－ 3.故阴影部分的面积为S △ACD －S 弓形AD ＝3－(2π3－3)＝2 3－2π3.12．(48π＋32)cm 2 [解析] 如图， 连接AO ，OB ，作OD ⊥AB 于点D .因为AB ︵＝90°，所以∠AOB ＝90°，所以胶皮面积S ＝S 扇形ACB ＋S △OAB ＝34×π×82＋12×8×8＝(48π＋32)cm 2.13．4π314．解：连接OC ，OD ，CD . ∵AC ︵＝BD ︵，∴∠CDA ＝∠DAB ，∴CD ∥AB ，∴S △ACD ＝S △OCD ，∴S 阴影＝S 扇形COD . 又∵∠COD ＝13∠AOB ＝60°，∴S 阴影＝S 扇形COD ＝n πR 2360＝16πR 2.15．解：(1)∵∠B ＝30°， ∴∠AOC ＝2∠B ＝60°. (2)∵∠AOC ＝60°，AO ＝CO ， ∴△AOC 是等边三角形． ∵OH ＝2 3，∴AO ＝4. ∵AD 与⊙O 相切，∴∠OAD ＝90°，∠D ＝30°，∴AD ＝4 3.(3)∵S 扇形OAC ＝60×π×42360＝83π，S △AOD ＝12×4×4 3＝8 3，∴S 阴影＝8 3－83π.16．]解：(1)∵在矩形ABCD 中，AB ＝2DA ， ∴AE ＝DC ＝2DA ，且∠ADE ＝90°. 又∵DA ＝2，∴AE ＝AB ＝4，∴DE ＝AE 2－AD 2＝42－22＝2 3， ∴EC ＝DC －DE ＝4－2 3. (2)由DA ＝2，DE ＝2 3，得tan ∠DAE ＝2 32＝3，∴∠DAE ＝60°.∴S 阴影＝S 扇形EAF －S △ADE ＝60×π×42360－12×2×2 3＝83π－2 3.17．解：根据题意，得AC 1＝AB ＝4，所以AC 2＝AB 1＝2 2， 所以AC 3＝AB 2＝2，所以AB 3＝2，所以阴影部分的面积S 3＝45π×22360－12×2×2＝π2－1.。

弧长及扇形的面积（2）附答案一、请准确填空(每小题3分，共24分)1.两个同心圆的半径差为5，其中一个圆的周长为15π，则另一个圆的周长为_____.2.已知a 、b 、c 分别是正六边形的一边、最短对角线和最长对角线，则a ∶b ∶c 为_____.3.已知Rt △ABC ，斜边AB =13 cm ，以直线BC 为轴旋转一周，得到一个侧面积为65π cm 2的圆锥，则这个圆锥的高等于_____.4.已知在同一平面内圆锥两母线在顶点最大的夹角为60°，母线长为8，则圆锥的侧面积为_____.5.已知圆柱的底面半径长和母线长是方程4x 2－11x +2=0的两个根，则该圆柱的侧面展开图的面积是_____.6.圆内接正方形的一边切下的一部分的面积等于2π－4，则正方形的边长是_____，这个正方形的内切圆半径是_____.7.要制造一个圆锥形的烟囱帽，如图1，使底面半径r 与母线l 的比r ∶l =3∶4，那么在剪扇形铁皮时，圆心角应取_____.8.将一根长24 cm 的筷子，置于底面直径为5 cm ，高为12 cm 的圆柱形水杯中(如图2).设筷子露在杯子外面的长为h cm ，则h 的取值范围是_____.图1 图2二、相信你的选择(每小题3分，共24分)9.已知正三角形的边长为a ，其内切圆的半径为r ，外接圆的半径为R ，则r ∶a ∶R 等于A.1∶23∶2B.1∶2∶23C.1∶2∶3D.1∶3∶210.如图3，△ABC 是正三角形，曲线ABCDEF …叫做“正三角形的渐开线”，其中、 、 、…圆心依次按A 、B 、C 循环，它们依次相连接，如果AB =1，那么曲线CDEF 的长是 A.8π B.6π C.4π D.2π11.如图4，一扇形纸扇完全打开后，外侧两竹条AB 、AC 的夹角为120°，AB 长为30 cm ，贴纸部分BD 长为20 cm ，贴纸部分的面积为A.800π cm 2B.500π cm 2 C .3800π cm 2D.3500π cm 2DEEF12.已知如图5，两同心圆中大圆的半径OA 、OB 交小圆于C 、D ，OC ∶CA =3∶2，则和的长度比为A.1∶1B.3∶2C.3∶ 5D.9∶2513.如图6，AB 为半圆O 的直径，C 是半圆上一点，且∠COA =60°，设扇形AOC 、△COB 、弓形BmC 的面积为S 1、S 2、S 3，则它们之间的关系是A.S 1<S 2<S 3B.S 2<S 1<S 3C.S 1<S 3<S 2D.S 3<S 2<S 1A BCDEFACD BO图3 图4 图5图614.如图7中，正方形的边长都相等，其中阴影部分面积相等的有(1)(2) (3)(4)图7A.(1)(2)(3)B.(2)(3)(4)C.(1)(3)(4)D.(1)(2)(3)(4)15.如果圆锥的母线长为5 cm ，底面半径为3 cm ，那么圆锥的表面积为 A.39π cm 2 B.30π cm 2 C.24π cm 2 D.15π cm 216.一个圆台形物体的上底面积是下底面积的41.如图8，放在桌面上，对桌面的压强是200 帕，翻过来放，对桌面的压强是A.50帕B.80帕C.600帕 D .800帕图8三、考查你的基本功(共14分)17.(6分)如图9，圆锥底面半径为r ，母线长为3r ，底面圆周上有一蚂蚁位于A 点，它从A 点出发沿圆锥面爬行一周后又回到原出发点，请你给它指出一条爬行最短的路径，并求出最短路径.AABC DOEF图9图1018.(8分)如图10，等腰Rt △ABC 中斜边AB =4，O 是AB 的中点，以O 为圆心的半圆分别与两腰相切于点D 、E ，图中阴影部分的面积是多少？请你把它求出来.(结果用π表示)四、生活中的数学(共18分)19.(8分)铅球比赛要求运动员在一固定圆圈内投掷，推出的铅球必须落在40°角的扇形区域内(以投掷圈的中心为圆心).如果运动员最多可投7 m ，那么这一比赛的安全区域的面积至少应是多少？(结果精确到0.1 m 2)20.(10分)如图11，有一直径是1 m 的圆形铁皮，要从中剪出一个最大的圆心角是90°的扇形CAB .(1)被剪掉的阴影部分的面积是多少？(2)若用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？(结果可用根号表示)A BO图11图12图13五、探究拓展与应用(共20分)21.(10分)现有总长为8 m 的建筑材料，用这些建筑材料围成一个扇形的花坛(如图12)，当这个扇形的半径为多少时，可以使这个扇形花坛的面积最大？并求最大面积.22.(10分)如图13，正三角形ABC 的中心恰好为扇形ODE 的圆心，且点B 在扇形内，要使扇形ODE 绕点O 无论怎样转动，△ABC 与扇形重叠部分的面积总等于△ABC 的面积的31，扇形的圆心角应为多少度？说明你的理由.参考答案一、1.5π或25π 2.1∶3∶2 3.12 cm 4.32π 5.π 6.4 22 7.270° 8.11≤h ≤12二、9.A 10.C 11.C 12.C 13.B 14.C 15.C 16.D三、17.解：把圆锥沿过点A 的母线展成如图所示扇形，则蚂蚁运动的最短路程为AA ′(线段).由此知：OA =OA ′=3r , 的长为2πr .∴2πr =1803rn ⋅π, n =120°,即∠AOA ′=120°, ∠OAC =30°.∴r OA OC 2321==.∴r CO OA AC 32322=-=. ∴AA ′=2AC =33r ,即蚂蚁运动的最短路程是33r . 18.解：AC =AB cos45°=22，连接OE . ∴OE ⊥BC , OE ∥AC .又OA =OB ，则OE =BE =EC =21AC =2, S 阴影=2(S △OBE －S 扇形OEF )=2－2π.四、19.解：S 扇形=3607402⨯⨯π≈17.2 m 2.20.(1)连接AB ，则AB 为⊙O 直径.∴S 阴影=S ⊙O －S 扇形ABC =π·(21)2－41π·8)22(2π=(cm 2).(2)设所剪成圆锥的底面圆的半径为r ,则2πr =1802290⋅π, ∴r =82(m).五、21.解：设扇形的半径为r ，∠AOB 的度数为n ，扇形花坛面积为S ，则扇形花坛周长为2r +π2n ·2πr =8, ①AOC A'S =π2nπr 2. ② 由①得：rrr r n πππ-=-=42282. ③ 将③代入②得：S =rrπ-4·πr 2=4r －r 2=－(r －2)2+4.故当r =2时，S 最大=4,即当扇形半径为2 m 时，花坛面积最大，其最大面积为4 m 2.22.当扇形的圆心角为120°时，△ABC 与扇形重合部分的面积为△ABC 面积的31，无论绕点O 怎样旋转，重合部分都等于△OAB 的面积.连接OB 、OC ，∴S △OBC =31S △ABC .∵∠BOC =120°，∠OBC =∠OCB =30°. 当∠DOE =120°时,扇形ODE 的两条半径OD 、OE 分别与OB 、OC 重合时，重合部分的面积为S △OBC .当OD 、OE 不与OB 、OC 重合时，设OD 交AB 于点G ，OE 交BC 于点H , 则∠BOG =∠COH ，OB =OC , ∠OBG =∠OCH =30°. ∴△OBG ≌△OCH .∴S △OBG +S △OBH =S △OCH +S △OBH ,即S 四边形OGBH =S △OBC =31S △ABC .16.如图是一管道的横截面示意图,某工厂想测量管道横截面的面积,工人师傅使钢尺与管道内圆相切并与外圆交于A 、B 两点,测量结果为AB=30cm, 求管道阴影部分的面积.BA17.一服装厂里有大量形状为等腰直角三角形的边角布料,如图所示,现找出其中一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形, 做成形状不同的玩具,使扇形的边缘半径恰好都在△ABC 的边上,且扇形的弧与△ABC 的其他边相切, 请设计出所有可能符合题意的方案示意图,并直接写出扇形的半径.C BA18.如图,正△ABC 的边长为1cm,将线段AC 绕点A 顺时针旋转120 °至AP 1, 形成扇形D 1;将线段BP 1绕点B 顺时针旋转120°至BP 2,形成扇形D 2;将线段CP 2绕点C 顺时针旋转120°至CP 3,形成扇形D 3;将线段AP 3绕点A 顺时针旋转120°至AP 4,形成扇形D 4,……设n l 为扇形n D 的弧长(n=1,2,3…),回答下列问题: (1)按要求填表:n1 2 3 4 n l(2)根据上表所反映的规律,试估计n 至少为何值时,扉形n D 的弧长能绕地球赤道一周?(设地球赤道半径为6400km)D 4D 3D 2D 1P 4P 3P 2P 1CBA16.设切点为C,圆心为O,连接OC,则OC ⊥AB,故AC=BC=15,连接OA,则OA 2-OC 2=AC 2=152=225,故S 阴影=2222()225AO CO AO CO ππππ-=-=g gcm 2. 17.如图所示.r=22CBAr=4CBAr=42-4OCBAr=2OCBA18.(1)依次填2468,,,3333ππππ.(2)根据表可发现: 23n l n π=g ,考虑 2264001000003n ππ≥⨯g g ,得n ≥1.92×109,∴n 至少应为1.92×109.。

39弧长及扇形的面积（一）一、选择题1．在半径为12 c 的圆中，150°的圆心角所对的弧长等于 ( ) A ．34πc B ．12πc C ．10πc D ．5π c2．一个扇形的弧长为20π c ，面积为240πc 2，则这个扇形的圆心角是 ( ) A ．120° B ．150° C ．210° D ．240°3． （2014•辽宁本溪，第7题3分）底面半径为4，高为3的圆锥的侧面积是（ ） A ． 12πB ． 15πC ． 20πD ． 36π4．（2014•内蒙古包头，第9题3分）如图，在正方形ABCD 中，对角线BD 的长为．若将BD 绕点B 旋转后，点D 落在BC 延长线上的点D′处，点D 经过的路径为，则图中阴影部分的面积是（ ）A﹣1 B﹣2 C﹣1 D π﹣25．如图3－147所示，图中有五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度爬行，甲虫沿1ADA ，12A EA ，23A FA ，3A GB 的路线爬行，乙虫沿ACB 的路线爬行，则下列结论正确的是 ( )A ．甲虫先到B 点 B ．乙虫先到B 点C ．甲、乙两虫同时到B 点D ．无法确定6（2014•甘肃天水，第10题4分）如图，是某公园的一角，∠AOB=90°，的半径OA 长是6米，点C 是OA 的中点，点D 在上，CD∥OB，则图中草坪区（阴影部分）的面积是（ ）A．（3π+）米B．（π+）米C．（3π+9）米D．（π﹣9）米二、填空题7．如图3－148所示，四边形OABC为菱形，点B，C在以点O为圆心的EF上．若OA＝3，∠OCB＝60°，∠1＝∠2，则扇形OEF的面积为．8．如图3－149所示，⊙A，⊙B，⊙C，⊙D，⊙E相互外离，它们的半径都为1，顺次连接五个圆心得到五边形ABCDE，则图中五个阴影部分的面积之和是．9．一个扇形的圆心角为30°，半径为12 c，则这个扇形的面积为．10．若一扇形的弧长是12π，圆心角是120°，则这个扇形的半径是．11．如图3－150所示，AB是半圆O的直径，以O为圆心，OE为半径的半圆交AB于E，F两点，弦AC切小半圆于点D．已知AO＝4，EO＝2，那么阴影部分的面积是．12 （2014•福建三明，第14题4分）如图，AB是⊙O的直径，分别以OA，OB为直径作半圆．若AB=4，则阴影部分的面积是．13 （2014•吉林，第14题3分）如图，将半径为3的圆形纸片，按下列顺序折叠．若和都经过圆心O，则阴影部分的面积是（结果保留π）三、解答题：14．如图3－151所示，在Rt△ABC中，∠BAC＝90°，AC＝AB＝2，以AB为直径的圆交BC于点D，求图中阴影部分的面积．15．（2014•辽宁本溪，第22题12分）如图，已知在R△ABC中，∠B=30°，∠ACB=90°，延长CA到O，使AO=AC，以O为圆心，OA长为半径作⊙O交BA延长线于点D，连接CD．（1）求证：CD是⊙O的切线；（2）若AB=4，求图中阴影部分的面积．参考答案1．C[提示：15012180π⨯＝10π(c)．]2．B[提示：先利用S ＝12lR ，求出R ＝24，再利用180n R l π=，求出n 即可．] 3C 4C5．C[提示：各小半圆弧长之和等于大半圆弧长．] 6A73π[提示：求扇形面积的关键是找半径和圆心角，现在半径OE ＝OC ＝OA ＝3．∵∠1＝∠2，∴∠EOF ＝∠AOC ＝∠180°－∠OCB ＝120°，∴S 扇形OEF ＝221203360360n r ππ⨯=＝3π．故填3π．］8．32π［提示：2(52)180313602ππ-=．］ 9．12π c 2[提示：23012360π⨯．＝12π(c 2)．]10．18［提示：120180·πr ＝12π，解得r ＝18．] 11．4233π+[提示：连接DO ，OC ，OC 交DF 于点G ，易证∠OAD ＝30°，则∠DOC ＝∠AOD ＝∠COB ＝60°，通过面积分割，可求得S 阴影＝S △ODC ＋S 扇形OCB －2S 扇ODG ＝4233π+．]122π 133π14．解：连接OD ，则OB ＝OD ＝12AB ＝1．∵AB ＝AC ，∠BAC ＝90°，∴∠B ＝45°．∵OD ＝OB ，∴∠BDO ＝45°，∴∠BOD ＝90°，∴S 阴影＝(S扇形OBD－S △OBD )＋(S梯形OACD－S扇形OAD)＝2901360π⨯－12×1×1＋12×(1＋2)×1－2901360π⨯＝1． 15．（1）证明：连接OD ， ∵∠BCA=90°，∠B=30°， ∴∠OAD=∠BAAC=60°， ∵OD=OA ，∴△OAD 是等边三角形， ∴AD=OA=AC，∠ODA=∠O=60°， ∴∠ADC=∠ACD=∠OAD=30°，∴∠ODC=60°+30°=90°，即OD⊥DC，∵OD为半径，∴CD是⊙O的切线；（2）解：∵AB=4，∠ACB=90°，∠B=30°，∴OD=OA=AC=AB=2，由勾股定理得：CD===2，∴S阴影=S△ODC﹣S扇形AOD=×2×2﹣=2﹣π．【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

弧长及扇形的面积1. (2017·黑龙江齐齐哈尔中考)一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图对应的扇形的圆心角是（）A．120° B．180° C．240° D．300°5．(2017·湖北十堰中考)如图，已知圆柱的底面直径BC＝6π，高AB＝3，小虫在圆柱表面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为（）A．3 2 B．3 5 C．6 5 D．6 23. 如图，已知□ABCD的对角线BD=4cm，将▱ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（）A．4π cm B．3π cm C．2π cm D．π cm4.如图1，水平地面上有一面积为30π平方厘米的灰色扇形OAB，其中OA的长度为6厘米，且与地面垂直．若在没有滑动的情况下，将图1的扇形向右滚动至OB垂直地面为止，如图2所示，则O点移动（）厘米．A．20 B．24 C．10π D．30π5.如图，点A、B、C都在⊙O上，⊙O的半径为2，∠ACB=30°，则的长是（）A．2π B．π C．23π D．13π6、如图，等边三角形ABC中，将边AC逐渐变成以BA为半径的AB，其他两边的长度不变，则∠ABC的度数大小由60变为（）A.180πB.120πC.90πD.60π7.如图，△ABC是等边三角形，AC=6，以点A为圆心，AB长为半径画弧DE，若∠1=∠2，则弧DE的长为（）A．1π B．1.5π C．2π D．3π8.在一个直径为6cm的圆中，小明画了一个圆心角为120°的扇形，则这个扇形的面积为（）A．πcm2 B．2πcm2 C．3πcm2 D．6πcm29.如图，梯形ABCD中，AD∥BC，∠C=90°，AB=AD=4，BC=6，以A为圆心在梯形内画出一个最大的扇形（图中阴影部分）的面积是（）A．π B．3π C．2π D．4π10.如图，四边形OCBA是菱形，点A、B在以点O为圆心的圆弧DE上，若AO=3，∠COE=∠DOA，则扇形ODE的面积为（）A．23π B．2π C．2.5 π D．3π11.已知一个半径为6的扇形面积是4π，则这个扇形的圆心角是（）A．30° B．40° C．45° D．60°12.如图，已知扇形AOB的半径为2，圆心角为90°，连接AB，则图中阴影部分的面积是（）A．π-2 B．π-4 C．4π-2 D．4π-413.如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC ，已知圆锥的高h 为12 cm ，OA ＝13 cm ，则扇形AOC 中AC ︵的长是__________cm .(结果保留π)14.已知扇形的圆心角为120°，弧长为2π，则它的半径为 . 15、如图，正六边形ABCDEF 内接于⊙O，⊙O 的半径为1，则AB 的长为16.如图，⊙A、⊙B、⊙C 两两不相交，且它们的半径都是2，图中三个阴影部分的面积之和是17.如图，在⊙O 中，半径OA⊥OB，过点OA 的中点C 作FD∥OB 交⊙O 于D ，F 两点，且CD ＝3，以O 为圆心，OC 为半径作CE ︵，交OB 于E 点．(1)求⊙O的半径OA的长；(2)计算阴影部分的面积．18.如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD．（1）求证：四边形ABCD是等腰梯形；（2）已知AC=6，求阴影部分的面积．参考答案1.答案：A2.答案：D3. 答案：C4.答案：C解析：解答：点O移动的距离为扇形的弧长，根据面积公式求出弧长，即30π=×l×6，解得l=10π．故选C．分析：点O移动的距离为扇形的弧长，根据弧长公式计算即可．5.答案：C解析：解答：∵∠ACB=30°，∴∠AOB=60°，∵OA=2，∴60221801803n rABπππ´===故选：C．分析：根据圆周角定理可得出∠AOB=60°，再根据弧长公式的计算即可．6、答案：A7.答案：C故选C．分析：先由等边三角形的性质得出AB=AC=6，∠CAB=60°．再由∠1=∠2得到∠CAB=∠DAE=60°，然后根据弧长公式解答即可．8.答案：C9.答案：D形的问题来解决．10.答案：D11.答案：B解得n=40；∴这个扇形的圆心角为40°． 故选B分析： 根据扇形的面积根据进行计算即可． 12.答案：A13.答案：10π 14. 答案：3解析：解答：∵l=180n Rπ ， ∴R=1802120ππ´=3．分析：根据弧长公式代入求解即可．15、答案：3π解析：解答：∵ABCDEF 为正六边形，∴∠AOB=360°÷ 6 =60°，AB 的长为601803ππ´=． 故答案为：3π．分析： 求出圆心角∠AOB 的度数，再利用弧长公式解答即可．16.答案：2π解析：解答： S 阴影 =1804360π´=2π．故答案是：2π．分析：由于三角形的内角和为180度，所以三个阴影扇形的圆心角的和为180°，由于它们的半径都为2，因此可根据扇形的面积公式直接求出三个扇形的面积和．17.解：(1)如图，连结OD.∵OA⊥OB，∴∠AOB＝90°.∵CD∥OB，∴∠OCD＝90°.在Rt△OCD 中，∵C 是AO 中点，CD ＝3，∴OD＝2CO.设OC ＝x ，∴x 2＋(3)2＝(2x)2，∴x＝1，∴OD＝2，∴⊙O 的半径为2.(2)∵sin∠CDO＝CO OD ＝12， ∴∠CDO＝30°.∵FD∥OB，∴∠DOB＝∠ODC＝30°，∴S 阴影＝S △CDO ＋S 扇形OBD －S 扇形OCE＝π3＋32－π4＝32＋π12.18..答案：(1)略；(2) 4π解析：解答： （1）证明：∵∠BAD=120°，AB=AD ，∴∠ABD=∠ADB=30°，∴弧AB 和弧AD 的度数都等于60°，又∵BC 是直径，∴弧CD 的度数也是60°，∴AB=CD 且∠CAD=∠ACB=30°，∴BC∥AD，∴四边形ABCD 是等腰梯形；（2）解：∵BC 是直径，∴∠BAC=90°∵∠ACB=30°，AC=6，∴BC=30°cos AC =4 ，故R=2 ，∵弧AB 和弧AD 的度数都等于60°，∴∠BOD=120°，连接OA 交BD 于点E ，则OA⊥BD，在Rt△BOE中：OE=OBsin30°= ，BE=OB•cos30°=3，BD=2BE=6，故S 阴影=S 扇形BOD -S △BOD=212013602 创-(π分析：（1）根据题意得出AB=CD 且∠CAD=∠ACB=30°，进而得出BC∥AD，即可得出答案；（2）利用S 阴影=S 扇形BOD -S △B OD ，进而求出即可．。