SPC理论基础知识

统计过程控制（S P C）培训资料一、什么叫SPCSPC即统计过程控制（Statistical Process Control），是一种统计分析工具，主要通过对过程数据的分析来对生产过程进行实时监控，区分出生产过程中产品质量的随机波动与异常波动，从而对生产过程的异常趋势提出预警，以便管理人员及时采取措施，消除异常，恢复过程的稳定，从而达到提高和控制质量的目的。

二、什么情况下要做SPC1.客户要求的关键特性2.内部确定的关键特性三、做SPC的前提1.过程数据易于采集2.过程处于受控状态四、SPC的理论知识变差1.变差的概念没有两件产品或者特性是彻底相同的，因为任何过程都存在许多引起变差的原因。

产品间的差距也许很大，也许小得无法测量，但这些差距总是存在。

例如一个冲压零件的尺寸易于受机器的稳定性、模具的磨损、材料的硬度、操作人员的操作方法、维修（润滑、零件的更换）及环境的影响. 产品间的差异即为变差。

2.变差的普通原因及特殊原因普通原因变差是向来在过程中浮现的变差(如模具的磨损、温度的变化等),过程惟独此类变差时,就认为过程是稳定的和可预测的, 我们称之为：“处于受控状态”。

---此类变差通常与管理者有关，通常采取系统措施来解决。

---此类变差是必然存在的，只能改善或者降低，不能彻底被消除。

特殊原因变差是由异常或者外部事件的影响产生的，在普通原因变差之外（如材料用错,操作方法错误等），当过程存在此类变差时，过程是不稳定的或者不受控的。

---此类变差通常是与该过程操作人员有关，通常采取局部措施来解决。

---此类变差是可以被消除的正态分布一种用于计量型数据的、连续的、对称的频率分布，它是计量型数据用控制图的基础。

，当一组测量数据服从正态分布时，有大约正态分布的两个参数：平均值U和标准差68.26%的测量值落在平均值处正负一个标准差的区间内,大约95.44%的测量值将落在平均值处于正负两个标准差的区间内;大约99.73%的值将落在平均值处正负三个标准偏差的区间内,超出三个标准差的惟独0.27%（如图一：正态分布图）。

spc质量管理SPC (Statistical Process Control)是指统计过程控制，是一种在生产过程中使用统计方法来监测和控制制造产品质量的方式。

SPC与传统的控制方法不同，它通过对过程数据的分析，使生产过程更可控，从而达到提高产品质量、减少浪费和成本的目的。

下面我们将就SPC的原理和方法以及在质量管理中的应用做详细介绍。

一、SPC理论基础1、过程变异在任何时刻，一种生产过程的输出不能百分百相同。

这种不同可以由多种因素产生，包括异常的原材料、工艺变更、机器磨损、操作者错误等等。

导致输出中变异的因素称为特殊因素，也称为系统性因素。

这种特殊因素变异是造成过程差异的主要原因。

2、常规变异除了特殊因素外，生产过程的输出也有常规变异。

常规变异是指，即使没有特殊因素，也会有一些小的差异在过程输出中出现。

常规变异主要由不可避免的自然因素或生产设备的某些功能限制引起。

3、SPC方法SPC方法的核心是确定过程总体的变异范围，并确定过程中的差异是否在可接受的范围内。

在某些情况下，它可以通过实施统计控制来消除这种变异。

SPC方法可以有效地降低过程差异，提高产品质量，减少成本，增加可靠性，提高客户满意度。

二、SPC的应用范围SPC方法可以应用于所有类型的制造过程，包括离散、连续、传统目视检验和自动化检验。

以下是SPC可以处理生产过程的举例：•\t安装对象的物理特性：例如长度、宽度、高度、重量、颜色、性质等。

•\t材料特性：例如硬度、强度、韧性、导电性等。

•\t流体特性：例如温度、压力、流量、粘度等。

•\t机器特性：例如速度、功率、电流、温度、气压等。

•\t操作员特性：例如工作时间、工作速度、操作标准等。

三、SPC的主要原理SPC的主要原理是基于过程变异性的持续监测和控制，包括以下步骤：1、控制图建立控制图以时间为横轴，测量数据为纵轴。

每次收集数据时，都将点绘制到控制图上。

然后通过绘制中心线、上界和下界来确定控制限。

SPC培训讲义—基础知识简介SPC（Statistical Process Control，统计过程控制）是一种基于统计方法的质量管理工具，旨在通过对过程数据的统计分析，帮助组织识别和解决可能导致质量问题的根本原因，从而提高产品的稳定性和可靠性。

本讲义将介绍SPC的基础知识，包括SPC的原理、常用的SPC 工具和应用案例等内容。

1. SPC的原理SPC的核心原理是基于过程数据的统计分析，通过对数据的收集和分析，识别和排除可能导致质量问题的特殊原因，同时通过控制图的使用，监控和改进过程的稳定性和可靠性。

1.1 正态分布在SPC中，数据的正态分布是一个重要的假设。

正态分布是一种对称的概率分布，其特点是均值和标准差能够完全描述分布的情况。

正态分布的图形呈钟形曲线，均值位于曲线的中央。

在实际应用中，SPC 通常假设数据是近似正态分布的，以方便进行统计分析。

1.2 变异性与稳定性在质量管理中，变异性是指同一过程在不同时间或不同条件下相同测量项的数值差异。

通过SPC的应用，可以发现原本被认为是随机变动的过程，实际上可能存在特殊原因造成的异常波动。

稳定性是指过程在一段时间内的变异性较小，并且符合预期的性能要求。

通过SPC 的控制图，可以监控过程的稳定性，并及时采取措施防止不稳定状态的出现。

2. 常用的SPC工具SPC工具是SPC实施过程中使用的具体方法和技术，下面介绍几种常用的SPC工具。

2.1 控制图控制图是SPC中最常用的一种工具，它用来监控过程在一段时间内的变异情况。

控制图是一种统计图表，将过程数据按时间顺序绘制在图表上，同时画出上下限和中心线。

如果过程数据处于控制限之内，说明过程处于稳定状态；如果过程数据超过控制限，说明过程发生了特殊原因的变异，需要进行分析和改进。

2.2 直方图直方图是一种用柱形表示数据分布的图表，它可以直观地展示数据的中心趋势、波动幅度以及偏态情况。

通过直方图，可以判断数据是否符合正态分布，如果数据呈现钟形分布，则可以认为数据符合正态分布的假设。

SPC基础知识及常用计算方法SPC基础知识一、SPC定义：1、SPC——统计制程管制：是指一套自制程中去搜集资料，并加以统计分析，从分析中去发气掘制程的异常，立即采取修正行动，使制程恢复正常的方法。

也就是说：品质不应再依赖进料及出货的抽样检验，而应该采取在生产过程中，认良好的管理方法，未获得良好的品质。

2、良好品质，必须做到下面几点：①变异性低②耐用度③吸引力④合理的价格3、变异的来源：大概来自5个方面：①机器②材料③方法④环境⑤作业人员应先从机器，材料方法，环境找变异，最后考虑人。

4、SPC不是一个观念，而是要行动的步骤一、确立制程流程——首先制程程序要明确，依据制程程序给制造流程图，并依据流程图订定工程品质管理表。

步骤二、决定管制项目——如果把所有对品质有影响的项目不论大小，轻重缓急一律列入或把客户不很重视的特性一并管制时，徒增管制成本浪费资料且得不赏失，反之如果重要的项目未加以管制时，则不能满足设计者，后工程及客户的需求，则先去管制的意义。

步骤三、实施标准化——欲求制程管制首先即得要求制程安定，例如：在风浪很大的船上比赛乒乓球，试部能否确定谁技高一筹，帮制程作业的安定是最重要的先决条件，所以对于制程上影响产品口质的重要原因，应先建立作业标准，并透过教育训练使作业能经标准进行。

步骤四、制程能力调查——为了设计、生产、销售客户满意且愿意购买的产品，制造该产品的制程能力务必符合客户的要求。

因此制程的能力不足时，必顺进行制程能力的改善，而且在制程能力充足后还必须能继续，所以在品质管理的系统中制程能力的掌握很重要。

步骤五、管制图运用——SPC的一个基本工具就是管制图，而管制图又分计量值管制图与计数值管制图。

步骤六、问题分析解决——制程能力调查与管制图是可筛提供问题的原因系由遇原因或非机遇原因所造成，但无法告知你确切的原因为何及如何解决决问题？解决问题？而问题的解决技巧，在于依据事实找出造成变异的确切原因，并提此对策加以改善，及如何防止再发生。

广州今朝科技有限公司SPC基础知识一SPC术语录1.控制图：SPC的核心工具。

一种标绘着根据相继抽取的样本或子组的某一统计量的值、并画有控制限的图，用于评估或检查一个过程是否处于控制状态之下。

画在坐标系中，横轴表示时间或样本号，纵轴表示数值大小，将采集到的数据以点的形式表示在图中。

2.运行图：一种代表过程特性的简单图形，上面描有一些从过程中收集到的统计数据（通常是单值）和一条中心线（通常是测量值的中位数），可用来进行链分析。

3.排列图：一种用于解决问题的简单工具，按照对成本或变差的影响程度对各种潜在的有问题区域或变差源进行排序。

一般情况下，大多数的成本（或变差）是由于少量原因造成的，所以解决问题的精力最好是首先集中在少量关键的原因上，而暂时忽视多数不重要的原因。

4.散点图（相关图）：把两个变量标在横轴与纵轴上，按照一一对应测量值点描绘成的图。

5.计量值：当质量特性值可以取给定范围内的任何一个可能的数值时，这样的质量特性值称为计量值。

6.计数值：当质量特性值只能取一组特定的数值,而不能取这些数值之间的数值时,称之为计数值。

7.过程：过程是指将输入转换成输出的一系列活8.9.10.628052366666611.动的总和。

12.样本：取自总体中的一个或多个个体，用于提供关于总体的信息，并作为可能做出对总体（或产生总体的过程）的某种判定的基础（引自GB3358-82）。

样本中所包含的样本单位数，称为样本大小。

13.样本容量（子组大小）：在抽检中抽出来的样本单位数。

14.不良品：指整件物品作为一个整体考虑而未满人意或不能接受。

一件不良品可能具有若干相同的或不相同的缺陷。

15.不良率控制图：即P图，用于控制对象的不合格率。

16.不良品数控制图：即Pn图，是一种计数值控制图，用于控制对象为不合格品数的场合。

）17.采集规划：采集规划指从某过程中选择质量特征值进行数据采集的一种工具。

18.单位缺陷数（U）控制图：是一种计数值控制图，它通过周期性抽取样本以统计单位产品的缺陷率并在控制图上绘制点来监控过程变化，样本的检测结果为平均每个样品包含的缺陷数。

SPC 基础知识一、基本概念：1、极差：测定值中最大值Xmax与最小值Xmin之差称为极差，用R表示：R=X max-X min2、平方和：各个测定值与平均值之差称为偏差。

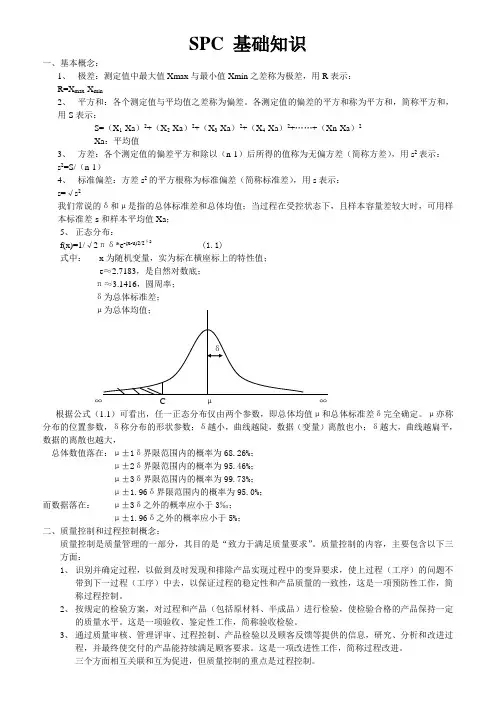
各测定值的偏差的平方和称为平方和，简称平方和，用S表示：S=（X1-Xa）2+（X2-Xa）2+（X3-Xa）2+（X4-Xa）2+……+（Xn-Xa）2Xa：平均值3、方差：各个测定值的偏差平方和除以（n-1）后所得的值称为无偏方差（简称方差），用s2表示：s2=S/（n-1）4、标准偏差：方差s2的平方根称为标准偏差（简称标准差），用s表示：s=√s2我们常说的δ和μ是指的总体标准差和总体均值；当过程在受控状态下，且样本容量差较大时，可用样本标准差s和样本平均值Xa；5、正态分布：f(x)=1/√2πδ*e-(x-u)2/2δ2 (1.1)式中：x为随机变量，实为标在横座标上的特性值；e≈2.7183，是自然对数底；π≈3.1416，圆周率；δ为总体标准差；μ-根据公式（1.1）可看出，任一正态分布仅由两个参数，即总体均值μ和总体标准差δ完全确定。

μ亦称分布的位置参数，δ称分布的形状参数；δ越小，曲线越陡，数据（变量）离散也小；δ越大，曲线越扁平，数据的离散也越大，总体数值落在：μ±1δ界限范围内的概率为68.26%；μ±2δ界限范围内的概率为95.46%；μ±3δ界限范围内的概率为99.73%；μ±1.96δ界限范围内的概率为95.0%；而数据落在：μ±3δ之外的概率应小于3‟；μ±1.96δ之外的概率应小于5%；二、质量控制和过程控制概念：质量控制是质量管理的一部分，其目的是“致力于满足质量要求”。

质量控制的内容，主要包含以下三方面：1、识别并确定过程，以做到及时发现和排除产品实现过程中的变异要求，使上过程（工序）的问题不带到下一过程（工序）中去，以保证过程的稳定性和产品质量的一致性，这是一项预防性工作，简称过程控制。