线性微分方程组的基本理论

第二讲 一阶线性微分方程组的一般概念与一阶线性齐次方程组的一般理论（4课时）一、 目的与要求: 了解一阶线性微分方程组的一般概念与一阶线性齐次方程组的一般理论, 掌握一阶线性齐次方程组的通解结构, 理解基本解矩阵, Wronsky 行列式等概念.二、重点：一阶线性齐次方程组的通解结构, 基本解矩阵, Wronsky 行列式.三、难点：基本解矩阵, Wronsky 行列式.四、教学方法：讲练结合法、启发式与提问式相结合教学法.五、教学手段：传统板书与多媒体课件辅助教学相结合.六、教学过程：1. 一阶线性微分方程组的一般概念如果在一阶微分方程组(3.1)中, 函数12(,,,,)(1,2,,)i n f x y y y i n =, 关于12,,,n y y y 是线性的, 即(3.1)可以写成1111122112211222221122()()()()()()()()()()()()n n n n n n n nn n n dy a x y a x y a x y f x dx dy a x y a x y a x y f x dx dy a x y a x y a x y f x dx ⎧=++++⎪⎪⎪=++++⎪⎨⎪⎪⎪=++++⎪⎩(3.6)则称(3.6)为一阶线性微分方程组. 我们总假设(3.6)的系数()(,1,2,,)ij a x i j n = 及()(1,2,,)i f x i n = 在某个区间I R ⊂ 上连续.为了方便, 可以把(3.6)写成向量形式. 为此, 记111212122212()()()()()()()()()()n n n n nn a x a x a x a x a x a x A x a x a x a x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦及12()()()()n f x f x F x f x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据第13讲的记号, (3.6)就可以写成向量形式()()dY A x Y F x dx=+ (3.7)如果在I 上, ()0F x ≡,方程组(3.7)变成()dY A x Y dx= (3.8)我们把(3.8)称为一阶线性齐次方程组.如果(3.8)与(3.7)中()A x 相同, 则称(3.8)为(3.7)的对应的齐次方程组.与第二章中关于一阶线性微分方程的结果类似, 我们可以证明如下的关于(3.7)的满足初始条件(3.2)′的解的存在与唯一性定理.定理 3.1′ 如果(3.7)中的()A x 及()F x 在区间[],I a b =上连续, 则对于[],a b 上任一0x 以及任意给定的0Y , 方程组(3.7)的满足初始条件(3.2)′的解在[],a b 上存在且唯一.这个定理的证明留给读者完成. 它的结论与定理3.1的不同之处是定理3.1的解的存在区间是局部的，而定理3.1′则指出解在整个区间[],a b 上存在.2. 一阶线性齐次方程组的一般理论⑴一阶线性齐次微分方程组解的性质本节主要研究一阶线性齐次方程组(3.8)的通解结构.为此我们首先从(3.8)的解的性质入手.定理3.2 如果11121212221212()()()()()()(),(),,()()()()m m m n n nm y x y x y x y x y x y x Y x Y x Y x y x y x y x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦是方程组(3.8)的m 个解，则1122m m Y C Y C Y C Y =+++ (3.9)也是(3.8)的解，其中12,,,m C C C 是任意常数.换句话说，线性齐次方程组(3.8)的任何有限个解的线性组合仍为(3.8)的解.证明 因为(1,2,,)i Y i m = 是(3.8)的解，即()()()i i dY x A x Y x dx = (1,2,,)i m =成立. 再由1122[()()()]m m d C Y x C Y x C Y x dx+++ 1212()()()m m dY x dY x dY x C C C dx dx dx=+++ 1122()()()()()()m m C A x Y x C A x Y x C A x Y x =+++ 1122()[()()()]m m A x C Y x C Y x C Y x =+++这就证明了(3.9)是(3.8)的解. 定理3.2告诉我们，一阶线性齐次微分方程组(3.8)的解集合构成了一个线性空间.为了搞清楚这个线性空间的性质，进而得到方程组(3.8)的解的结构，我们引入如下概念.定义3.1 设12(),(),,()m Y x Y x Y x 是m 个定义在区间I 上的n 维向量函数. 如果存在m 个不全为零的常数12,,,m C C C ，使得1122()()()0m m C Y x C Y x C Y x +++= 在区间I 上恒成立, 则称这m 个向量函数在区间I 上线性相关, 否则称它们在区间I 上线性无关.显然，两个向量函数12(),()Y x Y x 的对应分量成比例是它们在区间I 上线性相关的充要条件. 另外, 如果在向量组中有一零向量, 则它们在区间I 上线性相关.若12(),(),,()n Y x Y x Y x 是(3.8)的n 个解, 称下面的矩阵为这个解组对应的矩阵[]12()(),(),,()n x Y x Y x Y x Φ=111212122212()()()()()()()()()n n n n nn y x y x y x y x y x y x y x y x y x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦它的第i 个列向量为()i Y x . 如果这组解是线性无关的, 则称此矩阵为(3.8)的基本解矩阵例1 向量函数它21cos ()1,x Y x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 22sin 1()1x Y x x ⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦在任何区间(a , b )上是线性相关的. 事实上取121C C == 有1122()()0.C Y x C Y x +≡例2 向量函数3313(),x x x e Y x e e ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 6626()2x x x e Y x e e ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦在(-∞,+∞)上线性无关. 事实上，要使得1122()()0,(,)C Y x C Y x x +≡∈-∞+∞成立，或写成纯量形式，有3123123120,20,0,x x x C C e C C e C C e ⎧+=⎪-=⎨⎪+=⎩ (,)x ∈-∞+∞显然, 仅当120C C == 时, 才能使上面三个恒等式同时成立, 即所给向量组在(,)-∞+∞上线性无关.例3 向量函数212()0,x x e Y x e --⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦2220()x x Y x e e --⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦在(,)-∞+∞上线性无关. 事实上，由于1122()()0,(,)C Y x C Y x x +≡∈-∞+∞相当于纯量形式212222120,0,0,x x x x C e C e C e C e ----⎧≡⎪⎪≡⎨⎪--≡⎪⎩ (,)x ∈-∞+∞由此可以看出：仅当120C C ==时，才能使上面三个恒等式同时成立，即所给向量组在(,)-∞+∞上线性无关.例3中两个向量函数的各个对应分量都构成线性相关函数组. 这个例题说明，向量函数组的线性相关性和由它们的分量构成的函数组的线性相关性并不等价.下面介绍n 个n 维向量函数组12(),(),,()n Y x Y x Y x (3.10)在其定义区间I 上线性相关与线性无关的判别准则.我们考察由这些列向量所组成的行列式111212122212()()()()()()()()()()n n n n nn y x y x y x y x y x y x W x y x y x y x =通常把它称为向量组(3.10)的朗斯基(Wronsky)行列式.定理3.3 如果向量组(3.10)在区间I 上线性相关，则它们的朗斯基行列式()W x 在I 上恒等于零.证明 依假设，存在不全为零的常数12,,,n C C C ,使得1122()()()0,n n C Y x C Y x C Y x +++≡x I ∈把上式写成纯量形式, 有111212112122221122()()()0,()()()0,()()()0,n n n n n n n nn C y x C y x C y x C y x C y x C y x C y x C y x C y x +++≡⎧⎪+++≡⎪⎨⎪⎪+++≡⎩ x I ∈这是关于12,,,n C C C 的线性齐次代数方程组，且它对任一x I ∈，都有非零解12,,,n C C C .根据线性代数知识，它的系数行列式W (x )对任一x I ∈都为零.故在I 上有W (x )≡0.证毕.对于一般的向量函数组, 定理3.3的逆定理未必成立. 例如向量函数1(),0x Y x ⎡⎤=⎢⎥⎣⎦ 22()0x Y x ⎡⎤=⎢⎥⎣⎦的朗斯基行列式恒等于零，但它们却是线性无关的.然而，当所讨论的向量函数组是方程组(3.8)的解时，我们有下面的结论.定理3.4 如果12(),(),,()n Y x Y x Y x 是方程组(3.8)的n 个线性无关解，则它们的朗斯基行列式W (x )在I 上恒不为零. 证明(反证法) 如果有0x I ∈使得0()0W x =，考虑线性齐次代数方程组111021201012102220201102200()()()0,()()()0,()()()0,n n n n n n n nn C y x C y x C y x C y x C y x C y x C y x C y x C y x +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩由于系数行列式0()0W x =, 所以它存在非零解21(,,,)T T n C C C C =, 即1102200()()()0n n CY x C Y x C Y x +++=考虑函数 1122()()()()n n Y x CY x C Y x C Y x =+++由定理3.2知函数()Y x 是(3.8)的解，而且它满足初始条件0()0Y x ≡.另一方面，()0Y x ≡也是方程(3.8)的满足初值条件()0Y x =的解. 因此，根据定理3.1′有()0,Y x x I ≡∈即1122()()()0,n n CY x C Y x C Y x +++≡ x I ∈因为11,,,n C C C 不全为零，从而12(),(),,()n Y x Y x Y x 在I上线性相关，这与假设矛盾，定理证毕. 由定理3.3和定理3.4立即得到如下的推论.推论3.1 如果向量组(3.10)的朗斯基行列式W (x )在区间I 上的某一点0x 处不等于零，即0()0W x ≠, 则向量组(3.10)在I 上线性无关.实际上，这个推论是定理3.3的逆否命题.推论3.2 如果方程组(3.8)的n 个解的朗斯基行列式W (x )在其定义区间I 上某一点0x 等于零，即0()0W x =, 则该解组在I 上必线性相关.实际上，这个推论是定理3.4的逆否命题.推论3.3 方程组(3.8)的n 个解在其定义区间I 上线性无关的充要条件是它们的朗斯基行列式W (x )在I 上任一点不为零.条件的充分性由推论3.1立即可以得到． 必要性用反证法及推论3.2证明是显然的．证毕．3. 一阶线性齐次微分方程组解空间的结构．我们把一阶线性齐次方程组(3.8)的n 个线性无关解称为它的基本解组. 显然基本解组对应的矩阵中基本解矩阵.例4 易于验证向量函数11()1,()1tx t e y t -⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦222()1()2t x t e y t -⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 是方程组 ,xy = 2y x y =+的基本解组.定理3.5 方程组(3.8)必存在基本解组.证明 由定理(3.1)′可知，齐次方程组(3.8)必存在分别满足初始条件10200100010(),(),,(),000001n Y x Y x Y x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x I ∈(3.11)的n 个解12(),(),,()n Y x Y x Y x . 由于它们所构成的朗斯基行列式()W x 在0x x = 处有010000100()100001W x ==≠因而，由推论3.3知 12(),(),,()n Y x Y x Y x 是基本解组.满足初始条件(3.11)的基本解组称为方程组(3.8)的标准基本解组. 标准基本解组对应的矩阵称为标准基本解矩阵. 显然, 标准基本解矩阵在0x=时的值为单位阵. 下面我们可以给出齐次方程组(3.8)的基本定理了.定理3.6 如果12(),(),,()n Y x Y x Y x 是齐次方程组(3.8)的基本解组，则其线性组合1122()()()()n n Y x C Y x C Y x C Y x =+++(3.12)是齐次方程组(3.8)的通解,其中12,,,n C C C 为n 个任意常数.证明 我们仅需证明如下两点.首先，由定理3.2，对任意一组常数12,,,n C C C ,(3.12)是齐次方程组(3.8)的解.其次，证明：对于任何满足初始条件(3.2)′的齐次方程组(3.8)的解()Y x ，都可找到常12,,,n C C C ,使得1122()()()()n n Y x C Y x C Y x C Y x =+++为此，作方程组11022000()()()()n n C Y x C Y x C Y x Y x +++=或写成纯量形式11102120101012102220202011022000()()(),()()(),()()(),n n n n n n n nn n C y x C y x C y x y C y x C y x C y x y C y x C y x C y x y +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩(3.13)这是一个线性非齐次代数方程组，它的系数行列式恰是线性无关解12(),(),,()n Y x Y x Y x 的朗斯基行列式()W x 在0x x =处的值，由定理3.4知0()0W x ≠，从而方程组(3.13)有唯一解21(,,,)T T n C C C C =令1122()()()()n n Y x CY x C Y x C Y x =+++显然，()Y x 是(3.8)的一个解，且与()Y x 满足同一个初始条件，由解的唯一性，()()Y x Y x ≡定理得证.推论3.4 线性齐次方程组(3.8)的线性无关解的个数不能多于n 个.实际上，设121(),(),,()n Y x Y x Y x +是(3.8)的任意n +1个解. 现任取其中n 个解，如果它们线性相关，这时易证n +1个解当然也线性相关.如果它们线性无关，从而构成(3.8)的基本解组，由定理3.6，余下的这个解可由基本解组线性表出，这就说明这n +1个解是线性相关的.至此，我们证明了一阶线性齐次微分方程组(3.8)的解的全体构成一个n 维线性空间. 4．刘维尔公式齐次方程组(3.8)的解和其系数之间有下列联系. 定理3.7 如果12(),(),,()n Y x Y x Y x 是齐次方程组(3.8)的n 个解，则这n 个解的朗斯基行列式与方程组(3.8)的系数有如下关系式11220[()()()]0()()xnn x a t a t a t dtW x W x e+++⎰=(3.14)这个关系式称为刘维尔(Liouville)公式.证明 仅证n = 2情形，n 的情形类似．11111222211222()()()()dy a x y a x y dxdy a x y a x y dx⎧=+⎪⎪⎨⎪=+⎪⎩ （3.15）设11121()(),()y x Y x y x ⎡⎤=⎢⎥⎣⎦ 12222()()()y x Y x y x ⎡⎤=⎢⎥⎣⎦是（3.15）的两个解，它们的朗斯基行列式11122122()()()()()y x y x W x y x y x =1112111221222122()()()()()()()()()dy x dy x y x y x dW x dx dx dy x dy x dxy x y x dxdx=+因为12(),()Y x Y x 分别是（3.15）的解，所以有 11111112212121112221()()()()dy a x y a x y dxdy a x y a x y dx⎧=+⎪⎪⎨⎪=+⎪⎩ ,12111212222221122222()()()()dy a x y a x y dx dy a x y a x ydx⎧=+⎪⎪⎨⎪=+⎪⎩分别代入()dW x dx中，然后对每一个行列式进行化简，第一个行列式的第二行乘以12()a x -再与第一行相加，第二个行列式的第一行乘以21()a x -再与第二行相加，具体计算如下1111122111121222111221222111222121122222()()()()()a y a y a y a y y x y x dW x y x y x a y a y a y a y dx++=+++1111111211121122212222212222()()()()()()a y a y y x y x a a W x y x y x a y a y =+=+即1122()[()()]()dW x a x a x W x dx=+11220[()()]()xx a t a t dtW x ce+⎰=或11220[()()]0()()xx a t a t dtW x W x e+⎰=在代数学中，1()nkkk ax =∑称为矩阵()A x 的迹，记作()trA t ，因此刘维尔公式可表为0()0()()xx trA t dtW x W x e⎰=从公式（3.14）可以有显看出，齐次方程组（3.8）的几个解所构成的朗斯基行列式()W x 或者恒为零，或者恒不为零． 本讲要点：1． 一阶线性齐次微分方程组的所有解构成一个线性空间．2． 向量函数组和向量解组相关性判定 向量函数组 向量解组线性相关()0W x ⇒≡ 线性相关()0W x ⇔=线性无关0()0W x ⇐≠ 线性无关()0W x ⇔≠3． 齐次线性方程组通解基本定理解空间是n 维线性空间．4． 刘维尔公式解与系数关系．作业：练习3.3 1., 2., 3.。

线性微分方程组线性微分方程组是一组微分方程，它们具有相同的结构，可以用一般的线性微分方程来解释。

它们是研究动力学系统状态与其变化间重要手段，因此它们在数学、物理、工程、生物学、经济学等许多学科中都有重要应用。

线性微分方程组的基本元素是微分方程，它是用相关变量的变化率进行建模的函数的导数的形式。

用个别微分方程表达的变量可以是实数，但它们也可以是复数。

的变量可以是常数，也可以是连续的函数或定义在某个区域上的函数，甚至可以是多元函数，也可以是某种定义在空间上的函数。

线性微分方程组可以用一个向量表示，一般地，一个微分方程组可以用下面的基本形式表示：$$frac{dx}{dt}=Ax+f(t)$$其中，x是向量，t是时间变量，A是位置矩阵，并且f是一个不同于时间变量的函数。

线性微分方程组的解可以通过常规的数值方法和分析方法来求解。

数值方法的一般意义是，利用计算机程序将线性微分方程组的近似解计算出来。

常见的数值方法包括：*拉法：这种方法将线性微分方程组写成一阶微分方程，然后计算给定初始值时间t的解。

*跃法：这种方法是将线性微分方程组分解成一组一阶差分方程，然后利用差分方程的解计算出线性微分方程组的解。

*步逼近法：这种方法是用一步一步的方法找到线性微分方程组的近似解，它可以给出精确的解，也可以给出一定程度的近似解。

如果确定线性微分方程组的初始条件，则可以用分析方法解决这一问题。

常见的分析方案包括：*可比法：用一组复数幂函数解决线性微分方程组，这些复数幂函数具有一定的关系，并且可以用初始条件计算出相关系数。

*分法：用变分法求解线性微分方程组，它可以形式化地写出线性微分方程组的解，同时也可以求解非线性微分方程组的解。

*征值理论：主要是利用特征值理论求解线性微分方程组，它可以把线性微分方程组分解成一组数学表达式，然后根据表达式的系数来求解线性微分方程组。

线性微分方程组在数学、物理、工程、生物学、经济学等诸多学科中都有重要应用，也可以用于动力学系统的状态变化模拟。

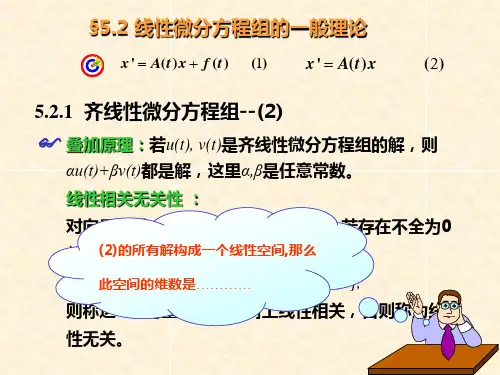
一．线性微分方程组的一般理论1. 线性微分方程组一般形式为：1111122112211222221122()()()(),()()()(), 1 ,()()()(),n n n n nn n nn n n x a t x a t x a t x f t x a t x a t x a t x f t x a t x a t x a t x f t '=++++⎧⎪'=++++⎪⎨⋅⋅⎪⎪'=++++⎩（） 记：111212122212111222()()()()()()()()()()()()(), , ()n n n n nn n n n a t a t a t a t a t a t A t a t a t a t f t x x f t x x f t x x f t x x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦'⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥'⎢⎥⎢⎥⎢⎥'===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦非齐次线性方程组表示为：()() x A t x f t '=+齐次线性方程组表示为：()x A t x '=2.齐次线性方程组的一般理论(1)定理 (叠加原理) 如果12(),(),,()n x t x t x t ⋯是齐次方程组()x A t x '=的k 个解，则它们的线性组合1212()()()n n c x t c x t c x t ++⋯+也是齐次方程组的解，这里12,,,n c c c ⋯是任意常数(2)向量函数线性相关性定义在区间],[b a 上的函数12(),(),,()n x t x t x t ⋯，如果存在不全为零的常数k c c c ,,,21⋯使得1212()()()0n n c x t c x t c x t ++⋯+≡在],[b a 上恒成立，我们称这些向量函数是线性相关的，否则称这些向量函数线性无关。

第三章 线性微分方程线性微分方程是常微分方程理论的重要组成部分，它在自然科学和工程技术方面有着极其广泛的应用，很多实际问题都可以用线性微分方程来处理.在第一章中，我们学习了一阶线性微分方程的处理方法，本章介绍高阶线性微分方程的概念以及常系数线性微分方程的解法.3.1 线性微分方程的一般理论在第一章，我们介绍了一阶线性微分方程)()(x q y x p y =+'的解法，这里介绍n 阶线性微分方程的概念，以及解的存在唯一性定理.首先来研究下面一个实际的例子.例1 弹簧振动设一质量为m 的物体A 悬挂在一上端固定的弹簧的末端（假设弹簧的质量相对于物体A 的质量可以忽略）试求该物体在外力)(t f 作用下的所满足的微分方程.当物体A 不受外力时，重力与弹簧的拉力平衡时的位置选为坐标轴x 的原点O ，向下的方向取为x 轴的正向.设t 时刻，物体A 的位移为)(t x ，速度为)(t v ，加速度为)(t a ，则22)(,)(dtx d t a dt dx t v ==. 由牛顿第二定律知，ma F =，其中m 是物体A 的质量，a 是加速度，F 是合外力.下面对物体A 所受到的力进行分析，由以下几个部分构成.（1）弹簧的拉力1f ，设弹簧的弹性系数为k ，在t 时刻，物体的位移为)(t x ，依据胡克定律知kx f -=1（2）空气的阻力2f ，当速度不太大时，空气的阻力与物体的速度成正比，设比例常数为)0(>μ，因为阻力的方向与速度的方向相反，所以dtdx v f μμ-=-=2 （3）外力)(t f因此，我们得到合外力)(t f dtdx kx F +--=μ 代入ma F =得物体A 所满足的微分方程为)(22t f kx dt dx dtx d m =++μ （3.1） 那么物体A 的运动规律方程)(t x 就是上述微分方程（3.1）的解，如何解该方程是我们本章学习的重点.方程（3.1）和我们第一章中所学的一阶线性微分方程一样，都是线性微分方程，因为方程（3.1）中的导数的最高阶数为2，所以（3.1）是二阶线性微分方程.一般的n 阶线性微分方程具有如下的形式：)0)((),()()()()(01)1(1)(0≠=+'+++--x a x y x a y x a y x a y x a n n n n ϕ因为0)(0≠x a ，所以上式可化为)()()()(1)1(1)(x f y x p y x p y x p y n n n n =+'+++-- （3.2） 其中)()()();,,2,1(,)()()(00x a x x f n i x a x a x p i i ϕ=== 方程（3.2）的初值条件为)1(00)1(0000)(,,)(,)(--='='=n n y x y y x y y x y （3.3） 方程（3.2）在什么条件下存在满足初值条件（3.3）的解呢？有解的话，其解是否唯一？存在区间又是什么呢？为了解决这些问题，我们先给出一般的n 阶方程),,,,()1()(-'=n n y y y x f y满足初值条件)1(00)1(0000)(,,)(,)(--='='=n n y x y y x y y x y 的解的存在唯一性定理.定理3.1 如果函数),,,,()1(-'n y y y x f 在闭区域1)1(0)1(100001,,,,:---+≤-≤'-'≤-≤-n n n n b y y b y y b y y a x x R上满足（1）),,,,()1(-'n y y y x f 在1+n R 上连续；（2）),,,,()1(-'n y y y x f 在1+n R 上关于变量)1(,,,-'n y y y 满足李普希兹条件，即存在正数N ，使得对于任何一对点1)1(222)1(111),,,,(),,,,,(+--∈''n n n R y y y x y y y x ，总有)(),,,,(),,,,()1(2)1(12121)1(222)1(111-----++'-'+-≤'-'n n n n y y y y y y N y y y x f y y y x f 则初值问题⎩⎨⎧='='='=---)1(00)1(0000)1()()(,,)(,)(),,,,(n n n n y x y y x y y x y y y y x f y 在0000h x x h x +≤≤-上存在唯一解)(x y ϕ=. 这里),,,,(max },,,,,min{)1(),,,,(11001)1(-∈'-'==+-n R y y y x n y y y x f M Mb M b M b a h n n . 定理3.1的证明和第二章中的解的存在唯一性定理的证明是相仿的，读者可以模仿定理2.1的证明，完成定理3.1的证明.n 阶线性微分方程（3.2）只是一般的n 解微分方程的一种特殊形式，和一阶线性微分方程类似，有如下的解的存在唯一性定理.定理3.2 如果方程（3.2）的系数),,2,1)((n i x p i =以及右端函数)(x f 在区间],[b a 上有定义而且都连续，则初值问题⎩⎨⎧='='==+'+++----)1(00)1(00001)1(1)()(,,)(,)()()()()(n n n n n n y x yy x y y x y x f y x p y x p y x p y 在],[b a 上存在唯一解)(x y ϕ=.该定理的证明可以利用定理3.1，只要),,2,1)((n i x p i =以及)(x f 在区间],[b a 上连续，则该初值问题就满足了定理3.1的两个条件，从而定理3.2是成立的.如无特别声明，在本章的讨论中，总假定方程（3.2）的系数),,2,1)((n i x p i =以及右端函数)(x f 在区间],[b a 上有定义而且都连续，从而，方程（3.2）满足初值条件（3.3）的解在闭区间],[b a 上存在且唯一.特别地，如果0)(=x f ，则方程（3.2）变为0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n （3.4）方程（3.4）称为n 阶线性齐次微分方程；如果0)(≠x f ，则称方程（3.2）为n 阶线性非齐次微分方程.这时，称方程（3.4）为方程（3.2）所对应的n 阶线性齐次微分方程.3.2 n 阶线性齐次微分方程的一般理论方程（3.4）称为n 阶线性齐次微分方程，对于这类方程应该如何处理呢？我们先研究方程（3.4）的解的性质（1）如果1y 是方程（3.4）的解，则对任意常数C ，1Cy 也是方程（3.4）的解.证明 因为1y 是方程（3.4）的解，所以0)()()(111)1(11)(1=+'+++--y x p y x p y x p y n n n n 从而有))(())(())(()(111)1(11)(1Cy x p Cy x p Cy x p Cy n n n n +'+++--00))()()((111)1(11)(1=⨯=+'+++=--C y x p y x p y x p y C n n n n 因此，1Cy 也是方程（3.4）的解.（2）如果21,y y 是方程（3.4）的解，则21y y +也是方程（3.4）的解.证明 因为21,y y 是方程（3.4）的解，所以0)()()(111)1(11)(1=+'+++--y x p y x p y x p y n n n n 0)()()(221)1(21)(2=+'+++--y x p y x p y x p y n n n n 从而有))(())(())(()(21211)1(211)(21y y x p y y x p y y x p y y n n n n ++'++++++--))(())((])())[(()()(21211)1(2)1(11)(2)(1y y x p y y x p y y x p y y n n n n n n ++'+'+++++=--- ))()()(())()()((221)1(21)(2111)1(11)(1y x p y x p y x p y y x p y x p y x p y n n n n n n n n +'+++++'+++=---- 000=+=因此，21y y +也是方程（3.4）的解.推论 如果n y y y ,,,21 是方程（3.4）的解，则对任意n 个常数n C C C ,,,21 ，线性组合n n y C y C y C +++ 2211也是方程（3.4）的解.该推论可由性质（1）和性质（2）直接推出.并且根据性质（1）和性质（2），我们可以得出，n 阶线性齐次微分方程（3.4）的解构成一个线性空间，称为解的线性空间.例1 易于验证函数x x e x y e x y -==)(,)(21是方程0=-''y y的解，因此，函数x x e C e C x y -+=21)(也是原方程的解.反过来，方程0=-''y y 的通解是不是x x e C e C x y -+=21)(呢？同样地，给出了方程（3.4）的n 个解)(,),(),(21x y x y x y n 后，含有n 个任意常数n C C C ,,,21 的函数)()()()(2211x y C x y C x y C x y n n +++=是否就是线性齐次微分方程的通解呢？为了解决这个问题，我们首先给出函数组的线性相关和线性无关的概念.定义3.1 函数组)(,),(),(21x y x y x y n 在区间I 上有定义，如果其中的某个函数可由其余的1-n 个函数线性表出，则称函数组)(,),(),(21x y x y x y n 在区间I 上是线性相关的.如果任何一个函数都不能由其余的1-n 个函数线性表出，则称函数组)(,),(),(21x y x y x y n 在区间I 上是线性无关的.定理3.3（判定定理）函数组)(,),(),(21x y x y x y n 在区间I 上有定义，如果存在一组不全为零的常数n k k k ,,,21 ，使得0)()()(2211=+++x y k x y k x y k n n则函数组)(,),(),(21x y x y x y n 在区间I 上线性相关.如果只有n k k k ,,,21 全为零时，0)()()(2211=+++x y k x y k x y k n n 才成立，则称函数组)(,),(),(21x y x y x y n 在区间I 上线性无关.证明 如果存在一组不全为零的常数n k k k ,,,21 ，使得0)()()(2211=+++x y k x y k x y k n n不妨假定01≠k ，则)()()(12121x y k k x y k k x y n n ---= 即)(1x y 可由)(,),(2x y x y n 线性表出，因此函数组)(,),(),(21x y x y x y n 在区间I 上线性相关.由线性相关与线性无关的定义，我们可以很容易的得出下面的结论：（1）在函数组)(,),(),(21x y x y x y n 中，如果含有一个零函数，比如0)(=x y i ，则函数组)(,),(),(21x y x y x y n 线性相关.事实上，)(x y i 可由其余1-n 个函数线性表出，即)(0)(0)(0)(0)(00)(1121x y x y x y x y x y x y n i i i ⨯++⨯+⨯++⨯+⨯=+-（2）如果函数组只含有两个函数)(),(21x y x y ，则它们线性相关等价于它们之比)()(21x y x y 为常数. 证明 如果)(),(21x y x y 线性相关，则其中的一个可以由另一个线性表出，不妨设)()(21x y x y →，则存在常数k ，使得)()(21x ky x y =，所以k x y x y =)()(21为常数. 反过来，如果)()(21x y x y 为常数，设k x y x y =)()(21，则)()(21x ky x y =， 即)()(21x y x y →，所以)(),(21x y x y 线性相关.例2 函数组x x e x y e x y -==)(,)(21在任意区间是线性无关的.证明 因为x e x y x y 221)()(=不是常数，所以x x e x y e x y -==)(,)(21线性无关. 例3 函数组x x y x x y x x y 23221sin )(,cos )(,2cos )(===在任意区间上是线性相关的.证明 因为x x x 22sin cos 2cos -=，即)()()(321x y x y x y -=，所以函数组 x x y x x y x x y 23221sin )(,cos )(,2cos )(===线性相关.对于一般的函数组，直接用线性相关和线性无关的定义，或者用定理3.3去判定是非常困难的.比如函数组1)(,cos )(,sin )(321===x y x x y x x y 是线性相关的，还是线性无关的呢？为了解决这个问题，我们下面给出朗斯基（Wronski ）行列式的定义.定义3.2 设函数组)(,),(),(21x y x y x y n 在区间I 上有定义，而且都存在1-n 阶导数，我们称行列式)()()()()()()()()()()1()1(2)1(12121x y x y x y x y x y x y x y x y x y x W n n n n n n ---'''=为函数组)(,),(),(21x y x y x y n 的朗斯基行列式.函数组的朗斯基行列式有如下的性质：定理3.4 函数组)(,),(),(21x y x y x y n 在区间I 上有定义而且线性相关，又对每个),,2,1)((n k x y k =存在1-n 阶导数，则它们的朗斯基行列式恒等于零.证明 因为函数组)(,),(),(21x y x y x y n 线性相关，所以其中的一个函数可由其余1-n 个函数线性表出，不妨设)(x y i 可由其余1-n 个函数线性表出，即存在1-n 个常数n i i k k k k k ,,,,,,1121 +-，使得)()()()()()(11112211x y k x y k x y k x y k x y k x y n n i i i i i ++++++=++--而且有)()()()()()(11112211x y k x y k x y k x y k x y k x y n n i i i i i '++'+'++'+'='++-- …………………………………………………………………………………………)()()()()()()1()1(11)1(11)1(22)1(11)1(x y k x y k x y k x y k x y k x y n nn n i i n i i n n n i --++------++++++= 则在朗斯基行列式)()()()()()()()()()()()()()1()1()1(2)1(12121x y x y x y x y x y x y x y x y x y x y x y x y x W n n n n n i n n i i ----''''=的计算中，第一列乘以1k -，第二列乘以2k -，…，第1-i 列乘以1--i k ，第1+i 列乘以1+-i k ，…，第n 列乘以n k -后，全加至第i 列，则第i 列中的每个元素全为零，所以0)()()(0)()(0)()(0)()()()1()1(2)1(12121='''=---x y x y x y x y x y x y x y x y x y x W n nn n n n推论1 函数组)(,),(),(21x y x y x y n 在区间I 上有定义，而且都存在1-n 阶导数，如果存在某一点I x ∈0，使得0)(0≠x W ，则函数组)(,),(),(21x y x y x y n 线性无关.该推论是定理3.4的逆否命题，所以显然是成立的.例4 函数组1)(,cos )(,sin )(321===x y x x y x x y 在任意区间上是线性无关的.证明 函数组1)(,cos )(,sin )(321===x y x x y x x y 的朗斯基行列式为01cos sin sin cos 0cos sin 0sin cos 1cos sin )(≠-=---=---=x x x x x x x x x x x W 所以函数组1)(,cos )(,sin )(321===x y x x y x x y 是线性无关的.例5 函数组x n x x n e x y e x y e x y λλλ===)(,,)(,)(2121 （其中n λλλ ,,21两两互异）在任意区间上是线性无关的.证明 函数组x n x x n e x y e x y e x y λλλ===)(,,)(,)(2121 的朗斯基行列式为1121121)(1121121111)(21212121---+++---==nnn n nx x nn x n x n x n x x x x xn n n n e e e e e e e e e e x W λλλλλλλλλλλλλλλλλλλλλλλλ∏≤<≤+++-=n j i i j xn e 1)()(21λλλλλ因为n λλλ ,,21两两互异，所以0)()(1)(21≠-=∏≤<≤+++n j i i j xn e x W λλλλλ ，因此，函数组x n x x n e x y e x y e x y λλλ===)(,,)(,)(2121 线性无关.由定理3.4知，函数组)(,),(),(21x y x y x y n 线性相关，则它们的朗斯基行列式恒为零；反过来，如果函数组)(,),(),(21x y x y x y n 的朗斯基行列式恒为零，能不能得出函数组)(,),(),(21x y x y x y n 线性相关呢？即朗斯基行列式恒为零是不是线性相关的充分必要条件呢？下面的例子给出了答案.例6 函数组,0,0)(21<≥⎩⎨⎧=x x x x y 0,0,0)(,22<≥⎩⎨⎧=x x x x y 显然是线性无关的，因为)()(21x y x y 不是常数.但是，它们的朗斯基行列式为 当0≥x 时，0020)(2==x x x W ，当0<x 时，0200)(2==xx x W . 即，对所有的R x ∈，朗斯基行列式恒为零.通过这个例子，我们可以看出即使函数组的朗斯基行列式恒为零，该函数组也有可能是线性无关的，所以函数组的朗斯基行列式恒为零是判定函数组线性相关的必要条件，而不是充分条件.我们只能用朗斯基行列式在某点处不为零，判定该函数组线性无关.但是，如果函数组)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n的n 个解，这时它们的朗斯基行列式恒为零是判定该函数组线性相关的充分必要条件.这可由下面的定理得到.定理3.5 如果函数组)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n定义在区间),(b a 上的n 个线性无关的解，则它们的朗斯基行列式0)(≠x W在区间),(b a 上恒成立.证明 假设0)(≠x W 在区间),(b a 上不恒成立，即存在),(0b a x ∈，使得0)(0=x W .构造n C C C ,,,21 的方程组⎪⎪⎩⎪⎪⎨⎧=+++='++'+'=+++---0)()()(0)()()(0)()()(0)1(0)1(220)1(1100220110022011x y C x y C x y C x y C x y C x y C x y C x y C x y C n n n n n n n n n因为方程组的系数行列式0)(0=x W ，所以方程组有非零解，设为)0()0(2)0(1,,,n C C C （)0()0(2)0(1,,,nC C C 不全为零） 以)0()0(2)0(1,,,nC C C 为系数，构造)(,),(),(21x y x y x y n 的线性组合)()()()()0(2)0(21)0(1x y C x y C x y C x y n n +++=根据齐次线性微分方程解的性质知，它是方程（3.4）的解.而且满足初始条件⎪⎪⎩⎪⎪⎨⎧=+++=='++'+'='=+++=----0)()()()(0)()()()(0)()()()(0)1()0(0)1(2)0(20)1(1)0(10)1(0)0(02)0(201)0(100)0(02)0(201)0(10x y C x y C x y C x yx y C x y C x y C x y x y C x y C x y C x y n n n n n n n n n n 而0)(≡x y 也是方程（3.4）的解，也满足0)(,,0)(,0)(0)1(00=='=-x y x y x y n .因为初值问题⎩⎨⎧=='==+'+++---0)(,,0)(,0)(0)()()(0)1(001)1(1)(x yx y x y y x p y x p y x p y n n n n n 的解是唯一的，所以0)()()()()0(2)0(21)0(1≡+++=x y C x y C x y C x y n n又)0()0(2)0(1,,,nC C C 不全为零，由定理3.3知，函数组)(,),(),(21x y x y x y n 是线性相关，这与函数组)(,),(),(21x y x y x y n 线性无关矛盾. 所以，假设不成立，因此，0)(≠x W 在区间),(b a 上恒成立. 推论2如果函数组)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n定义在区间),(b a 上的n 个解，如果存在),(0b a x ∈，使得它们的朗斯基行列式0)(0=x W则该解组在),(b a 上线性相关.该推论是定理3.5的逆否命题，所以显然是成立的. 推论3方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n的n 个解)(,),(),(21x y x y x y n 在其定义区间),(b a 上线性无关的充要条件是，存在),(0b a x ∈，使得它们的朗斯基行列式0)(0≠x W . 这样，我们就可以得出下面的结论：设函数组)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n在区间),(b a 上的n 个解，则)(,),(),(21x y x y x y n 线性相关⇔)),((0)(0)(00b a x x W x W ∈=⇔≡ )(,),(),(21x y x y x y n 线性无关⇔)),((0)(0)(00b a x x W x W ∈≠⇔≠.这样，我们判定方程的n 个解是线性相关还是线性无关就可以看),,(0b a x ∈∀ )(0x W 是否为零.解决了线性相关与线性无关的判定问题后，我们继续解决线性齐次微分方程的通解问题，首先给出基本解组的概念.定义3.3 方程（3.4）的定义在区间),(b a 上的n 个线性无关的解，称为方程（3.4）的基本解组.例7 在例1中，我们验证了函数x x e x y e x y -==)(,)(21是方程0=-''y y的解，而且x x e x y e x y -==)(,)(21是线性无关的两个解，即)(),(21x y x y 是方程0=-''y y的基本解组，那么x x e C e C x y -+=21)(是否为方程的通解呢？我们需要证明，方程的任一解是否可由基本解组线性表出？定理 3.6 如果函数组)(,),(),(21x y x y x y n 是方程（3.4）的一个基本解组，则对于（3.4）的任一解)(x y ，均可由函数组)(,),(),(21x y x y x y n 线性表出，即，存在一组数)0()0(2)0(1,,,nC C C ，使得 )()()()()0(2)0(21)0(1x y C x y C x y C x y n n +++= .证明 设)(x y 是方程（3.4）的任一解，并且满足初始条件)1(00)1(0000)(,,)(,)(--='='=n n y x y y x y y x y 构造n C C C ,,,21 的方程组⎪⎪⎩⎪⎪⎨⎧=+++'='++'+'=+++----)1(00)1(0)1(220)1(110002201100022011)()()()()()()()()(n n n n n n n n n n y x y C x y C x y C y x y C x y C x y C y x y C x y C x y C因为)(,),(),(21x y x y x y n 是方程（3.4）的基本解组，即)(,),(),(21x y x y x y n 是线性无关的，所以它们的朗斯基行列式在0x x =的值不为零，即方程组的系数行列式0)(0≠x W ，因此方程组存在唯一的解，设其解为)0()0(2)0(1,,,n C C C ，这样，我们可以用)0()0(2)0(1,,,nC C C 构造函数 )()()()()0(2)0(21)0(1~x y C x y C x y C x y n n +++=根据线性齐次微分方程解的性质知，)(~x y 是方程（3.4）的解，而且)(~x y 满足：⎪⎪⎩⎪⎪⎨⎧=+++='='++'+'='=+++=-----)1(00)1()0(0)1(2)0(20)1(1)0(10~)1(00)0(02)0(201)0(10~00)0(02)0(201)0(10~)()()()()()()()()()()()(n n n n n n n n n n n y x y C x y C x y C x yy x y C x y C x y C x y y x y C x y C x y C x y 又)(x y 是方程（3.4）的任一解，并且满足初始条件)1(00)1(0000)(,,)(,)(--='='=n n y x y y x y y x y 因为初值问题⎩⎨⎧='='==+'+++----)1(00)1(00001)1(1)()(,,)(,)(0)()()(n n n n n n y x y y x y y x y y x p y x p y x p y 的解是唯一的，所以)()()()()()0(2)0(21)0(1~x y C x y C x y C x y x y n n +++==即，)(x y 可由函数组)(,),(),(21x y x y x y n 线性表出. 由定理3.6，可以得出下面的基本定理.定理3.7（基本定理）如果函数组)(,),(),(21x y x y x y n 是方程（3.4）的一个基本解组，则)()()()(2211x y C x y C x y C x y n n +++=是方程（3.4）的通解，其中n C C C ,,,21 是n 个任意常数.证明 首先由线性齐次微分方程解的性质知，对任意的n C C C ,,,21)()()()(2211x y C x y C x y C x y n n +++=是方程（3.4）的解.其次，由定理3.6知，方程（3.4）的任一解均可由)(,),(),(21x y x y x y n 线性表出，即，任一解都可以表示成)()()()(2211x y C x y C x y C x y n n +++= 的形式. 因此，)()()()(2211x y C x y C x y C x y n n +++= 是方程（3.4）的通解. 由基本定理可知，方程（3.4）的求解，关键是找到方程（3.4）的一个基本解组，即，方程（3.4）的n 个线性无关的解)(,),(),(21x y x y x y n ，这样就可以很容易的写出方程（3.4）的通解：)()()()(2211x y C x y C x y C x y n n +++= .例8 求方程0=-''y y的通解.解 我们验证了函数x x e x y e x y -==)(,)(21是方程0=-''y y的两个线性无关的两个解，因此方程的通解为：x x e C e C x y -+=21)(.根据基本定理，我们可以得到下面的推论.推论4 n 阶线性齐次微分方程（3.4）的线性无关解的个数不超过n 个. 证明 设)(),(,),(),(121x y x y x y x y n n + 是方程（3.4）的任意1+n 个解.如果前n个解)(,),(),(21x y x y x y n 是线性相关的，则上述1+n 个解是线性相关的. 如果前n 个解)(,),(),(21x y x y x y n 是线性无关的，由定理3.6知，)(,),(),()(211x y x y x y x y n n →+所以)(),(,),(),(121x y x y x y x y n n + 是线性相关的. 因此，方程（3.4）的线性无关解的个数不超过n 个.由推论4知，n 阶线性齐次微分方程（3.4）的线性无关解的个数不超过n 个，那么方程（3.4）的线性无关解的个数是不是有且只有n 个呢？其基本解组存在吗？下面的定理可以回答这个问题.定理3.8 方程（3.4）总存在定义在),(b a 上的基本解组，即，总存在n 个线性无关的解.证明 在),(b a 上任取一点0x x =，由解的存在唯一性定理，方程（3.4）在),(b a 上必存在n 个解)(,),(),(),(321x y x y x y x y n ，它们分别满足下列初始条件：0)(,,0)(,0)(,1)(0)1(1010101==''='=-x y x y x y x y n 0)(,,0)(,1)(,0)(0)1(2020202==''='=-x y x y x y x y n 0)(,,1)(,0)(,0)(0)1(3030303==''='=-x y x y x y x y n………………………………………………………1)(,,0)(,0)(,0)(0)1(000==''='=-x y x y x y x y n n n n n由于这n 个解在0x x =点的朗斯基行列式的值011000010100001)(0≠==x W所以)(,),(),(),(321x y x y x y x y n 是线性无关的解，从而它们是方程（3.4）定义在),(b a 上的基本解组.由定理3.8知，线性齐次微分方程（3.4）的基本解组一定存在，且含有n 个线性无关的解.而且方程（3.4）的解与它的系数之间满足如下的刘维尔（Liouville ）公式.定理3.9 设)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n的任意n 个解，)(x W 是这n 个解的朗斯基行列式，则对),(b a 上的任一点0x x =，总有⎰=-xx dtt p ex W x W 01)(0)()(.在给出定理3.9的证明之前，先给出行列式函数求导法则 设n 阶行列式函数为)()()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a x D nn n n n n n =则+'''+'''=)()()()()()()()()()()()()()()()()()())((212222111211212222111211x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a dxx D d nn n n n n nn n n n n n)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a nn n nn n '''+证明 当2=n 时，这时)()()()()()()()()(21122211222112112x a x a x a x a x a x a x a x a x D -===dxx D d ))((2)]()()()([)]()()()([2112221121122211x a x a x a x a x a x a x a x a '-'+'-' )()()()()()()()(2221121122211211x a x a x a x a x a x a x a x a ''+''= 当3=n 时，)()()()()()()()()()()()()()()()(3231222113333123211233322322113x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x D +-==dx x D d ))((3)()()()()()()()()()()()()()()(323122211333312321123332232211x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a '+'-' ))()()()()(())()()()()(())()()()()((323122211333312321123332232211'+'-'+x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a)()()()()()()()()()()()()()()()()()()()()()()()()()()(333231232221131211333231232221131211333231232221131211x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a '''+'''+'''= 假设对1-n 阶方阵成立，则对于n 的情形有：)()()()()()()(1112121111x A x a x A x a x A x a x D n n n +++==dxx D d n ))(()]()()()()()([1112121111x A x a x A x a x A x a n n '++'+' )()([1111x A x a '+ )]()()()(111212x A x a x A x a n n '++'+ )()()()()()()()()()()()()()()()()()()()()()()()()()()(212222111211212222111211212222111211x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x a nnn nn n nn n n n n nn n n n n '''++'''+'''=下面，我们给出定理3.9的证明.证明 因为)()()()()()()()()()()1()1(2)1(12121x y x y x y x y x y x y x y x y x y x W n n n n n n ---'''=对朗斯基行列式求导得：)()()()()()()()()()()()()()()(2)(1)2()2(2)2(12121x y x y x y x y x y x y x y x y x y x y x y x y dxx dW n n n n n n n n n n---'''=分别用)(,),(),(21x p x p x p n n -乘以上述行列式的第一行，第二行，…，第1-n 行后，全部加至第n 行，这时第n 行元素为：),,2,1(,)()()(1)2(2)(n i y x p y x p y x p y i n i n n i n i =+'+++--因为)(,),(),(21x y x y x y n 均是方程（3.4）的解，即),,2,1(,0)()()()(1)2(2)1(1)(n i y x p y x p y x p y x p y i n i n n i n i n i ==+'++++--- 所以),,2,1(,)()()()()1(11)2(2)(n i y x p y x p y x p y x p y n i i n i n n i n i =-=+'+++--- 所以第n 行元素可以换为：),,2,1(,)()1(1n i y x p n i =--因此)()()()()()()()()()()()()()()()()()(1)1(1)1(21)1(11)2()2(2)2(12121x W x p x y x p x y x p x y x p x y x y x y x y x y x y x y x y x y dxx dW n n n n n n n n n n -=---'''=------即)()()(1x W x p dxx dW -= 即dx x p x W x dW )()()(1-= 从0x 到x 积分得：⎰=-xx dtt p ex W x W 01)(0)()(.在前面我们已经得出：如果函数组)(,),(),(21x y x y x y n 是方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n在区间),(b a 上的n 个解，则)(,),(),(21x y x y x y n 线性相关⇔)),((0)(0)(00b a x x W x W ∈=⇔≡ )(,),(),(21x y x y x y n 线性无关⇔)),((0)(0)(00b a x x W x W ∈≠⇔≠. 现在刘维尔公式直接给出了n 个解)(,),(),(21x y x y x y n 的朗斯基行列式的值与它在某一点0x x =处的值之间的关系：⎰=-xx dtt p ex W x W 01)(0)()(.下面给出刘维尔公式的一个简单应用：对于二阶线性齐次方程0)()(=+'+''y x q y x p y如果已知它的一个非零解)(1x y ，则由刘维尔公式可以求得与)(1x y 线性无关的另一个解，从而可求得方程的通解.设)(x y 是二阶线性齐次方程0)()(=+'+''y x q y x p y 的与)(1x y 线性无关的解，则由刘维尔公式得：)0()()(11≠⎰=''=-C Ce y y y y x W dxx p即⎰='-'-dxx p Ce y y y y )(11两边同时乘以211y 得： ⎰='-'-dx x p ey C y y y y y )(212111 积分得：⎰⎰⎰=⎰=--dx e y C dx e y C y y dxx p dx x p )(21)(2111 即⎰⎰=-dx e y Cy y dxx p )(2111 因此方程的通解为：⎰⎰+=-dx e y Cy y C x y dxx p )(2111*1)(. 例9 已知方程011)ln 1(2=-'+''-y xy x y x的一个解x y ln 1=，试求其通解.解 这里)1(ln 1)(--=x x x p ，由公式可得通解为：]ln 1[ln ]1[)1(ln 1ln 12*)1(ln 121*1⎰⎰⎰+=⎰+=---dx e xC C x dx e y C C y y x d x dx x x)]ln 1ln 1([ln ]ln 1ln [ln 2*2*⎰⎰⎰-+=-+=dx x dx x C C x dx xx C C x Cx x C xCx C x dx x x xd x x C C x +=+=--+=⎰⎰ln )ln (ln )]ln 1ln 1ln ([ln **2*. 上述例子表明，一个二阶的线性齐次微分方程，如果能得到其一个非零解，利用刘维尔公式可求得该线性齐次微分方程的通解.我们也可以采用换元法，将二阶线性齐次微分方程降阶为一阶微分方程，从而求得该方程的通解，下面介绍一下换元法.对于二阶线性齐次方程0)()(=+'+''y x q y x p y如果已知它的一个非零解)(1x y ，下面做变量代换，令z y y 1=则z y z y z y y z y z y y ''+''+''='''+'='111112,，代入原方程得： 0)())((2111111=+'+'+''+''+''z y x q z y z y x p z y z y z y 即0))(2())()((111111=''+'+'++'+''z y z y x p y z y x q y x p y 因为)(1x y 是原方程的解，所以0)()(111=+'+''y x q y x p y ，从而上式可化为： 0))(2(111=''+'+'z y z y x p y 令u z ='，则u z '=''，代入得：0))(2(111='++'u y u y x p y 降为了一阶微分方程，而且是变量可分离的方程，整理得：dx y y x p y u du111)(2+'-=102积分得：⎰=+'-dxy y x p y Ceu 111)(2.从而得到⎰⎰⎰=⎰=+'-+'-dx Cey y dx Cez dxy y x p y dxy y x p y 111111)(21)(2,.因此方程的通解为：⎰⎰+=+'-dx eCy y C x y dx y y x p y 111)(211*)(.例10 求方程066323=-'+''-'''y y x y x y x的通解，已知它的两个特解221,x y x y ==.解 令xz y =，则z z x y z z x y z z x y ''+'''=''''+''=''+'='3,2, 代入066323=-'+''-'''y y x y x y x 得：06)(6)2(3)3(23=-+'+'+''-''+'''xz z z x x z z x x z z x x即04='''z x ，所以,,,12321x z x z z ===因此33x y =故原方程的通解为：33221x C x C x C y ++=.习 题 3.21.试讨论下列各函数组在它们的定义区间上是线性相关的还是线性无关的？（1）;sin ,cos ,2sin t t t （2）;tan ,cos ,sin x x x （3）;42,2,322+++-x x x x x （4）.,,2t t t e t te e2.设在方程0)()(=+'+''y x q y x p y 中，)(x p 在某区间I 上连续且恒不为零，103试证它的任意两个线性无关的解的朗斯基行列式是区间I 上的严格单调函数.3.试证明：二阶线性齐次方程的任意两个线性无关解的朗斯基行列式之比是一个不为零的常数.4.已知方程022)1(2=+'-''-y y x y x 的一个解x y =1，试求其通解.5.已知方程0)1(=+'-''-y y x y x 的一个解x y =1，试求其通解.6.在方程0)()(=+'+''y x q y x p y 中，当系数满足什么条件时，其基本解组的朗斯基行列式等于常数.7.设)(1x y 是n 阶线性齐次方程0)()()(1)1(1)(=+'+++--y x a y x a y x a y n n n n的一个非零解.试证明：利用线性变换z x y y )(1=可将已知方程化为1-n 阶的齐次方程.3.3 n 阶线性非齐次微分方程的一般理论对于线性非齐次微分方程)()()()(1)1(1)(x f y x p y x p y x p y n n n n =+'+++-- （3.2）而言，我们首先研究其解与对应的线性齐次微分方程解之间的关系.（1）如果)(x y 是线性齐次微分方程（3.4）的解，)(*x y 是线性非齐次微分方程（3.2）的解，则)()(*x y x y +是线性非齐次微分方程（3.2）的解.证明 因为)(x y 是线性齐次微分方程（3.4）的解， 所以0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n因为)(*x y 是线性非齐次微分方程（3.2）的解， 所以)()())(())(()(**1)1(*1)(*x f y x p y x p y x p y n n n n =+'+++--因此))(())(())(()(**1)1(*1)(*y y x p y y x p y y x p y y n n n n ++'++++++--104))(())()(())()(()(**1)1(*)1(1)(*)(y y x p y y x p y y x p y y n n n n n n ++'+'+++++=--- )1(*1)(*1)1(1)())(()(())()()((---+++'+++=n n n n n n y x p y y x p y x p y x p y )()(0))())((**1x f x f y x p y x p n n =+=+'++- . 即，)()(*x y x y +是线性非齐次微分方程（3.2）的解.（2）如果)(),(*2*1x y x y 是线性非齐次微分方程（3.2）的解，则)()(*2*1x y x y -是线性齐次微分方程（3.4）的解.证明 因为)(),(*2*1x y x y 是线性非齐次微分方程（3.2）的解，所以)()())(())(()(*1*11)1(*11)(*1x f y x p y x p y x p y n n n n =+'+++-- )()())(())(()(*2*21)1(*21)(*2x f y x p y x p y x p y n n n n =+'+++--因此))(())(())(()(*2*1*2*11)1(*2*11)(*2*1y y x p y y x p y y x p y y n n n n -+'-++-+---))(())())((())())((()()(*2*1*2*11)1(*2)1(*11)(*2)(*1y y x p y y x p y y x p y y n n n n n n -+'-'++-+-=--- )1(*21)(*2*1*11)1(*11)(*1))(()(())())(())(()((---+-+'+++=n n n n n n y x p y y x p y x p y x p y 0)()())())((*2*21=-=+'++-x f x f y x p y x p n n . 即，)()(*2*1x y x y -是线性齐次微分方程（3.4）的解.根据上述两条性质，我们可以得到下面的定理. 定理3.10 n 阶线性非齐次微分方程)()()()(1)1(1)(x f y x p y x p y x p y n n n n =+'+++--的通解等于它对应的齐次方程0)()()(1)1(1)(=+'+++--y x p y x p y x p y n n n n的通解与它本身的一个特解之和.即)()()()()(*2211x y x y C x y C x y C x y n n ++++=证明 因为)()()(2211x y C x y C x y C n n +++ 是齐次方程（3.4）的解，)(*x y 是105非齐次方程（3.2）的解，由性质（1）知，)()()()()(*2211x y x y C x y C x y C x y n n ++++=是非齐次方程（3.2）的解.下面证明非齐次方程（3.2）的任一解)(x y 都可以表示成)()()()(*2211x y x y C x y C x y C n n ++++事实上，因为)(x y 和)(*x y 都是非齐次方程（3.2）的解，由性质（2）知，)()(*x y x y -是齐次方程（3.4）的解，所以可表示成方程（3.4）的通解形式，即)()()()()(2211*x y C x y C x y C x y x y n n +++=-因此)()()()()(*2211x y x y C x y C x y C x y n n ++++= .故非齐次方程（3.2）的通解可以表示为齐次方程的通解与非齐次方程的特解之和.由定理3.10知，求解一个线性非齐次方程（3.2）的关键是先找到对应的线性齐次方程（3.4）的通解，再找到一个非齐次方程的特解就可以了，这时有非齐通解=齐通解+非齐特解.假定我们已经求得了线性齐次微分方程（3.4）的齐通解)()()()(2211x y C x y C x y C x y n n +++=这时，可以采用常数变易法求非齐次方程的特解)(*x y .下面来看一下n 阶线性非齐次微分方程的常数变易法.已知)()()()(2211x y C x y C x y C x y n n +++= 是齐次方程（3.4）的通解，设)()()()()()()(2211*x y x C x y x C x y x C x y n n +++=是线性非齐次方程（3.2）的一个特解，为了将)(*x y 代入方程（3.2），我们需要首先计算)(*x y 的一阶，二阶，…，n 阶导数.则)()()()([)]()()()()()([))((22112211*x y x C x y x C x y x C x y x C x y x C x y n n '+'+'++'+'='106)]()(x y x C nn '++ 在求二阶导数之前，我们先研究一下特解)(*x y ，要想得到)(*x y ，必须求得)(,),(),(21x C x C x C n ，但是代入方程（3.2）只能得到一个等式，所以我们必须构造)(,),(),(21x C x C x C n 满足的另外1-n 个等式，因此在))((*'x y 中，令0)()()()()()(2211='++'+'x y x C x y x C x y x C n n 则)()()()()()())((2211*x y x C x y x C x y x C x y n n '++'+'=' 这时，再求))((*''x y ，有)()()()([)]()()()()()([))((22112211*x y x C x y x C x y x C x y x C x y x C x y n n ''+''+''++''+''='' )]()(x y x C n n ''++ 再令0)()()()()()(2211=''++''+''x y x C x y x C x y x C n n 则)()()()()()())((2211*x y x C x y x C x y x C x y n n ''++''+''='' 序行此法，可得)()([)]()()()()()([))(()1(11)2()2(22)2(11)1(*x y x C x y x C x y x C x y x C x y n n n n n n n -----+'++'+'= )]()()()()1()1(22x y x C x y x C n n n n --+++令0)()()()()()()2()2(22)2(11='++'+'---x y x C x y x C x y x C n n n n n则)()()()()()())(()1()1(22)1(11)1(*x y x C x y x C x y x C x y n n n n n n ----++++=这时，再求)(*))((n x y ，有)()([)]()()()()()([))(()(11)1()1(22)1(11)(*x y x C x y x C x y x C x y x C x y n n n n n n n +'++'+'=--- )]()()()()()(22x y x C x y x C n n n n +++107最后将求得的)(*x y 的一阶，二阶，…，n 阶导数代入方程（3.2）得：)()()()([)]()()()()()({[)(22)(11)1()1(22)1(11x y x C x y x C x y x C x y x C x y x C n n n n n n n ++'++'+'--- )]()()()()()()[()]}()()1()1(22)1(111)(x y x C x y x C x y x C x p x y x C n n n n n n n n ---++++++)()()[()]()()()()()()[(1122111x y x C x p x y x C x y x C x y x C x p n n n n +'++'+'++- )()]()()()(22x f x y x C x y x C n n =+++ 即)]()()()()()()()[(111)1(11)(11x y x p x y x p x y x p x y x C n n n n +'+++-- ++'++++--)]()()()()()()()[(221)1(21)(22x y x p x y x p x y x p x y x C n n n n )]()()()()()()()[(1)1(1)(x y x p x y x p x y x p x y x C n n n n n n n n n +'++++-- )()]()()()()()([)1()1(22)1(11x f x y x C x y x C x y x C n n n n n ='++'+'+---因为),,2,1(,0)()()()()()()(1)1(1)(n i x y x p x y x p x y x p x y i n i n n i n i ==+'+++-- 所以)()()()()()()()1()1(22)1(11x f x y x C x y x C x y x C n n n n n ='++'+'---这样，就得到了)(,),(),(21x C x C x C n ''' 的n 个方程 ⎪⎪⎪⎩⎪⎪⎪⎨⎧='++'+'='++'+'=''++''+''='++'+'------)()()()()()()(0)()()()()()(0)()()()()()(0)()()()()()()1()1(22)1(11)2()2(22)2(1122112211x f x y x C x y x C x y x C x y x C x y x C x y x C x y x C x y x C x y x C x y x C x y x C x y x C n n n n n n nn n n n n n n 该方程组的系数行列式为)(,),(),(21x y x y x y n 的朗斯基行列式)(x W ，因为这n 个解是线性无关的，所以0)(≠x W ，因此，该方程组存在唯一解，这样就可以求得)(,),(),(21x C x C x C n ''' ，再逐个积分，求得)(,),(),(21x C x C x C n ，从而得到特解)(*x y .例1 求方程10812-=-''x xe e y y的通解.解 齐次方程0=-''y y的通解为：x x e C e C y -+=21.设xxe x C e x C x y -+=)()()(21*为方程12-=-''x xe e y y 的一个特解，则⎪⎩⎪⎨⎧-='-'='+'--12)()(0)()(2121x x xx x x e e e x C e x C e x C e x C ， 解方程组得：⎪⎩⎪⎨⎧-='-='x xx e e x C e x C 1)(11)(221，所以x e de ee de e e dx e x C xx x x x x x x --=--=-=-=⎰⎰⎰1ln )111()1(111)(1 )1(ln )111(11)(22xx x x x x x x x e e de e de e e dx e e x C +--=+--=-=-=⎰⎰⎰ 因此非齐特解为)11ln (1ln )(*+----=-x x x x x e e xe e e x y故方程的通解为)11ln (1ln )(21+----++=--x x x x x x x e e xe e e e C e C x y .例2 求方程)(2t f x x =+∙∙ω的通解. 解 对应的齐次方程020=+∙∙x x ω的通解为t C t C t x 0201sin cos )(ωω+=.。