第六章 综合指数练习题

第六章统计指数分析习题一、填空题1．指数按其指标的作用不同，可分为和。

2．狭义指数是指反映由不能同度量的事物所构成的特殊总体变动或差异程度的特殊。

3．总指数的编制方法，其基本形式有两种：一是，二是。

4．平均指数是的加权平均数。

5．因素分析法的基础是。

6．在含有两个因素的综合指数中，为了观察某一因素的变动，则另一个因素必须固定起来。

被固定的因素通常称为，而被研究的因素则称为指标。

7．平均数的变动同时受两个因素的影响：一是各组的变量值水平，二是。

8．编制综合指数，确定同度量因素的一般原则是：数量指标指数宜以作为同度量因素，质量指标指数宜以作为同度量因素。

9．已知某厂工人数本月比上月增长6％，总产值增长12％，则该企业全员劳动生产率提高。

10．综合指数的重要意义，在于它能最完善地显示出所研究对象的经济内容，即不仅在相对数，而且还能在方面反映事物的动态。

二、单项选择1．统计指数按其反映的对象范围不同分为( )。

A简单指数和加权指数B综合指数和平均指数C个体指数和总指数D数量指标指数和质量指标指数2．总指数编制的两种形式是( )。

A算术平均指数和调和平均指数B个体指数和综合指数C综合指数和平均指数D定基指数和环比指数3．综合指数是一种( )。

A简单指数B加权指数C个体指数D平均指数4．某市居民以相同的人民币在物价上涨后少购商品15％，则物价指数为( )。

A 17．6％B 85％C 115％D 117．6％5．在掌握基期产值和各种产品产量个体指数资料的条件下，计算产量总指数要采用( )。

A综合指数B可变构成指数C加权算术平均数指数D加权调和平均数指数6．在由三个指数组成的指数体系中，两个因素指数的同度量因素通常( )。

A都固定在基期B都固定在报告期C一个固定在基期，另一个固定在报告期D采用基期和报告期的平均数7．某商店报告期与基期相比，商品销售额增长6．5％，商品销售量增长6．5％，则商品价格( )。

A增长13％B增长6．5％C增长1％D不增不减8．单位产品成本报告期比基期下降6％，产量增长6％，则生产总费用( )。

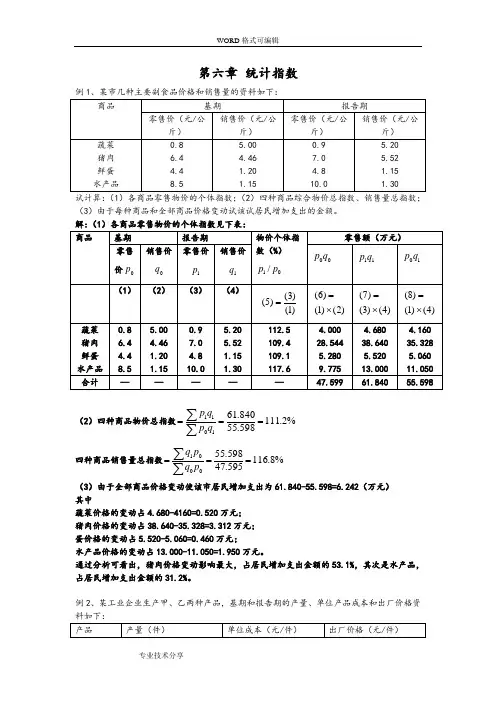
第六章 统计指数（3）由于每种商品和全部商品价格变动试该试居民增加支出的金额。

解：（1）各商品零售物价的个体指数见下表：（2）四种商品物价总指数%2.111598.55840.611011===∑∑qp q p四种商品销售量总指数%8.116595.47598.55001===∑∑pq p q（3）由于全部商品价格变动使该市居民增加支出为61.840-55.598=6.242（万元） 其中蔬菜价格的变动占4.680-4160=0.520万元； 猪肉价格的变动占38.640-35.328=3.312万元； 蛋价格的变动占5.520-5.060=0.460万元；水产品价格的变动占13.000-11.050=1.950万元。

通过分析可看出，猪肉价格变动影响最大，占居民增加支出金额的53.1%，其次是水产品，占居民增加支出金额的31.2%。

例2、某工业企业生产甲、乙两种产品，基期和报告期的产量、单位产品成本和出厂价格资试计算：（1）以单位成本为同度量因素的产量总指数 （2）以出厂价格为同度量因素的产量总指数 （3）单位成本总指数 （4）出厂价格总指数（1）以单位成本为同度量因素的产量总指数%7.1193100037100001===∑∑zq z q（2）以出厂价格为同度量因素的产量总指数%6.115550006360001===∑∑pq p q（3）单位成本总指数%2.14837100550001011===∑∑qz q z（4）出厂价格总指数%8.9963600635001011===∑∑qp q p例3、试根据例2的资料，从相对数和绝对数方面分析： （1）总成本变动受产量和单位成本变动的影响程度 （2）销售额变动受产量和出厂价格变动的影响程度 解：（1）总成本变动：总成本指数%4.1773100055000011===∑∑qz q z增加总成本∑∑=-=-2400031000550000011qz q z （元）其中由于产量变动的影响：产量指数%7.1193100037100001===∑∑zq z q由于产量增长而引起总成本增加：∑∑=-=-610031000371000001zq z q （元）由于单位成本变动的影响： 单位成本指数%2.1483710055000111===∑∑zq z q由于单位成本增长而引起总成本增加：∑∑=-=-1790037100550000111zq z q （元）177.4%=119.7%×148.2% 24000元=6100元+17900元计算表明，该厂两种产品总成本报告期比基期增长77.4%，是由于产品产量增加19.7%和单位成本提高48.2%两因素造成的。

第一章导论练习题1、现代统计学的核心是描述统计学。

（F）2、描述统计学是推断统计学的基础。

（T）3、统计指标可以分成数量指标和质量指标。

（T）4、所有标志都可以用数量表现。

（F）5、统计学是一门研究现象总体数量方面的方法论科学，所以它不关心、也不考虑个别现象的数量特征。

（F）6、三个同学的成绩不同，因此存在三个变量（F）7、统计数字的具体性是统计学区别于数学的根本标志（T）8、一般而言，指标总是依附于总体上的、而总体单位则是标志的直接承担者（T）9、统计研究中的变异是指总体单位质的差别（F）10、社会经济统计是在对质和量的联系中，观察和研究社会经济现象的数量方面（T）11、运用大量观察法，必须对研究对象的所有单位进行观察调查（F）12、综合为统计指标的前提是总体的同质性（T）13、单位产品原材料消耗量是数量指标，其值大小与研究的范围大小有关（F）14、质量指标是反映总体质的特征，因此，可以用文字来表述（F）第二章统计调查练习题1 、统计报表是我国定期取得统计资料的一种重要方式。

（T）2 、抽样调查在我国统计调查方法体系中处于主体地位。

（T）3 、我国的人口普查每10 年进行一次，因此，它是一种经常性调查方式。

（F）4 、统计报表有全面报表和非全面报表之分。

（T ）5 、抽样调查中存在抽样误差，因此，抽样推断是不准确的。

（F）6、重点调查的重点单位是根据当前的工作重点来确定的（F）7、调查时间是指进行调查工作所需的时间（F）8、对变化较小、变动较慢的现象应采用一次性调查来取得资料（T）9、调查对象就是统计总体，而统计总体不都是调查对象（F）10、在统计调查中，调查对象可以同时又是调查单位，调查单位可以同时又是总体单位（F）第三章统计整理练习题1、进行组距分组时，当标志值刚好等于相邻两组上下限数值时，一般把此值归并列为上限的那一组（F）2、直接观察法不能用于对历史资料的收集（T）3、为了解某县主要农产品生产成本可以进行经常性调查（F）第四章统计综合指标练习题1、某企业计划利润提高10% ，实际提高了5% ，则该企业的利润计划完成程度95%（F ）2、若两组数据的标准差相等，则其离散程度相同。

第六章 统 计 指 数一、单项选择题1、社会经济统计中的指数是指（ ）。

① 总指数 ② 广义的指数 ③ 狭义的指数 ④ 广义和狭义指数2、根据指数所包括的范围不同，可把它分为（ ）。

① 个体指数和总指数 ② 综合指数和平均指数 ③ 数量指数和质量指数 ④ 动态指数和静态指数3、编制综合指数时对资料的要求是须掌握（ ）。

① 总体的全面调查资料 ② 总体的非全面调查资料 ③ 代表产品的资料 ④ 同度量因素的资料 4、设P 表示商品的价格，q 表示商品的销售量，∑∑1011qp q p 说明了（ ）。

① 在报告期销售量条件下，价格综合变动的程度② 在基期销售量条件下，价格综合变动的程度 ③ 在报告期价格水平下，销售量综合变动的程度 ④ 在基期价格水平下，销售量综合变动的程度5、根据指数所反映现象的数量特征不同，可把它分为（ ）。

① 拉氏指数和帕氏指数 ② 综合指数和平均指数 ③ 数量指数和质量指数 ④ 动态指数和静态指数6、拉氏指数所选取的同度量因素是固定在（ ）。

① 报告期 ② 基期 ③ 假定期 ④ 任意时期7、帕氏指数所选取的同度量因素是固定在（ ）。

① 报告期 ② 基期 ③ 假定期 ④ 任意时期8、设P 表示商品的价格，q 表示商品的销售量，帕氏价格指数的公式是（ ）。

①∑∑1011qp qp ②∑∑01qp q p ③∑∑0111qp q p ④∑∑010qp q p9、设P 表示商品的价格，q 表示商品的销售量，拉氏销售量指数的公式是（ ）。

①∑∑1011qp q p ②∑∑01qp q p ③∑∑0111qp q p ④∑∑010qp q p10、编制数量指标综合指数的一般是采用（ ）作同度量因素。

① 报告期数量指标 ② 基期数量指标 ③ 报告期质量指标 ④ 基期质量指标11、编制质量指标综合指数的一般是采用（ ）作同度量因素。

① 报告期数量指标 ② 基期数量指标 ③ 报告期质量指标 ④ 基期质量指标 12、某地区职工工资水平本年比上年提高了5%，职工人数增加了2%，则工资总额增加了（ ）。

第六章 统 计 指 数一、单项选择题1、社会经济统计中的指数是指（ ）。

① 总指数 ② 广义的指数 ③ 狭义的指数 ④ 广义和狭义指数2、根据指数所包括的范围不同，可把它分为（ ）。

① 个体指数和总指数 ② 综合指数和平均指数 ③ 数量指数和质量指数 ④ 动态指数和静态指数3、编制综合指数时对资料的要求是须掌握（ ）。

① 总体的全面调查资料 ② 总体的非全面调查资料 ③ 代表产品的资料 ④ 同度量因素的资料 4、设P 表示商品的价格，q 表示商品的销售量，∑∑1011qp q p 说明了（ ）。

① 在报告期销售量条件下，价格综合变动的程度② 在基期销售量条件下，价格综合变动的程度 ③ 在报告期价格水平下，销售量综合变动的程度 ④ 在基期价格水平下，销售量综合变动的程度5、根据指数所反映现象的数量特征不同，可把它分为（ ）。

① 拉氏指数和帕氏指数 ② 综合指数和平均指数 ③ 数量指数和质量指数 ④ 动态指数和静态指数6、拉氏指数所选取的同度量因素是固定在（ ）。

① 报告期 ② 基期 ③ 假定期 ④ 任意时期7、帕氏指数所选取的同度量因素是固定在（ ）。

① 报告期 ② 基期 ③ 假定期 ④ 任意时期8、设P 表示商品的价格，q 表示商品的销售量，帕氏价格指数的公式是（ ）。

①∑∑1011qp qp ②∑∑001qp q p ③∑∑0111qp q p ④∑∑010qp q p9、设P 表示商品的价格，q 表示商品的销售量，拉氏销售量指数的公式是（ ）。

①∑∑1011qp q p ②∑∑001qp q p ③∑∑0111qp q p ④∑∑010qp q p10、编制数量指标综合指数的一般是采用（ ）作同度量因素。

① 报告期数量指标 ② 基期数量指标 ③ 报告期质量指标 ④ 基期质量指标11、编制质量指标综合指数的一般是采用（ ）作同度量因素。

① 报告期数量指标 ② 基期数量指标 ③ 报告期质量指标 ④ 基期质量指标 12、某地区职工工资水平本年比上年提高了5%，职工人数增加了2%，则工资总额增加了（ ）。

京改版七年级数学下册第六章整式的运算综合练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如果多项式x m-3＋5x －3是关于x 的三次三项式，那么m 的值为（ ）A ．0B ．3C ．6D ．9 2、下列说法正确的是（ ）A ．0不是单项式B ．单项式xy 的次数是1C ．单项式22a b 的系数是12D ．多项式2321x y x +-的一次项次数是—13、对代数式-(a -b )进行去括号运算，结果正确的是（ ）A ．a -bB ．-a -bC ．a +bD ．–a +b 4、单项式2223x yz -的系数和次数分别是（ ）A ．－2，5B ．23-，5 C ．23，2 D ．23-，2 5、下列计算中，正确的是（ ）A ．()2224a b a b +=+B ．44a a a ⋅=C ．623a a a ÷=D ．()2362a b a b =6、下列各式中，计算结果为x 10的是（ ）A ．x 5+x 5B ．x 2•x 5C ．x 20÷x 2D ．（x 5）27、已知26m =，23n =，则2m n +=（ ）A ．2B ．3C ．9D ．188、计算34a a ⋅的结果是（ ）A ．34aB ．43aC ．7aD ．12a9、 “数形结合”是一种重要的数学思维，观察下面的图形和算式：2111==21342+==213593++==21357164+++==213579255++++==解答下列问题：请用上面得到的规律计算：21＋23＋25＋27…＋101＝（）A ．2601B ．2501C ．2400D ．241910、下列各式中，计算结果为6a 的是（ ）A ．()42aB ．7a a ÷C ．82a a -D ．23a a ⋅第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、一个白色圆生成一个黑色圆，一个黑色圆生成一个白色圆和一个黑色圆，按如图方式排列，依此类推，第十行圆的个数为 _____．2、已知a ，b 两数在数轴上对应的点如图所示，化简||b a a --的结果是___．3、将初一年级的500名同学从1到500编号，并按编号从小到大的顺序站成一排报数1、2、3…，报到奇数的退下，偶数的留下，留下的同学从编号小的开始继续报数1、2、3…，报到奇数的退下，偶数的留下，…，如此继续，最后留下一个同学，则最后留下的这个同学编号是_____．4、把多项式332247x y xy x y -+--按x 的升幂重新排列____________．5、若式子x 2＋16x ＋k 是一个完全平方式，则k ＝______．三、解答题（5小题，每小题10分，共计50分）1、按照要求进行计算：（1）计算：()()()222223x x y xy xy y x xy xy ⎡⎤----÷⎣⎦ （2）利用乘法公式进行计算：()()22x y z x y z ++--2、先化简，再求值：（1）3（2x 2﹣xy ）﹣4（﹣6+xy +x 2），其中x ＝1，y ＝﹣1．（2）4xy ﹣（2x 2+5xy ﹣y 2）+2（x 2+3xy ），其中x ＝1，y ＝﹣2．3、已知a 2+b 2＝3，ab ＝﹣2，求代数式（7a 2+3ab +3b 2）﹣2（4a 2+3ab +2b 2）的值．4、完全平方公式：()2222a b a ab b ±=±+适当的变形，可以解决很多的数学问题．例如：若3,1a b ab +==，求22a b +的值．解：因为3,1a b ab +==所以()29,22a b ab +== 所以2229,22a b ab ab ++==得227a b +=．根据上面的解题思路与方法，解决下列问题：（1）若228,40x y x y +=+=，求xy 的值；（2）若()()458x x --=，则()22()45x x -+-= ； （3）如图，点C 是线段AB 上的一点，以AC BC 、为边向两边作正方形，设6AB =，两正方形的面积和1218S S +=，求图中阴影部分面积．5、先化简，再求值：()()2222432x y xy x y xy ---；其中3x =，2y =-．---------参考答案-----------一、单选题1、C【分析】直接利用多项式的定义得出m-3=3，进而求出即可．【详解】解：∵整式x m-3+5x-3是关于x的三次三项式，∴m-3=3，解得：m=6．故选：C．【点睛】本题考查了多项式的概念，几个单项式的和叫做多项式，多项式中的每个单项式都叫做多项式的项，其中不含字母的项叫做常数项，多项式的每一项都包括前面的符号，多项式中次数最高的项的次数叫做多项式的次数．2、C【分析】根据单项式的判断，单项式的系数与次数，多项式的次数、项数等概念逐项分析判断即可【详解】解：A. 0是单项式，故该选项不正确，不符合题意；B. 单项式xy的次数是2，故该选项不正确，不符合题意；C. 单项式22a b的系数是12，故该选项正确，符合题意；D. 多项式2321x y x +-的一次项次数是2，故该选项不正确，不符合题意；故选C【点睛】本题考查了单项式的判断，单项式的系数与次数，多项式的次数、项数等概念，掌握以上知识是解题的关键．单项式中，所有字母的指数和叫单项式的次数，数字因数叫单项式的系数，单项式中所有字母的指数的和叫做它的次数，通常系数不为0，应为有理数， 多项式的每一项都有次数，其中次数最高的项的次数，就是这个多项式的次数，一个多项式的项数就是合并同类项后用“＋”或“－”号之间的多项式个数，次数就是次数和最高的那一项的次数； 一个多项式中，次数最高的项的次数，叫做这个多项式的次数；多项式的项数就是多项式中包含的单项式的个数．3、D【分析】根据去括号法则进行计算即可．【详解】解：代数式-(a -b )进行去括号运算，结果是–a +b ．故选：D【点睛】本题考查了去括号法则，解题关键是明确括号前面是负号时，括号内各项都变号．4、B【分析】根据单项式系数及次数定义解答．【详解】 解：单项式2223x yz -的系数和次数分别是23-，2+1+2=5， 故选：B ．【点睛】此题考查了单项式的次数及系数的定义，熟记定义是解题的关键．5、D【分析】根据完全平方公式可判断A ，根据同底数幂的乘法同底数幂相乘底数不变指数相加可判断B ，根据同底数幂除法运算法则同底数幂相乘底数不变指数相减可判断C ，根据积的乘方每个因式分别乘方与幂的乘方法则底数不变指数相乘可判断D ．【详解】A. ()22222444a b a ab b a b +=++≠+，故选项A 不正确；B. 454a a a a ⋅=≠，故选项B 不正确；C. 664322a a a a a -=≠÷=，故选项C 不正确；D. ()()2236232a b a b a b ==，故选项D 正确． 故选：D ．【点睛】本题考查整式中幂指数运算与乘法公式，掌握整式中幂指数运算与乘法公式是解题关键．6、D【分析】利用合并同类项的法则，同底数幂的乘法的法则，同底数幂的除法的法则，幂的乘方的法则对各项进行运算即可．【详解】解：A 、x 5+x 5＝2x 5，故A 不符合题意；B 、x 2•x 5＝x 7，故B 不符合题意；C 、x 20÷x 2＝x 18，故C 不符合题意；D 、（x 5）2＝x 10，故D 符合题意；故选D ．【点睛】本题主要考查了合并同类项，同底数幂乘法，同底数幂除法，幂的乘方，熟知相关计算法则是解题的关键．7、D【分析】根据同底数幂的乘法逆运算进行整理，再代入求值即可．【详解】解：∵26m =，23n =，∴2226318m n m n +=⋅=⨯=．故选：D ．【点睛】本题主要考查求代数式的值，同底数幂乘法的逆用，解题的关键是把式子整理成整体代入的形式．8、C【分析】根据同底数幂乘法的计算方法，即可得到答案．【详解】34347a a a a +==⋅ 故选：C ．【点睛】本题考查了同底数幂乘法的知识；解题的关键是熟练掌握同底数幂乘法的计算方法，从而完成求解．9、B【分析】由题意根据图形和算式的变化发现规律，进而根据得到的规律进行计算即可．【详解】解：观察以下算式：1=1=121+3=4=221+3+5=9=321+3+5+7=16=421+3+5+7+9=25=52发现规律：1+3+5+7+9+…+19=100=102．∴1+3+5+7+9+…+19+21+23+25+27+…+101=512∴21+23+25+27+…+101=512-102=2501．故选：B．【点睛】本题考查规律型-图形的变化类、有理数的混合运算，解决本题的关键是根据图形和算式的变化寻找规律，并运用规律．10、B【分析】根据幂的运算法则即可求解．【详解】A. ()42a=8a，故错误；B. 7a a÷=6a，正确；C. 82-不能计算，故错误；a aD. 23a a⋅=5a，故错误；故选B．【点睛】此题主要考查幂的运算，解题的关键是熟知其运算法则．二、填空题1、55【分析】根据第一行有1个圆，第二行有1个圆，第三行有1+1=2个圆，第四行有1+2=3个圆，第五行有2+3=5个圆，第六行有3+5=8个圆，可知从第三行起，第n行圆的个数是第n-2行和第n-1行圆的个数和，由此求解即可．【详解】解：由题意得：第一行有1个圆，第二行有1个圆，第三行有1+1=2个圆，第四行有1+2=3个圆，第五行有2+3=5个圆，第六行有3+5=8个圆，∴第七行有5+8=13个圆，∴第八行有8+13=21个圆，第九行有13+21=34个圆，第10行有21+34=55个圆，故答案为：55．【点睛】本题主要考查了图形类的规律问题，解题的关键在于能够根据题意找到规律求解．2、b【分析】根据数轴可得b＜0＜a，根据有理数的加法法则可得b−a＜0，再计算绝对值后化简即可求解．【详解】解：由数轴可得0<<，b a则0b a-<，则||--b a aa b a=--=-．b故答案为：b-．【点睛】本题考查了数轴，绝对值，解答本题的关键是根据a、b在数轴上的位置进行绝对值的化简．3、256【分析】根据题意，可知一圈后留下的人是2的倍数的号；两圈后留下的人分别是4的倍数的号；三圈后留下的人是8的倍数的号；四圈后留下的人是16的倍数的号，…即只有256．【详解】解：由题意可知一圈后留下的人是2的倍数的号；两圈后留下的人分别是4的倍数的号；三圈后留下的人是8的倍数的号；四圈后留下的人是16的倍数的号∴经过n轮后（n为正整数），剩下同学的编号为2n；∵2n＜500，即n＜9，∴当圆圈只剩一个人时，n＝8，∴这个同学的编号为2n＝28＝256．故答案为：256．【点睛】本题主要考查了数字类的规律型问题，有理数的乘方，解题的关键在于发现留下的人的编号与2之间的关系．4、y3-4xy2-7x2y-x3【分析】先分清多项式的各项，然后按多项式中x的升幂排列的定义排列．【详解】解：多项式-x3+y3-4xy2-7x2y的各项为-x3，y3，-4xy2，-7x2y，按x的升幂排列为：y3-4xy2-7x2y-x3．故答案为：y3-4xy2-7x2y-x3．【点睛】本题考查了多项式的升序或降序排列．解题的关键是掌握多项式的升序或降序排列的方法，我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．5、64【分析】根据完全平方公式解答即可．【详解】解：∵（x+8）2=x2+16x+64=x2＋16x＋k，∴k=64．故填64．【点睛】本题主要考查了完全平方公式，掌握完全平方公式的结构特点成为解答本题的关键．三、解答题1、（1）1133xy-（2）22242x y yz z---【解析】【分析】（1）先计算中括号内的整式乘法，再运用多项式除以单项式的法则计算即可；（2）运用平方差公式计算即可．【详解】解：（1）()()()222223x x y xy xy y x xy xy ⎡⎤----÷⎣⎦=()()22322322233x y x y x y x y x y xy xy ⎡⎤----+÷⎣⎦=22322322233x y x y x y x y x y xy xy ⎡⎤--++-÷⎣⎦=23223x y xy xy ⎡⎤-÷⎣⎦=1133xy -（2）()()22x y z x y z ++--=()()222x y z -+=()22242x y yz z -++ =22242x y yz z ---．【点睛】本题考查了整式的乘除和乘法公式，解题关键是熟练掌握整式运算法则，熟练运用乘法公式进行计算．2、（1）2x 2﹣7xy +24，33；（2）5xy +y 2，－6【解析】【分析】（1）先去括号，再合并同类项把原式化简，最后代入计算即可．（2）先去括号，再合并同类项把原式化简，最后代入计算即可．【详解】（1）解：原式＝6x 2﹣3xy +24﹣4xy ﹣4x 2＝2x 2﹣7xy +24，当x ＝1，y ＝﹣1时，原式＝2×12﹣7×1×（﹣1）+24＝2+7+24＝33．（2）原式＝4xy ﹣2x 2﹣5xy +y 2+2x 2+6xy＝5xy +y 2，当x ＝1，y ＝﹣2时，原式＝5×1×（﹣2）+（﹣2）2＝﹣10+4＝﹣6．【点睛】本题考查的是整式的化简求值，掌握整式的加减混合运算法则是解题的关键．3、3【解析】【分析】先去括号，然后合并同类项化简，最后将已知式子的值代入求解即可．【详解】解：()()22227332432a ab b a ab b ++-++， 2222733864a ab b a ab b =++---，223a b ab =---，()223a b ab =-+-， 当223a b +=，2ab =-时，原式()332=--⨯-，3=．【点睛】题目主要考查整式的化简求值，熟练掌握整式的化简方法是解题关键．4、（1）12xy =；（2）17；（3）92【解析】【分析】（1）仿照题意，利用完全平方公式求值即可；（2）先求出()()54541x x x x ---=--+=，然后仿照题意利用完全平方公式求解即可； （3）设AC 的长为a ，BC 的长为b ，则AB =AC +BC =a +b =6，()222236a b a ab b +=++=，由1218S S +=，得到2218a b +=，由此仿照题意，利用完全平方公式求解即可．【详解】解：（1）∵8x y +=，2240x y +=，∴()22864x y +==，∴22264x xy y ++=，∴()222222644024xy x xy y x y =++-+=-=，∴12xy =；（2）∵()()458x x --=，()()54541x x x x ---=--+=，∴()()()()()()22254524551x x x x x x ---=----+-=⎡⎤⎣⎦，()()41625x x --=， ∴()()()22452(45117)x x x x -+-=--+=，故答案为：17；（3）设AC 的长为a ，BC 的长为b ，∴AB =AC +BC =a +b =6，∴()222236a b a ab b +=++= ∵1218S S +=，∴2218a b +=，∴()()222218ab a b a b =+-+=， ∴1922ab =，又∵四边形BCFG 是正方形，∴CF =CB ， ∴1119=2222S AC CF AC BC ab ⋅=⋅==阴影．【点睛】本题主要考查了完全平方公式的变形求值，解题的关键在于能够准确读懂题意．5、x 2y +5xy 2，42．【解析】【分析】先运用去括号法则去括号，然后合并同类项，化简整式，最后代入求值即可．【详解】解：原式=4x2y-xy2-3x2y+6xy2=x2y+5xy2．当x=3，y=-2时，原式=32⨯(-2)+5⨯3⨯(-2)2=-18+60=42．【点睛】本题考查了整式加减的化简求值．去括号时应注意：①不要漏乘；②括号前面是“-”，去括号后括号里面的各项都要变号．。

初级统计师《统计专业知识和实务》第六章习题（3）2017初级统计师《统计专业知识和实务》第六章习题7.下列关于综合指数的说法中，正确的有()。

A.是编制总指数的基本形式B.以两个总量指标形式对比形成的指数C.既有数量指标指数，又有质量指标指数D.在一定意义上，平均指数是综合指数的变形E.特点之一是先对比后综合【答案】ABCD【解析】E项，综合指数的特点是先综合后对比，平均指数的特点是先对比后综合。

8.在指数体系中，为保持有关指数在量上的对等关系，质量指标指数和数量指标指数()。

A.要用不同时期同度量因素计算B.都要以固定时期的指标作同度量因素C.都以报告期指标作同度量因素，并推算出共变影响的指数D.都以基期指标作同度量因素，并推算出共变影响的指数E.都要用综合指数公式进行计算【答案】AE【解析】在指数体系中，为保持有关指数在量上的对等关系，质量指标指数和数量指标指数都要用综合指数公式进行计算，遵守编制综合指数的一般原则：数量指标指数应以基期质量指标同度量(加权);质量指标指数应以报告期数量指标同度量(加权)。

9.同度量因素的作用有()。

A.平衡作用B.权数作用C.稳定作用D.同度量作用E.调和作用【答案】BD【解析】同度量因素是指媒介因素，借助媒介因素，把不能直接加总或直接对比的因素过渡到可以加总和对比。

同度量因素的作用有：①同度量作用;②权数作用。

10.加权算术平均数指数是一种()。

A.综合指数B.总指数C.平均指数D.加权调和平均指数E.质量指标指数【答案】BC【解析】平均指数是编制总指数的一种常用的形式，它是指以个体指数为基础，通过对个体指数加权平均计算的总指数，它又分为两种基本形式，一种是加权算术平均指数;另一种是加权调和平均指数。

11.平均指数()。

A.是两个平均数的比值B.是一种总指数C.是采用“先对比，后综合”的方法编制而成的D.主要有三种形式：算术平均指数，调和平均指数和几何平均指数E.计算结果大于综合指数【答案】BC【解析】A项，因为平均指数是指以个体指数为基础，通过对个体指数加权平均计算的总指数;D项，因为平均指数有两种基本形式：加权算术平均指数和加权调和平均指数;E项，因为在一定条件下，平均指数是综合指数的变形，其计算结果等于综合指数。

1.统计总论练习单项选择题1．对某市工业生产设备情况进行统计研究，这时，总体单位是该市（ 4 ）①每一个工业企业②每一台设备③每一台生产设备④每一台工业生产设备2．几位工人的工资分别是100元、120元、150元、200元这几个数字是（3 ）①指标②变量③变量值④标志3.标志是（ 3 ）①总体的特征②总体的数量特征③总体单位的属性或特征的名称④总体单位的数量特征多项选择题在全国人口普查中（235 ）①全国所有人口数是总体②每一个人是总体单位③人的年龄是变量④某人的性别为“女性”是一个品质标志⑤全部男性人口的平均寿命是统计指标2.统计调查练习一、单项选择题1、统计调查方案中调查期限是指_1____。

①调查工作的起迄时间②搜集资料的时间③时期现象资料所属的时间④时点现象资料所属的时间2、重点调查中的重点单位是指___4__。

①这些单位是工作的重点②这些单位举足轻重③这些单位数量占总体全部单位的比重很大④这些单位的标志总量在总体标志总量中占较大比重3、研究某型号炮弹的平均杀伤力，可以采用__4___。

①重点调查②普查③典型调查④抽样调查4、对某地食品物价进行一次全面调查，调查单位是__4__。

①该地区所有经营食品的商店②每一个经营食品的商店③全部零售食品④每一种零售食品二、多项选择题1、抽样调查和重点调查的主要区别有_24____。

①抽选调查单位的多少不同②抽选调查单位的方式方法不同③调查的组织形式不同④在对调查资料使用时，所发挥的作用不同⑤原始资料的来源不同2、第四次全国人口普查的标准时点是1990年7月1日零点，下列人员不应计入人口总数之中_135____。

①1990年7月1日23时出生的人口②1990年7月10日死亡的人口③1990年6月25日出生，30日23时死亡的人口④1990年6月29日出生，7月2日死亡的人口⑤1990年6月30日零点死亡的人口3、以系统为单位调查某市全部商业状况，调查对象是__34___。

第六章统计指数一、单项选择题(以下每小题各有四项备选答案，其中只有一项是正确的。

)1．广义上的指数是指( )。

A．价格变动的相对数B．物量变动的相对数C．所有通过比较计算的相对数D．综合说明复杂现象总体数量总变动程度的一种特殊相对数[答案] C[解析] 广义指数是指一切通过比较计算的相对数，均可称为指数。

例如，比较相对数、计划完成程度相对数、发展速度等等，前两种属于静态指数，后一种属于动态指数。

D项是狭义指数的概念。

2．编制总指数的两种形式是( )。

A．数量指标指数和质量指标指数 B．综合指数和平均数指数C．算术平均数指数和调和平均数指数 D．定基指数和环比指数[答案] B[解析] 统计指数的分类：①按所编制总指数的形式不同，分为综合指数和平均数指数；②按所考查现象的范围不同，分为个体指数与总指数；③按所反映现象的特征不同，分为数量指标指数与质量指标指数。

3．某地区某年多种工业产品成本计划完成百分数是一种( )。

A．个体指数 B．静态指数 C．动态指数 D．数量指标指数[答案] B[解析] 静态指数是指反映同类现象的数量在相同时间内不同空间的差异程度的指数。

题中，某地区某年多种工业产品成本计划完成百分数是一种静态指数，也是一种总指数和质量指标指数。

4．某商店2009年1月份微波炉的销售价格是350元，6月份的价格是342元，指数为 97.71%，该指数是( )。

A．综合指数 B．平均指数 C．总指数 D．个体指数[答案] D[解析] 个体指数是指反映单个事物变动程度的相对数。

题中指数97.71%仅仅反映微波炉价格降低了，故属于个体指数。

5．在一般情况下，商品销售量指数和工资水平指数的同度量因素分别为( )。

A．商品销售量、平均工资水平B．商品销售量、职工人数C．单位商品销售价格、平均工资水平D．单位商品销售价格、职工人数[答案] D[解析] 编制综合指数的一般原则：数量指标指数应以基期的质量指标同度量(加权)；质量指标指数应以报告期的数量指标同度量(加权)，所以商品销售量指数和工资水平指数的同度量因素分别为基期的单位商品销售价格、报告期的职工人数。

第六章统计指数一单项选择1、与数学上的指数函数不同，统计指数是（ C ）A、总量指标B、平均指标C、一类特殊的比较相对数D、百分数2、数量指标指数和质量指标指数的划分依据是( A )。

A.指数化指标的性质不同B.所反映的对象范围不同C.所比较的现象特征不同D.编制指数的方法不同3、编制总指数的两种形式是（ B ）。

A.数量指标指数和质量指标指数B.综合指数和平均数指数C.算术平均数指数和调和平均数指数D.定基指数和环比指数4、数量指标指数的同度量因素一般是（ A ）A、基期质量指标B、报告期质量指标C、基期数量指标D、报告期数量指标5. 以个体指数与报告期销售额计算的价格指数是（ D ）。

A.综合指数B.平均指标指数C.加权算术平均数指数D.加权调和平均数指数6.在设计综合指数的形式时，最关键的问题是( C )。

A.确定指数的公式形式B.确定对比基期C.确定同度量因素D.确定数量指标与质量指标7、若居民在某月以相同的开支额购买到的消费品比上月减少了10%，则消费价格指数应该为（ C ）A.110%B.90%C.111%D.100%8.销售量指数中指数化指标是( C )。

A.单位产品成本B.单位产品价格C.销售量D.销售额9.若物价上涨20%，则现在100元（）。

A.只值原来的0.80元B.只值原来的0.83元C.与原来的1元等值D.无法与过去比较10.已知劳动生产率可变构成指数为134.5%，职工人数结构影响指数为96.3%，则劳动生产率固定构成指数为( )。

A.139.67%B.129.52%C.71.60%D.39.67%1.商品销售额实际增加400元，由于销售量增长使销售额增加420元，由于价格（ C）。

A.增长使销售额增加20元B.增长使销售额增长210元C.降低使销售额减少20元D.降低使销售额减少210元2.某企业生产的甲、乙、丙3种产品价格，今年比去年分别增长3%、6%、7.5%，已知今年产品产值为：甲产品20400元、乙产品35000元、丙产品20500元，则3种产品价格总指数为（ C ）。

《统计学概论》第六章课后练习答案一、思考题1．什么是统计指数？其作用是什么？2．统计指数有哪些分类？3．综合指数的基本形式有哪几种？试就社会经济现象举一两个例子来说明。

4．什么是同度量因素？其作用是什么？5．编制综合指数时如何确定同度量因素的时期问题？6．什么是平均指数？它有哪些形式？7．试述平均指数与综合指数之间的相互关系？8．什么是指数体系？它与因素分析有什么关系？9．平均指标变动的因素分析应编制哪几种平均指标指数？如何分析？10．综合指数或平均指标指数因素分析的对象如何分辨？二、单项选择题1．在统计实践中，通常人们所说的指数一词的含义指的是（）。

A．广义的指数B．狭义的指数C．广义和狭义的指数D．拉氏和派氏指数2．从指数包括的范围不同,可以把指数分为（）。

A．个体指数和总指数B．简单指数和加权指数C．动态指数和静态指数D．定基指数和环比指数3．由两个平均指标对比形成的指数是（）。

A．平均指数值B．个体指数C．可变构成指数D．综合指数【解析】由两个平均指标对比形成的指数称为平均指标指数，具体包括三类：可变构成指数、固定构成指数和结构变动影响指数。

4．按个体价格指数和报告期销售额计算的价格指数是（）。

A．平均指标指数B．加权算术平均数指数C．综合指数D．加权调和平均数指数5．按个体产量指数和基期总产量值计算的产量指数是（）。

A．平均指标指数B．加权算术平均数指数C．综合指数D．加权调和平均数指数6．由三个指数组成的指数体系中，两个因素指数的同度量因素通常（）。

A．都固定在基期B．都固定在报告期C．一个固定在基期，另一个固定在报告期D．采用基期和报告期的平均7．拉氏指数所采用的同度量因素是固定在（）。

A．基期B．报告期C．假定期D．任意时期8．因素分析法的依据是（）。

A．指标体系B．指数体系C．拉氏指数D．派氏指数9．∑p1q1－∑p0q1表明（）。

A．由于销售量的变化对销售额的影响B．由于价格的变化对销售额的影响C．由于销售量的变动对价格的影响D．由于价格的变化对销售量的影响10．∑p0q1－∑p0q0表明（）。

.第六章指数分析一、填空题1、狭义的指数是反映及的社会经济现象的总动态的。

2、统计指数按其所反映对象范围不同，分为和。

3、统计指数按其所反映的不同，分为数量指标指数和指数。

4、统计指数按其所使用的基期不同，分为与。

5、综合指数分指数和指数。

6、编制数量指标和质量指标指数的一个重要的问题就是。

7、编制销售量指数，一般用作。

8、编制质量指标指数，一般用作。

9、在总体动态与各动态间形成的内在联系叫。

10、∑∑∑∑-+-=-)(_________________)(1111qppqqpqp11、._______111⨯=∑∑∑∑qppqqpqp12、商品销售量指数=商品销售额指数÷。

13、∑∑⨯=1pqpqqqKq是指数。

14、调和平均数指数用来编制质量指标指数时，是以指标为。

15、固定结构指数，就是把作为权数的这个因素。

16、分析工人总体结构变动对总平均工资变动的影响，必须把各组工人的这个因素固定在。

17、平均指标的动态，取决于和的变动程度。

18、算术平均数指数是用来编制指标指数的，它是以指标为。

19、若干有数量联系的统计指数所组成的整体称为。

利用它不仅可以进行指数间的，还可以分析各种因素的变动对的影响。

二、单项选择题（在每小题备选答案中，选出一个正确答案）1. 狭义的指数的含义是指( )。

a动态指数b总指数c定基指数d个体指数2. 反映个别事物动态变化的相对数称为( )。

a总指数b综合指数c定基指数d个体指数3. 总指数编制的两种形式是( )。

a算术平均法指数和调和平均法指数b个体指数和总指数c综合法指数和平均法指数d可变构成指数、固定构成指数和结构影响指数4. 综合法指数是总指数的( )。

a惟一形成b基本形成c变通形成d简单加总5. 说明现象总的规模和数量变动情况的统计指数是( )。

.a质量指标指数b平均数指数c数量指标指数d综合法指数6.编制销售量指数，一般是用( )。

a基期价格作用同度量因素b报告期价格作用度量因素c报告期销售量作同度量因素d基期销售量作同度量因素7. 编制价格指数，一般是用( )。

《应用统计学》练习题及答案《应用统计学》本科第一章导论一、单项选择题1．统计有三种涵义，其基础是( )。

(1)统计学 (2)统计话动 (3)统计方法 (4)统计资料 2．一个统计总体( )。

(1)只能有个标志 (2)只能有一个指标 (3)可以有多个标志 (4)可以有多个指标 3．若要了解某市工业生产设备情况，则总体单位是该市( )。

(1)每一个工业企业 (2)每一台设备 (3)每一台生产设备 (4)每一台工业生产设备 4．某班学生数学考试成绩分刷为65分、71分、80分和87分，这四个数字是( )。

(1)指标(2)标志(3)变量(4)标志值 5．下列属于品质标志的是( )。

(1)工人年龄 (2)工人性别 (3)工人体重(d)工人工资6．现要了解某机床厂的生产经营情况，该厂的产量和利润是( )。

(1)连续变量 (2)离散变量 ()3前者是连续变量，后者是离散变量 (4)前者是离散变量，后者是连续变量7．劳动生产率是( )。

(1)动态指标 (2)质量指标 (3)流量指标 (4)强度指标 8．统计规律性主要是通过运用下述方法经整理、分析后得出的结论( )。

(1)统计分组法 (2)大量观察法 (3)练台指标法(4)统计推断法 9．( )是统计的基础功能。

(1)管理功能 (2)咨询功能 (3)信息功能 (4)监督功能 10．( )是统计的根本准则，是统计的生命线。

(1)真实性 (2)及时件 (3)总体性 (4)连续性11．构成统计总体的必要条件是( )。

(1)差异性(2)综合性 (3)社会性 (4)同质性12．数理统计学的奠基人是( )。

(1) 威廉·配第 (2)阿亭瓦尔(3)凯特勒 (4)恩格尔13．统汁研究的数量必须是( )。

(1)抽象的量(2)具体的量(3)连续不断的量(4)可直接相加量 14．数量指标一般表现为( )。

(1)平均数(2)相对数(3)绝对数(1)众数 15．指标是说明总体特征的．标志则是说明总体单位特征的，所以( )。