热力学与统计物理-第一章-热力学与统计物理

《热力学与统计物理》课程教学大纲课程英文名称：Thermodynamics and Statistical Physics课程编号：0312043002课程计划学时：48学分：3课程简介：《热力学与统计物理》课是物理专业学生的专业基础课，与理论力学、量子力学、电动力学共同构成物理专业重要的四门必修课，通常称为物理专业的四大力学课。

热力学和统计物理的任务是研究热运动的规律，研究与热运动有关的物性及宏观物质系统的演化。

本课程的作用是使学生掌握热力学与统计物理的基本原理和处理具体问题的一些重要方法，并初步具有用这些方法解决较简单问题的能力。

一、课程教学内容及教学基本要求第一章热力学的基本规律本章重点：热力学的基本规律，热力学的三个定律，掌握热力学函数内能、焓、熵、自由能、吉布斯函数的物理意义.难点：熵增加原理的应用及卡诺循环及其效率。

本章学时:16学时教学形式:讲授教具:黑板，粉笔第一节热力学系统的平衡状态及其描述本节要求：掌握：系统、外界、子系统，系统的分类，热力学平衡态及其描述。

1系统、外界、子系统（①掌握：系统与外界概念。

②了解：界面的分类。

③了解：系统与子系统的相对性）2系统的分类（掌握：孤立系、闭系、开系的概念。

）3热力学平衡态及其描述（①掌握：热力学平衡态概念。

②掌握：状态参量的描述及引入。

）第二节热平衡定律和温度本节要求：掌握：热接触与热平衡，热平衡定律、温度、热平衡的传递性，存在态函数温度的数学论证，温度的测量(考核概率50%)。

1热接触与热平衡（①掌握：系统间没有热接触时系统状态参量的变化。

②掌握：系统间热接触时系统状态参量的变化。

）2热平衡定律、温度、热平衡的传递性（①掌握：热平衡定律。

②掌握：温度的数学论证，温标的确定及分类）（重点）第三节物态方程本节要求：理解：广延量与强度量。

掌握：物态方程的得出，实验系数及由实验系数k 、、βα 求物态方程。

（重点，难点）（考核概率100%） 1物态方程（①掌握：独立参量的选择与态函数的相对性。

马红孺热力学与统计物理讲义热力学和统计物理是物理学的两个重要分支，牵涉到研究热量、能量和物质转化的规律以及微观粒子行为的统计规律。

本文将为您介绍马红孺教授编写的热力学与统计物理讲义。

马红孺教授是中国科学院理论物理研究所的研究员。

他在热力学和统计物理领域具有丰富的研究经验和卓越的教学能力。

他的讲义以清晰简洁、思路严谨著称，是学习和研究热力学与统计物理的重要参考资料之一。

1. 热力学基础热力学是研究宏观物质的宏观性质、宏观状态和宏观变化规律的物理学分支。

马红孺热力学讲义主要包括热力学基本概念、热力学过程和热力学定律的介绍。

其中，热力学基本概念包括系统、热平衡、热力学性质等方面的内容。

热力学过程涉及绝热过程、等温过程等过程的研究。

热力学定律包括热力学第一定律、热力学第二定律等热力学定律。

这些内容构成了热力学的基础理论。

2. 统计物理基础统计物理是研究微观粒子行为的系统物理学分支，通过统计方法描述微观粒子在宏观尺度上的表现。

马红孺热力学与统计物理讲义的统计物理基础部分主要包括微观粒子的统计分布、独立粒子模型、热力学极限等基础知识。

通过这些内容的学习，读者可以了解粒子在宏观尺度上的统计规律，并将其应用于具体问题的求解。

3. 平衡态统计物理在马红孺热力学与统计物理讲义中，平衡态统计物理是一个重要的部分。

平衡态统计物理研究的是处于平衡状态的统计系统的性质。

这部分内容主要包括正则系综、统计物理量的计算、磁介质的统计模型等。

通过这些内容的学习，读者可以了解统计系统在平衡状态下的性质，并且可以应用统计物理的方法进行计算和研究。

4. 非平衡态统计物理除了平衡态统计物理，马红孺热力学与统计物理讲义还介绍了非平衡态统计物理的内容。

非平衡态统计物理研究的是处于非平衡状态的统计系统的性质。

这部分内容主要包括非平衡态统计物理的基本概念、涨落定理、输运过程等。

通过这些内容的学习，读者可以了解统计系统在非平衡状态下的行为规律，并且可以了解非平衡态统计物理的基本方法。

第一章统计物理的基本概念(The Fundamental Concepts of Statistical Physics §1.1统计物理简介(Simple Introduction of Statistical Physics历史:源于气体分子运动论(Kinetic Theory of Gases 1738Daniel Bernoulli提出。

Ludwig Bottzmann, 1844~1906J. Willard Gibbs, 1839~1903等人做了统计物理奠基性的工作,发展了统计系综理论,从而真正开创了统计物理的系统理论。

爱因斯坦(Einstein (1879~1955 , 普朗克(Planck (1858~1947等发扬光大。

在 20世纪(约 1910年后才被科学界广泛接受。

对这一事实确立起决定作用的是爱因斯坦的布朗运动的理论解释(1905年和 Jean Perrin (皮兰的实验验证。

统计物理起源于气体分子运动论,分子运动论的主要思想有三点:(1(2原子、分子处于不断热运动中。

(3原子、分子间有相互作用。

相互作用 Æ有序热运动 Æ无序这是一对矛盾。

热力学方法与统计物理方法的优缺点 :热力学方法的优缺点:逻辑推理和严格的数学运算来研究宏观物体的热学性质以及和热现象有关的一切规律。

所以热力学的结果较普遍、可靠,但不能求特殊性质。

统计物理方法的优缺点:现象有关的一切规律。

所以统计物理方法可求特殊性质,但其可靠性依赖于结构的假设,计算较麻烦。

此二者体现了归纳与演译的不同应用,可互相补充。

在统计物理方法中反映了三个问题 :(1微观结构?(2微观粒子运动态的描述?(3统计平均?这些是我们今后要特别关注的内容。

§1.2 系统微观运动状态的经典描述(Classical Description for Microscopic Motion State of System 一、物质的微观结构这是 20世纪三大基本理论问题之一,可以从不同层次进行讨论,从统计物理讨论物质的客观性质,主要在分子、原子层次。

热力学与统计物理课后习题答案第一章1.1 试求理想气体的体胀系数α,压强系数β和等温压缩系数κT 。

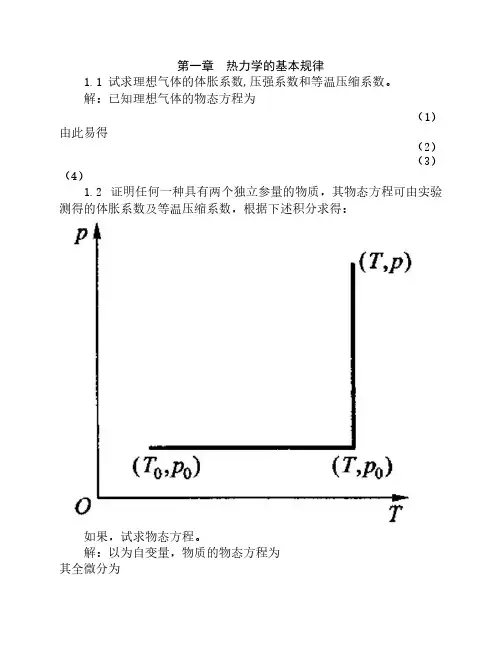
解：已知理想气体的物态方程为,pV nRT = （1）由此易得11,p V nR V T pV Tα∂⎛⎫=== ⎪∂⎝⎭ （2） 11,V p nR p T pV Tβ∂⎛⎫=== ⎪∂⎝⎭ （3） 2111.T T V nRT V p V p pκ⎛⎫⎛⎫∂⎛⎫=-=--= ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭ （4）1.2 证明任何一种具有两个独立参量,T p 的物质，其物态方程可由实验测得的体胀系数α及等温压缩系数κT ，根据下述积分求得：()ln T V =αdT κdp -⎰如果11,T T pακ==，试求物态方程。

解：以,T p 为自变量，物质的物态方程为(),,V V T p =其全微分为.p TV V dV dT dp T p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ （1） 全式除以V ，有11.p TdV V V dT dp V V T V p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭根据体胀系数α和等温压缩系数Tκ的定义，可将上式改写为.TdVdT dpVακ=-（2）上式是以,T p为自变量的完整微分，沿一任意的积分路线积分，有()ln.TV dT dpακ=-⎰（3）若11,TT pακ==，式（3）可表为11ln.V dT dpT p⎛⎫=-⎪⎝⎭⎰（4）选择图示的积分路线，从00(,)T p积分到()0,T p，再积分到（,T p），相应地体积由V最终变到V，有000ln=ln ln,V T pV T p-即00p VpVCT T==（常量），或.pV CT=（5）式（5）就是由所给11,T T pακ==求得的物态方程。

确定常量C 需要进一步的实验数据。

1.3 在0C 和1n p 下，测得一铜块的体胀系数和等温压缩系数分别为51714.8510K 7.810.n p ακ----=⨯=⨯T 和T ακ和可近似看作常量，今使铜块加热至10C 。

第一章 热力学的基本规律1.热力学的平衡状态⑴热力学的研究对象是由大量微观粒子组成的有限宏观系统.与系统发生相互作用的其他物体称为外界.按照系统与外界的相互作用状态,可将系统分为以下三种： ①孤立系：与外界既不发生质量交换,也不发生能量交换的系统； ②闭系：可与外界发生能量交换,而不发生质量交换的系统； ③开系：可与外界发生能量、质量交换的系统.⑵热力学平衡态：当一个孤立系经过足够长的时间,将会达到这样一种状态,在这种状态下,系统的各种宏观性质在长时间内部发生变化,称之为热力学平衡态.⑶状态参量：在热力学平衡态下,系统的各种宏观性质不再变化而拥有固定值,用这些固定值就可以确定系统的宏观状态.一般情况下,描述一个系统的状态参量有：热学参量温度T 、几何参量体积V 、力学参量压强p 和电磁参量D 、H .2.物态方程⑴描述系统的状态参量之间关系的方程称为物态方程,以简单的固液气系统为例,其物态方程可表示为：另外,定义几个与物态方程有关的物理量： ①等压膨胀系数：pT V V ⎪⎭⎫ ⎝⎛∂∂=1α； ②等容压力系数：VT p p ⎪⎭⎫ ⎝⎛∂∂=1β； ③等温压缩系数：Tp V V k ⎪⎪⎭⎫ ⎝⎛∂∂-=1τ. 根据物态方程,可得关系式：1-=⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂p V T V T T p p V ;故可得三个系数之间的关系为：p k βατ=.⑵气体的物态方程①理想气体状态方程：T Nk pV B =. ②实际气体的范德瓦尔斯方程：()nRT nb V V an p =-⎪⎪⎭⎫ ⎝⎛+22, 其中22Van 为压强修正项,nb 是体积修正项;⑶简单固体与液体的物态方程对于简单固体和液体,可通过实验测得体胀系数α和等温压缩系数τk ,它们的特点如下： ①固体和液体的膨胀系数是温度的函数,与压强近似无关;②α和τk 的数值都很小,在一定的温度范围内可以近似看成常量; 由此可得,物态方程为： ()()()()[]000001,,p p k T T p T V p T V ---+=τα;⑷顺磁性固体将顺磁性固体置于磁场中,顺磁性固体会被磁化;磁化强度M ,磁场强度H 与温度T 的关系： ()0,,=T H M f ;①实验测得一些顺磁性固体的磁物态方程为：H TCM =； ②另一些顺磁性固体的磁物态方程为：H T CMθ-=, 其中,C 和θ是常量,其数值因不同的物质而异; 3.功⑴气体准静态过程的体积功：pdV W -=δ;⑵液体表面张力做功：dA W σδ=,σ为单位长度的表面张力;⑶电介质准静态过程中电位移改变dD 时外界所作的功为：VEdD W =δ; 磁介质准静态过程中磁感应强度改变dB 时外界所作的功：VHdB W =δ; 4.热力学第一定律若系统经历一个无穷小的过程,则系统内能的增量与外界做功和外界传热的关系为：W Q dU δδ+=; 热力学第一定律表明,做功与热量传递在改变系统内能上是等效的; 5.热容与焓⑴热容：一个系统温度升高K 1所吸收的热量,即TQC T ∆∆=→∆0lim,热容是一个广延量,用m c 表示mol 1物质的热容,成为摩尔热容;⑵系统在等容过程的热容用符号V C 表示：VV T V T U T U C ⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∆∆=→∆0lim ;⑵系统在等压过程中的热容用符号p C 表示：pp p T p T p p T U T pdV U C ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∆+∆=→∆0lim ；引入状态函数焓：pV U H +=,则有pp T H C ⎪⎭⎫ ⎝⎛∂∂=;6.气体的内能⑴从微观角度看,在没有外场的情形下,气体无规则运动的能量包括分子的动能、分子之间相互作用的势能以及分子内部运动的能量;⑵根据焦耳的自由膨胀实验,理想气体的内能只是温度的函数,与体积无关,即从微观上看,理想气体的内能只是分子的动能;于是可得：①dT dU C V=；dTdHC p =； ②⎰+=dT C U U V 0；⎰+=dT C H H p 0;根据焓的定义：nRT U pV U H +=+=,可得nR C C V p +=,再设V p C =γ,得：1-=γnR C V ,nR C p 1-=γγ迈耶公式; 7.理想气体的准静态过程 ⑴等温过程：const pV =； ⑵等容过程：const Tp=；⑶等压过程：const T V=； ⑷绝热过程：const pV =γ;注：系数γ可通过测定空气中的声速获得;声音在空间中传播时,介质空间会发生周期性的压缩与膨胀,自然导致压强的变化;由于气体的导热系数很小,因此在声音传播过程中,热量传导很难发生,故可认为是绝热过程,因此根据牛顿的声速公式ρd dpa =可得 其中ρ为气体密度,ρυ1=为单位质量气体的体积;8.热力学第二定律⑴克劳修斯表述：不可能把热量从低温物体传到高温物体而不引起其它变化;⑵开尔文表述：不可能从单一热源吸收热量使之完全变成有用的功而不引起其它变化;热力学第二定律的开尔文表述表明,第二类永动机不可能造成;所谓第二类永动机是指能够从单一热源吸热,使之完全变成有用功而不引起其它影响的机器; 9.卡诺循环与卡诺定理 ⑴卡诺循环：卡诺循环过程以理想气体为研究对象研究热功转化的效率问题,由两个等温过程和两个绝热过程组成;在整个循环中,气体从高温热源吸收热量,对外做功,其效率为：1212111T T Q Q Q W -=-==η; ⑵卡诺定理：所有工作于两个一定温度之间的热机,以可逆机的效率为最高;推论：所有工作于两个一定温度之间的可逆热机的效率相等;⑶根据卡诺定理,工作于两个一定温度之间的热机的效率不可能大于可逆热机的效率,即由此可得克劳修斯不等式：02211≤+T Q T Q ,等号只适用于可逆循环过程 其中1Q 为热机从高温热源吸收的热量,2Q 也定义为热机从低温热源吸收的热量数值为负数; 将克劳修斯不等式推广到n 个热源的情形,可得：0≤∑i iiT Q , 对于更普遍的循环过程,应将求和号换成积分号,即0≤⎰TQδ;10.熵与热力学基本方程⑴根据克劳修斯不等式,考虑系统从初态A 经可逆过程R 到达终态B ,又从状态B 经另一可逆过程'R 回到状态A ;在上述循环过程中,有 可见,在可逆循环过程中,⎰T dQ与路径无关,由此定义状态函数熵S ,从状态A 到状态B 的熵变定义为：注：仅对可逆过程,⎰T dQ才与路径无关;对不可逆过程,B 和A 两态的熵变仍沿从A 态到B 态的可逆过程的积分来定义;在这种情形下,可逆过程与不可逆过程所引起的系统状态变化相同,但外界的变化是不同的;对前面熵变等式取微分：TQdSδ=,表示无穷小的可逆过程中的熵变;⑵根据热力学第二定律,可得可逆过程中TdS Q =δ,结合热力学第一定律可得热力学的基本微分方程：若系统与外界之间除了体积功,还有其他形式的功,可将上式表示为 ⑶热力学第二定律的数学表示：pdV TdS dU -≤,注：根据克劳修斯不等式和熵的定义,可知在任意无穷小过程中,Q TdS δ≥;⑷熵增加原理：系统在绝热条件下,熵永不减少,即0≥-A B S S 等号只适用于可逆过程;11.自由能与吉布斯函数⑴约束在等温条件下的系统,定义状态函数：TS U F -=;根据热力学第二定律可得,等温条件下pdV dF -≤,表明在等温条件下,系统自由能的增加量不大于外界对系统做的功;在等温等容过程中可得：0≤dF ,即等温等容条件下,系统的自由能永不增加,或者表述为在等温等容条件下的不可逆过程朝着使系统自由能减少的方向进行;⑵约束在等压条件下的系统,定义状态函数：pV TS U G +-=;同理可得：等温等压条件下,0≤dG ,即等温等压条件下,系统的吉布斯函数永不增加,或者表述为等温等压条件下的不可逆过程朝着使系统吉布斯函数减少的方向进行;第二章 均匀物质的热力学性质1.内能、焓、自由能和吉布斯函数的全微分⑴热力学基本方程即为内能的全微分形式：pdV TdS dU -=, 根据偏导数关系可得：VS S p V T ⎪⎭⎫⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂①； 内能的确定：dV p T p T dT C dUV V ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛∂∂+=;注：熵的确定：dV T p dT T C dS VV ⎪⎭⎫⎝⎛∂∂+=;⑵焓的全微分形式为：Vdp TdS dH +=,同理可得：p S S V p T ⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂②；焓的确定：dp T V T V dT C dH p p ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂++=; 注：熵的确定：dp T V dT T C dS pp ⎪⎭⎫⎝⎛∂∂-=;⑶自由能的全微分形式为：pdV SdT dF --=,同理可得：VT T p V S ⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂③;⑷吉布斯函数的全微分形式为：Vdp SdT dG +-=,同理可得：p TT V p S ⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫⎝⎛∂∂④; 其中,式①②③④称为麦克斯韦关系;2.气体的节流过程和绝热膨胀过程⑴气体从高压处通过多孔塞不断地流到低压处,并达到定常状态,这个过程叫做节流过程;在节流过程中,多孔塞两边的温度发生了明显变化,这个效应称为焦耳-汤姆孙效应; 经分析得,在节流过程中,气体的焓值不断,定义Hp T ⎪⎪⎭⎫⎝⎛∂∂=μ表示焓不变条件下,温度随压强的变化率,则根据1-=⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂T p H H p T H p T 可得： 上式给出了焦汤系数与物态方程和热容的关系;①对理想气体,T1=α,故0=μ,说明理想气体在节流过程前后温度不变； ②对实际气体,若1>T α,则气体在节流过程前后温度降低,称为制冷区；若1<T α,则气体在节流过程前后温度升高,称为制温区;利用节流过程的降温作用可使气体降温液化节流膨胀制冷效应; ⑵气体的绝热膨胀过程,熵保持不变,则定义Sp T ⎪⎪⎭⎫⎝⎛∂∂表示绝热过程中温度随压强的变化率,同上可得,上式表明,在绝热条件下,随着气体体积膨胀和压强降低,气体的温度必然下降;气体的绝热膨胀过程可用来使气体降温并液化绝热膨胀制冷效应; 3.热辐射的热力学理论⑴受热的固体会辐射电磁波,称为热辐射;一般情形下,热辐射的强度和强度随频率的分布于辐射体的温度和性质都有关;当辐射体对电磁波的吸收和辐射达到平衡,热辐射的特性将只取决于温度,与辐射体的其他特性无关,称为平衡辐射;⑵考虑一个封闭的空窖,窖壁保持一定的温度T ;窖壁将不断向空窖发射并吸收电磁波,当窖内辐射场与窖壁达到平衡后,二者具有相同的温度,显然空窖内的辐射就是平衡辐射;窖内的平衡辐射包含各种频率和沿着各个方向的电磁波,这些电磁波的振幅和相位是无规的;窖内平衡辐射是空间均匀和各项同性的,它的内能密度和内能密度按频率的分布只取决于温度; ⑶电磁理论中,关于辐射压强与辐射能量密度的关系为：u p 31=；由此根据热力学公式可得窖内平衡辐射的热力学函数为：4aT u =.⑷根据热力学基本方程,可得空窖辐射的熵为：V aT S 334=, 由上式可知,可逆绝热过程中辐射场的熵不变,此时有const V T =3.⑸若在窖壁上开一小孔,定义单位时间通过小孔的单位面积辐射出的能量,称为辐射能量密度u J .描述辐射能量密度u J 与辐射内能密度u 的关系称为斯特藩—玻尔兹曼定律,即444141T caT cu J u σ===,其中σ称为斯特藩常量. ⑹基尔霍夫定律：()ωωαωωωd T u cd e ,4=,其中,ωe 称为物体对频率在ω附近的电磁波的面辐射强度；ωα为物体对频率在ω附近的辐射能量的吸收系数.注：吸收系数为1的物体称为绝对黑体,此时有()ωωωωd T u cd e ,4=.4.磁介质的热力学⑴磁介质中磁场强度和磁化强度发生改变时,外界所做的功为：VHdMH Vd W 02021μμδ+⎪⎭⎫ ⎝⎛=,当热力学系统只包括介质而不包括磁场时,功的表达式只取第二项,即Hdm W 0μδ=, 其中,MV m =是介质的总磁矩.忽略磁介质的体积变化,可得热力学基本方程为,Hdm TdS dU 0μ+=,类比于理想气体,即H p 0μ→-,m V →.⑵绝热去磁制冷：根据吉布斯函数mdH SdT dG 0μ--=,可得：H T C CV H T HS 0μ=⎪⎭⎫⎝⎛∂∂, 上式说明,在绝热条件下减小磁场,磁介质的温度降低,称为绝热去磁制冷效应.第三章 单元系的相变 1.热动平衡判据⑴孤立系统的熵判据：0<∆S或0,02<=S S δδ熵增加原理；⑵等温等容系统的自由能判据：0>∆F 或0,02>=F F δδ等温等容系统自由能永不增加；⑶等温等压系统的吉布斯函数判据：0>∆G 或0,02>=G G δδ等温等压系统的吉布斯函数永不增加.⑷均匀系统的热动平衡条件：00,p p T T ==,即整个系统的温度和压强均匀. ⑸平衡的稳定性条件：0,0<⎪⎭⎫⎝⎛∂∂>TV V p C , 注：考虑系统与子系统简的变化,若子系统的温度由于涨落或外界影响而升高,则子系统通过向系统其他部分传热使温度降低；同样,若子系统的体积增大,则子系统与系统其他部分的压强差会使子系统的体积减小,从而使系统的平衡处于稳定. 2.开系的热力学基本方程⑴单元系是指化学上纯的物质系统,只含有一种化学组分.如果系统不是均匀的,可以分为若干个均匀的部分,该系统称为复相系.例如,冰、水和水蒸气共存构成一个单元三相系. ⑵物质的量发生变化的系统,其吉布斯函数的全微分可表示为：dn Vdp SdT dG μ++-=, 其中右方第三项代表由于物质的量改变dn 引起的吉布斯函数的变化. 定义pT n G ,⎪⎭⎫ ⎝⎛∂∂=μ,表示在温度、压强不变的条件下,增加mol 1物质时引起的吉布斯函数的改变,成为化学势.由于吉布斯函数是广延量,可得化学式与摩尔吉布斯函数的关系为：()p T G m ,=μ； 对单位物质的量系统的吉布斯函数可以写为：dp V dT S d m m +-=μ.⑶物质的量发生变化的系统的其他特性函数：①关于()n V S ,,的特性函数为内能,其全微分形式为：dn pdV TdS dU μ+-=； ②关于()n p S ,,的特性函数为焓,其全微分形式为：dn Vdp TdS dH μ++=； ③关于()n V T ,,的特性函数是自由能,其全微分形式为：dn pdV SdT dFμ+--=；④关于()μ,,V T 的特性函数是巨热力势,其全微分形式为：μnd pdV SdT dJ ---=.3.单元复相系的平衡热力学条件考虑一个单元两相系,这个单元两相系构成一个孤立系统.用α和β分别表示这两个相,用αααn V U ,,和βββn V U ,,分别表示两个相的内能,体积和物质的量.孤立系的总内能,总体积和总物质的量是恒定的,即 设想系统发生一个虚变动,引起两相的熵变为：⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=ββαααββαααβααβαμμδδδT T dn T p T p dV T TdU S S S 11, ⑴若复相系处于平衡条件下,则熵为极大值,即0=S δ.由此可得复相系的平衡热力学条件为：βαT T =热平衡条件 ββααTp T p =力学平衡条件ββααμμT T =相变平衡条件⑵若复相系平衡条件未能满足,则系统朝着熵增大的方向转变,即0>S δ.4.单元复相系的平衡性质第六章 近独立粒子的最概然分布1.粒子运动状态的经典描述设粒子的自由度为r ,则粒子的运动状态可用广义坐标和广义动量来描述,粒子的能量是广义坐标和广义动量的函数,即()r r p p q q ,,;,,11 εε=. 为了描述粒子的运动状态,用()r r p p q q ,,;,,11 这r 2变量构成一个r 2维的空间,称为μ空间,粒子在某一时刻的运动状态就表示为μ空间中的一个点.⑴自由粒子自由粒子不受力的作用而在三维空间中做自由运动,自由度为3,它的能量就是它的动能,即()22221zy x p p p m++=ε. ⑵线性谐振子粒子在线性回复力kx F-=的作用下做简谐运动,振动的圆频率为mk =ω.对自由度为1的线性谐振子,任意时刻的能量与粒子的位置和动量有关,即222212x m m p ωε+=.⑶转子粒子绕原点O 做转动,它的能量就是它的动能,可用球坐标表示,即()222222sin 21ϕθθε r r rm ++=. ①若考虑到粒子到原点的距离不变0=r ,则能量表示为： ()22222sin 21ϕθθε r r m +=； ②引入与ϕθ,共轭的动量：ϕθθϕθ 222sin ,mr p mr p ==,可将转子的能量写为： 其中,2mr I =是转子相对于原点的转动惯量.2.粒子运动的量子描述量子力学的观点中,微观粒子满足波粒二象性,有kp ==ωε；波粒二象性的粒子满足不确定关系,即不能同时具有确定的坐标与动量,分别用q ∆和p ∆表示坐标和动量的不确定度,则有h p q ≈∆⋅∆.在量子力学中,微观粒子的运动状态称为量子态,量子态由一组量子数表征,这组量子数的数目等于粒子的自由度数. ⑴线性谐振子圆频率为ω的线性谐振子,能量的可能值为：ωε ⎪⎭⎫ ⎝⎛+=21n n , ,1,0=n ；线性谐振子的自由度为1,n 是表征谐振子运动状态和能量的量子数. ⑵转子量子理论中,转子的能量为：(),1,0212=+=l Il l ，ε量子理论中,转子的角动量是分立的,()221 +=l l L ,对一定的l ,角动量在本征方向的投影z L 只能取分立值：l m m L z ±==,,0, ,转子的运动状态由m l ,两个量子数表征,能量只取决于量子数l ,因此转子的自由度为12+l .⑶自旋角动量基本粒子具有内禀的角动量,称为自旋角动量S,其平方的数值等于()221 +=S S S ,其中S 称为自旋量子数,可以是整数或半整数.自旋角动量的状态由自旋角动量的大小自旋量子数S 及自旋角动量在本征方向的投影确定,其中投影的大小表示为：S m m S S S z ±==,,0, , 因此,自旋角动量的自由度为12+S . ①电子的自旋角动量和自旋磁矩电子的自旋磁矩μ与自旋角动量S 之比为：me S-=μ； 电子在外磁场中的能量为：B me B H 2±=⋅-=μ.⑷自由粒子根据“箱归一化”条件,设自由粒子处于边长为L 的正方体容器中,则自由粒子的三个动量分量z y x p p p ,,的可能值为：,1,0,2,1,0,2,1,0,2±==±==±==z z z y y y x x x n n L p n n L p n n L p πππ；其中,z y x n n n ,,为表征自由粒子运动状态的量子数. 自由粒子能量的可能值为：()222222222221Ln n n m p p p m z y x z y x ++=++= πε, 自由粒子的运动状态由量子数z y x n n n ,,表征,能量只取决于222z y x n n n ++.①若粒子处于宏观大小的容器中运动,这时要考虑在体积3L V =内,在动量区间x x dp p +,y y dp p +和z z dp p +内的自由粒子量子态数：()dp p h V dp dp dp V dn dn dn z y x z y x 2332==π, 再根据m p22=ε,可得处于能量区间εεd +中的粒子状态数为：()()εεπεεd m hV d D 2123322=.3.系统微观运动状态的描述系统的微观运动状态就是它的力学运动状态.①全同粒子组成的系统就是由具有完全相同内禀属性相同的质量、电荷、自旋等的同类粒子组成的系统；②近独立粒子组成的系统是指系统中粒子之间相互作用很弱,系统的总能量等于各个粒子的能量之和,即∑==Ni i E 1ε.⑴系统微观运动状态的经典描述设粒子的自由度为r .第i 个粒子的力学运动状态由()r r p p q q ,,;,,11 这r 2个变量表示,考虑由N 个粒子组成的系统,则系统微观运动状态的确定需要Nr 2个变量,即()N i p p q q ir i ir i ,,2,1,,;,,11 =.单个粒子的运动状态可用μ空间中的一个点表示,则对于整个系统在某一时刻的运动状态可用μ空间中N 点表示.如果交换两个代表点在μ空间中的位置,相应的系统的运动状态是不同的. ⑵系统微观运动状态的量子描述①微观粒子的全同性原理：全同粒子是不可分辨的,在含有多个全同粒子的系统中,将任何两个全同粒子加以交换都不改变整个系统的微观运动状态.②假设全同粒子可以分辨,确定由全同近独立粒子组成的系统的微观运动状态归结为确定每个粒子的个体量子态；若全同粒子不可分辨,则归结为确定每个量子态上的粒子数.③自然界中的粒子分为两类：玻色子和费米子,其中自旋量子数是半整数的属于费米子,自旋量子数是整数的属于玻色子.a.由费米子组成的系统称为费米系统,遵从泡利不相容原理,即在含有多个全同近独立费米子的系统中,一个个体量子态最多可容纳一个费米子；b.由玻色子组成的系统称为玻色系统,粒子是不可分辨的,每个个体量子态可容纳的玻色子个数没有限制.4.分布与微观状态数⑴以() ,2,1=l l ε表示粒子的能级,l ω表示能级l ε的简并度,N 个粒子在各能级的分布如下：能级： ,,,,21l εεε简并度： ,,,,21l ωωω经典粒子表示为： ,,,,21r l r r hh h ωωω∆∆∆ 粒子数： ,,,,21l a a a以符号{}l a 表示系统的一个分布,它给出了系统中每个能级上的粒子数,为了确定系统的微观运动状态,还要清楚l a 个粒子如何占据能级l ε的各个简并态的. 对于具有确定的V E N ,,的系统,分布{}l a 满足约束条件：∑=ll a N ,∑=ll l a E ε⑵对于玻尔兹曼系统,粒子是可分辨的,且每个量子态上可容纳的粒子数没有限制,因此可以得到与分布{}l a 相应的系统的微观状态数为：∏∏=Ωla l ll B M l a N ω!!,, 其中最概然分布为：le a l l βεαω--=,其中βα,由约束条件∑∑----==ll l l ll le E e N βεαβεαεωω,确定.⑶对于玻色系统,粒子是不可分辨的,每个量子态上可容纳的粒子数没有限制,因此可得与分布{}l a 相应的系统微观状态数为：()()∏--+=Ωll l l l E B a a !1!!1,ωω, 其中最概然分布为：1-=+le a ll βεαω.⑷对于费米系统,粒子不可分辨,每个量子态上只能容纳一个粒子,因此可得与分布{}l a 相应的微观运动状态数为：()∏-=Ωll l l l D F a a !!!,ωω,其中最概然分布为：le a llβεαω++=1.注：对于三种系统的最概然分布,若满足条件11<<>>lla e ωα或,则玻色分布和费米分布近似于玻尔兹曼分布,这个条件称为经典极限条件或非简并性条件.⑸考虑个体量子态问题或者平均粒子数问题,设处在能量s ε的量子态s 上的粒子数为s f ,则各种系统的最概然分布可表示为：玻尔兹曼系统：se f s βεα--=玻色系统：11-=+s e f s βεα；费米系统：sef s βεα++=11. 第七章 玻尔兹曼统计1.热力学量的统计表达式定域系统和满足经典极限条件的玻色系统和费米系统都满足玻尔兹曼分布. 定义配分函数：∑-=ll l e Z βεω1或积分形式()⎰-⋅=r r p p q q rr r e h dp dp dq dq Z ,;,011111βε则系统的热力学量的统计表达式如下： ⑴内能：由玻尔兹曼分布的内能表达式∑--=lll le U βεαεω,可得：1ln Z NU β∂∂-=. ⑵外界对系统的广义作用力Y 为：1ln Z yN a y Y l ll ∂∂-=∂∂=∑βε. ⑶熵的统计表达式：⎪⎪⎭⎫ ⎝⎛∂∂-=11ln ln Z Z Nk S ββ. 2.理想气体的状态方程①利用统计力学求解热力学问题,首先要找到配分函数. 理想气体的配分函数为：②然后,再利用热力学量的统计表达式,得到相关热力学量： 3.麦克斯韦分布律根据玻尔兹曼分布,可以推导出麦克斯韦分布律气体分子的速度分布律.⑴以理想气体为研究对象,气体分子为自由粒子.在体积为V 的容器中,分布在动量区间z y x dp dp dp 内的微观状态数为：z y x dp dp dp h V3； 则分布在z y x dp dp dp 内的分子数为：而气体分子的总数为：因此可得,动量在z y x dp dp dp 范围内的分子数为：以VNn =表示单位体积内的分子数,则在单位体积内,速度在z y x dv dv dv 内的分子数为： ()()z y x v v v kT mz y x z y x dv dv dv ekT m n dv dv dv v v v f z y x 2222232,,++-⎪⎭⎫ ⎝⎛=π, 上式便是麦克斯韦速度分布律,其中()z y x v v v f ,,满足：()n vdv dv v v v f zy xzyx=⎰⎰⎰,,.⑵利用速度空间的球坐标转化,可得速率分布律：()dv v ekT m n dv v f mv kT 22123224-⎪⎭⎫ ⎝⎛=ππ, 分析速率分布律,可得以下特征数： ①最概然速率：mkTv m 2=； ②平均速率：m kTv π8=； ③方均根速率：mkTv v s 32==. ⑶计算单位时间内碰到单位面积器壁上的分子数,称为碰壁数.以dAdt d Γ表示在dt 时间内碰到dA 面积上,速度在z y x dv dv dv 范围内的分子数.这分子数就是位于以dA 为底、以()z y x v v v v ,,为轴线、以dt v x 为高的柱体内,速度在z y x dv dv dv 范围内的分子数.所以有：故可得单位时间内碰到单位面积上的分子数Γ为：mkTndv fv dv dv x x z y π20==Γ⎰⎰⎰∞+∞+∞-∞+∞-, 也可以表示为： 4.能均分定理能均分定理：对于处在温度T 的平衡状态的经典系统,粒子能量中每一个平方项的平均值等于kT 21. ⑴单原子分子只有平动,其能量为()22221zy x p p p m++=ε, 根据能均分定理,温度T 时,单原子分子的平均能量为：kT 23=ε.故单原子分子的内能为：NkT U 23=； 定容热容：Nk C V 23=； 定压热容：Nk Nk C C V p25=+=. ⑵双原子分子的能量为：如果不考虑相对运动,式中有5个平方项,根据能均分定理,双原子分子的平均能量为：kT 25=ε,双原子分子的内能、等容热容和等压热容分别为：⑶固体中的院子可以在平衡位置附近做微振动,假设各原子的振动是简谐运动,每个原子的能量为：只有两个平方项,而由于每个原子有三个自由度,根据能均分定理,每个原子的平均能量为：kT 3=ε,则固体的内能、等容热容分别为：固体热容之间的关系为：⑷平衡辐射问题考虑一个封闭的空窖,电磁辐射与窖壁达到平衡,称为平衡辐射,二者具有共同的温度空窖的辐射场可以分解为无穷多个单色平面波的叠加,分量可以表示为：其中ω是圆频率,k 是波矢.k的三个分量的可能值为：,1,0,2±==αααπn n L k ()z y x ,,=α.具有一定波矢k和一定偏振的单色平面波可以看做辐射场的一个自由度,它以圆频率ω随时间做简谐变化,因此相当于一个振动自由度.在体积V 内,在ωωωd +→的圆频率范围内,辐射场的振动自由度数为：()ωωπωωd cVd D 232=. 根据能均分定理,每一个振动自由度的平均能量为kT =ε.所以在体积V 内,在ωd 范围内平衡辐射的内能为：此式称为瑞利-金斯公式. 5.理想气体的内能与热容经典统计的能均分定理得到的关于理想气体内能和热容的结论与实验结果大体相同,但有几个问题没有得到合理的解释：原子内的电子对气体的热容为什么没有贡献；双原子分子的振动在常温范围内为什么对热容没有贡献；低温下氢的热容所得结果与实验结果不符. 本节以双原子分子为例,讲述理想气体内能和热容的量子统计理论.⑴暂不考虑原子中电子的运动,在一定近似下双原子分子的能量可以表示为平动能tε、振动能νε和转动能rε之和：r t εεεεν++=,以tω、νω和rω分别表示平动能、振动能和转动能的简并度,则配分函数1Z 可表示为： ①考虑平动对内能和热容的贡献：()2222212z y x t p p p mm p ++==ε,()2322312222⎪⎪⎭⎫ ⎝⎛==⎰++-βπβh m V dp dp dp e h V Z z y x p p p mt z y x ,因此,NkT Z NU t t 23ln 1=∂∂-=β, Nk T U C V tV 23=⎪⎭⎫ ⎝⎛∂∂=.②考虑振动对内能和热容的贡献：,2,1,0,21=⎪⎭⎫ ⎝⎛+=n n n ωεν, ()ωβωβωβν--+--==∑ee eZ nn 12211利用等比数列公式, 因此,引入振动特征温度νθ,ωθν =k ,可得。

《热力学与统计物理》考试大纲第一章 热力学的基本定律基本概念：平衡态、热力学参量、热平衡定律温度，三个实验系数（α，β，T κ）转换关系，物态方程、功及其计算，热力学第一定律（数学表述式）热容量（C ，C V ，C p 的概念及定义），理想气体的内能，焦耳定律，绝热过程及特性，热力学第二定律（文字表述、数学表述），可逆过程克劳修斯不等式，热力学基本微分方程表述式，理想气体的熵、熵增加原理及应用。

综合计算：利用实验系数的任意二个求物态方程，熵增（ΔS ）的计算。

第二章 均匀物质的热力学性质基本概念：焓（H ），自由能F ，吉布斯函数G 的定义，全微公式，麦克斯韦关系（四个）及应用、能态公式、焓态公式，节流过程的物理性质，焦汤系数定义及热容量（Cp ）的关系，绝热膨胀过程及性质，特性函数F 、G ，空窖辐射场的物态方程，内能、熵，吉布函数的性质。

综合运用：重要热力学关系式的证明，由特性函数F 、G 求其它热力学函数（如S 、U 、物态方程）第三章、第四章 单元及多元系的相变理论该两章主要是掌握物理基本概念：热动平衡判据（S 、F 、G 判据），单元复相系的平衡条件，多元复相系的平衡条件，多元系的热力学函数及热力学方程，一级相变的特点，吉布斯相律，单相化学反应的化学平衡条件，热力学第三定律标准表述，绝对熵的概念。

统计物理部分第六章 近独立粒子的最概然分布基本概念：能级的简并度，μ空间，运动状态，代表点，三维自由粒子的μ空间，德布罗意关系（k P =，＝ωε），相格，量子态数。

等概率原理，对应于某种分布的玻尔兹曼系统、玻色系统、费米系统的微观态数的计算公式，最概然分布，玻尔兹曼分布律（l l l e a βεαω--=）配分函数（∑∑-==-s l l sl e e Z βεβεω1），用配分函数表示的玻尔兹曼分布（l l l e Z N a βεω-=1），f s ，P l ，P s 的概念，经典配分函数（⎰⎰-=du e h Z l r βε 011）麦态斯韦速度分布律。

第一章热力学的基本规律习题试求理想气体的体胀系数α,压强系数β和等温压缩系数T κ; 解：由得：nRT PV=V nRTP P nRT V ==; 所以,TP nR V T V V P 11)(1==∂∂=α习题试证明任何一种具有两个独立参量的物质p T ,,其物态方程可由实验测得的体胀系数α及等温压缩系数T κ,根据下述积分求得:⎰-=)(ln dp dT V T κα如果1Tα=1T p κ=,试求物态方程;解：因为0),,(=p V T f ,所以,我们可写成),(p T V V =,由此,dp p V dT T V dV T p )()(∂∂+∂∂=,因为T T p p VV T V V )(1,)(1∂∂-=∂∂=κα 所以,dp dT VdVdp V dT V dVT T κακα-=-=,所以,⎰-=dp dT VT καln ,当p T T /1,/1==κα.习题测得一块铜块的体胀系数和等温压缩系数分别为1510*85.4--=K α和1710*8.7--=n T p κ,T κα,可近似看作常量,今使铜块加热至10°C;问1压强要增加多少np才能使铜块体积不变 2若压强增加100n p ,铜块的体积改多少解：分别设为V xp n ∆;,由定义得：所以,410*07.4,622-=∆=V p xn习题描述金属丝的几何参量是长度L ,力学参量是张力η,物态方程是0),,(=T L f η实验通常在n p 1下进行,其体积变化可忽略;线胀系数定义为ηα)(1T L L ∂∂=等杨氏摸量定义为T LA L Y )(∂∂=η其中A 是金属丝的截面积,一般说来,α和Y 是T 的函数,对η仅有微弱的依赖关系,如果温度变化范不大,可看作常数;假设金属丝两端固定;试证明,当温度由1T 降2T 时,其张力的增加为)(12T T YA --=∆αη解：),(,0),,(T L L T L f ηη==所以,dT TLd L dL T ηηη)()(∂∂+∂∂= 因AY L L L L T T T =∂∂∂∂=∂∂)(;)(1)(ηηη所以,)(12T T YA --=∆αη习题在C ︒25下,压强在0至1000n p 之间,测得水的体积13263)10046.010715.0066.18(---⨯+⨯-=mol cm p p V 如果保持温度不变,将1mol 的水从1n p 加压至1000n p ,求外界所做的功;解：外界对水做功: 习题解：外界所作的功：习题抽成真空的小匣带有活门,打开活门让气体充入;当压强达到外界压强p 0时将活门关上;试证明：小匣内的空气在没有与外界交换热量之前,它的内能U 与原来大气中的0U 之差为000V p U U =-,其中0V 是它原来在大气中的体积;若气体是理想气体,求它的温度和体积;解：假设先前的气体状态是P 0,dV 0,T 0内能是u 0,当把这些气体充入一个盒子时,状态为P 0,dV,T 这时的内能为u,压缩气体所做的功为：00dV p ,依绝热过程的热力学第一定律,得()000000=+-⎰dV P U U V积分得000V p U U=-对于理想气体,上式变为()001vRT T T vc V=-故有()01T R c T c V V +=所以001V T c c T VPγ==对于等压过程0101V T T V V γ==习题热泵的作用是通过一个循环过程将热量从温度较低的环境传送扫温度较高的物体上去;如果以理想气体的逆卡诺循环作为热泵的循环过程,热泵的效率可以定义为传送到高温物体的热量与外界所作的功的比值;试求热泵的效率;如果将功直接转化为热量而令高温物体吸收,则“效率”为何解：A →B 等温过程B →C 绝热过程 C →D 等温吸热D →A 绝热,2111Q Q Q A Q -==η由绝热过程泊松方程：1211--=r Cr B V T V T ；1112--=r Ar DV T V T∴D AC B V V V V =；CDB A V V V V =∴212212212111T T T T T T T T T T T -+=-+-=-=η将功A 直接转化为热量1Q ,令高温物体吸收;有A=Q 1∴11==AQ η; 习题假设理想气体的C p 和C V 之比γ是温度的函数,试求在准静态绝热过程中T 和V 的关系;该关系试中要用到一个函数FT ,其表达式为： 解：准静态绝热过程中：0=dQ,∴pdV dU -=1对于理想气体,由焦耳定律知内能的全微分为dT C dU v =2物态方程VnRT P nRT pV =⇒=32,3代入1得：dV VnRTdTC V -=其中1-=γnR C V ()dTVdV⎰⎰-=-11γ关系式γ为T 的函数∴V -1为T 的函数;∴VT F 1)(=1)(=V T F ; 第二章均匀物质的热力学性质习题已知在体积保持不变的情况下,一气体的压强正比于其绝对温度.试证明在温度保持不变时,该气体的熵随体积而增加; 解：由题意得：)()(V f T V k p +=;因V 不变,T 、p 升高,故kV >0T V S )(∂∂=V Tp)(∂∂=k VkV >0 由于kV >0,当V 升高时或V 0→V ,V >V 0,于是⇒T 不变时,S 随V 的升高而升高;设一物质的物态方程具有以下形式T V f P)(=,试证明其内能与体积无关;解：T V f P)(=,V T V U ∂∂),(T =T V T P)(∂∂-p =)()(V Tf V Tf -=0得证;习题求证：ⅰHP S )(∂∂<0ⅱU VS)(∂∂>0证VdP TdS dH +=等H 过程:H HVdP TdS )()(-=⇒PS ∂∂H=-TV <0V >0;T >0由基本方程：PdV TdS dU-=dV T pdU T dS +=⇒1;⇒VS ∂∂U =Tp>0.习题已知T VU)(∂∂=0,求证T p U )(∂∂=0;解T V U )(∂∂=T V T p )(∂∂-p ;⇒T V U )(∂∂=0;V TpT p )(∂∂= T VU )(∂∂=),(),(T V T U ∂∂=),(),(T p T U ∂∂),(),(T V T p ∂∂=0=T p U )(∂∂T Vp)(∂∂ ∵T Vp)(∂∂≠0;⇒T p U )(∂∂=0;习题试证明一个均匀物体在准静态等过程中熵随体积的增减取决于等压下温度随体积的增减;解：F =U-TS ,将自由能F 视为P ,V 的函数;F =Fp ,V=⎪⎭⎫⎝⎛∂∂p V S ()()p V p S ,,∂∂=()()⋅∂∂p T p S ,,()()p V p T ,,∂∂()()()()p T p V p T p S ,,,,∂∂∂∂==pp T V T S ⎪⎭⎫⎝⎛∂∂⎪⎭⎫⎝⎛∂∂由关系T C p=p T S ⎪⎭⎫ ⎝⎛∂∂;⇒=⎪⎭⎫⎝⎛∂∂pV S ⋅T C p pV T ⎪⎭⎫ ⎝⎛∂∂; 习题试证明在相同的压强降落下,气体在准静态绝热膨胀中的温度降落大于在节流过程中的温度降落;提示:证明S p T ⎪⎪⎭⎫⎝⎛∂∂-Hp T ⎪⎪⎭⎫⎝⎛∂∂>0证：()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==dS S H dp p H H T dp p T dH H T dp p T dT H p T T dS S T dp p T dT S p T T p S p H p Hp S),(1),(联立1,2式得：Sp T ⎪⎪⎭⎫⎝⎛∂∂-H p T ⎪⎪⎭⎫ ⎝⎛∂∂=p H T ⎪⎭⎫ ⎝⎛∂∂S p H ⎪⎪⎭⎫ ⎝⎛∂∂=pST H p H ⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂=pS C p H ⎪⎪⎭⎫⎝⎛∂∂据：pdV TdS dU-=熵不变时,dS =0,pdV dU -=Vdp TdS dH +=Sp H ⎪⎪⎭⎫⎝⎛∂∂=V⇒S p T ⎪⎪⎭⎫ ⎝⎛∂∂-Hp T ⎪⎪⎭⎫ ⎝⎛∂∂=0>p C V；原题得证;习题一弹簧在恒温下的恢复力X 与其伸长x 成正比,即.X =-Ax ；今忽略弹簧的热膨胀,试证明弹簧的自由能F 、熵S 和内能U 的表达式分别为； 解：),();(,x T U U T A A Ax X==-==dU dT T U x ⎪⎭⎫ ⎝⎛∂∂+dx x U T⎪⎭⎫⎝⎛∂∂⇒+-=;)(xdx T A SdT dF S T F x -=⎪⎭⎫ ⎝⎛∂∂;=x T A )(Tx F ⎪⎭⎫ ⎝⎛∂∂-=⇒S XT F ⎪⎭⎫⎝⎛∂∂=dT T dB x dT T dA )()(212--由于TS U F-=,）（2 dS S T dp p H H T p T p S p H ⎪⎭⎫⎝⎛∂∂+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂⋅⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂==⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-dT dB T T B x dT T dA T T A )()()(212∵X =0时,U =0,即不考虑自身因温度而带来的能量;实际上,dT dB TT B -)(=0或dTdBT T B -)(=)0,(T U 即得：2)()(21)0,(),(x dT T dA T T A T U X T U ⎥⎦⎤⎢⎣⎡-=-221)0,(),(Ax T F T X F +=;dT dA x T S T X S 2)0,(),(2-= 进而求U ∆略;代入abd c V V V V V aT uV U=⇒==；4习题如下图所示,电介质的介电常数EDT =)(ε与温度有关,试求电路为闭路时电介质的热容量与充电后再令电路断开后的热容量之差;解：当电路闭合时,电容器电场恒定 当电路断开时,电容器电荷恒定D T TED S )()(∂∂-=∂∂,因而 习题已知顺磁物质的磁化强度为：H TCm =,若维持物质温度不变,使磁场由0增至H,求磁化热;解：;H TCm =mV M =；TH S ⎪⎭⎫ ⎝⎛∂∂⇒=0μV H T m ⎪⎭⎫ ⎝⎛∂∂=H T C ⎪⎭⎫⎝⎛-20μ等T 下：22000H T CV HdH T C V S T Q H μμ⋅-=-=∆=∆⎰习题已知超导体的磁感应强度()00=+=m H B μ；求证:ⅰC m 与m 无关,只是T 的函数,其中C m 是在磁化强度m 保持不变时的热容量；ⅱ0202U m dT C U m +-=⎰μ；ⅲ0S dT TC S m+=⎰解：超导体()m H m H M B-=⇒=+=00ⅰT C H=HT S ⎪⎭⎫ ⎝⎛∂∂∵m H-=；T C C m H ==⇒HT S ⎪⎭⎫⎝⎛∂∂ⅱHdM TdS dU0μ+=;mV M =代入m C 表达式,其中U 0 为0K 时的内能;ⅲ由ii 中已应用了dT C TdSm =⇒T C T S mm=⎪⎭⎫⎝⎛∂∂；⇒0S dT TC S m+=⎰〈忽略因体积变化带来的影响〉; 习题实验测得顺磁介质的磁化率)(T χ;如果忽略其体积的变化,试求特性函数fm,t,并导出内能和熵;解：显然χ只与T 有关；)(T χ=TH m ⎪⎭⎫⎝⎛；()T H m m ,=HdMTdS dU 0μ+=;TS U f -=;SdT TdS dU df --=⇒HdM SdT df 0μ+-=;⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=dT T m dH H m V dM H T()H T V H f χμ0=⎪⎭⎫⎝⎛∂∂；()()()T f m V T f H T V f 02002022+=+=⇒χμχμ f 既已知：-=S ()02202S dT T d m V T f m+⋅=⎪⎭⎫⎝⎛∂∂χχμ HdMTdS dU 0μ+=；TS U f -=第三章单元系的相变习题试由0>vC 及0)(<∂∂T V p 证明0>p C 及0)(<∂∂S Vp; 证T C C V p =-⇒VT p ⎪⎭⎫⎝⎛∂∂pT V ⎪⎭⎫ ⎝⎛∂∂ =P C p T H ⎪⎭⎫ ⎝⎛∂∂=pT S T ⎪⎭⎫⎝⎛∂∂;=V C V T U ⎪⎭⎫⎝⎛∂∂V T S T ⎪⎭⎫ ⎝⎛∂∂= ⇒=⎪⎭⎫ ⎝⎛∂∂T V p V S p ⎪⎭⎫ ⎝⎛∂∂T V S ⎪⎭⎫ ⎝⎛∂∂+SV p ⎪⎭⎫⎝⎛∂∂1=⎪⎭⎫ ⎝⎛∂∂V T p VS p ⎪⎭⎫ ⎝⎛∂∂TT S ⎪⎭⎫⎝⎛∂∂2 ⇒=⎪⎭⎫ ⎝⎛∂∂S V T -VS p ⎪⎭⎫⎝⎛∂∂⇒V C V T S T ⎪⎭⎫ ⎝⎛∂∂=；即0>=⎪⎭⎫⎝⎛∂∂VV C T S T . 于是：0>=⎪⎭⎫⎝⎛∂∂T V p +⎪⎭⎫⎝⎛∂∂SV p 正数 于是：SV p ⎪⎭⎫⎝⎛∂∂<0 0>V C ;因而0>P C习题求证：1-=⎪⎭⎫⎝⎛∂∂n V T ,μV T n S ,⎪⎭⎫ ⎝⎛∂∂；2-=⎪⎪⎭⎫ ⎝⎛∂∂nT p ,μp T n V ,⎪⎭⎫⎝⎛∂∂ 证：1开系吉布斯自由能dn Vdp SdT dG μ++-=,),(T V p p =⇒VS T G n V +-=⎪⎭⎫⎝⎛∂∂,VT p ⎪⎭⎫⎝⎛∂∂① V V G nT =⎪⎭⎫⎝⎛∂∂,T V p ⎪⎭⎫⎝⎛∂∂② μ=⎪⎭⎫⎝⎛∂∂VT n G ,③ 由式①⇒n V n V T G T p V S ,⎪⎭⎫ ⎝⎛∂∂-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂=V T n S ,⎪⎭⎫ ⎝⎛∂∂nV T ,⎪⎭⎫ ⎝⎛∂∂-=μ第1式得证;习题试证明在相变中物质摩尔内能的变化为：⎪⎪⎭⎫⎝⎛⋅-=∆dp dT T p L u1如果一相是气相,可看作理想气体,另一相是凝聚相,试将公式化简; 解V p S T U∆-∆=∆VT L dT dp ∆=；S T L ∆=；dp dT T p L L U ⋅⋅-=∆⇒⎪⎪⎭⎫⎝⎛⋅-=dp dT T p L 1 习题在三相点附近,固态氨的蒸气压单位为a P 方程为：Tp 375492.27ln -= 液态氨的蒸气压方程为：Tp 306338.24ln -=,试求氨三相点的温度和压强,氨的汽化热、升华热及在三相点的熔解热;解：1固态氨的饱和蒸气压方程决定了固态-气态的相平衡曲线；液态氨的饱和蒸气压方程决定了氨的液态-气态的相平衡曲线;三相点是两曲线的交点,故三相点温度3T 满足方程：TT 306338.24375492.27-=-；由此方程可解出3T ,计算略； 2相变潜热可由RTLA p -=ln与前面实验公式相比较得到： 3754=RL S,从而求出S L ；类似可求出Q L ；计算略； 3在三相点,有r Q SL L L +=,可求得r L ,计算略;习题蒸汽与液相达到平衡;以dTdv 表在维持两相平衡的条件下,蒸汽体积随温度的变化率;试证明蒸汽的两相平衡膨胀系数为⎪⎭⎫ ⎝⎛-=⋅RT L T dT dv v 111; 解αV ～0.方程近似为：TVLT p ≈∆∆,V —气相摩尔比容;Vp T L T V V 11⋅∆=∆⋅⇒①气相作理想气体,pV=RT ②T R V p pV ∆=∆+∆⇒③联立①②③式,并消去△p 、P 得：TL TV VVP T R ∆=⋅∆-∆21RT LRT T V V -=⎪⎭⎫ ⎝⎛∆∆⇒；⎪⎭⎫ ⎝⎛-=-=⎪⎭⎫ ⎝⎛∂∂=⇒RT L T RT T T V V P 111112α 习题证明爱伦费斯公式：()()()()1212k k dT dp --=αα；()()()())(1212αα--=Tv c c dT dpp p 证：对二级相变0)(=∆dS ；即()2dS -()1dS =00)(=∆dV ；即()2dV -()1dV =0()2dS()dT T S ⎪⎪⎭⎫ ⎝⎛∂∂=2()dp p S ⎪⎪⎭⎫ ⎝⎛∂∂+1；()1dS ()dT T S ⎪⎪⎭⎫ ⎝⎛∂∂=1()dp p S ⎪⎪⎭⎫ ⎝⎛∂∂+1 )(0dS ∆=()2dS=-()1dS⇒()()=⎥⎦⎤⎢⎣⎡∂∂-∂∂dT T S TS 12()()dp p S p S ⎥⎦⎤⎢⎣⎡∂∂-∂∂-12 ()()()()⎥⎦⎤⎢⎣⎡∂∂-∂∂⎥⎦⎤⎢⎣⎡∂∂-∂∂-=⇒p S p S T S T S dT dp 1212;将pp T S T C ⎪⎭⎫ ⎝⎛∂∂=代入得;()()[]()()pS p S C C T dT dppP ∂∂-∂∂--=12121①即为：()-∂∂p S 2()()()()121αα--=∂∂V pS ；代入①得：()()()()1212αα--=TV C C dT dp p P类似地,利用0)(=∆dV 可证第二式;略第四章多元系的复相平衡和化学平衡习题若将U 看作独立变数T ,V ,n 1,…n k 的函数,试证明：1VUV n U n Ui ii∂∂+∂∂=∑；2VUv n U u i i i∂∂+∂∂=证：1),,,(),,,(11k k n n V T U n n V T U λλλλ=根据欧勒定理,f x fx iii=∂∂∑,可得 2i ii i i i i i iiu n V Uv n U n V U V n U n U∑∑∑=∂∂+∂∂=∂∂+∂∂=)( 习题证明),,,(1k i n n p T μ是k n n ,1的零次齐函数,0=⎪⎪⎭⎫⎝⎛∂∂∑j ij j n n μ; 证：),,,(),,,(11k m k n n p T n n p T μλλλμ=,化学势是强度量,必有m =0,习题二元理想溶液具有下列形式的化学势：其中g i T ,P 为纯i 组元的化学势,x i 是溶液中i 组元的摩尔分数;当物质的量分别为n 1、n 2的两种纯液体在等温等压下合成理想溶液时,试证明混合前后 1吉布斯函数的变化为)ln ln (2211x n x n RT G+=∆2体积不变0=∆V3熵变)ln ln (2211x n x n R S +-=∆4焓变0=∆H ,因而没有混合热;5内能变化如何解： 1222211112211ln ),(ln ),( x RT n p T g n x RT n p T g n n n n G i ii +++=+==∑μμμ所以22110ln ln x RT n x RT n G G G+=-=∆2p G V ∂∂=；0)(=∂∆∂=∆∴pG V ; 3T G S ∂∂-= ；2211ln ln )(x R n x R n TG S --=∂∆∂-=∆∴ 4TSH G -=50=∆-∆=∆V p H U习题理想溶液中各组元的化学势为：i i ix RT P T g ln ),(+=μ；(1) 假设溶质是非挥发性的;试证明,当溶液与溶剂蒸发达到平衡时,相平衡条件为其中'1g 是蒸汽的摩尔吉布斯函数,g 1是纯溶剂的摩尔吉布斯函数,x 是溶质在溶液中的摩尔分数; (2) 求证：在一定温度下,溶剂的饱和蒸汽压随溶液浓度的变化率为 (3) 将上式积分,得)1(0x p p x -=其中p 0是该温度下溶剂的饱和蒸汽压,p x 是溶质浓度为x 时的饱和蒸汽压;该公式称为拉乌定律; 解：1设“1”为溶剂,())1ln(,'111x RT P T g g -+==μ2由⇒=∂∂v p g Tp x x RT p g p g ⎪⎪⎭⎫⎝⎛∂∂--⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂)1(1'1Tp x ⎪⎪⎭⎫⎝⎛∂∂ -=⇒v v ')1(x RT-Tp x ⎪⎪⎭⎫ ⎝⎛∂∂；v’—蒸汽相摩尔热容 v —凝聚相摩尔热容故有v’-v ≈v’,又有pv’=RT 代入⇒ Tx p ⎪⎭⎫⎝⎛∂∂x p --=1 3积分2式得拉乌定律习题的气体A 1和n 0v 2mol 的气体A 2的混合物在温度T 和压强p 下所占体积为V 0,当发生化学变化,0A A A A 22114433=--+νννν；并在同样的温度和压强下达到平衡时,其体积为V e ;试证明反应度为 证：未发生化学变化时,有当发生化学变化时,原来有n 0v 1mol 的气体A 1,反应了n 0v 1εmol,未反应1-εn 0v 1mol,n 0v 2mol 的气体A 2,反应了εn 0v 2mol,未反应1-εn 0v 2mol,生成εn 0v 3molA 3和εn 0v 4molA 4,有习题根据第三定律证明,在T →0时;表面张力系数与温度无关;即0→dTd σ; 证：表面膜系统,dA SdT Fσ+-=S T F A -=⎪⎭⎫ ⎝⎛∂∂⇒;σ=⎪⎭⎫⎝⎛∂∂T A F=⎪⎭⎫ ⎝⎛∂∂T A S AT ⎪⎭⎫⎝⎛∂∂-σ;而实际上σ与A 无关,即=⎪⎭⎫⎝⎛∂∂TA S dT d σ-T →0时,根据热力学第三定律；()0lim 0=∆→TT S于是得：dT d σ0=⎪⎭⎫⎝⎛∂∂-=TA S ；原式得证; 习题试根据第三定律证明,在T →0时,一级相变两平衡曲线的斜率dTdp为零;证：VS dT dp ∆∆=；T →0；000=⎪⎭⎫⎝⎛∆∆=⎪⎭⎫⎝⎛→→T T V S dT dp ()0lim 0=∆→TT S ；原式得证;习题设在压强p 下,物质的熔点为T 0,相变潜热为L ,固相的定压热容量为C p ,液相的定压热容量为C p ’.试求液体的绝对熵表达式;解：为计算T 温度,p 压强下,液体绝对熵,可假想如下图过程;p液相 ABC 固相T 0T①A →B,等压过程：⎰=∆→0T p BA TdT C S②B 点相变过程.0T L S B =∆相变③B →C,等压过程：⎰=∆→TT p CB TdT C S 0'于是∑=∆+=S S S)0(⎰T p TdT C 0T L+⎰+TT p T dT C 0'习题试根据第三定律讨论图ab 两图中哪一个是正确的 图上画出的是顺磁性固体在H =0和H=H i 时的S-T 曲线;解：图b 正确;拒热力学第三定律;T →0；S 0=0;且T →0,0=⎪⎭⎫⎝⎛∂∂Tx S ； 即0K 附近,S 在等温过程中的变化与任何其它参量无关;第五章不可逆过程热力学简介习题带有小孔的隔板将容器分为两半,容器与外界隔绝,其中盛有理想气体,两侧气体存在小的温差ΔT 和压强差Δp 而各自处于局域平衡;以dt dn J n=和dtdUJ u =表示单位时间内通过小孔从一侧转移到另一侧的气体的物质的量和内能;试导出熵产生率公式,从而确定相应的动力; 解：根据热力学基本方程∑-=iii dn dU Tdsμ得dtdn T dt dU T dt ds i i i ∑-=μ11设温度为T +ΔT 的一侧熵为s 1;温度为T 的一侧熵为s 2,则 因为0 ;0='+='+n d dn U d dU所以dn n d dU U d -='-=';,dtdnT dt dU T dt ds μ+-=12熵产生率 dt ds dt ds dt s d i 21+==dtdnT dt dU T dt dn T T dt dU T T μμμ+-∆+∆+-∆+11 =dtdn T T T dt dU T T T ⎪⎭⎫ ⎝⎛-∆+∆+-⎪⎭⎫⎝⎛-∆+μμμ11=⎪⎭⎫ ⎝⎛∆-⎪⎭⎫⎝⎛∆T J T J n u μ1 相应的动力22 ,1T T T T X T T T X n u μμμ∆-∆=⎪⎭⎫ ⎝⎛∆-=∆-=⎪⎭⎫ ⎝⎛∆=第六章近独立粒子的最概然分布习题试证明,对子一维自由粒子,再长度L 内,在ε到εεd +的能量范围内,量子态数为：证：一维自由粒子,x P 附近的量子态为x dP hLdn =；x x x x x dP m dP m m m dP P d m P εεεε21222+=⋅+==⇒= 于是;()εεεεd mh Ld D2+=而±P x对应同一能量ε,于是：()mh L m h L D εεε2222=⎪⎪⎭⎫ ⎝⎛⨯=习题试证明,对于二维自由粒子,在长度L 2内,在ε到εεd +的能量范围内,量子态数为证：二维；在P x ,P y 附近dP x dP y 区间上内的粒子数;ϕPdPd hSdP dP h S dn y x 22==s －面积 因mP 22=ε只与P 有关P >0,故对ϕ积分可得：()⎪⎪⎭⎫ ⎝⎛==m P h S PdP h S d D 222222ππεε,επd h mSm 22= ()22hmS D πε=⇒s=L 2习题在极端相对论情形下,粒子的能量动量关系为cp =ε;试求在体积V 内,在ε到εεd +的能量范围内能量范围内三维粒子的量子态数; 解：φθθd dpd p hV dp dp dp h V dn z y x sin 233==由于cp =ε只与p 有关,与θ、φ无关,于是以上已经代入了cdp d cp =⇒=εε于是,32)(4)(hc V D επε=习题设系统含有两种粒子,其粒子数分别为N 和N ’.粒子间的相互作用很弱,可 看作是近独立的;假设粒子可分辨,处在一个个体量子态的粒子数不受限制;试证明, 在平衡态下两种粒子的最概然分布分别为：le a l lβεαω--=和'--'='l e a l lβεαω;其中l ε和'l ε是两种粒子的能级,l ω和'l ω是能级简并度;证：粒子A 能级,粒子数分布：l ε——{a l }——简并度l ω 粒子B 能级,粒子数分布：'l ε——{a ’l }——简并度'l ω由21Ω⋅Ω=Ω21ln ln ln Ω+Ω=Ω即使Ω最大,()11ln ΩΩ,()22ln ΩΩ达到最大;l e a l l εβαω''-'-'='注：'l a δ与l a δ在此情况下独立讨论,若将一系作为子系统,意味总能守恒,于是参照教材玻尔兹曼分布证明……0ln ln =⎪⎭⎫ ⎝⎛''+-''-'⎪⎪⎭⎫ ⎝⎛''+-⎪⎪⎭⎫ ⎝⎛⇒∑∑∑∑∑∑l l l l l l l l l llla a a a a a a a δεδεβδαδωδαδω同一0β,原题得证;这也是满足热平衡的要求;第七章玻耳兹曼统计习题根据公式∑∂∂-=lllVa Pε证明,对于非相对论粒子：)()2(21222222z y x n n n Lm m p s ++== π,z y x n n n ,,=0,±1,±2,…有VU p 32=,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立;证：∑∂∂-=lllVa Pε=⎥⎦⎤⎢⎣⎡++∂∂-∑)()2(212222z y x lln n n L m V a π=⎥⎦⎤⎢⎣⎡++∂∂-∑)()2(222223z y x l l n n n L m L V a π 其中Va ul l ε∑=;V ~3L 对同一l ,222zy x n n n ++=m a ll21∑-2)2( π)(222z y x n n n ++)32(35--V =m a ll21∑-22222)()2(L n n n z y x ++ π)32(3532--V V =V U32习题试根据公式∑∂∂-=lllVa Pε证明,对于极端相对论粒子：21222)(2z y x n n n L c cp ++== πε,z y x n n n ,,=0,±1,±2,…有VU p 31=,上述结论对玻耳兹曼分布、玻色分布和费米分布都成立;证：∑∂∂-=ll lVa Pε；对极端相对论粒子21222)(2z y x n n n Lc cp ++== πε类似得31212)()2(-∑∂∂-=∑V n V a P i ll π=VUVV a ll l 31)31(3431-=---∑ε 习题当选择不同的能量零点时,粒子第l 个能级的能量可以取为ll *εε或,以∆表示二者之差=∆l l εε-*;试证明相应的配分函数存在以下关系11Z e Z ∆-*=β,并讨论由配分函数Z 1和Z 1求得的热力学函数有何差别; 证：配分函数∑-=le Z l βεω1以内能U 为例,对Z 1:1ln Z NUβ∂∂-=对Z 1:()U N e N Z NU Z +∆=∂∂-=∂∂-=-1ln ln 1**βββ习题试证明,对于遵从玻尔兹曼分布的系统,熵函数可以表示为式中P s是总粒子处于量子态s 的概率,1Z e N e P ss s βεβεα---==,∑s对粒子的所有量子态求和;证法一：出现某状态s ψ几率为P s设S 1,S 2,……S k 状态对应的能级s 'ε；设S k+1,S k+2,……S w 状态对应的能级s 'ε；类似………………………………；则出现某微观状态的几率可作如下计算：根据玻尔兹曼统计Ne P sS βεα--=；显然NP s 代表粒子处于某量子态S 下的几率,Se NP Sβεα--=;于是Se βεα--∑代表处于S 状态下的粒子数;例如,对于s 'ε能级⎪⎪⎭⎫⎝⎛∑=--'K S S S S e 1βεα个粒子在s 'ε上的K 个微观状态的概率为： 类似写出：()⎪⎪⎭⎫ ⎝⎛''∑=''=''--k S S S s e S PS P1βεα ………………………………………………等等; 于是N 个粒子出现某一微观状态的概率; 一微观状态数P1=Ω,基于等概率原理将Se NP Sβεα--=带入S SS P P kN S ln ∑-=⇒；习题固体含有A 、B 两种原子;试证明由于原子在晶体格点的随机分布引起的混 合熵为k S=㏑[][][])1ln()1(ln !)1(!!x x x x N x N N N x --+-=-κ其中N 是总原子数,x 是A原子的百分比,1-x 是B 原子的百分比;注意x<1,上式给出的熵为正值; 证：显然[]!)1()!(!!!!21x N Nx N n n N -==ΩS=k ㏑Ω=-N k [])1ln()1(ln x x x x --+=)1()1(ln x x x x Nk ---；由于)1()1(x xx x--＜1,故0〉S ；原题得证;习题气体以恒定的速度沿方向作整体运动;试证明,在平衡状态下分子动量的最 概然分布为证：设能级l ε这样构成：同一l ε中,P z 相同,而P x 与P y 在变化,于是有：∑==0p a p p l z参照教材玻耳兹曼分布证明；有E N βδαδδ--Ωln -z p γ,其中）（22221Z y x lp p p m++=ε 由1知:N dp dp dp ehV z y x p z=⎰---γβεα3 将l ε代入并配方得:=N dp dp dp e hV z y x m p mm z y x =⎰+-+---2)(2)()22(3βγβεεββγα其中mp m p y y xx 2,222==εε整个体积内,分布在z z z y y y x x x dp p p dp p p dp p p +→+→+→,,内分子数为：由条件3知⎰=0),,(Np dp dp dp p p p f pz y x z y x z计算得 =z m p my x dp em dp dp emkTz y x ⎰⎰+-+--2)(2)(23)()21(βγβεεββγπ=0p Ndp dp fdp m zy x =-⎰βγ0p m -=⇒βγ代入得出分布：[]3)(22022"hdp dp Vdp ezy x p p p p mz y x-++--βα其中βγαα22'm -=,0p m -=βγ习题试根据麦克斯韦速度分布率导出两分子的相对速度12v v v r-=和相对速率rr v v =的概率分布,并求相对速率的平均值r v ;解：两分子的相对速度r v在rz ry rx dv dv dv 内的几率2122111])()()()[(23211)()2()()()(2212121212121--∞∞-+++++++-===⎰⎰⎰⎰kTm edv dv dv e kT m v V v V v d v V rx rz z ry y rx x z y x v kT m zy x v v v v v v v v v kT mr r ππ 同理可求得z y v v 11,分量为2122)(2--kTm ery v kT m π和2122)(2--kTm er v kT m π引进2m=μ,速度分布变为r r v kT mdv v e kT r 22232)2(-πμ 利用球极坐标系可求得速率分布为：r r v kT m dv v e kTr22232)2(4-πμπ 相对速率平均值v kT dv v e v kT v r r v kT m r r r28)2(4220232===-∞⎰πμπμπ习题试证明,单位时间内碰到单位面积上,速率介于v 与dv v +之间的分子数为：dv v e kTm n d kTmv 322/32)2(-=Γππ证：在斜圆柱体内,分速度为z v 的v 方向的分子数为:对于:0,,积分得从对从+∞→+∞→∞-z y x v v vdt 时间碰撞到ds 面积上的分子数dv v v +→=dsdt d dvd v ekTm n kTmv ϕθθπππcos )2(2/032202\32⎰⎰-得到：若只计算介于dv v v +→分子数则为：只对φθ,积分习题分子从器壁小孔射出,求在射出的分子束中,分子平均速度和方均根速度;解：dvv e kT m n dvv e kT m n v kT nv v kT m3022/30422/322)2()2(⎰⎰∞+-+∞-=ππππ；变量代换⇒==dx mkTdv x n kT m2;2 习题已知粒子遵从经典玻耳兹曼分布,其能量表达式为：bx ax p p p mz y x ++++=2222)(21ε其中b a ,是常数,求粒子的平均能量; 解：ab a b a bx x a m p 4)4(222222-+++=ε习题气柱的高度为H ,截面为S ,在重力场中;试求解此气柱的内能和热容量;解：配分函数⎰-++-=z y x mgz p p p mdp dp dxdydzdp ehZ z y x ββ)(232221 设⎥⎦⎤⎢⎣⎡=mg m hS A 1)2(2/33π；[]mgH e A Z ββ--+-=1ln ln )2/5(ln ln习题试求双原子理想气体的振动熵;解：振动配分函数ωβωβ ---=e e Z V 12/1代入式)1ln(2/ln 1ωβωβ ----=⇒e Z代入熵计算式V V k T Nk Nk S θωθ=+=⇒其中)./ln(;习题对于双原子分子,常温下kT 远大于转动的能级间距;试求双原子分子理 想气体的转动熵; 解转动配分函数212 βI Z r=);/ln(;/1ln ;2ln ln 121r T Nk Nk S Z I Z θβββ+=⇒-=∂∂=其中r k I h θ=22习题气体分子具有固有电偶极矩0d ,在电场ε下转动能量的经典表达式为：θεθεφθcos )sin 1(210222d p p I r -+=,证明在经典近似下转动配分函数： 解：经典近似下,rε视为准连续能量配分函数⎰⎰⎰⎰⎰⋅==∞∞-+⋅---πφθεβθβθβφθβεφθφθθ20cos sin 21222102211d dp d edp ehd d dp dpe hZ d I p Ir利用π=⎰∞∞--dx ex 2习题同19题,试证在高温10≤εβd 极限下,单位体积电偶极矩电极化强度为：εξkT d 320=; 解：电极化强度)1(1ln 0000001εβββεβξεβεβεβεβ--+=∂∂=--d d d d ee e d e d Z N 高温极限下,0→β,保留至20)(εβd εεβkTnd d 222020=⇒;其中VN n =习题试求爱因斯坦固体的熵;解：将ωβωβh h eeZ ---=121,代入至S 表达式即得,注意N 取3N;略第九章系综理论习题证明在正则分布中熵可表为∑-=ss s k S ρρln 其中sE s e Zβρ-=1是系统处在s 态的概率; 证：)ln (ln ββ∂∂-=Z Z k S多粒子配分函数)1(1ss E s E e Z e Z ββρ--=⇒=∑由1知[]s s s s s E Z E Z E Z esρβρβρβln ln 1;ln ln +=-+=-⇒=-代至2得[]∑∑+=+=∂∂ssss s s Z Z Z ρρββρρββln 1ln 1ln ln 1ln ;于是∑-=⎪⎪⎭⎫⎝⎛∂∂-=s ss k Z Z k Sρρββln ln ln习题试用正则分布求单原子分子理想气体的物态方程,内能和熵 证：()222121;iziy ix Ni s sE p p p mE eZs++==∑∑=-β符号∏=i iz iy ix dp dp dp dp符号∏=i ii i dz dy dx dq 利用式V NTk V Z Z Z P =∂∂=∂∂=⇒βββ1ln 1类似求S U ,;习题体积内盛有两种组元的单原子混合理想气体,其摩尔数为1n 和2n ,温度为T ; 试由正则分布导出混合理想气体的物态方程,内能和熵;解：习题利用范氏气体的配分函数,求内能和熵;解：Q m N Z N 2/32!1⎪⎪⎭⎫ ⎝⎛=βπ()⎰⎰⎰-----++=-=∂∂⇒dr f V N V dr e V N NTk U dr e V N Q N N N N 12121212122/3;22βφβφφφβ一般认为dr f VN 1222较小； 习题利用德拜频谱求固体在高温和低温下配分函数对数Z ln ,从而求内能和熵; 解：式 德拜频谱B ND 93=ω 对于振动())(1ln 1ln ln ln 2020020x d e e B d D e e e Z D D =⎪⎪⎪⎭⎫ ⎝⎛-+-=⎪⎪⎪⎭⎫ ⎝⎛-+=⎰⎰-----ωβωωβφωωωωβωβωωβωββφ 代换 S 计算略高温近似,∞→T ,0→ωβ()N N +--=ωββφ ln 30计算略习题用巨正则分布导出单原子分子理想气体的物态方程,内能,熵和化学势; 解：参照关于玻耳兹曼体系配分函数的处理过渡到连续能量分布得: 利用热力学式可求得kT N pV =,kT N U 23=等略 注:l ε--------单粒子处于l 能级的能量;习题利用巨正则分布导出玻耳兹曼分布; 解：∑∑--=ΞN S E N s eβα；由于玻耳兹曼系,粒子可分辨,从而为简单起见,考虑无简并有简并情况完全可类似处理 于是：(){}∏∞=+-=Ξ0ex p l a l l eβα即对无简并情况()l e a l βεα+-=对有简并者,类似处理可得()l e a l lβεαω+-=略 l ω——简并度。

热力学与统计物理热力学与统计学的研究任务：研究热运动的规律，研究与热运动有关的物质及宏观物质系统的演化。

热力学的局限性：不考虑物质的微观结构，把物质看作连续体，用连续函数表达物质的性质，不能解释涨落现象。

热力学部分第一章 热力学的基本规律1、热力学与统计物理学所研究的对象：由大量微观粒子组成的宏观物质系统 其中所要研究的系统可分为三类孤立系：与其他物体既没有物质交换也没有能量交换的系统；闭系：与外界有能量交换但没有物质交换的系统；开系：与外界既有能量交换又有物质交换的系统。

2、弛豫时间：系统由初始状态达到平衡态所经历的时间（时间长短由趋向平衡的性质决定），取最长的弛豫时间为系统的弛豫时间3、热力学平衡态：一个系统不论其初始状态如何复杂，经过足够长的时间后，将会达到这样的状态，即系统的各种宏观性质在长时间内不发生任何变化。

4、准静态过程：进行得非常缓慢的过程，系统在过程中经历的每一个状态都可以看成平衡态5、热力学系统平衡状态的四种参量：几何参量、力学参量、化学参量和电磁参量6、简单系统：只要体积和压强两个状态参量就可以确定的系统7、单相系（均匀系）：如果一个系统各个部分的性质完全一样，则该系统称为单相系； 复相系：如果整个系统是不均匀的，但可以分成若干个均匀的部分，称为复相系8、热平衡定律：如果物体A 和物体B 各自与处于同一状态的物体C 达到热平衡，若令A 与B 进行热接触，它们也将处于热平衡状态。

（得出温度的概念，比较温度的方法）9、物态方程：给出温度与状态函数之间参数的方程10、理想气体：符合玻意耳定律、阿氏定律和理想气体温标的气体11、焦耳定律：气体的内能只是温度的函数，与体积无关，即)(T U U =12、玻意耳定律：对于固定质量的气体，在温度不变时，压强和体积的乘积为常数13、阿氏定律：在相同的温度压强下，相同体积所含的各种气体的物质的量相同14、范德瓦尔斯方程：考虑了气体分子之间的相互作用力（排斥力和吸引力）,对理想气体状态方程作了修正之后的实际气体的物态方程15、广延量：热力学量与系统的n 、m 成正比强度量：热力学量与n 、m 无关（广延量除以n 、m 、V 变成强度量）16、能量守恒定律：自然界中一切物质都具有能量，能量有各种不同的形式，可以从一种形式转化为另一种；从一个物体传递到另一个物体，在传递和转化中能量的数量不变。

热力学与统计物理答案(汪志诚) 第一章热力学的基本规律1.1 热力学系统的平衡态及其描述1.什么是热力学系统？热力学系统有哪些分类？答：热力学系统是指由大量相互作用的粒子组成的集合体，可以用一些宏观物理量来描述其状态。

热力学系统可以分为孤立系统、封闭系统和开放系统。

2.什么是热力学平衡态？热力学平衡态有哪些性质？答：热力学平衡态是指在没有外界影响的情况下，系统的宏观性质不随时间变化的状态。

热力学平衡态具有均匀性、各向同性和稳定性等性质。

3.如何描述热力学系统的状态？常用的状态参量有哪些？答：热力学系统的状态可以用一组状态参量来描述，常用的状态参量有体积、温度、压力和熵等。

1.2 热力学第零定律温度1.热力学第零定律的内容是什么？如何理解？答：热力学第零定律的内容是：如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡(温度相同)，则它们彼此也必定处于热平衡。

这个定律说明了温度是描述热力学系统状态的一个重要参量，也是进行热交换的驱动力。

2.什么是温度？温度有哪些性质？答：温度是描述热力学系统状态的一个宏观参量，表示系统的冷热程度。

温度具有可加性和可比较性等性质，可以用温度计来测量。

3.温度与微观粒子运动的关系是什么？答：温度与微观粒子运动的关系可以通过麦克斯韦-玻尔兹曼分布来描述。

在一定温度下，系统中微观粒子的速度分布服从麦克斯韦-玻尔兹曼分布，粒子的平均动能与温度成正比。

1.3 热力学第一定律能量守恒定律1.热力学第一定律的内容是什么？如何理解？答：热力学第一定律的内容是：物体内能的增加等于物体吸收的热量和对物体所作的功的总和。

这个定律说明了能量守恒和转换的规律，即能量既不会凭空产生也不会凭空消失，只会从一种形式转换成另一种形式。

2.什么是内能？内能有哪些性质？答：内能是指热力学系统中所有微观粒子的动能和势能之和。

内能是一个状态函数，具有可加性和单调性等性质。