实验三_用matlab求极限和导数

matlab 《数学实验》报告9-matlab的极限和微分运算《数学实验》报告学号姓名成绩实验内容:Matlab的极限和微分运算。

一实验目的熟悉MATLAB软件中关于极限和微分运算的基本命令，掌握利用MATLAB软件求极限和微分运算的方法。

二预备知识(1)求函数的极限和微分的运算。

(2) Matlab基本命令limit，初等函数的表示方法。

三实验内容与要求1.求下列极限，将完成实验的程序写到文件sy31.m中xarctanF,(1); 1limxx,0Matlab命令结果clear%µÚ?þÖÖ???? =syms x atan(x)/xf=atan(x)/x ans =limit(f,'x',0) 1121，x,,F,(2) ,,2lim1,x,,x,0Matlab命令结果1clear F2 =syms x ((1+x)/(1-x))^(1/x) F2=((1+x)/(1-x))^(1/x) ans =limit(F2,'x',0) exp(2)xln(1x)，F,(3) 3lim2x,0sinxMatlab命令结果 clear F3 =syms x x*log(1+x)/sin(x^2) F3=x*log(1+x)/sin(x^2) ans = limit(F3,'x',0) 1xarctanF,(4) 4limxx,,Matlab命令结果 clear F4 =syms x atan(x)/xF4=atan(x)/x ans =limit(F4,'x',inf) 011,,limF,,(5) ,,531x,1x,,,x1,Matlab命令结果 clear F5 =1/(1-x)-1/(1-x^3) syms xF5=1/(1-x)-1/(1-x^3) ans =limit(F5,'x',1) NaN2、求下列函数的倒数，将完成实验的程序写到文件sy32.m中3(1); y,cosx,cos3x1Matlab命令结果2clear%diyi y1 =syms x cos(x)^3-cos(3*x) y1=(cos(x))^3-cos(3*x) ans = diff(y1,x) -3*cos(x)^2*sin(x)+3*sin(3*x) (2) y,xsinxlnx2 Matlab命令结果 clear%dier y2 =syms xy2=x*sin(x)*log(x) x*sin(x)*log(x)diff(y2,x) ans =sin(x)*log(x)+x*cos(x)*log(x)+sin(x)xxe,1(3)y, 3sinxMatlab命令结果 clear%disan y3 =syms x (x*exp(x)-1)/sin(x) y3=(x*exp(x)-1)/sin(x) ans =diff(y3,x)(exp(x)+x*exp(x))/sin(x)-(x*exp(x)-1)/sin(x)^2*cos(x)x，，4(4)，计算; y,ecosxy4Matlab命令结果 clear%disi y3 =exp(x)*cos(x) syms xans = y3=exp(x)*cos(x)diff(y3,x,4) -4*exp(x)*cos(x)2，，20y,xsin2x(5)，计算 yMatlab命令结果 clear%diwu y5 =syms x x^2*sin(2*x)y5=x^2*sin(2*x) ans =-99614720*sin(2*x)-20971520*x*cos(2*x)+1048576*x^2*sindiff(y5,x,20) (2*x)3谣言:吃太咸了会得病,导语:“人体每日摄入食盐不应过多，否则易患多种疾病。

数学实验二 用Matlab 软件求一元函数的导数和极（或最）值一、一元函数的导数1．调用格式一：diff(‘f(x)','x',n)式中，)(x f 为函数，x 为自变量，若未指明，按默认的自变量．n 为导数的阶数，缺省时，求一阶导数．例1 已知x x x f cos )(2=，求)(x f ′．解 在命令行中输入：dydx=diff('x^2*cos(x)') %未指明自变量，按默认的自变量输出导数结果结果如下：dydx =2*x*cos(x)-x^2*sin(x)即x x x x x f sin cos 2)(2−=′．例2 已知)arcsin(xt t y =(x 为常数)，求22dty d ． 解 在命令行中输入：d2ydt2=diff('t*asin(x*t)','t',2) %若不指明对t 求导，则默认对x 求导结果如下：d2ydt2 =2*x/(1-x^2*t^2)^(1/2)+t^2*x^3/(1-x^2*t^2)^(3/2)即3223222])(1[)(12xt t x xt x dt y d −+−=． 2．调用格式二：syms xdiff(f(x),x,n)例3 已知)arcsin(xt t y =(t 为常数)，求2dx y d ． 解 在命令行中输入：syms x td2ydx2=diff(t*asin(x*t),x,2)输出结果是：d2ydx2 =t^4/(1-x^2*t^2)^(3/2)*x即32422])(1[xt xt dx y d −=． 二、隐函数的导数在Matlab 中没有直接求隐函数导数的命令，但可调用Maple 中求隐函数导数的命令，调用格式如下：maple('implicitdiff(f(x,y)=0,y,x)')例4 求由方程05=−−+y x e xy 所确定的隐函数dxdy ． 解 在命令行中输入：dydx=maple('implicitdiff(x*y-exp(x+y)-5=0,y,x)')运行结果是：dydx =-(y-exp(x+y))/(x-exp(x+y))即 yx yx e x e y dx dy ++−−−=． 三、一元函数的极（或最）值在Matlab 中只有求极（或最）小值命令的函数．若要求函数)(x f 在),(21x x 内的极（或最）大值，可转化为求)(x f −在),(21x x 内的极（或最）小值．求极（或最）小值点和极（或最）小值的调用格式是：[x,fual]=fminbnd(‘fun ’,x1,x2)式中，fun 为函数，x1，x2为x 的取值范围，x 为极（或最）小点，fual 为极（或最）小值．例5 求函数x e x f x sin 2)(−=在)5,2(的最小值点和最小值．解 在命令行中输入：[xmin,fmin]=fminbnd('2*exp(-x)*sin(x)',2,5)输出结果如下：x min=3.9270fmin =-0.0279例6 求函数231)(x x x f −−=在]9,10[−的最值点和最值．解 在命令行中输入：[xmin,fmin]=fminbnd('1-3*x-x^2',-10,9); %求)(x f 的最小值点和最小值[xmax,zmin]=fminbnd('-1+3*x+x^2',-10,9); %转化为求)(x f −的最小值点和最小值 fmax=-zmin; %))((x f −−的最大值xmin,fmin,xmax,fmax %输出最小值点、最小值和最大值点、最大值运行结果为：xmin =9fmin =-107xmax =-1.5000fmax =3.2500四、上机实验1．用help命令查看函数diff，fminbnd等的用法．2．上机验证上面各例．3．作相关小节练习中函数的导数和求函数的极（或最）值．。

第三章微积分问题的计算机求解一、实验内容：题目1．试求出如下极限。

①limx→∞(3x +9x )1/ x，②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】：该题为单变量函数的极限。

极限问题可以用limit()函数直接求出。

要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限)，L=limit(fun,x,x0,’left’或’right’)(求极限)。

还需注意一开始要对函数的字符进行申明。

【解答】：（1）输入如下语句：>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下：L =9（2）输入如下语句：>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下：L =exp(-5)题目2.试求下面的双重极限。

①lim x→−1y→2 (x2y+xy3)/(x+y) 3，②limx→0 y→0 xy /√(xy+1)−1，③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。

【分析】：该题为多变量函数的极限问题。

他可以用嵌套使用limit()函数来解决。

在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。

其思想是所有的先关于X求导，再所有的关于y求导。

【解答】：(1)输入如下语句：>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下：L =-6(2)输入如下语句：>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键，语句运行后显示如下：L =2(3)输入如下语句：>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键，语句运行后显示如下：L =题目3.求出下面函数的导数。

实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。

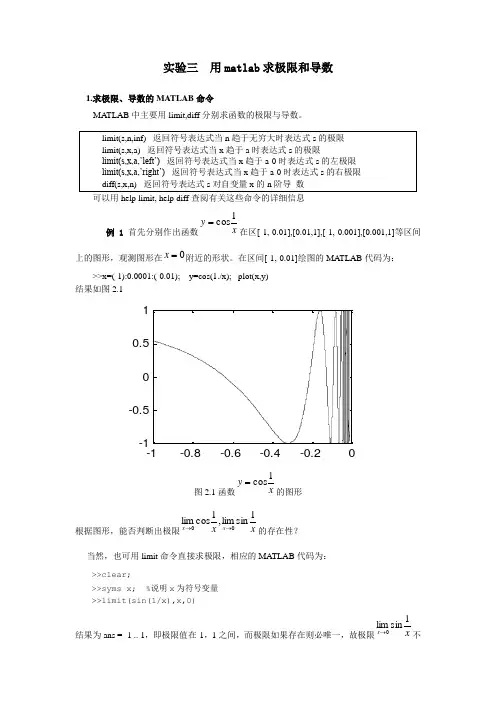
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形，观测图形在0=x 附近的形状。

在区间[-1,-0.01]绘图的MA TLAB 代码为： >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形，能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性？ 当然，也可用limit 命令直接求极限，相应的MATLAB 代码为：>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1，即极限值在-1，1之间，而极限如果存在则必唯一，故极限x x 1sinlim 0→不存在，同样，极限x x 1coslim 0→也不存在。

例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形，观测图形在0=x 附近的形状。

在区间[-1,-0.01]绘图的MA TLAB 代码为： >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形，能否判断出极限1sin lim0=→x xx 的正确性？当然，也可用limit 命令直接求极限，相应的MATLAB 代码为：>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时，数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。

matlab计算函数极限标题：用MATLAB计算函数极限在数学中，极限是研究函数在某个特定点附近的行为的重要概念之一。

计算函数的极限有助于我们了解函数在该点附近的性质，包括函数的趋势、连续性以及导数等。

在本文中，我们将使用MATLAB 来计算函数的极限，并通过实例来说明这一过程。

在MATLAB中，我们可以使用`limit`函数来计算函数的极限。

`limit`函数的语法为：```L = limit(f, x, a)```其中，`f`是输入的函数表达式，`x`是自变量，`a`是自变量趋于的点。

`limit`函数将返回函数在自变量趋于该点时的极限值`L`。

下面，我们通过一个具体的例子来演示如何使用MATLAB计算函数的极限。

假设我们要计算函数`f(x) = (x^2 - 1)/(x - 1)`在`x`趋于1时的极限。

我们定义函数`f`：```matlabsyms x;f = (x^2 - 1)/(x - 1);```然后，我们使用`limit`函数计算极限：```matlabL = limit(f, x, 1);```运行以上代码后，MATLAB将返回极限值`L`。

除了计算函数在某个点处的极限外，MATLAB还可以计算函数在正无穷或负无穷处的极限。

例如，我们要计算函数`g(x) = 1/x^2`在`x`趋于正无穷时的极限，可以使用以下代码：```matlabsyms x;g = 1/x^2;L = limit(g, x, inf);```同样地，MATLAB将返回极限值`L`。

除了计算极限值外，MATLAB还可以判断函数在某个点是否存在极限。

如果函数在某个点处的左极限和右极限相等，则称该函数在该点处存在极限。

我们可以使用`islimit`函数来判断函数在某个点是否存在极限。

例如，我们要判断函数`h(x) = sin(x)/x`在`x`趋于0时是否存在极限，可以使用以下代码：```matlabsyms x;h = sin(x)/x;exist_limit = islimit(h, x, 0);```运行以上代码后，MATLAB将返回布尔值`exist_limit`，若为`true`则表示函数在该点处存在极限，若为`false`则表示不存在。

Matlab 大作业本人选择了利用MATLAB解决高等数学问题。

1.极限计算limit(f,x,a):求函数f在x趋于常数a时的极限；limit(f):求函数f在x趋于0时的极限；limit(f,x,a,’right’):求函数f在x趋于常数a时的右极限；limit(f,x,a,’left’):求函数f在x趋于常数a时的左极限；具体计算如下：求极限M=（1-2x/n）^n(n->∞);>>syms n x；>>M=limit(‘(1-2*x/n)^n,n,inf)M=1/exp(2*x)相应图如下：2.导数计算diff(y,x,n):求y对x的n次导数；具体计算如下：设：y=sinax；求A=dy/dx, B=dy/da, C=d^2y/dx^2; >>syms a x; y=sin(a*x);>>A=diff(y,x)A=a*cos(a*x);>>B= diff(y,a)B=x*cos(a*x);>>C= diff(y,x,2)C=-a^2*sin(a*x)相应图如下：3.积分计算int(f):直接求函数f对x的不定积分；int(f,x1,x2):求函数f在积分区间为（x1，x2）的积分值；具体计算如下：求I=∫(x^2+1)/(x^2-2*x+2); J=∫cosx/(sinx+cosx)，x∈(0,π/2) K=e^(-x^2) x∈(0,+∞)；>>syms x>>f=(x^2+1)/(x^2-2*x+2)^2;>>g=cos(x)/(sin(x)+cos(x));>>h=exp(-x^2);I=int(f)I=(3*atan(x-1))/2+(x/2-3/2)/(x^2-2*x+2)；J=int(g,0,pi/2)J=Pi/4;K=int(h,0.inf)K= Pi^(1/2)/2;相应图如下：4.级数求和symsum(n的式子，a，b): 求的式子第a项到第b项的和。

一．计算下列极限： 1. xe e xx x sin lim 0-→- 解：y=sym(‘(exp(x)-exp(-x))/sin(x)’);y1=limit(y)结果：y1=2 2. nn mm a x a x a x --→lim 解：syms x a m ny=(x^m-a^m)/(x^n-a^n);y1=limit(y,x,a)结果：y1=na m a n m 3. nx x x 21lim ⎪⎭⎫ ⎝⎛+∞→ 解：syms x ny=((1+x)/x)^(2*n);y1=limit(y,x,inf)结果：y1=1 4. 111lim --→x x e解：y=exp(1/(x-1));y1=limit(y,x,1,‘left ’)结果：y1= 0 5. 111lim -+→x x e解：y=exp(1/(x-1));y1=limit(y,x,1,‘right ’)结果：y1= ∞二.创建表达式f=2x+4, g=4x^2+5x-2,并计算(1) f+g; (2) f-g; (3) f ×g;(4) f /g; (5) f [g(x)];(6) 求 g 的反函数。

解：syms xf=2*x+4;g=4*x^2+5*x-2;结果：(1) f+g= 7*x+2+4*x^2(2)f-g= -3*x+6-4*x^2(3)f*g= (2*x+4)*(4*x^2+5*x-2)(4)f/g= (2*x+4)/(4*x^2+5*x-2)(5) f [g(x)]=compose(f,g)=8*x^2+10*x(6)clearsyms xg=4*x^2+5*x-2;g1= finverse(g)结果：g1= ()2116578185x ++- 三.计算下列导数（1）)1ln(2x x e e y ++=解：syms xy=log(exp(x)+sqrt(1+exp(2*x)));z=diff(y,x);simple(z)结果：z=exp(x)/(exp(2*x) + 1)^(1/2)z=()2121+x xe e (2)xe y 1sin 2-=解：syms xy=exp(-(sin(1/x))^2);z=diff(y,x);simple(z)结果：z=(exp(cos(2/x)/2 - 1/2)*sin(2/x))/x^2 z=221)2cos()2sin(*x x ex - (3)212arcsint t y +=解： syms ty=asin(2*t/(1+t^2));z=diff(y,t);simple(z)结果：z=-(2*t^2 - 2)/((t^2 + 1)^2*((t^2 - 1)^2/(t^2 + 1)^2)^(1/2))z=11*)1(2222222+-+--t t t t (4)x x y =解：syms xy=x^(1/x);z=diff(y,x);simple(z)结果：z=-x^(1/x - 2)*(log(x) - 1) z=)1)*(ln 21(---x x x四．求曲线⎩⎨⎧==-t te y e x 2在t=0相应点处的切线方程和法线方程。

使用MATLAB软件求导数MATLAB是一种用于数值计算和科学编程的强大工具。

它不仅提供了丰富的函数库和工具箱，还可以轻松地进行符号和数值计算。

在MATLAB 中，求导数（即计算函数的导函数）非常简单。

下面将详细介绍在MATLAB中如何进行求导。

在MATLAB中，我们可以使用符号计算工具箱进行符号计算和求导。

这个工具箱提供了一系列函数来创建符号对象、进行符号计算，并计算与符号表达式相关的导数、积分和极限值等。

下面我们将介绍一些常用的符号计算函数。

首先，我们需要使用'sym'函数将数值变量转换为符号变量。

例如，我们可以将x转换为符号变量x，并将其赋值给变量x。

代码如下：```MATLABsyms x```接下来，我们可以使用符号变量来构建符号表达式。

例如，假设我们要计算函数f(x)的导数，可以通过以下方式创建符号表达式f(x)：```MATLABf = sin(x^2) + exp(x);```在这个例子中，我们创建了一个由sin(x^2)和exp(x)组成的符号表达式f(x)，其中x是我们之前定义的符号变量。

一旦我们创建了符号表达式，我们就可以使用'diff'函数计算其导数。

'diff'函数的语法如下：```MATLABdiff(f, x)```其中，f是我们要计算导数的符号表达式，x是我们要对其求导的变量。

例如，如果我们要计算上述函数f(x)相对于x的导数，可以使用以下代码：```MATLABdf = diff(f, x);```在这个例子中，我们计算了f(x)关于x的导数，并将结果赋值给变量df。

在MATLAB中，我们还可以使用'gradient'函数来计算多元函数的梯度向量。

梯度向量是由各个自变量的偏导数组成的向量。

'gradient'函数的语法如下：```MATLABgradient(f, [x, y, z, ...])```其中，f是我们要计算梯度的符号表达式，[x,y,z,...]是自变量向量。

matlab计算函数极值,如何⽤MATLAB求函数的极值点和最⼤值两种⽅法：1、求导的⽅法：syms x y；>>y=x^3+x^2+1>>diff(y)ans =3*x^2 + 2*x>>solve(ans)ans=-2/3极值有两点。

同时也是最值；2、直接⽤最⼩值函数：求最⼤值，既求-y的最⼩值：>>f=@(x)(-x^3-x^2-1)f =@(x)(-x^3-x^2-1)>>x=fminunc(f,-3,3)%在-3；-3范围内找Warning: Gradient must be provided fortrust-region method; using line-search methodinstead. > In fminunc at354Optimization terminated: relative infinity-norm of gradient lessthan options.TolFun.x =-0.6667>> f(x)ans =-1.1481在规定范围内的最⼤值是1.1481由于函数的局限性，求出的极值可能是局部最⼩(⼤)值。

求全局最值要⽤遗传算法。

例⼦：syms xf=(200+5*x)*(0.65-x*0.01)-x*0.45;s=diff(f);%⼀阶导数s2=diff(f,2);%⼆阶导数h=double(solve(s));%⼀阶导数为零的点可能就是极值点，注意是可能，详情请见⾼数课本fori=1:length(h)ifsubs(s2,x,h(i))<0disp(['函数在' num2str(h(i))'处取得极⼤值，极⼤值为' num2str(subs(f,x,h(i)))])elseifsubs(s2,x,h(i))>0disp(['函数在' num2str(h(i))'处取得极⼩值，极⼩值为'num2str(subs(f,x,h(i)))])elsedisp(['函数在' num2str(h(i))'处⼆阶导数也为0，故在该点处函数可能有极⼤值、极⼩值或⽆极值'])%%%详情见⾼数课本endend。

实验三导数及其中值定理实验目的：1掌握matlab求导数与高阶导数的方法。

2深入理解和掌握求隐函数的导数以及由参数方程定义的函数的导数的方法。

3理解中值定理的条件和结论；4会写函数的Taylor展开式和Maclaurin展开式；5掌握求函数的极值和最值的方法；6作出函数的图形。

实验使用的MATLAB函数：Matlab命令：求导数命令是diff,常用格式是：syms xdiff('f(x)',x)diff('f(x)',x,n) 求出f关于x的n阶导数Matlab 泰勒展开格式：taylor(f)求在x=0点展开6项taylor(f,n,x0) 求在x=x0点展开n项solve（方程,变量）：求解方程或方程组。

实验指导：一、导数概念与导数的几何意义：例：用定义求g(x)=2x3-4x2+x+1的导数输入：syms xdiff('2*x^3-4*x^2+x+1')输出：ans =6*x^2-8*x+1再输入：x=-1:0.1:3;y1=2*x.^3-4*x.^2+x+1;y2=6*x.^2-8*x+1;plot(x,y1,'b',x,y2,'r:')执行后得到函数y1与它的导函数y2的图像，如下图。

例：作函数f(x)=3x3+3x2-12x+7的图形和在x=1处的切线输入：syms xhanshu=3*x^3+3*x^2-12*x+7;daoshu=diff('3*x^3+3*x^2-12*x+7');x=1;hanshuzhi=eval(hanshu)daoshuzhi=eval(daoshu)输出：hanshuzhi =1daoshuzhi =3再输入:x=-4:0.1:3;y=3*x.^3+3*x.^2-12*x+7;y1=1+3*(x-1);plot(x,y,'b',x,y1,'r')输出：二、求函数的高阶导数以及函数在某点的导数值例：求函数y=x n 的一阶导数和二阶导数输入：syms xdiff('x^n',1)diff('x^n',2)输出：ans =x^n*n/xans =x^n*n^2/x^2-x^n*n/x^2例：求函数f(x)=sinaxcosbx 的一阶导数，并求f ’(1/(a+b))输入：syms x a bdaoshu=diff('sin(a*x)*cos(b*x)')x=1/(a+b);daoshuzhi=eval(daoshu)输出：daoshu =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*bdaoshuzhi =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b例：求函数910)10(2-+=x xy 的1阶到11阶导数输入：syms xy=x^10+2*(x-10)^9;for n=1:11diff(y,x,n)end 输出：ns =10*x^9+18*(x-10)^8ans =90*x^8+144*(x-10)^7ans =720*x^7+1008*(x-10)^6ans =5040*x^6+6048*(x-10)^5ans =30240*x^5+30240*(x-10)^4ans =151200*x^4+120960*(x-10)^3ans =604800*x^3+362880*(x-10)^2ans =1814400*x^2+725760*x-7257600ans =3628800*x+725760ans =3628800ans =三、求由隐函数、参数方程确定的函数的导数例：求由方程x 2-2xy+y 2+x+2y+1=0确定的隐函数的导数输入：syms x yz=x^2-2*x*y+y^2+x+2*y+1daoshu=-diff(z,x)/diff(z,y)输出：daoshu =(-2*x+2*y-1)/(-2*x+2*y+2)例：求由参数方程x=e t cost,y==e t sint 确定的函数的导数输入：syms tx=exp(t)*cos(t);y=exp(t)*sin(t);daoshu=diff(y,t)/diff(x,t)simple(daoshu)四、 理解中值定理的条件和结论；例1 针对函数()(1)(2)f x x x x =--观察罗尔定理的几何意义。

实验三 导数及应用实验目的1. 深入理解导数与微分的概念，导数的几何意义。

掌握MATLAB 求导数与高阶导数的方法。

深入理解和掌握求隐函数的导数及由参数方程定义的函数的导数的方法。

2. 掌握用函数的导数确定函数的单调区间、凹凸区间和函数的极值的方法。

掌握用MATLAB 求方程的根和求函数的极值的方法。

实验内容● 求导数的命令为：diff ，常用格式为 >> syms x>> diff('f(x)',x)diff(f,x)给出f 关于x 的导数，而表达式f 中的其它字母看作常量。

因此如果表达式是多元函数，则给出的是偏导数。

>> diff('f(x)',x,n) 给出f 关于x 的n 阶导数或者偏导数。

● 多项式方程00111=+++--a x a xa x a n n n n 求根命令是：roots具体格式：roots (c)● 求一般方程0)(=x f 近似根的命令，一般形式为：⑴ 建立函数：f=inline('表达 式 ')⑵ 求函数零点：c=fzero(f, [a, b]) % 求函数f(x) 在区间[a, b] 内的零点c ； c=fzero(f, x0) % 求函数f(x) 在x0 附近的零点c ； fsolve 非线性方程求解fzero 标量非线性方程求解● 求非线性函数f(x) 的极小值，求一元函数极小值命令是 fminbnd,常用格式为： x=fminbnd(fun,x1,x2);[x,fav1]=fminbnd(fun,x1,x2);[x,fav1,exitflag,output]=fminbnd(fun,x1,x2);其中：x=fminbnd(fun,x1,x2) 是求(x1,x2)上fun 函数的最小值x 。

[x,fav1]=fminbnd(fun,x1,x2)返回解x 处目标函数的值。

实验三多元函数的极值【实验目的】1．掌握MATLAB 软件有关的命令。

2．多元函数自由极值的求法3．多元函数条件极值的求法.【实验准备】1．计算多元函数的自由极值对于多元函数的自由极值问题,根据多元函数极值的必要和充分条件,可分为以下几个步骤:步骤1.定义多元函数),(y x f z =步骤2.求解正规方程0),(,0),(==y x f y x f y x ,得到驻点步骤3.对于每一个驻点),(00y x ,求出二阶偏导数,,,22222yz C y x z B x z A ∂∂=∂∂∂=∂∂=步骤4.对于每一个驻点),(00y x ,计算判别式2B AC −,如果02>−B AC ,则该驻点是极值点,当0>A 为极小值,0<A 为极大值;,如果02=−B AC ,判别法失效,需进一步判断;如果02<−B AC ,则该驻点不是极值点.2．计算二元函数在区域D 内的最大值和最小值设函数),(y x f z =在有界区域D 上连续，则),(y x f 在D 上必定有最大值和最小值。

求),(y x f 在D 上的最大值和最小值的一般步骤为：步骤1.计算),(y x f 在D 内所有驻点处的函数值；步骤2.计算),(y x f 在D 的各个边界线上的最大值和最小值；步骤3.将上述各函数值进行比较，最终确定出在D 内的最大值和最小值。

3．函数求偏导数的MATLAB 命令MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。

diff(f,x,n)求函数f关于自变量x的n阶导数。

jacobian(f,x)求向量函数f关于自变量x(x也为向量)的jacobian矩阵。

可以用help diff,help jacobian查阅有关这些命令的详细信息【实验内容】例1：求函数z=sin(x)sin(y)sin(x+y)在0<x<pi/2,0<y<pi/2内的极大值.理论分析知：当X=pi/3y=pi/3z有极大值3/8*3^(1/2)Matlab程序：%定义二元函数clc;clear;syms x y;z=sin(x)*sin(y)*sin(x+y);ezsurf(x,y,z,[0,pi/2,0,pi/2]);%求解驻点dzx=diff(z,x)dzy=diff(z,y)[xx,yy]=solve('cos(x)*sin(y)*sin(x+y)+sin(x)*sin(y)*cos(x+y)=0',...'sin(x)*cos(y)*sin(x+y)+sin(x)*sin(y)*cos(x+y)=0','x','y')%对于定义域内的驻点求解二阶偏导函数A=diff(z,x,2);B=diff(diff(z,x),y);C=diff(z,y,2);D=A*C-B^2;%判别极大值点D1=subs(subs(D,'x',xx(1)),'y',yy(1))A1=subs(subs(A,'x',xx(1)),'y',yy(1))D2=subs(subs(D,'x',xx(2)),'y',yy(2))A2=subs(subs(A,'x',xx(2)),'y',yy(2))%极大值点和极大值[xx(2)yy(2)]JDZ=subs(subs(z,'x',xx(2)),'y',yy(2))程序运行结果ans=[1/3*pi,1/3*pi]JDZ=3/8*3^(1/2)例2函数32824−+−=y xy x z 的极值点和极值求函数32824−+−=y xy x z 的极值点和极值.首先用diff 命令求z 关于x,y 的偏导数>>clear;syms x y;>>z=x^4-8*x*y+2*y^2-3;>>diff(z,x)>>diff(z,y)结果为ans =4*x^3-8*yans =-8*x+4*y 即.48,843y x yz y x x z +−=∂∂−=∂∂再求解正规方程，求得各驻点的坐标。

极限与导数1 函数对象与符号对象1.2 定义符号对象1.3 符号表达式 创建xx f )11()(+=，并求)10(f 值。

创建),(y x y x f +=]10,10[],10,10[-∈-∈y x1.5 输入2点绘制直线 技术准备：2 极限问题2.1 单变量函数的极限求解方法：)(lim 0x f L xx →= L= limit(f,x,x0);例2-1：求解xx )11(lim +∞→例2-2：求解ba x x x sin )1(lim +∞→例2-3：求解单边极限xx e x x sin cos 11lim3---+→例2-4：求解单边极限)tan(lim2t t +→π、)tan(lim 2t t -→π syms t;f=tan(t);L1=limit(f,t,pi/2, 'left'); % inf L2=limit(f,t,pi/2, 'right'); % -inf % 图形验证t1=pi/3:pi/100: pi/2; t2=2*pi/3:-pi/100: pi/2;y1=subs(f,t,t1); y2=subs(f,t,t2); plot(t1,y1); hold on; plot(t2,y2);2.2 多变量函数的极限 求解方法：),(lim 0y x f L y y xx →→= L= limit(limit(f,x,x0),y,y0);L= limit(limit(f,y,y0),x,x0);例2-5：求解222222)/(1/111sin lim y x x y y y x y x x eL ++-∞→→⎪⎪⎭⎫⎝⎛+=3 导数的解析解3.1 一元函数的导数求解方法：y=diff(fun,x); 一阶导数 y=diff(fun,x,n); n 阶导数 例3-1：给定函数sin )(2=x x f ，求x df )(例3-2：给定函数34sin )(2++=x x x x f ，求44)(dxx f d ，并化简之 syms x; f=sin(x)/(x^2+4*x+3);f4=diff(f,x,4);f41=collect (simple (f4),cos(x)); % 按cos(x)合并化简 f42=collect(simple(f41),sin(x)); % 按sin(x)合并化简% 测算高阶导数的计算时间 tic ; diff(f,x,50); toc ;例3-3：给定函数)(sin )(2t f t t t F ⋅=，求33)(dt t F d ，并得出te tf -=)(时的三阶导数，将结果与直接求导的结果向比较。