2019届江苏省泰州市高三第一次模拟考试数学试卷及答案

2019届江苏省泰州市高三第一次模拟考试数 学 文 科(满分160分，考试时间120分钟)99-参考公式：柱体的体积V ＝Sh ，锥体的体积V ＝13Sh一、 填空题：本大题共14小题，每小题5分，共计70分． 1. 函数f(x)＝sin 2x 的最小正周期为________．2. 已知集合A ＝{4，a 2}，B ＝{－1，16}，若A ∩B ≠∅，则实数a ＝________．3. 复数z 满足z i ＝4＋3i (i 是虚数单位)，则|z|＝________．4. 函数y ＝1－x 2的定义域是________．5. 从1，2，3，4，5这五个数中随机取两个数，则这两个数的和为6的概率为________．6. 一个算法的伪代码如图所示，执行此算法，最后输出的T 的值是________．7. 已知数列{a n }满足log 2a n ＋1－log 2a n ＝1，则a 5＋a 3a 3＋a 1＝________．8. 若抛物线y 2＝2px(p>0)的准线与双曲线x 2－y 2＝1的一条准线重合，则p ＝________．9. 如图，在直三棱柱ABCA 1B 1C 1中，M 为棱AA 1的中点，记三棱锥A 1MBC 的体积为V 1，四棱锥A 1BB 1C 1C 的体积为V 2，则V 1V 2的值是________．10. 已知函数f(x)＝2x 4＋4x 2，若f(a ＋3)>f(a －1)，则实数a 的取值范围为________．11. 在平面直角坐标系xOy 中，过圆C 1：(x －k)2＋(y ＋k －4)2＝1上任一点P 作圆C 2：x 2＋y 2＝1的一条切线，切点为Q ，则当线段PQ 的长最小时，k ＝________．12. 已知P 为平行四边形ABCD 所在平面上任一点，且满足PA →＋PB →＋2PD →＝0，λPA →＋μPB →＋PC →＝0，则λμ＝________．13. 已知函数f(x)＝⎩⎪⎨⎪⎧x 3－3x ＋2a ，x ≥a ，x 3＋3x －4a ，x<a ，若存在x 0＜0，使得f(x 0)＝0，则实数a 的取值范围是________．14. 在△ABC 中，已知sin A sin B sin (C －θ)＝λsin 2C ，其中tan θ＝12⎝⎛⎭⎫0<θ<π2，若1tan A ＋1tan B ＋2tan C 为定值，则实数λ＝________．二、解答题：本大题共6小题，共计90分．解答时应写出文字说明，证明过程或演算步骤． 15. (本小题满分14分)已知向量a ＝(sin x ，1)，b ＝⎝⎛⎭⎫12，cos x ，其中x ∈(0，π)．(1) 若a ∥b ，求x 的值；(2) 若tan x ＝－2，求|a ＋b |的值．16. (本小题满分14分)如图，在四棱锥PABCD 中，底面ABCD 为平行四边形，O 为对角线BD 的中点，E ，F 分别为棱PC ，PD 的中点，已知PA ⊥AB ，PA ⊥AD.求证：(1) 直线PB ∥平面OEF ； (2) 平面OEF ⊥平面ABCD.如图，三个小区分别位于扇形OAB 的三个顶点上，Q 是弧AB 的中点，现欲在线段OQ 上找一处开挖工作坑P(不与点O ，Q 重合)，为小区铺设三条地下电缆管线PO ，PA ，PB ，已知OA ＝2千米，∠AOB ＝π3，记∠APQ ＝θ rad ，地下电缆管线的总长度为y 千米．(1) 将y 表示成θ的函数，并写出θ的范围；(2) 请确定工作坑P 的位置，使地下电缆管线的总长度最小．如图，在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a>b>0)的左顶点为A ，B 是椭圆C 上异于左、右顶点的任意一点，P 是AB 的中点，过点B 且与AB 垂直的直线与直线OP 交于点Q ，已知椭圆C 的离心率为12，点A 到右准线的距离为6.(1) 求椭圆C 的标准方程；(2) 设点Q 的横坐标为x 0，求x 0的取值范围．设A ，B 为函数y ＝f(x)图象上相异两点，且点A ，B 的横坐标互为倒数，过点A ，B 分别作函数y ＝f(x)的切线，若这两条切线存在交点，则称这个交点为函数f(x)的“优点”．(1) 若函数f(x)＝⎩⎪⎨⎪⎧ln x ，0<x<1，ax 2， x>1不存在“优点”，求实数a 的值；(2) 求函数f(x)＝x 2的“优点”的横坐标的取值范围；(3) 求证：函数f(x)＝ln x 的“优点”一定落在第一象限．已知首项不为0的数列{a n}的前n项和为S n，2a1＋a2＝a3，且对任意的n∈N，n≥2都有2nS n＋1－(2n ＋5)S n＋S n－1＝ra1.(1) 若a2＝3a1，求r的值；(2) 数列{a n}能否是等比数列？说明理由；(3) 当r＝1时，求证：数列{a n}是等差数列．2019届高三年级第一次模拟考试(泰州)数学参考答案1. π2. ±43. 54. [－1，1]5. 15 6. 87. 4 8. 2 9. 14 10. (－1，＋∞) 11. 212. －34 13. [－1，0) 14. 51015. (1) 因为a ∥b ，所以sin x cos x ＝12，即sin 2x ＝1.因为x ∈(0，π)，所以x ＝π4.(2) 因为tan x ＝sin xcos x ＝－2，所以sin x ＝－2cos x .因为a ＋b ＝⎝⎛⎭⎫sin x ＋12，1＋cos x ， 所以|a ＋b |＝⎝⎛⎭⎫sin x ＋122＋（1＋cos x ）2＝94＋sin x ＋2cos x ＝32.16. (1) O 为BD 的中点，F 为PD 的中点， 所以PB ∥FO.因为PB ⊄平面OEF ，FO ⊂平面OEF ， 所以PB ∥平面OEF.(2) 连结AC ，因为四边形ABCD 为平行四边形， 所以AC 与BD 交于点O ，O 为AC 的中点． 因为E 为PC 的中点， 所以PA ∥OE.因为PA ⊥AB ，PA ⊥AD ，AB ∩AD ＝A ，AB ，AD ⊂平面ABCD ， 所以PA ⊥平面ABCD ， 所以OE ⊥平面ABCD. 因为OE ⊂平面OEF ，所以平面OEF ⊥平面ABCD.17. (1) 因为Q 为弧AB 的中点，由对称性，知PA ＝PB ，∠AOP ＝∠BOP ＝π6，又∠APO ＝π－θ，∠OAP ＝θ－π6，由正弦定理，得PA sin π6＝OA sin （π－θ）＝OPsin ⎝⎛⎭⎫θ－π6，又OA ＝2，所以PA ＝1sin θ，OP ＝2sin ⎝⎛⎭⎫θ－π6sin θ，所以y ＝PA ＋PB ＋OP ＝2PA ＋OP ＝2＋2sin ⎝⎛⎭⎫θ－π6sin θ＝3sin θ－cos θ＋2sin θ，因为∠APQ ＞∠AOP ，所以θ>π6，∠OAQ ＝∠OQA ＝12(π－π6)＝5π12，所以θ∈⎝⎛⎭⎫π6，5π12. (2) 令f(θ)＝3sin θ－cos θ＋2sin θ，θ∈⎝⎛⎭⎫π6，5π12， f′(θ)＝1－2cos θsin 2θ＝0，得θ＝π3， f(θ)在区间⎝⎛⎭⎫π6，π3上单调递减，在区间(π3，5π12)上单调递增， 所以当θ＝π3，即OP ＝233千米时，f(θ)有唯一的极小值，即是最小值，则f(θ)min ＝2 3.答：当工作坑P 与O 的距离为233千米时，地下电缆管线的总长度最小．18. (1) 依题意，得⎩⎨⎧c a ＝12，a ＋a 2c ＝6，解得⎩⎪⎨⎪⎧a ＝2，c ＝1，所以b ＝a 2－c 2＝3，所以椭圆C 的方程为x 24＋y 23＝1.(2) 由(1)知，A(－2，0)，设AB ：x ＝my －2，m ≠0，联立⎩⎪⎨⎪⎧x ＝my －2，3x 2＋4y 2＝12， 解得⎩⎪⎨⎪⎧x ＝6m 2－83m 2＋4，y ＝12m 3m 2＋4或⎩⎪⎨⎪⎧x ＝－2，y ＝0，即B(6m 2－83m 2＋4，12m 3m 2＋4)，则P(－83m 2＋4，6m 3m 2＋4)，所以k OP ＝－3m 4，OP ：y ＝－3m 4x.因为AB ⊥BQ ，所以k BQ ＝－m ，所以直线BQ 的方程为BQ ：y ＝－mx ＋6m 3＋4m3m 2＋4，联立⎩⎨⎧y ＝－3m 4x ，y ＝－mx ＋6m 3＋4m3m 2＋4，得x 0＝8（3m 2＋2）3m 2＋4＝8－163m 2＋4∈(4，8)．19. (1) 由题意可知，f′(x)＝f′⎝⎛⎭⎫1x 对x ∈(0，1)∪(1，＋∞)恒成立， 不妨取x ∈(0，1)，则f′(x)＝1x ＝2a x ＝f′⎝⎛⎭⎫1x 恒成立，即a ＝12， 经验证，a ＝12符合题意．(2) 设A(t ，t 2)，B ⎝⎛⎭⎫1t ，1t 2(t ≠0且t ≠±1)， 因为f′(x)＝2x ，所以A ，B 两点处的切线方程分别为y ＝2tx －t 2，y ＝2t x －1t 2，令2tx －t 2＝2t x －1t 2，解得x ＝12⎝⎛⎭⎫t ＋1t ∈(－∞，－1)∪(1，＋∞)， 所以“优点”的横坐标取值范围为(－∞，－1)∪(1，＋∞)． (3) 设A(t ，ln t)，b ⎝⎛⎭⎫1t ，－ln t ，t ∈(0，1)， 因为f ′(x)＝1x，所以A ，B 两点处的切线方程分别为y ＝1t x ＋ln t －1，y ＝tx －ln t －1，令1t x ＋ln t －1＝tx －ln t －1， 解得x ＝2ln tt －1t>0，所以y ＝1t ·2ln tt －1t ＋ln t －1＝t 2＋1t 2－1(ln t －t 2－1t 2＋1)，设h(m)＝ln m －m 2－1m 2＋1，m ∈(0，1)，则h′(m)＝（m 2－1）2m （m 2＋1）2>0，所以h(m)单调递增， 所以h(m)<h(1)＝0， 即ln t －t 2－1t 2＋1<0.因为t 2＋1t 2－1<0，所以y ＝1t ·2ln tt －1t＋ln t －1>0，所以“优点”的横坐标和纵坐标均为正数，在第一象限．20. (1)令n＝2，得4S3－9S2＋S1＝ra1，即4(a3＋a2＋a1)－9(a2＋a1)＋a1＝ra1，化简，得4a3－5a2－4a1＝ra1.因为2a1＋a2＝a3，a2＝3a1，所以4×5a1－5×3a1－4a1＝ra1，解得r＝1.(2) 假设数列{a n}是等比数列，公比为q，则由2a1＋a2＝a3得2a1＋a1q＝a1q2，且a1≠0，解得q＝2或q＝－1，由2nS n＋1－(2n＋5)S n＋S n－1＝ra1，得4S n＝2na n＋1－a n－ra1(n≥2)，所以4S n－1＝2(n－1)a n－a n－1－ra1(n≥3)，两式相减，整理得2na n＋1＋a n－1＝(2n＋3)a n，两边同除以a n－1，可得2n(q2－q)＝3q－1.因为q＝2或－1，所以q2－q≠0，所以上式不可能对任意n≥3恒成立，故数列{a n}不可能是等比数列．(3) r＝1时，令n＝2，整理得－4a1－5a2＋4a3＝a1，又由2a1＋a2＝a3可知a2＝3a1，a3＝5a1，令n＝3，可得6S4－11S3＋S2＝a1，解得a4＝7a1，由(2)可知4S n＝2na n＋1－a n－a1(n≥2)，所以4S n－1＝2(n－1)a n－a n－1－a1(n≥3)，两式相减，整理得2na n＋1＋a n－1＝(2n＋3)a n(n≥3)，所以2(n－1)a n＋a n－2＝(2n＋1)a n－1(n≥4)，两式相减，可得2n[(a n＋1－a n)－(a n－a n－1)]＝(a n－a n－1)－(a n－1－a n－2)(n≥4)．因为(a4－a3)－(a3－a2)＝0，所以(a n－a n－1)－(a n－1－a n－2)＝0(n≥4)，即a n－a n－1＝a n－1－a n－2(n≥4)，又因为a3－a2＝a2－a1＝2a1，所以数列{a n}是以a1为首项，2a1为公差的等差数列．。

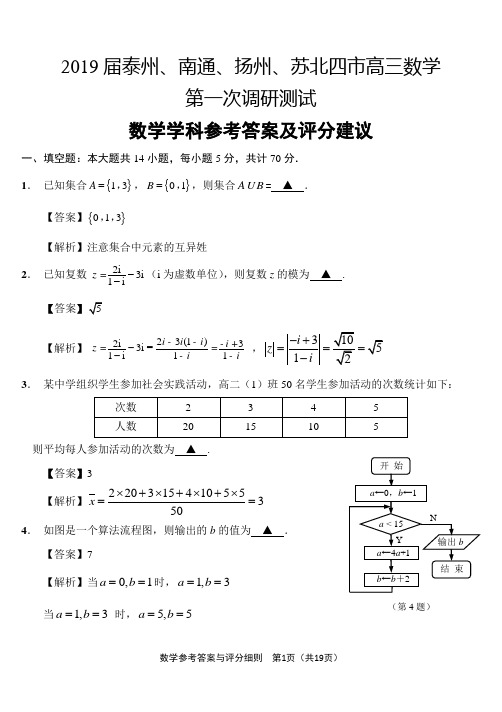
2019届泰州、南通、扬州、苏北四市高三数学第一次调研测试数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共计70分． 1． 已知集合{}13=A ，，{}01=B ，，则集合AB = ▲ ．【答案】{}013，，【解析】注意集合中元素的互异姓2． 已知复数2i 3i 1iz --=（i 为虚数单位），则复数z 的模为 ▲ .【答案【解析】23(1)2i 33i =1i 11i i i i z i i -----+==--，31i z i -+===-3． 某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：则平均每人参加活动的次数为 ▲ . 【答案】3 【解析】22031541055350x ⨯+⨯+⨯+⨯==4． 如图是一个算法流程图，则输出的b 的值为 ▲ ．【答案】7【解析】当0,1a b ==时，1,3a b == 当1,3a b == 时，5,5a b ==（第4题）当5,5a b ==时，21,7a b ==5． 有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参 加一个，则这两位同学参加不同兴趣小组的概率为 ▲ ． 【答案】23【解析】62333p ==⨯6． 已知正四棱柱的底面边长是3 cm ，侧面的对角线长是， 则这个正四棱柱的体积为 ▲ cm 3． 【答案】54【解析】6h == ，9654V =⨯=【应该改成体对角线比较好的哦，难道考查考生审题能力】 7． 若实数x y ，满足2+3x y x ≤≤，则x y +的最小值为 ▲ ．【答案】6-【解析】2333x y x x x +≤++≤+，23,3x x x ≤+≥- ，min ()3x y +≤8． 在平面直角坐标系xOy 中，已知抛物线22(0)=>y px p 的准线为l ，直线l 与双曲线2214x y -=的两条渐近线分别交于A ，B 两点，AB =p 的值为 ▲ ．【答案】【解析】双曲线渐近线方程，2x y =± ，根据双曲线对称性可知，24PAB =⨯=解之得p =9． 在平面直角坐标系xOy 中，已知直线3y x t =+与曲线()sin cos y a x b x a b t =+∈R ，，相切于点()01，，则()a b t +的值为 ▲ ．。

江苏省泰州市2019届高三第一次模拟考试高三数学（理）试卷★祝考试顺利★ 注意事项：1、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

2、选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3、非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5、考试结束后，请将本试题卷和答题卡一并上交。

一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1. 已知集合{}m P ,1-=，⎭⎬⎫⎩⎨⎧<<-=431x x Q ，若∅≠Q P ，则整数=m ▲ ． 2．已知α为第三象限的角，且4sin(),tan 25则παα+=-= ▲ ．3. 若函数()f x =a 的值为 ▲ ．4．已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若P (4，y )是角θ终边上一点，且sin θ＝－255，则y ＝ ▲ .5.若存在实数x ∈[1，2]满足2x 2﹣ax+2＞0，则实数a 的取值范围是 ▲ ．6.设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是 ▲ ． 7.已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝ ▲ ．8.设a ∈R ，函数f (x )＝e x＋a e x 是偶函数，若曲线y ＝f (x )的一条切线的斜率是32，则切点的横坐标为 ▲ ．9.已知x R ∈，()f x 为sin x 与cos x 中的较小者，设()m f x n ≤≤，则m n -= ▲ . 10．设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝ ▲ . 11．经过函数1y x=上一点M 引切线l 与x 轴、y 轴分别交于点A 和点B ，O 为坐标原点,记OAB ∆的面积为S ,则S = ▲ ．12．函数f(x)＝Asin(ωx ＋φ)(A ，ω，φ是常数，A>0，ω>0)的图象如右图所示，若2236f f f πππ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则ω= ▲ ． 13.若关于x 的方程4x e x kx -=有四个实数根，则实数k 的取值范围是 ▲ ．14.已知函数ax x x x f +-=ln )(在(0,e)上是增函数，函数)(x g =|a e x-|+22a 在[0,ln3]上的最大值M 与最小值m 的差为52，则a= ▲ ． 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 15（本题满分14分）已知函数f(x)=2x+k·2-x,k∈R.（1）若函数f(x)为奇函数，求实数k 的值；（2）若对任意的x∈[)0,+∞都有f(x)>2-x成立，求实数k 的取值范围.16. （本小题满分14分）已知πsin()410A +=ππ(,)42A ∈． （Ⅰ）求cos A 的值； （Ⅱ）求函数5()cos 2sin sin 2f x x A x =+的值域．17．(本小题满分14分)北京市某旅游景点预计2017年1月份起前x 个月的旅游人数的和p(x) (单位：万人)与x 的关系近似满足1()(1)(392),(,12)2p x x x x x N x *=+∙-∈≤已知第x 月的人均消费额q(x)(单位：元)与x 的近似关系是 q(x)=352,(,16)16,(,712)x x N x x N x x**⎧-∈≤≤⎪⎨∈≤≤⎪⎩ (1)写出2017年第x 月的旅游人数f(x)(单位：万人)与x 的函数关系式； (2)试问2017年哪个月的旅游消费总额最大，最大旅游消费额为多少万元？18．(本小题满分16分)已知cos ⎝⎛⎭⎪⎫π6＋αcos ⎝ ⎛⎭⎪⎫π3－α＝－14，α∈(π3，π2)． (1) 求sin 2α的值； (2) 求tan α－1tan α的值．19. （本题满分16分）已知函数2()(21)ln f x x a x a x =-++(1)当a=1时，求函数f(x)的单调增区间；(2)求函数f(x)区间[]e ,1上的最小值； (3)设()(1)g x a x =-，若存在01,x e e ⎡⎤∈⎢⎥⎣⎦，使得00()()f x g x ≥成立，求实数a 的取值范围.20．（本题满分16分） 已知函数2()ln f x a x x =-。

-2019年江苏省泰州市、南通市、扬州市、苏北四市七市高考数学一模试卷一、填空题：本大题共14小题，每小题5分，共计70分．1．（5分）已知集合A ＝{1，3}，B ＝{0，1}，则集合A ∪B ＝．2．（5分）已知复数（i 为虚数单位），则复数z 的模为．3．（5分）某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：次数2345人数2015105则平均每人参加活动的次数为．4．（5分）如图是一个算法流程图，则输出的b 的值为．5．（5分）有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为．6．（5分）已知正四棱柱的底面边长为3cm ，侧面的对角线长是3cm ，则这个正四棱柱的体积是cm 3．7．（5分）若实数x ，y 满足x ≤y ≤2x+3，则x+y 的最小值为．8．（5分）在平面直角坐标系xOy 中，已知抛物线y 2＝2px （p ＞0）的准线为l ，直线l 与双曲线的两条渐近线分别交于A ，B 两点，，则p 的值为．9．（5分）在平面直角坐标系xOy 中，已知直线y ＝3x+t 与曲线y ＝asinx+bcosx （a ，b ，t ∈R ）相切于点（0，1），则（a+b ）t 的值为．10．（5分）已知数列{a n }是等比数列，有下列四个命题：①数列{|a n |}是等比数列；②数列{a n a n+1}是等比数列；③数列是等比数列；④数列{lga n 2}是等比数列．其中正确的命题有个．11．（5分）已知函数f （x ）是定义在R 上的奇函数，且f （x+2）＝f （x ）．当0＜x ≤1时，f （x ）＝x 3﹣ax+1，则实数a 的值为．12．（5分）在平面四边形ABCD 中，AB ＝1，DA ＝DB ，＝3，＝2，则|的最小值为．13．（5分）在平面直角坐标系xOy 中，圆O ：x 2+y 2＝1，圆C ：（x ﹣4）2+y 2＝4．若存在过点P （m ，0）的直线l ，l 被两圆截得的弦长相等，则实数m 的取值范围．14．（5分）已知函数f （x ）＝（2x+a ）（|x ﹣a|+|x+2a|）（a ＜0）．若f （1）+f （2）+f （3）+…+f （672）＝0，则满足f （x ）＝2019的x 的值为．二、解答题：本大题共6小题，共计90分．15．（14分）如图，在四棱锥P ﹣ABCD 中，M ，N 分别为棱PA ，PD 的中点．已知侧面P AD⊥底面ABCD ，底面ABCD 是矩形，DA ＝DP ．求证：（1）MN ∥平面PBC ；（2）MD ⊥平面PAB ．16．（14分）在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对边的长，，．（1）求角B 的值；（2）若，求△ABC 的面积．17．（14分）如图，在平面直角坐标系xOy 中，椭圆（a ＞b ＞0）的左焦点为F ，右顶点为A，上顶点为B．（1）已知椭圆的离心率为，线段AF中点的横坐标为，求椭圆的标准方程；（2）已知△ABF外接圆的圆心在直线y＝﹣x上，求椭圆的离心率e的值．18．（16分）如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别为和4m，上部是圆心为O的劣弧CD，．（1）求图1中拱门最高点到地面的距离；（2）现欲以B点为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示．设BC与地面水平线l所成的角为θ．记拱门上的点到地面的最大距离为h，试用θ的函数表示h，并求出h的最大值．19．（16分）已知函数．（1）讨论f（x）的单调性；（2）设f（x）的导函数为f'（x），若f（x）有两个不相同的零点x1，x2．①求实数a的取值范围；②证明：x1f'（x1）+x2f'（x2）＞2lna+2．20．（16分）已知等差数列{a n}满足a4＝4，前8项和S8＝36．（1）求数列{a n}的通项公式；（2）若数列{b n}满足．①证明：{b n}为等比数列；②求集合．【选做题】本题包括21、22、C23三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．[选修4-2：矩阵与变换]（本小题满分0分）21．已知矩阵，，且，求矩阵M．[选修4-4：坐标系与参数方程]（本小题满分0分）22．在平面直角坐标系xOy中，曲线C的参数方程是（t为参数）．以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是ρsin（θ﹣）＝．求：（1）直线l的直角坐标方程；（2）直线l被曲线C截得的线段长．[选修4-5：不等式选讲]（本小题满分0分）23．已知实数a，b，c满足a 2+b2+c2≤1，求证：．【必做题】第22、23题，每小题0分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．24．“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位“回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4，其结果记为X；从9个不同2位“回文数”中任取2个相加，其结果记为Y．（1）求X为“回文数”的概率；（2）设随机变量ξ表示X，Y两数中“回文数”的个数，求ξ的概率分布和数学期望E （ξ）．25．设集合B是集合A n＝{1，2，3，……，3n﹣2，3n﹣1，3n}，n∈N *的子集．记B中所有元素的和为S（规定：B为空集时，S＝0）．若S为3的整数倍，则称B为A n的“和谐子集”．求：（1）集合A1的“和谐子集”的个数；（2）集合A n的“和谐子集”的个数．2019年江苏省泰州市、南通市、扬州市、苏北四市七市高考数学一模试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共计70分．1．（5分）已知集合A＝{1，3}，B＝{0，1}，则集合A∪B＝{0，1，3}．【解答】解：根据题意，集合A＝{1，3}，B＝{0，1}，则A∪B＝{0，1，3}；故答案为：{0，1，3}．2．（5分）已知复数（i为虚数单位），则复数z的模为．【解答】解：＝，则复数z的模为．故答案为：．3．（5分）某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：次数2345人数2015105则平均每人参加活动的次数为3．【解答】解：根据题意，计算这组数据的平均数为：＝×（20×2+15×3+10×4+5×5）＝3．故答案为：3．4．（5分）如图是一个算法流程图，则输出的b的值为7．【解答】解：模拟程序的运行，可得a＝0，b＝1满足条件a＜15，执行循环体，a＝1，b＝3满足条件a＜15，执行循环体，a＝5，b＝5满足条件a＜15，执行循环体，a＝21，b＝7此时，不满足条件a＜15，退出循环，输出b的值为7．故答案为：7．5．（5分）有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为．【解答】解：有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，基本事件总数n＝3×3＝9，这两位同学参加不同兴趣小组包含的基本事件个数m＝3×2＝6，则这两位同学参加不同兴趣小组的概率为p＝＝．故答案为：．6．（5分）已知正四棱柱的底面边长为3cm，侧面的对角线长是3cm，则这个正四棱柱的体积是54cm3．【解答】解：设正四棱柱的高为h，∵正四棱柱的底面边长为3cm，侧面的对角线长是3cm，∴＝3，解得h＝6（cm），∴这个正四棱柱的体积V＝Sh＝3×3×6＝54（cm3）．故答案为：54．7．（5分）若实数x，y满足x≤y≤2x+3，则x+y的最小值为﹣6．【解答】解：画出实数x，y满足x≤y≤2x+3的平面区域，如图示：由，解得A（﹣3，﹣3），由z＝x+y得：y＝﹣x+z，显然直线过A时z最小，z的最小值是﹣6，故答案为：﹣6．8．（5分）在平面直角坐标系xOy 中，已知抛物线y 2＝2px （p ＞0）的准线为l ，直线l 与双曲线的两条渐近线分别交于A ，B 两点，，则p 的值为．【解答】解：抛物线y 2＝2px （p ＞0）的准线为l ：x ＝﹣，双曲线的两条渐近线方程为y ＝±x ，可得A （﹣，﹣），B （（﹣，），|AB|＝＝，可得p ＝2．故答案为：2．9．（5分）在平面直角坐标系xOy 中，已知直线y ＝3x+t 与曲线y ＝asinx+bcosx （a ，b ，t ∈R ）相切于点（0，1），则（a+b ）t 的值为4．【解答】解：根据题意得，t ＝1y ′＝acosx ﹣bsinx ∴k ＝acos0﹣bsin0＝a ∴a ＝3，bcos0＝1∴a ＝3，b ＝1故答案为4．10．（5分）已知数列{a n }是等比数列，有下列四个命题：①数列{|a n |}是等比数列；②数列{a n a n+1}是等比数列；③数列是等比数列；④数列{lga n 2}是等比数列．其中正确的命题有3个．【解答】解：由{a n}是等比数列可得＝q（q为常数，q≠0），①＝＝|q|为常数，故是等比数列；②＝＝q2为常数，故是等比数列；③＝＝常数，故是等比数列；④数列a n＝1是等比数列，但是lga n2＝0不是等比数列；故答案为：311．（5分）已知函数f（x）是定义在R上的奇函数，且f（x+2）＝f（x）．当0＜x≤1时，f（x）＝x 3﹣ax+1，则实数a的值为2．【解答】解：∵f（x）是定义在R上的奇函数，且f（x+2）＝f（x）．∴当x＝﹣1时，f（﹣1+2）＝f（﹣1）＝f（1），即﹣f（1）＝f（1），则f（1）＝0，∵当0＜x≤1时，f（x）＝x3﹣ax+1．∴f（1）＝1﹣a+1＝0，得a＝2，故答案为：212．（5分）在平面四边形ABCD中，AB＝1，DA＝DB，＝3，＝2，则|的最小值为2．【解答】解：如图，以A为原点，建立平面直角坐标系，则A（0，0），B（1，0），因为DA＝DB，可设D（，m），因为?＝3，AB＝1，所以可设C（3，n），又?＝2，所以+mn＝2，即mn＝，+2＝（4，n+2m）|+2|＝＝≥＝2，当且仅当n＝2m，即n＝1，m＝时，等号成立．故答案为：213．（5分）在平面直角坐标系xOy 中，圆O ：x 2+y 2＝1，圆C ：（x ﹣4）2+y 2＝4．若存在过点P （m ，0）的直线l ，l 被两圆截得的弦长相等，则实数m 的取值范围﹣4＜m．【解答】解：显然直线l 有斜率，设直线l ：y ＝k （x ﹣m ），即kx ﹣y ﹣km ＝0，依题意得1﹣（）2＝4﹣（）2＞0有解，即，∴13﹣8m ＞0且3m 2+8m ﹣16＜0解得﹣4＜m ＜，故答案为：﹣4＜m ．14．（5分）已知函数f （x ）＝（2x+a ）（|x ﹣a|+|x+2a|）（a ＜0）．若f （1）+f （2）+f （3）+…+f （672）＝0，则满足f （x ）＝2019的x 的值为337．【解答】解：注意到：，又因为：，，因此．所以，函数f （x ）关于点对称，所以，解得：a ＝﹣673，f （x ）＝（2x ﹣673）（|x+673|+|x ﹣2×673|）＝2019，显然有：0＜2x ﹣673＜2019，即，所以，f （x ）＝（2x ﹣673）（x+673+2×673﹣x ）＝2019，2x﹣673＝1，解得：x＝337．故答案为：337．二、解答题：本大题共6小题，共计90分．15．（14分）如图，在四棱锥P﹣ABCD中，M，N分别为棱PA，PD的中点．已知侧面P AD ⊥底面ABCD，底面ABCD是矩形，DA＝DP．求证：（1）MN∥平面PBC；（2）MD⊥平面PAB．【解答】证明：（1）在四棱锥P﹣ABCD中，M，N分别为棱PA，PD的中点，所以MN∥AD．……………………2分又底面ABCD是矩形，所以BC∥AD，所以MN∥BC．…………………………………………………………………4分又BC?平面PBC，MN?平面PBC，所以MN∥平面PBC．…………………………………………………………6分（2）因为底面ABCD是矩形，所以AB⊥AD．又侧面PAD⊥底面ABCD，侧面PAD∩底面ABCD＝AD，AB?底面ABCD，所以AB⊥侧面P AD．……………………………………………………………8分又MD?侧面PAD，所以AB⊥MD．………………………………………………………………10分因为DA＝DP，又M为AP的中点，从而MD⊥P A．………………………………………………………………12分又P A，AB在平面PAB内，P A∩AB＝A，所以MD⊥平面P AB．…………………………………………………………14分16．（14分）在△ABC中，a，b，c分别为角A，B，C所对边的长，，．（1）求角B的值；（2）若，求△ABC的面积．【解答】（本题满分为14分）解：（1）在△ABC中，因为，0＜A＜π，所以．………………………………………………………2分因为，由正弦定理，得．所以cosB＝sinB．…………………………………………………………………4分若cosB＝0，则sinB＝0，与sin2B+cos2B＝1矛盾，故cosB≠0．于是．又因为0＜B＜π，所以．…………………………………………………………………………7分（2）因为，，由（1）及正弦定理，得，所以．………………………………………………………………………9分又sin C＝sin（π﹣A﹣B）＝sin（A+B）＝sinAcosB+cosAsinB＝．……………………………………………12分所以△ABC的面积为．……14分17．（14分）如图，在平面直角坐标系xOy中，椭圆（a＞b＞0）的左焦点为F，右顶点为A，上顶点为B．（1）已知椭圆的离心率为，线段AF中点的横坐标为，求椭圆的标准方程；（2）已知△ABF外接圆的圆心在直线y＝﹣x上，求椭圆的离心率e的值．【解答】解：（1）因为椭圆（a＞b＞0）的离心率为，所以，则a＝2c．因为线段AF中点的横坐标为，所以．所以，则a2＝8，b2＝a2﹣c2＝6．所以椭圆的标准方程为．…………………………………………………4分（2）因为A（a，0），F（﹣c，0），所以线段AF的中垂线方程为：．又因为△ABF外接圆的圆心C在直线y＝﹣x上，所以． (6)分因为A（a，0），B（0，b），所以线段AB的中垂线方程为：．由C在线段AB的中垂线上，得，整理得，b（a﹣c）+b2＝ac，…………………………………………………………10分即（b﹣c）（a+b）＝0．因为a+b＞0，所以b＝c．……………………………………………………………12分所以椭圆的离心率．…………………………………………14分18．（16分）如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别为和4m，上部是圆心为O的劣弧CD，．（1）求图1中拱门最高点到地面的距离；（2）现欲以B点为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示．设BC与地面水平线l所成的角为θ．记拱门上的点到地面的最大距离为h，试用θ的函数表示h，并求出h的最大值．【解答】解：（1）如图，过O作与地面垂直的直线交AB，CD于点O1，O2，交劣弧CD 于点P，O1P的长即为拱门最高点到地面的距离．在Rt△O2OC中，，，所以OO2＝1，圆的半径R＝OC＝2．所以O1P＝R+OO1＝R+O1O2﹣OO2＝5．答：拱门最高点到地面的距离为5m．…………………4分（2）在拱门放倒过程中，过点O作与地面垂直的直线与“拱门外框上沿”相交于点P．当点P在劣弧CD上时，拱门上的点到地面的最大距离h等于圆O的半径长与圆心O到地面距离之和；当点P在线段AD上时，拱门上的点到地面的最大距离h等于点D到地面的距离．由（1）知，在Rt△OO1B中，．以B为坐标原点，直线l为x轴，建立如图所示的坐标系．（2.1）当点P在劣弧CD上时，．由，，由三角函数定义，得O，则．…………………………………………………………8分所以当即时，h取得最大值．……………………………………………………10分（2.2）当点P在线段AD上时，．设∠CBD＝φ，在Rt△BCD中，，．由∠DBx＝θ+φ，得．所以＝．……………………………………14分又当时，．所以在上递增．所以当时，h取得最大值5．因为，所以h的最大值为．答：；艺术拱门在放倒的过程中，拱门上的点到地面距离的最大值为（）m．……………………………………………16分19．（16分）已知函数．（1）讨论f（x）的单调性；（2）设f（x）的导函数为f'（x），若f（x）有两个不相同的零点x1，x2．①求实数a的取值范围；②证明：x1f'（x1）+x2f'（x2）＞2lna+2．【解答】解：（1）f（x）的定义域为（0，+∞），且．（i）当a≤0时，f'（x）＞0成立，所以f（x）在（0，+∞）为增函数；………2分（ii）当a＞0时，①当x＞a时，f'（x）＞0，所以f（x）在（a，+∞）上为增函数；②当0＜x＜a时，f'（x）＜0，所以f（x）在（0，a）上为减函数．………4分（2）①由（1）知，当a≤0时，f（x）至多一个零点，不合题意；当a＞0时，f（x）的最小值为f（a），依题意知f（a）＝1+lna＜0，解得．……………………………………6分一方面，由于1＞a，f（1）＝a＞0，f（x）在（a，+∞）为增函数，且函数f（x）的图象在（a，1）上不间断．所以f（x）在（a，+∞）上有唯一的一个零点．另一方面，因为，所以，，令，当时，，所以又f（a）＜0，f（x）在（0，a）为减函数，且函数f（x）的图象在（a2，a）上不间断．所以f（x）在（0，a）有唯一的一个零点．综上，实数a的取值范围是．……………………………………………10分②证明：设．又则p＝2+ln（x1x2）．………………………………………12分下面证明．不妨设x1＜x2，由①知0＜x1＜a＜x2．要证，即证．因为，f（x）在（0，a）上为减函数，所以只要证．又f（x1）＝f（x2）＝0，即证．……………………………………14分设函数．所以，所以F（x）在（a，+∞）为增函数．所以F（x2）＞F（a）＝0，所以成立．从而成立．所以p＝2+ln（x1x2）＞2lna+2，即x1f'（x1）+x2f'（x2）＞2lna+2成立．…16分20．（16分）已知等差数列{a n}满足a4＝4，前8项和S8＝36．（1）求数列{a n}的通项公式；（2）若数列{b n}满足．①证明：{b n}为等比数列；②求集合．【解答】解：（1）设等差数列{a n}的公差为d．因为等差数列{a n}满足a4＝4，前8项和S8＝36，所以，解得所以数列{a n}的通项公式为a n＝n．（2）①设数列{b n}前n项的和为B n．由（1）及得，由③﹣④得3（2n﹣1）﹣3（2n﹣1﹣1）＝（b1a2n﹣1+b2a2n﹣3+…+b n﹣1a3+b n a1+2n）﹣（b1a2n ﹣3+b2a2n﹣5+…+b n﹣1a1+2n﹣2）＝[b1（a2n﹣3+2）+b2（a2n﹣5+2）+…+b n﹣1（a1+2）+b n a1+2n]﹣（b1a2n﹣3+b2a2n﹣5+…+b n﹣1a1+2n﹣2）＝2（b1+b2+…+b n﹣1）+b n+2＝2（B n﹣b n）+b n+2．所以3?2n﹣1＝2B n﹣b n+2（n≥2，n∈N*），又3（21﹣1）＝b1a1+2，所以b1＝1，满足上式．所以当n≥2时，由⑤﹣⑥得，．＝，所以，，所以数列{b n}是首项为1，公比为2的等比数列．②由，得，即．记，由①得，，所以，所以c n≥c n+1（当且仅当n＝1时等号成立）．由，得c m＝3c p＞c p，所以m＜p；设t＝p﹣m（m，p，t∈N*），由，得．当t＝1时，m＝﹣3，不合题意；当t＝2时，m＝6，此时p＝8符合题意；当t＝3时，，不合题意；当t＝4时，，不合题意．下面证明当t≥4，t∈N*时，．不妨设f（x）＝2x﹣3x﹣3（x≥4），f'（x）＝2x ln2﹣3＞0，所以f（x）在[4，+∞）上单调增函数，所以f（x）≥f（4）＝1＞0，所以当t≥4，t∈N*时，，不合题意．综上，所求集合＝{（6，8）}．【选做题】本题包括21、22、C23三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．[选修4-2：矩阵与变换]（本小题满分0分）21．已知矩阵，，且，求矩阵M．【解答】解：由题意，，则．……………………………………4分因为，则．……………………………………………………6分所以矩阵．………………………………………………10分[选修4-4：坐标系与参数方程]（本小题满分0分）22．在平面直角坐标系xOy中，曲线C的参数方程是（t为参数）．以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是ρsin（θ﹣）＝．求：（1）直线l的直角坐标方程；（2）直线l被曲线C截得的线段长．【解答】解：（1）直线l的极坐标方程是ρsin（θ﹣）＝．转换为直角坐标方程为：x﹣y+2＝0；（2）曲线C的参数方程是（t为参数）：转换为直角坐标方程为：x2＝y．由，得x2﹣x﹣2＝0，所以直线l与曲线C的交点A（﹣1，1），B（2，4）．所以直线l被曲线C截得的线段长为．[选修4-5：不等式选讲]（本小题满分0分）23．已知实数a，b，c满足a 2+b2+c2≤1，求证：．【解答】证明：由柯西不等式，得， (5)分所以．…………………………10分【必做题】第22、23题，每小题0分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．24．“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位“回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4，其结果记为X；从9个不同2位“回文数”中任取2个相加，其结果记为Y．（1）求X为“回文数”的概率；（2）设随机变量ξ表示X，Y两数中“回文数”的个数，求ξ的概率分布和数学期望E （ξ）．【解答】解：（1）记“X是‘回文数’”为事件A．9个不同2位“回文数”乘以4的值依次为：44，88，132，176，220，264，308，352，396．其中“回文数”有：44，88．所以，事件A的概率．……………………………………………………3分（2）根据条件知，随机变量ξ的所有可能取值为0，1，2．由（1）得．…………………………………………………………………5分设“Y是‘回文数’”为事件B，则事件A，B相互独立．根据已知条件得，．；；……………………………………………………8分所以，随机变量ξ的概率分布为ξ012P所以，随机变量ξ的数学期望为：． (10)分25．设集合B是集合A n＝{1，2，3，……，3n﹣2，3n﹣1，3n}，n∈N *的子集．记B中所有元素的和为S（规定：B为空集时，S＝0）．若S为3的整数倍，则称B为A n的“和谐子集”．求：（1）集合A1的“和谐子集”的个数；（2）集合A n的“和谐子集”的个数．【解答】解：（1）由题意有：A1＝，则集合A1的“和谐子集”为：?，，，共4个，故答案为：4；（2）记A n的“和谐子集”的个数等于a n，即A n有a n个所有元素的和为3的整数倍的子集，另记A n有b n个所有元素的和为3的整数倍余1的子集，有c n个所有元素的和为3的整数倍余2的子集，易知：a1＝4，b1＝2，c1＝2，集合A n+1＝{1，2，3，……，3n﹣2，3n﹣1，3n，3n+1，3n+2，3n+3}的“和谐子集”有以下4种情况，（考查新增元素3n+1，3n+2，3n+3）①集合集合A n＝{1，2，3，……，3n﹣2，3n﹣1，3n}的“和谐子集”共a n个，②仅含一个元素3（n+1）的“和谐子集”共a n个，同时含两个元素3n+1，3n+2的“和谐子集”共a n个，同时含三个元素3n+1，3n+2，3（n+1）的“和谐子集”共a n个，③仅含一个元素3n+1的“和谐子集”共c n个，同时含两个元素3n+1，3n+3的“和谐子集”共c n个，④仅含一个元素3n+2的“和谐子集”共b n个，同时含两个元素3n+2，3n+3的“和谐子集”共b n个，所以集合A n+1的“和谐子集”共有a n+1＝4a n+2b n+2c n，同理：b n+1＝4b n+2a n+2c n，c n+1＝4c n+2a n+2c n，所以a n+1﹣b n+1＝2（a n﹣b n），所以数列是以a1﹣b1＝2为首项，2为公比的等比数列，求得：a n＝b n+2n，同理a n＝c n+2n，又a n+b n+c n＝23n，解得：a n＝+（n∈N*）故答案为：+（n∈N*）。

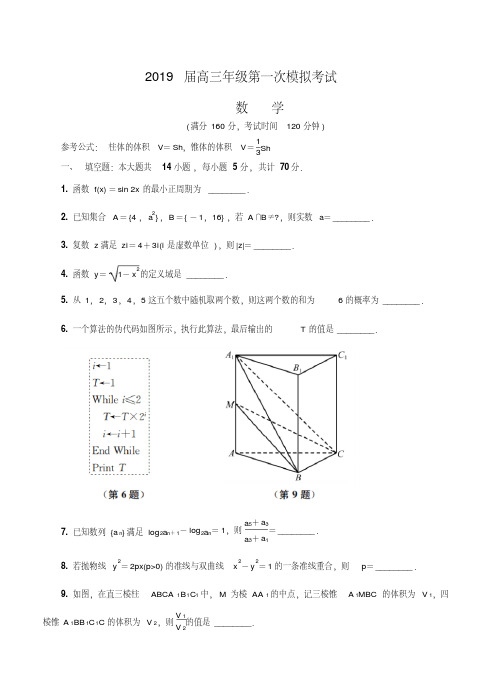
2019届高三年级第一次模拟考试数学(满分160分，考试时间120分钟)参考公式：柱体的体积V ＝Sh ，锥体的体积V ＝13Sh 一、填空题：本大题共14小题，每小题5分，共计70分．1. 函数f(x)＝sin 2x 的最小正周期为________．2. 已知集合A ＝{4，a 2}，B ＝{－1，16}，若A ∩B ≠∅，则实数a ＝________．3. 复数z 满足z i ＝4＋3i (i 是虚数单位)，则|z|＝________．4. 函数y ＝1－x 2的定义域是________．5. 从1，2，3，4，5这五个数中随机取两个数，则这两个数的和为6的概率为________．6. 一个算法的伪代码如图所示，执行此算法，最后输出的T 的值是________．7. 已知数列{a n }满足log 2a n ＋1－log 2a n ＝1，则a 5＋a 3a 3＋a 1＝________． 8. 若抛物线y 2＝2px(p>0)的准线与双曲线x 2－y 2＝1的一条准线重合，则p ＝________．9. 如图，在直三棱柱ABCA 1B 1C 1中，M 为棱AA 1的中点，记三棱锥A 1MBC 的体积为V 1，四棱锥A 1BB 1C 1C 的体积为V 2，则V 1V 2的值是________． 10. 已知函数f(x)＝2x 4＋4x 2，若f(a ＋3)>f(a －1)，则实数a 的取值范围为________．11. 在平面直角坐标系xOy 中，过圆C 1：(x －k)2＋(y ＋k －4)2＝1上任一点P 作圆C 2：x 2＋y 2＝1的一条切线，切点为Q ，则当线段PQ 的长最小时，k ＝________．12. 已知P 为平行四边形ABCD 所在平面上任一点，且满足PA →＋PB →＋2PD →＝0，λPA →＋μPB →＋PC →＝0，则λμ＝________．13. 已知函数f(x)＝⎩⎪⎨⎪⎧x 3－3x ＋2a ，x ≥a ，x 3＋3x －4a ，x<a ，若存在x 0＜0，使得f(x 0)＝0，则实数a 的取值范围是________．14. 在△ABC 中，已知sin A sin B sin (C －θ)＝λsin 2C ，其中tan θ＝12⎝⎛⎭⎫0<θ<π2，若1tan A ＋1tan B ＋2tan C 为定值，则实数λ＝________．二、解答题：本大题共6小题，共计90分．解答时应写出文字说明，证明过程或演算步骤．15. (本小题满分14分)已知向量a ＝(sin x ，1)，b ＝⎝⎛⎭⎫12，cos x ，其中x ∈(0，π)．(1) 若a ∥b ，求x 的值；(2) 若tan x ＝－2，求|a ＋b |的值．16. (本小题满分14分)如图，在四棱锥PABCD 中，底面ABCD 为平行四边形，O 为对角线BD 的中点，E ，F 分别为棱PC ，PD 的中点，已知PA ⊥AB ，PA ⊥AD.求证：(1) 直线PB ∥平面OEF ；(2) 平面OEF ⊥平面ABCD.17. (本小题满分14分)如图，三个小区分别位于扇形OAB 的三个顶点上，Q 是弧AB 的中点，现欲在线段OQ 上找一处开挖工作坑P(不与点O ，Q 重合)，为小区铺设三条地下电缆管线PO ，PA ，PB ，已知OA ＝2千米，∠AOB ＝π3，记∠APQ ＝θ rad ，地下电缆管线的总长度为y 千米． (1) 将y 表示成θ的函数，并写出θ的范围；(2) 请确定工作坑P 的位置，使地下电缆管线的总长度最小．。

江苏省泰州市2019-2020学年第一次高考模拟考试数学试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()ln f x x =，()()23g x m x n =++，若对任意的()0,x ∈+∞总有()()f x g x ≤恒成立，记()23m n +的最小值为(),f m n ，则(),f m n 最大值为（ ）A ．1B ．1eC ．21eD 【答案】C 【解析】 【分析】对任意的()0,x ∈+∞总有()()f x g x ≤恒成立，因为ln (23)x m x n ≤++，对()0,x ∈+∞恒成立，可得230m +>，令ln (23)y x m x n =-+-，可得1(23)y m x'=-+，结合已知，即可求得答案. 【详解】Q 对任意的()0,x ∈+∞总有()()f x g x ≤恒成立∴ln (23)x m x n ≤++，对()0,x ∈+∞恒成立， ∴230m +>令ln (23)y x m x n =-+-，可得1(23)y m x'=-+ 令0y '=，得123x m =+ 当123x m >+，0y '<当1023x m <<+0y '> ∴123x m =+，max 1ln1023y n m =--≤+，123n m e --+≥ 故1(23)(,)n nm n f m n e ++≥=Q 11(,)n nf m n e+-'=令110n ne+-=，得 1n = ∴当1n >时，(,)0f m n '<当1n <，(,)0f m n '>∴当1n =时，max 21(,)f m n e=故选：C. 【点睛】本题主要考查了根据不等式恒成立求最值问题，解题关键是掌握不等式恒成立的解法和导数求函数单调性的解法，考查了分析能力和计算能力,属于难题.2．设等差数列{}n a 的前n 项和为n S ，若31425a a a =+=，，则6S =（ ） A ．10 B ．9C ．8D ．7【答案】B 【解析】 【分析】 根据题意3141152223a a a a d a d =+=+=+=，，解得14a =，1d =-，得到答案.【详解】3141152223a a a a d a d =+=+=+=，，解得14a =，1d =-，故616159S a d =+=.故选：B . 【点睛】本题考查了等差数列的求和，意在考查学生的计算能力.3．设复数z 满足()117i z i +=-，则z 在复平面内的对应点位于（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】C 【解析】 【分析】化简得到34z i =--，得到答案. 【详解】()117i z i +=-，故()()()()1711768341112i i i iz i i i i -----====--++-，对应点在第三象限. 故选：C . 【点睛】本题考查了复数的化简和对应象限，意在考查学生的计算能力.4．已知向量(1,2),(3,1)a b =-=-r r，则（ ）A ．a r∥b rB ．a r⊥b rC ．a r∥(a b -rr)D ．a r⊥( a b -rr)【答案】D【解析】 【分析】由题意利用两个向量坐标形式的运算法则，两个向量平行、垂直的性质，得出结论. 【详解】∵向量a =r（1，﹣2），b =r（3，﹣1），∴a r和b r的坐标对应不成比例，故a r、b r不平行，故排除A ； 显然，a r •b =r3+2≠0，故a r、b r不垂直，故排除B ；∴a b -=rr（﹣2，﹣1），显然，a r和a b -rr的坐标对应不成比例，故a r和a b -rr不平行，故排除C ；∴a r •（a b -r r ）＝﹣2+2＝0，故 a r ⊥（a b -r r ），故D 正确，故选：D. 【点睛】本题主要考查两个向量坐标形式的运算，两个向量平行、垂直的性质，属于基础题.5．已知向量a r 与a b +r r的夹角为60︒，1a =r ，b =r ，则a b ⋅=r r ( )A ．B ．0C ．0或32-D ．32-【答案】B 【解析】 【分析】由数量积的定义表示出向量a r 与a b +r r的夹角为60︒，再由22a a =r r ，22b b =r r 代入表达式中即可求出a b ⋅r r .【详解】由向量a r 与a b +r r的夹角为60︒，得()2cos 60a a b a a b a a b ⋅+=+⋅=+︒r r r r r r r r r，所以21122a ab +⋅==r r r r又1a =r ，b =r ，22a a =r r ，22b b =r r ，所以1112a b +⋅=⨯r r 0a b ⋅=r r .故选：B 【点睛】本题主要考查向量数量积的运算和向量的模长平方等于向量的平方，考查学生的计算能力，属于基础题. 6．函数sin ln ||2y x x π⎛⎫=-⋅ ⎪⎝⎭图像可能是（ ）A ．B ．C ．D ．【答案】D 【解析】 【分析】先判断函数的奇偶性可排除选项A,C ，当0x +→时，可分析函数值为正，即可判断选项. 【详解】sin ln ||cos ln ||2y x x x x π⎛⎫=-⋅=- ⎪⎝⎭Q ,cos()ln ||cos ln ||x x x x ∴---=-,即函数为偶函数， 故排除选项A,C ，当正数x 越来越小，趋近于0时，cos 0,ln ||0x x -<<，所以函数sin ln ||02y x x π⎛⎫=-⋅> ⎪⎝⎭，故排除选项B,故选：D 【点睛】本题主要考查了函数的奇偶性，识别函数的图象，属于中档题. 7．已知复数(1)(3)(z i i i =+-为虚数单位） ，则z 的虚部为（ ） A ．2 B ．2iC ．4D ．4i【答案】A 【解析】 【分析】对复数z 进行乘法运算，并计算得到42z i =+，从而得到虚部为2. 【详解】因为(1)(3)42z i i i =+-=+，所以z 的虚部为2. 【点睛】本题考查复数的四则运算及虚部的概念，计算过程要注意21i =-.8．二项式22)nx+的展开式中只有第六项的二项式系数最大，则展开式中的常数项是( ) A ．180 B ．90C ．45D ．360【答案】A 【解析】试题分析：因为22)nx+的展开式中只有第六项的二项式系数最大，所以10n =，551021101022•?()2r r rr r rr T C C x x--+==，令5502r -=，则2r =，23104180T C ==.考点：1.二项式定理；2.组合数的计算.9．在ABC V 中，AD 为BC 边上的中线，E 为AD 的中点，且||1,||2AB AC ==u u u r u u u r，120BAC ∠=︒，则||EB =u u u r（ ）A B ．C D 【答案】A 【解析】 【分析】根据向量的线性运算可得3144EB AB AC =-u u u r u u u r u u u r ,利用22||B EB E =u u r u u u r u 及||1,||2AB AC ==u u u r u u u r ，120BAC ∠=︒计算即可. 【详解】因为11131()22244EB EA AB AD AB AB AC AB AB AC =+=-+=-⨯++=-u u u r u u u r u u u r u u u r u u u r u u ur u u u r u u u r u u u r u u u r ,所以22229311216441||6EB AB AB B AC AC E =-⨯=⨯⋅+u u u r u u u r u u ur u u u r u u r u u u r u 229311112()2168216=⨯-⨯⨯⨯-+⨯ 1916=，所以||EB =u u u r ，故选：A 【点睛】本题主要考查了向量的线性运算，向量数量积的运算，向量数量积的性质，属于中档题. 10．阅读如图所示的程序框图，运行相应的程序，则输出的结果为（ ）A ．1112B ．6C ．112D ．223【答案】D 【解析】 【分析】用列举法，通过循环过程直接得出S 与n 的值，得到8n ＝时退出循环,即可求得. 【详解】执行程序框图，可得0S =，2n =，满足条件，12S =，4n ＝，满足条件，113244S =+=，6n =，满足条件，1111124612S =++=，8n ＝，由题意，此时应该不满足条件，退出循环，输出S 的值为11228123⨯=. 故选D ． 【点睛】本题主要考查了循环结构的程序框图的应用,正确依次写出每次循环得到的S 与n 的值是解题的关键,难度较易.11．定义在上的函数满足，且为奇函数，则的图象可能是（ ）A ．B ．C ．D ．【答案】D 【解析】 【分析】 根据为奇函数，得到函数关于中心对称，排除，计算排除，得到答案.为奇函数，即，函数关于中心对称，排除.，排除.故选：. 【点睛】本题考查了函数图像的识别，确定函数关于中心对称是解题的关键.12．已知复数为纯虚数(为虚数单位)，则实数（ ） A ．-1 B ．1C ．0D ．2【答案】B 【解析】 【分析】 化简得到，根据纯虚数概念计算得到答案.【详解】为纯虚数，故且，即.故选：. 【点睛】本题考查了根据复数类型求参数，意在考查学生的计算能力. 二、填空题：本题共4小题，每小题5分，共20分。

2019届高三第一次调研测试数学试题一、填空题：本大题共14小题，每小题5分，共计70分．1． 已知集合{}13=A ，，{}01=B ，，则集合A B = ▲ ．2． 已知复数2i 3i 1iz --=（i 为虚数单位），则复数z 的模为 ▲ . 3． 某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：则平均每人参加活动的次数为 ▲ .4． 如图是一个算法流程图，则输出的b 的值为 ▲ ． 5． 有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为 ▲ ． 6． 已知正四棱柱的底面边长是3 cm ，侧面的对角线长是cm ，则这个正四棱柱的体积为 ▲ cm 3．7． 若实数x y ，满足2+3x y x ≤≤，则x y +的最小值为 ▲ ．8． 在平面直角坐标系xOy 中，已知抛物线22(0)=>y px p 的准线为l ，直线l 与双曲线2214x y -=的两条渐近线分别交于A ，B 两点，AB p 的值为 ▲ ．9． 在平面直角坐标系xOy 中，已知直线3y x t =+与曲线()sin cos y a x b x a b t =+∈R ，，相切于点()01，，则()a b t +的值为 ▲ ．10．已知数列{}n a 是等比数列，有下列四个命题：①数列{}n a 是等比数列； ②数列{}1+n n a a 是等比数列； ③数列1⎧⎫⎨⎬⎩⎭n a 是等比数列； ④数列{}2lg n a 是等比数列．其中正确的命题有 ▲ 个．11．已知函数()f x 是定义在R 上的奇函数，且(2)()f x f x +=．当01<x ≤时，()=f x 31x ax -+，则实数a 的值为 ▲ ．（第4题）12．在平面四边形ABCD 中，1AB DA DB ==，，32AB AC AC AD ⋅=⋅=，，则2AC AD +的最小值为 ▲ ．13．在平面直角坐标系xOy 中，圆221O x y +=：，圆()2244C x y -+=：．若存在过点()0P m ，的直线l ，l 被两圆截得的弦长相等，则实数m 的取值范围是 ▲ ．14．已知函数()()()2|||2|(0)f x x a x a x a a =+-++<．若(1)(2)(3)f f f +++…(672)0f +=，则满足()2019f x =的x 的值为 ▲ ．二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）如图，在四棱锥P ABCD -中，M ，N 分别为棱P A ，PD 的中点．已知侧面P AD ⊥底面ABCD ，底面ABCD 是矩形，DA =DP ．求证：（1）MN ∥平面PBC ； （2）MD ⊥平面P AB ．16．（本小题满分14分）在△ABC 中，a ，b ，c 分别为角A ，B ，C所对边的长，cos cos a B A =，cos A =． （1）求角B 的值；（2）若a =ABC 的面积．（第15题）BCDPMN如图，在平面直角坐标系xOy 中，椭圆22221y x a b+=(0)a b >>的左焦点为F ，右顶点为A ，上顶点为B ．（1）已知椭圆的离心率为12，线段AF，求椭圆的标准方程；（2）已知△ABF 外接圆的圆心在直线y x -=上，求椭圆的离心率e 的值．18．（本小题满分16分）如图1，一艺术拱门由两部分组成，下部为矩形ABCD ，AB AD ，的长分别为和 4m ，上部是圆心为O 的劣弧CD ，=3COD 2π∠．（1）求图1中拱门最高点到地面的距离；（2）现欲以B 点为支点将拱门放倒，放倒过程中矩形ABCD 所在的平面始终与地面垂直，如图2、图3、图4所示．设BC 与地面水平线l 所成的角为θ．记拱门上的点到地面 的最大距离为h ，试用θ的函数表示h ，并求出h 的最大值．OOODDDCCAAACDO（第17题）已知函数()()ln a f x x a x =+∈R ．（1）讨论()f x 的单调性；（2）设()f x 的导函数为()f x '，若()f x 有两个不相同的零点12x x ，．① 求实数a 的取值范围；② 证明：1122()()2ln 2x f x x f x a ''+>+．20．（本小题满分16分）已知等差数列{}n a 满足44a =，前8项和836S =． （1）求数列{}n a 的通项公式；（2）若数列{}n b 满足()()212123(21)nn k n k n k b a a n *+-=+=-∈∑N ，．① 证明：{}n b 为等比数列；② 求集合*3()=p m m p a a m p m p b b ⎧⎫⎪⎪∈⎨⎬⎪⎪⎩⎭N ，，，．21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题，并在．．．．．．．．．答题卡．．．相应的答题区域内作答．．．．．．．．．．． 若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A ．[选修4-2：矩阵与变换]（本小题满分10分）已知矩阵=a b c d ⎡⎤⎢⎥⎣⎦M ，10=102⎡⎤⎢⎥⎢⎥⎣⎦N ，且()110402-⎡⎤⎢⎥=⎢⎥⎣⎦MN ，求矩阵M ．B ．[选修4-4：坐标系与参数方程]（本小题满分10分）在平面直角坐标系xOy 中，曲线C 的参数方程是2x t y t =⎧⎨=⎩，（t 为参数）．以原点O 为极点， x 轴正半轴为极轴建立极坐标系，直线l的极坐标方程是sin()4ρθπ-=求：（1）直线l 的直角坐标方程； （2）直线被曲线C 截得的线段长．C ．[选修4-5：不等式选讲]（本小题满分10分）已知实数a b c ，，满足222a b c ++≤1，求证：22211191114a b c +++++≥．l【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出 文字说明、证明过程或演算步骤． 22．(本小题满分10分)“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位 “回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4， 其结果记为X ；从9个不同2位“回文数”中任取2个相加，其结果记为Y ． （1）求X 为“回文数”的概率；（2）设随机变量ξ表示X ，Y 两数中“回文数”的个数，求ξ的概率分布和数学期望()E ξ．23．(本小题满分10分)设集合B 是集合{123n A =，，，…，32313}n n n n *--∈N ，，，的子集．记B 中所有元素的 和为S （规定：B 为空集时，S =0）．若S 为3的整数倍，则称B 为n A 的“和谐子集”． 求：（1）集合1A 的“和谐子集”的个数；（2）集合n A 的“和谐子集”的个数．2019届高三第一次调研测试 数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共计70分．1． 已知集合{}13=A ，，{}01=B ，，则集合A B = ▲ ．【答案】{}013，，2． 已知复数2i 3i 1iz --=（i 为虚数单位），则复数z 的模为 ▲ . 【答案】3． 某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：则平均每人参加活动的次数为 ▲ . 【答案】34． 如图是一个算法流程图，则输出的b 的值为 ▲ ．【答案】75． 有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为 ▲ ． 【答案】236． 已知正四棱柱的底面边长是3 cm ，侧面的对角线长是，则这个正四棱柱的体积为 ▲ cm 3． 【答案】547． 若实数x y ，满足2+3xy x ≤≤，则x y +的最小值为 ▲ ．【答案】6-8． 在平面直角坐标系xOy 中，已知抛物线22(0)=>y px p 的准线为l ，直线l 与双曲线221x y -= 的两条渐近线分别交于A ，B 两点，AB p 的值为 ▲ ． 【答案】9． 在平面直角坐标系xOy 中，已知直线3y x t =+与曲线()sin cos y a x b x a b t =+∈R ，，相切于（第4题）点()01，，则()a b t +的值为 ▲ ． 【答案】410．已知数列{}n a 是等比数列，有下列四个命题：①数列{}n a 是等比数列； ②数列{}1+n n a a 是等比数列； ③数列1⎧⎫⎨⎬⎩⎭n a 是等比数列； ④数列{}2lg n a 是等比数列．其中正确的命题有 ▲ 个．【答案】311．已知函数()f x 是定义在R 上的奇函数，且(2)()f x f x +=．当01<x ≤时，()=f x 31x ax -+，则实数a 的值为 ▲ ． 【答案】212．在平面四边形ABCD 中，1AB DA DB ==，，32AB AC AC AD ⋅=⋅=，，则2AC AD +的最小值为 ▲ ．【答案】13．在平面直角坐标系xOy 中，圆221O x y +=：，圆()2244C x y -+=：．若存在过点()0P m ，的直线l ，l 被两圆截得的弦长相等，则实数m 的取值范围是 ▲ ．【答案】()44-，14．已知函数()()()2|||2|(0)f x x a x a x a a =+-++<．若(1)(2)(3)f f f +++…(672)0f +=，则满足()2019f x =的x 的值为 ▲ ．【答案】337二、解答题：本大题共6小题，共计90分．15．（本小题满分14分）如图，在四棱锥P ABCD -中，M ，N 分别为棱P A ，PD 的中点．已知侧面P AD ⊥底面ABCD ，底面ABCD 是矩形，DA =DP ．求证：（1）MN ∥平面PBC ； （2）MD ⊥平面P AB ．【证明】（1）在四棱锥P ABCD -中，M ，N 分别为（第15题）ABCDPMN棱P A ，PD 的中点，所以MN ∥AD ．……………………2分 又底面ABCD 是矩形， 所以BC ∥AD ．所以MN ∥BC ． …………………………………………………………………4分 又⊂⊄BC PBC MN PBC 平面，平面，所以MN ∥平面PBC ． …………………………………………………………6分（2）因为底面ABCD 是矩形， 所以AB ⊥AD ．又侧面P AD ⊥底面ABCD ，侧面P AD ∩底面ABCD =AD ，AB ⊂底面ABCD ， 所以AB ⊥侧面P AD ．……………………………………………………………8分 又MD ⊂侧面P AD ，所以AB ⊥MD ． ………………………………………………………………10分 因为DA =DP ，又M 为AP 的中点，从而MD ⊥PA ． ………………………………………………………………12分 又PA ，AB 在平面P AB 内，=PAAB A ，所以MD ⊥平面P AB ．…………………………………………………………14分 16．（本小题满分14分）在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对边的长，cos cos a B A =，cos A =．（1）求角B 的值；（2）若a =ABC 的面积．【解】（1）在△ABC 中，因为cos A ，0π<<A ，所以sin =A ．………………………………………………………2分因为cos cos a B A =，由正弦定理=a b ，得sin cos cos A B B A ．所以cos sin =B B ． ………………………………………………………………… 4分若cos =0B ，则sin =0B ，与22sin cos 1B B +=矛盾，故cos 0B ≠．于是sin tan 1cos ==B B B ．又因为0π<<B ，所以π4B =． …………………………………………………………………………7分（2）因为a =sin A ，由（1）及正弦定理sin sin =a b A B，所以=b ． ………………………………………………………………………9分又()()sin sin πsin C A B A B =--=+sin cos cos sin =+A B A B．……………………………………………12分 所以△ABC的面积为11sin ==S ab C .……14分17．（本小题满分14分）如图，在平面直角坐标系xOy 中，椭圆22221y x a b+=(0)a b >>的左焦点为F ，右顶点为A ，上顶点为B ．（1）已知椭圆的离心率为12，线段AF，求椭圆的标准方程；（2）已知△ABF 外接圆的圆心在直线y x -=上，求椭圆的离心率e 的值．【解】（1）因为椭圆22221x y a b +=(0)a b >>的离心率为12，所以12c a =，则2a c =．因为线段AF，所以2a c -．所以c 28a =，2226b a c -==．所以椭圆的标准方程为22186x y +=． …………………………………………………4分（2）因为(0)(0)A a F c -，，，， 所以线段AF 的中垂线方程为：2a cx -=．（第17题）又因为△ABF 外接圆的圆心C 在直线y x -=上， 所以()22a c a cC ---，．…………………………………………………………………6分 因为(0)(0)A a B b ，，，， 所以线段AB 的中垂线方程为：()22b a ay x b --=． 由C 在线段AB 的中垂线上，得()2222a cb a ac ab -----=，整理得，2()b a c b ac -+=，…………………………………………………………10分 即()()0b c a b -+=．因为0a b +>，所以b c =．……………………………………………………………12分所以椭圆的离心率c e a ===． …………………………………………14分18．（本小题满分16分）如图1，一艺术拱门由两部分组成，下部为矩形ABCD ，AB AD ，的长分别为和 4m ，上部是圆心为O 的劣弧CD ，=3COD 2π∠．（1）求图1中拱门最高点到地面的距离；（2）现欲以B 点为支点将拱门放倒，放倒过程中矩形ABCD 所在的平面始终与地面垂直，如图2、图3、图4所示．设BC 与地面水平线l 所成的角为θ．记拱门上的点到地面 的最大距离为h ，试用θ的函数表示h ，并求出h 的最大值．【解】（1）如图，过O 作与地面垂直的直线交A B，于点12O O ，，交劣弧CD 于点P ，1O P 的长即为拱门最高点到地面的距离． 在2Rt O OC △中，23O OC π∠=，2CO = 所以21OO =，圆的半径2R OC ==． 所以11122=5O P R OO R O O OO +=+-=．答：拱门最高点到地面的距离为5m ． …………………4分OOODDDCCAAACDO（2）在拱门放倒过程中，过点O 作与地面垂直的直线与“拱门外框上沿”相交于点P ．当点P 在劣弧CD 上时，拱门上的点到地面的最大距离h 等于圆O 的半径长与圆心O 到地面距离之和；当点P 在线段AD 上时，拱门上的点到地面的最大距离h 等于点D 到地面的距离． 由（1）知，在1Rt OO B △中，OB =以B 为坐标原点，直线l 为x 轴，建立如图所示的坐标系．（2.1）当点P 在劣弧CD 上时，ππ62θ<≤． 由π6OBx θ∠=+，OB =由三角函数定义，得O ππ))66()θθ++，则π2)6h θ=++． …………………………………………………………8分所以当ππ62θ+=即π3θ=时， h取得最大值2+ ……………………………………………………10分（2.2）当点P 在线段AD 上时，06θπ≤≤．设=CBD ϕ∠，在Rt BCD △中，DBsin cos ϕϕ===． 由DBx θϕ∠=+，得))()D θϕθϕ++，．所以)h θϕ=+4sin θθ=+．……………………………………14分 又当06θπ<<时，4cos 4cos 066h θθππ'=->-．所以4sin h θθ=+在[0]6π，上递增．所以当6θπ=时，h 取得最大值5．因为25+，所以h的最大值为2+θODCB Axy答：4sin 06π2)662h θθθθθπ⎧+⎪⎪=⎨ππ⎪++<⎪⎩，≤≤，，≤；艺术拱门在放倒的过程中，拱门上的点到地面距离的最大值为（2+m ． ……………………………………………16分19．（本小题满分16分）已知函数()()ln a f x x a x =+∈R ． （1）讨论()f x 的单调性；（2）设()f x 的导函数为()f x '，若()f x 有两个不相同的零点12x x ，．① 求实数a 的取值范围；② 证明：1122()()2ln 2x f x x f x a ''+>+．【解】（1）()f x 的定义域为()0+∞，，且2()x a f x x-'=． （1.1）当0a ≤时，()0f x '>成立，所以()f x 在()0+∞，为增函数； ………2分 （1.2）当0a >时，（i ）当x a >时，()0f x '>，所以()f x 在()+a ∞，上为增函数； （ii ）当0x a <<时，()0f x '<，所以()f x 在()0a ，上为减函数．………4分 （2）①由（1）知，当0a ≤时，()f x 至多一个零点，不合题意；当0a >时，()f x 的最小值为()f a ，依题意知()=f a 1ln 0a +<，解得10a <<．……………………………………6分一方面，由于1a >，()10f a =>，()f x 在()+∞a ，为增函数，且函数()f x 的图 象在()1a ，上不间断． 所以()f x 在()a +∞，上有唯一的一个零点． 另一方面， 因为10e a <<，所以210e <<<a a ．2211()ln 2ln f a a a =+=+，令()12ln =+g a a ，当10e a <<时，()2212210-'=-+=<a g a a a，所以()()211()2ln 20f a g a a g e a e==+>=->又()0f a <，()f x 在()0a ，为减函数，且函数()f x 的图象在()2a a ，上不间断．所以()f x 在()0a ，有唯一的一个零点． 综上，实数a 的取值范围是()10e ，．……………………………………………10分 ② 设()()1122121211=2+a a a a p x f x x f x x x x x ⎛⎫''=+=-+-- ⎪⎝⎭．又1122ln 0ln 0a x x a x x ⎧+=⎪⎪⎨⎪+=⎪⎩，， 则()122ln p x x =+．………………………………………12分 下面证明212x x a >．不妨设12x x <，由①知120x a x <<<． 要证212x x a >，即证212a x >．因为()2120a x a x ∈，，，()f x 在()0a ，上为减函数， 所以只要证()212a f f x x >⎛⎫ ⎪⎝⎭． 又()()12==0f x f x ，即证()222a f f x x >⎛⎫ ⎪⎝⎭．……………………………………14分 设函数()()()()22ln 2ln a x a F x f f x x a x a x a x=-=--+>． 所以()()220x a F x ax -'=>，所以()F x 在()+a ∞，为增函数.所以()()20F x F a >=，所以()222a f f x x >⎛⎫ ⎪⎝⎭成立． 从而212x x a >成立.所以()122ln 2ln 2p x x a =+>+，即()()11222ln 2''+>+x f x x f x a 成立. …16分20．（本小题满分16分）已知等差数列{}n a 满足44a =，前8项和836S =． （1）求数列{}n a 的通项公式；（2）若数列{}n b 满足()()212123(21)nn k n k n k b a a n *+-=+=-∈∑N ，．① 证明：{}n b 为等比数列；② 求集合*3()=p m m pa a m p m pb b ⎧⎫⎪⎪∈⎨⎬⎪⎪⎩⎭N ，，，．【解】（1）设等差数列{}n a 的公差为d ．因为等差数列{}n a 满足44a =，前8项和836S =， 所以1134878362a d a d +=⎧⎪⎨⨯+=⎪⎩，，解得111a d =⎧⎨=⎩，． 所以数列{}n a 的通项公式为n a n =． ………………………………………………3分（2）①设数列{}n b 前n 项的和为n B ．由（1）及()()212123(21)nn k n k n k b a a n *+-=+=-∈∑N ，得，()()()()()()21211121213212321212nnk n k k n n k n k k b a n b an n +-=----=⎧-=+⎪⎪⎨⎪-=+-⎪⎩∑∑，③≥， ④ 由③-④得()()()1121223131321321+2n n n n n n b a b a b a b a n -------=++++ ()12322511+22n n n b a b a b a n ----+++-[]123225111(2)(2)+(2)2n n n n b a b a b a b a n ---=+++++++()12322511+22n n n b a b a b a n ----+++-()()1212+222n n n n n b b b b B b b -=++++=-++．所以13222n n n B b -⋅=-+()2n n *∈N ≥，， 又()1113212b a -=+，所以11b =，满足上式． 所以()12232n n n B b n -*-+=⋅∈N ⑤…………………………………………6分 当2n ≥时，2112232n n n B b ----+=⋅⑥由⑤-⑥得，2132n n n b b --+=⋅．………………………………………………………8分()12122n n n n b b ----=--=()()11120n b -=--=，所以12n n b -=，12n nb b +=， 所以数列{}n b 是首项为1，公比为2的等比数列．………………………………10分②由3=p m m p a a b b ，得11322m p p m --=，即32p mp m -=． 记n n n a c b =，由①得，12n n n n an c b -==， 所以1112n n c n c n++=≤，所以1n n c c +≥（当且仅当1n =时等号成立）． 由3=p m m pa ab b ，得3m p pc c c =>， 所以m p <．…………………………………………………………………………12分 设t p m =-()*m p t ∈N ，，，由32p m pm -=，得323t t m =-． 当1t =时，3m =-，不合题意；当2t =时，6m =，此时8p =符合题意； 当3t =时，95m =，不合题意；当4t =时，121m =<，不合题意．下面证明当4t t *∈N ≥，时，3123t t m =<-． 不妨设()233x f x x =--()4x ≥，()2ln 230x f x '=->，所以()f x 在4+[)∞，上单调增函数， 所以()(4)10f x f =>≥，所以当4t t *∈N ≥，时，3123t t m =<-，不合题意． 综上，所求集合*3()=p m m p a a m p m p b b ⎧⎫⎪⎪∈⎨⎬⎪⎪⎩⎭N ，，，(){}=68，．………………16分21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题，并在．．．．．．．．．答题卡．．．相应的答题区域内作答．．．．．．．．．．． 若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A ．[选修4-2：矩阵与变换]（本小题满分10分）已知矩阵=a b c d ⎡⎤⎢⎥⎣⎦M ，10=102⎡⎤⎢⎥⎢⎥⎣⎦N ，且()110402-⎡⎤⎢⎥=⎢⎥⎣⎦MN ，求矩阵M ． 【解】由题意，()110402-⎡⎤⎢⎥=⎢⎥⎣⎦MN ，则40102⎡⎤⎢⎥=⎢⎥⎣⎦MN ． ……………………………………4分因为10=102⎡⎤⎢⎥⎢⎥⎣⎦N ，则110=02-⎡⎤⎢⎥⎣⎦N ．……………………………………………………6分 所以矩阵401040=1020102⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦M ．………………………………………………10分 B ．[选修4-4：坐标系与参数方程]（本小题满分10分）在平面直角坐标系xOy 中，曲线C 的参数方程是2x t y t =⎧⎨=⎩，（t 为参数）．以原点O 为极点， x 轴正半轴为极轴建立极坐标系，直线l的极坐标方程是sin()4ρθπ-=求：（1）直线l 的直角坐标方程； （2）直线被曲线C 截得的线段长．【解】（1）直线l的极坐标方程可化为(sin cos cos sin )44ρθθππ-sin cos 2ρθρθ-=．又cos sin x y ρθρθ==，， 所以直线l 的直角坐标方程为20x y -+=． …………………………4分（2）曲线C : 2x t y t =⎧⎨=⎩，（t 为参数）的普通方程为2x y =． 由220x y x y ⎧=⎨-+=⎩，，得220x x --=，所以直线l 与曲线C 的交点()11A -，，()24B ，． ……………………………8分 所以直线被曲线C 截得的线段长为AB ．………10分C ．[选修4-5：不等式选讲]（本小题满分10分）已知实数a b c ，，满足222a b c ++≤1，求证：22211191114a b c +++++≥． 【证明】由柯西不等式，得()()()222222111111111a b c ++a b c ⎛⎫⎡⎤+++++ ⎪⎣⎦+++⎝⎭29=≥，…………………………5分 所以2222221119991113134++a b c a b c =+++++++≥≥． …………………………10分 【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出 文字说明、证明过程或演算步骤． 22．(本小题满分10分)l l“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位 “回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4， 其结果记为X ；从9个不同2位“回文数”中任取2个相加，其结果记为Y ． （1）求X 为“回文数”的概率；（2）设随机变量ξ表示X ，Y 两数中“回文数”的个数，求ξ的概率分布和数学期望()E ξ． 【解】（1）记“X 是‘回文数’”为事件A ．9个不同2位“回文数”乘以4的值依次为：44，88，132，176，220，264，308， 352，396．其中“回文数”有：44，88．所以，事件A 的概率2()9P A =．……………………………………………………3分（2）根据条件知，随机变量ξ的所有可能取值为0，1，2．由（1）得2()9P A =．…………………………………………………………………5分设“Y 是‘回文数’”为事件B ，则事件A ，B 相互独立．根据已知条件得，()29205=9P B C =． ()()()()()2528=0=119981P P A P B ξ=--=；()()()()()()()252543=1=11999981P P A P B P A P B ξ+=-+-=；()()()2510=2=P P A P B ξ=⋅= ……………………………………………………8分 所以，随机变量ξ的概率分布为所以，随机变量ξ的数学期望为2843107()0128181819E ξ=⨯+⨯+⨯=．……………10分23．(本小题满分10分)设集合B 是集合{123n A =，，，…，32313}n n n n *--∈N ，，，的子集．记B 中所有元素的 和为S （规定：B 为空集时，S =0）．若S 为3的整数倍，则称B 为n A 的“和谐子集”． 求：（1）集合1A 的“和谐子集”的个数；（2）集合n A 的“和谐子集”的个数．【解】（1）集合{}1=123A ，，的子集有：φ，{}1，{}2，{}3，{}12，，{}13，，{}23，，{}123，，．其中所有元素和为3的整数倍的集合有：φ，{}3，{}12，，{}123，，． 所以1A 的“和谐子集”的个数等于4．……………………………………………3分 （2）记n A 的“和谐子集”的个数等于n a ，即n A 有n a 个所有元素和为3的整数倍的子集；另记n A 有n b 个所有元素和为3的整数倍余1的子集，有n c 个所有元素和为3的整数 倍余2的子集．由（1）知，111=4=2=2a b c ，，．集合()+1{12332313313231}n A n n n n n n =--+++，，，，，，，，，的“和谐子集” 有以下四类（考察新增元素()313231n n n +++，，）：第一类 集合{123n A =，，，…，32313}n n n --，，的“和谐子集”，共n a 个； 第二类 仅含一个元素()31n +的“和谐子集”，共n a 个；同时含两个元素3132n n ++，的“和谐子集”，共n a 个；同时含三个元素()313231n n n +++，，的“和谐子集”，共n a 个；第三类 仅含一个元素31n +的“和谐子集”，共n c 个；同时含两个元素()313+1n n +，的“和谐子集”，共n c 个；第四类 仅含一个元素32n +的“和谐子集”，共n b 个；同时含有两个元素()3231n n ++，的“和谐子集”，共n b 个，所以集合+1n A 的“和谐子集”共有1422n n n n a a b c +=++个．同理得1422n n n n b b c a +=++，1422n n n n c c a b +=++．………………………………7分 所以+112()n n n n a b a b +-=-，112a b -=，所以数列{}n n a b -是以2为首项，公比为2 的等比数列． 所以=2n n n a b -．同理得=2n n n a c -．又3=2n n n n a b c ++，所以()321=2233n n n a n *⨯+⨯∈N ，． ………………………10分。

2019年江苏省泰州市、南通市、扬州市、苏北四市七市高考数学一模试卷一、填空题：本大题共14小题，每小题5分，共计70分．1．（5分）已知集合A＝{1，3}，B＝{0，1}，则集合A∪B＝．2．（5分）已知复数（i为虚数单位），则复数z的模为．3．（5分）某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：则平均每人参加活动的次数为．4．（5分）如图是一个算法流程图，则输出的b的值为．5．（5分）有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为．6．（5分）已知正四棱柱的底面边长为3cm，侧面的对角线长是3cm，则这个正四棱柱的体积是cm3．7．（5分）若实数x，y满足x≤y≤2x+3，则x+y的最小值为．8．（5分）在平面直角坐标系xOy中，已知抛物线y2＝2px（p＞0）的准线为l，直线l与双曲线的两条渐近线分别交于A，B两点，，则p的值为．9．（5分）在平面直角坐标系xOy中，已知直线y＝3x+t与曲线y＝a sin x+b cos x（a，b，t∈R）相切于点（0，1），则（a+b）t的值为．10．（5分）已知数列{a n}是等比数列，有下列四个命题：①数列{|a n|}是等比数列；②数列{a n a n+1}是等比数列；③数列是等比数列；④数列{lga n2}是等比数列．其中正确的命题有个．11．（5分）已知函数f（x）是定义在R上的奇函数，且f（x+2）＝f（x）．当0＜x≤1时，f（x）＝x3﹣ax+1，则实数a的值为．12．（5分）在平面四边形ABCD中，AB＝1，DA＝DB，＝3，＝2，则|的最小值为．13．（5分）在平面直角坐标系xOy中，圆O：x2+y2＝1，圆C：（x﹣4）2+y2＝4．若存在过点P（m，0）的直线l，l被两圆截得的弦长相等，则实数m的取值范围．14．（5分）已知函数f（x）＝（2x+a）（|x﹣a|+|x+2a|）（a＜0）．若f（1）+f（2）+f（3）+…+f（672）＝0，则满足f（x）＝2019的x的值为．二、解答题：本大题共6小题，共计90分．15．（14分）如图，在四棱锥P﹣ABCD中，M，N分别为棱P A，PD的中点．已知侧面P AD ⊥底面ABCD，底面ABCD是矩形，DA＝DP．求证：（1）MN∥平面PBC；（2）MD⊥平面P AB．16．（14分）在△ABC中，a，b，c分别为角A，B，C所对边的长，，．（1）求角B的值；（2）若，求△ABC的面积．17．（14分）如图，在平面直角坐标系xOy中，椭圆（a＞b＞0）的左焦点为F，右顶点为A，上顶点为B．（1）已知椭圆的离心率为，线段AF中点的横坐标为，求椭圆的标准方程；（2）已知△ABF外接圆的圆心在直线y＝﹣x上，求椭圆的离心率e的值．18．（16分）如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别为和4m，上部是圆心为O的劣弧CD，．（1）求图1中拱门最高点到地面的距离；（2）现欲以B点为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示．设BC与地面水平线l所成的角为θ．记拱门上的点到地面的最大距离为h，试用θ的函数表示h，并求出h的最大值．19．（16分）已知函数．（1）讨论f（x）的单调性；（2）设f（x）的导函数为f'（x），若f（x）有两个不相同的零点x1，x2．①求实数a的取值范围；②证明：x1f'（x1）+x2f'（x2）＞2lna+2．20．（16分）已知等差数列{a n}满足a4＝4，前8项和S8＝36．（1）求数列{a n}的通项公式；（2）若数列{b n}满足．①证明：{b n}为等比数列；②求集合．【选做题】本题包括21、22、C23三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．[选修4-2：矩阵与变换]（本小题满分0分）21．已知矩阵，，且，求矩阵M．[选修4-4：坐标系与参数方程]（本小题满分0分）22．在平面直角坐标系xOy中，曲线C的参数方程是（t为参数）．以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是ρsin（θ﹣）＝．求：（1）直线l的直角坐标方程；（2）直线l被曲线C截得的线段长．[选修4-5：不等式选讲]（本小题满分0分）23．已知实数a，b，c满足a2+b2+c2≤1，求证：．【必做题】第22、23题，每小题0分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．24．“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位“回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4，其结果记为X；从9个不同2位“回文数”中任取2个相加，其结果记为Y．（1）求X为“回文数”的概率；（2）设随机变量ξ表示X，Y两数中“回文数”的个数，求ξ的概率分布和数学期望E （ξ）．25．设集合B是集合A n＝{1，2，3，……，3n﹣2，3n﹣1，3n}，n∈N*的子集．记B中所有元素的和为S（规定：B为空集时，S＝0）．若S为3的整数倍，则称B为A n的“和谐子集”．求：（1）集合A1的“和谐子集”的个数；（2）集合A n的“和谐子集”的个数．2019年江苏省泰州市、南通市、扬州市、苏北四市七市高考数学一模试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共计70分．1．【解答】解：根据题意，集合A＝{1，3}，B＝{0，1}，则A∪B＝{0，1，3}；故答案为：{0，1，3}．2．【解答】解：＝，则复数z的模为．故答案为：．3．【解答】解：根据题意，计算这组数据的平均数为：＝×（20×2+15×3+10×4+5×5）＝3．故答案为：3．4．【解答】解：模拟程序的运行，可得a＝0，b＝1满足条件a＜15，执行循环体，a＝1，b＝3满足条件a＜15，执行循环体，a＝5，b＝5满足条件a＜15，执行循环体，a＝21，b＝7此时，不满足条件a＜15，退出循环，输出b的值为7．故答案为：7．5．【解答】解：有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，基本事件总数n＝3×3＝9，这两位同学参加不同兴趣小组包含的基本事件个数m＝3×2＝6，则这两位同学参加不同兴趣小组的概率为p＝＝．故答案为：．6．【解答】解：设正四棱柱的高为h，∵正四棱柱的底面边长为3cm，侧面的对角线长是3cm，∴＝3，解得h＝6（cm），∴这个正四棱柱的体积V＝Sh＝3×3×6＝54（cm3）．故答案为：54．7．【解答】解：画出实数x，y满足x≤y≤2x+3的平面区域，如图示：由，解得A（﹣3，﹣3），由z＝x+y得：y＝﹣x+z，显然直线过A时z最小，z的最小值是﹣6，故答案为：﹣6．8．【解答】解：抛物线y2＝2px（p＞0）的准线为l：x＝﹣，双曲线的两条渐近线方程为y＝±x，可得A（﹣，﹣），B（（﹣，），|AB|＝＝，可得p＝2．故答案为：2．9．【解答】解：根据题意得，t＝1y′＝a cos x﹣b sin x∴k＝a cos0﹣b sin0＝a∴a＝3，b cos0＝1∴a＝3，b＝1故答案为4．10．【解答】解：由{a n}是等比数列可得＝q（q为常数，q≠0），①＝＝|q|为常数，故是等比数列；②＝＝q2为常数，故是等比数列；③＝＝常数，故是等比数列；④数列a n＝1是等比数列，但是lga n2＝0不是等比数列；故答案为：311．【解答】解：∵f（x）是定义在R上的奇函数，且f（x+2）＝f（x）．∴当x＝﹣1时，f（﹣1+2）＝f（﹣1）＝f（1），即﹣f（1）＝f（1），则f（1）＝0，∵当0＜x≤1时，f（x）＝x3﹣ax+1．∴f（1）＝1﹣a+1＝0，得a＝2，故答案为：212．【解答】解：如图，以A为原点，建立平面直角坐标系，则A（0，0），B（1，0），因为DA＝DB，可设D（，m），因为•＝3，AB＝1，所以可设C（3，n），又•＝2，所以+mn＝2，即mn＝，+2＝（4，n+2m）|+2|＝＝≥＝2，当且仅当n＝2m，即n＝1，m＝时，等号成立．故答案为：213．【解答】解：显然直线l有斜率，设直线l：y＝k（x﹣m），即kx﹣y﹣km＝0，依题意得1﹣（）2＝4﹣（）2＞0有解，即，∴13﹣8m＞0且3m2+8m﹣16＜0解得﹣4＜m＜，故答案为：﹣4＜m．14．【解答】解：注意到：，又因为：，，因此．所以，函数f（x）关于点对称，所以，解得：a＝﹣673，f（x）＝（2x﹣673）（|x+673|+|x﹣2×673|）＝2019，显然有：0＜2x﹣673＜2019，即，所以，f（x）＝（2x﹣673）（x+673+2×673﹣x）＝2019，2x﹣673＝1，解得：x＝337．故答案为：337．二、解答题：本大题共6小题，共计90分．15．【解答】证明：（1）在四棱锥P﹣ABCD中，M，N分别为棱P A，PD的中点，所以MN∥AD．……………………2分又底面ABCD是矩形，所以BC∥AD，所以MN∥BC．…………………………………………………………………4分又BC⊂平面PBC，MN⊄平面PBC，所以MN∥平面PBC．…………………………………………………………6分（2）因为底面ABCD是矩形，所以AB⊥AD．又侧面P AD⊥底面ABCD，侧面P AD∩底面ABCD＝AD，AB⊂底面ABCD，所以AB⊥侧面P AD．……………………………………………………………8分又MD⊂侧面P AD，所以AB⊥MD．………………………………………………………………10分因为DA＝DP，又M为AP的中点，从而MD⊥P A．………………………………………………………………12分又P A，AB在平面P AB内，P A∩AB＝A，所以MD⊥平面P AB．…………………………………………………………14分16．【解答】（本题满分为14分）解：（1）在△ABC中，因为，0＜A＜π，所以．………………………………………………………2分因为，由正弦定理，得．所以cos B＝sin B．…………………………………………………………………4分若cos B＝0，则sin B＝0，与sin2B+cos2B＝1矛盾，故cos B≠0．于是．又因为0＜B＜π，所以．…………………………………………………………………………7分（2）因为，，由（1）及正弦定理，得，所以．………………………………………………………………………9分又sin C＝sin（π﹣A﹣B）＝sin（A+B）＝sin A cos B+cos A sin B＝．……………………………………………12分所以△ABC的面积为．……14分17．【解答】解：（1）因为椭圆（a＞b＞0）的离心率为，所以，则a＝2c．因为线段AF中点的横坐标为，所以．所以，则a2＝8，b2＝a2﹣c2＝6．所以椭圆的标准方程为．…………………………………………………4分（2）因为A（a，0），F（﹣c，0），所以线段AF的中垂线方程为：．又因为△ABF外接圆的圆心C在直线y＝﹣x上，所以． (6)分因为A（a，0），B（0，b），所以线段AB的中垂线方程为：．由C在线段AB的中垂线上，得，整理得，b（a﹣c）+b2＝ac，…………………………………………………………10分即（b﹣c）（a+b）＝0．因为a+b＞0，所以b＝c．……………………………………………………………12分所以椭圆的离心率．…………………………………………14分18．【解答】解：（1）如图，过O作与地面垂直的直线交AB，CD于点O1，O2，交劣弧CD 于点P，O1P的长即为拱门最高点到地面的距离．在Rt△O 2OC中，，，所以OO2＝1，圆的半径R＝OC＝2．所以O1P＝R+OO1＝R+O1O2﹣OO2＝5．答：拱门最高点到地面的距离为5m．…………………4分（2）在拱门放倒过程中，过点O作与地面垂直的直线与“拱门外框上沿”相交于点P．当点P在劣弧CD上时，拱门上的点到地面的最大距离h等于圆O的半径长与圆心O到地面距离之和；当点P在线段AD上时，拱门上的点到地面的最大距离h等于点D到地面的距离．由（1）知，在Rt△OO1B中，．以B为坐标原点，直线l为x轴，建立如图所示的坐标系．（2.1）当点P在劣弧CD上时，．由，，由三角函数定义，得O，则．…………………………………………………………8分所以当即时，h取得最大值．……………………………………………………10分（2.2）当点P在线段AD上时，．设∠CBD＝φ，在Rt△BCD中，，．由∠DBx＝θ+φ，得．所以＝．……………………………………14分又当时，．所以在上递增．所以当时，h取得最大值5．因为，所以h的最大值为．答：；艺术拱门在放倒的过程中，拱门上的点到地面距离的最大值为（）m．……………………………………………16分19．【解答】解：（1）f（x）的定义域为（0，+∞），且．（i）当a≤0时，f'（x）＞0成立，所以f（x）在（0，+∞）为增函数；………2分（ii）当a＞0时，①当x＞a时，f'（x）＞0，所以f（x）在（a，+∞）上为增函数；②当0＜x＜a时，f'（x）＜0，所以f（x）在（0，a）上为减函数．………4分（2）①由（1）知，当a≤0时，f（x）至多一个零点，不合题意；当a＞0时，f（x）的最小值为f（a），依题意知f（a）＝1+lna＜0，解得．……………………………………6分一方面，由于1＞a，f（1）＝a＞0，f（x）在（a，+∞）为增函数，且函数f（x）的图象在（a，1）上不间断．所以f（x）在（a，+∞）上有唯一的一个零点．另一方面，因为，所以，，令，当时，，所以又f（a）＜0，f（x）在（0，a）为减函数，且函数f（x）的图象在（a2，a）上不间断．所以f（x）在（0，a）有唯一的一个零点．综上，实数a的取值范围是．……………………………………………10分②证明：设．又则p＝2+ln（x1x2）．………………………………………12分下面证明．不妨设x1＜x2，由①知0＜x1＜a＜x2．要证，即证．因为，f（x）在（0，a）上为减函数，所以只要证．又f（x1）＝f（x2）＝0，即证．……………………………………14分设函数．所以，所以F（x）在（a，+∞）为增函数．所以F（x2）＞F（a）＝0，所以成立．从而成立．所以p＝2+ln（x1x2）＞2lna+2，即x1f'（x1）+x2f'（x2）＞2lna+2成立．…16分20．【解答】解：（1）设等差数列{a n}的公差为d．因为等差数列{a n}满足a4＝4，前8项和S8＝36，所以，解得所以数列{a n}的通项公式为a n＝n．（2）①设数列{b n}前n项的和为B n．由（1）及得，由③﹣④得3（2n﹣1）﹣3（2n﹣1﹣1）＝（b1a2n﹣1+b2a2n﹣3+…+b n﹣1a3+b n a1+2n）﹣（b1a2n+b2a2n﹣5+…+b n﹣1a1+2n﹣2）＝[b1（a2n﹣3+2）+b2（a2n﹣5+2）+…+b n﹣1（a1+2）+b n a1+2n]﹣3﹣（b1a2n﹣3+b2a2n﹣5+…+b n﹣1a1+2n﹣2）＝2（b1+b2+…+b n﹣1）+b n+2＝2（B n﹣b n）+b n+2．所以3•2n﹣1＝2B n﹣b n+2（n≥2，n∈N*），又3（21﹣1）＝b1a1+2，所以b1＝1，满足上式．所以当n≥2时，由⑤﹣⑥得，．＝，所以，，所以数列{b n}是首项为1，公比为2的等比数列．②由，得，即．记，由①得，，所以，所以c n≥c n+1（当且仅当n＝1时等号成立）．由，得c m＝3c p＞c p，所以m＜p；设t＝p﹣m（m，p，t∈N*），由，得．当t＝1时，m＝﹣3，不合题意；当t＝2时，m＝6，此时p＝8符合题意；当t＝3时，，不合题意；当t＝4时，，不合题意．下面证明当t≥4，t∈N*时，．不妨设f（x）＝2x﹣3x﹣3（x≥4），f'（x）＝2x ln2﹣3＞0，所以f（x）在[4，+∞）上单调增函数，所以f（x）≥f（4）＝1＞0，所以当t≥4，t∈N*时，，不合题意．综上，所求集合＝{（6，8）}．【选做题】本题包括21、22、C23三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．[选修4-2：矩阵与变换]（本小题满分0分）21．【解答】解：由题意，，则．……………………………………4分因为，则．……………………………………………………6分所以矩阵．………………………………………………10分[选修4-4：坐标系与参数方程]（本小题满分0分）22．【解答】解：（1）直线l的极坐标方程是ρsin（θ﹣）＝．转换为直角坐标方程为：x﹣y+2＝0；（2）曲线C的参数方程是（t为参数）：转换为直角坐标方程为：x2＝y．由，得x2﹣x﹣2＝0，所以直线l与曲线C的交点A（﹣1，1），B（2，4）．所以直线l被曲线C截得的线段长为．[选修4-5：不等式选讲]（本小题满分0分）23．【解答】证明：由柯西不等式，得， (5)分所以．…………………………10分【必做题】第22、23题，每小题0分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．24．【解答】解：（1）记“X是‘回文数’”为事件A．9个不同2位“回文数”乘以4的值依次为：44，88，132，176，220，264，308，352，396．其中“回文数”有：44，88．所以，事件A的概率．……………………………………………………3分（2）根据条件知，随机变量ξ的所有可能取值为0，1，2．由（1）得．…………………………………………………………………5分设“Y是‘回文数’”为事件B，则事件A，B相互独立．根据已知条件得，．；；……………………………………………………8分所以，随机变量ξ的概率分布为所以，随机变量ξ的数学期望为：． (10)分25．【解答】解：（1）由题意有：A1＝，则集合A1的“和谐子集”为：∅，，，共4个，故答案为：4；（2）记A n的“和谐子集”的个数等于a n，即A n有a n个所有元素的和为3的整数倍的子集，另记A n有b n个所有元素的和为3的整数倍余1的子集，有c n个所有元素的和为3的整数倍余2的子集，易知：a1＝4，b1＝2，c1＝2，集合A n+1＝{1，2，3，……，3n﹣2，3n﹣1，3n，3n+1，3n+2，3n+3}的“和谐子集”有以下4种情况，（考查新增元素3n+1，3n+2，3n+3）①集合集合A n＝{1，2，3，……，3n﹣2，3n﹣1，3n}的“和谐子集”共a n个，②仅含一个元素3（n+1）的“和谐子集”共a n个，同时含两个元素3n+1，3n+2的“和谐子集”共a n个，同时含三个元素3n+1，3n+2，3（n+1）的“和谐子集”共a n个，③仅含一个元素3n+1的“和谐子集”共c n个，同时含两个元素3n+1，3n+3的“和谐子集”共c n个，④仅含一个元素3n+2的“和谐子集”共b n个，同时含两个元素3n+2，3n+3的“和谐子集”共b n个，所以集合A n+1的“和谐子集”共有a n+1＝4a n+2b n+2c n，同理：b n+1＝4b n+2a n+2c n，c n+1＝4c n+2a n+2c n，所以a n+1﹣b n+1＝2（a n﹣b n），所以数列是以a1﹣b1＝2为首项，2为公比的等比数列，求得：a n＝b n+2n，同理a n＝c n+2n，又a n+b n+c n＝23n，解得：a n＝+（n∈N*）故答案为：+（n∈N*）。

2019年江苏省泰州市高考数学一模试卷学校:________ 班级:________ 姓名:________ 学号:________一、填空题（共14小题）1.函数f（x）＝sin2x的最小正周期为．2.已知集合A＝{4，a2}，B＝{﹣1，16}，若A∩B≠∅，则a＝．3.复数z满足zi＝4+3i（i是虚数单位），则|z|＝．4.函数y＝的定义域为﹣．5.从1，2，3，4，5这5个数中，随机抽取2个不同的数，则这2个数的和为6的概率是．6.一个算法的伪代码如图所示，执行此算法，最后输出的T的值是．7.已知数列{a n}满足log2a n+1﹣log2a n＝1，则＝．8.若抛物线y2＝2px（p＞0）的准线与双曲线x2﹣y2＝1的一条准线重合，则p＝．9.如图，在直三棱柱ABC﹣A1B1C1中，点M为棱AA1的中点，记三棱锥A1﹣MBC的体积为V1，四棱锥A1﹣BB1C1C的体积为V2，则的值是．10.已知函数f（x）＝2x4+4x2，若f（a+3）＞f（a﹣1），则实数a的取值范围为﹣11.在平面直角坐标系xOy中，过圆C1：（x﹣k）2+（y+k﹣4）2＝1上任一点P作圆C2：x2+y2＝1的一条切线，切点为Q，则当线段PQ长最小时，k＝．12.已知点P为平行四边形ABCD所在平面上任一点，且满足，，则λμ＝﹣．13.已知函数，若存在x0＜0，使得f（x0）＝0，则实数a的取值范围是﹣．14.在△ABC中，已知sin A sin B sin（C﹣θ）＝λsin2C，其中，若为定值，则实数λ＝．二、解答题（共6小题）15.已知向量，，其中x∈（0，π）．（1）若，求x的值；（2）若tan x＝﹣2，求||的值．16.如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，点O为对角线BD的中点，点E，F分别为棱PC，PD的中点，已知P A⊥AB，P A⊥AD．求证：（1）直线PB∥平面OEF；（2）平面OEF⊥平面ABCD．17.如图，三个校区分别位于扇形OAB的三个顶点上，点Q是弧AB的中点，现欲在线段OQ上找一处开挖工作坑P（不与点O，Q重合），为小区铺设三条地下电缆管线PO，P A，PB，已知OA＝2千米，∠AOB＝，记∠APQ＝θrad，地下电缆管线的总长度为y千米．（1）将y表示成θ的函数，并写出θ的范围；（2）请确定工作坑P的位置，使地下电缆管线的总长度最小．18.如图，在平面直角坐标系xOy中，椭圆C：的左顶点为A，点B是椭圆C上异于左、右顶点的任一点，P是AB的中点，过点B且与AB垂直的直线与直线OP交于点Q，已知椭圆C 的离心率为，点A到右准线的距离为6．（1）求椭圆C的标准方程；（2）设点Q的横坐标为x0，求x0的取值范围．19.设A，B为函数y＝f（x）图象上相异两点，且点A，B的横坐标互为倒数，过点A，B分别做函数y＝f（x）的切线，若这两条切线存在交点，则称这个交点为函数f（x）的“优点”．（1）若函数不存在“优点，求实数a的值；（2）求函数f（x）＝x2的“优点”的横坐标的取值范围；（3）求证：函数f（x）＝lnx的“优点”一定落在第一象限．20.已知数列{a n}的前n项和为S n，2a1+a2＝a3，且对任意的n∈N*，n≥2都有2nS n+1﹣（2n+5）S n+S n﹣1＝ra1．（1）若a1≠0，a2＝3a1，求r的值；（2）数列{a n}能否是等比数列？说明理由；（3）当r＝1时，求证：数列{a n}是等差数列．2019年江苏省泰州市高考数学一模试卷参考答案一、填空题（共14小题）1.【分析】利用函数y＝A sin（ωx+φ）的周期为，得出结论．【解答】解：函数f（x）＝sin2x的最小正周期为＝π，故答案为：π．【知识点】三角函数的周期性及其求法2.【分析】利用交集定义直接求解．【解答】解：∵集合A＝{4，a2}，B＝{﹣1，16}，A∩B≠∅，∴a2＝16，解得a＝±4．故答案为：±4．【知识点】交集及其运算3.【分析】把已知等式变形，再由复数代数形式的乘除运算化简，利用复数模的计算公式求解．【解答】解：由zi＝4+3i，得z＝，∴|z|＝．故答案为：5．【知识点】复数求模4.【分析】令被开方数大于等于0，解不等式求出定义域．【解答】解：要使函数有意义，需满足1﹣x2≥0解得﹣1≤x≤1故答案为{x|﹣1≤x≤1}【知识点】函数的定义域及其求法5.【分析】基本事件总数n＝＝10，这2个数的和为6包含的基本事件有2个，由此能求出这2个数的和为6的概率．【解答】解：从1，2，3，4，5这5个数中，随机抽取2个不同的数，基本事件总数n＝＝10，这2个数的和为6包含的基本事件有：（1，5），（2，4），共2个，则这2个数的和为6的概率是p＝＝．故答案为：．【知识点】古典概型及其概率计算公式6.【分析】模拟程序的运行过程，即可得出程序运行后输出的S值．【解答】解：模拟程序的运行，可得i＝1，T＝1满足条件i≤2，执行循环体，T＝1×21＝2，i＝2满足条件i≤2，执行循环体，T＝2×22＝8，i＝3不满足条件i≤2，退出循环，输出T的值为8．故答案为：8．【知识点】伪代码7.【分析】由对数的运算性质结合等比数列的通项公式可得结果．【解答】解：∵log2a n+1﹣log2a n＝1，∴＝2，∴数列{a n}是公比q为2的等比数列，∴＝q2＝4．故答案为：4．【知识点】等比数列8.【分析】求出抛物线的准线方程，双曲线的左准线方程，建立关系，即可求出p的值．【解答】解：抛物线y2＝2px的准线为：x＝﹣，双曲线x2﹣y2＝1的左准线为：x＝﹣＝﹣，由题意可知﹣＝﹣，p＝．故答案为：．【知识点】圆锥曲线的综合9.【分析】设出棱柱的棱长，然后求解三棱锥A1﹣MBC的体积为V1，四棱锥A1﹣BB1C1C的体积为V2，推出结果．【解答】解：在直三棱柱ABC﹣A1B1C1中，点M为棱AA1的中点，A到BC是距离为：t，记三棱锥A1﹣MBC的体积为V1＝•t＝•t四棱锥A1﹣BB1C1C的体积为V2＝则＝＝．故答案为：．【知识点】棱柱、棱锥、棱台的体积10.【分析】根据f（x）的解析式可看出f（x）是偶函数，并且在（0，+∞）上单调递增，从而由f（a+3）＞f（a﹣1）得到f（|a+3|）＞f（|a﹣1|），从而得出|a+3|＞|a﹣1|，两边平方即可解出a的范围．【解答】解：f（x）＝2x4+4x2是偶函数，且在（0，+∞）上单调递增；∴由f（a+3）＞f（a﹣1）得：f（|a+3|）＞f（|a﹣1|）；∴|a+3|＞|a﹣1|；∴（a+3）2＞（a﹣1）2；解得a＞﹣1；∴实数a的取值范围为（﹣1，+∞）．故答案为：（﹣1，+∞）．【知识点】奇偶性与单调性的综合11.【分析】根据题意，由圆C1的方程求出圆心的坐标，分析可得圆心在直线y＝﹣x﹣4上，结合圆与圆的位置关系分析可得当C1C2的连线与直线y＝﹣x+4垂直时，线段PQ长最小，据此可得＝1，解可得k的值，即可得答案．【解答】解：根据题意，圆C1：（x﹣k）2+（y+k﹣4）2＝1的圆心为（k，4﹣k），半径r＝1，则圆心在直线y＝﹣x+4上，点P为圆C1上任意一点，过点P作圆C2：x2+y2＝1的一条切线，切点为Q，当C1C2的连线与直线y＝﹣x+4垂直时，线段PQ长最小，此时有＝1，解可得：k＝2；故答案为：2．【知识点】圆方程的综合应用12.【分析】利用向量加减法把所给两个条件中的向量都转化为，对比可得解．【解答】解：由，得＝，即；…①由，得，即，∴，即（μ+1），∴，…②由①②可得，得，∴，故答案为：﹣【知识点】平面向量的基本定理及其意义13.【分析】分别求得x＜a，x≥a时f（x）的导数，求得单调性、极值，讨论a＝0，a＜0，a＞0，结合函数f（x）存在负的零点，可得a的范围．【解答】解：由f（x）＝x3+3x﹣4a的导数为f′（x）＝3x2+3＞0，可得x＜a为增函数，可得f（x）＜a3﹣a，且x≥a时，f（x）＝x3﹣3x﹣4a的导数为f′（x）＝3x2﹣3，即有﹣1＜x＜1时，f（x）递减；x＞1或x＜﹣1时，f（x）递增，可得x＝1为极小值﹣2+2a，x＝﹣1处取得极大值2+2a，a＝0时，x＜0时，f（x）＜0；x≥0时，f（x）在（0，1）递减，（1，+∞）递增，无负的零点；0＜a＜1时，x＜a时，f（x）＜f（a）＜0，函数f（x）无负的零点；当a≥1时，x＜a时，f（x）递增，x≥a，f（x）递增，f（x）也无负的零点；当a＜0时，由f（a）≥0即a3﹣a≥0，解得﹣1≤a＜0，可得f（x）存在负的零点．故答案为：[﹣1，0）．【知识点】分段函数的应用14.【分析】由，可求sinθ，cosθ，然后由sin A sin B sin（C﹣θ）＝λsin2C，结合两角差的正弦公式可求sin A sin B，然后进行化简，结合其特点及为定值可求λ．【解答】解：由，可得，sinθ＝，cosθ＝，∵sin A sin B sin（C﹣θ）＝λsin2C，sin A sin B sin C﹣sin A sin B cos C＝λsin2C，∴sin A sin B＝＝∵＝＝，＝＝为定值，∴则实数λ＝故答案为：【知识点】两角和与差的余弦函数二、解答题（共6小题）15.【分析】（1）根据即可得出，从而得出sin2x＝1，根据x∈（0，π）即可得出2x∈（0，2π），从而得出2x＝，从而得出x的值；（2）根据tan x＝﹣2可得出sin x＝﹣2cos x，可求出，从而可求出．【解答】解：（1）∵；∴sin x cos x＝，即sin2x＝1；∵x∈（0，π）；∴；（2）∵tan x＝＝﹣2；∴sin x＝﹣2cos x；∵；∴＝＝．【知识点】平面向量共线（平行）的坐标表示16.【分析】（1）由O为PB中点，F为PD中点，得PB∥FO，由此能证明PB∥平面OEF．（2）连结AC，推导出P A∥OE，由P A⊥AB，P A⊥AD，得P A⊥平面ABCD，从而OE⊥平面ABCD，由此能证明平面OEF⊥平面ABCD．【解答】证明：（1）O为PB中点，F为PD中点，∴PB∥FO，而PB⊄平面OEF，FO⊂平面OEF，∴PB∥平面OEF．（2）连结AC，∵ABCD为平行四边形，∴AC与BD交于点O，O为AC中点，又E为PC中点，∴P A∥OE，∵P A⊥AB，P A⊥AD，AB∩AD＝A，∴P A⊥平面ABCD，∴OE⊥平面ABCD，又OE⊂平面OEF，∴平面OEF⊥平面ABCD．【知识点】直线与平面平行的判定、平面与平面垂直的判定17.【分析】（1）由题意在△∠AOP中利用正弦定理求得P A、OP，把y表示为θ的函数，再求出θ的取值范围；（2）由（1）构造函数，利用导数f（θ）的单调性，求出f（θ）的最小值以及对应θ的值即可．【解答】解：（1）因为Q为弧AB的中点，由对称性知P A＝PB，∠AOP＝∠BOP＝，又∠APO＝π﹣θ，∠OAP＝，由正弦定理，得：，又OA＝2，所以，P A＝，OP＝，所以，y＝P A+PB+OP＝2P A+OP＝＝，又∠APQ＞∠AOP，所以，，∠OAQ＝∠OQA＝（π+）＝，所以，θ∈（，）；（2）令，θ∈（，），令，得：，所以，f（θ）在上单调递减，在（，）上单调递增；所以，当，即OP＝时，f（θ）有唯一的极小值，即是最小值：f（θ）min＝2，答：当工作坑P与O的距离为时，地下电缆管线的总长度最小．【知识点】已知三角函数模型的应用问题18.【分析】（1）根据已知条件列有关a、c的方程组，解出a和c的值，进而可得出b的值，从而求出椭圆C的标准方程；（2）设直线AB的方程为x＝my﹣2，m≠0，将直线AB的方程与椭圆C的方程联立，求出点B的坐标，进而求出点P的坐标，分别写出直线OP和直线BQ的方程，联立这两条直线方程，求出x0的表达式，利用不等式的性质求出x0的取值范围．【解答】解：（1）依题意，有：，即，又＝6，所以，＝6，解得：a＝2，c＝1，b＝＝，所以，椭圆C的方程为：；（2）由（1）知，A（﹣2，0）、设AB：x＝my﹣2，m≠0，将直线AB的方程与椭圆C的方程联立，解得，即点B的坐标为，则，所以，直线OP的斜率为，则直线OP的方程为，直线BQ的斜率为k BQ＝﹣m，所以，直线BQ的方程为，将直线OP的方程与直线BQ的方程联立，得出．因此，x0的取值范围是（4，8）．【知识点】直线与椭圆的位置关系19.【分析】（1）由题意可得f′（x）＝f′（）对x∈（0，1）∪（1，+∞）恒成立，不妨取0＜x＜1，求得导数，可得a的范围；（2）设A（t，t2），B（，），（0＜t＜1），求得导数和切线方程，求得交点的横坐标，结合基本不等式可得所求范围；（3）设A（t，lnt），B（，﹣lnt），0＜t＜1，求得导数，以及切线方程，求交点，由构造函数法，即可得到交点的坐标均为正数．【解答】解：（1）若函数不存在“优点，可得f′（x）＝f′（）对x∈（0，1）∪（1，+∞）恒成立，不妨取0＜x＜1，可得f′（x）＝＝＝f′（），即3a＝x，即有a∈（0，），故存在两条切线平行，且a的范围是（0，）；（2）设A（t，t2），B（，），（t≠0），f′（x）＝2x，以A，B为切点的切线方程为y＝2tx﹣t2，y＝x﹣，令2tx﹣t2＝x﹣，可得x＝（t+）＞1或x＜﹣1，可得“优点”的横坐标的取值范围为（1，+∞）∪（﹣∞，﹣1）；（3）证明：设A（t，lnt），B（，﹣lnt），0＜t＜1，由f′（x）＝，以A，B为切点的切线方程为y＝+lnt﹣1；y＝tx﹣lnt﹣1，可令tx﹣lnt﹣1＝+lnt﹣1，可得x＝＞0，y＝（lnt2﹣），设t2＝m∈（0，1），可令h（m）＝lnm﹣，h′（m）＝﹣＝＞0，即h（m）递增，h（m）＜h（1）＝0，即lnt2﹣＜0，又＜0，则y＝（lnt2﹣）＞0，函数f（x）＝lnx的“优点”的横坐标和纵坐标均为正数，一定落在第一象限．【知识点】利用导数研究曲线上某点切线方程20.【分析】（1）在已知数列递推式中，取n＝2，可得4a3﹣5a2﹣4a1＝ra1，结合已知2a1+a2＝a3即可求得r值；（2）假设数列{a n}是等比数列，公比为q，求得q＝2或q＝﹣1，再由已知可得2n（q2﹣q）＝3q﹣1，不能得到对任意n≥3恒成立，故数列{a n}不可能是等比数列；（3）当r＝1时，令n＝2，整理得：﹣4a1﹣5a2+4a3＝ra1，结合已知可得a2＝3a1，a3＝5a1，令n＝3，得a4＝7a1．由（2）可知，4S n＝2na n+1﹣a n﹣ra1（n≥2），进一步得到2na n+1+a n﹣1＝（2n+3）a n（n≥3），可得2（n﹣1）a n+a n﹣2＝（2n+1）a n﹣1（n≥4）．得到2n[（a n+1﹣a n）﹣（a n﹣a n﹣1）]＝（a n﹣a n﹣1）﹣（a n﹣1﹣a n﹣2）（n≥4）．从而得到（a n﹣a n﹣1）﹣（a n﹣1﹣a n﹣2）＝0（n≥4）．即a n﹣a n﹣1＝a n﹣1﹣a n﹣2（n≥4），由此可得数列{a n}是以a1为首项，以2a1为公差的等差数列．【解答】解：（1）令n＝2，得：4S3﹣9S2+S1＝ra1，即：4（a3+a2+a1）﹣9（a2+a1）+a1＝ra1，化简，得：4a3﹣5a2﹣4a1＝ra1，∵2a1+a2＝a3，a2＝3a1，∴4×5a1﹣5×3a1﹣4a1＝ra1，解得：r＝1；（2）假设数列{a n}是等比数列，公比为q，则，且a1≠0，解得q＝2或q＝﹣1．由2nS n+1﹣（2n+5）S n+S n﹣1＝ra1，可得4S n＝2na n+1﹣a n﹣ra1（n≥2）．∴4S n﹣1＝2（n﹣1）a n﹣a n﹣1﹣ra1，两式相减得：2na n+1+a n﹣1＝（2n+3）a n，两边同除以a n﹣1，可得2n（q2﹣q）＝3q﹣1，∵q≠1，∴q2﹣q≠0，则上式不可能对任意n≥3恒成立，故数列{a n}不可能是等比数列；证明：（3）当r＝1时，令n＝2，整理得：﹣4a1﹣5a2+4a3＝ra1，又由2a1+a2＝a3，可得a2＝3a1，a3＝5a1，令n＝3，可得6S4﹣11S3+S2＝a1，解得a4＝7a1．由（2）可知，4S n＝2na n+1﹣a n﹣ra1（n≥2），∴4S n﹣1＝2（n﹣1）a n﹣a n﹣1﹣ra1（n≥3），两式相减得：2na n+1+a n﹣1＝（2n+3）a n（n≥3），∴2（n﹣1）a n+a n﹣2＝（2n+1）a n﹣1（n≥4）．∴2n[（a n+1﹣a n）﹣（a n﹣a n﹣1）]＝（a n﹣a n﹣1）﹣（a n﹣1﹣a n﹣2）（n≥4）．∵（a4﹣a3）﹣（a3﹣a2）＝0，∴（a n﹣a n﹣1）﹣（a n﹣1﹣a n﹣2）＝0（n≥4）．即a n﹣a n﹣1＝a n﹣1﹣a n﹣2（n≥4），又∵a3﹣a2＝a2﹣a1＝2a1，∴数列{a n}是以a1为首项，以2a1为公差的等差数列．【知识点】等比数列、数列递推式、等差数列。