中考数学压轴题专题动点问题

初中数学动点问题及练习题附参考答案专题一：建立动点问题的函数解析式函数提醒了运动变化过程中量与量之间的变化规律,是初中数学的重要容.动点问题反映的是一种函数思想,由于*一个点或*图形的有条件地运动变化,引起未知量与量间的一种变化关系,这种变化关系就是动点问题中的函数关系.则,我们怎样建立这种函数解析式呢"下面结合中考试题举例分析.一、应用勾股定理建立函数解析式。

二、应用比例式建立函数解析式。

三、应用求图形面积的方法建立函数关系式。

专题二：动态几何型压轴题动态几何特点----问题背景是特殊图形，考察问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性〔特殊角、特殊图形的性质、图形的特殊位置。

〕动点问题一直是中考热点，近几年考察探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

下面就此问题的常见题型作简单介绍，解题方法、关键给以点拨。

一、以动态几何为主线的压轴题。

〔一〕点动问题。

〔二〕线动问题。

〔三〕面动问题。

二、解决动态几何问题的常见方法有:1、特殊探路，一般推证。

2、动手实践，操作确认。

3、建立联系，计算说明。

三、专题二总结，本大类习题的共性：1．代数、几何的高度综合〔数形结合〕；着力于数学本质及核心容的考察;四大数学思想：数学结合、分类讨论、方程、函数．2．以形为载体，研究数量关系；通过设、表、列获得函数关系式；研究特殊情况下的函数值。

专题三：双动点问题点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体，运动变化为主线，集多个知识点为一体，集多种解题思想于一题. 这类题综合性强，能力要求高，它能全面的考察学生的实践操作能力，空间想象能力以及分析问题和解决问题的能力. 其中以灵活多变而著称的双动点问题更成为今年中考试题的热点，现采撷几例加以分类浅析，供读者欣赏.1 以双动点为载体，探求函数图象问题。

D C BA PQ K E D C B A 中考压轴题之动点问题1. （2011吉林）如图，梯形ABCD 中，AD ∥BC ，∠BAD =90°，CE ⊥AD 于点E ，AD =8cm ，BC =4cm ，AB =5cm ．从初始时刻开始，动点P ，Q 分别从点A ，B 同时出发，运动速度均为1cm/s ，动点P 沿A -B -C -E 方向运动，到点E 停止；动点Q 沿B -C -E -D 方向运动，到点D 停止，设运动时间为x s ，△P AQ 的面积为y cm 2，（这里规定：线段是面积为0的三角形）解答下列问题：（1） 当x =2s 时，y =_____ cm 2；当x =92s 时，y =_______ cm 2． （2）当5 ≤ x ≤ 14时，求y 与x 之间的函数关系式．（3）当动点P 在线段BC 上运动时，求出154 y S 梯形ABCD 时x 的值． （4）直接写出在整个．．运动过程中，使PQ 与四边形ABCE 的对角线平行的所有x 的值．2. （2007河北）如图，在等腰梯形ABCD 中，AD ∥BC ，AB =DC =50，AD =75，BC =135．点P 从点B 出发沿折线段BA -AD -DC 以每秒5个单位长的速度向点C 匀速运动；点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动，过点Q 向上作射线QK ⊥BC ，交折线段CD -DA -AB 于点E ．点P 、Q 同时开始运动，当点P 与点C 重合时停止运动，点Q 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当点P 到达终点C 时，求t 的值，并指出此时BQ 的长；（2）当点P 运动到AD 上时，t 为何值能使PQ ∥DC ？（3）设射线QK 扫过梯形ABCD 的面积为S ，分别求出点E 运动到CD 、DA 上时，S 与t 的关系式；（4）△PQE 能否成为直角三角形？若能，写出t 的取值范围；若不能，请说明理由．备用图3. （2008河北）如图，在Rt ABC △中，∠C=90°，AB =50，AC =30，D ，E ，F 分别是AC ，AB ，B C 的中点．点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动；点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动，过点Q 作射线QK AB ⊥，交折线BC -CA 于点G ．点P Q ，同时出发，当点P 绕行一周回到点D 时停止运动，点Q 也随之停止．设点P Q ，运动的时间是t 秒（0t >）．（1）D F ，两点间的距离是 ；（2）射线QK 能否把四边形CDEF 分成面积相等的两部分？若能，求出t 的值．若不能，说明理由；（3）当点P 运动到折线EF FC -上，且点P 又恰好落在射线QK 上时，求t 的值；（4）连结PG ，当PG AB ∥时，请直接．．写出t 的值．4. （2011山西太原）如图，在平面直角坐标系中，四边形OABC 是平行四边形．直线l 经过O 、C 两点．点A 的坐标为(8，0)，点B 的坐标为(11，4)，动点P 在线段OA 上从点O 出发以每秒1个单位的速度向点A 运动，同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动，过点P 作PM 垂直于x 轴，与折线O -C -B 相交于点M ．当P 、Q 两点中有一点到达终点时，另一点也随之停止运动，设点P 、Q 运动的时间为t 秒(0t >)，△MPQ 的面积为S ．（1）点C 的坐标为________，直线l 的解析式为__________．（2）试求点Q 与点M 相遇前S 与t 的函数关系式，并写出相应的t 的取值范围．（3）试求题(2)中当t 为何值时，S 的值最大，并求出S 的最大值．（4）随着P 、Q 两点的运动，当点M 在线段CB 上运动时，设PM 的延长线与直线l 相交于点N ．试探究：当t 为何值时，△QMN 为等腰三角形？请直接写出t 的值．B 备用图F E DC BAF E O P D C B F E O P D C B F E O P D C B 5. （2011四川重庆）如图，矩形ABCD 中，AB ＝6，BC ＝23，点O 是AB 的中点，点P 在AB 的延长线上，且BP ＝3．一动点E 从O 点出发，以每秒1个单位长度的速度沿OA 匀速运动，到达A 点后，立即以原速度沿AO 返回；另一动点F 从P 点出发，以每秒1个单位长度的速度沿射线P A 匀速运动，点E 、F 同时出发，当两点相遇时停止运动．在点E 、F 的运动过程中，以EF 为边作等边△EFG ，使△EFG 和矩形ABCD 在射线P A 的同侧，设运动的时间为t 秒（t ≥0）．（1）当等边△EFG 的边FG 恰好经过点C 时，求运动时间t 的值；（2）在整个运动过程中，设等边△EFG 和矩形ABCD 重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围；（3）设EG 与矩形ABCD 的对角线AC 的交点为H ，是否存在这样的t ，使△AOH 是等腰三角形？若存在，求出对应的t 的值；若不存在，请说明理由．备用图1 备用图26. （2011山东烟台）如图，在直角坐标系中，梯形ABCD 的底边AB 在x 轴上，底边CD 的端点D 在y 轴上．直线CB 的表达式为41633y x =-+，点A 、D 的坐标分别为（－4，0），（0，4）．动点P 自A 点出发，在AB 上匀速运动．动点Q 自点B 出发，在折线BCD 上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P 运动t （秒）时，△OPQ 的面积为S （不能构成△OPQ 的动点除外）．（1）求出点B 、C 的坐标；（2）求S 随t 变化的函数关系式；（3）当t 为何值时S 有最大值？并求出最大值．备用图。

九年级中考压轴——动点问题集锦1、已知等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动。

过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点，线段MN运动的时间为t秒。

1) 当四边形MNQP为矩形时，有MN=QP，即MN在运动t秒后，线段QP的长度为3+t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的面积为2根号3*t平方+2t。

2) 四边形MNQP的面积为S，运动时间为t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的高为2根号3.由于四边形MNQP是矩形，所以MN=QP=3+t，PQ=2根号3.因此，S=PQ*MN=2根号3*(3+t)。

函数关系式为S=2根号3*t+6根号3，t的取值范围为t≥0.2、在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=42，∠B=45度。

动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动。

设运动的时间为t 秒。

1) 因为三角形ABD和三角形CBD相似，所以BD=AB-AD=39.由于三角形BCD是直角三角形，所以BC=BD/根号2=39/根号2.2) 当MN∥AB时，由于三角形BMD和三角形BAC相似，所以BD/AB=MD/MN，即39/42=2t/(3+t)，解XXX13秒。

3) 当△MNC为等腰三角形时，由于三角形MNC和三角形ABD相似，所以CN/AD=MN/BD，即CN/3=(3+t)/39，XXX13秒。

3、在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为(6，0)，点B的坐标为(4，3)，点C在y轴的正半轴上。

动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点。

中考数学压轴题型研究（一）——动点几何问题例1：在△ABC 中，∠B=60°,BA=24CM,BC=16CM, (1)求△ABC 的面积；(2)现有动点P 从A 点出发，沿射线AB 向点B 方向运动，动点Q 从C 点出发，沿射线CB 也向点B 方向运动。

如果点P 的速度是4CM/秒，点Q 的速度是2CM/秒，它们同时出发，几秒钟后，△PBQ的面积是△ABC 的面积的一半？(3)在第（2）问题前提下，P ,Q 两点之间的距离是多少？例2: ()已知正方形ABCD 的边长是1，E 为CD 边的中点， P 为正方形ABCD 边上的一个动点，动点P 从A 点出发，沿A →B → C →E 运动，到达点E.若点P 经过的路程为自变量x ，△APE 的面积为函数y ，（1）写出y 与x 的关系式 (2)求当y ＝13时，x 的值等于多少？例3：如图1 ，在直角梯形ABCD 中，∠B=90°，DC ∥AB ，动点P 从B 点出发，沿梯形的边由B →C → D → A 运动，设点P 运动的路程为x ,△ABP 的面积为y , 如果关于x 的函数y 的图象如图2所示 ，那么△ABC 的面积为（ ）A ．32B ．18C ．16D ．10ACB By例4：直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．（1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式； （3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．例5：已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．（1）线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积； （2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．例6：如图（3），在梯形ABCD 中，906DC AB A AD ∠==∥，°，厘米，4DC =厘米，BC 的坡度34i =∶，动点P 从A 出发以2厘米/秒的速度沿AB 方向向点B 运动，动点Q 从点B 出发以3厘米/秒的速度沿B C D →→方向向点D 运动，两个动点同时出发，当其中一个动点到达终点时，另一个动点也随之停止．设动点运动的时间为t秒．（1）求边BC 的长；（2）当t 为何值时，PC 与BQ 相互平分；图（3）BC PQBA MN（3）连结PQ ，设PBQ △的面积为y ，探求y 与t 的函数关系式，求t 为何值时，y 有最大值？最大值是多少？二、利用函数与方程的思想和方法将所解决图形的性质（或所求图形面积）直接转化为函数或方程。

专题15动点综合问题【考点1】动点之全等三角形问题【例1】1．如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时，△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【变式1-1】已知正方形ABCD的对角线AC与BD交于点O，点E、F分别是线段OB、OC上的动点（1）如果动点E 、F 满足BE ＝OF （如图），且AE ⊥BF 时，问点E 在什么位置？并证明你的结论；（2）如果动点E 、F 满足BE ＝CF （如图），写出所有以点E 或F 为顶点的全等三角形（不得添加辅助线）．【变式1-2】如图①，将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ，其中AB ＝8cm ，BC ＝6cm ，AC ＝10cm ．现将△ABC 和△EDF 按如图②的方式摆放（点A 与点D 、点B 与点E 分别重合）．动点P 从点A 出发，沿AC 以2cm /s 的速度向点C 匀速移动；同时，动点Q 从点E 出发，沿射线ED 以acm /s （0＜a ＜3）的速度匀速移动，连接PQ 、CQ 、FQ ，设移动时间为ts （0≤t ≤5）．（1）当t ＝2时，S △AQF ＝3S △BQC ，则a ＝；（2）当以P 、C 、Q 为顶点的三角形与△BQC 全等时，求a 的值；（3）如图③，在动点P 、Q 出发的同时，△ABC 也以3cm /s 的速度沿射线ED 匀速移动，当以A 、P 、Q 为顶点的三角形与△EFQ 全等时，求a 与t 的值．【考点2】动点之直角三角形问题【例2】如图，在四边形纸片ABCD 中，//AB CD ，60A ∠=︒，30B ∠=︒，2CD =，4BC =，点E 是AB 边上的动点，点F 是折线A D C --上的动点，将纸片ABCD 沿直线EF 折叠，使点A 的对应点A '落在AB 边上，连接A C '，若A BC ' 是直角三角形，则AE 的长为________．【变式2-1】（2019·辽宁中考模拟）如图，已知二次函数y ＝ax 2+bx+4的图象与x 轴交于点A(4，0)和点D(﹣1，0)，与y 轴交于点C ，过点C 作BC 平行于x 轴交抛物线于点B ，连接AC(1)求这个二次函数的表达式；(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动；点N 从点B 同时出发，以每秒1个单位长度的速度向点C 运动，其中一个动点到达终点时，另一个动点也随之停动，过点N 作NQ 垂直于BC 交AC 于点Q ，连结MQ.①求△AQM 的面积S 与运动时间t 之间的函数关系式，写出自变量的取值范围；当t 为何值时，S 有最大值，并求出S 的最大值；②是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．【变式2-2】如图，在矩形OAHC 中，8,12OC OA ==，B 为CH 中点，连接AB .动点M 从点O 出发沿OA 边向点A 运动，动点N 从点A 出发沿AB 边向点B 运动，两个动点同时出发，速度都是每秒1个单位长度，连接,,CM CN MN ，设运动时间为t （秒）(010)t <<.则t =_____时，CMN ∆为直角三角形【考点3】动点之等腰三角形问题【例3】如图，AB 是⊙O 的直径，BC 是弦，10cm AB =，6cm BC =．若点P 是直径AB 上一动点，当PBC 是等腰三角形时，AP =__________cm ．【变式3-1】如图①，已知正方形ABCD 边长为2，点P 是AD 边上的一个动点，点A 关于直线BP 的对称点是点Q ，连结PQ 、DQ 、CQ 、BQ .设AP=x.（1）当1x =时，求BP 长；（2）如图②，若PQ 的延长线交CD 边于E ，并且90CQD ∠=o ，求证：CEQ ∆为等腰三角形；（3）若点P 是射线AD 上的一个动点，则当CDQ ∆为等腰三角形时，求x 的值.【变式3-2】（2019·河南中考模拟）如图，抛物线y=ax 2+bx+3交y 轴于点A ，交x 轴于点B （-3，0）和点C （1，0），顶点为点M ．（1）求抛物线的解析式；（2）如图，点E 为x 轴上一动点，若△AME 的周长最小，请求出点E 的坐标；（3）点F 为直线AB 上一个动点，点P 为抛物线上一个动点，若△BFP 为等腰直角三角形，请直接写出点P 的坐标．【变式3-3】（2019·广西中考真题）已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -，点O 为坐标原点，点P 为抛物线上的动点，直线y x b =-+与x 轴、y 轴分别交于A B 、两点．（1）求m b 、的值；（2）当PAM ∆是以AM 为底边的等腰三角形时，求点P 的坐标；（3）满足（2）的条件时，求sin BOP ∠的值．【考点4】动点之相似三角形问题【例4】如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC 是相似三角形，求AP的长．【变式4-1】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝3 4AC（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【变式4-2】如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．（1）请找出图中一对相似三角形，并证明；（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．【考点5】动点之平行四边形问题（含特殊四边形）【例5】如图，抛物线23y ax bx =++与x 轴交于(3,0),(1,0)A B -两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 是抛物线上的动点，且满足2PAO PCO S S ∆∆=，求出P 点的坐标；（3）连接BC ，点E 是x 轴一动点，点F 是抛物线上一动点，若以B 、C 、E 、F 为顶点的四边形是平行四边形时，请直接写出点F 的坐标．备用图【变式5-1】（2019·江西中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．（1）如图1，当点与点重合时，________°；（2）如图2，连接．①填空：_________（填“>”，“<”，“=”）；②求证：点在的平分线上；（3）如图3，连接，，并延长交的延长线于点，当四边形是平行四边形时，求的值．【变式5-2】（2019·湖南中考真题）如图，二次函数213y x bx c =-++的图象过原点，与x 轴的另一个交点为()8,0（1）求该二次函数的解析式；（2）在x轴上方作x轴的平行线1y m=，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（0t>）．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．【变式5-3】．如图，在平面直角坐标系中，AOB∆的顶点O是坐标原点，点A坐标为()1,3，A、B两点关于直线y x=对称，反比例函数()0ky xx=>图象经过点A，点P是直线y x=上一动点.（1）B点的坐标为______；（2）若点C是反比例函数图象上一点，是否存在这样的点C，使得以A、B、C、P四点为顶点的四边形是平行四边形？若存在，求出点C坐标；若不存在，请说明理由；（3）若点Q 是线段OP 上一点（O 不与O 、P 重合），当四边形AOBP 为菱形时，过点Q 分别作直线OA 和直线AP 的垂线，垂足分别为E 、F ，当QE QF QB ++的值最小时，求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图，在平面直角坐标系中，平行四边形如图放置，将此平行四边形绕点O 顺时针旋转90°得到平行四边形．抛物线经过点A 、C 、A′三点．（1）求A 、A′、C 三点的坐标；（2）求平行四边形和平行四边形重叠部分的面积；（3）点M 是第一象限内抛物线上的一动点，问点M 在何处时，的面积最大？最大面积是多少？并写出此时M 的坐标．【变式6-1】（1）发现：如图1，点A 为线段BC 外一动点，且BC =α，AB b =(0)a b >>，当点A 位于时，线段AC 的长取得最大值，最大值为（用含,a b 的式子表示）；（2）应用：如图2，点A 为线段BC 外一动点，4BC =，2AC =，以AB 为边作等边ABD ∆，连接CD ，求线段CD 的最大值；（3）拓展：如图3，线段3AB =，点P 为线段AB 外一动点，且2AP =，PM PB =，90BPM ∠=︒，求线段AM 长的最大值及此时PBM ∆的面积．【变式6-2】如图，矩形ABCD 中，3,4AD AB ==，点P 是对角线AC 上一动点（不与A C 、重合），连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，以线段,PE PB 为邻边作矩形BPEF ，过点P 作GH CD ⊥。

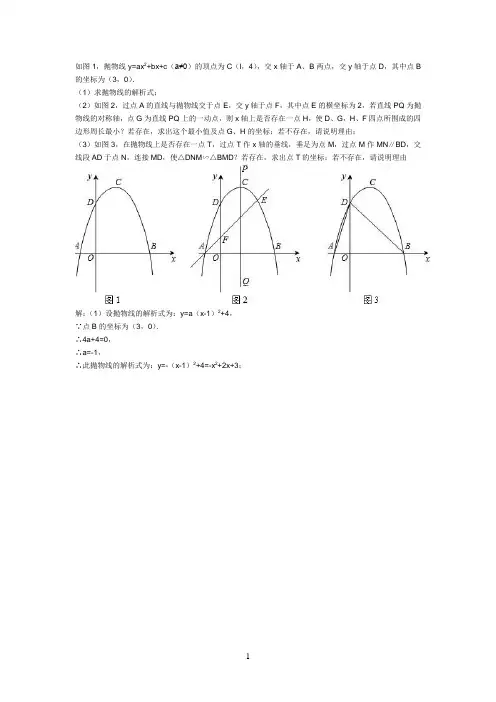
如图1，抛物线y=ax2+bx+c（a≠0）的顶点为C（l，4），交x轴于A、B两点，交y轴于点D，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，过点A的直线与抛物线交于点 E，交y轴于点F，其中点E的横坐标为2，若直线PQ为抛物线的对称轴，点G为直线 PQ上的一动点，则x轴上是否存在一点H，使D、G，H、F四点所围成的四边形周长最小？若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由；（3）如图3，在抛物线上是否存在一点T，过点T作x轴的垂线，垂足为点M，过点M作MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD？若存在，求出点T的坐标；若不存在，请说明理由解：（1）设抛物线的解析式为：y=a（x-1）2+4，∵点B的坐标为（3，0）．∴4a+4=0，∴a=-1，∴此抛物线的解析式为：y=-（x-1）2+4=-x2+2x+3；如图1，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）．已知AM=BC．（1）求二次函数的解析式；（2）证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；（3）在（2）的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N．①若直线l⊥BD，如图1，试求的值；②若l为满足条件的任意直线．如图2．①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例．四边形OABC是等腰梯形，OA∥BC，在建立如图的平面直角坐标系中，A（10，0），B（8，6），直线x=4与直线AC交于P点，与x轴交于H点；（1）直接写出C点的坐标，并求出直线AC的解析式；（2）求出线段PH的长度，并在直线AC上找到Q点，使得△PHQ的面积为△AOC面积的1/5，求出Q 点坐标；（3）M点是直线AC上除P点以外的一个动点，问：在x轴上是否存在N点，使得△MHN为等腰直角三角形？若有，请求出M点及对应的N点的坐标，若没有，请说明理由．如图1，平面直角坐标系xOy中，抛物线y= x2+bx+c与x轴交于A、B两点，点C是AB的中点，CD ⊥AB且CD=AB．直线BE与y轴平行，点F是射线BE上的一个动点，连接AD、AF、DF．（1）若点F的坐标为（9/2，1），AF=①求此抛物线的解析式；②点P是此抛物线上一个动点，点Q在此抛物线的对称轴上，以点A、F、P、Q为顶点构成的四边形是平行四边形，请直接写出点Q的坐标；（2）若2b+c=-2，b=-2-t，且AB的长为kt，其中t＞0．如图2，当∠DAF=45°时，求k的值和∠DFA的正切值．如图，在平面直角坐标系中，已知点A、B、C的坐标分别为（-1，0），（5，0），（0，2）．（1）求过A、B、C三点的抛物线解析式；（2）若点P从A点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．若点P运动的时间为t秒，（0≤t≤6）设△PBF的面积为S；①求S与t的函数关系式；②当t是多少时，△PBF的面积最大，最大面积是多少？（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE．（1）填空：点D的坐标为（），点E的坐标为（）．（2）若抛物线y=ax2+bx+c（a≠0）经过A、D、E三点，求该抛物线的解析式．（3）若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在y轴上时，正方形和抛物线均停止运动．①在运动过程中，设正方形落在y轴右侧部分的面积为s，求s关于平移时间t（秒）的函数关系式，并写出相应自变量t的取值范围．②运动停止时，求抛物线的顶点坐标．如图，矩形OABC中，A（6，0），C（0，），D（0，），射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO=60°．（1）①点B的坐标是（）；②∠CAO= 度；③当点Q与点A重合时，点P的坐标为（）；（直接填写答案）（2）设点P的横坐标为x，△OPQ与矩形OABC的重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．已知抛物线y=a（x+1）2+c（a＞0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，其顶点为M，已知直线MC的函数表达式为y=kx-3，与x轴的交点为N，且cos∠BCO=（1）求抛物线的解析式；（2）在此抛物线上是否存在异于点C的点P，使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．（3）如图2，过点A作x轴的垂线，交直线MC于点Q，若将抛物线沿其对称轴上下平移，使抛物线与线段NQ总有公共点，则抛物线向上最多可平移多少单位长度？向下最多可平移多少个单位长度？。

专题8填空题压轴题之动点问题（原卷版）模块一 2022中考真题训练类型一用函数观点描述几何图形1．（2022•烟台）如图1，△ABC中，∠ABC＝60°，D是BC边上的一个动点（不与点B，C重合），DE∥AB，交AC于点E，EF∥BC，交AB于点F．设BD的长为x，四边形BDEF的面积为y，y与x的函数图象是如图2所示的一段抛物线，其顶点P的坐标为（2，3），则AB的长为．2．（2022•营口）如图1，在四边形ABCD中，BC∥AD，∠D＝90°，∠A＝45°，动点P，Q同时从点A 出发，点P以√2cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x（s），△APQ的面积为y（cm2），若y与x之间的函数关系的图象如图2所示，当x=72（s）时，则y＝cm2．3．（2022•湖北）如图1，在△ABC中，∠B＝36°，动点P从点A出发，沿折线A→B→C匀速运动至点C 停止．若点P的运动速度为1cm/s，设点P的运动时间为t（s），AP的长度为y（cm），y与t的函数图象如图2所示．当AP恰好平分∠BAC时t的值为．类型二三角形、多边形上的动点问题4．（2022•遵义）如图，在等腰直角三角形ABC中，∠BAC＝90°，点M，N分别为BC，AC上的动点，且AN＝CM，AB=√2．当AM+BN的值最小时，CM的长为．5．（2022•黄石）如图，等边△ABC中，AB＝10，点E为高AD上的一动点，以BE为边作等边△BEF，连接DF，CF，则∠BCF＝，FB+FD的最小值为．6．（2022•广州）如图，在矩形ABCD中，BC＝2AB，点P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段BP′，连接PP′，CP′．当点P′落在边BC上时，∠PP′C的度数为；当线段CP′的长度最小时，∠PP′C的度数为．7．（2022•柳州）如图，在正方形ABCD中，AB＝4，G是BC的中点，点E是正方形内一个动点，且EG＝2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为．8．（2022•辽宁）如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，点P为斜边AB上的一个动点（点P不与点A、B重合），过点P作PD⊥AC，PE⊥BC，垂足分别为点D和点E，连接DE，PC交于点Q，连接AQ，当△APQ为直角三角形时，AP的长是．9．（2022•陕西）如图，在菱形ABCD中，AB＝4，BD＝7．若M、N分别是边AD、BC上的动点，且AM＝BN，作ME⊥BD，NF⊥BD，垂足分别为E、F，则ME+NF的值为．10．（2022•盘龙区）如图，已知四边形ABCD中，AB＝10cm，BC＝8cm，CD＝12cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3cm/s的速度沿B﹣C﹣B运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为cm/s时，能够使△BPE与△CQP全等．类型三有关圆的动点问题11．（2022•宁波）如图，在△ABC中，AC＝2，BC＝4，点O在BC上，以OB为半径的圆与AC相切于点A．D是BC边上的动点，当△ACD为直角三角形时，AD的长为．12．（2022•东城区模拟）如图，在平面直角坐标系xOy中，点A与点B的坐标分别是（1，0）与（7，0）．对于坐标平面内的一动点P，给出如下定义：若∠APB＝45°，则称点P为线段AB的“等角点”．①若点P为线段AB在第一象限的“等角点”，且在直线x＝4上，则点P的坐标为；②若点P为线段AB的“等角点”，并且在y轴正半轴上，则点P的坐标为．模块二2023中考押题预测13．（2022•驻马店二模）如图，四边形ABCD中，AB∥CD，∠ABC＝60°，AD＝BC＝CD＝4，点M是四边形ABCD内的一个动点，满足∠AMD＝90°，则点M到直线BC的距离的最小值为．14．（2022•普定县模拟）如图，点M是∠AOB平分线上一点，∠AOB＝60°，ME⊥OA于E，OE=√5，如果P是OB上一动点，则线段MP的取值范围是．15．（2022•徐州二模）如图，在等边三角形ABC中，AB＝2，点D，E，F分别是边BC，AB，AC边上的动点，则△DEF周长的最小值为．16．（2022•仁怀市模拟）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝8，点D为边AB的中点，点P为边AC上的动点，则PB+PD的最小值为．17．（2022•亭湖区校级三模）在平面直角坐标系中，A（3，3），B（6，0），点D、E是OB的三等分点，点P是线段AB上的一个动点，若只存在唯一一个点P使得PD+PE＝a，则a需满足的条件是：．18．（2022•夏邑县校级模拟）如图，在等腰三角形ABC中，∠A＝30°，BC＝2，点D为AC的中点，点E 为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF，当EF⊥AC时，AE的长为．19．（2022•新昌县模拟）在△ABC中，∠A＝60°，点P和点Q分别是边AC和BC上的两个动点，分别连结BP和PQ．把△ABC分割成三个三角形．若分割成的这三个三角形都是等腰三角形，则∠ABC的度数可以是．20．（2022•新化县一模）已知在Rt△ABC中，∠C＝90°，∠ABC＝75°，AB＝5．点E为边AC上的动点，点F为边AB上的动点，则线段FE+EB的最小值是．21．（2022•顺城区模拟）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AC＝6，点M是射线AC上的一个动点，MC＝1，连接BM，以AB为边在AB的上方作∠ABE＝∠AMB，直线BE交AC的延长线于点F，则CF＝．23．（2022•碧江区一模）如图，在△ABC中，AB＝6，BC＝7，AC＝4，直线m是△ABC中BC边的垂直平分线，P是直线m上的一动点，则△APC的周长的最小值为．24．（2022•抚顺县二模）如图，在Rt △ABO 中，∠OBA ＝90°，A （4，4），点C 在边AB 上，且AC CB =13，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为 ．25．（2022•德保县二模）如图，在平面直角坐标系中，△OAB 是边长为4的等边三角形，OD 是AB 边上的高，点P 是OD 上的一个动点，若点C 的坐标是（0，−√3），则P A +PC 的最小值是 ．26．（2022•元宝区校级一模）如图，在△ABC 中，∠C ＝90°，AC ＝6，BC ＝8，动点P 从点B 出发以每秒1个单位长度的速度沿B →A 匀速运动；同时点Q 从点A 出发以同样的速度沿A →C →B 匀速运动．当点P 到达点A 时，P 、Q 同时停止运动，设运动时间为t 秒，当t 为 时，以B 、P 、Q 为顶点的三角形是等腰三角形．27．（2022•大理州二模）如图，Rt △ACB 中，∠ACB ＝90°，AB ＝13cm ，AC ＝5cm ，动点P 从点B 出发沿射线BC 以2cm /s 的速度运动，设运动时间为ts ，当△APB 为等腰三角形时，t 的值为 ．28．（2022•锡山区校级模拟）如图，△ABC 中，∠C ＝90°，BC ＝6，∠ABC 的平分线与线段AC 交于点D ，且有AD ＝BD ，点E 是线段AB 上的动点（与A 、B 不重合），连结DE ，当△BDE 是等腰三角形时，则AE 的长为 ．29．（2022•衡南县校级二模）等腰△ABC的底边BC＝8cm，腰长AB＝5cm，一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动，当点P运动到P A与腰垂直的位置时，点P运动的时间应为秒．30．（2022•大冶市校级模拟）如图，已知四边形ABCD是正方形AB=2√2，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连CG．（1）CE+CG＝；（2）若四边形DEFG面积为5时，则CG＝．31．（2022•玉树市校级一模）如图，菱形ABCD中，∠A＝60°，AD＝4，P是AB边一个动点，E、F分别是DP、BP的中点，则线段EF的长为．32．（2022•浉河区校级模拟）如图，在矩形纸片ABCD中，AB＝4，AD＝5，点F是AB的中点，点E为AD上一动点，作△AEF关于直线EF的对称图形，点A的对应点为点A′，作△A′EF关于直线A′E 的对称图形，点F的对应点为F'．当点F'落在矩形ABCD的边上时，AE的长为．33．（2022•嵩县模拟）如图，四边形ABCD和AEFG都是正方形，点E是AB边上一个动点，点G在AD 边上，AB=√2cm，连接BF，CF，若△BCF恰为等腰三角形，则AE的长为cm．34．（2022•赣州模拟）如图，矩形ABCD中，AB＝6，AD＝2，点E是边CD的中点，点P在AB边上运动，点F为DP的中点；当△DEF为等腰三角形时，则AP的长为．35．（2022•华龙区校级模拟）如图，正方形ABCD中，AB＝6，点E为对角线AC上的动点，以DE为边作正方形DEFG，点H是CD上一点，且DH=23CD，连接GH，则GH的最小值为．36．（2022•柘城县校级二模）如图，在矩形ABCD中，AB＝1，BC=√2，点E为射线AD上的动点（不与点A，D重合），点A关于直线BE的对称点为A'，连接A'B，A'D，A'C，当△A'BC是以BC为底边的等腰三角形时，AE的长为．37．（2022•武汉模拟）如图，菱形ABCD中，AB＝5，BD＝4√5，动点E、F分别在边AD、BC上，且AE ＝CF，过点B作BP⊥EF于P，当E点从A点运动到D点时，线段CP的长度的取值范围为．38．（2022•保亭县二模）如图1，在矩形ABCD中，点E在CD上，∠AEB＝90°，点P从点A出发，沿A →E→B的路径匀速运动到点B停止，作PQ⊥CD于点Q，设点P运动的路程为x，PQ长为y，若y与x 之间的函数关系图象如图2，则BC的长为；当x＝6时，PQ的长为．39．（2022•丹江口市模拟）已知定点P（a，b），且动点Q（x，y）到点P的距离等于定长r，根据平面内两点间距离公式可得（x﹣a）2+（y﹣b）2＝r2，这就是到定点P的距离等于定长r圆的方程．已知一次函数的y＝﹣2x+10的图象交y轴于点A，交x轴于点B，C是线段AB上的一个动点，则当以OC为半径的⊙C 的面积最小时，⊙C的方程为40．（2022•香洲区校级三模）如图正方形ABCD的边长为3，E是BC上一点且CE＝1，F是线段DE上的动点．连接CF，将线段CF绕点C逆时针旋转90°得到CG，连接EG，则EG的最小值是．41．（2022•韶关模拟）如图，已知正方形ABCD中，AB＝2，点E为BC边上一动点（不与点B、C重合），连接AE，将AE绕点E顺时针旋转90得到EF，连接CF，连接AF与CD相交于点G，连接DF，当DF 最小时，四边形CEGF的面积是．42．（2022•珠海校级三模）如图，在矩形ABCD中，AB＝4，BC＝6，点P是线段BC上一动点，将线段P A 绕点P顺时针转90°得到线段P A'，连接DA'，则DA'的最小值为．43．（2022•仁怀市模拟）如图，在等边△ABC中，AD是BC边上的高，点E是AD上一动点，连接CE，将线段CE绕点E顺时针旋转60°得到线段FE，连接AF，若AB＝4，AF=√19，则CF的长为．44．（2022•大庆二模）如图是边长为2的等边三角形ABC，D为△ABC内（包括△ABC的边）一动点，且满足CD2＝AD2+BD2，则CD的长度m的取值范围为．45．（2022•雁塔区校级模拟）如图，正方形ABCD中，AB＝4，点E为边BC上一动点，将点A绕点E顺时针旋转90°得到点F，则DF的最小值为．46．（2022•沈阳二模）如图，在矩形ABCD中，AB＝5，BC＝6，点E（不与点B重合）是BC边上一个动点，将线段EB绕点E顺时针旋转90°得到线段EF，当△DFC是直角三角形时，那么BE的长是．47．（2022•台山市校级一模）△ABC中，AB＝AC＝13，BC＝24，点D为△ABC的对称轴上一动点，过点D作⊙O与BC相切，BD与⊙O相交于点E，那么AE的最大值为．48．（2022•蓬江区校级一模）矩形ABCD中，AB＝2，BC＝6，点P为矩形内一个动点．且满足∠PBC＝∠PCD，则线段PD的最小值为．49．（2022•芜湖二模）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝4．点F为射线CB上一动点，过点C作CM⊥AF于M，交AB于E，D是AB的中点，则DM长度的最小值是．50．（2022•周至县一模）如图，在Rt△ABC中，∠B＝90°，∠C＝30°，AD平分∠BAC，BC＝6，点O 为线段AD上的动点，若以点O为圆心，1为半径的⊙O在△ABC内（⊙O可以与△ABC的边相切），则点D到⊙O上的点的距离最大值为．51．（2022•丹东模拟）在平面直角坐标系中，已知点A（﹣4，0），B（2，0），点M是y轴上的一个动点，当∠BMA＝30°时，点M的坐标为．52．（2022•常山县模拟）如图，在矩形ABCD中，AB＝6，BC＝8，E为AD上一点，且AE＝2，F为BC 边上的动点，以EF为直径作⊙O，当⊙O与矩形的边相切时，BF的长为．53．（2022•元宝区校级模拟）如图，四边形ABCD中，AB∥CD，∠ABC＝60°，AD＝BC＝CD＝4，点M 是四边形ABCD内的一个动点，满足∠AMD＝90°，则△MBC面积的最小值为．54．（2022•亭湖区校级一模）如图，AB为⊙O的直径，C为⊙O上一点，过B点的切线交AC的延长线于点D，E为弦AC的中点，AD＝6，BD＝4，若点P为直径AB上的一个动点，连接EP，若△AEP与△ABD相似，AP的长．55．（2022•柯桥区一模）如图，在平面直角坐标系中，M 、N 、C 三点的坐标分别为（1，2），（6，2），（6，0）．点A 为线段MN 上的一个动点，连接AC ，过点A 作AB ⊥AC 交y 轴于点B ．当点A 从M 运动到N 时，点B 随之运动，点B 经过的路径长是 ．。