力学静水压强实验分析

实验一 静水压强实验一、实验目的1、通过实验加深对流体静力学基本方程h p p γ+=0的理解。

2、验证静止流体中不同点对于同一基准面的测压管水头为常数，即=+γpz 常数3、实测静水压强，掌握静水压强的测量方法。

4、巩固绝对压强、相对压强、真空度的概念，加深理解位置水头、压力水头以及测压管水头之间的关系。

5、已知一种液体重度测定另一种液体的重度。

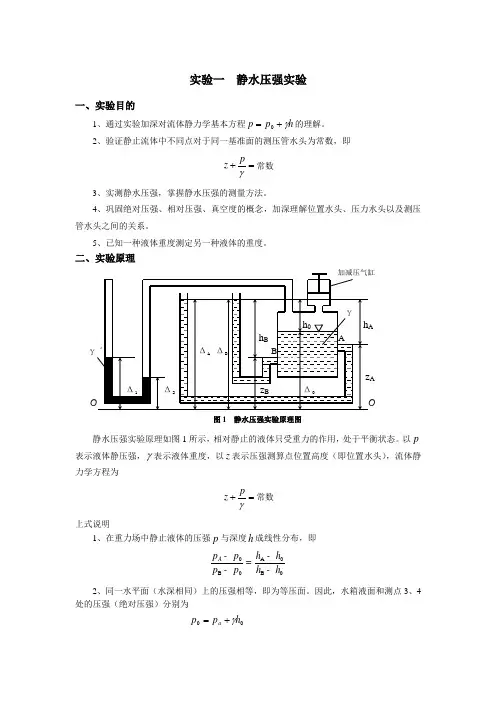
二、实验原理γA图1 静水压强实验原理图静水压强实验原理如图1所示，相对静止的液体只受重力的作用，处于平衡状态。

以p 表示液体静压强，γ表示液体重度，以z 表示压强测算点位置高度（即位置水头），流体静力学方程为=+γpz 常数上式说明1、在重力场中静止液体的压强p 与深度h 成线性分布，即0A 0B 0B 0A p p h h p p h h --=--2、同一水平面（水深相同）上的压强相等，即为等压面。

因此，水箱液面和测点3、4处的压强（绝对压强）分别为00h p p a γ+=()A 0a p g =+D -D ()B 0a p g =+D -DA A a p p h g =+()a A A p z g =+D -B a B p p h g =+()a B B p z g =+D - 与以上各式相对应的相对压力（相对压强）分别为a p p p -='000h γ= ()0A g =D -D ()0B g =D -Da p p p -='333h γ= ()A A z g =D -BB a p p p ¢=-B h g = ()B B z g =D -式中 a p —— 大气压力，Paγ—— 液体的重度，3m N0h —— 液面压力水头，m 0∆ —— 液面位置水头，mA D 、B D —— A 、B 处测压管水头，mA z 、B z —— A 、B 处位置水头，m A h 、B h —— A 、B 处压力水头，m3、静水中各点测压管水头均相等，即A B D =D或 A B A B p p z z g gⅱ+=+ 或 A A B B z h z h +=+ 即测压管A 、B 的液位在同一平面上。

水静压强实验一、实验目的1、加深理解静力学基本方程式及等压面的概念；2、理解封闭容器内静止液体表面压力及其液体内部某空间点的压力；3、观察压力传递现象。

二、实验仪器外形图三、实验原理对密封容器的液体表面加压时，设其压力为P ，即P0> P a。

从U 形管可以看到有压差产生，U 形管与密封容器上部连通的一面，液面下降，而与大气相通的一面，液面上升，由此可知液面下降的表面压力即是密闭容器内液体表面压力P0，即P0= P a+ρgh，h是U 形管液面上升的高度。

当密闭容器内压力P0下降时，U 形管内的液面呈现相反的现象，即P0<P a，这时密闭容器内液面压力P0=P a -ρgh 。

H 为液面下降高度。

四、实验步骤1、向水箱内注水至2/3 处，拧紧加压器并打开排气阀门，关闭与烧杯相连的导管上的阀门，打开与U 形管相连的阀门；2、用加压器缓慢加压，关闭排气阀门及与U 形管相连的阀门，读取Z1（靠近水箱一侧液柱的高度）、Z2（同一个U 形管另一侧的液柱高度），同时观察A、B 管内液柱变化情况并重复三次；3、打开与烧杯相连的导管上的阀门，不再有气泡冒出后，关闭该阀门；4、关闭排气阀门，打开水箱下端排水阀门，放出少量水，读取Z1、Z2,同时观察A、B 管内液柱变化情况，并重复三次。

五、数据处理六、演示步骤如果对密闭容器的液体表面加压时，其容器内部的压力向各个方向传递，在右侧的测压管中，可以看到由于A、B 两点在容器内的淹没深度h 不同，在压力向各点传递时，先到A 点后到B 点。

在测压管中反应出的是 A 管的液柱先上升而B 管的液柱滞后一点也在上升，当停止加压时，A、B 两点在同一水平面上。

1、关闭排气阀，用加压器缓慢加压，U 形管出现压差Δh，在加压的同时，观察右侧A、B 管的液柱上升情况；2、打开排气阀，使液面恢复到同一水平面上，关闭排气阀，打开密闭容器底部的水门，放出一部分水，造成容器内压力下降。

竭诚为您提供优质文档/双击可除静水压强的测定实验报告篇一：静水压强量测实验(完成)(1)武汉大学教学实验报告篇二：静水压强实验完成版1-1静水压强实验（experimentofstastichydraulicspressure）一、实验目的要求、1、掌握用测压管测量流体静压强的技能；2、验证不可压缩流体静力学基本方程；3、通过对诸多流体静力学现象的实验分析研讨，进一步提高解决静力学实际问题的能力。

4、巩固绝对压强、相对压强、真空度概念。

二、实验装置、图1.1静水压强实验装置图1、测压管；2、带标尺测压管；3、连通管；4、真空测压管；5、u型测压管；6、通气阀；7、加压打气球；8、截止阀；9、油柱；10、水柱；11、减压放水阀。

说明：1、所有测压管液面标高均以标尺（测压管2）零读数为基准；2、仪器铭牌所注?b、?c、?D系测点b、c、D标高；若同时取标尺零点作为静力学基本方程的基准点，则?b、?c、?D亦为zb、zc、zD；3、本仪器所有阀门旋柄顺管轴线为开。

三、实验原理、1、在重力作用下不可压缩流体静力学基本方程为：pz+?=const或：p?p0h（1.1）式中：z——被测点在基准面以上的位置高度；p——被测点的静水压强，用相对压强表示，以下同；p0——水箱中液面的表面压强；?——液体容重；h——被测点的液体深度。

另对装有水油（图1.2及图1.3）u型测管，应用等压面原理可得油的比重s0有下列关系：?0h1s0=??=h1?h2（1.2）据此可用仪器直接测得s0四、实验方法与步骤、1、搞清仪器组构及其用法，包括：1）阀门开关；2）加压方法——关闭所有阀门（包括截止阀），然后用打气球充气；3）减压方法——开启筒底阀11放水；4）检查仪器是否密封——加压后检查测管1、2、5液面高程是否恒定。

若下降，表明漏气，应查明原因并加以处理。

2、记录仪器编号及各常数（记入表1.1）。

五、实验数据记录及分析1、量测点静压强（各点压强用厘米水柱高表示）。

平面静水总压力实验分析报告班级：大禹港航姓名：张成君学号：1119010509实验原理：作用于任意形状平面上的静水总压力等于该平面形心点的压强与平面面积的乘积。

矩形平面上的静水总压力等于压强分布图的体积，即P=V=Ω*b。

对于三角形分布：P=（1/2）Hb，e=（1/3）H对于梯形分布：P=（1/2）（H1+H2）ab，e=（a/3）（2H1+H2）/（H1+H2）数据处理与分析：班级一共分为15组，每组三角形分布与梯形分布各三组数据，故，平面静水总压力实验共有45组数据，按照水位读数H由小到大的顺序排列。

（数据表格见反面）相对值均值：y=0.95 相对值方差：s²=∑（yi-0.95）²=0.2783由数据可以看出，实际静水总压力与理论静水点压力P理在误差允许范围内大致相等，相对值y在1.00附近，均值0.95，实验精确度较高。

有实验数据可验证得静水压力理论的正确性，即：作用于任意形状平面上的静水总压力P 等于该平面形心点的压强与平面面积A的乘积。

即P=pc·A。

由数据可分别绘制出三角形分布与梯形分布的压力P与e的关系曲线。

直线方程为y=1.248x-1.1107，与理论公式近似相等。

直线方程为y=4.4055x-11.594，与理论公式近似相等。

实验产生误差的原因及避免误差的方法：1、实验仪器所带来的误差。

①、砝码表面磨损，质量未达标注质量，致实际静水总压力略小于理论静水点压力，y值略小于1.00。

仪器老化所导致的实验误差，可通过对仪器的保养养护来减小误差，必要时，可更换仪器。

②、实验仪器上支点位置的影响。

扇形体的圆柱形曲面上各点处的静水总压力均通过其圆心，故支点必须在圆心上。

否则，圆柱形曲面上的静水总压力就会对杠杆受力发生作用，产生测量误差。

实验前检查仪器上支点的位置是否通过圆心，若不通过，需调节使其符合要求。

2、实验操作中产生的误差。

①、读数误差。

由于眼睛读数时的俯视或仰视，导致水位读数偏大或偏小，带来误差。

试验一：静水压强实验
一、实验目的
1、验证静水力学基本方程；
2、测定静止液体内某点的静水压强；
3、验证压强的特性。

二、实验原理
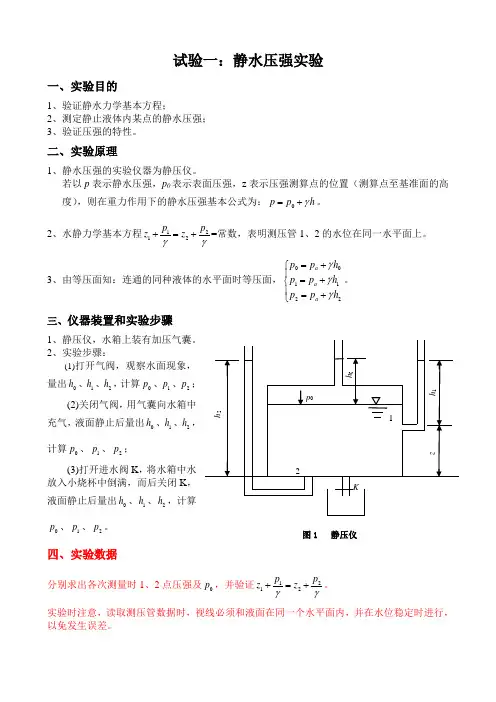
1、静水压强的实验仪器为静压仪。

若以p 表示静水压强，p 0表示表面压强，z 表示压强测算点的位置（测算点至基准面的高度），则在重力作用下的静水压强基本公式为：0p p h γ=+。

2、水静力学基本方程1
2
12p p z z γγ
+
=+
=常数，表明测压管1、2的水位在同一水平面上。

3、由等压面知：连通的同种液体的水平面时等压面，00
112
2a a a p p h p p h p p h
γγγ=+⎧⎪
=+⎨⎪=+⎩。

三、仪器装置和实验步骤 1、静压仪，水箱上装有加压气囊。

2、实验步骤：
(1)打开气阀，观察水面现象，量出0h 、1h 、2h ，计算0p 、1p 、2p ；
(2)关闭气阀，用气囊向水箱中充气，液面静止后量出0h 、1h 、2h ，计算0p 、1p 、2p ；
(3)打开进水阀K ，将水箱中水放入小烧杯中倒满，而后关闭K ，液面静止后量出0h 、1h 、2h ，计算
0p 、1p 、2p 。

四、实验数据
分别求出各次测量时1、2点压强及0p ，并验证1
2
12p p z z γ
γ
+
=+。

实验时注意，读取测压管数据时，视线必须和液面在同一个水平面内，并在水位稳定时进行，以免发生误差。

图1 静压仪
单位：mm。

实验八静水压强水静力学主要研究液体在平衡状态下的静水压强分布规律，进而进行建筑物的平面及曲面静水总压力的计算。

处于静止状态的液体质点之间以及液体质点与固体边壁之间的相互作用，是通过压强的形式来表现的。

下面我们进行室内的静水压强实验。

一、实验目的1．加深理解水静力学基本方程式及等压面的概念。

2．计算密封容器内静止液体表面及其内部某空间点的静水压强。

3.观察液体表面压强变化时，液体压强的传递现象和传递规律。

4.学会用静水压强法求液体的容重。

二、实验原理假设密封容器的液体表面压强为P0，当对液体的表面加压时，即使P0＞Pa，从U形管C可以看到有压力差产生，U形管C与密封容器上部空气连通的一面，液面下降，而与大气相通的一面，液面上升。

由此可知，液面下降的表面压力，即是密封容器内液体表面压力P0，即：P0＝Pa＋ρgh，是U形管液面上升的高度。

当密封容器内压力P0下降时，U形管液面呈现相反的现象，即：P0＜Pa，这时密封容器内液体表面压力P0＝Pa-ρgh，h为液面下降的高度。

如果对密封容器的液体表面加压时，其容器内部的压力向各个方向传递，在右侧的测压管中，可以看到由于A、B两点在容器内的淹没深度h不同，在压力向各个点传递时，先到A点后到B点。

在测压管中反映出的是A管的液体柱先上升，而B管的液柱滞后A上升，当停止加压时，A、B两点在同一水平面上。

静水压强：液体内垂直于单位面积上的压应力叫做静水压强。

其单位可以用kPa、kg/cm2、mmHg或水柱高度表示。

静水压强方程式：P=P0+ h (8－1)式中：P ——计算点的压强。

P 0——液体表面所受气体的压强，也叫做表面压强。

γ——水的容重。

h ——计算点的深度。

γh ——相对压强。

等压面是由静水压强相等的各点所构成的面。

静止液体表面是一水平面，也是一个等压面。

在同一液体内等压面是一系列的水平面。

两种液体的分界也是一个等压面。

根据压强方程式： P 0 +11h γ=Pa 22h γ+所以：11h γ=22h γ （8—2）根据上式可计算液体的容重。

静水压强实验报告
实验目的：研究静水的压强分布规律。

实验器材：水槽、塞子、刻度尺、玻璃管、手柄塞、气泵、橡胶管、水柱
实验原理：静水压强是指水柱的压力作用在一定面积上的力，即单位面积上的压力。

静水压强与水柱的高度，液体的密度和重力加速度有关，可用公式P = ρgh计算，其中P为静水压强，ρ为液体的密度，g为重力加速度，h为液体的高度。

实验步骤：
1. 将水槽中水平放置，并将塞子拔掉。

2. 在水槽中放入玻璃管，使其底部接触水面，并固定在水槽边缘。

3. 在玻璃管中装入水柱，使其高度适当。

4. 用刻度尺测量水柱的高度h，并记录下来。

5. 在水柱上方插入手柄塞，并用气泵将其固定。

6. 运用压力表测量手柄塞上受到的压力，并记录下来。

7. 重复实验3至6，分别改变水柱的高度，得到不同高度下的
压力值。

实验数据：
水柱高度h (cm) 手柄塞上压力P (Pa)
-----------------------------
10 1000
20 2000
30 3000
40 4000
50 5000
实验结果分析：根据实验数据，可以计算得到水柱高度与静水压强的关系，绘制压强-高度的图形。

根据实验结果可以得出
结论，当水柱的高度增加时，静水压强也随之增加，并且压强与高度之间呈线性关系。

实验结论：静水压强与水柱的高度成正比，当水柱高度增加时，静水压强也随之增加。

该实验结果验证了静水压强与水柱高度之间的关系。

静水压强实验报告静水压强实验报告引言：静水压强是物理学中的一个基本概念，它描述了液体在静止状态下对物体施加的压力。

通过实验，我们可以直观地观察到液体的压强与液体的深度、液体的密度以及重力加速度等因素有关。

本实验旨在通过测量不同深度下的静水压强，验证静水压强与液体深度的关系，并探究其它可能的影响因素。

实验目的：1. 验证静水压强与液体深度的关系；2. 探究静水压强与液体密度、重力加速度的关系；3. 分析可能的误差来源。

实验器材：1. 透明的容器；2. 液体（如水）；3. 液位计；4. 垂直刻度尺；5. 实验平台；6. 数字电子秤。

实验步骤：1. 将透明容器放置在实验平台上，并用液体（如水）填满容器；2. 将液位计固定在容器的一侧，以便测量液体的深度；3. 使用垂直刻度尺，测量液体的深度，并记录数据；4. 使用数字电子秤，测量液体的质量，并记录数据；5. 重复步骤3和步骤4，测量不同深度下的液体质量和深度数据。

实验结果与分析：根据实验数据，我们可以得出以下结论：1. 静水压强与液体深度成正比关系。

当液体深度增加时，静水压强也随之增加。

这符合物理学中的基本原理，即液体的压强与液体的深度成正比，与液体的密度和重力加速度有关。

2. 静水压强与液体密度成正比关系。

当液体密度增加时，静水压强也随之增加。

这是因为液体的压强与液体的密度成正比，密度越大，分子间的相互作用力越大，压强也就越大。

3. 静水压强与重力加速度成正比关系。

当重力加速度增加时，静水压强也随之增加。

这是因为压强是由液体的重力引起的，重力加速度越大，液体受到的压力也就越大。

误差分析：在实验过程中，可能存在以下误差来源：1. 液体表面的波动：由于外界因素的干扰，液体表面可能会产生波动，导致液体深度的测量不准确。

为减小误差，可以等待液体表面稳定后再进行测量。

2. 容器形状不规则：如果容器的形状不规则，液体深度的测量结果可能会受到影响。

为减小误差，可以使用规则形状的容器，并确保液体充满整个容器。

静水压强实验成果分析及小结静水压强实验是一种经典的物理实验，通过实验可以观察到静水的压强随深度的增加而增加的规律。

在本次实验中，我们在一个长方形玻璃容器中注入了一定深度的水，并使用一根透明的竹竿在水中测量了不同深度处的水压。

通过实验数据的分析，我们得到了以下实验成果：1. 静水的压强随深度的增加而增加，这符合物理学中的基本原理。

根据压强公式P = ρgh，其中P为压强，ρ为水的密度，g为重力加速度，h为深度。

实验中我们可以观察到，当深度增加时，水的压强也相应增加，验证了该公式的正确性。

2. 实验数据符合线性关系。

我们将实验数据绘制在图表上，发现水的压强与深度之间呈现出线性关系。

这表明静水的压强随深度的变化是一个直线关系，增加的速率是恒定的。

3. 压强的大小受到水的密度的影响。

实验中，我们也可以通过改变水的密度来观察压强的变化。

在实验中，我们在水中溶入了一定量的食盐，使水的密度增加。

结果显示，密度较大的水压强较大，密度较小的水压强较小。

通过这次实验，我们得到了对静水压强的一些认识。

静水压强与深度的增加成正比，即水的压强是随着深度的增加而增加的。

压强的大小受到水的密度的影响，密度越大，压强越大。

在实验过程中，我们也发现了一些问题，例如竹竿插入水中后可能会出现读数的误差，对于这个问题，我们可以通过使用更精确的测量工具来减少误差。

总的来说，通过静水压强实验，我们对静水的特性有了更深入的了解。

通过观察实验数据和分析实验结果，我们认识到了静水压强与深度和密度之间的关系，以及如何利用压强公式进行计算。

这些认识对于我们理解和应用物理学中有关压强的知识具有重要意义。

静水压强实验报告实验目的：本实验旨在探究液体静水压强与液体高度、液体密度及重力加速度等因素之间的关系。

实验原理：液体所受到的压力称为液压，液体对容器壁的压力称为静水压强。

液体中某一点的静水压强与该点的深度成正比，与液体密度及重力加速度成正比。

公式为：P = ρgh，其中P表示静水压强，ρ表示液体的密度，g表示重力加速度，h表示液体的高度。

实验器材：1. 液体容器：透明的圆柱形容器2. 静水压强计：用于测量液体的静水压强3. 液体：可以选择水或其他无色透明液体4. 标尺：用于测量液体的高度5. 实验平台：用于将实验器材固定在一起实验步骤：1. 将液体容器放在实验平台上，并固定好。

2. 将液体倒入容器中，使其高度适中，不要超过容器的高度。

3. 将静水压强计插入液体中，确保其完全浸入。

4. 读取静水压强计的读数，并记录下来。

5. 使用标尺测量液体的高度，并记录下来。

6. 重复以上步骤，改变液体的高度，记录对应的静水压强计读数和液体高度。

7. 将实验数据整理并计算静水压强。

8. 根据计算结果绘制静水压强与液体高度的关系图。

实验数据处理：1. 根据实验记录的数据，计算每组实验的静水压强值。

2. 绘制静水压强与液体高度的关系图。

3. 分析实验结果，探究静水压强与液体高度、液体密度及重力加速度之间的关系。

实验结果分析：根据实验数据处理得出的结果，在静水条件下，液体的静水压强与液体高度成正比，与液体密度及重力加速度成正比。

即静水压强P = ρgh。

不同液体的静水压强相同液体高度的静水压强不同，与液体密度有关。

一、实验目的1. 理解流体静力学基本方程式及等压面的概念；2. 计算密封容器内静止液体表面及其内部某空间点的静水压强；3. 观察液体表面压强变化时，液体压强的传递现象和传递规律；4. 学会用静水压强法求液体的容重。

二、实验原理静水压强实验是基于流体静力学原理进行的。

在重力作用下的均质静止液体中，任一点的压强为pp0 h。

式中p0为液面压强，h为该点处于液面下的深度，为液体容重，h就是从该点到液面的单位面积上的液柱重量。

静止液体内任一点相对于某一水平基准面的位置高度z与该点的压强高度之和，等于同一常数，即常数。

如果作用在静止液体边界上的压强有所增减，则液体内部任意点任意方向上的压强将发生同样大小的增减。

这就是静水压强传递的帕斯卡定律。

三、实验装置1. 静压强实验仪：包括U形管、测压管、连通器、密封水箱、调压箱等；2. 量筒：用于测量液体体积；3. 仪器架：用于固定实验装置。

四、实验步骤1. 将实验装置组装完毕，确保各部件连接牢固；2. 向水箱中加入一定量的液体，注意液面高度；3. 调整调压箱，使密封水箱内气体压强与大气压相等；4. 观察U形管中液面高度，记录液面压强；5. 改变密封水箱内气体压强，观察U形管中液面高度变化，记录液面压强；6. 改变水箱中液体深度，观察测压管中液面高度变化，记录液面压强；7. 改变水箱中液体深度，测量不同深度处的液体体积，计算液体容重；8. 比较不同深度处的液体压强，验证帕斯卡定律。

五、实验结果与分析1. 实验数据表1：不同深度处的液体压强数据深度h（m） | 液面压强p（Pa）--------- | -------------0.1 | 980.60.2 | 1961.20.3 | 2932.80.4 | 3904.40.5 | 4875.02. 实验结果分析（1）根据实验数据，可以看出随着液体深度的增加，液面压强也随之增大，符合流体静力学基本方程式pp0 h；（2）在改变密封水箱内气体压强时，U形管中液面高度变化，验证了帕斯卡定律；（3）根据液体深度和液体体积，计算得到不同深度处的液体容重，与理论值基本一致。

静水压强实验报告引言：静水压强是指水体在静止状态下对物体所产生的压力。

在工程学、物理学和生物学等领域，我们经常会遇到静水压强的概念。

本实验旨在通过实际操作，观察和测量静水压强的变化规律，以加深对静水压强的理解。

实验背景：静水压强是由重力引起的，与所放物体的形状和所处的深度有关。

根据压力定义，压强等于力除以面积。

在静水中，压强只与水的密度、重力加速度以及深度有关，与容器形状、装载条件等无关。

实验中我们将通过测量不同深度下的压强值，验证这一观点，并研究压强与深度的关系。

实验准备：实验所需材料包括透明的塑料容器、刻度尺、水桶、水银压力计和水。

先清洗塑料容器，确保内壁干净，然后填充足够的水，准备好其他实验设备。

实验步骤：1. 将塑料容器放在平稳的桌面上。

2. 使用刻度尺测量容器的高度，并记录下来。

3. 在容器的底部放置水银压力计，确保其与塑料容器底部紧密贴合。

4. 缓慢注水，同时观察水银压力计上的读数。

5. 当注水到水面接触到压力计刻度0时，停止注水。

6. 重复步骤4和5，每次注水增加一定深度，至少5次，记录下每次的压力计读数。

7. 将实验数据整理并绘制图表，分析压力与深度的关系。

实验结果与分析：根据实验数据，我们得到了不同深度下的压力计读数。

通过整理数据并绘制图表，我们可以看到随着深度增加，压力计的读数也相应增加。

这一结果符合我们的预期，表明压强与深度有正相关的关系。

根据实验结果绘制的图表，我们可以观察到以下特点：1. 当深度增加时，压力的增加幅度呈指数衰减。

也就是说，刚开始深度增加时，压力增加较快，但随着深度进一步增加，压力增加的速度减慢。

2. 在同一深度下，压强的数值相同。

这是因为重力对水的压力是均匀的，在同一深度处的压强是相等的。

3. 随着深度的增加，压强的变化越来越小。

这是因为随着深度增加，所受压力的面积也在增大，导致单位面积上的压力减小。

实验结论：通过本实验，我们验证了静水压强与深度的关系，得到的实验结果与理论预期相一致。

实验一 静水压强实验1.1实验目的和要求1. 掌握用测压管测量静水压强的方法，通过对水静力学现象的实验分析，加深理解水静力学方程的物理意义和几何意义，提高解决实际问题的能力。

2.观察在重力作用下液体任意点的位置水头Z 、压强水头γp 和测压管水头p Z +，验证不可压缩流体静力学的基本方程；3.测量当a p p =0、a p p >0和a p p <0时静水中某一点的压强，分析各测压管水头变化规律，加深对绝对压强、相对压强、表面压强、真空压强和真空度的理解；4.学习测量液体比重的方法；1.2静水压强实验的原理在重力作用下，处于静止状态下不可压缩的均质液体，其基本方程为 C p Z p Z ==+=+γγ2211 （1-1）式中，Z 为单位重量液体相对于基准面的位置高度或称位置水头；p 为单位重量液体的压能或称压强水头；p 为静止液体中任意点的压强；γ为水的重度；γp Z +称为测压管水头。

方程（1-1）的物理意义是：静止液体中任一点的单位位能和单位压能之和为一常数，而γp Z +表示单位重量液体具有的总势能，因此也可以说，在静止液体内部各点的单位重量液体的势能均相等。

几何意义是：静止液体中任一点的位置高度和该点压强的液柱高度之和为一常数。

静水压强方程也可以写成h p p γ+=0 （1-2） 式中，0p 为作用在液体表面的压强；h 为由液面到液体中任一点的深度。

上式说明， 在静止液体中，任一点的静水压强p ，等于表面压强0p 加上该点在液面下的深度h 与液体容重γ的乘积之和。

表面压强遵守巴斯家原理，等值地传递到液体内部所有各点上，所以当表面压强0p 一定时，由式（1-2）可知，静止液体中某一点的静水压强p 与该点在液面下的深度h 成正比。

如果作用在液面上的是大气压强a p ，则式（1-2）可写为h p p a γ+= （1-3） 上式说明当作用在液面上的压强为大气压强时，其静水压强等于大气压强a p 与液体重度γ和水深h 乘积之和。

02静水压强量测实验报告
实验目的：
通过实验，掌握测量液体静水压强的方法和技巧。

实验器材：
实验装置包括U型管、U型管的底部有一个扩张室和一只水箱。

U型管底部的扩张室上方有一个压强传感器。

实验原理：
液体静水压强的大小与液体的密度、深度、重力加速度等因素有关。

公式为P=ρgh，其中P为液体静水压强，ρ为液体的密度，g为重力加速度，h为液体深度。

在实验中，扩张室中的液体的深度与U型管中液体的深度相等。

通过测量扩张室中液体的压强传感器所测得的压强大小，即可得到液体的静水压强。

实验步骤：
1.首先将水箱中的水注入U型管中，直至水平面高度一致。

2.将压强传感器连接到扩张室上方的导管，并连接到计算机上进行数据测量。

3.随着沉入U型管中的扩张室体积的增加，压强传感器所测量的液体压强也会随之增加。

记录不同扩张室深度时的压强数值。

4.根据测量数据，计算得到液体静水压强，并绘制出深度与静水压强的关系曲线。

实验结果：
通过测量结果，我们得到深度与液体静水压强的关系曲线如下：
其中，横坐标为液体深度，单位为厘米；纵坐标为液体静水压强，单位为千帕。

由曲线可知，液体静水压强随液体深度的增加而线性增加，与实验原理相符合。

通过本次实验，我们深入了解了液体静水压强的测量原理，学会了运用实验装置测量液体静水压强，并通过数据计算得到了液体深度与静水压强的关系曲线。

同时，我们还发现液体静水压强与液体深度呈线性关系。

总之，本次实验让我们更加了解了液体静水压强的含义和概念，为我们日后学习和实践提供了参考。

02静水压强量测实验报告静水压强量测实验报告一、实验原理1.根据流体平衡规律，在重力场中静止液体的压强分布可表示为：Cgpz，即在连通的同种静止液体中各点对于同一基准面的测压管水头相等。

2.测压管的一端接大气，这样就把测管水头揭示出来了。

再利用液体的平衡规律，可知连通的静止液体区域中任何一点的压强，包括测点处的压强。

这就是测压管量测静水压的原理。

3.压强水头gp和位置水头z之间的互相转换，决定了液柱高和压差的对应关系：hgp.在压差相同的情况下，不同的液体对应不同的液柱高。

用这个原理可以测定液体的重度。

二、实验装置1.在一全透明密封有机玻璃箱内注水，并由一乳胶管将水箱与一可升降的调压筒相连，调压筒的顶部与大气连通。

水箱顶部装有排气阀K1，另从孔口K2接出管子与测压排中的三个U形比压计中的测管1，3，5相通，U形比压计1-2与水箱不连通，内装液体为未知液体，未知可能大于水的密度也可能小于水的密度，U形比压计3-4、5-6在测点A和B（底部）与水箱接通。

从开关K3接出的管子插入另一容器中的染色水中。

打开K1时，水箱内液体的表面压强为大气压，当K1关闭时，可通过升降调压筒调节水箱内液体的表面压强，使它高于或低于大气压。

实验设备简图：三、实验目的和要求1．通过实验加深对水静力学基本方程物理意义的理解。

加深理解位置水头、压强水头及测管水头的概念。

2．通过实验加深对水静力学基本方程物理意义的理解。

加深理解位置水头、压强水头及测管水头的概念。

3．验证静止液体中，不同点对于同一基准面的测压管水头为常数，即Cgpz。

4．实测静水压强，掌握静水压强的测量方法。

5．观察真空现象，加深对真空压强、真空度的理解。

66．．测定未知液体的重度。

四、实验步骤7．认真阅读实验目的要求、实验原理和注意事项。

8．熟悉仪器，测记有关常数。

9．将调压筒放置适当高度，打开排气阀K1，使水箱内的液面与大气相通，此时液面压强p0=pa.待水面稳定后，观察各测管中的液面位置，以验证等压面原理。

流体力学实验一：静水压强特性实验一、实验目的1．验证流体静力学基本方程；2．掌握用测压管测量流体静压强的技能；3．通过对诸多流体静力学现象的实验分析研讨，进一步提高解决流体静力学实际问题的能力。

二、实验仪器及耗材静水压强特性试验仪三、实验原理在重力作用下，不可压缩流体的静力学方程为：p Z const gρ+=或0p p gh ρ=+z ——被测点在基准面以上的位置高度；p ——被测点的静水压强，用相对压强表示，以下同； p 0——水箱中液面的表面压强； ρ——液体密度；h ——被测点的液体深度。

四、实验内容及步骤1．选定基准面，测定A 、B 点的位置高度Z A 、Z B 并记录；2．打开排气阀，U 型通气阀，调压管置于适当高度，此时水箱液面压强0p =0； 3．关闭排气阀，适当提高调压筒位置到适当高度，此时0p >0；4．测度并记录水箱液面高度0Z （或0∇），测压管开口管1、2、3的液面高度▽1、▽2、▽3及闭口管1的液面高度▽1’；5．再次升高调压筒至新位置，并记录水箱高度▽0及开口管液面高度▽1、▽2、▽3；6．打开排气阀，调压筒置适当位置，使之平衡；7．关闭排气阀，从0p =0位置处降低调压筒的位置，此时0p <0；8．连续降低2次调压筒至新位置，并记录水箱高度▽0及开口管液面高度▽1、▽2、▽3及闭口管1的液面高度▽1’； 8．实验结束，打开排气阀。

五、注意事项1．要保持容器具有良好的密闭性，如果容器加压后，测压管水位及水箱页面高度持续变化，则说明容器的密闭性不能满足实验要求； 2．校核标尺位置，以保证所取基准面及测压管读数无误； 3．必须等待页面稳定后再读数，按正确读数要求操作。

六、实验数据与计算1．实验原始数据表A Z = ，B Z =2．相关计算公式011(')p g ρ=∇-∇，00()A A p p g ρ=+∇-∇，00()B B p p g ρ=+∇-∇，A 点测压管水头AA p Z g ρ+，B 点测压管水头BB p Z gρ+。

同济大学流体力学实验报告静水压强实验和伯努利方程实验前言流体力学是一门实用性很强的学科，它研究的对象是流体中的运动和相应的力学问题，其广泛应用于水利、水电、船舶、机械、化工等各个领域。

为了更好地理解流体力学，本次实验我们进行了静水压强实验和伯努利方程实验。

一、实验目的1.了解静水压强的概念及其计算方法。

2.了解流体静压力的产生原理。

3.掌握用皮托管和风洞测量差压的方法。

4.理解伯努利方程的物理意义。

5.熟悉伯努利方程的实验方法及结果分析。

二、实验原理1.静水压强实验原理静水压强是指静止不动的流体所产生的压强，它是由于流体分子间的相互作用力所产生的压强。

在静止的流体中，由于流体的不可压缩性和流体分子的连续性，任何一点处的压强都是相等的。

静水压强公式为P=ρgh，其中ρ为流体的密度，g是重力加速度，h是液体的压头。

液体的压强只与液体高度有关，与液体横截面积无关。

2.伯努利定理实验原理伯努利方程是流体力学中的重要定理，它是热力学第一定律在流体中的应用，描述了在流体中沿着流线的稳恒流动中，流体的总能量守恒。

伯努利方程的数学形式为：P1+1/2ρv1²+ρgh1=P2+1/2ρv2²+ρgh2，其中P1、v1、h1为流体在点1处的压强、速度和位置，P2、v2、h2为流体在点2处的压强、速度和位置。

3.实验器材(1) 双口皮托管：测量速度压强。

(2) 多孔板：掩盖直线流动的速度分布，使得速度分布在整个试验区内保持恒定。

(3) 一个风洞(4) 数字压力计：测量压强差。

(5) 液位计：测量流体的高度。

三、实验步骤1. 静水压强实验(1) 将实验装置包括双口皮托管、数字压力计、液面计等连接起来。

(2) 把双口皮托管放置在液体里，保证口向上，在关闭口塞之前，先打开两口塞的短小孔，確認双口管内外的压力相同。

(3) 关闭型式口塞和长小孔，使双口管的两个端口分别与数字压力计连接，并依次对三个接口进行防漏。