二倍角的三角函数2

三角函数二倍角公式大全三角函数的二倍角公式是一组与角的两倍相关的方程，我们可以通过这些公式来计算角的两倍的正弦、余弦和正切值。

以下是常见的三角函数的二倍角公式：正弦的二倍角公式：sin(2θ) = 2sin(θ)cos(θ)余弦的二倍角公式：cos(2θ) = cos²(θ) - sin²(θ) = 2cos²(θ) - 1 = 1 -2sin²(θ)正切的二倍角公式：tan(2θ) = (2tan(θ))/(1 - tan²(θ))割的二倍角公式：sec(2θ) = (1 + tan²(θ))/(1 - tan²(θ))余割的二倍角公式：csc(2θ) = (1 + cot²(θ))/(1 - cot²(θ))这些公式可以通过基本的三角函数公式和三角恒等式推导得出。

下面我们将逐个证明这些公式。

1.正弦的二倍角公式：我们知道sin(α + β) = sin(α)cos(β) + cos(α)sin(β)当α和β相等时sin(2θ) = sin(θ + θ) = sin(θ)cos(θ) + cos(θ)sin(θ) = 2sin(θ)cos(θ)2.余弦的二倍角公式：正弦的平方加上余弦的平方等于1，即sin²(θ) + cos²(θ) = 1、将sin²(θ)替换为1 - cos²(θ)得到cos(2θ) = cos²(θ) - sin²(θ)又可以推导得到cos(θ + θ)，然后用cos(θ)替换掉其中的一项：cos(2θ) = cos²(θ) - sin²(θ) = cos²(θ) - (1 - cos²(θ)) = 2cos²(θ) - 13.正切的二倍角公式：tan(α + β) = (tan(α) + tan(β))/(1 - tan(α)tan(β))当α和β相等时tan(2θ) = tan(θ + θ) = (tan(θ) + tan(θ))/(1 - tan²(θ)) = 2tan(θ)/(1 - tan²(θ))4.割的二倍角公式：割(α+β)=(割(α)割(β))/(割(α)+割(β))当α和β相等时sec(2θ) = sec(θ + θ) = (sec(θ)sec(θ))/(sec(θ) +sec(θ)) = (1 + tan²(θ))/(1 - tan²(θ))5.余割的二倍角公式：余割(α+β)=(余割(α)余割(β))/(余割(α)+余割(β))当α和β相等时csc(2θ) = csc(θ + θ) = (csc(θ)csc(θ))/(csc(θ) +csc(θ)) = (1 + cot²(θ))/(1 - cot²(θ))这些二倍角公式在解决一些三角函数问题时非常有用。

二倍角的正弦余弦正切公式二倍角指的是角度的两倍，即一个角度的两倍。

在三角函数中，我们通常使用θ来代表一个角度，那么二倍角就用2θ表示。

接下来，让我们来看一下二倍角的正弦、余弦和正切公式：1.二倍角的正弦公式：sin(2θ) = 2sinθcosθ这个公式表示了一个角度的二倍角的正弦值与这个角度的正弦值、余弦值的关系。

具体来说，这个公式表明一个角度的二倍角的正弦值等于这个角度的正弦值和余弦值的乘积的2倍。

2.二倍角的余弦公式：cos(2θ) = cos^2θ - sin^2θ= 2cos^2θ - 1= 1 - 2sin^2θ这个公式表示了一个角度的二倍角的余弦值与这个角度的正弦值、余弦值的关系。

具体来说，这个公式有三种等价的形式，它们分别表示一个角度的二倍角的余弦值等于这个角度的余弦值的平方减去正弦值的平方、等于2倍的余弦值的平方减去1、等于1减去2倍的正弦值的平方。

3.二倍角的正切公式：tan(2θ) = 2tanθ / (1 - tan^2θ)这个公式表示了一个角度的二倍角的正切值与这个角度的正切值的关系。

具体来说，这个公式表明一个角度的二倍角的正切值等于角度的正切值的两倍除以1减去角度的正切值的平方。

使用这些二倍角公式可以方便地计算二倍角的三角函数值，从而简化三角函数的计算。

此外，二倍角公式还有很多应用，例如在解三角方程、求和差化积等问题中。

需要注意的是，这些公式只适用于特定的角度范围，通常是0到360度或者0到2π弧度之间。

当角度超过这个范围时，可能需要利用三角函数的周期性质进行转化。

另外，这些公式的推导可以通过三角函数的定义、三角恒等式和半角公式来完成。

总结起来，二倍角的正弦、余弦和正切公式是三角函数中的重要公式，它们可以方便地计算二倍角的三角函数值，简化三角函数的计算，并且在解三角方程、求和差化积等问题中有广泛的应用。

三角函数的2倍角公式三角函数的2倍角公式是初中数学中的一个重要概念，它是由三角函数的和差公式推导而来的。

在本文中，我们将详细介绍三角函数的2倍角公式及其应用。

一、正弦函数的2倍角公式正弦函数的2倍角公式是指：sin(2θ) = 2sinθcosθ其中，θ为任意角度。

这个公式的含义是，一个角的正弦值的2倍等于这个角的两倍角的正弦值。

也就是说，通过2倍角公式，我们可以用已知角度的正弦函数值来求解该角度的两倍角的正弦函数值。

例如，如果我们知道sinθ的值，想要求解sin(2θ)的值，只需要将sinθ代入2倍角公式中即可。

二、余弦函数的2倍角公式余弦函数的2倍角公式是指：cos(2θ) = cos^2θ - sin^2θ同样地，θ为任意角度。

这个公式的含义是，一个角的余弦值的2倍等于这个角的两倍角的余弦值。

通过2倍角公式，我们可以通过已知角度的余弦函数值来求解该角度的两倍角的余弦函数值。

例如，如果我们知道cosθ的值，想要求解cos(2θ)的值，只需要将cosθ代入2倍角公式中即可。

三、正切函数的2倍角公式正切函数的2倍角公式是指：tan(2θ) = (2tanθ) / (1 - tan^2θ)同样地，θ为任意角度。

通过2倍角公式，我们可以通过已知角度的正切函数值来求解该角度的两倍角的正切函数值。

例如，如果我们知道tanθ的值，想要求解tan(2θ)的值，只需要将tanθ代入2倍角公式中即可。

四、2倍角公式的应用三角函数的2倍角公式在解三角方程、证明恒等式和简化复杂表达式等方面都有广泛的应用。

在解三角方程时，我们可以利用2倍角公式将复杂的三角方程转化为简单的一次方程或二次方程，从而更容易求解。

在证明恒等式时，2倍角公式可以帮助我们将一个角的三角函数值转化为另一个角的三角函数值，从而证明两个角的三角函数值相等。

在简化复杂表达式时，2倍角公式可以将一个角的三角函数值表示为另一个角的三角函数值的形式，从而简化表达式的求值过程。

二倍角和半倍角公式在三角函数中，二倍角和半倍角公式是非常重要的公式之一。

它们可以将一个三角函数的角度转化为另一个三角函数的角度，并且可以简化一些复杂的三角函数表达式。

下面将介绍二倍角和半倍角公式的定义以及推导过程。

1. 二倍角公式：正弦函数的二倍角公式：sin(2θ) = 2sinθcosθ余弦函数的二倍角公式：cos(2θ) = cos^2θ - sin^2θ = 1 - 2sin^2θ = 2cos^2θ - 1正切函数的二倍角公式：tan(2θ) = 2tanθ / (1 - tan^2θ)这些二倍角公式的推导可以通过使用三角函数的和差角公式得出。

假设有一个角度为θ的三角函数表达式，通过和、差角公式可以得到theta和-θ的三角函数表达式。

然后将这两个表达式相加或者相乘，就可以得到二倍角的三角函数表达式。

2. 半倍角公式：正弦函数的半倍角公式：sin(θ/2) = ±√[(1 - cosθ) / 2]余弦函数的半倍角公式：cos(θ/2) = ±√[(1 + cosθ) / 2]正切函数的半倍角公式：tan(θ/2) = ±√[(1 - cosθ) /(1 + cosθ)]这些半倍角公式的推导可以通过使用二倍角公式得出。

假设有一个角度为2θ的三角函数表达式，通过二倍角公式可以得到2θ的三角函数表达式。

然后将这个表达式中的θ替换成θ/2，就可以得到半倍角的三角函数表达式。

二倍角和半倍角公式在解决三角函数相关问题时非常有用。

通过将角度转化为二倍角或者半倍角，可以简化复杂的三角函数表达式，从而更容易进行计算和推导。

总结：二倍角公式和半倍角公式是解决三角函数相关问题的重要工具。

它们可以将一个角度的三角函数表达式转化为另一个角度的三角函数表达式，并且可以简化复杂的三角函数表达式。

通过熟练掌握和灵活运用二倍角和半倍角公式，可以更快速地解决各种三角函数问题。

初中数学三角函数的二倍角公式有哪些小编已经为大家找来了二倍角公式，而且小编还整理了三角函数的两角和差公式及常用三角函数，赶快跟随小编一起来看看吧。

三角函数的二倍角公式sin2α=2sinαcosαcos2α=cos(α)^2-sin(α)^2=2cos(α)^2-1=1-2sin(α)^2tan2α=2tanα/[1-tan(α)]两角和差公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)常用三角函数α=30°(π/6) sinα=1/2 cosα=√3/2 tαnα=√3/3 cotα=√3 secα=2√3/3 cscα=2α=45°(π/4) sinα=√2/2 cosα=√2/2 tαnα=1 cotα=1 secα=√2cscα=√2α=60°(π/3) sinα=√3/2 cosα=1/2 tαnα=√3 cotα=√3/3 secα=2 cscα=2√3/3α=90°(π/2) sinα=1 cosα=0 tαnα→∞ cotα=0 secα→∞ cscα=1三角函数定义三角函数（也叫做"圆函数"）是角的函数；在研究三角形和建模周期现象和许多其他应用中是很重要的。

三角函数通常定义为包含这个角的直角三角形的两个边的比率，也可以等价的定义为单位圆上的各种线段的长度。

更现代的定义把它们表达为无穷级数或特定微分方程的解，允许它们扩展到任意正数和负数值，甚至是复数值。

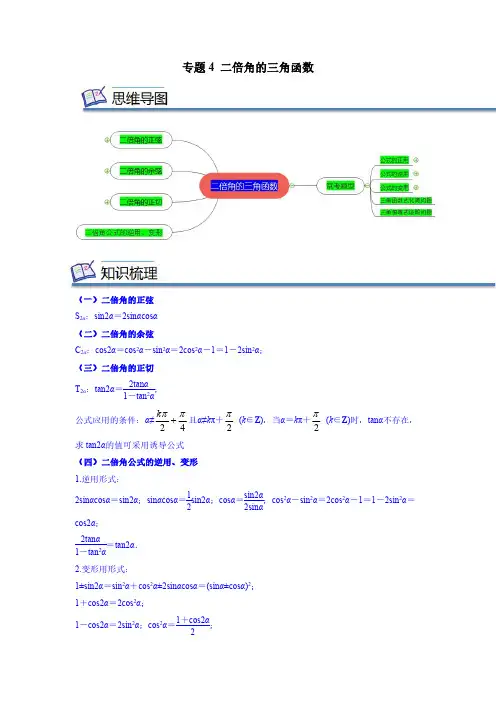
专题4二倍角的三角函数（一）二倍角的正弦S 2α：sin2α＝2sin αcos α（二）二倍角的余弦C 2α：cos2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α；（三）二倍角的正切T 2α：tan2α＝2tan α1－tan 2α；公式应用的条件：α≠24k ππ+且α≠k π＋2π(k ∈Z )，当α＝k π＋2π(k ∈Z )时，tan α不存在，求tan2α的值可采用诱导公式（四）二倍角公式的逆用、变形1.逆用形式：2sin αcos α＝sin2α；sin αcos α＝12sin2α；cos α＝sin2α2sin α；cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α＝cos2α；2tan α1－tan 2α＝tan2α．2.变形用形式：1±sin2α＝sin 2α＋cos 2α±2sin αcos α＝(sin α±cos α)2；1＋cos2α＝2cos 2α；1－cos2α＝2sin 2α；cos 2α＝1＋cos2α2；sin 2α＝1－cos2α2．题型一公式的正用【典例1】（2022春·江苏南京·高一南京航空航天大学附属高级中学校考期中）已知()0,απ∈，1tan 2α=，则cos2α＝（）A ．15B ．35C ．45D ．1225【典例2】（2022春·江苏苏州·高一统考期末）已知向量3sin ,2,1,1cos a b αα=-=-，若2a b ⋅=-，则tan2α=（）A ．1213-B ．613-C ．125-D ．65-【典例3】（2022春·江苏徐州·高一校考竞赛）求sin sin sin 181818的值.由给出的某些角的三角函数值，求另外一些角的三角函数值，关键在于“变角”使“目标角”变成“已知角”，另外角的范围应根据所给条件进一步缩小，避免出现增解．题型二公式的逆用【典例4】（2022春·江苏盐城·高一江苏省响水中学校考阶段练习）设212tan13cos 66,,21tan 13a b c ︒=︒-︒==-︒则有（）A ．a b c >>B ．a b c <<C ．a c b<<D ．b<c<a正确的是（）A ．tan 25tan 3525tan 35︒+︒+︒⋅︒=B ．22ππ1cos sin 12122-=C ．2tan22.51tan45tan 22.52︒=︒-︒D．12sin10=(1)求值()4sin 67cos 27sin 23cos 27tan 40-- ；(2)已知ππ1sin sin 634αα⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭，ππ,32α⎛⎫∈ ⎪⎝⎭，求sin 2α的值当出现（或可化成）公式右端结构形式时，注意“逆用”公式，简化解题过程.题型三公式的变用【典例7】（2023秋·重庆沙坪坝·=（）A ．1BCD 122122212212222sin cos sin cos π，Z sin cos sin cos sin θθθθθk θθθθθ⎛⎫+-+++=≠∈ ⎪+++-⎝⎭．【典例9】（2023·江苏·高一专题练习）已知cos 2,252θθπ=<<．(1)求tan θ的值；(2)求22cos sin 24θθπθ-⎛⎫+ ⎪⎝⎭的值．公式变形的主要形式有1±sin2α＝sin 2α＋cos 2α±2sin αcos α＝(sin α±cos α)2,1＋cos2α＝2cos 2α，1－cos2α＝2sin 2α，cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2．题型四三角函数式化简问题【典例10】（2022秋·河北承德·高一河北承德第一中学校考期末）化简：1cos15sin15·sin170cos15sin15⎫︒+︒-⎪⎪︒︒-︒⎝⎭____.sin21tan tan2ααα⎛⎫+=⎪⎝⎭__．︒-︒cos40sin501︒+︒︒1.三角公式化简求值的策略(1)使用倍角公式，首先要记住公式的结构特征和符号变化规律．(2)使用公式求值，应注意与同角三角函数基本关系、诱导公式的综合应用．(3)使用公式求值，应注意配方法、因式分解和整体代换思想的应用．2.注意三角函数公式逆用、变形用及“变角、变名、变号”的“三变”问题(1)公式逆用时一定要注意公式成立的条件和角之间的关系．(2)注意特殊角的应用，当式子中出现12，1，,23入特殊角，把“值变角”构造适合公式的形式．题型五三角恒等式证明问题【典例13】（2023·江苏·高一专题练习）证明：ππ2sin sin cos 244ααα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭；【典例14】（2023·江苏·高一专题练习）求证：tan 1sin 2cos 2ααα=++【典例15】（2023春·湖北黄冈·高一校考阶段练习）（1）化简：cos()2sin sin αβαβ--；（2）求证：1sin cos sin 1sin cos 1cos θθθθθθ+-=+++．三角恒等式的证明方法(1)从等式的比较复杂的一边化简变形到另一边，相当于解决化简题目．(2)等式两边同时变形，变形后的结果为同一个式子．(3)先将要证明的式子进行等价变形，再证明变形后的式子成立．提醒：开平方时正负号的选取易出现错误，所以要根据已知和未知的角之间的关系，恰当地把角拆分，根据角的范围确定三角函数的符号．一、单选题1．（2023·江苏·高一专题练习）1sin cos ,sin25ααα+=-=（）A ．2425-B ．2425C ．1225D ．1225-2．（2023春·安徽·高三合肥市第六中学校联考开学考试）已知2sin 2cos24θ+=，则sin 2θ=A ．1516-B ．1516C ．34-D ．34tan 26πα⎛⎫+= ⎪⎝⎭，则4tan 23πα⎛⎫+= ⎪⎝⎭（）A ．512B ．43-C ．34D ．43A ．0B ．2cos αC π4α⎛⎫- ⎪⎝⎭D π4α⎛⎫+ ⎪⎝⎭5．（2022春·江苏宿迁·高一统考期末）若51sin 123⎛⎫+= ⎪⎝⎭πα，则cos 26πα⎛⎫- ⎪⎝⎭的值为（）A ．9B ．9-C ．79D ．79-sin (1sin 2)sin cos θθθθ+=+（）A ．25B ．25-C ．65D ．65-7．（2022春·江苏苏州·高一江苏省沙溪高级中学校考期中）已知0,απ∈，且sin cos 5αα-=，则22sin2cos sin ααα=-（）A ．247B ．12C ．12-D ．247-，且，则α=（）A ．9B ．18C ．27oD ．36o【答案】D【分析】根据二倍角公式和逆用余弦的差角公式化简得到()cos 29sin 9α+=，结合090α<< 得到29909α+=- ，求出α.【详解】因为()()sin181sin 22sin 9cos 91sin 2αα+=+，所以()22cos 9cos 22sin 9cos 91sin 2αα=+，整理得：cos9cos 2sin 9sin 2sin 9αα=+ ，cos9cos 2sin 9sin 2sin 9αα-= ，()cos 29sin 9α+= ，因为090α<< ，所以929189α<+< ，所以29909α+=- ，解得：36α= 故选：D.二、多选题9．（2022春·江苏盐城·高一盐城市伍佑中学校考期中）下列等式成立的是（）A ．22cos 15sin 15-B ．sincos 882ππ=C ．1sin 4040sin 702=D ．tan152=10．（2022春·江苏徐州·高一统考期中）已知sin cos 5αα+=，以下选项正确的是（）A ．24sin 225α=±B ．7sin cos 5αα-=±C ．7cos 225α=±D ．447sin cos 25αα-=±11．（2023秋·宁夏银川·高一银川唐徕回民中学校考期末）24cos 20︒=___________.12.（2022春·江苏盐城·高一统考期中）若(,2)2απ∈_____．13．（2022秋·上海宝山·高一上海交大附中校考阶段练习）已知tan 2θ=-π02θ<<.(1)求tan θ；(2)求22cos sin 12π4θθθ+-⎛⎫- ⎪⎝⎭.14．（2023秋·陕西渭南·高一统考期末）（1）已知2sin sin 22α=-，求sin cos cos2ααα+的值；（2）已知ππ22x -<<，1sin cos 5x x +=，则2sin22sin 1tan x x x+-．15．（2023·江苏·高一专题练习）已知向量()()sin ,1,3,cos m n αα=-=-，其中,π2α⎛⎫∈ ⎪⎝⎭，且m n ⊥ ．(1)求tan α和sin 2α的值；(2)若sin()αβ+=0,2πβ⎛⎫∈ ⎪⎝⎭，求角β的值．16．（2022春·江苏盐城·高一盐城中学校考期中）已知向量()cos ,sin a αα=，122b ⎫=-⎪⎪⎝⎭，02πα<<．(1)若a b ⊥时，求sin 21cos 2αα+的值；(2)若a b -= sin 212απ⎛⎫+ ⎪⎝⎭的值．。

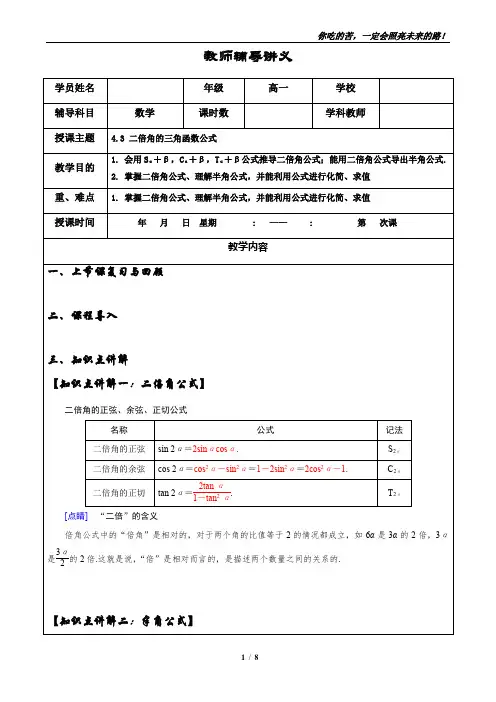
教师辅导讲义半角三角函数的公式(半角公式)sin α2＝± 1－cos α2；cos α2＝± 1＋cos α2； tanα2＝±1－cos α1＋cos α＝sin α1＋cos α＝1－cos αsin α.在这些公式中，根号前面的符号由α2所在象限相应的三角函数值的符号确定，若α2所在象限无法确定，则应保留根号前面的正、负两个符号.【知识点讲解三：二倍角余弦公式的运用】在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛.常用形式： ①1＋cos 2α＝2cos 2 α；②cos 2 α＝1＋cos 2α2；③1－cos 2α＝2sin 2 α；④sin 2 α＝1－cos 2 α2. 【例题解析1】利用二倍角公式求值[例1] (1)求下列各式的值：①23－43sin 2 15°； ②cos π5cos 2π5.(2)已知cos ⎝⎛⎭⎫α＋π4＝35，π2≤α<3π2，求cos ⎝⎛⎭⎫2α＋π4的值.【巩固练习1】1.(1)已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan 2x ＝( )【本知识点小结2】【例题解析3】三角函数性质与恒等变换的综合应用[例3] 已知函数f (x )＝4tan x sin ⎝⎛⎭⎫π2－x ·cos ⎝⎛⎭⎫x －π3－ 3.(1)求f (x )的定义域与最小正周期； (2)讨论f (x )在区间⎣⎡⎦⎤－π4，π4上的单调性.【巩固练习3】3.(1)函数y ＝32sin x ＋cos 2 x2的最小正周期为________. (2)函数y ＝cos x ＋cos ⎝⎛⎭⎫x ＋π3⎝⎛⎭⎫x ∈⎣⎡⎦⎤－π3，π2的最大值是________，最小值是________.【本知识点小结3】 四、当堂检测限时（分钟） 用时（分钟）难度 分值 得分 得分率1.判断正误(正确的打“√”，错误的打“×”)(1)对于任意的角α，都有sin 2α＝2sin α成立.( )(2)存在角α，使cos 2α＝2cos α成立.( ) (3)cos 3αsin 3α＝12sin 6α对任意的角α都成立.( )(4)cosα2＝1＋cos α2.( ) 2.若sin α＝13，则cos 2α＝( )A.89B.79C.－79D.－893.已知sin α＝3cos α，那么tan 2α的值为( )A.2B.－2C.34D.－344.已知2π<θ<4π，且sin θ＝－35，cos θ<0，则tan θ2的值等于( )A.－3B.3C.－13D.135.若cos ⎝⎛⎭⎫π4－α＝35，则sin 2α＝( )A.725 B.15 C.－15D.－7256.若cos 2αsin ⎝⎛⎭⎫α＋π4＝12，则sin 2α的值为( )A.－78B.78C.－47D.477.设α∈⎝⎛⎭⎫0，π2，β∈⎝⎛⎭⎫0，π2，且tan α＝1＋sin βcos β，则( )A.3α－β＝π2B.2α－β＝π2C.3α＋β＝π2D.2α＋β＝π28.(多选题)下列各式中，值为32的是( ) A.2sin 15°cos 15° B.cos 2 15°－sin 2 15° C.1－2sin 2 15°D.sin 2 15°＋cos 2 15°9.(多选题)设a ＝12cos 6°－32sin 6°，b ＝2sin 13°cos 13°，c ＝1－cos 50°2，则下列结论不正确的是( )A.a >b >cB.a <b <cC.a <c <bD.b <c <a10.已知|cos θ|＝35且5π2<θ<3π，则tan θ2的值为________.11.已知tan α＝2，则sin 2α－cos 2α1＋cos 2 α＝________.12.函数f (x )＝sin 2x ＋3sin x cos x 在区间⎣⎡⎦⎤π4，π2上的最大值是________.13.若tan ⎝⎛⎭⎫π4－α＝12，则tan 2α＋1cos 2α＝________. 14.已知sin x 2－2cos x2＝0.(1)求tan x 的值； (2)求cos 2xcos⎝⎛⎭⎫5π4＋x sin （π＋x ）的值.15.设函数f (x )＝cos ⎝⎛⎭⎫2x ＋π3＋sin 2 x －12.(1)当x ∈[0，π]时，求f (x )的单调递减区间； (2)当f ⎝⎛⎭⎫α－π8＝33时，求f (2α)的值.。

三角函数二倍角公式大全1.正弦函数的二倍角公式：sin(2θ) = 2sin(θ)cos(θ)这个公式可以用来计算任意角度的正弦值。

它的推导可以通过将一个角度θ分成两个相等的角度来完成。

2.余弦函数的二倍角公式：cos(2θ) = cos²(θ) - sin²(θ)这个公式可以用来计算任意角度的余弦值。

它的推导可以通过将一个角度θ分成两个相等的角度来完成。

3.正切函数的二倍角公式：tan(2θ) = 2tan(θ) / (1 - tan²(θ))这个公式可以用来计算任意角度的正切值。

它的推导可以通过将sin(2θ)除以cos(2θ) 来完成。

4.余切函数的二倍角公式：cot(2θ) = cot²(θ) - 1这个公式可以用来计算任意角度的余切值。

它的推导可以通过将cos(2θ)除以sin(2θ)来完成。

5.正割函数的二倍角公式：sec(2θ) = (1 + tan²(θ)) / (1 - tan²(θ))这个公式可以用来计算任意角度的正割值。

它的推导可以通过将1除以cos²(2θ)来完成。

6.余割函数的二倍角公式：csc(2θ) =2csc(θ)cos(θ)这个公式可以用来计算任意角度的余割值。

它的推导可以通过将sin(2θ)除以sin(θ)来完成。

这些三角函数二倍角公式在解决三角函数相关问题、证明三角恒等式以及计算复杂的三角函数表达式时非常有用。

它们可以帮助我们简化计算，以及更深入地理解三角函数的性质与关系。

除了上述常见的三角函数二倍角公式，还有其他一些特殊的二倍角公式，例如：1. sin(θ + π) = -sin(θ)2. cos(θ + π) = -cos(θ)3. tan(θ + π) = tan(θ)4. cot(θ + π) = cot(θ)5. sec(θ + π) = -sec(θ)6. csc(θ + π) = -csc(θ)这些公式可以帮助我们计算任意角度的三角函数值。

二倍角和半角公式在数学中，二倍角和半角公式是用于求解三角函数的重要工具。

它们可以帮助我们简化复杂的三角函数表达式，从而更方便地进行计算和推导。

一、二倍角公式二倍角公式是指将一个角的两倍表示为另一个角的函数表达式。

在三角函数中，我们常用的二倍角公式有以下几个：1. 正弦函数的二倍角公式：sin(2θ) = 2sinθcosθ这个公式告诉我们，一个角的正弦函数的两倍等于该角的正弦函数乘以它的余弦函数。

2. 余弦函数的二倍角公式：cos(2θ) = cos^2θ - sin^2θ这个公式告诉我们，一个角的余弦函数的两倍等于该角的余弦函数的平方减去它的正弦函数的平方。

3. 正切函数的二倍角公式：tan(2θ) = (2tanθ) / (1 - tan^2θ)这个公式告诉我们，一个角的正切函数的两倍等于该角的正切函数的两倍除以1减去该角的正切函数的平方。

二、半角公式半角公式是指将一个角的一半表示为另一个角的函数表达式。

在三角函数中，我们常用的半角公式有以下几个：1. 正弦函数的半角公式：sin(θ/2) = √[(1 - cosθ) / 2]这个公式告诉我们，一个角的正弦函数的一半等于1减去该角的余弦函数的一半再开平方。

2. 余弦函数的半角公式：cos(θ/2) = √[(1 + cosθ) / 2]这个公式告诉我们，一个角的余弦函数的一半等于1加上该角的余弦函数的一半再开平方。

3. 正切函数的半角公式：tan(θ/2) = sinθ / (1 + cosθ)这个公式告诉我们，一个角的正切函数的一半等于该角的正弦函数除以1加上该角的余弦函数。

以上就是二倍角和半角公式的简要介绍。

通过这些公式，我们可以将复杂的三角函数表达式转化为简单的形式，从而更方便地进行数学推导和计算。

在解决实际问题中，二倍角和半角公式也起到了重要的作用，帮助我们更好地理解和应用三角函数。

总结一下，二倍角和半角公式是数学中常用的工具，它们可以帮助我们简化复杂的三角函数表达式，从而更方便地进行计算和推导。

三角函数二倍角公式大全三角函数是数学中的重要内容，而三角函数的二倍角公式更是其中的关键部分。

本文将为大家详细介绍三角函数的二倍角公式，希望能够帮助大家更好地理解和掌握这一知识点。

1. 正弦函数的二倍角公式。

正弦函数的二倍角公式是，sin(2θ) = 2sinθcosθ。

这个公式可以通过正弦函数的和差角公式推导得出，它可以帮助我们求解一些复杂的三角函数问题，特别是在解决一些三角函数方程时非常有用。

2. 余弦函数的二倍角公式。

余弦函数的二倍角公式是，cos(2θ) = cos^2θ sin^2θ。

这个公式也可以通过余弦函数的和差角公式推导得出，它在解决一些三角函数方程和证明三角函数恒等式时起到非常重要的作用。

3. 正切函数的二倍角公式。

正切函数的二倍角公式是，tan(2θ) = (2tanθ)/(1-tan^2θ)。

这个公式可以通过正切函数的和差角公式推导得出，它在解决一些三角函数方程和简化三角函数表达式时非常有用。

4. 三角函数的二倍角公式的应用。

三角函数的二倍角公式在解决三角函数方程、证明三角函数恒等式以及简化复杂的三角函数表达式时都起到非常重要的作用。

通过灵活运用这些公式，我们可以更快更准确地解决各种三角函数相关的问题，提高解题效率。

5. 总结。

三角函数的二倍角公式是数学中的重要知识点，它们在解决各种三角函数相关问题时起到至关重要的作用。

希望大家通过本文的介绍和总结，能够更好地掌握三角函数的二倍角公式，提高数学学习的效率和水平。

通过以上内容的介绍，我们可以看到三角函数的二倍角公式在数学中的重要性和应用价值。

希望大家能够认真学习和掌握这些公式，提高解决三角函数问题的能力，为今后的学习和工作打下坚实的数学基础。