现代光学系统第四章习题答案

解：对方位，的第二个次最大位
对 的第三个次最大位
即：
9、波长为的平行光垂直地射在宽的缝上，若将焦距为的透镜紧贴于缝的后面，并使光聚焦到屏上，问衍射图样的中央到⑴第一最小值；⑵第一最大值；⑶第三最小值的距离分别为多少？
解：⑴第一最小值的方位角为：
⑵第一最大值的方位角为：
⑶第3最小值的方位角为：
10、钠光通过宽的狭缝后，投射到与缝相距的照相底片上。所得的第一最小值与第二最小值间的距离为，问钠光的波长为多少？若改用X射线（）做此实验，问底片上这两个最小值之间的距离是多少？
解：
⑴
⑵级光谱对应的衍射角为：
即在单缝图样中央宽度内能看到条（级）光谱
⑶由多缝干涉最小值位置决定公式：
第3xx 几何光学的基本原理
1、证明反射定律符合费马原理
证明：
设A点坐标为，B点坐标为
入射点C的坐标为
光程ACB为：
令
即：
*2、根据费马原理可以导出近轴光线条件下，从物点发出并会聚到像点的所有光线的光程都相等。由此导出薄透镜的物像公式。
另一个气泡
， 即气泡离球心
13、直径为的球形鱼缸的中心处有一条小鱼，若玻璃缸壁的影响可忽略不计，求缸外观察者所看到的小鱼的表观位置和横向放大率。
解：由球面折射成像公式：
解得 ，在原处
14、玻璃棒一端成半球形，其曲率半径为。将它水平地浸入折射率为的水中，沿着棒的轴线离球面顶点处的水中有一物体，利用计算和作图法求像的位置及横向放大率，并作光路图。
解：
由球面折射成像公式：
15、有两块玻璃薄透镜的两表面均各为凸球面及凹球面，其曲率半径为。一物点在主轴上距镜处，若物和镜均浸入水中，分别用作图法和计算法求像点的位置。设玻璃的折射率为，水的折射率为。

第四章 光的偏振（2）一．选择题：（共30分）1．在双缝干涉实验中，用单色自然光，在屏上形成干涉条纹，若在两缝后放一个偏振片，则[ ]（A ） 干涉条纹的间距不变，但明纹的亮度加强。

（B ） 干涉条纹的间距不变，但明纹的亮度减弱。

（C ） 干涉条纹的间距不窄，但明纹的亮度减弱。

（D ） 无干涉条纹。

2．光强为I 0的自然光垂直通过两个偏振片，它们的偏振化方向之间的夹角α =600，设偏振片没有吸收，则出射光强I 与入射光强I 0之比为 [ ]（A ）1/4 （B ） 3/4 （C ）1/8 （D ）3/83．如果两个偏振片堆叠在一起，且偏振化方向之间夹角为600，假设二者对光无吸收，光强为I 0的自然光垂直入在偏振片上，则出射光强为 [ ](A) I 0/8 (B) 3I 0 /8 (C) I 0 /4 (D) 3 I 0/44．光强为I 0的自然光依次通过两个偏振片和，若的偏振化方向的夹角，则透射偏振光的强度是[ ](A) I 0/4 (B) √3 I 0/4 (C) √3 I 0/2 (D) I 0/8 (E) 3I 0 /85．两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过。

当其中一偏振片慢慢转动1800时透射光强度发生变化为： [ ](A) 光强单调增加。

(B) 光强先增加，后有减小至零(C) 光强先增加，后减小，再增加(D) 光强先增加，然后减小，再增加，再减小至零6．一束自然光自空气射向 一块平板玻璃（如图），设入射角等于布儒斯特角i 0 ，则在界面2的反射光 [ ](A) 是自然光(B) 是完全偏振光且光矢量的振动方向垂直入射面 (C) 是完全偏振光且光矢量的振动方向平行入射面(D) 是部分偏振光7．一束单色平面偏振光，垂直投射到一块用方解石（负晶体）制成的四分之一波片（对投射光的频率）上，如图所示，如果入射光的振动面与光轴成450角，则对着光看从波片射出的光是(A) 逆时针方向旋转的圆偏振光(B) 逆时针方向旋转的椭圆偏振光(C) 顺时针方向旋转的圆偏振光(D) 顺时针方向旋转的椭圆偏振光8(A) 线偏振光 (B) 部分偏振光(C) 和原来旋转方向相同的圆偏振光(D) 和原来旋转方向相反的圆偏振光9（对投射光的频率）上，如图所示 成300角，则对着光看从波片射出的光是(A) 逆时针方向旋转的圆偏振光(B) 逆时针方向旋转的椭圆偏振光(C) 顺时针方向旋转的圆偏振光(D) 顺时针方向旋转的椭圆偏振光10．一束单色线偏振光其偏振化方向与1/4波片的光轴夹角α =π/4。

(2)由 ，得到 ，即若欲使光轴向上、向下各偏移5mm，平板应正、反转过0.25rad角度.
8.有一等边折射三棱镜，其折射率为1.65，求1)光线经该棱镜的二个折射面折射后产生最小偏角时的入射角；2)最小偏角值。
解：
（1）如上图，因为仅当 时，才产生最小偏向角，由公式 ，可得I1=55.6度
（2）如上图，根据折射定律，可得最小偏向角与 ， 的关系 ，把 ， 带入上式，可解得最小偏向角δm=51.2度。
9.一正薄透镜将物体成像于屏幕上时，测得其放大率β=－3×， 而当透镜向物体移近180mm时，屏上像的放大率为－4×，问该透镜的焦距为多少？
解：由 ，其中 为物体移动的距离，所以该透镜的焦距 mm， mm
该系统的焦距为2160mm
11.一焦距为10cm的正薄透镜在某一共轭距时，二个成清晰像的透镜位置相距15cm； 现若将共轭距加倍，问此时能成清晰像的二个透镜位置相距多少？
解：
2.一块厚度为15mm的平凸透镜放在报纸上，当平面朝上时， 报纸上的文字的虚像在平面下10mm处；当凸面朝上时，像的放大率为β=3，求透镜的折射率和凸面的曲率半径。
解：
26.某望远镜物镜由正、负分离的二个薄透镜组组成，已知 ，求其焦距。若用此望远镜来观察前方200m处的物体时，仅用第二个负透镜组来调焦以使其像仍位于物镜的原始焦平面上，问该镜组应向什么方向移动多少距离？此时物镜的焦距为多少？
解: 由薄透镜的物象位置关系
（1）l’=-250代入 得l=-60.607mm
4.有一实物被成一实像于薄透镜后300mm处时，其放大率正好为1倍。问放大率为50倍时，实像应位于透镜后什么位置？
解：由薄透镜的物象位置关系 和 。
由 和 ，解得焦距 mm;

第四章习题4.1 若光波的波长宽度为λΔ，频率宽度为νΔ，试证明：λλννΔΔ=。

设光波波长为nm 8632=.λ，nm 8-10⨯2=λΔ，试计算它的频宽νΔ。

若把光谱分布看成是矩形线型，那么相干长度?=c l证明：参阅苏显渝，李继陶《信息光学》P349，第4.1题答案。

421.510c λνλ∆∆==⨯赫，32010()c c cl ct m ν===⨯∆4.2 设迈克尔逊干涉仪所用的光源为nm 0589=1.λ，nm 6589=.2λ的钠双线，每一谱线的宽度为nm 010.。

（1）试求光场的复自相干度的模。

（2）当移动一臂时，可见到的条纹总数大约为多少？（3）可见度有几个变化周期？每个周期有多少条纹？ 答：参阅苏显渝，李继陶《信息光学》P349，第4.2题答案。

假设每一根谱线的线型为矩形，光源的归一化功率谱为 ()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G式中12ννν-=∆，复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆，故第一个因子是τ的慢变化非周期函数，第二个因子是τ的快变化周期函数。

相干时间由第一个因子决定，它的第一个零点出现在δντ1=c 的地方，c τ为相干时间，故相干长度δλλδλλδντ22≈===cc l c c 。

（2）可见到的条纹总数589301.05893====δλλλcl N （3）复相干度的模中第二个因子的变化周期ντ∆=1，故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N4.3假定气体激光器以N 个等强度的纵模振荡，其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ 式中，νΔ是纵模间隔，ν为中心频率并假定N 为奇数。

• 上式分母中的a′相对于x′而言，是一个很小的值， 可以略去。
• 放大镜放大率的公式，通常采用以下形式
M 250 f'
• 放大镜的放大率仅由放大镜的焦距f ′ 所决定，焦 距越大则放大率越小。
§4-3 目 镜
放大镜是一种通过直接放大实物达到增大视角的助视仪器。下面将介绍 一种放大像的助视仪器——目镜。 一、目镜
• 由于场镜的物为虚物，所以这种目镜无法对物镜所成的像进行测量。
• 此目镜的视角较大（可达400），在250范围内像更清晰。而且结构 紧凑，适用于生物显微镜。
2、冉斯登目镜 1
Q 'Q
2
⑴ 结构：如图示 3
⑵ 特点：
F2 F
o1
• 场镜、视镜均为同种材
3
F1' 3
o2
2
2
料的平凸透镜，二镜凸 面相向，平面朝外。
网膜 脉络膜 黄斑中心凹
前室
晶状体
盲斑
总能将像成在网膜上。
后室
角膜和晶状体之间的空间称为前室；充满1.336的水状液；
晶状体和网膜所包围的空间称为后室;充满1.336的玻状体
人眼的构造剖视图
瞳孔 虹膜 角膜
1.376
前室
1.336
晶状体
巩膜
网膜 脉络膜 黄斑中心凹
视轴
光轴
盲斑
后室 1.336
眼睛的像方节点与中心凹的连线为眼睛的视轴, 在观察物 体时眼睛本能地把物体瞄准在这根轴上。
x'
f1' f1'
• 物镜的像被目镜放大，其放大率为
Me
250 f2 '
• 式中： f2' 为目镜的焦距。由此，显微镜系统的

解：设能看见 个亮纹。从中心往外数第 个亮纹对透镜中心的倾角 ，成为第N个条纹的角半径。设 为中心条纹级数， 为中心干涉极小数，令 ( , )，从中心往外数，第N个条纹的级数为 ，则
，
两式相减，可得 ，利用折射定律和小角度近似，得 ，( 为平行平板周围介质的折射率)
对于中心点，上下表面两支反射光线的光程差为 。因此，视场中心是暗点。由上式，得 ，因此，有12条暗环，11条亮环。
解：由题意，得，波列长度 ，
由公式 ，
又由公式 ，所以频率宽度
。
某种激光的频宽 Hz，问这种激光的波列长度是多少？
解：由相干长度 ，所以波列长度 。
第二章光的干涉及其应用
在与一平行光束垂直的方向上插入一透明薄片，其厚度 ，若光波波长为500nm，试计算插入玻璃片前后光束光程和相位的变化。
解：由时间相干性的附加光程差公式
，所以
。
杨氏干涉实验中，若波长 =600nm，在观察屏上形成暗条纹的角宽度为 ，（1）试求杨氏干涉中二缝间的距离（2）若其中一个狭缝通过的能量是另一个的4倍，试求干涉条纹的对比度
解：角宽度为 ，
所以条纹间距 。
由题意，得 ，所以干涉对比度
若双狭缝间距为，以单色光平行照射狭缝时，在距双缝远的屏上，第5级暗条纹中心离中央极大中间的间隔为，问所用的光源波长为多少是何种器件的光源
解：由公式 ，所以
= 。
此光源为氦氖激光器。
在杨氏干涉实验中，照明两小孔的光源是一个直径为2mm的圆形光源。光源发光的波长为500nm，它到小孔的距离为。问两小孔可以发生干涉的最大距离是多少？
解：因为是圆形光源，由公式 ，
则 。
月球到地球表面的距离约为 km，月球的直径为3477km，若把月球看作光源，光波长取500nm，试计算地球表面上的相干面积。

1λ第四章 习题及答案 １。

双缝间距为１mm ，离观察屏１m ，用钠灯做光源，它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ，问两种单色光的第10级这条纹之间的间距是多少？ 解：由杨氏双缝干涉公式，亮条纹时：dDm λα=（m=0, ±1, ±2···） m=10时，nm x 89.511000105891061=⨯⨯⨯=-，nm x 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆２。

在杨氏实验中，两小孔距离为1mm ，观察屏离小孔的距离为50cm ，当用一片折射率1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ，试决定试件厚度。

21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆-3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前，在观察屏上观察到稳定的干涉条纹系。

继后抽去气室中的空气，注入某种气体，发现条纹系移动了２５个条纹，已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。

试求注入气室内气体的折射率。

0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ４。

垂直入射的平面波通过折射率为n 的玻璃板，透射光经透镜会聚到焦点上。

玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。

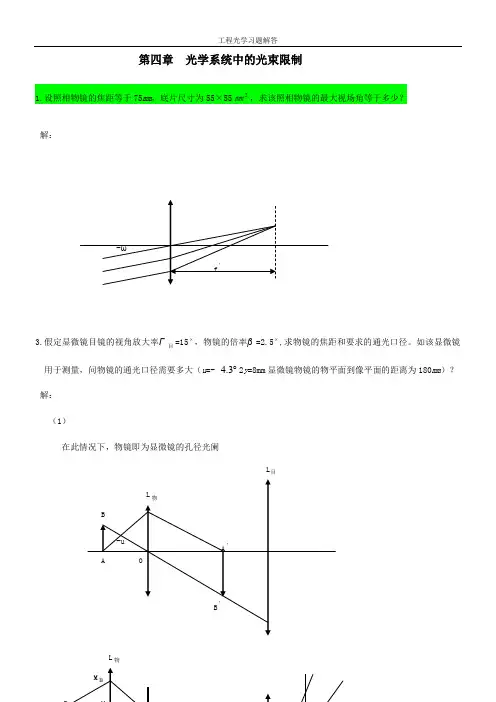
第四章 光学系统中的光束限制1.设照相物镜的焦距等于75mm ，底片尺寸为55×55㎜2，求该照相物镜的最大视场角等于多少？解：3.假定显微镜目镜的视角放大率Γ目=15⨯，物镜的倍率β=2.5⨯,求物镜的焦距和要求的通光口径。

如该显微镜用于测量，问物镜的通光口径需要多大（u =-︒3.42y =8mm 显微镜物镜的物平面到像平面的距离为180mm ）？ 解： （1）在此情况下，物镜即为显微镜的孔径光阑L 目（2）用于测量时，系统中加入了孔径光阑，目镜是视场光阑 由于u 已知，根据u 可确定孔径光阑的大小在中M M B B '∆ OA P AB A O M B A D B ‘‘’‘’‘孔=++21 答：物镜的焦距为36.73mm ，物镜的孔径为7.734mm ，用于测量时物镜孔径为15.726mm 。

4. 在本章第二节中的双目望远镜系统中，假定物镜的口径为30mm ，目镜的通光口径为20mm ，如果系统中没有视场光阑，问该望远镜最大的极限视场角等于多少？渐晕系数k =0.5的视场角等于多少？ 解：（1）A ’F 2出瞳L 目αω'F '1f ‘物L '-目fL ‘Z-uOB‘（2）答：极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。

5. 如果要求上述系统的出射瞳孔离开目镜像方主面的距离为15mm，求在物镜焦面上加入的场镜焦距。

解：D 物对场镜成像，位置为mm f l 1081-=-=’物对目镜有’目f l l 1112'2=- l mm l Z 15''2== mm f 18=‘目 可得 mm l 902=对场镜‘场f l l 1111'1=- 答：场镜焦距为54mm 。

6.思考题：当物点在垂直光轴方向上下移动时，系统的孔径光阑是否改变？答：当物点在垂直光轴方向上下移动时，孔径光阑对来自不同点的成像光束 口径限制最大，所以系统的孔径光阑不变。

2.单薄透镜成像时，若共轭距(物与像之间的距离)为250mm ， 求下列情况下透镜应有的焦距：1)实物，β=－4；2)实物，β=－1/4；3)虚物，β=－4；4)实物，β=4；5)虚物， β=4。

解：由薄透镜的物象位置关系''111fl l =-和l l '=β，共轭距mm l l 250'=-（1） 实物，β=－4。

由mm l l 250'=-和4'-==ll β,解得mm l 200'=，mm l 50-=,代入''111fl l =-得到焦距40'=f mm （2） 实物，β=－1/4。

由mm l l 250'=-和41'-==l l β,解得mm l 50'=，mm l 200-=,代入''111fl l =-得到焦距40'=f mm （3） 虚物，β=－4。

由mm l l 250'=-和4'-==ll β,解得mm l 200'-=，mm l 50=,代入''111fl l =-得到焦距40'-=f mm （4） 实物，β=4。

由mm l l 250'=-和4'==l l β,解得mm l 31000'-=，mm l 3250-=,代入''111fl l =-得到焦距11.111'=f mm （5） 虚物， β=4。

由mm l l 250'=-和4'==l l β，解得mm l 31000'=，mm l 3200=,代入''111fl l =-得到焦距11.111'-=f mm 。

3.一个f '＝80mm 的薄透镜当物体位于其前何处时，正好能在1)透镜之前250mm 处；2) 透镜之后250mm 处成像？ 解: 由薄透镜的物象位置关系''111fl l =- （1）l’=-250代入'111'l l f -=得l=-60.6061mm（2）l’=250代入'111'l l f -=得l=-117.647mm 4.有一实物被成一实像于薄透镜后300mm 处时，其放大率正好为1倍。

39
第2章 线性系统概论
以上结论推广到n个线性不变系统组成的串联系统，其
传递函数、调制传递函数和相位传递函数分别为
(2.3-3)
40
第2章 线性系统概论 2. 并联系统 图2.3-2所示为两个独立的线性不变系统的并联系统，
两独立系统的传递函数分别为
41
第2章 线性系统概论
图 2.3-2 并联复合系统示意图 42
状不变，其输出函数位置仅产生相同的移动，则称该系统为 位移不变系统，即若
L｛f(x)｝=g(x)
则
L｛f(x－x0)｝=g(x－x0)
(2.1-7)
式中: x0为实常数。
7
第2章 线性系统概论 一个系统既是线性的，又是位移不变的，则称为线性位
移不变系统，简称为线性不变系统。该系统用算符表示为
(2.1-8)
式中: x1和x2为实常数。
8
第2章 线性系统概论
2.2 线性系统分析方法
2.2.1 线性系统对基元函数的响应 1. 脉冲响应
当系统的输入是一个用δ函数表示的脉冲时，其对应的 输出称为系统的脉冲响应。如果线性系统对位于x=x0处的输 入脉冲δ(x－x0)的响应用h(x；x0)表示，即
(2.2-1)
性不变系统的脉冲响应可以简化为
(2.2-4a) 和
(2.2-4b)
11
第2章 线性系统概论
2. 复指数函数的响应 当线性不变系统的输入为复指数函数 出为
时，其输
(2.2-5)
式中： ξ0为一任意实参数。若输入为位移形式 (其中x0为实常数)，则由线性性质可得
(2.26)
12
第2章 线性系统概论 由位移不变性得
(2.2-7) 因此有

为拉普
拉斯算符。把式(3.1-2)代入式(3.1-3)，得到自由空间单色
光场满足的波动方程为
(3.1-4)
式中: k=2πν/c=2π/λ为波矢量的大小。该式称为亥姆霍
兹方程。这表明自由空间传播的任何单色光波的复振幅必然 满足亥姆霍兹方程。
6
第3章 傅里叶光学基础 3. 格林定理 格林定理是基尔霍夫衍射积分定理的数学基础。格林定
(3.1-10) 14
第3章 傅里叶光学基础
式中: Ω为Sε面对P点所张开的立体角。将式(3.1-10)代入
式(3.1-8)得
(3.1-11)
15
第3章 傅里叶光学基础 2. 基尔霍夫衍射公式 现在讨论无限大不透明屏幕上透光孔所引起的衍射问题。
衍射装置如图3.1-3所示，从点源P0发出的单色光波，传播并 通过不透明屏S′上的一个小孔Σ，在屏后的P点观察。假设 开孔Σ的线度、P0点和P点到孔Σ的距离远大于波长λ，P0和 P到Σ上任一点P1的矢径分别为r0和r。
根据1.1节的知识，光波场中P点在t时刻的光振动用复值标 量函数u(P,t)表示，对于单色光场，有
(3.1-2)
式中: U(P)为光波场中P点的复振幅； ν为光波的时间频率。
根据电磁场理论，光波场中的每一个无源点上，光振5
第3章 傅里叶光学基础
式中: c为光在真空中的速度;
(3.1-7)
10
第3章 傅里叶光学基础
在V′中,G和U都满足亥姆霍兹方程
把上式代入式(3.1-7)，得到
11
第3章 傅里叶光学基础 于是式(3.1-7)简化为 或
(3.1 -8) 12
第3章 傅里叶光学基础
在Sε面上，n与r处处反向，有

∴ 透镜为有效光阑，也是整个光具组的入射光瞳和 出射光瞳， 对主轴上P点的位置均为12cm，其大小 为6cm。
1 1 1 (2) . s s f 1 1 1 1 1 1 1 7 s f s 5 12 5 12 60 60 故：s 8.57（cm) 8.6 (cm) . 7
4.10 有一光阑直径为5cm，放置在薄透镜后3厘 米处，透镜焦距为5cm，孔径为6cm，现有一高为 3cm的物PQ置于透镜前12cm处，试求：（1）计算对 主轴上P点的入射光瞳和出射光瞳的大小和位置； （2）象的位置；（3）作光路图。 解：（1）首先计算光阑对其前面的透镜所成 的象的位置和大小 1 1 1 f 5 cm s 3 c m s s f
（3）注意光阑经透镜L成象时，其实图中F是象 方焦点，但PQ经透镜L成象时，F为物方焦点。
A´ Q O P F
s
A
光阑
2.5 7.5
6.25
P´ Q´ B´
B
若为凹透镜，则 s = - 3.53cm
4.11 图中 H H 为光具组的主点， F F 为焦点， E为对于物点P的入射光瞳，EO为其半径。 已知 EO ， 2 , HP 20 , HF 15 , HO 5 , H F 15 物长 PQ 0.5 （单位都是cm）。作光路图计算：（1） 像的位置；（2）像长；（3）入射孔径角；（4）对 P点的出射光瞳半径和出射孔径角。
1 1 1 s s f
1 1 1 5 1 1 2 1 0 0 f近 0 0
1 0 0 f近 1 .9 6 1 c m 5 1
3 0 0 f 1 . 9 8 7 c m 远 1 5 1

高等光学第4-5章习题答案第四章标量衍射理论基础4.1证明（4-21）式所示的索末菲辐射条件成立。

证明：球面2S是中心位于1S面上的发散球面波的波面，假定2S面上的光场分布表示为rjkr)exp(=U式中r表示产生发散球面波的点光源到球面2S上任意一点的距离。

1exp()cos()cos(,)r jkrjkn r n r r r∂∂∂∂===−∂∂∂∂U U Un,r n r当∞→R时，有∞→r，所以这时有1),cos(≈rn2)exp()exp(1rjkrjkrjkrrjkjkn−≅−−=−∂∂UUU当∞→R时，上式分母中的r可用R来代替，于是2exp()1lim lim lim(cos sin)R R RjkrR jk R kr j krn R R→∞→∞→∞∂−=−=−+∂UUlim0jkrReR→∞=−=4.2 参考图4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即010110101exp()exp()()jkr jkrPr r+=+G(1)证明+G的法线方向的导数在孔径平面上为零。

(2)利用这个格林函数，求出用孔径上的任意扰动来表示()pU的表达式，要得到这个结果必须用什么样的边界条件。

(3)利用(2)的结果，求出当孔径被从2P点发散的球面波照明时()pU的表达式证明: 下面是教材中图4-8（1）)(1P +G 由两项迭加而成，它们分别表示从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球面波。

孔径平面1S 上任一点1P 的+G 值为010101011~)~exp()exp()(r r jk r jkr P +=+G （P4.2-1） 1()P +G 的法向导数为0101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n −+ −=∂∂+ （P4.2-2） 对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n −= 0101~r r = （P4.2-3）将以上关系式代入（P4.2-2）式，得到0n+∂=∂G （P4.2-4） （2）根据（4-22）式，观察点0P 的光扰动可以用整个平面1S 上的光扰动U 和它的法向导数来表示∫∫∂∂−∂∂=1d 41)(0S s n n P G U G U U π（P4.2-5） 由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式一同代入（P4.2-5）式，得到∫∫∫∫∂∂=∂∂=+11d )exp(21d 41)(01010S S s r jkr ns G n P U U U ππ（P4.2-7）为了将上式所表示的结果进一步简化，根据孔径Σ上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径Σ上，场分布的法向导数n U ∂∂与不存在衍射屏时的值完全相同。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

五年高考三年联考绝对突破系列新课标：选修3-4光学光的波动性以及光的粒子性三部分,高考对本考点的考查一般以选项题的形式出现，重点放在考查光学一些重要的规律和概念上，注重课本，加强理解；“考课本”、“不回避陈题”是高考对光学命题的特点。

“联系实际、联系生活、联系高科技”已成为高考命题的新趋向；也是这几年光学命题的热点．目前高考中几何光学已淡化了“像”的概念，侧重于“光路”的考查（折射、全反射、棱镜等），一般是考查光线的去向的定性分析和定量计算问题；同时几何光学还常与力学中的直线运动、平抛运动、圆周运动、万有引力定律等相结合命题，考查学生的分析综合能力，估计以后高考试题不会有太大的变化，但会加强对光学的物理规律的理解和对物理现象、物理情景的分析能力的考查。

光的波动内容近两年命题频率较高，对光的波动性进行考查，主要是以干涉和衍射以及电磁波谱知识为要点,考查波动光学的一些初步理论、以及建立这些理论的实验基础和一些重要的物理现象；尤其是波动光学近年新增知识点有“双缝干涉的条纹间距与波长的关系”、“光的偏振现象”、“物质波”、“激光的特性及应用”等也在高考中有所体现．光的粒子性主要考查光电效应规律理解和爱因斯坦光电效应方程的熟练应用．第一部分五年高考题荟萃两年高考·精选（2008～2009）考点1 光的折射和全反射1.（09·全国卷Ⅰ·15）某物体左右两侧各有一竖直放置的平面镜，两平面镜相互平行，物体距离左镜4m，右镜8m，如图所示，物体在左镜所成的像中从右向左数的第三个像与物体的距离是（ B ）A．24mB．32mC．40mD．48m解析：本题考查平面镜成像.从右向左在左镜中的第一个像是物体的像距离物体8cm,第二个像是物体在右镜所成像的像,第3个像是第一个像在右镜中的像在左镜中的像距离物体为32cm.2.（09·全国卷Ⅱ·21）一玻璃砖横截面如图所示，其中ABC 为直角三角形（AC 边末画出），AB 为直角边∠ABC=45°；ADC 为一圆弧，其圆心在BC 边的中点。

第一章测试1【判断题】(10分)规范的光学工程制图在光电领域设计及生产中非常重要。

A.错B.对2【多选题】(10分)光学工程制图标准对哪些方面提出要求A.图形画法B.线条形式C.尺寸标注D.图纸格式3【单选题】(10分)以下哪个不属于标题栏上应有的内容A.材料名称B.图纸编号C.单位名称D.制图者住址4【单选题】(10分)以下哪个比例代表图中图形要素为实物的一半？A.1:2B.1:1C.2:1D.1.5：15【判断题】(10分)实物大小不是由图中所标注的尺寸所确定的A.对B.错6【单选题】(10分)粗实线一般应用在以下哪种场合A.过渡线B.可见轮廓线C.中断线D.尺寸线7【多选题】(10分)细点画线一般应用在哪种场合A.对称中心线B.轴线C.过渡线D.剖面线8【判断题】(10分)每个尺寸一般只标注一次，并应标注在最能反应该结构特征的视图上。

A.错B.对9【判断题】(10分)图样中的尺寸，以毫米为单位，如采用其它单位时，不需要注明单位名称。

A.对B.错10【单选题】(10分)尺寸标注时以下哪个缩写词代表厚度A.E QSB.S RC.RD.t第二章测试1【多选题】(10分)常用的基本视图有哪三个A.俯视图B.左视图C.右视图D.主视图2【多选题】(10分)按剖切范围的大小来分，剖视图可分为A.全剖视图B.局部剖视图C.半剖视图3【多选题】(10分)基本视图的“三等关系”为A.宽相等B.长对正C.高平齐4【多选题】(10分)按剖切面来分，剖视图可分为A.斜剖B.旋转剖C.单一剖D.阶梯剖5【多选题】(10分)剖视图的标注包括三部分内容A.字母B.箭头C.剖切线D.剖切面6【判断题】(10分)省略一切标注的剖视图，说明它的剖切平面通过机件的对称平面A.错B.对7【判断题】(10分)重合断面图画在视图上的，其轮廓线用粗实线绘制A.错B.对8【多选题】(10分)断面图用来表达零件的某部分的断面形状，剖面可分为A.引出断面B.移出断面C.重合断面9【单选题】(10分)当机件外形比较简单,内形比较复杂而且又不对称时,常采用（）来表达.A.全剖视图B.半剖视图C.局部剖视图10【判断题】(10分)用剖切面局部地剖开机件所得到的剖视图称为半剖视图A.错B.对第三章测试1【判断题】(10分)对标准件需要单独绘制零件图。

1. 证：设两个均匀介质的分界面是平面，它们的折射率为n 1和n2。

光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。

为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，O O '是他们的交线，则实际 光线在界面上的反射点C 就可由费马原理来确定（如右图）。

（1）反正法：如果有一点C '位于线外，则对应于C '，必可在O O '线上找到它的垂足C ''.由于C A >C A ,B C >B C ,故光谱B C A '总是大于光程B C A ''而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。

（2）在图中建立坐oxy 标系，则指定点A,B 的坐标分别为（y x 11,）和（y x22,），未知点C 的坐标为（0,x ）。

C 点在B A '',之间是，光程必小于C 点在B A ''以外的相应光程，即xx x 21<<，于是光程ACB为：y x x n y x x n n n n 2211221221111)()(+-++-=+=根据费马原理，它应取极小值，即：i i 11='，∴0)(1=ACB n dxd取的是极值，符合费马原理。

故问题得证。

0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n CB B C AC C A n y x x x x n y x x x x n ACB n dx d2.(1)证：如图所示，有位于主光轴上的一个物点S 发出的光束 经薄透镜折射后成一个明亮的实象点S '。

由于球面AC 是由S 点 发出的光波的一个波面，而球面DB 是会聚于S '的球面波的一个 波面，固而SB SC =,BS D S '='.又光程FD EF n CE CEFD ++=，而光程AB n AB =。