2008-2009(1)自动控制原理试题B卷

自动控制原理考试题及答案b卷一、单项选择题（每题2分，共20分）1. 自动控制系统中，开环传递函数G(s)H(s)的极点是系统（）。

A. 稳定性的决定因素B. 稳态误差的决定因素C. 动态性能的决定因素D. 稳态性能的决定因素答案：A2. 一个二阶系统，其阻尼比ζ=0.5，自然频率ωn=4rad/s，其过渡过程是（）。

A. 欠阻尼B. 临界阻尼C. 过阻尼D. 等阻尼答案：A3. 在控制系统中，若系统开环传递函数为G(s)，则闭环传递函数为（）。

A. 1/G(s)B. G(s)/[1+G(s)]C. 1/[1+G(s)]D. G(s)/[1-G(s)]答案：C4. 线性时不变系统的稳定性可以通过（）来判断。

A. 劳斯-赫尔维茨判据B. 奈奎斯特判据C. 波特判据D. 根轨迹法答案：B5. 对于一个单位反馈系统，其开环传递函数为G(s)，闭环传递函数为T(s)，则（）。

A. T(s) = G(s)B. T(s) = 1/[1+G(s)]C. T(s) = G(s)/[1+G(s)]D. T(s) = 1/G(s)答案：C6. 根轨迹法中，根轨迹的分支数等于（）。

A. 开环传递函数的极点数B. 开环传递函数的零点数C. 开环传递函数的极点数减去零点数D. 开环传递函数的极点数加上零点数答案：C7. 奈奎斯特判据中，系统的开环传递函数G(s)H(s)在复平面的右半部分有P个极点，则闭环系统将有（）个极点在右半平面。

A. PB. P-NC. N-PD. N答案：B8. 对于一个二阶系统，其阻尼比ζ=0.5，自然频率ωn=4rad/s，其过渡过程的调节时间大约为（）。

A. 2/ωnB. 4/ωnC. 2/ζωnD. 4/ζωn答案：D9. 系统的时间常数τ与系统的自然频率ωn之间的关系是（）。

A. τ = 1/ωnB. τ = ωnC. τ = 2/ωnD. τ = ωn^2答案：A10. 对于一个单位反馈系统，其开环传递函数为G(s)=1/s(s+1)(s+2)，其闭环传递函数为（）。

01．分析定值控制系统时，常用的典型输入信号是（ ） A.脉冲函数B.斜坡函数C.阶跃函数D.正弦函数02．如下传递函数所表示的系统为非最小相位系统的是（ ） A ．()()1121-+s T s T K B ．()1+Ts s K C ． ()()()11121+++s T s T s K τ D ．()()1121++s T s T K03．单位负反馈控制系统的开环传递函数为()s G K ，则其闭环传递函数为（ ） A ．()()()s G s G s K K -=Φ1 B ．()()s G s K +=Φ11 C ．()()()s G s G s K K +=Φ1 D ．()()s G s K -=Φ1104．开环传递函数()()()∏∏==++=n i i mj j K p s s z s K s G 11ν，则其根轨迹条数和渐近线条数分别为（ ）A ．n +ν和m n ++νB ．n +ν和m n --νC ．n -ν和m n -+νD ．n +ν和m n -+ν 05．一阶系统G (s )=1+Ts K的放大系数T 愈小，则系统的动态输出响应（ ） A ．不变B ．越快C ．越慢D ．不定06．二阶系统当0<ζ<1时，如果增加ζ，则输出响应的最大超调量%σ将（ ） A ．增加B ．减小C ．不变D ．不定07．自动控制系统稳定的充要条件是闭环传递函数在（ ） A ．S 平面左半平面无极点 B ．S 平面右半平面无极点 C ．S 平面左半平面无零点D ．S 平面右半平面无零点08．某最小相位系统稳定，则其相角裕量（ ） A ．0=γ B ．0>γ C ．0<γ D ．不定09．一阶系统12+Ts 的单位阶跃响应为（ ） A ．⎪⎭⎫ ⎝⎛++T te 12B ．⎪⎭⎫ ⎝⎛--T t e 12C ．⎪⎭⎫ ⎝⎛-+T te 12D ． ⎪⎭⎫ ⎝⎛+-T t e 1210．超前校正装置最大超前角的频率是（ ） A ．21ωωω+=m B ．()2121ωωω+=m C ．21ωωω=m D ．()2121ωωω=m 二、系统微分方程组如下：()()()12i o x t u t u t =-，()()()2212dx t x t x t dt+=，()()()322o x t x t u t =-，()du t间变量。

东北大学考试试卷（B 卷）2008—2009 学年第 1 学期 课程名称： 自动控制原理 一、（10分）简要回答下列问题（每小题各5分）。

1. 简述自动控制系统一般是由那些基本环节组成，并画出控
制系统结构框图。

2. 简述什么是无差系统。

得分
二、（10分）控制系统如图1所示，其中)(s W c 为补偿校正装置，
试求该系统扰动误差传递函数)()(s N s X c ，并从理论上说明如何设计补偿校正装置)(s W c 可以使系统补偿后的扰动误差为零。

图1 题二图
得分
三、（10分）已知某三阶单位负反馈系统具有一个有限零点为
1.5-，三个极点分别为6.1
2.1j ±-和 1.49-，且系统传递函数根的
形式放大系数为4。

试求系统在单位阶跃函数作用下，系统的动态性能指标超调量%σ、调整时间5s t ±（%）和峰值时间m t 。

得分
四、（14分）设单位负反馈系统的开环传递函数为
)
2)(1()(++=
s s s k s W g
k
1． 绘制闭环系统根轨迹（写出具体绘制过程并标出关键点）； 2． 试确定系统呈单调动态响应以及衰减振荡动态响应的g k 取
值范围。

得分
r
五、（20分）一单位负反馈最小相位系统的开环对数幅频特性
如图2所示，其中虚线为校正前特性，实线为加入串联校正装置后的特性。

1． 试写出串联校正装置的传递函数，并说明此校正主要是利
用该装置的什么特性；
2． 求校正后系统的相位裕量()c γω。

图2 题五图
得分。

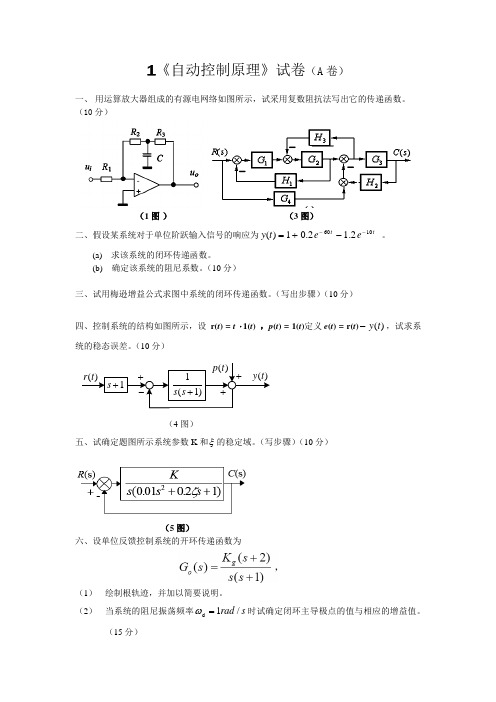
1《自动控制原理》试卷（A 卷）一、 用运算放大器组成的有源电网络如图所示，试采用复数阻抗法写出它的传递函数。

（10分）（1图 ）（3图）二、假设某系统对于单位阶跃输入信号的响应为t te et y 10602.12.01)(---+= 。

(a) 求该系统的闭环传递函数。

(b) 确定该系统的阻尼系数。

（10分）三、试用梅逊增益公式求图中系统的闭环传递函数。

（写出步骤）（10分）四、控制系统的结构如图所示，设 r(t ) = t ⋅ 1(t ) ，p (t ) = 1(t )定义e (t ) = r(t ))(t y -，试求系统的稳态误差。

（10分）)(t p )(t r -++)(t y 1+s )1(1+s s +（4图）五、试确定题图所示系统参数K 和ξ的稳定域。

（写步骤）（10分）（5图）六、设单位反馈控制系统的开环传递函数为（1） 绘制根轨迹，并加以简要说明。

（2） 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。

（15分）七、最小相位系统的开环对数幅频特性的渐近线如图所示，确定系统的开环传递函数。

（10分）八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示，其中Lo(ω)为校正前特性，L开(ω)为校正后特性。

（1）试作出校正装置的对数幅频特性Lc(ω)(折线)；（2）试写出校正装置的传递函数Gc(s);（3）计算校正后系统的相位裕度γ。

（15分）cp为s右半平面上的开环根的个数，v为开九、设开环系统的奈氏曲线如下图所示，其中，环积分环节的个数，试判别闭环系统的稳定性。

(10分)（a）(b)2《自动控制原理》试卷（B 卷）一、 求下图所示系统的传递函数)(/)(0s U s U i 。

（10分）（1图） （3图）二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。

(a) 求该系统的闭环传递函数。

1《自动控制原理》试卷（A 卷）一、 用运算放大器组成的有源电网络如图所示，试采用复数阻抗法写出它的传递函数。

（10分）（1图 ）（3图）二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。

(a) 求该系统的闭环传递函数。

(b) 确定该系统的阻尼系数。

（10分）三、试用梅逊增益公式求图中系统的闭环传递函数。

（写出步骤）（10分）四、控制系统的结构如图所示，设 r(t ) = t ⋅ 1(t ) ，p (t ) = 1(t )定义e (t ) = r(t ))(t y -，试求系统的稳态误差。

（10分）（4图）五、试确定题图所示系统参数K 和ξ的稳定域。

（写步骤）（10分）（5图）六、设单位反馈控制系统的开环传递函数为（1） 绘制根轨迹，并加以简要说明。

（2） 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。

（15分）七、最小相位系统的开环对数幅频特性的渐近线如图所示，确定系统的开环传递函数。

（10分）八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示，其中Lo(ω)为校正前特性，L开(ω)为校正后特性。

（1）试作出校正装置的对数幅频特性Lc(ω)(折线)；（2）试写出校正装置的传递函数Gc(s);（3）计算校正后系统的相位裕度γ。

（15分）cp为s右半平面上的开环根的个数，v为开九、设开环系统的奈氏曲线如下图所示，其中，环积分环节的个数，试判别闭环系统的稳定性。

(10分)（a）(b)2《自动控制原理》试卷（B 卷）一、 求下图所示系统的传递函数)(/)(0s U s U i 。

（10分）（1图） （3图）二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。

(a) 求该系统的闭环传递函数。

(b) 确定该系统的阻尼系数。

（10分）三、系统的信号流图如图所示，求输出C （S ）的表达式。

经典控制理论习题解答第一章考试题库1、重庆三峡学院04至05学年度第2 期自动控制原理课程考试试题册A卷（02级电信)一、填空（本题共20 分，共10小题，每题各2 分）l．自动控制是。

2．反馈控制的基本原理是。

3．一个反馈控制系统通常由、、、、、等几个部分组成。

4．按给定量的运动规律，控制系统可分为、、。

5．系统的频率特性是指。

6．一个设计性能良好的控制系统，应当满足、、三个方面的要求。

7．根轨迹的模值方程为 ,相角方程为。

8．非线性特性的描述函数定义为。

9．对于高阶系统，系统主导极点是指。

10．采样系统的脉冲传递函数定义为：。

二、（本题共15 分）某工业过程温度控制系统如图所示，电位器上设定的电压u r是系统的输入量，箱体内液体的实际温度θ为输出量，插入箱体内的热电偶的输出Uθ与θ成正比。

试分析该系统的工作原理并画出方框图。

二、（本题共15分）测得某二阶系统的单位阶跃响应c(t)如图所示，已知该系统具有单位负反馈，试确定其开环传递函数。

四、（本题共15 分，共2小题）1）设某系统的特征方程式为：，试用劳斯稳定判据判别系统的稳定性。

2）下图表示开环传递函数G(s)的奈奎斯待图，P为G(s)的正实部极点数目，判定闭环系统的稳定性。

（a）（b）五、（本题共15分）已知最小相位开环系统的渐近对数幅频特性如图所示。

试求取系统的开环传递函数。

六、（本题共20分）已知单位反馈系统的开环传递函数为：试设计一个串联超前校正环节，使系统的相角裕量不小于45度，截止频率不低于50rad／s。

自动控制原理课程考试试题A卷评分标准一、（本题共20 分，共10小题，每题各2 分）1、在没有人直接干预的情况下，通过控制装置使被控对象或过程自动按照预定的规律运行，使之达到一定的状态和性能。

2、检测误差，用于纠正误差。

3、控制器、测量装置、比较装置、参考输入变换装置、执行机构、被控对象。

4、随动控制系统、定值控制系统、程序控制系统5、线性定常系统，在正弦信号作用下，输出的稳态分量与输入的复数比。

⾃动控制原理试题库套和答案详解完整版⾃动控制原理试题库套和答案详解⼀、填空（每空1分，共18分）1．⾃动控制系统的数学模型有、、、共4种。

2．连续控制系统稳定的充分必要条件是。

离散控制系统稳定的充分必要条件是。

3．某统控制系统的微分⽅程为：dtt dc )(+(t)=2r(t)。

则该系统的闭环传递函数Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是阶型系统；其开环放⼤系数K= 。

5则该系统开环传递函数ωC = 。

67系统)()1()1()(10210T T e Z Z e Z G -----=（单位反馈T=）当输⼊r(t)=t 时.该系统稳态误差为。

求：（（2（1（2（3五.已知某系统L （ω）曲线，（12分）（1）写出系统开环传递函数G （s ）（2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=，⼀. 2. 微分环节的传递函数为 3.并联⽅框图的等效传递函数等于各并联传递函数之 4.单位冲击函数信号的拉⽒变换式5.系统开环传递函数中有⼀个积分环节则该系统为型系统。

6.⽐例环节的频率特性为。

7. 微分环节的相⾓为。

8.⼆阶系统的谐振峰值与有关。

9.⾼阶系统的超调量跟有关。

10. 在零初始条件下输出量与输⼊量的拉⽒变换之⽐，称该系统的传递函数。

⼆．试求下图的传第函数(7分)10K 值s T s s s G 25.0,)4(1)(=+=五．在系统的特征式为A （s ）=6s +25s +84s +123s +202s +16s+16=0，试判断系统的稳定性（8分） .⼋．设采样控制系统饿结构如图所⽰，其中试判断系统的稳定性。

（10分）九．试绘制K 由0 ->+值范围。

(15分) ⼀、填空题：(每空分，共15分)1.当扰动信号进⼊系统破坏系统平衡时，有重新恢复平衡的能⼒则该系统具有。

第一学期《自动控制原理》试卷（自03-1、2、3、4用）1（10分）某复合控制系统如图1所示： ⑴ 求取系统的传递函数()()Y s U s ；⑵ 要使系统对于任何输入无静差，应如何选取()k s 。

图12（20分）系统结构如图2所示，若要求系统在输入()1()r t t t = 作用下的静态误差0.1ss e ≤，试确定参数1k 的取值范围。

图23（15分）系统结构如图3所示，试确定阻尼比0.6ξ=时的f k 值，并求出这时系统阶跃响应的调节时间s t 和超调量%∂。

图34（15分）系统结构如图4所示，绘出该系统以K 为参变量的根轨迹，并指出系统稳定的K 值范围。

图45（10分）单位反馈系统的开环传递函数()()()1211kG s s T s T s =++ （120,0,0T T k >>>），画出()G s 对应的Nyquist 曲线，并用Nyquist 稳定判据给出闭环系统稳定的条件。

6（20分） 已知系统串联校正前后的对数幅频特性折线图L w 和L w k 如图5所示：图5⑴ 绘制出校正装置的对数幅频特性折线图L w c ，求出校正装置的传递函数()c W s ，并确定采用的为何种校正装置.⑵ 确定校正前及校正后系统的开环传递函数()W s 、()k W s .7（10分）离散系统如图6所示，已知10,0T K >>，T 为采样周期，试证明系统的稳定条件是112(1)01T T T T eK e--+<<-图6内蒙古科技大学2005-2006春学期试题课程名称：自动控制原理 课程号：050512、050529 使用专业：自动化、测控一. 求取图1所示系统的传递函数Y(S)/U(S)？（10分）图1二. 设有一系统的闭环传递函数为222()()2nn nC s R s s s ωξωω=++，为了使系统对单位阶跃输入的响应有约4.3%的超调量和2秒的过渡过程时间（允许误差范围为2%±），试求n ξω和值应等于多大？（10分）三. ①线性系统稳定的充分必要条件是什么？（5分）②已知一控制系统如图2所示，试确定使系统稳定的K 的取值范围？（10分）图2四. 应用根轨迹法确定使图3所示系统阶跃响应无超调的K 值范围？（15分）图3五. 对于图4所示系统，试求r （t ）= 4 + 6t ，f （t ）= -1（t ）时系统的静态误差ess ？（20分）图4六. 已知某最小相位系统的开环折线对数幅频特性如图5所示图5①求出系统的开环传递函数G 0（S ） （7分） ②画出开环相频特性曲线 （8分）③求出截止角频率ωc （5分） 七. 图6所示采样系统的()()()0.3680.26410.368z G z z z +=--，试判断该采样系统的稳定性？（10分）图6内蒙古科技大学2006/2007学年第1学期《自动控制原理》（A 卷）考试试题 课程号：05106207考试方式： 闭卷使用专业、年级：自动化04、电气04、仪表04 任课教师：崔桂梅、李爱莲、刘慧博 考试时间：2007年1月11日一、判断对错（10小题，每小题2分，共20分）1对1对于欠阻尼的二阶系统：（1）阻尼系数ξ保持不变，无阻尼自振角频率n ω越大，系统超调量pσ越大。