奇妙的图形密铺
教学目标
1.通过观察生活中常见的密铺图案,初步理解密 铺的含义。 2.通过拼摆各种图形,认识一些可以密铺的平面 图形,初步探索密铺的特点,在探究规律的过程 中培养同学们的观察、猜测、验证、推理和交流 的能力。 3.通过欣赏密铺图案和设计简单的密铺图案,体 会到图形之间的转换,充分感受数学知识与生活 的密切联系,经历欣赏数学美、创造数学美的过 程。
Please Criticize And Guide The Shortcomings
演讲人:XXXXXX 时 间:XX年XX月XX日
埃 舍 尔 的 作 品
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
感谢聆听
不足之处请大家批评指导
正三角形能密铺Biblioteka 五边形不 能密铺你知道吗?
密铺图形奇妙而美丽,古往今来,不少艺术 家都在这方面进行过研究,其中最富有趣味的是 荷兰艺术家埃舍尔,他到西班牙旅行参观时,对 一种名为阿罕伯拉宫的建筑有很深刻的印象,并 得到启发,创造了各种并不局限于几何图形的密 铺图案。这些图案包括鱼、青蛙、狗、人、蜥蜴, 甚至是他凭空想象的物体。他创造的艺术作品, 结合了数学与艺术,给人留下深刻印象,更让人 对数学产生另一种看法。
这些图片分别是由哪些图形拼成的 ?
这些平面图形在拼的时候有没有什么共
同的地方?
无空隙 不重叠
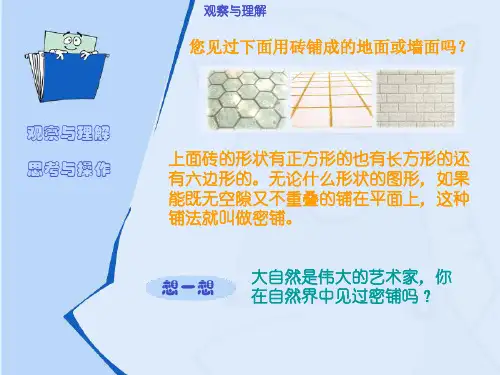
像这样把一种或几种平面图形既无空隙,又 不重叠地铺在平面上,这种铺法数学上称它为 “密铺”
下面的三幅图,可以看作是密铺吗?为 什么?