历年中国同欧洲各国进出口数据,完整版(100%真实统计数据)

二聚丙烯醛(稳定的)化学品安全技术说明书第一部分：化学品名称化学品中文名称：二聚丙烯醛(稳定的) 化学品英文名称：acrolein dimer(stabilized) 英文名称2：pyranaldehyde 技术说明书编码：2247CAS No.：100-73-2 分子式：C 6H 8O 2分子量：112.14第二部分：成分/组成信息有害物成分含量CAS No.第三部分：危险性概述健康危害：本品有毒。

其蒸气和烟雾对皮肤、眼睛和粘膜有刺激作用。

环境危害：对环境可能有危害。

燃爆危险：本品易燃，具刺激性。

第四部分：急救措施皮肤接触：脱去污染的衣着，用流动清水冲洗。

眼睛接触：提起眼睑，用流动清水或生理盐水冲洗。

就医。

吸入：迅速脱离现场至空气新鲜处。

保持呼吸道通畅。

如呼吸困难，给输氧。

如呼吸停止，立即进行人工呼吸。

就医。

食入：饮足量温水，催吐。

就医。

第五部分：消防措施危险特性：其蒸气与空气可形成爆炸性混合物，遇明火、高热能引起燃烧爆炸。

与氧化剂可发生反应。

容易自聚，聚合反应随着温度的上升而急骤加剧。

若遇高热，容器内压增大，有开裂和爆炸的危险。

有害燃烧产物：一氧化碳、二氧化碳。

灭火方法：消防人员须佩戴防毒面具、穿全身消防服，在上风向灭火。

尽可能将容器从火场移至空旷处。

喷水保持火场容器冷却，直至灭火结束。

处在火场中的容器若已变色或从安全泄压装置中产生声音，必须马上撤离。

灭火剂：雾状水、泡沫、干粉、二氧化碳、砂土。

第六部分：泄漏应急处理有害物成分 含量 CAS No.:二聚丙烯醛(稳定的) 100-73-2应急处理：迅速撤离泄漏污染区人员至安全区，并进行隔离，严格限制出入。

切断火源。

建议应急处理人员戴自给式呼吸器，穿防静电工作服。

不要直接接触泄漏物。

尽可能切断泄漏源。

防止流入下水道、排洪沟等限制性空间。

小量泄漏：用砂土吸收。

大量泄漏：构筑围堤或挖坑收容。

用泵转移至槽车或专用收集器内，回收或运至废物处理场所处置。

贵州省部分学校2025届高三上学期11月联考考试试题一、单选题（本大题共8小题）1．在等比数列{}n a 中，12a =，45678a a a a a =，则25a a +=（）A．36B．32C．16D．122．若复数()2i 1i z a a =+-+是纯虚数，则实数a =（）A．1B．1-C．1±D．03．已知直线1y kx =+与圆224x y +=相交于,M N 两点，若MN =，则k =（）A．12B．1C．D．24．高二年级进行消防知识竞赛，统计所有参赛同学的成绩，成绩都在[50,100]内，估计所有参赛同学成绩的第75百分位数为（）A．65B．75C．85D．955．记ABC V 的内角A ，B ，C 的对边分别是a ，b ，c ，已知3a =，2239b c c =++，ABC ∠的平分线交边AC 于点D ，且2BD =，则b =（）A．B．C．6D．6．2024年春节档贺岁片《热辣滚烫》《飞驰人生2》《熊出没·逆转时空》异常火爆，甲、乙等5人去观看这三部电影，每人只观看其中一部，甲、乙不观看同一部电影，则选择观看的方法有（）A．243种B．162种C．72种D．36种7．已知函数()()2log 41x f x x =+-x 的不等式()()22f x f x +>解集为（）A．2,23⎛⎫- ⎪⎝⎭B．211,232⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ ,C．211,,2322纟轹琪--È琪棼滕D．111,,222纟轹琪--È琪棼滕8．已知抛物线2:2E y x =，圆()()2200:11,,M x y N x y -+=为圆M 外一点，过点N 作圆M 的两条切线1l ，2l ，直线1l 与抛物线E 交于点()()1122,,,A x y B x y ，直线2l 与抛物线E 交于点()()3344,,C x y D x y ，，若22001x y +=，则1234y y y y =（）A．16B．8C．4D．1二、多选题（本大题共3小题）9．设离散型随机变量X 的分布列如表，若离散型随机变量Y 满足21Y X =-，则（）X01234P0.10.4x0.20.2A．0.2x =B．()2E X =，() 1.8D X =C．()2E X =，() 1.4D X =D．()3E Y =，()7.2D Y =10．已知一元二次不等式20ax bx c ++>的解集为M ，则下列说法正确的是（）A．不等式解集M =∅的充要条件为240a b ac <⎧⎨-≤⎩B．若111a b c a b c==，则关于x 的不等式21110a x b x c ++>的解集也为M C．若{}23M x x =-<<，则关于x 的不等式20cx bx a -+<的解集是1|3x x ⎧<-⎨⎩，或>D．若2b M x x a ⎧⎫=≠-⎨⎬⎩⎭，且a b <，则24a b c b a ++-的最小值为811．已知函数()f x ，()g x 的定义域均为R ，它们的导函数分别为'，()g x '，且()()25f x g x +-=，()()43g x f x --=，若+2是偶函数，则下列正确的是（）．A．()20g '=B．4为函数()f x 的一个周期C．()1f x +是奇函数D．()25g =，则()202412024k f k ==∑三、填空题（本大题共3小题）12．集合A 满足{}1,3**15,,A x y x N y N x ⎧⎫⊆=∈∈⎨⎬⎩⎭，则集合A 的个数有个.13．已知函数()()3,02,0x x f x f x x ⎧>⎪=⎨+≤⎪⎩，则31log 16f ⎛⎫=⎪⎝⎭．14．已知M 是椭圆22110x y +=上一点，线段AB 是圆()22:64C x y +-=的一条动弦,且AB =则MA MB ⋅的最大值为.四、解答题（本大题共5小题）15．在ABC 中，角,,A B C所对的边分别为,,a b c ，已知sin cos a B A =，角A 的平分线交边BC 于点D ，且1AD =.(1)求角A 的大小；(2)若BC =，求ABC 的面积.16．如图，在四棱锥P ABCD -中，底面ABCD 为梯形，//,AB CD CD BC ⊥，24,,AB CD BD BP PCD === 为等边三角形.(1)证明：⊥BC 平面PCD .(2)若ABD △为等边三角形，求平面PBD 与平面PAD 夹角的余弦值.17．篮球运动深受青少年喜爱，2024《街头篮球》SFSA 全国超级联赛赛程正式公布，首站比赛将于4月13日正式打响，于6月30日结束，共进行13站比赛.(1)为了解喜爱篮球运动是否与性别有关，某统计部门在某地随机抽取了男性和女性各100名进行调查，得到22⨯列联表如下：喜爱篮球运动不喜爱篮球运动合计男性6040100女性2080100合计80120200依据小概率值0.001α=的独立性检验，能否认为喜爱篮球运动与性别有关？(2)某校篮球队的甲、乙、丙、丁四名球员进行传球训练，第1次由甲将球传出，每次传球时，传球者都等可能将球传给另外三个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到.记甲第n 次触球的概率为n P ，则11P =.（i）证明：数列（ii）判断第24次与第25次触球者是甲的概率的大小.附：22()()()()()n ad bc a b c d a c b d χ-=++++.α0.10.050.010.0050.001x α2.7063.8416.6357.87910.82818．已知椭圆E ：221164x y +=，椭圆上有四个动点A ，B ，C ，D ，//CD AB ，AD 与BC相交于P 点.如图所示.(1)当A ，B 恰好分别为椭圆的上顶点和右顶点时，试探究：直线AD 与BC 的斜率之积是否为定值？若为定值，请求出该定值；否则，请说明理由；(2)若点P 的坐标为()8,6，求直线AB 的斜率.19．已知函数()1e ln -=-xf x a x ．(1)当1a =-时，求曲线()y f x =在()()1,1f 处的切线方程；(2)当0a >，若不等式()ln f x a a a ≥+恒成立，求a 的取值范围．参考答案1．【答案】A【详解】因为数列{}n a 为等比数列，所以45678a a a a a =化为31221311a q a q ⋅=⋅，解得1a q =，又因为12a =，所以2q =，所以112n nn a q a -=⋅=，所以4251143236a a a q a q +=⋅+⋅=+=.故选：A 2．【答案】B【详解】由()()22i 1i 11i z a a a a =+-+=-+-，根据题意可知210110a a a ⎧-=⇒=-⎨-≠⎩.故选：B 3．【答案】B【分析】先计算直线10kx y -+=到圆心O 的距离d ，然后根据勾股定理得到22144d MN +=，再代入条件即可解出2k ，从而得到k .【详解】如图所示：设坐标原点O 到直线10kx y -+=的距离为d ，则d =.设线段MN 的中点为P ，则MN OP ⊥，根据勾股定理，有22222144OMOP PMd MN ==+=+.由MN =22211144414d MN k =+=++，故21112k =+，解得21k =，故1k =.故选B.4．【答案】C【详解】因为2101a ⨯=，所以0.05a =.参赛成绩位于[50,80)内的频率为()100.010.0150.0350.6⨯++=，第75百分位数在[)80,90内，设为80y +，则0.030.15y =，解得y =5，即第75百分位数为85，故选：C.5．【答案】D【详解】因为3a =及2239b c c =++，可得222b a c ac =++，由余弦定理得2221cos 22a cb B ac +-==-，又由0πB <<，所以2π3B =，因为ABC ABD BCD S S S =+△△△，即11sin ()sin 22ac ABC BD a c ABD ∠=⋅+∠，解得6c =，由余弦定理得222263263cos633b π=+-⨯⨯⨯=，即b =故选：D．6．【答案】B【详解】先安排甲、乙两人，有23A 种方法，再安排其余3人，每人有3种安排方法，故共有23A 333162⨯⨯⨯=（种）方法.故选：B.7．【答案】C 【详解】因为()()()222241log 41log 41log 2log 2x xxxx f x x +=+-++-++()2log 22x x -=+由210x -≥可得1x ≤-或1x ≥，即函数()f x 的定义域为(][),11,-∞-+∞ ，因为()()()()22log 22log 22x x x x f x f x ---=+=+=，所以，函数()f x 为偶函数，任取1x 、[)21,x ∈+∞，且12x x >，则12222x x >≥，122x x +>，1224x x +>，令22x x u -=+，则()1212121212111122222222x x x xx x x x u u ⎛⎫⎛⎫⎛⎫-=+-+=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()12121212121222212222022x x x x x x x x x x x x +++---=--=>，即12u u >，所以，函数22x x u -=+在[)1,+∞上为增函数，又因为函数2log y u =在()0,∞+上为增函数，所以，函数()2log 22x xy -=+在[)1,+∞上为增函数，又因为函数y =[)1,+∞上为增函数，故函数()f x 在[)1,+∞上为增函数，由()()22f x f x +>可得()()22f x f x +>，可得221x x +>≥，解得2132x -<≤-或122x ≤<，因此，原不等式的解集为211,,2322纟轹琪--È琪棼滕.故选：C.8．【答案】C【详解】由题意()00,N x y ，且12,l l 都与抛物线有两个不同的交点，所以00x ≠，故设过点N 且与圆M 相切的切线方程为()00y y k x x -=-，即000kx y y kx -+-=，由题意得1=，整理得，()()220000022110x x k y x k y ---+-=（*），设直线12,l l 的斜率分别为12,k k ，则12,k k 是方程（*）的两个实根，故()()()20000121200000211,222y x y x k k k k x x x x x --+===---，由00202kx y y kx y x-+-=⎧⎨=⎩，得()200220k y y y kx -+-=，因为()()()()11223344,,,,A x y B x y C x y D x y ，，，，所以()()010*********22,y k x y k x y y y y k k --==，所以()()()22012000120100201234121244y k k x y x k k y k x y k x y y y y k k k k ⎡⎤-++--⎣⎦==()()220000000000220000214224442y x x y x y x x x x y x x x ⎡⎤--+⋅⎢⎥--⎣⎦==+=-.故选C.9．【答案】BD【详解】因为0.10.40.20.21x ++++=，所以0.1x =，A 选项错误；由()00.110.420.130.240.22E X =⨯+⨯+⨯+⨯+⨯=，故22222()(02)0.1(12)0.4(22)0.1(32)0.2(42)0.2 1.8D X =-⨯+-⨯+-⨯+-⨯+-⨯=，因此选项B 正确；又21Y X =-，所以，()2()13E Y E X =-=，()4()7.2D Y D X ==，故C 错D 对.故选：BD 10．【答案】AD【详解】解：选项A：不等式20ax bx c ++>解集M =∅，等价于一元二次函数2y ax bx c =++的图象没有在x 轴上方的部分，故等价于2040a b ac <⎧⎨-≤⎩，所以选项A 正确；选项B：取值1,2,3a b c ==-=-，1112,31,a b c ===-，此时能满足111a b c a b c==，而2230x x -->的解集为{|1x x <-，或}3x >，2230x x -++>的解集为{}|13x x -<<，故B 选项错误；选项C：因为一元二次不等式20ax bx c ++>的解集为{}23M x x =-<<，所以得到2-与3是20ax bx c ++=的根且a<0，故有2323b aca ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，解得60b a c a a =-⎧⎪=-⎨⎪<⎩，所以不等式20cx bx a -+<即为260ax ax a -++<，等价于不等式2610x x --<的解集1132M x x ⎧⎫=-<<⎨⎬⎩⎭，所以选项C 错误；选项D：因为2b M x x a ⎧⎫=≠-⎨⎬⎩⎭，所以240b ac ∆=-=，即24b c a=，令()0b a t t -=>，所以()()()222222222244b a b a a t a t a a ab b a at ta b a a b a at at++++++++++===--4448a t t a =++≥+=，当且仅当4a t t a =即3b a =取“=”，选项D 正确.故选：AD.11．【答案】ABD【详解】A 选项，+2为偶函数，故()()22g x g x -+=+，两边求导得，()()22g x g x --+='+'，令0x =得()()22g g -'='，解得()20g '=，A 正确；B 选项，因为()()25f x g x +-=，()()22g x g x -+=+，所以()()25f x g x ++=①，因为()()43g x f x --=，所以()()223g x f x +--=②，则①②相减得，()()22f x f x +-=③，又()()242f x f x -+-=④，则③④相减得()()40f x f x --=，即()()4f x f x =-，故4为函数()f x 的一个周期，B 正确；C 选项，假如()1f x +为奇函数，则()()110f x f x -+++=，当1x =时，可得()()020f f +=，但()()22f x f x +-=，当2x =可得()()202f f +=，显然不满足要求，故()1f x +不是奇函数，C 错误；D 选项，因为()()25f x g x +-=，所以()()025f g +=，又()25g =，故()00f =，由B 选项得()()22f x f x +-=，故()()202f f +=，解得()22f =，且()()312f f +=，由B 选项知()f x 的一个周期为4，故()()400f f ==，所以()()()()12344f f f f +++=，则()()()()()20241506123450642024k f k f f f f =⎡⎤=+++=⨯=⎣⎦∑，D 正确.故选：ABD 12．【答案】3【详解】因为{}1,3**15,,A x y x N y N x ⎧⎫⊆=∈∈⎨⎬⎩⎭，即{}1,3{}1,3,5,15A ⊆，所以{}13,5A =,，{}1,3,15A =，{}1,3,5,15A =，即集合A 的个数有3个.故答案为：3.13．【答案】8116【分析】根据分段函数解析式结合自变量范围求解即可.【详解】331log log 1616=-Q ，233163<<，313log 216∴-<<-，381log 1633331118181log log 2log 22log 31616161616f f f f ⎛⎫⎛⎫⎛⎫⎛⎫∴=+=++===⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭故答案为：8116.14．【答案】70【详解】如图，设AB 中点为N ，由AB AN =⇒=CN =N 的轨迹为以()0,6为圆心，r =()()()()2222MA MB MN NA MN NB MN NA MN NA MN NA MN ⋅=+⋅+=+⋅-=-=- ，max max MN MC r =+，设),cos Mθθ，则MC ===，当且仅当2cos 3θ=-时，max MC ==所以max max MN MC r =+==()2maxmax272270MA MBMN⋅=-=-=故答案为：7015．【答案】(1)2π3(2)4【分析】（1）由两角和的正弦公式以及正弦定理可得tan A =，可得结果；（2）由三角形面积公式并利用ABD ACD ABC S S S +=△△△，可得b c bc +=，再由余弦定理即可求得5bc =,由三角形的面积公式可得结果.【详解】（1）因为sin cos a B A =，由正弦定理可得sin sin sin cos A B B A=sin 0B ≠，所以sin A A =，故tan A =2π3A =.（2）由题意可知ABD ACD ABC S S S +=△△△，即1π1π12πsin sin sin 232323c b bc +=，化简可得b c bc +=，在ABC 中，由余弦定理得()2222221cos 222b c bc a b c a A bc bc +--+-===-，从而()2220122bc bc bc --=-，解得5bc =或4bc =-（舍去），所以11sin 5sin120224ABC S bc A ==⨯⨯︒=△.16．【答案】(1)证明见解析(2)35【详解】（1）记E 为PD 的中点，连接,BE CE .因为PCD △为等边三角形，所以PD CE ⊥，因为BD BP =，所以PD BE ⊥，又,,BE CE E BE CE =⊂ 平面BCE ，所以PD ⊥平面BCE ，因为⊂BC 平面BCE ，所以PD BC ⊥，又,,,CD BC CD PD D CD PD ⊥=⊂ 平面PCD ，所以⊥BC 平面PCD .（2）以C 为原点，,CD CB 所在直线分别为,x y轴建立如图所示的空间直角坐标系，因为PCD △为等边三角形，2CD =，所以P 到底边CD的距离为因为ABD △为等边三角形，4AB =，所以D 到底边AB的距离为则(0,(2,0,0),(4,P B D A ，所以(2,(1,0,(2,BD PD DA =-== ，设平面PBD 的法向量为(,,)m x y z = ，则00m BD m PD ⎧⋅=⎪⎨⋅=⎪⎩，即200x x ⎧-=⎪⎨=⎪⎩，令1y =，则1x z ==，故)m = ，设平面PAD 的法向量为 =s s ，则00n DA n PD ⎧⋅=⎪⎨⋅=⎪⎩即200a a ⎧+=⎪⎨=⎪⎩，令1c =，则1a b ==-，故1,1)n =- ，因为3cos ,5m n m n m n ⋅〈〉== ，所以平面PBD 与平面PAD 夹角的余弦值为35.17．【答案】(1)能认为喜爱篮球运动与性别有关(2)（i）证明见解析；（ii）甲第25次触球者的概率大【详解】（1）假设0H ：喜爱篮球运动与性别独立，即喜爱篮球运动与性别无关.根据列联表数据，经计算得220.001200(60802040)10010.828100*********x χ⨯⨯-⨯==>=⨯⨯⨯，依据小概率值0.001α=的独立性检验，我们推断0H 不成立，即能认为喜爱篮球运动与性别有关，此推断犯错误的概率不超过0.001.（2）（i）由题意，()11111101333n n n n P P P P ---=⋅+-⋅=-+，所以1111434n n P P -⎛⎫-=-- ⎪⎝⎭又113044P -=≠，所以14n P ⎧⎫-⎨⎬⎩⎭是以34为首项，13-为公比的等比数列.（ii）由（i）得，1311434n n P -⎛⎫=⋅-+ ⎪⎝⎭，所以232431114344P ⎛⎫=⋅-+< ⎪⎝⎭，242531114344P ⎛⎫=⋅-+> ⎪⎝⎭.故甲第25次触球者的概率大.18．【答案】(1)是定值，定值为14(2)13-【详解】（1）由题意知，4a =，2b =，所以(0,2)A ，()4,0B ，所以12AB k =-，设直线CD 的方程为()122y x t t =-+≠，设()11,D x y ，()22,C x y ，联立直线CD 与椭圆的方程22116412x y y x t ⎧+=⎪⎪⎨⎪=-+⎪⎩，整理得222280x tx t -+-=，由()2244280t t ∆=-->，解得t -<<2t ≠，则122x x t +=，21228x x t =-，所以()()12121212111222244AD BC x t x t y y k k x x x x x ⎛⎫⎛⎫-+--+ ⎪⎪-⎝⎭⎝⎭==--21212212111()2424x x t x x t x t x x x -+++-=-2221121121442222244t t x t t x t x x x x x x --+-+--==--21214122844t x t x --==--，故直线AD 与BC 的斜率之积是定值，且定值为14.（2）设()33,A x y ，()44,B x y ，(),D x y ，记PD DA λ= (0λ≠)，得3386x x x y y y λλλλ-=-⎧⎨-=-⎩.所以338161x x y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩.又A ，D 均在椭圆上，所以22332233116486111164x y x y λλλλ⎧+=⎪⎪⎪⎨++⎛⎫⎛⎫⎪ ⎪ ⎪++⎝⎭⎝⎭⎪+=⎪⎩，化简得3331220x y λλλ++-=，因为CD AB ∥，所以PC CB λ= ，同理可得4431220x y λλλ++-=，即直线AB ：31220x y λλλ++-=，所以AB 的斜率为13-.19．【答案】(1)210x y --=(2)(]0,1【详解】（1）当1a =-时，()1e ln x f x x -=+，则()11e x f x x-'=+，()01e 12f '∴=+=，又()01e ln11f =+=，()y f x ∴=在()()1,1f 处的切线方程为：()121y x -=-，即210x y --=.（2）方法一：令()()1ln e ln ln x g x f x a a a a x a a a -=--=---，则()0g x ≥恒成立，()g x 的定义域为()0,∞+，()1e x a g x x -'=-且0a >；令()()h x g x ='，则()12e 0x a h x x -'=+>，()h x ∴在()0,∞+上单调递增，即()g x '在()0,∞+上单调递增，又()11e e 1011aa a g a a a '+=-=-+>++，11e 101a a g a a -+⎛⎫'=--< ⎪+⎝⎭，0,11a x a a ⎛⎫∴∃∈+ ⎪+⎝⎭，使得()00g x '=，且当()00,x x ∈时，()0g x '<；当()0,x x ∈+∞时，()0g x '>；()g x ∴在()00,x 上单调递减，在()0,x +∞上单调递增，()()0100min e ln ln x g x g x a x a a a -∴==---，由()00g x '=得：010e x a x -=，00ln 1ln x x a ∴+-=，010e x a x -=，()()000011110000000e e ln e e ln 1x x x x g x x x x x x x ----∴=---+-()012000e 12ln x x x x -=--，()012000e 12ln 0x x x x -∴--≥，即00012ln 0x x x --≥，令()12ln u x x x x=--，则()u x 在()0,∞+上单调递减，又()000012ln 0u x x x x =--≥，()10u =，001x ∴<≤，设()()1e 01x t x x x -=<≤，则()()11e 0x t x x -'=+>，()t x ∴在(]0,1上单调递增，()01t x ∴<≤，0100e 1x x -∴<≤，又010e x a x -=，a ∴的取值范围为(]0,1.方法二：由()ln f x a a a ≥+得：1e ln ln x a a a a x -≥++，()()()()ln 111e 1ln ln ln 1ln 1e ax x x ax a x ax ax ax +-⎡⎤-⎣⎦∴≥++=+=+⎡⎤⎡⎤⎣⎦⎣⎦，当()ln 10ax +≤时，()1e 0ln 1x x ax ->≥+在0a >，0x >时恒成立，0a ∴>；当()ln 10ax +>时，设()()1e 0x h x x x -=>，则()()()ln 1h x h ax ≥+，()()11e 0x h x x -'=+> ，()h x ∴在()0,∞+上单调递增，()ln 1x ax ∴≥+，即()1e 0x ax x -≤>，()1e 0x a x x-∴≤>，令()()1e 0x u x x x -=>，则()()121e x x u x x--'=，∴当()0,1x ∈时，()0u x '<；当()1,x ∈+∞时，()0u x '>；()u x ∴在()0,1上单调递减，在()1,+∞上单调递增，()()min 11u x u ∴==，1a ∴≤，又0a >，01a ∴<≤；综上所述：实数a 的取值范围为(]0,1.方法三：()f x 定义域为()0,∞+，()ln f x a a a ≥+恒成立，()11ln f a a a ∴=≥+必然成立；令()ln S a a a a =+，则()2ln S a a '=+，∴当()20,e a -∈时，()0S a '<；当()2e ,a -∈+∞时，()0S a '>；()S a ∴在()20,e -上单调递减，在()2e ,-+∞上单调递增，又()11S =，当10e a -<<时，()()1ln 0S a a a =+<，∴当01a <≤时，ln 1a a a +≤；下面证明：当01a <≤时，()ln f x a a a ≥+恒成立.ln 0a a ≤ ，()ln ln ln ln 1a x a a a a x a a x ∴++≤+=+，()11e ln ln e ln 1x x a x a a a a x --∴---≥-+，令()()1e ln 1x F x a x -=-+，则()1e x a F x x -'=-，令()()G x F x '=，则()12e0x a G x x -'=+>，()F x '∴在()0,∞+上单调递增，当1a =时，()11e x F x x-'=-，()10F '=，∴当()0,1x ∈时，()0F x '<；当()1,x ∈+∞时，()0F x '>；()F x ∴在()0,1上单调递减，在()1,+∞上单调递增，()()10F x F ∴≥=，1e ln ln 0x a x a a a -∴---≥恒成立，即()ln f x a a a ≥+恒成立；当01a <<时，()110F a '=->，()1e 10a F a -'=-<，()0,1x a ∴∃∈，使得()00F x '=，且当()00,x x ∈时，()0F x '<；当()0,x x ∈+∞时，()0F x '>；()F x ∴在()00,x 上单调递减，在()0,x +∞上单调递增，()()()0100e ln 1x F x F x a x -∴≥=-+，由()00F x '=得：010e x a x -=，00ln ln 1x a x =+-，()()000001ln 1ln a F x a a x a x a a a x x ⎛⎫∴=-+-=+-- ⎪⎝⎭，()0,1x a ∈ ，0012x x ∴+>，()()0001ln ln 1ln 0F x a x a a a a a a a a x ⎛⎫∴=+-->-=-> ⎪⎝⎭，()()00F x F x ∴≥>，1e ln ln 0x a x a a a -∴---≥恒成立，即()ln f x a a a ≥+恒成立；当1a >时，()()111ln ln f a a a a a =<+=+，显然不满足()ln f x a a a ≥+恒成立；综上所述：实数a 的取值范围为(]0,1.1.通过直接构造函数的方式，将问题转化为含参数函数的单调性的讨论和最值的求解问题，利用最值求得参数的取值范围；2.采用同构法，将问题转化为同一函数的不同函数值的大小关系的问题，从而通过求解函数的单调性得到自变量的大小关系；3.采用由特殊到一般的思路，通过特殊位置必然成立的思路得到a 的一个取值范围，再证明在此范围时不等式恒成立，并通过反例说明不在此范围时不等式不恒成立来得到最终范围.。

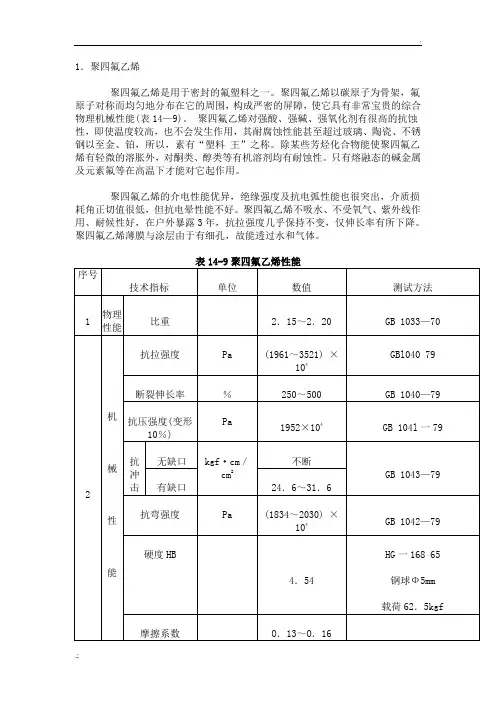
1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。

聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。

聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。

除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。

只有熔融态的碱金属及元素氟等在高温下才能对它起作用。

聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。

聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。

聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。

聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。

但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。

聚四氟乙烯分子间的范德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。

聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。

其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。

在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。

聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。

常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。

如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。

第七章动量守恒定律第1讲动量动量定理课标要求核心考点五年考情核心素养对接1.理解冲量和动量.2.通过理论推导和实验，理解动量定理，能用其解释生产生活中的有关现象.动量、冲量及动量变化量的理解2023：新课标T19、T20，天津T5；2022：湖北T7，湖南T7；2021：湖南T2，北京T10 1.物理观念：理解动量、冲量等基本概念，掌握动量定理，深化运动与相互作用观念.2.科学思维：经历科学论证过程，理解动量定理的物理实质与牛顿第二定律的一致性；领会求解变力的冲量时的极限思想.3.科学探究：经历寻求碰撞中不变量的过程，体会探究过程中猜想、推理和证据的重要性.4.科学态度与责任：通过对动量、冲量的学习，让学生逐渐形成探索自然的内在动力.动量定理的应用2023：江苏T15，广东T10；2022：山东T2，湖南T14，全国乙T20；2021：湖北T3，全国乙T19，重庆T13，浙江1月T20，天津T7；2020：全国ⅠT14，海南T8；2019：全国ⅠT16，全国ⅡT25介质流模型2021：福建T4命题分析预测动量和动量定理是本章的基础，在高考中常以选择题的形式考查，主要考查应用动量定理解释生活现象等，难度不大.考点1动量、冲量及动量变化量的理解1.动量（1）定义：物体的[1]质量与[2]速度的乘积叫作物体的动量.（2）表达式：p＝[3]mv，单位kg·m/s.（3）动量为矢量，方向与[4]速度的方向相同.2.动量的变化量（1）因为动量是矢量，动量的变化量Δp也是[5]矢量，其方向与速度的改变量Δv的方向[6]相同.（2）动量的变化量Δp的大小，一般用末动量p'减去初动量p进行计算，也称为动量的增量，即Δp＝[7]p'－p.3.冲量（1）定义：[8]力与[9]力的作用时间的乘积叫作力的冲量.（2）表达式：I＝FΔt，单位为N·s.（3）冲量为矢量，方向与[10]力的方向相同.如图，一个质量为0.1kg的物体在光滑水平面上以6m/s的速度向右运动，碰到坚硬的墙壁后，沿着同一直线以6m/s的速度水平向左弹回，g取10m/s2.（1）以向右为正方向，则碰到墙壁之前物体的动量为0.6kg·m/s，弹回后物体的动量为－0.6kg·m/s，碰撞过程中物体的动量变化量为－1.2kg·m/s.（2）如果水平面粗糙，物体与水平面间的动摩擦因数为0.1，物体向右运动3s内（未碰墙壁），重力的冲量大小为3N·s，支持力的冲量大小为3N·s，摩擦力的冲量大小为0.3N·s.命题点1动量及其变化量的理解和计算1.[动量/多选]在光滑水平面上，原来静止的物体在水平力F的作用下，经过时间t、通过位移L后动量变为p、动能变为E k.以下说法正确的是（BD）A.在F作用下，若这个物体经过位移2L，其动量等于2pB.在F作用下，若这个物体经过位移2L，其动能等于2E kC.在F作用下，若这个物体经过时间2t，其动能等于2E kD.在F作用下，若这个物体经过时间2t，其动量等于2p解析在光滑水平面上，合力大小等于F的大小，根据动能定理知FL＝12mv2-0，位移变为原来的2倍，动能变为原来的2倍，根据p＝2B k，知动量变为原来的2倍，故A错误，B正确；根据动量定理知，Ft＝mv，时间变为原来的2倍，则动量变为原来的2倍，根据E k＝22知，动能变为原来的4倍，故C错误，D正确.方法点拨动量与动能的比较k下沿直线做加速运动，经过一段时间后动能大小变为2E k，则这段时间内物体动量变化量的大小为（D）B.（2－2）C.B kD.（2－2）B k解析由动能与动量的表达式E k＝12mv2，p＝mv可知p＝2B k，故动能大小由E k变为2E k的这段时间内物体动量变化量的大小为Δp＝2×2k−2B k＝(2-2)B k，故D 正确.命题点2冲量的理解和计算3.[冲量]如图所示，车载玩具——弹簧人公仔固定在车的水平台面上，公仔头部的质量为m，静止在图示位置.现用手竖直向下压公仔的头部，使之缓慢下降至某一位置，之后迅速放手.公仔的头部经过时间t，沿竖直方向上升到另一位置时速度为零.此过程弹簧始终处于弹性限度内，不计空气阻力及弹簧质量.在公仔头部上升的过程中（C）A.公仔头部的机械能守恒B.公仔头部的加速度先增大后减小C.弹簧弹力冲量的大小为mgtD.弹簧弹力对头部所做的功为零解析弹簧弹力对公仔头部做功，公仔头部的机械能不守恒，故A错误；公仔头部上升过程中，弹簧弹力先减小后反向增大，加速度先减小后反向增大，故B错误；公仔头部上升过程中，取向上为正方向，根据动量定理有I弹-mgt＝0，则弹簧弹力冲量的大小为I弹＝mgt，故C正确；公仔头部上升过程中，根据动能定理有W弹-mgh＝0，则弹簧弹力对头部所做的功为W弹＝mgh≠0，故D错误.命题拓展命题条件不变，一题多设问整个过程中合力对公仔头部的冲量大小为0，弹簧弹力对公仔底部的冲量大小为mgt.解析公仔头部的初速度为0，末速度也是0，动量变化量为0，则合力的冲量也是0，公仔头部整个过程中只受到弹簧弹力的冲量和重力的冲量，所以弹簧弹力对公仔头部的冲量大小为mgt，弹簧弹力对公仔底部的冲量大小也是mgt.方法点拨冲量与功的比较冲量功公式I＝Ft（F为恒力）W＝Fl cosα（F为恒力）标矢性矢量标量意义表示力对时间的累积，是动量变化的量度表示力对空间的累积，是能量变化的量度联系都是过程量，都与力的作用过程相互联系命题点3F－t图像的应用4.[多选]如图所示，物体从t＝0时刻开始由静止做直线运动，0～4s内其合力随时间变化的关系图线为某一正弦函数图像.下列表述正确的是（ABD）A.0～2s内合力的冲量一直增大B.0～4s内合力的冲量为零C.2s末物体动量的方向发生变化D.0～4s内物体动量的方向一直不变解析根据F-t图像中图线所围面积表示冲量可知，在0～2s内合力的冲量一直增大，A 正确；0～4s内合力的冲量为零，B正确；2s末力的方向发生变化，物体的动量开始减小，但方向不发生变化，0～4s内物体动量的方向一直不变，C错误，D正确.命题拓展命题条件不变，一题多设问[多选]下列说法正确的是（CD）A.第2s末，物体的动量为零B.第4s末，物体回到出发点C.在0～2s时间内，力F的瞬时功率先增大后减小D.在1～3s时间内，力F的冲量为零解析在前2s内力与运动的方向相同，物体经历了一个加速度逐渐增大的加速运动和加速度逐渐减小的加速运动，所以第2s末，物体的速度最大，动量最大，故A错误；该物体在2～4s内受到的力与0～2s内受到的力的方向相反，前半个周期内做加速运动，后半个周期内做减速运动，所以物体在0～4s内的位移为正，即第4s末，物体没有回到出发点，故B错误；0～2s内，速度在增大，力F先增大后减小，根据瞬时功率P＝Fv得力F瞬时功率开始时为0，2s末的瞬时功率为0，所以在0～2s 时间内，F的瞬时功率先增大后减小，故C正确；在F-t图像中，图线与坐标轴围成图形的面积表示力F的冲量，由图可知，1～2s的面积与2～3s的面积大小相等，一正一负，所以和为0，则在1～3s时间内，F的冲量为0，故D正确.方法点拨冲量的四种计算方法1.内容：物体在一个过程中所受的冲量等于它在这个过程始末的[11]动量变化量.2.公式：[12]I＝p'－p或[13]F（t'－t）＝mv'－mv.3.动量定理的理解（1）动量定理反映了合力的冲量与动量变化量之间的因果关系，即合力的冲量是原因，物体的动量变化量是结果.（2）动量定理中的冲量是合力的冲量，而不是某一个力的冲量，它可以是合力的冲量，可以是各力冲量的矢量和，也可以是外力在不同阶段冲量的矢量和.（3）动量定理的表达式是矢量式，等号包含了大小相等、方向相同两方面的含义.图甲为码头上河岸边悬挂的旧轮胎，图乙为轿车的安全气囊在剧烈碰撞时自动弹出的情境.判断下列说法的正误.（1）码头上河岸边悬挂的旧轮胎减小了船靠岸时的冲量.（✕）（2）码头上河岸边悬挂的旧轮胎减小了船靠岸时动量的变化量.（✕）（3）轿车的安全气囊在剧烈碰撞时自动弹出可以延长作用时间，减小司机或乘员受到的作用力.（√）（4）旧轮胎和气囊均起到延长作用时间、减小作用力的效果，即起到缓冲作用.（√）命题点1动量定理的简单计算5.[2024湖南常德模拟]城市进入高楼时代后，高空坠物已成为危害极大的社会安全问题.如图所示为一则安全警示广告，非常形象地描述了高空坠物对人伤害的严重性.某同学用下面的实例来检验广告词的科学性：设一个50g的鸡蛋从16楼的窗户自由落下，与地面撞击时间约为3ms，相邻楼层的高度差为3m，不计空气阻力，重力加速度g取10m/s2，则从16楼下落的鸡蛋对地面的平均冲击力约为（C）一个鸡蛋的威力从4楼抛下会让人起肿包从8楼抛下可以砸破人的头皮从18楼抛下可以砸裂行人头骨从25楼抛下可能使人当场死亡A.5000NB.900NC.500ND.250N解析鸡蛋下落高度h＝15×3m＝45m，鸡蛋自由下落过程，由动能定理有mgh＝12mv2-0，在鸡蛋与地面撞击时间内，规定竖直向下为正方向，由动量定理得mgt-Ft＝0-mv，其中F为地面对鸡蛋的作用力，由牛顿第三定律知，鸡蛋对地面的平均冲击力F'＝F＝500.5N，方向竖直向下，故选C.命题点2动量定理的综合应用6.跑酷是以日常生活的环境为运动场所的极限运动.质量m＝50kg的跑酷运动员，在水平高台上水平向右跑到高台边缘，以v0的速度从边缘的A点水平向右跳出，运动t1＝0.3s后落在一倾角为53°的斜面上的B点，速度方向与斜面垂直.此时运动员迅速转身并调整姿势，以02的速度从B点水平向左蹬出，刚好落到斜面的底端C点.假设该运动员可视为质点，不计空气阻力，重力加速度g取10m/s2，sin53°＝0.8，cos53°＝0.6.（1）求运动员从高台边缘跳出的水平速度v0大小；（2）求运动员落到斜面底端C时的速度；（3）假设与斜面的作用时间为0.3s，求运动员与斜面作用过程中运动员对斜面的作用力.答案（1）4m/s（2，方向与水平方向夹角的正切值为83（3）10002N，方向斜向右下方与水平方向夹角为45°解析（1）运动员落至斜面上B点时竖直分速度为v y＝gt1＝3m/s由于速度方向与斜面垂直，满足tan53°＝0解得v0＝4m/s即运动员从高台边缘跳出的水平速度大小为4m/s.（2）从B点水平向左蹬出的速度为02＝2m/s设从B点蹬出到落至C点的时间为t2，由位移公式可得x＝02t2，y＝12g22由位移偏角公式可得tan53°＝落至C点的竖直分速度为v'y＝gt2运动员落到斜面底端C 时的速度大小为v 速度方向与水平方向夹角的正切值为tan α＝'02联立代入数据解得v ，tan α＝8运动员落到斜面底端C ，方向与水平方向夹角的正切值为83.（3）设斜面对运动员的作用力在竖直方向的分量为F 1，在水平方向的分量为F 2，在竖直方向上，以向上为正方向，由动量定理可得（F 1－mg ）Δt ＝0－（－mv y ）在水平方向上，以向左为正方向，由动量定理可得F 2Δt ＝m ·02－（－mv 0）解得F 1＝F 2＝1000N故斜面对运动员的作用力大小为F ＝12＋22＝10002N斜向左上方与水平方向成45°角，由牛顿第三定律可知，运动员对斜面的作用力大小为10002N ，方向斜向右下方，与水平方向夹角为45°.方法点拨1.用动量定理解题的思路2.动量定理的两点说明（1）动量定理不仅适用于恒力，也适用于变力.对变力使用时，动量定理中的力F 应理解为变力在作用时间内的平均值.（2）动量定理的研究对象可以是单体，也可以是整体.其中“整体”含义：对象或过程.动量定理的整体表达式：I ＝Δp 1＋Δp 2＋…＋Δp n （矢量和）.考点3介质流模型研究对象流体类：液体流、气体流等，通常给出流体的密度ρ微粒类：电子流、光子流、尘埃等，通常给出单位体积内的粒子数n分析步骤①建构“柱状”模型：沿流速v 的方向选取一段小柱体，其横截面积为S②微元研究小柱体的体积ΔV ＝vS Δt小柱体质量m ＝ρΔV ＝ρvS Δt 小柱体内粒子数N ＝nvS Δt 小柱体动量p ＝mv ＝ρv 2S Δt③建立方程，应用动量定理F Δt ＝Δp 研究命题点1流体类“柱状”模型7.如图所示为清洗汽车用的高压水枪.设水枪喷出的水柱直径为D ，水流速度为v ，水柱垂直于汽车表面，水柱冲击汽车后水的速度为零.手持高压水枪操作，进入水枪的水流速度可忽略不计，已知水的密度为ρ.下列说法正确的是（D）A.高压水枪单位时间喷出的水的质量为ρπvD 2B.高压水枪单位时间喷出的水的质量为14ρvD 2C.水柱对汽车的平均冲力为14ρD 2v 2D.当高压水枪喷口的出水速度变为原来的2倍时，喷出的水对汽车的压强变为原来的4倍解析高压水枪单位时间内喷出水的质量m 0＝ρV ＝ρπ·24v ＝14πρvD 2，故A 、B 错误；以t 时间内喷出的水为研究对象，设汽车对水柱的平均作用力大小为F ，水柱对汽车的平均冲力大小为F'，由动量定理得Ft ＝mv ，即Ft ＝14πρvD 2·t ·v ，可得F'＝F ＝14πρv 2D 2，故C 错误；高压水枪喷出的水对汽车产生的压强p ＝＝14πB 2214π2＝ρv 2，则当高压水枪喷口的出水速度变为原来的2倍时，压强变为原来的4倍，故D 正确.方法点拨命题点2微粒类“柱状”模型8.正方体密闭容器中有大量运动粒子，每个粒子的质量均为m ，单位体积内粒子数量n 为恒量.为简化问题，我们假定：粒子大小可以忽略，其速率均为v ，且与器壁各面碰撞的机会均等，与器壁碰撞前后瞬间，粒子速度方向都与器壁垂直，且速率不变.利用所学力学知识，导出器壁单位面积所受粒子压力f 与m 、n 和v 的关系.答案f ＝13nmv 2解析一个粒子每与器壁碰撞一次对器壁的作用力的冲量ΔI＝2mv如图所示，以器壁上面积为S的部分为底、vΔt为高构成柱体，由题设可知，其内有16的粒子在Δt时间内与器壁上面积为S的部分发生碰撞，碰壁粒子总数N＝16n·SvΔtΔt时间内粒子对器壁的作用力的冲量I＝N·ΔI＝13nSmv2Δt器壁上面积为S的部分受到粒子的压力F＝Δ则器壁单位面积所受粒子的压力f＝＝13nmv2.方法点拨流体碰撞的两类模型解法热点8应用动量定理解决实际问题动量和冲量是力学中两个重要的物理概念，动量定理揭示了冲量和动量变化量之间的关系，成为近年高考命题的热点内容.试题紧密联系生产生活实际，内容丰富，考查角度灵活，对学生的综合应用能力及物理建模能力要求较高.题型既有选择题，又有计算题.1.[2023天津]质量为m的列车以速度v匀速行驶，突然以大小为F的力制动刹车直到列车停止，整个过程中列车还受到大小恒为f的阻力，下列说法正确的是（C）A.减速运动过程的加速度大小a＝B.力F的冲量大小为mvC.刹车距离为B22（＋）D.匀速行驶时功率为（f＋F）v解析一题多解刹车过程，由动能定理得-(F＋f)x＝0-12mv2，解得x＝B22(＋p，C正确.2.[2022山东]我国多次成功使用“冷发射”技术发射长征十一号系列运载火箭.如图所示，发射仓内的高压气体先将火箭竖直向上推出，火箭速度接近零时再点火飞向太空.从火箭开始运动到点火的过程中（A）A.火箭的加速度为零时，动能最大B.高压气体释放的能量全部转化为火箭的动能C.高压气体对火箭推力的冲量等于火箭动量的增加量D.高压气体的推力和空气阻力对火箭做功之和等于火箭动能的增加量解析从火箭开始运动到点火的过程中，火箭先加速运动后减速运动，当加速度为零时，动能最大，A正确；高压气体释放的能量转化为火箭的动能和重力势能及火箭与空气间因摩擦产生的热量，B错误；根据动量定理可得高压气体对火箭的推力F、火箭自身的重力mg和空气阻力f的冲量矢量和等于火箭动量的变化量，C错误；根据动能定理可得高压气体对火箭的推力F、火箭自身的重力mg和空气阻力f对火箭做的功之和等于火箭动能的变化量，D错误.3.[2022重庆]在测试汽车的安全气囊对驾乘人员头部防护作用的实验中，某小组得到了假人头部所受安全气囊的作用力随时间变化的曲线（如图）.从碰撞开始到碰撞结束过程中，若假人头部只受到安全气囊的作用，则由曲线可知，假人头部（D）A.速度变化量的大小等于曲线与横轴围成的面积B.动量大小先增大后减小C.动能变化量的大小正比于曲线与横轴围成的面积D.加速度大小先增大后减小解析4.[2023广东/多选]某同学受电动窗帘的启发，设计了如图所示的简化模型.多个质量均为1kg的滑块可在水平滑轨上滑动，忽略阻力，开窗帘的过程中，电机对滑块1施加一个水平向右的恒力F，推动滑块1以0.40m/s的速度与静止的滑块2碰撞，碰撞时间为0.04s，碰撞结束后瞬间两滑块的共同速度为0.22m/s .关于两滑块的碰撞过程，下列说法正确的有（BD ）A.该过程动量守恒B.滑块1受到合力的冲量大小为0.18N·sC.滑块2受到合力的冲量大小为0.40N·sD.滑块2受到滑块1的平均作用力大小为5.5N 解析规定水平向右为正方向动量定理：物体所受合力的冲量等于动量的变化量滑块1受到合力的冲量I 1＝mv －mv 0＝－0.18N·s ，负号表示方向向左，B 对滑块2受到合力的冲量2＝B －0=0.22N ·s ，方向向右，C 错滑块1的平均作用力满足2＝2Δ→2=.5N ，D 对两滑块碰撞过程，I 1＋I 2≠0，碰撞过程动量不守恒，A 错深入讲解碰撞过程中，对滑块1根据动量定理有F Δt -F 2Δt ＝I 1，解得滑块1所受外力F ＝1N ，不远小于两滑块碰撞过程中的相互作用力F 2＝5.5N ，因此该碰撞过程不满足动量守恒定律.1.[W －t 图像＋动量/2022重庆/多选]一物块在倾角为45°的固定斜面上受到方向与斜面平行、大小与摩擦力相等的拉力作用，由静止开始沿斜面向下做匀变速直线运动，物块与斜面间的动摩擦因数处处相同.若拉力沿斜面向下时，物块滑到底端的过程中重力和摩擦力对物块做的功随时间的变化分别如图中曲线①、②所示，则（BC ）A.B.当拉力沿斜面向上，重力做的功为9J 时，物块动能为3JC.当拉力分别沿斜面向上和向下时，物块的加速度大小之比为1∶3D.当拉力分别沿斜面向上和向下时，物块滑到底端时的动量大小之比为1∶2解析2.[v－t图像＋动量/2022湖南/多选]神舟十三号返回舱进入大气层一段时间后，逐一打开引导伞、减速伞、主伞，最后启动反冲装置，实现软着陆.某兴趣小组研究了减速伞打开后返回舱的运动情况，将其运动简化为竖直方向的直线运动，其v－t图像如图所示.设该过程中，重力加速度不变，返回舱质量不变，下列说法正确的是（AC）A.在0～t1时间内，返回舱重力的功率随时间减小B.在0～t1时间内，返回舱的加速度不变C.在t1～t2时间内，返回舱的动量随时间减小D.在t2～t3时间内，返回舱的机械能不变解析由题知，返回舱的运动可简化为竖直方向的直线运动，所以重力的功率P＝mgv，因此在0～t1时间内，结合v-t图像可知返回舱重力的功率随时间减小，A项正确；v-t图像的斜率表示返回舱的加速度，故0～t1时间内，返回舱的加速度不断减小，B项错误；返回舱的动量大小与其速度大小成正比，所以t1～t2时间内，返回舱的动量随时间减小，C项正确；在t2～t3时间内，返回舱匀速下降，机械能不守恒，D项错误.3.[动量定理的应用/2022北京]“雪如意”是我国首座国际标准跳台滑雪场地，如图所示.跳台滑雪运动中，裁判员主要根据运动员在空中的飞行距离和动作姿态评分.运动员在进行跳台滑雪时大致经过四个阶段：①助滑阶段，运动员两腿尽量深蹲，顺着助滑道的倾斜面下滑；②起跳阶段，当进入起跳区时，运动员两腿猛蹬滑道快速伸直，同时上体向前伸展；③飞行阶段，在空中运动员保持身体与雪板基本平行、两臂伸直贴放于身体两侧的姿态；④着陆阶段，运动员落地时两腿屈膝，两臂左右平伸.下列说法正确的是（B）A.助滑阶段，运动员深蹲是为了减小与滑道之间的摩擦力B.起跳阶段，运动员猛蹬滑道主要是为了增加向上的速度C.飞行阶段，运动员所采取的姿态是为了增加水平方向速度D.着陆阶段，运动员两腿屈膝是为了减少与地面的作用时间解析不同阶段1.[2024山东烟台统考/多选]下列说法正确的是（BC ）A.当力与物体的位移垂直时，该力的冲量为零B.如果物体（质量不变）的速度发生变化，则其所受合外力的冲量不为零C.物体所受合外力的冲量越大，它的动量变化量也越大D.做竖直上抛运动的物体，在一定时间内所受重力的冲量可能为零解析因力的冲量为I ＝Ft ，可知当力与物体的位移垂直时，该力的冲量不为零，故A 错误；如果物体(质量不变)的速度发生变化，则物体的动量发生变化，根据动量定理可知，物体所受合外力的冲量不为零，故B 正确；物体所受合外力的冲量越大，根据动量定理可知，物体的动量变化量一定越大，故C 正确；做竖直上抛运动的物体，在Δt 时间内所受重力的冲量I G ＝G Δt ＝mg Δt ，可知做竖直上抛运动的物体，在Δt 时间内所受重力的冲量不可能为零，故D 错误.2.[情境创新/2023新课标/多选]使甲、乙两条形磁铁隔开一段距离，静止于水平桌面上，甲的N 极正对着乙的S 极，甲的质量大于乙的质量，两者与桌面之间的动摩擦因数相等.现同时释放甲和乙，在它们相互接近过程中的任一时刻（BD ）A.甲的速度大小比乙的大B.甲的动量大小比乙的小C.甲的动量大小与乙的相等D.甲和乙的动量之和不为零解析根据F -μmg ＝ma 可得a ＝1F -μg ，因m 甲＞m 乙、μ甲＝μ乙，故a 甲＜a 乙，则任意时刻甲的速度大小比乙的小，A 错误；m 甲＞m 乙，又μ甲＝μ乙，则f 甲＞f 乙，故甲和乙组成的系统合外力的冲量方向向左，即甲的动量大小比乙的小，BD 正确，C 错误.3.[2024浙江宁波余姚中学校考]一位质量为m 的运动员从下蹲状态向上起跳，经Δt 时间，身体伸直并刚好离开地面，速度为v .对此过程的描述，错误的是（A ）A.地面对运动员的弹力做的功为12mv 2B.运动员所受合力的冲量大小为mvC.地面对运动员弹力的冲量大小为mv＋mgΔtD.重力的冲量大小为mgΔt解析在跳起过程中，运动员在支持力方向上没有位移，地面对运动员的支持力不做功，故A错误；重力的冲量大小I G＝mgΔt，故D正确；根据动量定理可得运动员所受合力的冲量大小I F＝mv，故B正确；以运动员为研究对象，受到地面的支持力和自身的重力，规定向上为正方向，根据动量定理可知(N-mg)Δt＝mv，所以地面对运动员弹力的冲量为NΔt＝mgΔt＋mv，故C正确.4.一个质量为50kg的蹦床运动员，从离水平网面1.8m高处自由下落，着网后沿竖直方向蹦回离水平网面2.45m高处.已知运动员和网接触的时间为1s，g取10m/s2.网对运动员的平均作用力大小为（D）A.150NB.550NC.650ND.1150N解析运动员从h1高度处下落，刚触网时的速度大小为v1＝2K1＝6m/s，方向竖直向下，运动员反弹到高度h2，离网时的速度大小为v2＝2K2＝7m/s，方向竖直向上，在接触网的过程中，运动员受到竖直向上的弹力和竖直向下的重力mg，设竖直向上为正方向，由动量定理有(-mg)t＝mv2-(-mv1)，解得＝1150N，故选D.5.[联系生活实际/2024贵州阶段联考]新能源汽车工业的快速发展，使人们的出行更方便环保，电动汽车逐渐成为家庭的重要交通工具.暑假结束了，某同学乘坐自家的电动汽车返回学校，电动汽车在行驶过程中，以恒定速率通过一段水平圆弧弯道，对于电动汽车的这一运动过程，下列说法正确的是（C）A.电动汽车的动量不变B.在任意相等时间内，电动汽车所受合力的冲量相同C.电动汽车的动能不变D.路面对电动汽车作用力的冲量竖直向上解析电动汽车在行驶过程中，以恒定速率通过一段水平弯道，速度大小不变，方向发生变化，所以小球的动量改变，动能不变，故A错误，C正确；电动汽车做匀速圆周运动，受到的合力的大小不变，方向不断改变，所以在任意相等时间内，电动汽车所受合力的冲量大小相等，方向不相同，故B错误；路面给电动汽车竖直向上的支持力和水平方向指向圆心的摩擦力，所以路面对电动汽车作用力的冲量与水平面有一定夹角，而不是竖直向上，故D错误.6.[2024辽宁沈阳名校联考]海洋馆中一潜水员把一小球以初速度v0从手中竖直向上抛出.从抛出开始计时，4t0时刻小球返回手中.小球始终在水中且在水中所受阻力大小不变，抛出后小球的速度随时间变化的图像。

2024年普通高等学校招生全国统一考试（新课标II 卷）数学本试卷共10页，19小题，满分150分.注意事项：1.答题前，先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后，请将本试卷和答题卡一并上交.一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上.1．已知1i z =--，则z =（）A ．0B ．1CD ．22．已知命题p ：x ∀∈R ，|1|1x +>；命题q ：0x ∃>，3x x =，则（）A ．p 和q 都是真命题B ．p ⌝和q 都是真命题C ．p 和q ⌝都是真命题D ．p ⌝和q ⌝都是真命题3．已知向量,a b满足1,22a a b =+= ，且()2b a b -⊥ ，则b = （）A ．12B．2CD ．14．某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量（单位：kg ）并整理如下表亩产量[900，950）[950，1000）[1000，1050）[1050，1100）[1100，1150）[1150，1200）频数61218302410根据表中数据，下列结论中正确的是（）A ．100块稻田亩产量的中位数小于1050kgB ．100块稻田中亩产量低于1100kg 的稻田所占比例超过80%C ．100块稻田亩产量的极差介于200kg 至300kg 之间D ．100块稻田亩产量的平均值介于900kg 至1000kg 之间5．已知曲线C ：2216x y +=（0y >），从C 上任意一点P 向x 轴作垂线段B '，P '为垂足，则线段B '的中点M 的轨迹方程为（）A ．221164x y +=（0y >）B ．221168x y +=（0y >）C ．221164y x +=（0y >）D ．221168y x +=（0y >）6．设函数2()(1)1f x a x =+-，()cos 2g x x ax =+，当(1,1)x ∈-时，曲线()y f x =与()y g x =恰有一个交点，则a =（）A ．1-B ．12C ．1D ．27．已知正三棱台111ABC A B C -的体积为523，6AB =，112A B =，则1A A 与平面ABC 所成角的正切值为（）A ．12B ．1C ．2D ．38．设函数()()ln()f x x a x b =++，若()0f x ≥，则22a b +的最小值为（）A ．18B ．14C ．12D ．1二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得6分，选对但不全的得部分分，有选错的得0分.9．对于函数()sin 2f x x =和π()sin(2)4g x x =-，下列说法中正确的有（）A ．()f x 与()g x 有相同的零点B ．()f x 与()g x 有相同的最大值C ．()f x 与()g x 有相同的最小正周期D ．()f x 与()g x 的图象有相同的对称轴10．抛物线C ：24y x =的准线为l ，P 为C 上的动点，过P 作22:(4)1A x y +-=⊙的一条切线，Q 为切点，过P 作l 的垂线，垂足为B ，则（）A ．l 与A 相切B ．当P ，A ，B 三点共线时，||PQ =C ．当||2PB =时，PA AB⊥D ．满足||||PA PB =的点P 有且仅有2个11．设函数32()231f x x ax =-+，则（）A ．当1a >时，()f x 有三个零点B ．当a<0时，0x =是()f x 的极大值点C ．存在a ，b ，使得x b =为曲线()y f x =的对称轴D ．存在a ，使得点()()1,1f 为曲线()y f x =的对称中心三、填空题：本大题共3小题，每小题5分，共15分.12．记n S 为等差数列{}n a 的前n 项和，若347a a +=，2535a a +=，则10S =.13．已知α为第一象限角，β为第三象限角，tan tan 4αβ+=，tan tan 1αβ=，则sin()αβ+=.14．在如图的4×4的方格表中选4个方格，要求每行和每列均恰有一个方格被选中，则共有种选法，在所有符合上述要求的选法中，选中方格中的4个数之和的最大值是．四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15．记ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin 2A A +=．(1)求A ．(2)若2a =sin sin 2C c B =，求ABC V 的周长．16．已知函数3()e x f x ax a =--．(1)当1a =时，求曲线()y f x =在点()1,(1)f 处的切线方程；(2)若()f x 有极小值，且极小值小于0，求a 的取值范围．17．如图，平面四边形ABCD 中，8AB =，3CD =，AD =，90ADC︒∠=，30BAD ︒∠=，点E ，F 满足25AE AD = ，12AF AB =，将AEF △沿EF 翻折至PEF !，使得PC =．(1)证明：EF PD ⊥；(2)求平面PCD 与平面PBF 所成的二面角的正弦值．18．某投篮比赛分为两个阶段，每个参赛队由两名队员组成，比赛具体规则如下：第一阶段由参赛队中一名队员投篮3次，若3次都未投中，则该队被淘汰，比赛成绩为0分；若至少投中一次，则该队进入第二阶段.第二阶段由该队的另一名队员投篮3次，每次投篮投中得5分，未投中得0分.该队的比赛成绩为第二阶段的得分总和．某参赛队由甲、乙两名队员组成，设甲每次投中的概率为p ，乙每次投中的概率为q ，各次投中与否相互独立．(1)若0.4p =，0.5q =，甲参加第一阶段比赛，求甲、乙所在队的比赛成绩不少于5分的概率．(2)假设0p q <<，（i ）为使得甲、乙所在队的比赛成绩为15分的概率最大，应该由谁参加第一阶段比赛？（ii ）为使得甲、乙所在队的比赛成绩的数学期望最大，应该由谁参加第一阶段比赛？19．已知双曲线()22:0C x y m m -=>，点()15,4P 在C 上，k 为常数，01k <<．按照如下方式依次构造点()2,3,...n P n =：过1n P -作斜率为k 的直线与C 的左支交于点1n Q -，令n P 为1n Q -关于y 轴的对称点，记n P 的坐标为(),n n x y .(1)若12k =，求22,x y ；(2)证明：数列{}n n x y -是公比为11kk+-的等比数列；(3)设n S 为12n n n P P P ++ 的面积，证明：对任意正整数n ，1n n S S +=.1．C【分析】由复数模的计算公式直接计算即可.【详解】若1i z =--，则z ==故选：C.2．B【分析】对于两个命题而言，可分别取1x =-、1x =，再结合命题及其否定的真假性相反即可得解.【详解】对于p 而言，取1x =-，则有101x +=<，故p 是假命题，p ⌝是真命题，对于q 而言，取1x =，则有3311x x ===，故q 是真命题，q ⌝是假命题，综上，p ⌝和q 都是真命题.故选：B.3．B【分析】由()2b a b -⊥ 得22b a b =⋅ ，结合1,22a a b =+= ，得22144164a b b b +⋅+=+=，由此即可得解.【详解】因为()2b a b -⊥ ，所以()20b a b -⋅= ，即22b a b =⋅，又因为1,22a a b =+=，所以22144164a b b b +⋅+=+= ，从而=b 故选：B.4．C【分析】计算出前三段频数即可判断A ；计算出低于1100kg 的频数，再计算比例即可判断B ；根据极差计算方法即可判断C ；根据平均值计算公式即可判断D.【详解】对于A,根据频数分布表可知,612183650++=<,所以亩产量的中位数不小于1050kg ,故A 错误；对于B ，亩产量不低于1100kg 的频数为341024=+，所以低于1100kg 的稻田占比为1003466%100-=，故B 错误；对于C ，稻田亩产量的极差最大为1200900300-=，最小为1150950200-=，故C 正确；对于D ，由频数分布表可得，平均值为1(692512975181025301075241125101175)1067100⨯⨯+⨯+⨯+⨯+⨯+⨯=，故D 错误.故选；C.5．A【分析】设点(,)M x y ，由题意，根据中点的坐标表示可得(,2)P x y ，代入圆的方程即可求解.【详解】设点(,)M x y ，则0(,),(,0)P x y P x '，因为M 为PP '的中点，所以02y y =，即(,2)P x y ，又P 在圆2216(0)x y y +=>上，所以22416(0)x y y +=>，即221(0)164x y y +=>，即点M 的轨迹方程为221(0)164x y y +=>.故选：A 6．D【分析】解法一：令()()21,cos F x ax a G x x =+-=，分析可知曲线()y F x =与()y G x =恰有一个交点，结合偶函数的对称性可知该交点只能在y 轴上，即可得2a =，并代入检验即可；解法二：令()()()(),1,1h x f x g x x =-∈-，可知ℎ为偶函数，根据偶函数的对称性可知ℎ的零点只能为0，即可得2a =，并代入检验即可.【详解】解法一：令()()f x g x =，即2(1)1cos 2a x x ax +-=+，可得21cos a x ax -=+，令()()21,cos F x ax a G x x =+-=，原题意等价于当(1,1)x ∈-时，曲线()y F x =与()y G x =恰有一个交点，注意到()(),F x G x 均为偶函数，可知该交点只能在y 轴上，可得()()00F G =，即11a -=，解得2a =，若2a =，令()()F x G x =，可得221cos 0x x +-=因为∈−1,1，则220,1cos 0x x ≥-≥，当且仅当0x =时，等号成立，可得221cos 0x x +-≥，当且仅当0x =时，等号成立，则方程221cos 0x x +-=有且仅有一个实根0，即曲线()y F x =与()y G x =恰有一个交点，所以2a =符合题意；综上所述：2a =.解法二：令()()()2()1cos ,1,1h x f x g x ax a x x =-=+--∈-，原题意等价于ℎ有且仅有一个零点，因为()()()()221cos 1cos h x a x a x ax a x h x -=-+---=+--=，则ℎ为偶函数，根据偶函数的对称性可知ℎ的零点只能为0，即()020h a =-=，解得2a =，若2a =，则()()221cos ,1,1h x x x x =+-∈-，又因为220,1cos 0x x ≥-≥当且仅当0x =时，等号成立，可得()0h x ≥，当且仅当0x =时，等号成立，即ℎ有且仅有一个零点0，所以2a =符合题意；故选：D.7．B【分析】解法一：根据台体的体积公式可得三棱台的高h =的结构特征求得3AM =，进而根据线面夹角的定义分析求解；解法二：将正三棱台111ABC A B C -补成正三棱锥P ABC -，1A A 与平面ABC 所成角即为PA 与平面ABC 所成角，根据比例关系可得18P ABC V -=，进而可求正三棱锥P ABC -的高，即可得结果.【详解】解法一：分别取11,BC B C 的中点1,D D ，则11AD A D ==可知1111166222ABC A B C S S =⨯⨯⨯=⨯⨯ 设正三棱台111ABC A B C -的为h ，则(11115233ABC A B C V h -==，解得h =如图，分别过11,A D 作底面垂线，垂足为,M N ，设AM x =，则1AA=DN AD AM MN x=--=，可得1DD==结合等腰梯形11BCC B可得22211622BB DD-⎛⎫=+⎪⎝⎭,即()221616433x x+=++，解得3x=，所以1A A与平面ABC所成角的正切值为11tan1A MA ADAMÐ==；解法二：将正三棱台111ABC AB C-补成正三棱锥P ABC-，则1A A与平面ABC所成角即为PA与平面ABC所成角，因为11113PA A BPA AB==，则111127P A B CP ABCVV--=，可知1112652273ABC A B C P ABCV V--==，则18P ABCV-=，设正三棱锥P ABC-的高为d，则11661832P ABCV d-=⨯⨯⨯⨯，解得d=，取底面ABC的中心为O，则⊥PO底面ABC，且AO=所以PA与平面ABC所成角的正切值tan1POPAOAO∠==.故选：B.8．C【分析】解法一：由题意可知：()f x 的定义域为(),b -+∞，分类讨论a -与,1b b --的大小关系，结合符号分析判断，即可得1b a =+，代入可得最值；解法二：根据对数函数的性质分析ln()x b +的符号，进而可得x a +的符号，即可得1b a =+，代入可得最值.【详解】解法一：由题意可知：()f x 的定义域为(),b -+∞，令0x a +=解得x a =-；令ln()0x b +=解得1x b =-；若-≤-a b ，当(),1x b b ∈--时，可知()0,ln 0x a x b +>+<，此时()0f x <，不合题意；若1b a b -<-<-，当(),1x a b ∈--时，可知()0,ln 0x a x b +>+<，此时()0f x <，不合题意；若1a b -=-，当(),1x b b ∈--时，可知()0,ln 0x a x b +<+<，此时()0f x >；当[)1,x b ∈-+∞时，可知()0,ln 0x a x b +≥+≥，此时()0f x ≥；可知若1a b -=-，符合题意；若1a b ->-，当()1,x b a ∈--时，可知()0,ln 0x a x b +<+>，此时()0f x <，不合题意；综上所述：1a b -=-，即1b a =+，则()2222211112222a b a a a ⎛⎫=++=++≥ ⎪⎝⎭+，当且仅当11,22a b =-=时，等号成立，所以22a b +的最小值为12；解法二：由题意可知：()f x 的定义域为(),b -+∞，令0x a +=解得x a =-；令ln()0x b +=解得1x b =-；则当(),1x b b ∈--时，()ln 0x b +<，故0x a +≤，所以10b a -+≤；()1,x b ∈-+∞时，()ln 0x b +>，故0x a +≥，所以10b a -+≥；故10b a -+=，则()2222211112222a b a a a ⎛⎫=++=++ ⎪⎝⎭+，当且仅当11,22a b =-=时，等号成立，所以22a b +的最小值为12.故选：C.【点睛】关键点点睛：分别求0x a +=、ln()0x b +=的根，以根和函数定义域为临界，比较大小分类讨论，结合符号性分析判断.9．BC【分析】根据正弦函数的零点，最值，周期公式，对称轴方程逐一分析每个选项即可.【详解】A 选项，令()sin 20f x x ==，解得π,2k x k =∈Z ，即为()f x 零点，令π()sin(2)04g x x =-=，解得ππ,28k x k =+∈Z ，即为()g x 零点，显然(),()f x g x 零点不同，A 选项错误；B 选项，显然max max ()()1f x g x ==，B 选项正确；C 选项，根据周期公式，(),()f x g x 的周期均为2ππ2=，C 选项正确；D 选项，根据正弦函数的性质()f x 的对称轴满足πππ2π,224k x k x k =+⇔=+∈Z ，()g x 的对称轴满足πππ3π2π,4228k x k x k -=+⇔=+∈Z ，显然(),()f x g x 图像的对称轴不同，D 选项错误.故选：BC 10．ABD【分析】A 选项，抛物线准线为1x =-，根据圆心到准线的距离来判断；B 选项，,,P A B 三点共线时，先求出P 的坐标，进而得出切线长；C 选项，根据2PB =先算出P 的坐标，然后验证1PA AB k k =-是否成立；D 选项，根据抛物线的定义，PB PF =，于是问题转化成PA PF =的P 点的存在性问题，此时考察AF 的中垂线和抛物线的交点个数即可，亦可直接设P 点坐标进行求解.【详解】A 选项，抛物线24y x =的准线为1x =-，A 的圆心(0,4)到直线1x =-的距离显然是1，等于圆的半径，故准线l 和A 相切，A 选项正确；B 选项，,,P A B 三点共线时，即PA l ⊥，则P 的纵坐标4P y =，由24P P y x =，得到4P x =，故(4,4)P ，此时切线长PQ ===，B 选项正确；C 选项，当2PB =时，1P x =，此时244P P y x ==，故(1,2)P 或(1,2)P -，当(1,2)P 时，(0,4),(1,2)A B -，42201PA k -==--，4220(1)AB k -==--，不满足1PA AB k k =-；当(1,2)P -时，(0,4),(1,2)A B -，4(2)601PA k --==--，4(2)60(1)AB k --==--，不满足1PA AB k k =-；于是PA AB ⊥不成立，C 选项错误；D 选项，方法一：利用抛物线定义转化根据抛物线的定义，PB PF =，这里(1,0)F ，于是PA PB =时P 点的存在性问题转化成PA PF =时P 点的存在性问题，(0,4),(1,0)A F ，AF 中点1,22⎛⎫ ⎪⎝⎭，AF 中垂线的斜率为114AF k -=，于是AF 的中垂线方程为：2158x y +=，与抛物线24y x =联立可得216300y y -+=，2164301360∆=-⨯=>，即AF 的中垂线和抛物线有两个交点，即存在两个P 点，使得PA PF =，D 选项正确.方法二：（设点直接求解）设2,4t P t ⎛⎫⎪⎝⎭，由PB l ⊥可得()1,B t -，又(0,4)A ，又PA PB =，214t =+，整理得216300t t -+=，2164301360∆=-⨯=>，则关于t 的方程有两个解，即存在两个这样的P 点，D 选项正确.故选：ABD11．AD【分析】A 选项，先分析出函数的极值点为0,x x a ==，根据零点存在定理和极值的符号判断出()f x 在(1,0),(0,),(,2)a a a -上各有一个零点；B 选项，根据极值和导函数符号的关系进行分析；C 选项，假设存在这样的,a b ，使得x b =为()f x 的对称轴，则()(2)f x f b x =-为恒等式，据此计算判断；D 选项，若存在这样的a ，使得(1,33)a -为()f x 的对称中心，则()(2)66f x f x a +-=-，据此进行计算判断，亦可利用拐点结论直接求解.【详解】A 选项，2()666()f x x ax x x a '=-=-，由于1a >，故()(),0,x a ∞∞∈-⋃+时()0f x '>，故()f x 在()(),0,,a ∞∞-+上单调递增，(0,)x a ∈时，()0f x '<，()f x 单调递减，则()f x 在0x =处取到极大值，在x a =处取到极小值，由(0)10=>f ，3()10f a a =-<，则(0)()0f f a <，根据零点存在定理()f x 在(0,)a 上有一个零点，又(1)130f a -=--<，3(2)410f a a =+>，则(1)(0)0,()(2)0f f f a f a -<<，则()f x 在(1,0),(,2)a a -上各有一个零点，于是1a >时，()f x 有三个零点，A 选项正确；B 选项，()6()f x x x a '=-，0a <时，(,0),()0x a f x '∈<，()f x 单调递减，(0,)x ∈+∞时()0f x '>，()f x 单调递增，此时()f x 在0x =处取到极小值，B 选项错误；C 选项，假设存在这样的,a b ，使得x b =为()f x 的对称轴，即存在这样的,a b 使得()(2)f x f b x =-，即32322312(2)3(2)1x ax b x a b x -+=---+，根据二项式定理，等式右边3(2)b x -展开式含有3x 的项为303332C (2)()2b x x -=-，于是等式左右两边3x 的系数都不相等，原等式不可能恒成立，于是不存在这样的,a b ，使得x b =为()f x 的对称轴，C 选项错误；D 选项，方法一：利用对称中心的表达式化简(1)33f a =-，若存在这样的a ，使得(1,33)a -为()f x 的对称中心，则()(2)66f x f x a +-=-，事实上，32322()(2)2312(2)3(2)1(126)(1224)1812f x f x x ax x a x a x a x a +-=-++---+=-+-+-，于是266(126)(1224)1812a a x a x a-=-+-+-即126012240181266a a a a -=⎧⎪-=⎨⎪-=-⎩，解得2a =，即存在2a =使得(1,(1))f 是()f x 的对称中心，D 选项正确.方法二：直接利用拐点结论任何三次函数都有对称中心，对称中心的横坐标是二阶导数的零点，32()231f x x ax =-+，2()66f x x ax '=-，()126f x x a ''=-，由()02af x x ''=⇔=，于是该三次函数的对称中心为,22a a f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，由题意(1,(1))f 也是对称中心，故122aa =⇔=，即存在2a =使得(1,(1))f 是()f x 的对称中心，D 选项正确.故选：AD【点睛】结论点睛：（1）()f x 的对称轴为()(2)x b f x f b x =⇔=-；（2）()f x 关于(,)a b 对称()(2)2f x f a x b ⇔+-=；（3）任何三次函数32()f x ax bx cx d =+++都有对称中心，对称中心是三次函数的拐点，对称中心的横坐标是()0f x ''=的解，即,33b b f aa ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭是三次函数的对称中心12．95【分析】利用等差数列通项公式得到方程组，解出1,a d ，再利用等差数列的求和公式节即可得到答案.【详解】因为数列n a 为等差数列，则由题意得()1111237345a d a d a d a d +++=⎧⎨+++=⎩，解得143a d =-⎧⎨=⎩，则()10110910104453952S a d ⨯=+=⨯-+⨯=.故答案为：95.13．3-【分析】法一：根据两角和与差的正切公式得()tan αβ+=-αβ+的范围，最后结合同角的平方和关系即可得到答案；法二：利用弦化切的方法即可得到答案.【详解】法一：由题意得()tan tan tan 1tan tan αβαβαβ++===--，因为π3π2π,2π,2ππ,2π22k k m m αβ⎛⎫⎛⎫∈+∈++ ⎪⎝⎭⎝⎭，,Z k m ∈，则()()()22ππ,22π2πm k m k αβ+∈++++，,Z k m ∈，又因为()tan 0αβ+=-，则()()3π22π,22π2π2m k m k αβ⎛⎫+∈++++ ⎪⎝⎭，,Z k m ∈，则()sin 0αβ+<，则()()sin cos αβαβ+=-+()()22sin cos 1αβαβ+++=，解得()sin αβ+=法二：因为α为第一象限角，β为第三象限角，则cos 0,cos 0αβ><,cos α==cos β==则sin()sin cos cos sin cos cos (tan tan )αβαβαβαβαβ+=+=+4cos cos 3αβ=====-故答案为：3-.14．24112【分析】由题意可知第一、二、三、四列分别有4、3、2、1个方格可选；利用列举法写出所有的可能结果，即可求解.【详解】由题意知，选4个方格，每行和每列均恰有一个方格被选中，则第一列有4个方格可选，第二列有3个方格可选，第三列有2个方格可选，第四列有1个方格可选，所以共有432124⨯⨯⨯=种选法；每种选法可标记为(,,,)a b c d ，a b c d ,,,分别表示第一、二、三、四列的数字，则所有的可能结果为：(11,22,33,44),(11,22,34,43),(11,22,33,44),(11,22,34,42),(11,24,33,43),(11,24,33,42)，(12,21,33,44),(12,21,34,43),(12,22,31,44),(12,22,34,40),(12,24,31,43),(12,24,33,40)，(13,21,33,44),(13,21,34,42),(13,22,31,44),(13,22,34,40),(13,24,31,42),(13,24,33,40)，(15,21,33,43),(15,21,33,42),(15,22,31,43),(15,22,33,40),(15,22,31,42),(15,22,33,40)，所以选中的方格中，(15,21,33,43)的4个数之和最大，为152********+++=.故答案为：24；112【点睛】关键点点睛：解决本题的关键是确定第一、二、三、四列分别有4、3、2、1个方格可选，利用列举法写出所有的可能结果.15．(1)π6A =(2)2+【分析】（1）根据辅助角公式对条件sin 2A A +=进行化简处理即可求解，常规方法还可利用同角三角函数的关系解方程组，亦可利用导数，向量数量积公式，万能公式解决；（2）先根据正弦定理边角互化算出B ，然后根据正弦定理算出,b c 即可得出周长.【详解】（1）方法一：常规方法（辅助角公式）由sin 2A A =可得1sin 122A A +=，即sin()1π3A +=，由于ππ4π(0,π)(,333A A ∈⇒+∈，故ππ32A +=，解得π6A =方法二：常规方法（同角三角函数的基本关系）由sin 2A A =，又22sin cos 1A A +=，消去sin A 得到：24cos 30(2cos 0A A A -+=⇔-=，解得cos A =又(0,π)A ∈，故π6A =方法三：利用极值点求解设()sin (0π)f x x x x =<<，则π()2sin (0π)3f x x x ⎛⎫=+<< ⎪⎝⎭，显然π6x =时，max ()2f x =，注意到π()sin 22sin(3f A A A A =+==+，max ()()f x f A =，在开区间(0,π)上取到最大值，于是x A =必定是极值点，即()0cos sin f A A A '==，即tan 3A =，又(0,π)A ∈，故π6A =方法四：利用向量数量积公式（柯西不等式）设(sin ,cos )a b A A ==，由题意，sin 2a b A A ⋅=+=，根据向量的数量积公式，||||cos ,2cos ,a b a b a b a b ⋅== ，则2cos ,2cos ,1a b a b =⇔= ，此时,0a b =，即,a b 同向共线，根据向量共线条件，1cos sin tan 3A A A ⋅=⇔=，又(0,π)A ∈，故π6A =方法五：利用万能公式求解设tan 2A t =，根据万能公式，2222)sin 211tt A A t t-==++，整理可得，222(2(20((2t t t --+-==--，解得tan22A t ==22tan 1t A t ==-又(0,π)A ∈，故π6A =（2）由题设条件和正弦定理sin sin 2sin 2sin sin cos C c B B C C B B =⇔=，又,(0,π)B C ∈，则sin sin 0B C ≠，进而cos 2B =，得到π4B =，于是7ππ12C A B =--=，sin sin(π)sin()sin cos sin cos 4C A B A B A B B A =--=+=+=，由正弦定理可得，sin sin sin a b cA B C ==，即2ππ7πsin sin sin6412bc==，解得b c ==故ABC V 的周长为2+16．(1)()e 110x y ---=(2)()1,+∞【分析】（1）求导，结合导数的几何意义求切线方程；（2）解法一：求导，分析0a ≤和0a >两种情况，利用导数判断单调性和极值，分析可得2ln 10a a +->，构建函数解不等式即可；解法二：求导，可知()e '=-x f x a 有零点，可得0a >，进而利用导数求()f x 的单调性和极值，分析可得2ln 10a a +->，构建函数解不等式即可.【详解】（1）当1a =时，则()e 1x f x x =--，()e 1x f x '=-，可得(1)e 2f =-，(1)e 1f '=-，即切点坐标为()1,e 2-，切线斜率e 1k =-，所以切线方程为()()()e 2e 11y x --=--，即()e 110x y ---=.（2）解法一：因为()f x 的定义域为，且()e '=-x f x a ，若0a ≤，则()0f x '≥对任意∈恒成立，可知()f x 在上单调递增，无极值，不合题意；若0a >，令()0f x '>，解得ln x a >；令()0f x '<，解得ln x a <；可知()f x 在(),ln a ∞-内单调递减，在()ln ,a ∞+内单调递增，则()f x 有极小值()3ln ln f a a a a a =--，无极大值，由题意可得：()3ln ln 0f a a a a a =--<，即2ln 10a a +->，构建()2ln 1,0g a a a a =+->，则()120g a a a+'=>，可知()g a 在0,+∞内单调递增，且()10g =，不等式2ln 10a a +->等价于()()1g a g >，解得1a >，所以a 的取值范围为1,+∞；解法二：因为()f x 的定义域为，且()e '=-x f x a ，若()f x 有极小值，则()e '=-x f x a 有零点，令()e 0x f x a '=-=，可得e x a =，可知e x y =与y a =有交点，则0a >，若0a >，令()0f x '>，解得ln x a >；令()0f x '<，解得ln x a <；可知()f x 在(),ln a ∞-内单调递减，在()ln ,a ∞+内单调递增，则()f x 有极小值()3ln ln f a a a a a =--，无极大值，符合题意，由题意可得：()3ln ln 0f a a a a a =--<，即2ln 10a a +->，构建()2ln 1,0g a a a a =+->，因为则2,ln 1y a y a ==-在0,+∞内单调递增，可知()g a 在0,+∞内单调递增，且()10g =，不等式2ln 10a a +->等价于()()1g a g >，解得1a >，所以a 的取值范围为1,+∞.17．(1)证明见解析【分析】（1）由题意，根据余弦定理求得2EF =，利用勾股定理的逆定理可证得EF AD ⊥，则,EF PE EF DE ⊥⊥，结合线面垂直的判定定理与性质即可证明；（2）由（1），根据线面垂直的判定定理与性质可证明PE ED ⊥，建立如图空间直角坐标系E xyz -，利用空间向量法求解面面角即可.【详解】（1）由218,,52AB AD AE AD AF AB ====，得4AE AF ==，又30BAD ︒∠=，在AEF △中，由余弦定理得2EF ,所以222AE EF AF +=，则AE EF ⊥，即EF AD ⊥，所以,EF PE EF DE ⊥⊥，又,PE DE E PE DE =⊂ 、平面PDE ，所以⊥EF 平面PDE ，又PD ⊂平面PDE ，故⊥EF PD ；（2）连接CE，由90,3ADC ED CD ︒∠===，则22236CE ED CD =+=，在PEC中，6PC PE EC ===，得222EC PE PC +=，所以PE EC ⊥，由（1）知PE EF ⊥，又,EC EF E EC EF =⊂ 、平面ABCD ，所以PE ⊥平面ABCD ，又ED ⊂平面ABCD ，所以PE ED ⊥，则,,PE EF ED 两两垂直，建立如图空间直角坐标系E xyz -，则(0,0,0),(0,0,(2,0,0),(0,E P D C F A -，由F 是AB的中点，得(4,B ，所以(4,22(2,0,2PC PD PB PF =-===-，设平面PCD 和平面PBF 的一个法向量分别为111222(,,),(,,)n x y z m x y z ==，则11111300n PC x n PD ⎧⋅=+-=⎪⎨⋅=-=⎪⎩，222224020m PB x m PF x ⎧⋅=+-=⎪⎨⋅=-=⎪⎩，令122,y x =11220,3,1,1x z y z ===-=，所以(0,2,3),1,1)n m ==- ，所以cos ,65m n m n m n⋅==，设平面PCD 和平面PBF 所成角为θ，则sin 65θ==，即平面PCD 和平面PBF所成角的正弦值为65.【点睛】18．(1)0.686(2)（i ）由甲参加第一阶段比赛；（i ）由甲参加第一阶段比赛；【分析】（1）根据对立事件的求法和独立事件的乘法公式即可得到答案；（2）（i ）首先各自计算出331(1)P p q ⎡⎤=--⎣⎦甲，331(1)Pq p ⎡⎤=--⋅⎣⎦乙，再作差因式分解即可判断；(ii)首先得到X 和Y 的所有可能取值，再按步骤列出分布列，计算出各自期望，再次作差比较大小即可.【详解】（1）甲、乙所在队的比赛成绩不少于5分，则甲第一阶段至少投中1次，乙第二阶段也至少投中1次，∴比赛成绩不少于5分的概率()()3310.610.50.686P =--=.（2）（i ）若甲先参加第一阶段比赛，则甲、乙所在队的比赛成绩为15分的概率为331(1)P p q ⎡⎤=--⎣⎦甲，若乙先参加第一阶段比赛，则甲、乙所在队的比赛成绩为15分的概率为331(1)P q p ⎡⎤=--⋅⎣⎦乙，0p q << ，3333()()P P q q pq p p pq ∴-=---+-甲乙()2222()()()()()()q p q pq p p q p pq q pq p pq q pq ⎡⎤=-+++-⋅-+-+--⎣⎦()2222()333p q p q p q pq =---3()()3()[(1)(1)1]0pq p q pq p q pq p q p q =---=---->，P P ∴>甲乙，应该由甲参加第一阶段比赛.(ii)若甲先参加第一阶段比赛，比赛成绩X 的所有可能取值为0，5，10，15，333(0)(1)1(1)(1)P X p p q ⎡⎤==-+--⋅-⎣⎦，()()()3213511C 1P X p q q ⎡⎤==--⋅-⎣⎦，3223(10)1(1)C (1)P X p q q ⎡⎤==--⋅-⎣⎦，33(15)1(1)P X p q ⎡⎤==--⋅⎣⎦，()332()151(1)1533E X p q p p p q⎡⎤∴=--=-+⋅⎣⎦记乙先参加第一阶段比赛，比赛成绩Y 的所有可能取值为0，5，10，15，同理()32()1533E Y q q q p=-+⋅()()15[()()3()]E X E Y pq p q p q pq p q ∴-=+---15()(3)p q pq p q =-+-，因为0p q <<，则0p q -<，31130p q +-<+-<，则()(3)0p q pq p q -+->，∴应该由甲参加第一阶段比赛.【点睛】关键点点睛：本题第二问的关键是计算出相关概率和期望，采用作差法并因式分解从而比较出大小关系，最后得到结论.19．(1)23x =，20y =(2)证明见解析(3)证明见解析【分析】（1）直接根据题目中的构造方式计算出2P 的坐标即可；（2）思路一：根据等比数列的定义即可验证结论；思路二：利用点差法和合比性质即可证明；（3）思路一：使用平面向量数量积和等比数列工具，证明n S 的取值为与n 无关的定值即可.思路二：使用等差数列工具，证明n S 的取值为与n 无关的定值即可.思路三：利用点差法得到()11111n n n n n n P P n n n n x y x y k x y x y +++++++-=+--，()1222112211n n n n n n P P n n n n x y x y k x y x y -+++--++--++-=+--，再结合（2）中的结论得()1122n n n n x y q x y +++++=+，最后证明出112n n n n P P P P k k +-+=即可.【详解】（1）由已知有22549m =-=，故C 的方程为229x y -=.当12k =时，过()15,4P 且斜率为12的直线为32x y +=，与229x y -=联立得到22392x x +⎛⎫-= ⎪⎝⎭.解得3x =-或5x =，所以该直线与C 的不同于1P 的交点为()13,0Q -，该点显然在C 的左支上.故()23,0P ，从而23x =，20y =.（2）方法一：由于过(),n n n P x y 且斜率为k 的直线为()n n y k x x y =-+，与229x y -=联立，得到方程()()229n n x k x x y --+=.展开即得()()()2221290n n n n k x k y kx x y kx ------=，由于(),n n n P x y 已经是直线()n n y k x x y =-+和229x y -=的公共点，故方程必有一根n x x =.从而根据韦达定理，另一根()2222211n n n n nn k y kx ky x k x x x k k ---=-=--，相应的()2221n n nn n y k y kx y k x x y k +-=-+=-.所以该直线与C 的不同于n P 的交点为222222,11n n n n n n n ky x k x y k y kx Q k k ⎛⎫--+- ⎪--⎝⎭，而注意到n Q 的横坐标亦可通过韦达定理表示为()()2291n n ny kx k x ----，故n Q 一定在C 的左支上.所以2212222,11n n n n n n n x k x ky y k y kx P k k +⎛⎫+-+- ⎪--⎝⎭.这就得到21221n n n n x k x ky x k ++-=-，21221n n nn y k y kx y k ++-=-.所以2211222211n n n n n nn n x k x ky y k y kx x y k k +++-+--=---()()222222221211111n n n n n n n n n n x k x kx y k y ky k k kx y x y k k k k+++++++=-=-=-----.再由22119x y -=，就知道110x y -≠，所以数列{}n n x y -是公比为11k k+-的等比数列.方法二：因为(),n n n P x y ，()11,n n n Q x y ++-，11n n n n y y k x x ++-=-+，则111111n n n nn n n nx x y y k k x x y y +++++-++=-++-，由于22112299n n nn x y x y ++⎧-=⎨-=⎩，作差得()()()()1111n n n n n n n n x y x y x y x y ++++-+=-+，1111n n n n n n n n x y x y x y x y ++++-+=-+，利用合比性质知1111111111n n n n n n n n n n n n n n n n x y x y x y x y kx y x y x y x y k ++++++++-+-+++===-+-++-，因此{}n n x y -是公比为11kk+-的等比数列.（3）方法一：先证明一个结论：对平面上三个点,,U V W ，若(),UV a b = ，(),UW c d =，则12UVW S ad bc =- .（若,,U V W 在同一条直线上，约定0UVW S = ）证明：11sin ,22UVW S UV UW UV UW UV UW =⋅=⋅12UV UW =⋅==12ad bc ===-.证毕，回到原题.由于上一小问已经得到21221n n n n x k x ky x k ++-=-，21221n n nn y k y kx y k ++-=-，故()()22211222221211111n n n n n n n n n nn n x k x ky y k y kx k k kx y x y x y k k k k+++-+-+--+=+=+=+---+.再由22119x y -=，就知道110x y +≠，所以数列{}n n x y +是公比为11k k-+的等比数列.所以对任意的正整数m ，都有n n m n n mx y y x ++-()()()()()()1122n n m n n m n n m n n m n n m n n m n n m n n m x x y y x y y x x x y y x y y x ++++++++=-+-----()()()()1122n n n m n m n n n m n m x y x y x y x y ++++=-+-+-()()()()11112121mmn n n n n n n n k k x y x y x y x y k k -+⎛⎫⎛⎫=-+-+- ⎪ ⎪+-⎝⎭⎝⎭()22111211mmn n k k x y k k ⎛⎫-+⎛⎫⎛⎫=-- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭911211mmk k k k ⎛⎫-+⎛⎫⎛⎫=- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭.而又有()()()111,n n n n n n P P x x y y +++=---- ，()122121,n n n n n n P P x x y y ++++++=-- ，故利用前面已经证明的结论即得()()()()1212112112n n n n P P P n n n n n n n n S S x x y y y y x x ++++++++==---+-- ()()()()12112112n n n n n n n n x x y y y y x x ++++++=-----()()()1212112212n n n n n n n n n n n n x y y x x y y x x y y x ++++++++=-+---2219119119112211211211k k k k k k k k k k k k ⎛⎫-+-+-+⎛⎫⎛⎫⎛⎫⎛⎫=-+--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-+-+-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.这就表明n S 的取值是与n 无关的定值，所以1n n S S +=.方法二：由于上一小问已经得到21221n n n n x k x ky x k ++-=-，21221n n n n y k y kx y k ++-=-，故()()22211222221211111n n n n n n n n n nn n x k x ky y k y kx k k kx y x y x y k k k k+++-+-+--+=+=+=+---+.再由22119x y -=，就知道110x y +≠，所以数列{}n n x y +是公比为11k k-+的等比数列.所以对任意的正整数m ，都有n n m n n mx y y x ++-()()()()()()1122n n m n n m n n m n n m n n m n n m n n m n n m x x y y x y y x x x y y x y y x ++++++++=-+-----()()()()1122n n n m n m n n n m n m x y x y x y x y ++++=-+-+-()()()()11112121mmn n n n n n n n k k x y x y x y x y k k -+⎛⎫⎛⎫=-+-+- ⎪ ⎪+-⎝⎭⎝⎭()22111211mmn n k k x y k k ⎛⎫-+⎛⎫⎛⎫=-- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭911211mmk k k k ⎛⎫-+⎛⎫⎛⎫=- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭.这就得到232311911211n n n n n n n n k k x y y x x y y x k k ++++++-+⎛⎫-=-=- ⎪+-⎝⎭，以及22131322911211n n n n n n n n k k x y y x x y y x k k ++++++⎛⎫-+⎛⎫⎛⎫-=-=- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭.两式相减，即得()()()()232313131122n n n n n n n n n n n n n n n n x y y x x y y x x y y x x y y x ++++++++++++---=---.移项得到232131232131n n n n n n n n n n n n n n n n x y y x x y y x y x x y y x x y ++++++++++++--+=--+.故()()()()321213n n n n n n n n y y x x y y x x ++++++--=--.而()333,n n n n n n P P x x y y +++=--，()122121,n n n n n n P P x x y y ++++++=-- .所以3n n P P + 和12n n P P ++平行，这就得到12123n n n n n n P P P P P P S S +++++= ，即1n n S S +=.方法三：由于22112299n n n n x y x y ++⎧-=⎨-=⎩，作差得222211n n n n x x y y ++-=-，变形得()111111111n n n n n n n n n nP P n n n n n n n n y y x x x y x y k x x y y x y x y +++++++++-+++-===-++--①，同理可得()122121221121212211n n n n n n n n n n P P n n n n n n n n y y x x x y x y k x x y y x y x y -++-+-++--+-+-++---+++-===-++--，由（2）知{}n n x y -是公比为11kk +-的等比数列，令11k q k+=-则()11n n n n x y q x y ---=-②，同时{}n n x y +是公比为1q的等比数列，则()1122n n n n x y q x y +++++=+③，将②③代入①，()()()()()()2211111221111122112211n n n n n n n n n nn n n n n n n n n n n n n n n n n n q x y q x y y y x y x y x y x y x x x y x y q x y q x y x y x y ++--+++++--+++++--++--++--++-++-===-+--+--+--即112n n n n P P P P k k +-+=，从而1n n S S -=，即1n n S S +=.【点睛】关键点点睛：本题的关键在于将解析几何和数列知识的结合，需要综合运用多方面知识方可得解.。

2024届NCS高三摸底测试数学2023.9.08本试卷共4页，22小题，满分150分．考试时间120分钟．一．单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．l ．已知集合P={xly=✓句，Q={yl y=2x}，则A.Q�PB.P 已2C.P=QD.Q 己[,._p1 2.复数z＝一—-的虚部是3+4i3_ 3._ 4 A .-—B.－—iC.__i_ D.－土i2525c .2525－ －－ － 3.已知向噩a=(2,m),b=(m+l,l)，若a II b,则m=2 A.-=-B.1C.2或－1D.1或一234.已知公比为q 的等比数列{a n }的前n项和S n =2t2i -2q n,则t2i=1A.iB. 1C. 2D.45.已知抛物线C:x 2=4y 的焦点为F,P 是抛物线C 在第一象限的一点，过P 作C 的准线的垂线，垂足为M,FM的中点为N，若直线PN经过点(0,-3)，则直线PN的斜率为A.1B.2c .五D.36.已知函数y=e x 和y=lnx 的图象与直线y=2-x 交点的横坐标分别为a,b,则A.a >bB.a+b<2C.ab>lD.a 2+bf >27.已知函数f(x)的值域为A,函数g (x)=f(x) 2的值域为B ,则“A=[rl,l]“是f�(x)+l1 1 “B =［－一，一］”的2 2 A.充分不必要条件c.充要条件B.必要不充分条件D.既不充分也不必要条件兀兀8.若函数f(x)= c osx,a e（一，兀］，则函数f(x)在［一，a ］上平均变化率的取值范围为2 22A.(-1,0]B.(-1，一一］兀2 C.（女，O]D.(-00，一一］兀—高三数学第1页（共4页）－．二．多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求，全部选对得5分，部分选对的得2分，有选错的得0分·.9.“未来之星“少儿才艺大赛，选手通过自我介绍和才艺表演，展示仪表形象、表达能力、风度气质等自身的整体形象，评委现场打分．若九位评委对某选手打分分别是石，x 2,…，为，记这组数据的平均分、中位数、标准差、极差分别为歹，z,s,j,去掉这组数据的一个最高分和一个砐低分后，其平均分、中位数、标准差、极差分别为了',z',s',j'，则下列判断中一定正确的是A.x ＝艾＇B.z=zC.s2::s'D.}2::j'10.在下列四棱锥中，A,B,C,M ,N 是四棱锥的顶点或棱的中点，则MN/／平面ABC 的有,JBCN CNA BC D11.f(x)是定义在R 上连续可导函数，其导函数为J'（x)，下列命题中正确的是A.若f(x)= f (-x)，则f'(x)= -f'(-x)B.若f'(x)=f'(x+T)(T,;:. 0)，则f(x)=f (x+T)C.若f(x)的图象关千点(a,b)中心对称，则f'(x)的图象关千直线x=a 轴对称D.若f(-l+x)+f(-1-x)=2,f'(x+2)的图象关千原点对称，则f(-1)+/'(2)=112.已知双曲线C:x 2-y 2=2,点M为双曲线右支上的一个动点，过点M分别作两条渐近线的垂线，垂足分别为A,B 两点，则下列说法正确的是A．双曲线的离心率为✓1B.存在点M ，使得四边形OAMB 为正方形c.直线AB,OM 的斜率之积为2D.存在点M ，使得IMAl+JMBJ=✓3三填空题：本题共4小题，每小题5分，共20分13.已知直线x+y+2=0与圆f+y 2=r 2相切，则半径r=.14.(l-x+x 2)(l+x)6展开式中x 1的系数是一—-·15.如图，高度均为3的封闭玻璃圆锥和圆柱容器内装入等体积的水，此时水面高度均为h,若h=2,记圆锥的底面半径R 为R,圆柱的底面半径为r,则一＝h.... L ..16.已知函数y =A sin(x+rp)(A > 0)的图象与直线y=m (O<m <A)连续的三个公共点从m左到右依次为M ,N,P,若IPNl=3IMNI,则一＝．A一高三数学第2页（共4页）－四．解答题：共70分．17题10分，其余大题12分一道，解答应写出文字说明、证明过程或演算步骤亢17.00分）在A钮C中，角A,B ,C所对的边分别为a,b,c,C=-:;-, acosB+bcosA= abc. 3(I)求A钮C的面积：(2)若c=1，求丛BC的周长．18.(12分）如图，在三棱锥P-AB C中，AB .LBC ,M,N分别为AC,A B的中点，B.(l)求证：AB.LPN:(2)若AB=BC= 2, BP= PM= 3,求二面角N-PM-B的余弦值．P.ABc19.（l2分）如图，第n个图形是由棱长为n+l的正方体挖去棱长为n的正方体得到的，记其体积为包｝．勹第1个图第2个图(1)求证：a n = 3n 2 + 3n + 1 ;(2)求和：12+22+32+…+n 2.•••••• 第3个图••••••一高三数学第3页（共4页）－X y 3 20.(12分）已知椭圆C:勹·+—=l(a > b > O)经过点M (l，一a b 2 23为坐标原点，tiOFM的面积为—.4(1)求椭圆C 的标准方程：), F 为椭圆C 的右焦点，O (2)过点P(4,0)作一条斜率不为0的直线与椭圆C 相交千A,B 两点(A 在B,P 之间），直线BF与椭圆C的另一个交点为D,求证；点A,D关千x 轴对称．21. (12分）迎“七一＂党建知识竞赛，竞赛有两关，某学校代表队有四名队员，这四名队员若有机会参加这两关比赛，通过的概率见下表：队员第一关第二关甲3 24 3乙32 43 丙2 13 2 丁2 13 2比赛规则是：从四名队员中随机选出两名队员分别参加比赛，每个队员通过第一关可以得60分，且有资格参加第二关比赛，若没有通过，得0分且没有资格参加第二关比赛，若通过第二关可以再得40分，若没有通过，不再加分两名参赛队员所得总分为该代表队的得分，代表队得分不低于160分，可以获得“党建优秀代表队啼尔号．假设两名参赛队员不相互影响．(l)1求这次比赛中，该校获得“党建优秀代表队”称号的概率；(2)若这次比赛中，选中了甲乙两名队员参赛，记该代表队的得分为X,求随机变世X 的分布列和期望．22.(12分）已知函数f(x)= a x(a > 1).1(1)求函数g(x)= J(x) + f （一）在(0，七吩上的单调区间和极值；X1(2)若方程f （一）＝I-xlog a X有两个不同的正根，求a的取值范围．X一高三数学第4页（共4页）－一．单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．|＝: 1 ; I :I ; |； I : I ; l : I : I二多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求，全部选对得5分，部分选对的得2分，有选错的得0分，|:： IB 乙）1 ；： I A心）1 ；； |三填空题：本题共4小题，每小题5分，共20分，13.✓2;14.5;15.3忘五:16.— 13.·-· 2. 四．解答题：共70分．17题10分，其余大题12分一道，解答应写出文字说明，证明过程或演舞步骤17.【解析】（I )由已知，si n AcosB +si n BcosA = ab s n C ,即si n (A + B)= a b s n C ,si n C=absi n C,所以ab=I,故.MBC 的面积为－absi n C=..:.x Ix ....:...=....:.... ＄五22 24 (2)由余弦定理，cosC=a 2 +b 2 -c 2 ___ a 2+b 2 -I I可得a ＝－ 2a b2 2' ........................ 3分························ 5分所以矿＋b 2= 2, ························ 7分所以(a +b)2=a 2 +b l + 2ab = 4,即a+b=2,所以凶BC 的周长为3………......…...…10分18.【解析】(I )因为M ,N 分别为AC,AB 的中点，所以NM II BC,........................ 2分因为AB.lBC,所以AB.lMN,因为AB.lPM,PMnMN=M, 所以AB.l 平面P1vf N,所以AB.lPN:(2)因为AB =BC = 2, BP= P M = 3,则NM =NB=I,所以LIPNB = LIPNM,因为AB.lPN,所以PN.lNM,因为NB门NM=N,所以PN.l 平面ABC,因为AB=BC= 2,BP = PM =3,所以PN=2五伽，以NB 为x 轴，NM 为y 轴，NP 为z 轴，建立如图所示的空间直角坐标系，则M (O,l,O),B(l,0,0), P(0,0,2✓2),所以啼＝（1,-1,0)，而＝（0,-1,2五），设平面PMB 的法向揽为n 1=(x,y,z),则尸B 元＝0x -y =0，所以MP fl l =0{-y +2迈z=O '........................ 5分........................ 7分pAc令z = I,得到元＝（2J5,2J5,l),平面PMN的法向蜇为闪＝（1,0,0)所以cos < n 1,n 2 >= n 1世迈2尽-－= ＝, 仇I|n 21而172尽则二面角N-PM -B的余弦值为——1719.【解析】(I )棱长为n +）的正方体的体积为(n + 1)3,棱长为n的正方体的体积为矿，3 3. � 2 所以a ,,=(n + 1)3 -n = n 3 + 3n 2 + 3n + 1-,i 3 = 3n 2 + 3n + 1: (2)由(I)可知an = (n + 1)3 -n 3 = 3n 2 + 3n + l,........................ 10分........................ 12分........................ 3分........................ 5分........................ 7分则a 1+ a 2 +···+a,,=3 x I 2+ 3xl + l + 3x22+ 3x2 +l + · ·· +3 x n 2 + 3xn + l 2-. -... n(n +I) =3x(l 2 +22 +···+n 2)+3x(l +2+···+n)+n =3x(I 2 +22 +···+n 2)+3x-—+n2又a 1+ a 2 +···+a ,, == 2仁13+ 33-23 + · · · +(n + 1)3 -n 3 = (n + 1)3 -I = n 3 + 3n 2 + 3n, 2'.,., n(n +l) 所以3x(l 2+22 +..·+ n 2)+3x�+n = n 3 +3n 2 +3n, 22 2n 3+ 3n 2 + n n(n + I )(2n + I) 即I 2+ 22+ 32+... + n 2 = 6 = 6........................ 12分3 l3 3 20.【解析】(I )因为AOFM 的面积为－，则有－xcx -＝一，解得c =l,……2分又因为M (l ,%)在椭圆C 上则［：：：：＝1舟2年得厂：：22x-. y 所以椭圆C的标准方程为—-＋—-＝l :...………...……... 5分4 3(2)根据椭圆的对称性，欲证A,D关干x轴对称，只需证忆＝－k F D'即证k FA +k PB = 0,设A (x 2,y 2),B (x ,y,)，直线AB方程为x=m y +4,由{x =m y +4消去x 得(3m 2+4)y 2 +24m y +36 = 0,3x 2+4y 2=12-24m36 所以y 1+y 2 = ，y l y 2 = 3m 2 +4 3m 2+4........................ 9分则k FA +k 吓＝——-＋——-＝ y l y 2片(x 2-l )＋y 2(x 1 -l ) = Y凸＋y凸－（y 1+y 2)x 1-I ;飞:2-I (;飞l-l)(入;2-1) (x 1 -I)（]飞·2-l)36-24m 因为y凸＋y凸－（Y i +Y 2)=2my凸＋3(y 1+ y 2)=2mx �+3�=0 3m 2 + 4 · -3m 2+ 4所以k F A +k FB = 0,即A,D 关于x 轴对称...………………... 12分21.【解析】(I )记选出甲乙两名队员参赛为事件A I '选出甲乙、丙丁各一人参赛为事件4,选出丙丁两名队员参赛为事件4,活动”党建优秀代表队”称号为事件Bc 2 l C扂2C2l 则P(A,)＝－主＝－，P (A 2)=——-＝ －,P(A J =�=-;. ························ 3分@ 6C : 3 @ 6 P(B) =P(A 1B + A i B + A 3B) l 3 2 2 2 l 2 3 2 2 l l l 2 1=－x(－）2 x[（－） ＋2x-X-］＋－X-X-x(－X-＋－X-+－X-）+6 4 33 3 34 3 3 2 3 2 3 2 l 2 2 1 2.l l l5 1 5 -x (－） x [（－） ＋ 2 x -X -］ ＝—+ -＋—=—.．．．．．．．．．．．．．．．．．．．．．．．6分6'3'. "2'. -2. 2'12. 18. 18 12(2)X 的可能取伯为：0,60, I 00, 120,160,200,l l 3) l lP(X= 0) = (�)2=—, P(X=60)＝2x -X -X -=-, 4 164 3 4 8 3 2 1 1 3 2 l lP(X = 100) = 2x.=;.x 7x"7="7, P(X = 120)＝（一）x（－）2 =－,4 3 4 4 4 3 16 3 2 1 l 3 2 2 P(X=160) ＝（－）2x2x -x-＝－，P(X=200) ＝（-)2x(－） ＝－14 3 3 4 4 34 所以随机变噩X 的分布列为：勹60 JOO 120 16020016l -8-416 -4-4l l l l l l所以EX=Ox —+60x ..:.+ 1oox ..:..+ 120x —+l60x ..:..+20ox ..:.. =130.16 8 4 16 4 4........................ 12分22.【解析】(I)g(x)＝矿＋a;,(a>I),Ia 'Ina Ina 则g'(x)= a "'Ina --了-= ---,-(x切－a ')'x-.!. l l 设h(x)= x 切－矿，则h'(x)= 2xa -'+ x 切X Ina+—a;lna>O,X2 ........................ 2分故h(x)在（0，七o )单调递增，又因为h(l)= 0, 故g(x)在(0,l)单谓递减，在(l ,+oo)单调递增则g(x)的极小值为g(l)=2a,无极大值．........................ 5分L .. --....!. (2)因为八－）＝1-x-log. x ，所以1-xlog,,x=a·',XI I .:..a x = lo g.(.:...a x ),XXI］ －令t =.:..a x'显然t=－矿在(0,+oo)单调递减，XXI故有八－）＝1-x -log� x 两个正根，等价于h(t)= t-log,, t 有两个零点X........................ 7分l lh'(t) = 1-—，易然t E (0，一一）时，h'(t)< 0, lna ·t· · 1naltE(—,+oo)时，h'(t)> 0,Inall故h(t)在(0,—-）递减，（—－，+oo)递增，lna lna l l l h(t)min = h (—) ＝—-log 0—=log 0(a 古ln a),lna ln a lnaI令log0（产lna)<O,所以a i;;;;·lna<L 则a 石<IIn al.!....!...l设x 。

专题11.8多边形及其内角和（精选精练）（专项练习）一、单选题（本大题共10小题，每小题3分，共30分）1．（23-24六年级下·山东烟台·期中）过多边形一个顶点的所有对角线将这个多边形分成3个三角形，这个多边形是（）A ．五边形B ．六边形C ．七边形D ．八边形2．（23-24八年级下·安徽阜阳·阶段练习）一个正多边形的内角和为1080︒．则这个正多边形的边数为（）A ．9B ．8C ．7D ．63．（2024·福建福州·模拟预测）如图1是颐和园小长廊五角加膛窗，其轮廓是一个正五边形，如图2是它的示意图，它的一个外角α的度数为（）A ．70︒B ．72︒C ．60︒D ．108︒4．（2020·辽宁葫芦岛·三模）如图，多边形ABCDEFG 中，108E F G ∠=∠=∠=︒,72C D ∠=∠=︒，则A B ∠∠+的值为（）A ．108︒B ．72︒C ．54︒D ．36︒5．（2024·内蒙古赤峰·三模）如果一个正多边形的一个外角是45︒，则这个正多边形是正（）边形A ．六B ．八C ．十D ．十二6．（2024·湖北荆门·模拟预测）小聪利用所学的数学知识，给同桌出了这样一道题：假如从点A 出发，沿直线走9米后向左转θ，接着沿直线前进9米后，再向左转θ，…，如此下去，当他第一次回到点A 时，发现自己一共走了72米，则θ的度数为（）A．60︒B．75︒C．30︒D．45︒7．（2024·云南玉溪·三模）若一个正多边形的每一个外角都是36︒，则该正多边形的内角和的度数是（）．A．1440︒B．360︒C．1800︒D．2160︒∠=︒，则1∠的度数为8．（2024·河北石家庄·三模）如图，五边形ABCDE是正五边形，AF DG∥，若226（）A．86︒B．64︒C．62︒D．52︒9．（23-24九年级下·河北邯郸·期中）综合实践课上，嘉嘉用八个大小相等的含45°角的直角三角板拼成了一个环状图案，如图1，若淇淇尝试用含60°角的直角三角板拼成类似的环状图案，如图2，除了图上3个还需要含60°角的直角三角板的数量为（）A．3个B．6个C．9个D．12个10．（2024·河北沧州·二模）用“筝形”和“镖形”两种不同的瓷砖铺设成如图所示的地面，则“筝形”瓷砖中的∠的度数为（）内角BCDA．120︒B．135︒C．144︒D．150︒二、填空题（本大题共8小题，每小题4分，共32分）11．（2024八年级下·全国·专题练习）一个八边形的内角和是．12．（23-24六年级下·山东济南·期中）若从n边形的一个顶点最多能引出2条对角线，则n是．13．（2024·湖北咸宁·一模）一个多边形的内角和为540︒，这个多边形的边数是．14．（2024·陕西宝鸡·模拟预测）一个正多边形的内角比外角大90︒，则这个多边形的内角和为．15．（23-24八年级上·辽宁营口·期中）如果把一个多边形剪去一个内角，剩余部分的内角和为1440︒，那么原多边形有条边．16．（19-20七年级下·江苏扬州·期末）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝．17．（2024·陕西西安·模拟预测）一个正多边形的外角和与内角和的比为1:3，则这个多边形是正边形．18．（2024·云南昆明·二模）如图，一个正n边形被树叶遮掩了一部分，若直线a，b所夹锐角为36︒，则n的值是．三、解答题（本大题共6小题，共58分）19．（8分）（21-22八年级下·广西桂林·期中）列式计算：求图中x的值．20．（8分）（23-24八年级上·江西南昌·期末）如果多边形的每个内角都比与它相邻的外角的4倍多30︒．（1）这个多边形的内角和是多少度？（2）求这个多边形的对角线的总条数．21．（10分）（23-24八年级上·新疆昌吉·期中）如图，在五边形ABCDE 中，100120AE CD A B �靶=，，∥（1）若110D ∠=︒，请求E ∠的度数；（2）试求出C ∠及五边形外角和的度数．22．（10分）（23-24七年级下·湖南衡阳·阶段练习）如图，阅读佳佳与明明的对话，解决下列问题：（1）多边形内角和为什么不可能为2020︒？（2）明明求的是几边形的内角和？（3）错当成内角的那个外角为多少度？23．（10分）（2024·浙江杭州·一模）问题情境：在探索多边形的内角与外角关系的活动中，同学们经历了观察、猜想、实验、计算、推理、验证等过程，提出了问题，请解答．（1）若四边形的一个内角的度数是α．①求和它相邻的外角的度数（用含α的代数式表示）；②求其他三个内角的和（用含α的代数式表示）．n>，除了一个内角，其余内角的和为920︒，求n的值．（2）若一个n边形(3)深入探究：n>的一个外角与和它不相邻的(n)1-个内角的和之间满足的等量关系，说明理由．（3）探索n边形(3)24．（12分）（1）已知图①中的三角形ABC，分别作AB，BC，CA的延长线BD，CE，AF，测量∠CBD，∠ACE，∠BAF的度数，并计算∠CBD+∠ACE+∠BAF．由此你有什么发现？请利用所学知识解释说明；（2）类似地，已知图②中的四边形PQRS，分别作PQ，QR，RS，SP的延长线QG，RH，SM，PN，测量∠RQG，∠SRH，∠PSM，∠QPN的度数，并计算∠RQG+∠SRH+∠PSM+∠QPN．由此你又有什么发现？（3）综合（1）（2）的发现，你还能进一步得到什么猜想？参考答案：1．A【分析】本题考查了多边形的对角线数量问题，根据n 边形从一个顶点出发可引出()3n -条对角线，可组成()2n -个三角形，依此可求出n 的值，得到答案．【详解】解：设这个多边形是n 边形，由题意得：23n -=，解得：5n =，即这个多边形是五边形，故选：A ．2．B【分析】本题多边形内角和公式，解题关键是理解并熟记多边形内角和公式．根据多边形内角和定理：可得方程()18021080x ︒⨯-=︒，再解方程即可．【详解】解：设多边形边数有x 条，由题意得：()18021080x ︒⨯-=︒解得：8x =故选B3．B【分析】本题主要考查多边形的内角和外角，熟练掌握正多边形的外角和为360︒是解题的关键．根据多边形的外角和为360︒即可作答．【详解】解：360572÷=︒．故选：B ．4．B【分析】连接CD ，设AD 与BC 交于点O ，根据多边形的内角和公式即可求出∠E ＋∠F ＋∠G ＋∠EDC ＋∠GCD ，根据各角的关系即可求出∠ODC ＋∠OCD ，然后根据对顶角的相等和三角形的内角和定义即可求出结论．【详解】解：连接CD ，设AD 与BC 交于点O∵∠E ＋∠F ＋∠G ＋∠EDC ＋∠GCD=180°×（5－2）=540°，108E F G ∠=∠=∠=︒，72∠=∠=︒GCB EDA ，∴108°＋108°＋108°＋72°＋∠ODC ＋72°＋∠OCD=540°∴∠ODC ＋∠OCD=72°∵∠AOB=∠COD∴∠A ＋∠B=180°－∠AOB=180°－∠COD=∠ODC ＋∠OCD=72°故选B ．【点拨】此题考查的是多边形的内角和公式和对顶角的性质，掌握多边形的内角和公式和对顶角相等是解决此题的关键．5．B【分析】本题考查了正多边形的外角性质，根据正多边形的外角都相等以及外角和为360︒，列式36045︒÷︒进行计算，即可作答．【详解】解：∵一个正多边形的一个外角是45︒，∴360458︒÷︒=，∴这个正多边形是正八边形，故选：B ．6．D【分析】本题考查了多边形的内角与外角，解决本题的关键是明确第一次回到出发点A 时，所经过的路线正好构成一个正多边形．第一次回到出发点A 时，所经过的路线正好构成一个正多边形，用8972=÷，求得边数，再根据多边形的外角和为360︒，即可求解．【详解】解：∵第一次回到出发点A 时，所经过的路线正好构成一个正多边形，∴正多边形的边数为：8972=÷，根据多边形的外角和为360︒，∴则他每次转动θ的角度为：360845︒÷=︒，故选：D ．7．A【分析】本题主要考查了多边形的内角和与外角和，掌握内角和公式是解题的关键．根据任何多边形的外角和都是360︒，可以求出多边形的边数，再根据多边形的内角和公式，就得到多边形的内角和．【详解】解：根据题意得：该多边形的边数为：3601036︒=︒，∴该正多边形的内角和为：()1021801440-⨯︒=︒．故选：A ．8．C【分析】此题考查了多边形的内角和外角及平行线的性质，熟记多边形内角和公式及平行线的性质是解题的关键．连接AD ，根据多边形的内角和及平行线的性质求解即可．【详解】如图,连接AD ,∵五边形ABCDE 是正五边形，()521801085E BAE -⨯︒∴∠=∠==︒，EA ED =，()34180108236∴∠=∠=︒-︒÷=︒，5108472∴∠=︒-∠=︒，226∠=︒ ，2598,DAF ∴∠=∠+∠=︒,AF DG 98,ADG ∴∠=︒1362.ADG ∴∠=∠-∠=︒故选:C ．9．C【分析】本题主要考查了正多边形的外角和．多边形由拼图方法可知：环状图案的外围是正多边形，根据正多边形外角和等于360︒即可求出正多边形的边数．【详解】解：依题意可知：用含60°角的直角三角板按图示拼成类似的环状图案是正多边形，正多边形的外角180(9060)30=︒-︒+︒=︒，故正多边形的边数为3603012︒÷︒=（条）∴除了图上3个还需要含60°角的直角三角板的数量为1239-=（个）故选C ．10．C【分析】本题主要考查了多边形内角和定理，根据5个“筝形”组成一个正十边形，结合多边形内角和定理求解即可【详解】解；由图可知，5个“筝形”组成一个正十边形，∴()180********BCD ︒⨯-∠==︒，故选：C11．1080︒/1080度【分析】本题考查了多边形内角和定理，直接套用多边形的内角和()2180n -⋅︒进行计算可求八边形的内角和，【详解】解：内角和：()8218061801080-⨯︒=⨯︒=︒．故答案为：1080︒12．5【分析】本题考查了多边形的对角线，牢记n 边形从一个顶点出发可引出(3)n -条对角线是解题的关键．据此求解即可．【详解】解：∵从n 边形的一个顶点最多能引出2条对角线，∴32n -=，∴5n =．故答案为：5．13．5【分析】本题考查多边形的内角和公式，n 边形的内角和公式为()2180n -⨯︒，由此列方程即可得到答案．【详解】解：设这个多边形的边数为n ，则()2180540n -⨯︒=︒，解得5n =，故答案为：5．14．1080︒/1080度【分析】本题考查了多边形外角和与内角和，掌握其计算公式是解题的关键．多边形的内角和公式为：()2180n -⨯︒（其中n 为多边形的边数），多边形的外角和是360︒．因为多边形的外角和是360︒，且正多边形的每个内角都相等，每个外角也都相等，设这个正多边形的一个外角为x ，则内角为90x +︒，根据内角与外角的和为180︒可列出方程．【详解】设外角是x ，则内角是180x ︒-，则18090x x ︒--=︒，解得45x =︒．则多边形的边数是：360458︒÷︒=．∴内角和是：()821801080-⨯︒=︒．故答案为：1080︒．15．11或10或9【分析】本题考查了多边形的内角和度数，熟记相关结论是解题关键．【详解】解：以五边形为例，如图所示：剪去一个内角后，多边形的边数可能加1，可能不变，也可能减1设新多边形的边数为n ，则()21801440n -⨯︒=︒，解得：10n =∴原多边形可能有11或10或9条边．故答案为：11或10或9．16．540°【分析】连接ED ，由三角形内角和可得∠A+∠B=∠BED+∠ADE ，再由五边形的内角和定理得出结论．【详解】连接ED ，∵∠A+∠B=180°-∠AOB ，∠BED+∠ADE=180°-∠DOE ，∠AOB=∠DOE ，∴∠A+∠B=∠BED+∠ADE ，∵∠CDE+∠DEF+∠C+∠F+∠G=(5-2)×180°=540°，即∠CDO+∠ADE+BED+∠BEF+∠C+∠F+∠G=540°，∴∠A+∠B+∠C+∠CDO+∠BEF+∠F+∠G=540°．故答案为：540°．【点拨】本题考查了三角形的内角和公式，以及多边形的内角和公式，熟记多边形的内角和公式为(n -2)×180°是解答本题的关键．17．八【分析】本题主要考查了多边形的内角和，熟练掌握多边形的内角和公式，是解决问题的关键设这个正多边形的边数为n ，根据正多边形的外角和与内角和的比为1:3，利用多边形内角和公式与外角和列方程解答并检验，即得【详解】设这是个正n 边形，∵这个正多边形的外角和与内角和的比为1:3，∴()360121803n =-⨯，解得，8n =，经体验8n =是所列方程的解，且符合题意，∴这是个正八边形，故答案为：八18．5【分析】本题主要考查了多边形的内角和外角，解题关键是熟练掌握正多边形的定义及性质和外角和．先根据题意画出图形，再根据已知条件求出2∠和3∠的度数，然后根据正多边形的性质和外角和，求出正多边形的边数即可．【详解】解：如图所示：由题意得：136∠=︒，123180∠+∠+∠=︒ ，2318036144∴∠+∠=︒-︒=︒，正多边形每个外角都相等，23144272∴∠=∠=︒÷=︒，正多边形的外角和为360︒，∴它的边数为：360725÷=，n ∴的值为5，故答案为：5．19．100【分析】本题考查了四边形的内角和定理，根据题意，列式109060360x x +++︒+︒=︒计算即可．【详解】根据题意，列式109060360x x +++︒+︒=︒，解得100x =，故图中x 的值为100．20．(1)1800︒(2)54【分析】本题主要考查多边形内角与外角的知识点，此题要结合多边形的内角和公式寻求等量关系，构建方程求解即可．另外还要注意从n 边形一个顶点可以引3n -（）条对角线．（2）求出多边形的边数，利用多边形内角和公式即可得到答案；（3）根据n 边形有()32n n -条对角线，即可解答．【详解】（1）解：设这个正多边形的一个外角为x ︒，依题意有430180x x ++=，解得30x =，3603012︒÷︒=∴这个正多边形是十二边形．∴这个正多边形的内角和为(122)1801800-⨯︒=︒（2）解：对角线的总条数为4(1231)252-=⨯(条)．21．(1)70E ∠=︒(2)140C ∠=︒，五边形外角和的度数是360︒【分析】本题主要考查多边形内角和、外角和及平行线的性质，熟练掌握多边形内角和及平行线的性质是解题的关键．（1）根据平行线的性质可进行求解；（2）根据多边形内角和、外角和及平行线的性质可进行求解．【详解】（1）解：∵AE CD ∥，∴180D E ∠+∠=︒，∴180********E D ∠∠=︒-=︒-︒=︒；（2）解：五边形ABCDE 中，()52180540A B C D E ∠+∠+∠+∠+∠=-⨯︒=︒，∵180D E ∠+∠=︒，100A ∠=︒，120B ∠=︒，∴()540C D E A B∠∠∠∠∠=︒-+--140=︒；五边形外角和的度数是360︒．22．(1)见解析(2)十三边形或十四边形(3)110︒或20︒【分析】本题主要考查了多边形内角和定理，多边形内角和外角的关系以及二元一次方程组的应用．（1）根据多边形内角和定理公式计算判断即可．（2）设应加的内角为x ，多加的外角为y ，依题意可列方程为()21802020n y x -=-+ ，结合角的属性建立不等式求整数解即可．（3）分别计算十三边形的内角和以及十四边形的内角和，分别列出关于x ，y 的二元一次方程组求解即可．【详解】（1）设多边形的边数为n ，由题意得()18022020n -= ，解得2139n =，∵n 为正整数，∴多边形的内角和不可能为2020︒．（2）设应加的内角为x ，多加的外角为y ，依题意可列方程为()21802020n y x -=-+ ，∵180180x y -<-< ，∴()202018018022020180n -<-<+ ，解得22121499n <<，又∵n 为正整数，∴n 13=或14n =．故明明求的是十三边形或十四边形的内角和．（3）十三边形的内角和为()1801321980⨯-= ，∴2020198040y x -=-= ，又180x y += ，∴70x = ，110y = ．十四边形的内角和为()1801422160⨯-= ，∴21602020140x y -=-= ，又180x y += ，∴160x = ，20y = ．所以错当成内角的那个外角为110︒或20︒．23．（1）①180α︒-，②360α︒-（2）8n =；（3）(3)180n βα-=-⨯︒，理由见解析【分析】（1）①根据一个内角与它相邻的外角的和是180︒进行计算即可；②四边形的内角和是360︒进行计算即可；（2）根据多边形的内角和的计算方法进行计算即可；（3）表示出和它不相邻的(n )1-个内角的和即可．【详解】解：（1）①四边形的一个内角的度数是α，则与它相邻的外角的度数180α︒-；②由于四边形的内角和是360︒其中一个内角为α，则其它三个内角的和为360α︒-；（2）由题意得，(2)180920n α-⨯︒-=︒，3n > 的正整数，0180α︒<<︒，8n ∴=，即这个多边形为八边形；（3）设n 边形(3)n >的一个外角为α，它不相邻的(n )1-个内角的和为β，则有180(2)180n αβ︒-+=-⨯︒，即(3)180n βα-=-⨯︒．24．（1）见解析，∠CBD +∠ACE +∠BAF ＝360°，三角形中的外角和为360°，见解析；（2）∠RQG +∠SRH +∠PSM +∠QPN ＝360°，见解析；（3）多边形的外角和和都是360°，见解析【分析】（1）经测量得出∠CBD ＝138°，∠ACE ＝117°，∠BAF ＝105°，∠CBD +∠ACE +∠BAF ＝360°，则据此得出结论三角形中的外角和为360°，根据平角是180°和多边形内角和证明即可；（2）分别测量出几个角并求出这几个角的和，得出结论：在四边形的外角和是360°；根据（1）中证明方法证明即可；（3）猜想：多边形的外角和和都是360°．根据（1），（2）方法证明即可；【详解】解：（1）经测量知∠CBD ＝138°，∠ACE ＝117°，∠BAF ＝105°，∴∠CBD +∠ACE +∠BAF ＝360°，发现：三角形中的外角和为360°，理由：∵∠CBD+∠ABC＝180°，∠ACE+∠ACB＝180°，∠BAC+∠BAF＝180°，∴∠CBD+∠ACE+∠BAF+∠ABC+∠ACB+∠BAC＝540°，又∵∠ABC+∠ACB+∠BAC＝180°，∴∠CBD+∠ACE+∠BAF＝360°；（2）∠RQG＝125°，∠SRH＝113°，∠PSM＝48°，∠QPN＝74°，所以∠RQG+∠SRH+∠PSM+∠QPN＝360°；发现：在四边形的外角和是360°；∵∠RQG+∠PQR＝180°，∠SRH+∠QRS＝180°，∠PSM+∠RSP＝180°，∠QPN+∠QPS＝180°，∵∠RQG+∠PQR+∠SRH+∠QRS+∠PSM+∠RSP+∠QPN+∠QPS＝720°，∵∠PQR+∠QRS+∠RSP+∠QPS＝360°，∴∠RQG+∠SRH+∠PSM+∠QPN＝360°．（3）猜想：多边形的外角和都是360°．设多边形为n边形，则n边形的每一个内角与它相邻的外角的和为180°，∴n边形的外角和＝180°n﹣（n﹣2）×180°＝180°n﹣180°n+360°＝360°．【点拨】此题考查多边形外角和的知识，利用平角是180°结合多边形内角和证明即可．。

S7-1500与S7-1200的Profinet通信实例一一、 1515与1214 S7通信：第一步创建”项目名称“如1500练习20170110。

第二步：此界面点击“新手上路”内的任何一个菜单，都可以进入相应的编程界面。

第三步：点击创建PLC设备。

第四步：选择“控制器", SIMATIC S7-1500,CPU 1515-2PN,6ES7-S515-2AM01-0ABO,设备名称可更改，点击确定。

•,,·, 嗣岫压，七士七,女子-.:.;l'i:几已，印'i >J 九,r o 11w 凇出H 拉I I们1日�• �·(•.ti:,!'t l 芯令II｀j'L/夕．心ll田片1凸品t3膏。

门'Ill亡h 开叩H � 认,e r ,f 片，令含第五步：双击"M ain"或者点击”项目视图＇，进入编程界面。

日冒第六步：项目视图包括多个编程界面：项目树、菜单栏、信息窗口、指令窗口、库窗口等。

第七步：点击“添加新设备“添加1214CPU, 确定后，会自动跳到“设备和网络”窗口。

可直接点击“设备和网络＂配置CPU的别的模块。

�'f I第八步：在“设备和网络＂窗口，将显示添加的PLC,直接将“硬件目录”下相应的模块拖到轨”上。

?!_!-,I I?;, 业第九步：相同的方法配置1515CPU的电源模块。

"E己，寸ll第十步：点击"PLC_l"下的设备组态，点击CPU模块，在“信息窗口”设置CPU的I P地址。

用同样的方法，配置其他CPU的I P地址。

第十一步：各PLC间使用S7通信，在“设备和网络＂窗口下，选择“网络视图”，点击“连接”，选择"S7连接＂，鼠标左键按住PLC3的网线接口，拖动连接到PLCl的网线接口，相同的方法连接PLC2与PLCl.第十二步：点击“在线＇选择每个P L C,点击“转至在线＇。

第1章习题1.1隧道空气中常见的有害气体有哪些？隧道空气中常见的有害气体主要指的是机动车辆通过隧道时所排放出的废气，它包含的主要有害气体有一氧化碳(CO)、一氧化氮(NO)、二氧化氮(N02)及其他氮氧化合物(NO x)、硫化气体(H2S,S02)、甲醒(H C H O)、乙醋(C H3C H O)、粉尘以及未燃烧完全的燃料微粒所形成的烟尘等。

1.2隧道空气的主要成分有哪些？隧道内空气即地面空气，地面空气是由干空气和水蒸气组成的混合气体，通常称为湿空气。

湿空气中仅含有少量的水蒸气，但其含噩的变化会引起湿空气的物理性质和状态发生变化。

干空气是指完全不含有水蒸气的空气，它是由氧、氮、二氧化碳、氪、氖和其他一些微量气体所组成的混合气体。

隧道内地面大气中还含有各类细微颗粒，如尘埃、微生物等。

这些物质不计入空气的组分，也不影响主要成分之间的比例关系。

1.3什么叫隧道气候？隧道气候是指隧道空气的温度、湿度和流速这三个参数的综合作用状态。

这三个参数的不同组合，便构成了不同的隧道气候条件。

隧道气候条件对作业人员的身体健康和劳动安全有重要的影响。

第2章习题2.1描述隧道空气物理状态的参数主要有哪些？并简要说明其定义。

(1)描述隧道空气物理状态的参数主要有压力、温度、湿度、比容、密度、粘度、比热、焙等状态参数。

(2)空气的压力（压强在隧道通风中习惯称为压力）也称为空气的静压，用符号P表示，它是空气分子热运动对器壁碰撞的宏观表现，其大小取决于在重力场中的位噩（相对高度）、空气温度、湿度（相对湿度）和气体成分等参数。

(3)温度是物体冷热程度的标志。

根据分子运动理论，气体的温度是气体分子运动动能的度量。

(4)空气的湿度是指空气的潮湿程度，有两种度量方法：绝对湿度和相对湿度。

(5)空气和其他物质一样具有质量，单位体积空气所具有的质量称为空气的密度，用P(kg/m3)表示。

(6)单位质量物质所占的容积称为比容，用u Cm勺kg)表示。

阳新县2022-2023学年度下学期期末考试八年级数学试卷班级姓名一一－考号注意事项1.本试卷分为试题卷和答题卡两部分。

考试时间为120分钟，满分为120分。

2.考生在答题前请阅读答题卡中的“注意事项”，然后按要求答题。

3.所有答案均须做在答题卡相应区域，做在其他区域无效。

一、单选题〈每小题3分，共30分〉l代数式豆互有意义的x的取值范围是（A. x 二三－1且X;t:0B.x 二三－12.下列二次根式是最简二次根式的是（ C.x<-1 D.x＞－］且X;t:0A 而3B.$5c.J王D在3一次函数y=-x+5的图象经过（）A 一、二、三象限B 一、二、四象限C 一、三、四象限D.二、三、四象限4.为庆祝中国共产主义青年团成立LOO 周年，某区举办了因i架知识竞赛，甲、乙两所中学各派5名学生参加，两队学生的竞赛成绩如图所示，下列关系正确的是（成绩‘－O A－－··J ··．． ．． ·a i 40，－en －－· ··－．．，e ie－t ．． －··M T ’··iT ．．． ．．． r e b －－‘， ．．． ．．． r ·‘，自··．，．．． ．．． rlLflr ∞MH MW I 。

，，，l ’‘剧。

）－－－伽－－伽－－·－－·－－‘··咱’‘”』’。

I 23 •S学尘＂号审剧费100吁·－r--r--T--T －－俨－、90卡－－』··‘－……－乡＿＿.. ω＋－·卜p 半－＋ct �，－－斗70� －－￥－＇－�－－』－三牛二斗’ 「－�－r ’－，－－，…，－…． ω「’－「－－「－－卜－7－－�－－才50卡··卜，；．．卜－＋－－，－斗40｝…卜’←·←·←－·－－吨。

2024年苏科版高二数学上册月考试卷515考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共6题，共12分)1、的二项展开式中，项的系数是（）A. 45B. 90C. 135D. 2702、【题文】为了得到函数的图象，只需把函数图象上的所有点（）A. 纵坐标伸长到原来的2倍，横坐标不变B. 横坐标伸长到原来的2倍，纵坐标不变C. 纵坐标缩短到原来的倍，横坐标不变D. 横坐标缩短到原来的倍，纵坐标不变3、若b＜0＜a，d＜c＜0，则下列不等式中必成立的是（）A. ac＞bdB.C. a+c＞b+dD. a﹣c＞b﹣d4、已知函数f(x0在R上连续可导，则等于（）A.B.C.D.5、如图，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB和△PAD都是等边三角形，则直线PC与平面ABCD所成角的正切值为（）A.B.C.D.6、复数z=5+3i的共轭复数对应的点所在的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限评卷人得分二、填空题(共9题，共18分)7、【题文】已知ΔABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则ΔABC的周长的取值范围是__________.8、【题文】高二某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：，．左上图是按上述分组方法得到的频率分布直方图. 则成绩大于等于 14秒且小于16秒的学生人数为____．9、【题文】_________10、【题文】如图给出的是求的值的一个程序框图；其中判断框内应填入的条件是_____________11、“存在x∈（0，+∞）使不等式mx2+2x+m＞0成立”为假命题，则m的取值范围为____．12、已知F1、F2分别是椭圆C：=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF1的中点在y 轴上，若2∠PF1F2=∠F1PF2，那么椭圆的离心率为____．13、如果随机变量ξ～N（-1，σ2），且P（-3≤ξ≤-1）=0.4，则P（ξ≥1）= ______ ．14、已知向量a鈫�=(2,鈭�1),b鈫�=(0,1)则|a鈫�+2b鈫�|= ______ ．15、在3名男教师和3名女教师中选取3人参加义务献血，要求男、女教师都有，则有 ______ 种不同的选取方法(用数字作答)．评卷人得分三、作图题(共5题，共10分)16、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？17、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）18、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？19、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）20、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）评卷人得分四、解答题(共4题，共20分)21、（本题满分12分）已知命题方程表示圆；命题双曲线的离心率若命题“”为假命题，“”为真命题，求实数的取值范围．22、某工厂有工人1000名；其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）．现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）．（Ⅰ）A类工人中和B类工人各抽查多少工人？（Ⅱ）从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2表1：。

河南省郑州外国语中学2024-2025学年九年级上学期期中考试数学试卷一、单选题1．公元前5世纪，古希腊数学家毕达哥拉斯首次提出了关于一元二次方程的概念．下列关于x的方程中，是一元二次方程的为（）A．210xx+=B．20 x xy-=C．221x x+=D．20ax bx+=（a、b为常数）2．“斗”是我国古代称量粮食的量器，它无盖．如图所示.下列图形是“斗”的俯视图的是（）A．B．C．D．3．已知线段a、b、c，作线段x，使b：a＝x：c，则正确的作法是（）A．B．C．D．4．将标有“最”“美”“河”“南”的四个小球装在一个不透明的口袋中（每个小球上仅标一个汉字），这些小球除所标汉字不同外，其余均相同．从中随机摸出一个球，放回后再随机摸出一个球，则摸到的球上的汉字可以组成“河南”的概率是（）A ．13B ．14C ．16D ．185．若把方程2410x x --=化为2()x m n +=的形式，则n 的值是（）A ．5B ．2C ．2-D ．5-6．如图，已知矩形ABCD 中，E 为BC 边上一点，DF AE ⊥于点F ，且6AB =，12AD =，10AE =，则DF 的长为（）A ．5B ．113C ．365D ．87．如图是某地下停车场的平面示意图，停车场的长为40m ，宽为22m ．停车场内车道的宽都相等，若停车位的占地面积为2520m ，求车道的宽度（单位：m ）．设停车场内车道的宽度为m x ，根据题意所列方程为（）A ．(402)(22)520x x --=B ．(40)(22)520x x --=C ．(40)(222)520x x --=D ．(40)(22)520x x -+=8．下列给出的条件不能得出ABD ACB ∽△△的是（）A ．AD BDAB BC=B ．ABD ACB ∠=∠C ．2AB AD AC=⋅D ．ADB ABC∠=∠9．如图，在平面直角坐标系中，正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形，且相似比为13，点A ，B ，E 在x 轴上，若正方形BEFG 的边长为6，则D 点坐标为（）A ．1,22⎛⎫ ⎪⎝⎭B ．1,13⎛⎫ ⎪⎝⎭C ．()1,2D ．1,24⎛⎫ ⎪⎝⎭10．如图（1），正方形ABCD 的对角线相交于点O ，点P 为OC 的中点，点M 为边BC 上的一个动点，连接OM ，过点O 作OM 的垂线交C 于点N ，点M 从点B 出发匀速运动到点C ，设BM x =，PN y =，y 随x 变化的图象如图（2）所示，图中m 的值为（）AB ．1C D ．2二、填空题11．若1x =是关于x 的一元二次方程260x mx +-=的一个根，则m 的值为．12．工人师傅做铝合金窗框分下面三个步骤进行：先截出两对符合规格的铝合金窗料（如图①），使AB CD =、EF GH =；然后摆放成如图②四边形；将直角尺紧靠窗框的一个角（如图③）调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是形，根据的数学原理是：．13．如图，四边形ABCD 是菱形，∠DAB ＝48°，对角线AC ，BD 相交于点O ，DH ⊥AB 于H ，连接OH ，则∠DHO ＝度．14．如图，在平行四边形ABCD 中，E 是线段AB 上一点，连结AC DE 、交于点F ．若23AE EB =，则ADFAEFS S =△△．15．如图，在矩形纸片ABCD中，2AD AB ==，点P 是AB 的中点，点Q 是BC 边上的一个动点，将PBQ 沿PQ 所在直线翻折，得到PEQ ，连接DE CE ，，则当DEC 是以DE 为腰的等腰三角形时，BQ 的长是．三、解答题16．解方程：(1)2630x x -+=；(2)23210x x --=．17．在一个不透明的袋子里装了只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：摸球的次数n 1002003005008001000摸到黑球的次数m 65118189310482602摸到黑球的频m na0.590.630.620.6030.602(1)当n 很大时，摸到黑球的频率将会趋近（精确到0.1）；(2)某小组成员从袋中拿出1个黑球，3个白球放入一个新的不透明袋子中，随机摸出两个球，请你用列表或树状图的方法求出随机摸出的两个球颜色不同的概率．18．一张矩形纸ABCD ，将点B 翻折到对角线AC 上的点M 处，折痕CE 交AB 于点E ．将点D 翻折到对角线AC 上的点H 处，折痕AF 交DC 于点F ，折叠出四边形AECF ．（1）求证：AF //CE ；（2）当∠BAC ＝度时，四边形AECF 是菱形？说明理由．19．已知关于x 的一元二次方程210x ax a -+-=．(1)求证：该方程总有两个实数根；(2)若方程的两个实数根1x 、2x 满足123x x -=，求a 的值；20．2024年巴黎奥运会顺利闭幕，吉祥物“弗里热”深受奥运迷的喜爱，一商场以20元的进价进一批“弗里热”纪念品，以30元每个的价格售出，每周可以卖出500个，经过市场调查发现，价格每涨10元，就少卖100个．若商场计划一周的利润达到8000元，并且更大优惠让利消费者，售价应定为多少钱？21．求证：相似三角形对应边上的中线之比等于相似比．要求：①根据给出的△ABC 及线段A 'B ′，∠A ′（∠A ′=∠A ），以线段A ′B ′为一边，在给出的图形上用尺规作出△A 'B ′C ′，使得△A 'B ′C ′∽△ABC ，不写作法，保留作图痕迹；②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．22．一数学兴趣小组为了测量校园内灯柱A 的高度，设计了以下三个方案：方案一：在操场上点C 处放一面平面镜，从点C 处后退1m 到点D 处，恰好在平面镜中看到灯柱的顶部A 点的像；再将平面镜向后移动4m （即4m FC =）放在F 处．从点F 处向后退1.5m 到点H 处，恰好再次在平面镜中看到灯柱的顶部A 点的像，测得的眼睛距地面的高度ED 、GH 为1.5m ，已知点B ，C ，D ，F ，H 在同一水平线上，且GH FH ⊥，ED CD ⊥，AB BH⊥（平面镜的大小忽略不计）．方案二：利用标杆C 测量灯柱的高度，已知标杆C 高1.5m ，测得2m DE =， 2.5m CE =．方案三：利用自制三角板的边C 保持水平，并且边C 与点M 在同一直线上，已知两条边0.4m CE =，0.2m EF =，测得边CE 离地面距离0.3m DC =．三种方案中，方案不可行，请根据可行的方案求出灯柱的高度．23．在ABC V 中，AB AC =，BAC α∠=，点D 为线段CA 延长线上一动点，连接DB ，将线段DB 绕点D 逆时针旋转，旋转角为α，得到线段DE ，连接BE ，CE ．(1)如图1，当60α=︒时，ADCE的值是______；DCE ∠的度数为______︒；(2)如图2，当90α=︒时，请写出ADCE的值和DCE ∠的度数，并就图2的情形说明理由；(3)如图3，当120α=︒时，若8AB =，7BD =，请直接写出点E 到CD 的距离．。

第1部分化学品及企业标识化学品中文名：2-甲酰基-3,4-二氢吡喃化学品英文名：3,4-dihydro-2H-pyran-2-carbaldehydeCAS号：100-73-2分子式：C6H8O2分子量：112.13产品推荐及限制用途：工业及科研用途。

第2部分危险性概述紧急情况概述：易燃液体和蒸气。

皮肤接触有害。

造成皮肤刺激。

造成严重眼损伤。

吸入有害。

可引起呼吸道刺激。

GHS危险性类别：易燃液体类别3急性经皮肤毒性类别4皮肤腐蚀/刺激类别2严重眼损伤/眼刺激类别1急性吸入毒性类别4特异性靶器官毒性一次接触类别3标签要素：象形图：警示词：危险危险性说明：H226易燃液体和蒸气H312皮肤接触有害H315造成皮肤刺激H318造成严重眼损伤H332吸入有害H335可引起呼吸道刺激防范说明：•预防措施：——P210远离热源/火花/明火/热表面。

禁止吸烟。

——P233保持容器密闭。

——P240容器和装载设备接地/等势联接。

——P241使用防爆的电气/通风/照明/设备。

——P242只能使用不产生火花的工具。

——P243采取防止静电放电的措施。

——P280戴防护手套/穿防护服/戴防护眼罩/戴防护面具。

——P264作业后彻底清洗。

——P261避免吸入粉尘/烟/气体/烟雾/蒸气/喷雾。

——P271只能在室外或通风良好处使用。

•事故响应：——P303+P361+P353如皮肤(或头发)沾染：立即脱掉所有沾染的衣服。

用水清洗皮肤/淋浴。

——P370+P378火灾时：使用灭火器灭火。

——P302+P352如皮肤沾染：用水充分清洗。

——P312如感觉不适，呼叫解毒中心/医生——P362+P364脱掉沾染的衣服，清洗后方可重新使用——P332+P313如发生皮肤刺激：求医/就诊。

——P305+P351+P338如进入眼睛：用水小心冲洗几分钟。

如戴隐形眼镜并可方便地取出，取出隐形眼镜。

继续冲洗。

——P310立即呼叫解毒中心/医生——P304+P340如误吸入：将人转移到空气新鲜处，保持呼吸舒适体位。

基础课35数列的综合问题考点考向课标要求真题印证考频热度核心素养等差、等比理解2022年全国甲卷（文）T***逻辑推理数列的综合18数学运算2021年全国乙卷（文）T19数列与其他理解2023年北京卷T21***逻辑推理知识的交汇2020年新课标II卷（理）T数学运算12命题分析预从近几年高考的情况来看，一般以压轴题的形式出现，属千中档题测或较难题，命题热点以递推式为载体，常常与不等式、函数、方程交汇，具有知识点多、覆盖面广、综合性强的特点预计2025年高考命题情况变化不大，但应加强对阅读、理解、迁移和运算的训练一基础知识．诊断穷实基础一、数列与函数数列与函数的综合问题主要有以下两类：＿1. 已知函数条件，解决数列问题，此类问题一般是利用函数的性质、图象研究数列问题；2. 已知数列条件，解决函数问题，解决此类问题一般要充分利用数列的范围、公式、求和方法等对式子化简变形．二、数列中不等式恒成立的问题数列中有关项或前n 项和的恒成立问题，往往转化为数列的最值问题；项或前n 项和的不等关系可以利用不等式的性质或基本不等式求解．诊断自测题组1走出误区1. 判－判（对的打"✓"'错的打"X")(1) 已知等差数列{a n }的公差d>0, 等比数列{b n }的公比为q ,若a 1= b 1 = 1, a 2 = b z ,a 14 = b 3'则d + q = 25.(X )(2) 已知数列{a n }满足a l 'a 2'a 3成等差数列，a l ,a 2'a 4成等比数列，若a l a l + a 4+ a 2 + a 3 = a 4'则a3= 3.(X )(3) 若数列{a n }的前n项和S n =2n+l_C ,则"c=2"是“数列{a n }为等比数列＂的充分不必要条件.(X )(4) 若数列{a n }满足a n+1 = 2a n (a n *0,n EN勹，且a z与a 4的等差中项是5,则a l +a z +…+ a n = 2n -1.(✓)2. (易错题）记数列{a n }的前n项和为S n '已知a 1= 1, 5 n + 1 = 4a n + 1设丸＝a n+1-2a n 'e n = l b n -1001, T n 为数列{e n }的前n 项和，则T l O =尥甡．【易错点】忽视对伲-100忡b n -100的符号的分类讨论致错．［解析］由S n+1= 4a n + 1得S n=4a n -l + l(n�2,n EN勹，两式相减得a n+1 = 4 bnan+1-2an 2(an-2an_1) 妇-a n _1)(n �2),即a n+1-2a n = 2妇-2a n -1)'所以＝＝bn-1an -2an-1an -2an-1= 2(n �2),故数列{b n }是首项b 1= a 2-2a 1 = 4-2 = 2, 公比为2的等比数列，即丸=2.2n -l = 2n (n EN 勹，所以e n =I泸-1001= {100-2n,n:::; 6,2n-100,n > 6,T 10 = 600-2 X (1-26)切+22+…+26)+27+28+29+210-400=200-1-2+27+28+29+沪=200 + 2 + 28 + 29 + 210 = 1994. 题组2走进教材3. (人教A版选修@P56•TIO改编）已知等差数列{a n }的前n 项和为S n '且s 4= 4S 2,a 2n = 2a n + l(n EN*)若b n = 3n -l,c n = a n b n 'T n 为数列{e n }的前n项和，则T n = 1 + (n-1)·3n.［解析］设等差数列{a n }的公差为d,由a 2n = 2a n + 1得a 1+ (2n-1)d = 2a 1 + 2 (n-l)d + 1, 即d= a 1 + 1, CD 由S 4= 4S 2得4a 1+ 6d= 4(2a 1 + d ), 即d= 2a 1 , ＠）联立(D(Z)解得{a 1=1,d = 2, 故数列{a n }的通项公式是a n =2n -1, n EN 勹所以e n =a 九=(2n-1)·3n -1(n EN 勹，则飞=1 X 3+ 3 X 31+ 5 X 32+…+ (2n-3)·3n -Z + (2n-1)·3n -l , @3T n= 1 X 31+ 3 X 32+…+ (2n-5)·3n -Z + (2n-3)·3n -l + (2n-1)·3n, @由＠－句得-2T n = 1 + 2 X 31+ 2 X 32+…+ 2 X 3n -l -(2n-1)·3n= 1 + 2 X3(1-3n -l )1_3 -(2n-1)·3n = -2 + (2-2n)·3气故T n= 1 + (n-1)·3n.4. (人教A 版选修@P37•例9改编）设等比数列{an}的前n 项和为S n '若鸟＝9, S 6=36, 则a 7+ a 8 + a 9 = (B ). A .. 144B .. 81C . .45D .. 63［解析］由等比数列的性质可知s 3,s 6-s 3, s 9-s 6,成新的等比数列，设这个27新数列的公比为q,由s 6-s 3= 36-9 = 27, 得q =了=3, 所以a 7+ a 8 + a 9 = S 9-S 6 =27 x 3 = s 1. 故选B.题组3走向高考5. [2021• 新高考11卷］（多选题）设正整数n =a。

ot · tiom r -_ ris -i ,e rUSEI ·,s I ANUAL J a nu a r y 2018No. 150-704-00 FTable of C ontentsIntroduction 1 1 3 6 0.sCfipt i on Calibration InstallationInstallation in H azardous Locations Specific Conditions of U se Maintenance & Troubleshoot i ng4S�LIVERY�llld kt � TOL L F REE 1-800-999-2900U n 'ei!d K ifio d OfflF REE PHONE0800 525107 ... , .... TOLL mEE008 261928l 06$0�CIO!ll.,...1 S..,wcll,, C.bN Ill� U .SA. ltt 18181 8'11,7111 • T Iii! 8S-JSt.i F�:(,18)891•2'1•OONt<et�WS(l'Ul.VEOA , uo,,,,. co...,,.� AoJo •, °'-"rW &u.-RH 1f)201J ,UriWld '°"domT -0'2li0 S I • ... • T tlc 87&67F AX:0:53�Moore Industries" STAR" C ent e r has a w i de variety of quaJ i ty instrumentat i on in stock and ready to s h i p .•S i gnal Transm i tters• Temperature Transm i tters • P /1 and 1/P Converters •Isolators and Converters • I nd i cators and D i splays • A l ann Trips•Integrators and Total i zers •Power Transducers•Instrument Power Suppl i es • R acks, Rails and Enc l osuresMost instruments can be custom i zed to m eet yoor needs. Even then, you·n never have to wa i t more than a few days.8118IntroductionMoore l ndustflos' IOO P-PQWe<ed P oteot l ometer Transmll1er, t he PTX, s a dev i oe u sed to converts1andard, three-w i r e pot entlomttor (poQ i n put 10pl'0p011i0na l curre n t output.Th i s ma n ual cont a i ns all o f the i ntotmatiO,n nt tded 10 ca l ibrate, CIS*'att, and m a i n ta i n lhe P TX. 11 al soi ncludes a brief descriptio n of t he u ni! and its c.apa·biti i es and oplk)n s,a llstlng of u n it specif ica t i ons, and a n overview o4 Moort l nct.,str l es' u nll data lraeklng system and lab eling.A A awe,ndix a.t l ht tnd � lhe manual provid es th9 tionnatlo n reql.A'ed tOJ l n st.al i ng N PTX i n h aJard·ous e n v i r ontl'ltf'IIS. Such inStaHatlo n$ r equ i r e o n e o l ht availab&e l n t.rl n sic S afety (S) o ptions. de scribed la1e<.I.Nhere they appea, a, '9lt1 o r f igur.s, "N OTES'" art uS6d to draw at t ef'lli O n to p taetioe s t hal cou l d olhef­wiSe r esul I n lnoonv enienoes to t he user. "WARN· INGS" po i nt o ut practices that, u.-U avoic5td, could result in pe r so n a l injury,DescriptionThe PTX tra n srrittor is a va i l ab&t n e i ther a D IN-style, or Moo r e l rd.tst r i es'hOCMy·p.,ck (HP) hOus l ng. n measu r es variable reSiSUve l l'l)UI b y oon,parfno Input m i lli vo lt$ wl h 1ht drop across a n Interna l,pr ec i sio n vo l tage dMder. II p rovides co n stant voltage ox:cila·tlo n l o a Slanda r d, 3-wir e pot, and OUtpulS a p,opor·tlo n aS 4-20 °' 1 ()..50 mAcurre n t based on the pors w i pe r pos i tio n. t accepts� f rom any 100 10 10,000n.3-w i,e pot.The unil IS IOOp-powe r eCI (12·42 Vdc-). Some S options req.ii r e 12�24 or 12-28 V dc powe r i ng. Re:tet 10 t h& l n S1ala!ion Sect ion of th i s manuat f or i n lonna­tioo on u ni e l9Ctrieal con n oeliOns.1"N a vai1'ble hOus l ng styles ro r the PTX, t he H P-o r DIN-style, a flon:I t he use, w ith a wide vatiely of mounthg options. I n additio n to lh8 Sland·ak>ne unil. mounthg hardware optio n s nclude tl3"0&$ l o, u se wih re l ay track O f surf a ce mount, e xp l osiOnptOOt enclosu r es,and NEMA bO xes. co n sult wh h you r Moore l nc:klstrics' Sa l e$ RepresenlaJ l ve fo r mo r ei nformauon o o ava�1e mounlfng h ardwa r e options.Pag e 1PTXTht HP•Style PTX. This styt& oC u nit S inl e nded 10 runot l on as a modutar rep&aoomenl n appllcatio ns whe r e conduit a nd encfO-Su res may alr e ady be i n place. when a special en closure i s n()1 1&qui-ed, or In appllcatlons where the O N•sty l e u n i t 1$ not otherwise appropri at e,l l i s atso avallab l e mou n ted in a separate, dQme<I, explos l onproof enclosure. secured n s i de with s pr�clips; n o drilli ng o, lapp i ng s r equ i red. Othe r r if·slo n s h:WG h;a,ctwsre l o r surf ace mounl and retay tractt1n sianatto n s.Tho D N·stYIJO PTX. Th i s style soaps on t o G·YP8 DIN rails (01N EN50035), I I ii most O lte n used In applic a lions ,e�l r l ng a la r ge n urrt>e, of units In are l atlvefy smal space. TeSl j adl.$ o n the t,o n t panel allow tor basic f uncliOn Check$ wtl hOOI having tor emove the PTX l rom the process l oop,Tab l e 1 IISls t he p erf o rmance and operat10n a1 speclfl. catio n s k>r M oo r e l ndustr i os' P TX. Flgv r e 1 shows the r elationsh i p between the po wer souroe u sed i n a PTX ai,s:lli l ion and t he u n it's load capab i l ity,Controls and IndicatorsLabe l ed pots 10 oo n trO unit zero and sp a n are located on !he fro n t p ane l o1 bo th the D N-and H P·sty l o PTX. The Calibration Sectio n Of t h i s ma n ua lde&Cflbes hOw these pois ca n be a djusted. Sc:,ec l l'l­catiOns to r ad j uslabll ity appea r in table 1,OptionsThe follow i ng li SI provides a n oveNlew o f some of the PTX optio n s. Comp&e l e n formatio n o n mour¥i ng harttNam and f unclion&optio n s, o r curr80lfy avai­able c ert ll icatio n s and approva l s is avalab l e trom yQUr Moore l nd.Jstries Salos ROPf0$0nlatlv e. Usef'S may also con tact the factory Clite,ct l y at 1--800-999-2900 in t he U.S.A.IS(X) o,mo n-Intrinsic Sa lety.U n hs equi pped w l l h options such a s tSB and SC a r e rna n ufac:tu r eo acoo r d l n g 10 t he specifications of thit'di)any cenlfy l r q agencies l o meet vamus teQJitements 10f l nt r l n s l·cally safe flsta11ation i n haza r(IOus e n viro n me n ts. Refe r 10 lht PTX d�l{I Sheet.o r consu l t the lactory lor i n lo,tmalion on currenl IS oe rtif i cali0n$,Page2PIXno,-1. PTX Pa tformaf'IC6 and Opa ratlonal Spec{fica6onsCh1ractertsUc:Spectr J ca U o n slnpY t k i t e poientlome,1-rtated f rom 0·100 O to 0-10,000 a Sen.« Current; l mA,, maximumftan9e:M i n i mums,�n Is 15%0, potv-.i•. Mall l n-..m o'™'t l o r � 18 (t00%• -0%')-10%• po l v a l ueo u t putF eic.Ory-.ML 4-20 m A 01 10-50 m Aacco rd in g ID ou s llo m or spoc il icmion ill li mo or otdo r Limit ing: ,.20 m A units 1rnc.d 10 30 m A . maxltnl.lTI 10-so m A 1,W!h & fm l � 10 65 fflA tnax lmu m .... ,12-42 V d oSome IS options require other pow9r r.i�. Refer to � o r <XltliUII wllh your Moor• fndustlios' Sa l es Ropte:Mnlilllv• l or (l etah,,M ax im u m : Un l e3n s lJSIUI u p to 80 V do w l hio ut darn a g ci Contro l •Z.ro : Labs l ed pot o n f ron t p,;,M,I pn,v ido s ad ju stmcinl ID O"-o f ou!p t.C s p an 11()%. wit h O"-l'l pu tZ.ro Ran g •: Min1nwm zero Is 15%Cf inputpo t v aruo Spa n : Labo l od pot on f lQnl panel .cl j i..1, f u ll «* 10 100%PlorformanoeAccuracy: i-0.1% ot tplVI ltldud l ng l nta r ly at'l d 1tp&atabifty Load Capebllity: Sae r-.;w• l Loop Load t Un• Voflege) E H•ct: :t0.002'% oC span 1)61 VOl tel\tlnge, as m.asured' at the inpultarmilalsA ,,..,._. T empe r •t w e Effect : .t0.01%oi s pan po, •F c h ange Env 1r on me n ia JA � Amb i e n t �allng Tem p e r a1u,. Rango : -29 lo 82•c (--20 ID 1so •F )Rat ingWe l g :11HP.atyto : Appw l m .i !el)' 141.8 g (5 Ol)O I N •aty le : App 10x i m a,8'y 224 g {7SI OZ)NOT ES : 1. Consult your Moo re Industrias'$"" Rop,ettnlllllve l or Information Ct'I 81)41(:IIM!tlliof'lt. Pf lc l ng a nda vailabii t y oi oplions .2. Rotor to the In stal l ation 1on t or PTX outJne <f lll'let1sbne.RF Op tion -RadiO F rllQUOllcy a nd Elec.tromagnetlc lntorlerence (RFVEMI) Filtering. F1Jielf:d term i na l sand cuep rovid0$50 V/m eter. a bc:. 0.1% of f u ll ·sca l e s p anWhe n I H1ed aocotd i ng 10 PMC SAMA SUtfldard 33. 1,RTB Opflon -Removeable Terminal BIOCk. Pt0videst o r unn rep1a,Cemen1 w ithoutw i ri ng d i soonnect.J>W l i eable to 0/l'ktyte PTX�on,y.untt D ata Tracklng -ModCIJSOfla l NumbOr. MooroI ndustr i es keeps a record o l pr oduct l nlorma!io n on overy u n i t sold or s ervioed. Th i s record Is keyed t o I .he u nl model and �l'iO l ,.,.rr(lers.On DIN·$1)11e PTX's.. IOOk l ()t the model and st.ria l nul Tber& o n one o l the hous i n g side pane l s. The l ab e l on HP·Sly l e u n i ts i$ found c,1th0r on tho unit beck or front paneJ.Page 3P TX2400 ----..-----.------,-----.----�::!l:IO l-----------�-----1-..;,..._---+------...111"--'2000 1----"-----li-----t....&,,.. __ ...a..,,6.. __The e-xa"l)le on'Ll'lo following page '5how.s a tvpt:alP rx m::idei n umbor, breaking out ils �tq 1l e ltb forl ustr atb n purposes. Actor kl lh8 example Indeeil)l'lnt i ng the mode l n�r on your unil.H sol'Yice a6i&is1anc e Is ever fl oct u i rodl. m.ae e na1e or11'16 unit. model 1a1�er 1:1e,or-e contacti n g Lhe factory.1For rast:Ht as.sis t e nce. �l s.o no t e 100 IJf'lil t.oriaJnu l'l1'0r, o b 1a1n1Jer, and llrJe purCM$ ord'et mr.JEBrl.ffido, whic:.h it waS :shtppea. TlliS lntormatiOn assls1slh r ac:,o,y tepresenJetlve n p110viding )'OU with �heMS-wors you need a� e i1ilcie n l'.ty as po:s.sil1e.CalibrationP rio r 10 5h lpme n1, every P1X is m u ly t es.1e d IO enrureco mpliance with Moore lndustrles· slr1d Cl,.JaliLyoontfol ,guidelines. ee1·01e n s1al l3l lo ri, �·ov e r. yourunH(s) :smuld be benc h �ed In order to sol andwrir)r Lhe desired operamlng levels..This procedure should b e oonal!docJ in an o nvwo n­mont co ns ide r ed awropriete •or general l es t� 04olcu::tronic atu:I pnel!lmatic equipment I t Is recom­rnoncted lha11he pl'Dcedure5 In lhls :s.ea l o n no, beca rr i e d Otl'I In the IT-e.ld. Use a technician� ti cncn orin a Simi l a r lab-type selup, SQ lhat any u n i1 damag�um rnay have occt.1fifed during stilpmenll can bediS'.t'XMU ecl !iilfely, h.e., s:ewate-ll lrom tile lntcn(t(ldprocess 01 applfcstlon.POQG4PIXI EXAMPLE IPTX / 1K--0-100 / 4-20MA / 12-42DC / •RTB ·RF [HP)�--a�Unit T ypeTota l Res i stance of Po 1anOometer % o t PotonliOmoterTrave J IOObta i n0% O utpu1'Yo o t Poienlk>meter T rave l to Ctita l n F ull·&eale ( 100%) Outpu1Powot Optlon(s) Hou$1ngCalibration SetupTab l e 2 l ists t he OCJJ i pment you wil l ne&d to calbrate the PTX . These i tems aro not �plied by Moore Industries. rut shOuld be ava i lable I n env i rorwnents qua l if i ed to p erform the p,ooodure.'Ille termila l s t01oo mection of the c aM>rat i on equ i pme nt ate located on the unit fronl panel. H P · style un i ts U$O a she-place, n orrt>ered terminal block w i th term i na l 5 fl'l acttve , O I N·style units aJso h ave a six-place terminal l*x::k w ith the non-labeled l &rminal inadive. The term i na l s on both types of uM a e clear l y labeled.. Use +PS and -PS tOJ connection of the approp riate loop po wer and term i nals ·A·, "8", and ·c· t or conn(lclion o t pot i npu t Flgure 2 i ltlstra t es the hookup I Of standard PTX callbrat l o n The desfgnator "f\ • r efers to the eppn,.prlate p,ec:lslon res i stor.use the appropriate materials listed I n t l)ble 2 I n the l�up, app l y appr opriate power , and allow approx:!·mal e l y 5 m i n..r les for unil w�up a n d hoolQJp scab i llzaUo nCalibration ProcedureWith l he �l bratlon s etup c�l et8d as ShOwn. set bolh decade resistar.::e boxes to p rov i de z ero ohms ot res i stance. apply t he appropl'iale 10-42 voe powor , a nd 1um both the Z ero and Span pds on tne 1ro n t panel 011he PTX tu.lly oo unterdock w ise. AllOW appmximate l y l l ve m i n utes tor u n i t warm�p and se.tup stabi i z.a l i o n .1.Se1 d ecad e box A l o p r o v id i&r &&i s t a noo eq u ro to th e va l ue catted o ut in t he "% T rav el M>, 0%Ou 1pu1" fi e ld 01 vour un � mode l nu mbe r:2$e l box B t o v a ll e spec ified i n ..,..lo T r ave l t o,1� 0\11pur t l eld o f u nit mo de l num oo rFOR E XAMP L E ;For a PTXw i th •1K �25.75� l i st ed t n mo d elrunti er, s et d ec a de bo x A to 250 n afl(f b O x B t o p(OV lde 750 0.PIXEqufpment Spff:1Jle1Uo11sAlli.tafl� De.Id� BoltH Oallbnlted. Aeeura1a 10 :f0.05� mlnlrrwum.(2, Reci;,mm9.lld ESDI l!)Qieiibo• mock! 0862, or a:puivi1klnL00Vi:111milr GaJibtatiid. AIX.Ul--mei to :t0.005%. mlrinwm.Rocomrn a tal' K•lliikly mod 197, or e,q,ut.ralent.PIKl11Gn AN111or 2.50ll, ±0..01 ,I,. pr«lJl:!11 re 'klr 1or 4-20 mA L!llit5,1000. ±0..01 % remicr ior 1 o-5(1mA unia.P'Jw,arSoura C albr�id. Vwbii &Quro9 � of r�utz lm O:tJlpJ L .in Om12-42 Vdc r�.SCNwdmta-, Bli!dlili "'1idlh 2..5-4 rJlril [O. 1 ntti�. trWIITIIJffl.(·ilO� � ·�pt)10 0 0 0,,1 A10 0 0 O�I CDECADE R0!1STAHJC!;! BOX D3.14m zero pol CIOCkvdse u fMJ I' vottmeter reads 1-V, t-4mV,"· C:ti:ange "1t l PCJo• �e 'bo x A.Jo.pro,yli1ereSi:S t anc_p �Nd In stop 2 {% T tavel lor 1g o%� ft(!� �I 11R.inlb$r).PTX-5. Set decat;lel box B to Y al.Je 1rom s tep 1 t'¾ Tr.aveS.Of 0%}.X'.PS I I +��2\100l?OWEA,SOt.JACE-ff AV J\V� -DCVOLTMETER6.li'Um Span r::tOt" �lae U1iTII YOltrne'ler reads SV,.±4 mV.7.Aepeet s.1eps 11hrough 4 uhtll PTX oo1iiut is x:stable at !»In O¾o aoo l\ull-seale Input.8.Check linearity D')' cal'cula1ing 25%. 50'%, arid75o/ii o t ratod span W"h On setting on decadeto� 13-, set box A to eech level derived fro.,, tt.esucalcula11oPS.. error In u n o u t p u l wiU not ttxoood'0. 1 % 01 span.Pago 6PIXInstallationI nstallation of th e PTX i s p,osent.Od � th i s matlJa l i n 1w o phases. FirSI Is t he physical m ount i n g o f th eu n i t This I s fo l low e d by the e tectr l ca l con n ectio n s. hi s recommondod that i nsta.ll alion bO ca tfiOd out 111 lhlsotdOI.Befor e PTX I n st a llation.• l s 61tong l)' rec:olffll e nded that each urjl b e bonCh choeked,Re'lot to thei nstruct i ons f or triS p rocOOJte i n the C alibra t ion Stction, ea r l iet i n t h i s marua1.Atso. any requ i romenlS I Ot NMSic satoty i n t he Nended application must be considered.Intrinsic Safety Considerations Electrical ConnectionsF,gul'O 5i s the PTX �stall a t l oo hOokup d i ag ram. Wh e n th e u n it s have been ptOPOrty mou rned, ref e r to figure 5 t o connect them to power and other t l ekt devlees.As l he PTX i s a loop-pow e ted dO v iee n o addlllonaf elect r ical oonnecOons art re,qu l recl. Check t he "Powe,. l retd 01 vour u n lt'S mod e l n umber to venty appropr i ate IOOP volage.R e f e r 10 th e exp l anation Of the model n.,mt>er In t h e Oescq)tion S&ctiOn of th i s maf' l, and 10 th e speciica6ons liStOd i n l able 1 lor mor e I nforma t ion.A s s how n I n 1he f i gur es con n oct t he +P$ term i n a l of lhe PTX to the po sit i v e� tmm the power souroe In t h e loop. Co n n ect the -PS PTX torm l nal I n ser l e$w ith t h e pos i tive torm i n.alS or the other de v ices I n t he loop and th& negative term i nal of the loop power suppty.The po1enti0motcr w i t i ng I s oonnected to th e term i­na l s ta be l Od A B.and c.Connoct.-.g w i te.s u se<I ShOu l d b e betw e e n,,. a n d 22 AWG.Connections are mad e w i lh oomprossiOn­screw socket s Use a slott e d·l:4> screwdl'Worwilh a head w idth n o g r e at e r lhan 2.54 nm (0,1inch). Ground i ng. To ground the HP·Sly l e unll. m ake s u,e a shie lded g rounding lead iS c:onnected to the GND screw o n l h8 u nit front panel Th i$ screw Is loca ted to th e rigft of the Z•ro act j ustmenl pot, and Is l y p l·cally fitted w ith a w i re or wlt e term i nat i ng lu g. Typieally, whe n MP·style unlls are equ_,ped w ith explOS I Of'C.\l'OOf e.n ctosures,th e u n it gro unding s crew 1$ attac:heci lo th e en closur e ground pr l0< to Ship­ment.To ground tho O I N•Sly l e PTX, the use ot sh l e tded twiStOd•pait w i Mg, QtOUncle<f as ne a r a s poss i ble 10 the u n it Ilse.It l s recomm en ded.Physical Mounting of the PTXF I QUte 3 shOws the mount i ng d l me n sJo n s k>r the H P·&tyle PTX, and th e O I N•51y l e PTX hous i ng d i l'l'IOn­slOns are ShOw n i n t igure 4Tht M P musltatiOn shc>w'S ttwt u anoe mouni hat<fwa re option.Whe n us i n g 1he H P PTX wilh e x p l o.s i O(l)roof eocto-sures,spring t;t l p$ ex1end from the uni fronlpa n el Reier 10 t he approp r1ale Moore l ndU$l t\es Cata)Og d a1asheet ro r enctosure d i me n s i ons.Installation in Hazardous LocationsThis section contains important information regarding the installation of the PTX in Hazardous Area Locations.Specific Conditions of UseCSA InstallationsInstallation of the Model PTX into a Class 1 Division 1 location requires the use of a CSA Certified Intrinsic Safety Barrier with the following output parameters.Uz = 27V, Imax out = 100mA, Wmax out =0.68W or Uz = 28V, Imax out = 93mA, Wmax out = 0.67W.4-4.S.mn:11 �(1,75 h] -.U,7f811"141e;e1,1.rn�tl'!m--------[�.87in)-----lll"iI Cle ll!'l rl',,.. _____ (4,251f\J _____ _-:\'' ,, '',,II'' ''. ,,l:-: =�p1J KPIX{_�3,W :R E POT 0-1000ID 0-,0,0000 114 ,PS B PTX C -PS �12-42.\!DC POWER SOURCE -.. DLIRREJff DRi\10\1 --SEB NOTE!DEYVlCE NOTE; Som e as a� rBqlite dilfilll!nt Wlhlil!i r ana • a �r � ••�,I!� cw aiodl l ilt:1;1,y bf lnformalio� Maintenance & TroubleshootingOnce pmpcdy 1nsta11ee1 an.1 oonneded, IJ'to PTX i u nc Uons: u n :ane n de<I , A 'Simp e , perloo!C c:heok or @Meclbns. � a ll th.at Is re-q u l fed •o rna ln 1a1n u nll ope r a1km. Moore I nd u5:tl1es. 5ug9es.1, a &-im:>mti 9dledu l e fo r mal nte n anc e Checks .t problems. �e ln the �l,ll"il;lon o1 �he u n � In I t � awllc.a'lbn,•Maka SIJilO lhat 1npu1. and o u 1pu1. eoM«tlon.s .aro clean Md Ugh'l.•Ro mo ve · tM unill I m m Hrviee aM iltc.alibra,e,� su,e that bench inSlruments. usedl are pr,ope.l'il!,' c a ll bla t e(I .Vern loop p!Wt'4r IIOvels,tr, afte r re-ca.tbratlan. me PTX rails lo pe-f1o rm u p 1o sp;eciUcatiOM, co nl aci your 10cal Cl.iSlome r Service D-epartroont. Pl'IDne l'IU!fbers o4 o� STAR cen,ats are lls.1ed Inside lhe fr(lnl OOYTilt ol Urli:S mainu l �n.i clk>n !ii lor 1he r,etu m of tne u ,o tho tactory IOr fur1he r lesliflg or ran.m can bOi lound on lh.e back OOv,&t.Wha 1 cal 101 aulsJan::e, ahNays. r e tM mbe r ,o �i:, t taotory with ltte mod.el and !i(l!ilel number' 011no ot r e � unh, and i. po�1e. �ith Uis fob oomber alld tile !PUrc�e, order ni,imbet u ndB r whiCh Ote unit was ordered. Test J�k,. The OIN-�le PTX Is equipped ww, W.'O Leos4 Jacu. Locat� on Lhe f'ronl pan o l , mese Jaci<.s p ro,v ld'e a. convenient lltlsa.M om votifying l oo p ClU ff ie nt when th e uni:C is Installed! aild op rating,. CoooeeJlng a: m l ll �a e r to the [a.ck&, l abelled ·+ l'" and ·-T", when ·til e u n � b powenKI up. �cs a reedino, 111 mTil!ami;,e. ot lhe cu�nt in tno klop, i'O. 1¾. II desired. �s.u r a ttie vOflaga Cll'Op across a 1 o n cto.OS%) r es l 5,1or 00meo1ed 1o 'the �. The o-urnmt In ·t he ilQop �hQujj �,ch that obt;eii\'o dl iln lhe reslst o r , ±0.01%.© 2018 Moore Industries-International, Inc.Specifications and Information subject to change without notice.。