下载文档原格式
卷积码的编码及解码（Viterbi 解码）一、实验目的1、了解卷积码的基本原理；2、掌握卷积码编码的电路设计方法；2、掌握卷积码 Viterbi 译码的基本方法和电路设计方法。
二、实验仪器1、移动通信实验箱一台；2、台式计算机一台；三、实验原理1.卷积码编码原理卷积码是一个有限记忆系统，它也将信息序列切割成长度 k的一个个分组，与分组码不同的是在某一分组编码时，不仅参看本时刻的分组而且参看本时刻以前的 L 个分组。
我们把 L＋1 称为约束长度。
2.卷积码的译码算法（硬判决 Viterbi 译码）Viterbi译码算法是一种最大似然算法，它不是在网络图上依次比较所有可能的路径，而是接收一段，计算，比较一段，保留最有可能的路径，从而达到整个码序列是一个最大似然序列。
Viterbi解码算法的基本步骤如下：1、从某一时间单位j＝m开始，对进入每一状态的所有长为j段分支的部分路径，计算部分路径度量。
对每一状态，挑选并存储一条有最大度量的部分路径及其部分度量，称此部分路径为留选（幸存）路径。
2、j增加1，把此时刻进入每一状态的所有分支度量，和同这些分支相连的前一时刻的留选路径的度量相加，得到了此时刻进入每一状态的留选路径，加以存储并删去其他所有的路径。
因此留选路径延长了一个分支。
3、若j<L+m，则重复以上步骤，否则停止，译码器得到了有最大路径度量的路径。
上面的过程可以简单的总结为“加、比、选”（也称ACS）。
四、实验步骤1、将实验箱和计算机通过串行口连接好，为实验箱上电。
2、将与实验箱相连的电脑上的学生平台程序打开。
在“实验选择”栏中选择“卷积码”实验，点击确认键。
从而进入此实验界面。
3、在实验界面上点“生成数据”，让系统生成待编码的随机比特。
也可在界面上直接双击所显示的 bit，修改其值。
4、在界面上点击下发“原始数据”，该数据将被送入单片机（或 CPLD）进行卷积编码然后经过编码的数据被送回学生平台并显示在“编码数据”栏。
【报告】卷积码实验报告一、实验目的本次卷积码实验的主要目的是深入理解卷积码的编码与译码原理，掌握其在数字通信系统中的应用，并通过实际实验操作和结果分析，评估卷积码的纠错性能和对通信质量的改善效果。
二、实验原理（一）卷积码的基本概念卷积码是一种有记忆的非分组码，它将输入的信息序列经过特定的编码器生成输出的码序列。
卷积码的编码过程不仅取决于当前输入的信息位，还与之前的若干个信息位有关。
（二）编码原理卷积码的编码器通常由若干个移位寄存器和模 2 加法器组成。
输入的信息位在时钟的控制下依次进入移位寄存器，同时与寄存器中的内容进行模 2 加法运算，生成输出的编码位。
（三）译码原理卷积码的译码方法有多种，常见的有维特比译码算法。
维特比译码算法基于最大似然准则，通过在码的网格图上寻找最有可能的路径来实现译码。
三、实验环境与设备本次实验在计算机上进行，使用了以下软件和工具：1、 MATLAB 编程环境，用于实现卷积码的编码、传输和译码过程，并进行性能分析。
2、通信系统仿真工具，用于构建通信系统模型，模拟信号的传输和接收。
四、实验步骤（一）编码实现1、在 MATLAB 中定义卷积码的编码器结构，包括移位寄存器的数量和连接方式，以及模 2 加法器的位置。
2、编写编码函数，输入信息序列，按照编码器的工作原理生成编码后的序列。
（二）信道传输1、模拟加性高斯白噪声信道，设置不同的信噪比条件。
2、将编码后的序列通过信道传输，引入噪声干扰。
（三）译码实现1、使用维特比译码算法对接收序列进行译码。
2、编写译码函数，输入接收序列和信道参数，输出译码后的信息序列。
（四）性能评估1、计算误码率，即错误译码的比特数与总传输比特数的比值。
2、绘制误码率曲线，分析卷积码在不同信噪比条件下的纠错性能。
五、实验结果与分析（一）不同卷积码参数对性能的影响1、改变卷积码的约束长度，观察其对纠错性能的影响。
结果表明，约束长度越长，卷积码的纠错能力越强，但编码效率会有所降低。
卷积码实验报告篇一：卷积码实验报告实验五信道编解码（）本章目标掌握数字频带传输系统调制解调的仿真过程掌握数字频带传输系统误码率仿真分析方法 5.1实验目的1. 使用MATLAB进行卷积码编/译码器的仿真。
2. 熟练掌握MATLAB软件、语句。
3. 了解卷积码编/译码器的原理、知识。
5.2实验要求1. 编写源程序、准备测试数据。
2. 在 MATLAB环境下完成程序的编辑、编译、运行，获得程序结果。
如果结果有误，应找出原因，并设法更正之。
5.3 实验原理（一）卷积码编码器 1. 连接表示卷积码由3个整数n，k，N描述。
k/n也表示编码效率（每编码比特所含的信N称为约束长度，息量）；但n与线性分组码中的含义不同，不再表示分组或码子长度；表示在编码移位寄存器中k元组的级数。
卷积码不同于分组码的一个重要特征就是编码器的记忆性，即卷积码编码过程中产生的n元组，不仅是当前输入k元组的函数，而且还是前面N?1个输入k元组的函数。
实际情况下，n和k经常取较小的值，而通过N的变化来控制编码的能力和复杂性。
下面以图1中的卷积码编码器为例介绍卷积码编码器。
该图表示一个约束长度K?3的（2，1）卷积译码器，模2加法器的数目为n?2，因此，编码效率k/n?1/2。
在每个输入比特时间上，1位信息比特移入寄存器最左端的一级，同时将寄存器中原有比特均右移一级，接着便交替采样两个模2加法器，得到的码元就是与该输入比特相对应的分支字。
对每一个输入信号比特都重复上述采样过程。
图1卷积码编码器（编码效率1/2，K?3）用于描述反馈移位寄存器实现循环码时所使用的生成多项式也可用户描述卷积码编码器的连接。
应用n个生成多项式描述编码的移位寄存器与模2加法器的连接方式，n个生成多项式分别对应n个模2加法器，每个生成多项式不超过K?1阶。
仍以图1中的编码器为例，用生成多项式g1(X)代表上方连接，g2(X)代表下方连接，则有：g1(X)?1?X?X2g2(X)?1?X2多项式中的最低阶项对应于寄存器的输入级。
实验九 (2,1,5）卷积码编码译码技术一、实验目的1、掌握(2,1,5）卷积码编码译码技术2、了解纠错编码原理。
二、实验内容1、(2,1,5）卷积码编码。
2、(2,1,5）卷积码译码。
三、预备知识1、纠错编码原理。
2、(2,1,5）卷积码的工作原理。
四、实验原理/卷积码是将发送的信息序列通过一个线性的，有限状态的移位寄存器而产生的编码。
通常卷积码的编码器由K级（每级K比特）的移位寄存器和n个线性代数函数发生器（这里是模2加法器）组成。
若以（n,k,m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n 为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。
卷积码将k 元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。
与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。
卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。
在编码器复杂性相同的情况下，卷积码的性能优于分组码。
编码器随着信息序列不断输入，编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列，所以图3所示状态图可以简单直观的描述编码器的编码过程。
因此通过状态图很容易给出输入信息序列的编码结果，假定输入序列为110100，首先从零状态开始即图示a状态，由于输入信息为“1”，所以下一状态为b并输出“11”，继续输入信息“1”，由图知下一状态为d、输出“01”……其它输入信息依次类推，按照状态转移路径a->b->d->c->b->c->a输出其对应的编码结果“”。
译码方法⒈代数代数译码是将卷积码的一个编码约束长度的码段看作是[n0(m+1），k0(m+1)]线性分组码，每次根据（m+1）分支长接收数字，对相应的最早的那个分支上的信息数字进行估计，然后向前推进一个分支。
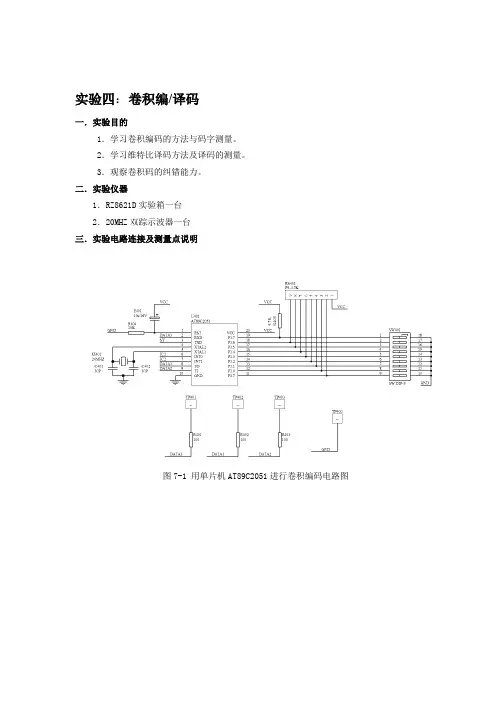
实验四：卷积编/译码一．实验目的1．学习卷积编码的方法与码字测量。
2．学习维特比译码方法及译码的测量。
3．观察卷积码的纠错能力。
二．实验仪器1．RZ8621D实验箱一台2．20MHZ双踪示波器一台三．实验电路连接及测量点说明图7-1 用单片机AT89C2051进行卷积编码电路图图7-2 用单片机AT89C2051进行维特比译码电路图差错控制编码的方法很多，卷积码是一种既能纠随机错，又能纠实发错的编码，在同样的传输速率和设备复杂的条件下，性能较优良的一种编码。
卷积码常采用维特比软判决译码，具有较好的纠错功能。
本实验为卷积码的编译码，它是由一片AT80C2051芯片用软件编程方法实现。
其编译码电路框图如下：图中各主要测量点说明如下：TP401—源码序列TP402—卷积码序列TP403—加错或不加错卷积码序列(模拟信道的传输)TP405—卷积码译码输出序列四．实验步骤及内容（一）卷积码编码1．拨线开关介绍。
用拨动开关SW401设置输入信息。
开关拨动至上面为1，下面为0。
拨动开关共9位，左起1-8位为信息位，第九位为状态位。
第九位为“1”表示无错误，第九位为“0”表示有错误。
2．信息码设置。
如上所述，信息码设置共8位，由SW401开关位置决定，例如设置信息为DCH则八位码为1101 1100。
3．信息码观察。
为了示波器上能看到周期性的信息码和编出的卷积码，本机规定在信息位第一位前加一个“1”，在末位加两个“0”。
因此信息码序列变成1 1101 110000，我们称它们为源码序列。
将示波器1通道探头接于TP401（DTAT3），便可看到该序列波形。
4．卷积编码序列手工编码。
根据源码序列和（2.1.3）卷积码编码规秩，写出卷积码编码序列。
上述源码序列的卷积码为1101 1001 0001 1001 110000。
5．无错卷积码编码序列观察。
将拨动开关第九位（状态位）置于“1”表示无错码。
示波器1通道探头接至TP402（DATA1），2通道探头接至TP403（DATA2），观察示波器上显示的波形，看看它是否与上述卷积编码的码型一致。
实验二--卷积码编码及译码实验实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。
二、实验内容1、观察NRZ基带信号及其卷积编码信号。
2、观察帧同步信号的生成及巴克码的特性。
3、观察卷积编码信号打孔及码速率匹配方法。
4、观察接收端帧同步过程及帧同步信号。
5、观察译码结果并深入理解维特比译码的过程。
6、观察随机差错及突发差错对卷积译码的影响。
三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。
卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k 段，共Nk 个寄存器；一组n 个模2和相加器；一个由n 级组成的输出移位寄存器,对应于每段k 个比特的输入序列,输出n 个比特。
12…k 12…k …12…k12…n 卷积码输出序列信息比特一次移入k 个Nk 级移位寄存器…图17-1 卷积编码器的一般形式由图17-1可以看到，n 个输出比特不仅与当前的k 个输入信息有关,还与前（N -1）k 个信息有关。
通常将N 称为约束长度（有的书中也把约束长度定为nN 或N -1）。
常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。
编码效率定义为：/c R k n (17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。
一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。
（1）图解表示法（2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。
（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。
卷积码是一种纠错编码技术，通常用于无线通信和数字通信系统中，以提高数据传输的可靠性。
卷积码的编码和译码是两个关键步骤，下面分别介绍这两个步骤：**编码：**1. **选择卷积码的参数：** 在编码之前，您需要确定卷积码的参数，包括约束长度（constraint length）、生成多项式（generator polynomial）和码率（code rate）。
这些参数将决定编码器的结构和性能。
2. **构建编码器：** 卷积码编码器通常是一个有限状态自动机（Finite State Machine，FSM）。
根据所选的生成多项式，配置编码器的状态转移图。
编码器的输入是要编码的数据位，输出是编码后的码字。
3. **编码操作：** 对每个输入位进行编码操作。
编码器的状态会根据输入位的不同而变化，从而生成不同的编码输出。
通常，每个输入位都会产生多个输出位，这是卷积码的特点之一。
4. **输出码字：** 编码器将生成的码字传送出来，以便传输或存储。
**译码：**1. **构建译码器：** 卷积码的译码器通常是使用一种称为Viterbi算法的最大似然译码方法来实现的。
译码器需要与编码器具有相同的约束长度和生成多项式。
2. **接收和测量：** 译码器接收传输的码字，并测量接收到的码字与每个可能的发送码字之间的距离或差异。
这些度量值用于决定哪个发送码字最有可能是原始数据。
3. **路径追踪：** Viterbi算法使用路径追踪技术来跟踪可能的状态序列，并根据度量值来选择最有可能的路径。
这个过程可以看作是在状态图上搜索最佳路径的过程。
4. **译码操作：** 根据最佳路径上的状态序列，译码器重建原始数据位。
这些数据位就是译码器的输出。
卷积码的译码是一种计算密集型的过程，通常需要高效的硬件支持，特别是在高速通信系统中。
Viterbi算法是一种复杂的算法，但它在纠错性能方面非常出色，可以大大提高数据传输的可靠性。
实验九 (2,1,5）卷积码编码译码技术一、实验目的1、掌握(2,1,5）卷积码编码译码技术2、了解纠错编码原理。
二、实验内容*1、(2,1,5）卷积码编码。
2、(2,1,5）卷积码译码。
三、预备知识1、纠错编码原理。
2、(2,1,5）卷积码的工作原理。
:四、实验原理卷积码是将发送的信息序列通过一个线性的，有限状态的移位寄存器而产生的编码。
通常卷积码的编码器由K级（每级K比特）的移位寄存器和n个线性代数函数发生器（这里是模2加法器）组成。
若以（n,k,m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n 为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。
卷积码将k 元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。
与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。
卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。
在编码器复杂性相同的情况下，卷积码的性能优于分组码。
编码器随着信息序列不断输入，编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列，所以图3所示状态图可以简单直观的描述编码器的编码过程。
因此通过状态图很容易给出输入信息序列的编码结果，假定输入序列为110100，首先从零状态开始即图示a状态，由于输入信息为“1”，所以下一状态为b并输出“11”，继续输入信息“1”，由图知下一状态为d、输出“01”……其它输入信息依次类推，按照状态转移路径a->b->d->c->b->c->a输出其对应的编码结果“”。
译码方法⒈代数代数译码是将卷积码的一个编码约束长度的码段看作是[n0(m+1），k0(m+1)]线性分组码，每次根据（m+1）分支长接收数字，对相应的最早的那个分支上的信息数字进行估计，然后向前推进一个分支。
上例中信息序列=(10111），相应的码序列c=(1）。
若接收序列R=(1），先根据R的前三个分支（101000）和码树中前三个分支长的所有可能的8条路径(000000…）、（000011…）、（001110…）、（001101…）、（111011…）、（111000…）、（110101…）和（110110…）进行比较，可知（111001）与接收序列（101000）的距离最小，于是判定第0分支的信息数字为0。
然后以R的第1～3分支数字（100001）按同样方法判决，依此类推下去，最后得到信息序列的估值为=(10111），遂实现了纠错。
这种译码法，译码时采用的接收数字长度或译码约束长度为（m+1)n0，所以只能纠正不多于（dmin-1)/2个错误（n长上的）。
实用中多采用反馈择多逻辑译码法实现。
⒉维特比维特比译码是根据接收序列在码的格图上找出一条与接收序列距离（或其他量度）为最小的一种算法。
它和运筹学中求最短路径的算法相类似。
若接收序列为R=(1），译码器从某个状态，例如从状态ɑ出发，每次向右延伸一个分支（对于l<L，从每个节点出发都有2=2种可能的延伸，其中L是信息序列段数，对l≥L，只有一种可能），并与接收数字相应分支进行比较，计算它们之间的距离，然后将计算所得距离加到被延伸路径的累积距离值中。
对到达每个状态的各条路径（有2=2条）的距离累积值进行比较，保留距离值最小的一条路径，称为幸存路径（当有两条以上取最小值时，可任取其中之一），译码过程如图。
图中标出到达各级节点的幸存路径的距离累积值。
对给定R的估值序列为=(10111）。
这种算法所保留的路径与接收序列之间的似然概率为最大，所以又称为最大似然译码。
这种译码的译码约束长度常为编码约束长度的数倍，因而可以纠正不多于（df/2）个错误。
维特比译码器的复杂性随m呈指数增大。
实用中m不大于10。
它在卫星和深空通信中有广泛的应用。
在解决码间串扰和数据压缩中也可应用。
⒊序贯译码序贯译码是根据接收序列和编码规则，在整个码树中搜索（既可以前进，也可以后退）出一条与接收序列距离（或其他量度）最小的一种算法。
由于它的译码器的复杂性随m值增大而线性增长，在实用中可以选用较大的m值（如20～40）以保证更高的可靠性。
许多深空和海事通信系统都采用序贯译码。
五、:六、实验仿真这里我用c语言实现(2,1,5)卷积码编码，viterbi解码。
七、实验仿真程序#include <>、#include ""#define N 34#include ""#include <>#include<>、#define randomize() srand((unsigned)time(NULL))int s[16]={0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15};encode(unsigned int *symbols, /*编码输出*/，unsigned int *data, /*编码输入*/unsigned int nbytes, /*nbytes=n/16,n为实际输入码字的数目*/ unsigned int startstate /*定义初始化状态*/){|int j;unsigned int input,a0=0,a1=0,a2=0,a3=0;for(j=0;j<nbytes;j++){input=*data;￥data++;*symbols = input^a0^a1;symbols++;*symbols = input^a0^a2^a3;symbols++;，a3=a2;a2=a1;a1=a0;a0=input;}》return 0;}int trandistance(int m, int stat1,int stat2) /*符号m与从state1到state2时输出符号的汉明距离,`如果state1无法到state2则输出度量值为10000*/{int c;int sym,sym1,sym2;sym1=((stat2>>3)&1)^((stat1>>3)&1)^((stat1>>2)&1);*sym2=((stat2>>3)&1)^((stat1>>3)&1)^((stat1>>1)&1)^(stat1&1);sym=(sym1<<1) | sym2;if((((stat1>>3)&1)==((stat2>>2)&1))&&(((stat1>>2)&1)==((stat2>>1)&1))&&( ( (stat1>>1)&1)==(s tat2&1)))c=((m&1)^(sym&1))+(((m>> 1)&1)^((sym >> 1)&1));else~c=10000;return(c);}[int traninput(int a,int b) /*状态从a到b时输入卷积码的符号*/{int c;if ((((a>>3)&1)==((b>>2)&1))&&(((a>>2)&1)==((b>>1)&1))&&(((a>>1)&1)==(b&1))) c=((b>>3)&1);；elsec=-1;return(c);}~int tranoutput(int a,int b) /*状态从a到b时卷积码输出的符号*/{int c,s1,s2;s1=((b>>3)&1)^((a>>3)&1)^((a>>2)&1);s2=((b>>3)&1)^((a>>3)&1)^((a>>1)&1)^(a&1);#if((((a>>3)&1)==((b>>2)&1))&&(((a>>2)&1)==((b>>1)&1))&&(((a>>1)&1)==(b&1))) c=(s1<<1)|s2;elsec=-1;return(c);，}void viterbi(int initialstate, /*定义解码器初始状态*/int *viterbiinput, /*解码器输入码字序列*/int *viterbioutput) /*解码器输出码字序列*/%{struct sta /*定义网格图中每一点为一个结构体,其元素包括*/{int met; /*转移到此状态累计的度量值*/int value; /*输入符号*/~struct sta *last; /*及指向前一个状态的指针*/ };struct sta state[16][N];struct sta *g;int i,j,p,q,t,r,u,l;:for(i=0;i<16;i++) /* 初始化每个状态的度量值*/{for(j=0;j<N;j++)state[i][j].met=0;'}for(int m=0;m<16;m++){state[m][0].met=trandistance(*viterbiinput,initialstate,s[m]);、state[m][0].value=traninput(initialstate,s[m]);state[m][0].last=NULL;}for(t=1;t<N;t++)*{for(p=0;p<8;p++)for(q=0;q<16;q++){if((trandistance(viterbiinput[t],s[p],s[q])==10000)||(trandistance(viterbiinput[t],s[p+8],s[q ])==10000))-{ast=NULL;0continue;}；else{int met1=state[p][t-1].met+trandistance(viterbiinput[t],s[p],s[q]);int met2=state[p+8][t-1].met+trandistance(viterbiinput[t],s[p+8],s[q]);if(met1>met2){{state[q][t].met=met2;state[q][t].value=traninput(s[p+8],s[q]);state[q][t].last=&state[p+8][t-1];}|else{state[q][t].met=met1;state[q][t].value=traninput(s[p],s[q]);state[q][t].last=&state[p][t-1];%}}}}|r=state[0][N-1].met; /*找出n步后度量值最小的状态，准备回溯路由*/g=&state[0][N-1];。
