电液比例位置控制系统建模与仿真

水轮机筒阀电液同步控制系统数学建模与仿真1. 引言嘿，朋友们！今天咱们聊聊一个非常酷的主题，那就是水轮机筒阀电液同步控制系统。

听起来复杂，但其实就像做饭一样，只要掌握了步骤，就能做出美味的菜肴。

水轮机，这个名字一听就知道是跟水打交道的东西，简单来说，它就像是大自然的动力工厂，利用水流来发电。

筒阀嘛，简单点说，就是水流的“开关”，它能控制水的流动，咱们今天的目标就是让这个“开关”与电液系统协同工作，达到最优效果。

2. 数学建模2.1 模型的建立首先，咱们得从建模开始。

数学模型就像是这个系统的“身份证”，没有它，系统就无法运转。

我们需要定义几个关键参数，比如水流速、压力，以及筒阀的开度。

这些参数就像是乐队的乐器，各自演奏自己的旋律，但最终得和谐地结合在一起。

就像煮汤，如果火候不对，味道肯定不行。

咱们的目标是建立一个精确的数学模型，能够反映出这些参数之间的关系。

数学模型的建立过程并不简单，首先得用一些基础方程来描述水流的运动，比如连续性方程和动量方程。

听起来有点复杂，但别担心，只要你有耐心，逐步来，总能找到答案。

可以想象成拼拼图，最初的几片可能很难对上，但随着拼图的逐步完善，最后的画面就会展现出它的美丽。

2.2 关键方程的推导接着，我们要推导出几个关键方程。

这些方程就像是我们的“秘密武器”，能够帮助我们解决各种问题。

比如说，如何计算筒阀的开度对水流速的影响。

这就需要运用到流体力学的一些基本原理，虽然听起来有点高深，但其实就像是在观察小溪里的水流，你只需关注水流的变化，慢慢摸索其中的规律。

建立好数学模型后，咱们就能进行仿真了。

仿真就像是在计算机上演一场精彩的舞台剧，所有的角色都得恰如其分。

通过仿真，我们可以预测系统在不同情况下的表现，避免了实地测试中可能遇到的各种麻烦。

就好比你在家里练习做菜，总能发现那些“意想不到的惊喜”。

3. 仿真分析3.1 仿真结果的解读仿真完成后，咱们得仔细分析结果。

结果就像是小孩子的成绩单，得一分就得一分，看能不能考出个好成绩。

引言液压伺服系统是以液体压力能为动力的机械量（位移、速度和力）自动控制系统按系统。

控机械量的不同，它又可以分为电液位置伺服系统、电液速度伺服控制系统和电液力控制系统三种。

电液控制系统的基本元件包括电磁阀、电液开关控制阀、光电耦合器、功率放大器、电—机械转换器、普通电液伺服阀(频宽数十赫)、高频电液伺服阀(国内产品 400 赫)、电液比例流量阀、电液比例压力阀、电液比例方向阀、电液复合阀、电液比例泵、电液通断控制阀、电液数字阀、电液数字缸、电液数字泵等。

它们广泛用于机床工业、冶金工业、船舶工业、煤炭工业和工程机械等的控制系统中。

本文要研究的是电液速度控制系统及其仿真分析，是对电液速度控制系统的各个环节进行了数学模型的建立，并应用Matlab/Simulink对电液速度控制系统进行了仿真分析,通过幅频特性和相频特性的变化得到数学模型中各个部分对整个控制系统的影响。

1 绪论液压控制是液压技术领域的重要分支。

近20年来，许多工业部门和技术领域对高响应、高精度、高功率—重量比和大功率液压控制系统的需要不断扩大，促使液压控制技术迅速发展。

特别是控制理论在液压系统中的应用、计算及电子技术与液压技术的结合，使这门技术不论在元件和系统方面、理论与应用方面都日趋完善和成熟，并形成一门学科。

目前液压技术已经在许多部门得到广泛应用，诸如冶金、机械等工业部门及飞机、船舶部门等。

我国于50年代开始液压伺服元件和系统的研究工作，现已生产几种系列电液伺服产品，液压控制系统的研究工作也取得很大进展。

1.1电液控制技术的发展及趋势液压技术的发展与流体力学理论研究相互关联。

自1650年帕斯卡提出静态液体中的压力传播规律--帕斯卡原理以来，1686年牛顿揭示了粘性液体的内摩擦定律，18世纪建立了流体力学的连续性方程。

这些理论的建立为液压技术的发展奠定了理论基础。

从1795年，英国人首先制造出世界上第一台水压机起，液压传动开始进入工程领域。

高技术的现代战争要求地面雷达具有良好的机动性能。

雷达天线车的快速架设、调平和撤收系统是雷达的重要系统之一，直接影响到雷达的机动性能。

电液比例控制技术填补了开关液压控制技术与伺服控制技术之间的空白，已成为液压技术中最富活力的分支。

把电液比例阀控技术成功地应用雷达车调平系统中，对于提升雷达机动性能具有重要的意义。

本文所介绍的电液比例阀控液压自动调平系统，采用了比例多路阀控制，多个调平支腿执行元件可以实现不受负载约束的无级调速控制，这是实现高效调平性能的关键。

1 调平系统特点某雷达天线车自重45 t，要求工作状态时天线水平基准小于3’，整车展开并完成调平的时间控制在2 min以内。

雷达车采用四点支撑实现系统调平的方式。

系统设计采用液压作为动力源，由电机一液压泵驱动，通过液压控制阀控制四条液压支腿的升降运动，将天线车由运输状态转架为正常工作状态，并保持水平状态的稳定。

要实现本系统的功能有两个关键技术需要解决：一是调平支腿的性能问题；二是驱动控制方式和控制策略问题。

本系统方案摒弃了常规的开关阀控设计，采用性能更为先进的电液比例控制技术，提升液压系统执行机构的控制性能，实现多个执行元件同时相互独立地在不同的速度和压力下工作，使得调平控制更为灵活，实现柔性的控制策略；功能上解决了落地检测的问题，实现了一键式调平的全自动功能，有效地保证了调平时间指标的实现。

调平支腿采用带抱闸制动功能的液压马达驱动滚珠丝杆的结构设计，机械效率高，承载能力强，满足了大吨位雷达车的使用要求；通过专门研制的液压马达制动控制阀集成模块对调平支腿实施驱动和控制。

该设计方案在满足系统要求的前提下，具备了技术的先进性，同时具有很好的通用性和可扩展性。

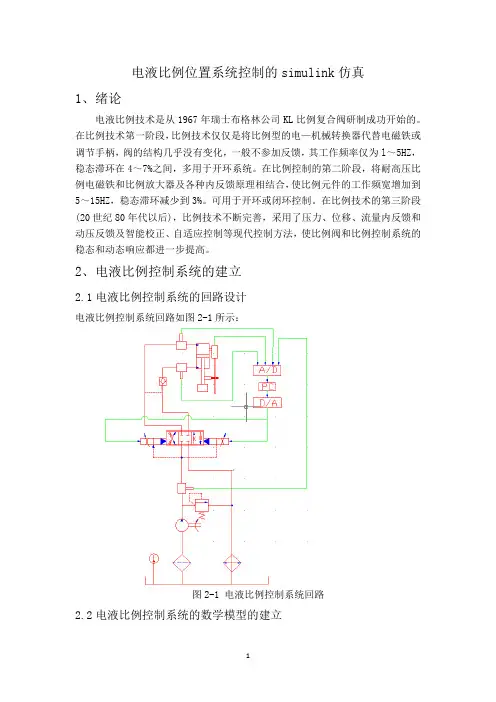
2 系统设计2．1液压系统工作原理及工作过程液压调平系统原理图如图1所示，液压泵采用负载敏感恒功率变量泵，泵源额定压力为180 bar，最大流量为90 L／min，电机功率11 kW。

图1液压系统原理图液压比例控制阀为负载敏感式换向阀，从执行元件通路引出的控制油信号经过换向滑阀中的信号孔引出，然后合成一个公共的信号通路，并且保证只是从某一侧获得的控制压差作用于流量调节装置。

电液比例方向阀控位置系统仿真研究摘 要：为了满足生产工艺的设计要求，电液比例控制系统的静态性能和动态性能往往需要进行校核，本文结合比例控制元件的特性和自动控制原理设计方法，通过参数计算建立了电液比例方向阀控位置系统的数学模型，利用MA TLAB 仿真校核比例控制系统的动态性能，实现了对系统参数的校正。

关键词：电液比例阀；数学建模；MA TLAB0 前言电液比例阀是在通断式控制元件和伺服控制元件的基础上发展起来的一种电－液控制元件，它可以接受电信号的指令，连续地控制液压系统的压力、流量和方向等参数，使之与输入信号成比例地变化。

电液比例控制技术作为连结现代微电子技术和大功率工程控制设备之间的桥梁，已经成为现代控制工程的基本技术构成之一。

与传统的电液伺服技术相比，它具有可靠、节能和廉价等明显特点，已经赢得相当广泛的应用领域。

实际应用中，为了改进和优化电液控制系统的控制特性，需要对系统进行理论分析和实验研究。

理论分析通常借助自动控制理论，为了分析便利常引入一些假设使问题简化，往往难以得到令人满意的结果；实验研究一般以建立实际系统或相似物理模型为前提，需要在时间、空间、费用等方面花费较大的代价。

相对而言，采用计算机仿真手段对电液控制系统进行研究则具有非常突出的优点[1]。

本文利用MA TLAB 仿真具有改变参数方便，与客观实际一致性好，省工省时，研究质量高的优点对比例方向阀控闭环位置系统进行了动态性能分析。

1 系统数学建模图1为采用比例方向阀构成的闭环位置控制系统，其基本组成与相应各环节的传递函数如图2所示。

建立只有惯性负载的动态数学模型方法如下[2]：1）比例放大器：其转折频率比系统的频宽高得多，可近似为比例环节，设增益为a K 。

2）位置检测传感器：其频宽也比系统频宽高得多，亦可近似为比例环节，设增益为m K 。

3）比例方向阀：根据测试结果，工程上将比例方向阀视为一个二阶环节，传递函数为1)(222++=vv vssqpv K s W ωδω，式中q K 为比例方向阀的流量增益（A s m⋅3）；v ω为比例方向阀的相频宽（s rad ）；v δ为比例方向阀的阻尼比，取值范围为0.5～0.7。

M A T L A B电液位置伺服控制系统设计及仿真数控机床工作台电液位置伺服控制系统设计及仿真姓名：雷小舟专业:机械电子工程子方向：机电一体化武汉工程大学机电液一体化实验室位置伺服系统是一种自动控制系统。

因此，在分析和设计这样的控制系统时，需要用自动控制原理作为其理论基础，来研究整个系统的动态性能，进而研究如何把各种元件组成稳定的和满足稳定性能指标的控制系统。

若原系统不稳定可通过调整比例参数和采用滞后校正使系统达到稳定，并选取合适的参数使系统满足设计要求。

1 位置伺服系统组成元件及工作原理数控机床工作台位置伺服系统有不同的形式，一般均可以由给定环节、比较环节、校正环节、执行机构、被控对象或调节对象和检测装置或传感器等基本元件组成[1]。

根据主机的要求知系统的控制功率比较小、工作台行程比较大，所以采用阀控液压马达系统。

系统物理模型如图1所示。

图1 数控机床工作台位置伺服系统物理模型系统方框图如图2所示。

图2 数控机床工作台位置伺服系统方框图数控机床工作台位置伺服系统是指以数控机床工作台移动位移为控制对象的自动控制系统。

位置伺服系统作为数控机床的执行机构，集电力电子器件、控制、驱动及保护为一体。

数控机床的工作台位置伺服系统输出位移能自动地、快速而准确地复现输入位移的变化，是因为工作台输出端有位移检测装置（位移传感器）将位移信号转化为电信号反馈到输入端构成负反馈闭环控制系统。

反馈信号与输入信号比较得到差压信号，然后把差压信号通过伺服放大器转化为电流信号，送入电液伺服阀（电液转换、功率放大元件）转换为大功率的液压信号（流量与压力）输出，从而使液压马达的四通滑阀有开口量就有压力油输出到液压马达，驱动液压马达带动减速齿轮转动，从而带动滚珠丝杠运动。

因滚珠丝杠与工作台相连所以当滚珠丝杠 运动时，工作台也发生相应的位移。

2数控工作台的数学模型 2.1 工作台负载分析工作台负载主要由切削力c F ,摩擦力f F 和惯性力a F 三部分组成，则总负载力为:a f c L F F F F ++=2.2液压执行机构数学模型工作台由液压马达经减速器和滚珠丝杠驱动。

电液伺服控制系统的设计与仿真引言电液伺服系统具有响应速度快、输出功率大、控制精确性高等突出优点，因而在航空航天、军事、冶金、交通、工程机械等领域得到广泛应用。

随着电液伺服阀的诞生，使液压伺服技术进入了电液伺服时代，其应用领域也得到广泛的扩展。

随着液压系统逐渐趋于复杂和对液压系统仿真要求的不断提高，传统的利用微分方程和差分方程建模进行动态特性仿真的方法已经不能满足需要。

因此，利用AMESim、Matlab／Simulink等仿真软件对电液伺服控制系统进行动态仿真，对于改进系统的设计以及提高液压系统的可靠性都具有重要意义。

1 液压系统动态特性研究概述随着液压技术的不断发展与进步和应用领域与范围的不断扩大，系统柔性化与各种性能要求更高，采用传统的以完成执行机构预定动作循环和限于系统静态性能的系统设计远远不能满足要求。

因此，现代液压系统设计研究人员对系统动态特性进行研究，了解和掌握液压系统动态工作特性与参数变化，以提高系统的响应特性、控制精度以及工作可靠性，是非常必要的。

1.1 液压系统动态特性简述液压系统动态特性是其在失去原来平衡状态到达新的平衡状态过程中所表现出来的特性，原因主要是由传动与控制系统的过程变化以及外界干扰引起的。

在此过程中，系统各参变量随时间变化性能的好坏，决定系统动态特性的优劣。

系统动态特性主要表现为稳定性（系统中压力瞬间峰值与波动情况）以及过渡过程品质（执行、控制机构的响应品质和响应速度）问题。

液压系统动态特性的研究方法主要有传递函数分析法、模拟仿真法、实验研究法和数字仿真法等。

数字仿真法是利用计算机技术研究液压系统动态特性的一种方法。

先是建立液压系统动态过程的数字模型——状态方程，然后在计算机上求出系统中主要变量在动态过程的时域解。

该方法适用于线性与非线性系统，可以模拟出输入函数作用下系统各参变量的变化情况，从而获得对系统动态过程直接、全面的了解，使研究人员在设计阶段就可预测液压系统动态性能，以便及时对设计结果进行验证与改进，保证系统的工作性能和可靠性，具有精确、适应性强、周期短以及费用低等优点。

8科技资讯 SC I EN C E & TE C HN O LO G Y I NF O R MA T IO N高 新 技 术本文以冶金行业某型提升装置为研究对象,合理选用电液比例方向阀、减压阀、速度传感器等元件构建控制系统并建立数学模型,最后利用计算机工程软件Matlab/Simulink,研究分析了系统的控制性能,使其更好的满足实际生产需要。

1 提升机电液比例控制系统设计提升机的一个重要参数是提升速度,提升速度的平稳性、快速性、准确性是衡量其性能的一个重要指标,直接影响着产品质量及生产效率。

为了对提升机的速度进行精确控制,设计了一种采用电液比例速度控制系统,提高提升机的速度控制精度,相关分析结果可对提升机的设计及改造维护提供理论参考。

根据实际生产要求提出控制系统的技术要求及性能指标如下:液压原理图如图1所示。

(1)速度控制频域动态指标: 相位裕度: 45~70 ;增益裕度: 8K dB dB;-3dB频宽: 8 Hz;(2)速度控制时域动态指标(在单位阶跃信号作用下): 上升时间: 0.2r t s s; 超调量: 10%p ; 调整时间: 0.2s t s s;(3)技术经济指标:位置控制精度 2% ; 工作噪声:<85dB。

2 提升机电液比例控制系统仿真根据系统原理建立相关元件的数学模型,得到系统传递函数,并带入相关参数如下。

系统的开环传递函数:1022()21qe d s m k h hhK K K K R K D G s ss22225.120.1551236.7236.7s s 系统的闭环传递函数:102120()21qe s mq h e d h hs m K K K R K D W s K K K s s K R K D 22225120.155226.1236.7236.7s s 根据式系统开环传递函数编写MATLAB程序,基本程序如下。

%Draw Bode clear all;clc;num=[1];den=[0.0000178,0.00131,1];G=tf(225.1*num,den);bode(G);grid;绘制系统开环Bode图如图2所示。

电液比例马达速度同步控制系统建模与仿真杨前明;孔令奇;李健;王世刚;郭建伟【摘要】以船携式溢油回收机围油栏布放驱动控制系统为研究对象，针对双马达速度同步控制问题，提出以可编程逻辑控制器（programmable logic controller ，PLC）为控制核心的电液比例阀控马达主从速度同步控制方案。

建立其速度同步控制系统数学模型，利用MATLAB／Simulink软件进行稳定性、输出速度与速度同步误差分析；为提高系统稳定性同时减小速度同步误差，引入P ID控制环节。

仿真结果表明，控制系统引入P ID整定环节后，其稳态性能明显提高，马达输出速度稳定性与同步性均有满意的设计效果。

在同步精度要求不高的情况下，基于PLC的主从同步控制策略是切实可行的。

%Taking the driving control systemof oil boom uncoil and rewound for the ship carrying oil spill recovery machine as the research object ,aiming at the problem of synchronousco ntrol of dual‐motor speed synchronization , the electric‐hydraulic proportional valve controlled motor speed synchronous scheme of master‐slave based on PLC w as proposed .T he mathematical model of speed synchronous control system was established and the MATLAB/Simulink software was also used to analyze the stability ,the output speed and the speed synchronization error .The PID unit had been introduced into this system for improving the stability and reducing the speed syn‐chronization error .The simulation results showed that the stable performance was improved sig‐nificantly ,the motor output speed stability and the synchronization performance had satisfied de‐sign effect after the PID unit being introduced into the system .The synchronous controlstrate gy of master‐slave based on PLC is feasible w hen the demand of synchronous precision is not high .【期刊名称】《工程设计学报》【年(卷),期】2015(000)004【总页数】7页(P330-336)【关键词】溢油回收机;马达速度同步;电液比例;Simulink;PID【作者】杨前明;孔令奇;李健;王世刚;郭建伟【作者单位】山东科技大学机械电子工程学院，山东青岛266590;山东科技大学机械电子工程学院，山东青岛266590;山东科技大学机械电子工程学院，山东青岛266590;青岛华海环保工业有限公司，山东青岛266400;青岛华海环保工业有限公司，山东青岛266400【正文语种】中文【中图分类】TP202;TP271船携式双内嵌溢油回收系统用于牵引围油栏进行海洋溢油收集，通过对机身本体转速与围油栏卷筒转速的协调控制，使其在抓握点处线速度同步，以实现围油栏布放机械化作业.实际作业情况分析表明，线速度同步精度控制在15～20mm／s以内是系统稳定作业的基本保证.文献［1］就扫油臂系抓握点位置精准运动控制采用“D－H位移矩阵法”进行了分析，解决了动点运动轨迹规划策略问题.实现线速度同步控制是解决系统机械化稳定作业的技术关键，而线速度同步控制的实质是解决扫油臂端部与围油栏卷筒布放线速度同步问题.文献资料研究表明，同步闭环控制采用了自适应控制和智能控制理论设计控制策略及其控制器，如PI与PID优化调节器、模型跟随自适应控制器（AMFC）、参考模型自适应控制器（MRAC）、神经网络自适应同步控制算法和神经网络相关学习等同步控制算法［2－5］.本文根据实际设计要求，提出基于PLC控制的双路比例阀控马达速度“主从控制”实现方法，建立速度控制系统数学模型，引入PID控制环节，对控制系统进行仿真分析与校正.1 双马达驱动系统组成与速度控制1.1 系统组成图1所示为围油栏收放装置示意图.机身本体以及围油栏卷筒均采用马达－减速机驱动方案，机身本体马达经行星轮减速机、外啮合齿轮对减速后驱动扫油臂转动；卷筒马达经行星轮减速机减速后驱动卷筒转动，最终实现抓握点（浮筒）处的线速度保持同步.图1 围油栏收放装置示意图Fig.1 The schematic diagram of oil boomdevice1—卷筒；2—导向辊；3—围油栏；4—扫油臂；5—机身本体；6—浮筒；7，10—马达；8，11—减速机；9—齿轮对.1.2 速度控制目标围油栏的一端缠绕在卷筒1上，另一端则固定在扫油臂端部浮筒6上，围油栏实际布放过程中，考虑到海浪冲击及围油栏自身的柔性，要求围油栏布放过程中具有一定张紧长度.围油栏牵引端线速度良好的同步性、协调性与可控性是布放系统实现稳定作业的前提.实际设计过程中将两端线速度误差限制在15～20mm／s范围内.1.3 主从同步控制策略双马达同步控制的常用方式有同等控制与主从控制两种方式.主从控制方式即以2个马达中其一的输出作为理想输出，并以此输出作为另一马达的指令控制信号，即速度跟随实现同步控制；而同等方式是指2个需同步控制的液压马达同时分别受到相同的控制指令信号，实现同步驱动控制.同等控制方式的液压同步闭环控制系统中，各执行、反馈、检测与控制元件需有严格的匹配关系［5－6］.在本文研究的双马达控制系统中，2个液压马达在实现两者速度良好协调性的同时，允许两者有一定的先后启动顺序，因此选用主从方式进行控制.图2所示为双马达速度同步控制系统原理图，系统由PLC、D／A模块、比例放大器、电磁比例换向阀、液压马达、编码器等组成.主动回路采用开环控制方案，将设定值输入PLC，通过D／A模块将设定值转化为与之对应的电压模拟信号.比例放大器将电压模拟信号转换为对应的比例阀驱动电流信号，实现其流量输出调节，从而实现马达转速控制.马达1转速输出作为马达2速度控制指令的输入值，并与马达2的速度测定返回值进行比较处理后作为比例阀2控制信号，实现马达2的转速跟随控制.图2 双马达速度同步控制系统原理图Fig.2 The schematic diagram of speed synchronous control system of dual－motor2 数学模型图3所示为双马达速度协调控制系统方框图，分别用G1（S），G2（S），G3（S），G4（S）表示D／A模块、比例放大器、比例方向阀、液压马达与负载的传递函数，用H1（S），H2（S）表示速度传感器与速度调整因子的传递函数［7］，系统为典型的“主从控制”方式，马达1的输出信号经采集后作为马达2的跟随输出控制信号.图3 双马达速度同步控制系统方框图Fig.3 The block diagram of speed synchronous control system of dual－motor为正确把握控制系统特征，对系统稳定性、同步误差进行分析.以下首先建立其组成各环节及系统传递函数数学模型，为仿真分析奠定基础.2.1 D／A模块和比例放大器D／A模块、比例放大器两者的输出与输入均可视为比例环节［8］，其传递函数可分别表述如下：式中：U（S）为D／A模块输出电压，V；SV（S）为PLC设定输入值；I（S）为比例放大器输出电流，mA.2.2 比例方向阀当阀固有频率与液压固有频率接近时，阀可近似为2阶震荡环节，其表达式为［8］当阀固有频率大于液压固有频率的3～5倍时，阀可近似为惯性环节，其表达式为［8］其中：Ksv由按实际供油压力下的实际空载流量确定，即式中：Ksv——比例阀流量增益，m3／（s·A）；Tsv——比例阀时间常数，s；qn——比例阀的In额定流量，m3／s；In——比例阀的额定电流，mA；ps——实际供油压力，MPa；psn——通过额定流量时的规定阀压降，MPa［9］；Q0——比例阀的空载流量，m3／s.2.3 液压马达与负载负载主要为海水阻力，属惯性负载，因此液压马达及负载可看作纯惯量，其输出角速度的传递函数表述［8］为其中：式中：Q——比例阀输出空载流量，m3／s；Dm——液压马达排量，m3／rad；wh——液压固有频率，rad／s；ξh——液压阻尼比；βe——液体有效体积弹性模量，取βe＝700×106 Pa；Vt——阀控对称马达的总控制容积，取Vt＝（1.25～3.5）×2πDm；Jt——液压马达轴上总等效转动惯量，kg·m2.2.4 速度传感器速度传感器的输出与输入为比例环节［8］，其传递函数为式中：P（S）为脉冲输出数；v（S）为马达输出转速，r／s.2.5 速度调整因子将速度传感器的脉冲输出值与PLC的设定值进行比较时，须将单位进行统一，即令马达最高转速与PLC数字量输出最大值相统一，因此，调整因子是不可或缺的.首先由马达最高转速对应的PLC数字量最大设定值折算得出初始值，再由Simulink中开环响应结果逐步试凑获得，最终选定Kv1＝60，Kv2＝14.5.综合以上控制系统各环节传递函数，可得图4所示控制系统传递函数方框图.由图4传递函数框图不难获得2个液压马达的输出传递函数［9］.马达1开环传递函数［10］为图4 控制系统传递函数方框图Fig.4 The block diagram of transfer function of the control system马达2闭环传递函数［10］为其中，分析马达2闭环传递函数可知：除Ksv2外，其余参数均为常量，即影响马达2转速的参量为比例放大器输出电流，马达2转速由PLC设定值SV、马达1速度调整因子Kv1确定.同理，由马达1开环传递函数分析可知，马达1转速仅取决于PLC设定值SV.换言之，对于双马达速度主从同步控制系统，在构成控制系统元件及外界因素如海况等级、作业程序及外界其他干扰相对稳定的情况下，通过调整PLC设定值可以便捷实现2个液压马达的主从速度跟随同步控制.3 系统Simulink仿真3.1 原始参数利用MATLAB仿真软件中的Simulink软件包将系统闭环传递函数方框图转化为液压系统仿真模型进行仿真，系统有关原始参数选取可参见表1.表1 原始参数Table 1 Original parameters注：1）由于围油栏在海水中展开时阻力较大，因此折算在液压马达轴上的负载惯量较大，导致液压阻尼比常值大很多，远超过0.1～0.2的一般值.Kd D／A模块增益 1／3200 Ka／（A／V）比例放大器增益0.1 ξsv 比例阀阻尼比 0.6 wsv／（rad／s）比例阀固有频率60 Kq1／（m3／（s·A））比例阀1流量增益8.67×10－4 Kq2／（m3／（s·A））比例阀2流量增益2.55×10－3 ξh1 液压阻尼比11）7.57 ξh2 液压阻尼比21）1.36 wh1 液压固有频率1 10.55 wh2 液压固有频率2 27 Kf1 传感器1增益 39 Kf2 传感器2增益35 Kv1 速度1调整因子 60 Kv2 速度2调整因子14.5 Dm1／（m3／rad）马达1排量10×10－6 Dm2／（m3／rad）马达2排量6.5×10－6 Jt1／（kg·m2）马达1负载惯量 20 Jt2／（kg·m2）马达2负载惯量10 Kce／（m2·（s·Pa）－2）流量压力系数［11］3.3×10－12 K1 动态柔度系数［11］0.013 63.2 系统稳定性在对系统马达速度同步输出仿真前，首先对系统进行频域稳定性及阶跃响应分析.图5所示为双马达速度同步控制系统在Simulink中的传递函数框图.图5 Simulink中传递函数方框图Fig.5 The block diagram of transfer function in Simulink图6所示为马达2开环系统的Bode图，图中曲线1表示未加入PID环节时的频率特性曲线.图6 开环系统Bode图Fig.6 The open－loop Bode diagram系统的相位裕量为16.8°，幅值裕量为1.92 dB，而较稳定的控制系统的相位裕量为30°～60°，幅值裕量应大于6dB，因此稳定性较差［10］.选择单位阶跃信号作为阶跃响应系统的输入信号，马达1、马达2（以示波器2、示波器3分别表示）的输出响应如图7中曲线1与曲线2所示，马达2具有明显的稳态误差.由式（8）可知，马达2的闭环传递函数为0型系统，其阶跃响应存在稳态误差.Ⅰ型系统对阶跃响应的位置误差为零［10］，所以需加入积分环节（1／S）对控制系统的稳态误差进行校正，现采用PLC自带PID指令对系统进行调节［12－15］.图6中曲线2为PID整定后的系统Bode图，系统的相位裕量为57°，幅值裕量为12.2dB，因此系统的稳定性较好.图7中曲线3为校正后的阶跃响应曲线，显然其稳态误差与同步精度均有显著提高.图7 主从控制下的马达阶跃响应曲线Fig.7 The step response curve of motor under the control of master－slave图7中曲线1，3为马达1开环控制、PID整定后马达2闭环控制系统响应曲线，均具有良好的响应稳定性，无震荡，无超调；到达稳态值的75%所需时间在2.5s 左右，能够满足实际控制系统稳定性及速度响应要求.3.3 马达输出速度与同步误差双马达速度协调主从控制是通过改变调整因子Kv1，实现2个马达的速度比例关系，本系统实际要求2个马达速度比约为1∶6.4.图8所示为双马达速度主从同步控制系统扫油臂端部与卷筒围油栏线速度输出v1，v2曲线.图8 主从控制下扫油臂端部与卷筒线速度曲线Fig.8 The curve of linear velocities of the arm ends and the drum under the control of master－slave由图8中曲线可以看出，马达1，2的实际速度输出v1，v2同步性好.开始阶段，速度差逐渐变大，此后在约1.2s时间内迅速减小为零，并继续下降为负值，稳定在Δv＝7mm／s左右.速度误差由正转为负反映了马达1、马达2在开始阶段主动控制马达输出转速略高于跟随马达输出速度；当系统运行趋于稳定后，跟随马达输出速度略高于主动控制马达.稳定后的线速度接近43cm／s，速度误差Δv≈7mm ／s，远小于15～20mm／s，满足系统控制要求.4 结论本文针对海面溢油回收机围油栏自动布放液压牵引系统的同步控制问题进行了研究.根据围油栏自动化布放作业要求，采取“主从方式”控制策略，实现液压牵引系统同步控制；建立了围油栏自动化布放双马达速度同步控制系统数学模型，提出了主从控制策略，利用Simulink软件对系统进行稳定性分析；在控制系统中引入PID 调节环节，改善了主从控制系统响应稳定性；在分析主从马达同步控制传递函数的基础上，提出通过PLC设定值SV实现马达主从同步速度控制的方法.实际系统仿真结果表明，系统同步性良好，同步误差小于设计要求.本文提出的双马达主从同步速度控制原理与方法为本课题后续研究奠定基础，也为同类问题设计提供参考.参考文献：［1］杨前明，闫久祥，王世刚，等.基于D－H位移矩阵法的溢油回收系统扫油臂运动学建模［J］.山东科技大学学报：自然科学版，2014，33（1）：92－97.YANG Qian－ming，YAN Jiu－xiang，WANG Shi－gang，etal.Kinematic modeling for telescopic jib arm of oil spill recovery system based on D－H displacement matrix method［J］.Journal of Shandong University of Science and Technology：Natural Science，2014，33（1）：92－97.［2］胡寿松，周川，胡维礼.基于神经网络的模型跟随鲁棒自适应控制［J］.自动化学报，2000，26（5）：623－629.HU Shou－song，ZHOU Chuan，HU Wei－li.Model－following robust adaptive control based on neural networks［J］.Acta Automatica Sinica，2000，26（5）：623－629.［3］刘晓峰，刘昕晖，王龙山.基于模糊PID控制的大型履带起重机双马达速度同步控制［J］.吉林大学学报：工学版，2011，41（3）：659－664.LIU Xiao－feng，LIU Xi－hui，WANG Long－shan.Speed synchronization control of dual－motor in large crawler crane based on fuzzy PID control［J］.Journal of Jilin University：Engineering and Technology Edition，2011，41（3）：659－664.［4］逄波，王占林，白国长.工程机械液压底盘试验台双马达同步的研究［J］.系统仿真学报，2007，19（9）：2018－2021.PANG Bo，WANG Zhan－lin，BAI Guo－chang.Study of dual motors synchronism drive based on engineering machine hydraulics under pan test－bed［J］.Journal of System Simulation，2007，19（9）：2018－2021.［5］吴保林，裘丽华，祁小野，等.单泵驱动双马达速度同步控制技术研究［J］.系统仿真学报，2006，18（6）：1585－1588.WU Bao－lin，QIU Li－hua，QIXiao－ye，et al.Research on rotational speed synchronization control of one pump driving two motors［J］.Journal of System Simulation，2006，18（6）：1585－1588.［6］苏东海，韩国惠，于江华，等.液压同步控制系统及应用［J］.沈阳工业大学学报，2005，27（4）：364－367.SU Dong－hai，HAN Guo－yu，YU Jiang－hua，et al.Design and application of hydraulic synchronization control system［J］.Journal of Shenyang University of Technology，2005，27（4）：364－367.［7］董建园，曹旭妍，委培，等.电液比例位置控制系统的研究［J］.机床与液压，2013，41（7）：40－47.DONG Jian－yuan，CAO Xu－yan，WEI Pei，et al.Research on electro－hydraulic proportional position servo system ［J］.Machine Tool ＆Hydraulics，2013，41（7）：40－47.［8］张利平.液压控制系统及设计［M］.北京：化学工业出版社，2007：239－253.ZHANG Li－ping.The hydraulic control system and design［M］.Beijing：Chemical Industry Press，2007：239－253.［9］宋又廉.比例换向阀压降的计算方法和阀通径选择［J］.机床与液压，2007，35（5）：150－152.SONG You－puting method for evaluating pressure drop of proportional direction valves and the selection of valve nominal diameter［J］.Machine Tool ＆Hydraulics，2007，35（5）：150－152.［10］陈康宁，王馨，李天石，等.机械工程控制基础［M］.修订本.西安：西安交通大学出版社，2010：179－187.CHEN Kang－ning，WANG Xin，LI Tian－shi，et al.Mechanical Engineering control［M］.Rev.ed.Xi′an：Xi′an Jiaotong University Press，2010：179－187.［11］吴根茂，邱敏秀，王庆丰，等.新编实用电液比例技术［M］.杭州：浙江大学出版社，2010：203－211.WU Gen－mao，QIU Min－xiu，WANG Qing－feng，et al.Electro－hydraulic proportional technique in theory and application［M］.Hangzhou：Zhejiang University Press，2010：203－211. ［12］李艳杰，崔天宇，王海，等.比例阀控液压缸位置PID闭环控制的PLC软件实现［J］.沈阳理工大学学报，2013，32（4）：37－41.LI Yan－jie，CUI Tian－yu，WANG Hai，et al.Software implementation of hydraulic cylinder position PID closed loop control in proportional value control system using PLC［J］.Journal of Shenyang Ligong University，2013，32（4）：37－41. ［13］AYMAN A Aly.Model reference PID control of an electro－hydraulic drive［J］.International Journal of Intelligent Systems and Applications，2012，4（11）：24－32.［14］SHAO Jun－peng，WANG Zhong－wen，LIN Jian－ying.Model identification and control of electro－hydraulic position servo system ［C］.Intelligent Human－Machine Systems and Cybernetics.Hangzhou，Zhejiang，China，Aug.26－27，2009.［15］李丽霞，毛向阳，边东岩，等.基于PLC的电液比例流量控制系统设计［J］.机床与液压，2013，41（4）：130－133.LI Li－xia，MAO Xiang－yang，BIAN Dong－yan，et al.Design of the electrohydraulic proportional flow control system based on PLC［J］.Machine Tool ＆Hydraulics，2013，41（4）：130－133.。

电液比例铲斗联控制系统建模与联合仿真孙畅励;贾文华【摘要】基于挖掘机SY215C8M样机,分析铲斗联系统的结构组成原理并对其进行电液比例系统改造,利用AMEsim建模并仿真验证.为提高控制精度,提出模糊自整定PID控制策略,用AMESim-Simulink联合仿真,观察比较传统pid控制和模糊pid控制的区别.【期刊名称】《软件》【年(卷),期】2019(040)005【总页数】6页(P134-139)【关键词】铲斗联系统;电液比例控制;模糊控制;联合仿真【作者】孙畅励;贾文华【作者单位】南京工程学院,江苏南京 211100;南京工程学院,江苏南京 211100【正文语种】中文【中图分类】TP2730 引言挖掘机（如图 1）在工程上应用十分广泛。

本文基于三一重机SY215C8M样机铲斗联电铲斗联液比例系统，分析其工作原理并进行电液比例改造，推导挖掘机铲斗联电液比例系统数学模型并利用AMEsim进行建模并仿真验证系统改造的合理性。

采用模糊PID控制策略代替传统pid对液压缸位置进行控制，利用AMESim-Simulink进行联合仿真，观察比较传统pid控制器和模糊pid控制器在控制效果上的区别。

图1 挖掘机的广泛应用Fig.1 Widespread application of excavators1 系统组成原理及改造1.1 挖掘机铲斗联系统组成挖掘机工作装置中应用最为广泛的是铰接反铲式工作装置，主要由动臂、斗杆、铲斗及其相应的液压油缸组合而成，本文是基于挖掘机铲斗联系统进行研究。

铲斗作为挖掘机进行挖掘动作的执行元件，主要有内收和外摆两个动作，两个动作之间的切换主要来实现[1-2]，液压回路如图2。

在挖掘机作业之前，铲斗主控阀1处于左位，铲斗合流阀2关闭，前泵单独供油，液压缸有杆腔进油，铲斗活塞后缩实现铲斗外摆动，进入准备挖掘动作状态。

当铲斗开始挖掘作业时，铲斗主控阀1处于右位，液压油经过主控阀流入液压缸无杆腔，活塞外伸，铲斗内收。

电液位置伺服控制系统设计方法本文将介绍电液位置伺服控制系统设计的方法，并针对其中的几个关键环节进行详细说明。

一、系统建模几何方法是通过几何分析来建立系统的几何关系方程，例如通过机械结构的分析来推导出负载移动和油液角位移的关系。

物理方法是通过物理定律和原理来建立系统的动态方程，例如利用牛顿第二定律和液压力学原理来推导出系统的动态方程。

数学方法是通过系统的输入和输出响应数据来建立系统的数学模型，例如通过实验数据拟合出系统的传递函数或状态空间模型。

二、控制策略选择在电液位置伺服控制系统中，常用的控制策略包括PID控制、模糊控制和自适应控制等。

PID控制是最常用的控制策略之一，通过调节比例、积分和微分三个控制参数来实现位置控制。

PID控制具有简单、稳定的特点，适用于许多工业领域。

模糊控制是一种基于模糊逻辑的控制策略，能够处理非线性、模糊的系统。

模糊控制通过建立模糊规则和模糊推理机制来实现控制。

自适应控制是一种根据系统状态和参数变化进行自动调节的控制策略。

自适应控制能够实时调节控制参数，以适应系统的变化。

根据具体的系统动态特性和控制性能要求，选择适合的控制策略。

三、控制器设计根据选定的控制策略，设计合适的控制器参数，例如PID控制中的比例、积分和微分参数。

控制器参数的选择通常通过试验和调整得到，常用的方法包括试探法、经验法和优化算法。

试探法是最常用的方法，通过对控制器参数进行调整，观察系统的响应，找到最佳的控制参数。

经验法是通过工程经验来选择控制器参数，常用的经验法包括Ziegler-Nichols 方法和Chien-Hrones-Reswick 方法等。

优化算法是一种通过优化方法来寻找最优控制参数的方法，例如遗传算法、粒子群算法等。

四、系统仿真和调试在设计完成后，应进行系统仿真和调试，以验证系统的性能和稳定性。

系统仿真可以通过利用系统的数学模型，使用仿真软件（如Matlab/Simulink）进行。

仿真可以帮助设计人员评估系统的性能，并对控制器参数进行进一步调整。