神经网络学习 之 BP神经网络

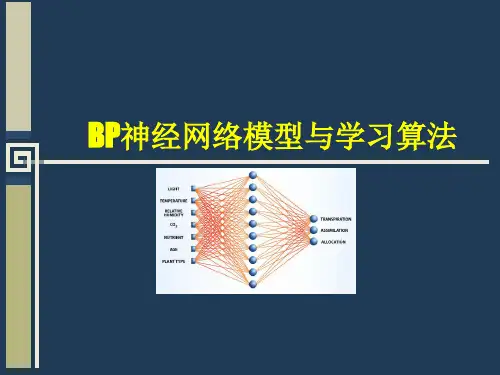
bp神经网络BP神经网络（Backpropagation Network）是一种被广泛应用于分类、预测和优化问题中的人工神经网络模型。

BP神经网络具有简单易懂、易于理解和易于实现的特点，因此在工程实践中被广泛应用。

BP神经网络的基本思想是将信息通过一层层的神经元传递，然后反向调节神经元的权重和偏置，从而实现对模型参数的优化。

BP神经网络通常包含输入层、隐层和输出层三个层次。

其中输入层用于接收输入数据，隐层用于处理输入数据，输出层用于给出模型的预测结果。

BP神经网络通过不断反向传播误差信号来调整各层神经元之间的连接权重，从而实现对模型参数的逐步优化。

BP神经网络的训练过程通常分为前向传播和反向传播两个阶段。

在前向传播阶段，输入数据被输入到神经网络中，经过一系列计算后得到输出结果。

在反向传播阶段，将输出结果与真实值进行比较，计算误差信号，并通过反向传播算法将误差信号逐层传递回到输入层，从而实现对神经网络参数（权重和偏置）的不断调整。

通过多次迭代，直到神经网络的输出结果与真实值的误差达到一定的精度要求为止。

BP神经网络的优点在于可以处理非线性问题，并且可以自适应地调整模型参数。

然而，BP神经网络也存在一些缺点，例如容易陷入局部极小值，训练速度较慢，需要大量的训练数据等等。

在实际应用中，BP神经网络已经被广泛应用于分类、预测和优化等方面。

例如，BP神经网络可以用于识别手写数字、预测股票市场走势、自动驾驶和机器人控制等方面。

另外，BP 神经网络还可以与其他机器学习算法相结合，共同解决各种复杂问题。

总之，BP神经网络是一种简单实用的人工神经网络模型，具有广泛的应用前景。

在实际应用中，需要根据具体问题对模型进行适当的改进和优化，以提高其预测精度和鲁棒性。

載师信号（期望输出信号）图1-7神经网络学习系统框图输入部接收外来的输入样本X,由训练部进行网络的权系数W调整，然后由输岀部输岀结果。

在这个过程中，期望的输出信号可以作为教师信号输入，由该教师信号与实际输出进行比较，产生的误差去控制修改权系数W学习机构可用图1—8所示的结构表示。

在图中，X，X2，…，X n，是输入样本信号，W，W，…，W是权系数。

输入样本信号X可以取离散值0”或1”输入样本信号通过权系数作用，在u产生输岀结果口WX，即有：u=B/VX =WX i +WX2 + …+WX n再把期望输岀信号丫(t)和u进行比较，从而产生误差信号e。

即权值调整机构根据误差e去对学习系统的权系数进行修改，修改方向应使误差e变小，不断进行下去，使到误差e为零，这时实际输出值u和期望输出值丫(t)完全一样，则学习过程结束。

期望辑出y图学可机构神经网络的学习一般需要多次重复训练，使误差值逐渐向零趋近，最后到达零。

则这时才会使输岀与期望一致。

故而神经网络的学习是消耗一定时期的，有的学习过程要重复很多次，甚至达万次级。

原因在于神经网络的权系数W有很多分量W，W，----W n ；也即是一个多参数修改系统。

系统的参数的调整就必定耗时耗量。

目前，提高神经网络的学习速度，减少学习重复次数是十分重要的研究课题，也是实时控制中的关键问题。

、感知器的学习算法感知器是有单层计算单元的神经网络，由线性元件及阀值元件组成。

感知器如图感知器的数学模型:v=f[加讯-e] (1-12)其中：f[.]是阶跃函数，并且有pl 2二主W凶-0工01 —1>u=SW i X^-0<O“1(1-13)9是阀值。

感知器的最大作用就是可以对输入的样本分类，故它可作分类器，感知器对输入信号的分类如下:卩，A类Y = * —B 类(1-14)1-9所示。

f [sw iX£-O]1时，输入样本称为A类；输岀为-1时，输入样本称为B类。

BP神经网络学习及算法1.前向传播：在BP神经网络中，前向传播用于将输入数据从输入层传递到输出层，其中包括两个主要步骤：输入层到隐藏层的传播和隐藏层到输出层的传播。

(1)输入层到隐藏层的传播：首先，输入数据通过输入层的神经元进行传递。

每个输入层神经元都与隐藏层神经元连接，并且每个连接都有一个对应的权值。

输入数据乘以对应的权值，并通过激活函数进行处理，得到隐藏层神经元的输出。

(2)隐藏层到输出层的传播：隐藏层的输出被传递到输出层的神经元。

同样，每个隐藏层神经元与输出层神经元连接，并有对应的权值。

隐藏层输出乘以对应的权值，并通过激活函数处理，得到输出层神经元的输出。

2.反向传播：在前向传播后，可以计算出网络的输出值。

接下来，需要计算输出和期望输出之间的误差，并将误差通过反向传播的方式传递回隐藏层和输入层，以更新权值。

(1)计算误差：使用误差函数（通常为均方差函数）计算网络输出与期望输出之间的误差。

误差函数的具体形式根据问题的特点而定。

(2)反向传播误差：从输出层开始，将误差通过反向传播的方式传递回隐藏层和输入层。

首先，计算输出层神经元的误差，然后将误差按照权值比例分配给连接到该神经元的隐藏层神经元，并计算隐藏层神经元的误差。

依此类推，直到计算出输入层神经元的误差。

(3)更新权值：利用误差和学习率来更新网络中的权值。

通过梯度下降法，沿着误差最速下降的方向对权值和阈值进行更新。

权值的更新公式为：Δwij = ηδjxi，其中η为学习率，δj为神经元的误差，xi为连接该神经元的输入。

以上就是BP神经网络的学习算法。

在实际应用中，还需要考虑一些其他的优化方法和技巧，比如动量法、自适应学习率和正则化等，以提高网络的性能和稳定性。

此外，BP神经网络也存在一些问题，比如容易陷入局部极小值、收敛速度慢等，这些问题需要根据实际情况进行调优和改进。

BP神经网络的基本原理_一看就懂BP神经网络（Back Propagation Neural Network）是一种常用的人工神经网络模型，用于解决分类、回归和模式识别问题。

它的基本原理是通过反向传播算法来训练和调整网络中的权重和偏置，以使网络能够逐渐逼近目标输出。

1.前向传播：在训练之前，需要对网络进行初始化，包括随机初始化权重和偏置。

输入数据通过输入层传递到隐藏层，在隐藏层中进行线性加权和非线性激活运算，然后传递给输出层。

线性加权运算指的是将输入数据与对应的权重相乘，然后将结果进行求和。

非线性激活指的是对线性加权和的结果应用一个激活函数，常见的激活函数有sigmoid函数、ReLU函数等。

激活函数的作用是将线性运算的结果映射到一个非线性的范围内，增加模型的非线性表达能力。

2.计算损失：将网络输出的结果与真实值进行比较，计算损失函数。

常用的损失函数有均方误差（Mean Squared Error）和交叉熵（Cross Entropy）等，用于衡量模型的输出与真实值之间的差异程度。

3.反向传播：通过反向传播算法，将损失函数的梯度从输出层传播回隐藏层和输入层，以便调整网络的权重和偏置。

反向传播算法的核心思想是使用链式法则。

首先计算输出层的梯度，即损失函数对输出层输出的导数。

然后将该梯度传递回隐藏层，更新隐藏层的权重和偏置。

接着继续向输入层传播，直到更新输入层的权重和偏置。

在传播过程中，需要选择一个优化算法来更新网络参数，常用的优化算法有梯度下降（Gradient Descent）和随机梯度下降（Stochastic Gradient Descent）等。

4.权重和偏置更新：根据反向传播计算得到的梯度，使用优化算法更新网络中的权重和偏置，逐步减小损失函数的值。

权重的更新通常按照以下公式进行：新权重=旧权重-学习率×梯度其中，学习率是一个超参数，控制更新的步长大小。

梯度是损失函数对权重的导数，表示了损失函数关于权重的变化率。

BP神经网络框架BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。

BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)。

1BP神经网络基本原理BP神经网络的基本原理可以分为如下几个步骤：（1）输入信号Xi→中间节点（隐层点）→输出节点→输出信号Yk；（2）网络训练的每个样本包括输入向量X和期望输出量t，网络输出值Y 和期望输出值t之间的偏差。

（3）通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度取值Tjk，以及阈值，使误差沿梯度方向下降。

（4）经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），训练到此停止。

（5）经过上述训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线性转换的信息。

2BP神经网络涉及的主要模型和函数BP神经网络模型包括输入输出模型、作用函数模型、误差计算模型和自学习模型。

输出模型又分为：隐节点输出模型和输出节点输出模型。

下面将逐个介绍。

（1）作用函数模型作用函数模型，又称刺激函数，反映下层输入对上层节点刺激脉冲强度的函数。

一般取（0,1）内的连续取值函数Sigmoid函数：f x=11+e^(−x)（2）误差计算模型误差计算模型反映神经网络期望输出与计算输出之间误差大小的函数：Ep=12(tpi−Opi)2其中，tpi为i节点的期望输出值；Opi为i节点的计算输出值。

（3）自学习模型自学习模型是连接下层节点和上层节点之间的权重矩阵Wij的设定和修正过程。

bp神经网络算法原理BP神经网络算法（Backpropagation algorithm）是一种监督学习的神经网络算法，其目的是通过调整神经网络的权重和偏置来实现误差的最小化。

BP神经网络算法基于梯度下降和链式法则，在网络的前向传播和反向传播过程中进行参数的更新。

在前向传播过程中，输入样本通过网络的各个神经元计算，直到达到输出层。

每个神经元都会对上一层的输入进行加权求和，并经过一个非线性激活函数得到输出。

前向传播的结果即为网络的输出。

在反向传播过程中，首先需要计算网络的输出误差。

误差是实际输出与期望输出的差异。

然后，从输出层开始，沿着网络的反方向，通过链式法则计算每个神经元的误差贡献，并将误差从输出层反向传播到输入层。

每个神经元根据自身的误差贡献，对权重和偏置进行调整。

这一过程可以看作是通过梯度下降来调整网络参数，以最小化误差。

具体而言，对于每个样本，BP神经网络算法通过以下步骤来更新网络的参数：1. 前向传播：将输入样本通过网络，计算得到网络的输出。

2. 计算误差：将网络的输出与期望输出进行比较，计算得到输出误差。

3. 反向传播：从输出层开始，根据链式法则计算每个神经元的误差贡献，并将误差沿着网络反向传播到输入层。

4. 参数更新：根据每个神经元的误差贡献，使用梯度下降方法更新神经元的权重和偏置。

5. 重复以上步骤，直到达到预设的训练停止条件，例如达到最大迭代次数或误差小于某个阈值。

总的来说，BP神经网络算法通过计算输出误差和通过反向传播调整网络参数的方式，实现对神经网络的训练。

通过不断迭代优化网络的权重和偏置，使得网络能够更准确地进行分类、回归等任务。

bp神经网络第一篇：BP神经网络的基本原理BP神经网络是一种最为经典的人工神经网络之一，它在模拟神经元之间的信息传输和处理过程上有很高的效率，可以被应用于多种领域，如图像处理、模式识别、预测分析等。

BP神经网络的核心思想是通过将神经元之间的权值调整来达到优化网络结构的目的，从而提高网络的准确率和泛化能力。

BP神经网络包含三个基本部分：输入层、隐层和输出层。

其中，输入层用于接收原始数据，隐层是神经元之间信号处理的地方，而输出层则用于输出最终的结果。

与其他的神经网络不同，BP神经网络使用了反向传播算法来调整神经元之间的权值。

这个算法是一种基于梯度下降的优化方法，通过最小化目标函数来优化权值，从而获得最小的误差。

具体来说，反向传播算法分为两个步骤：前向传播和反向传播。

前向传播是指从输入层开始，将数据经过神经元的传递和处理，一直到输出层，在这个过程中会计算每一层的输出值。

这一步完成后，就会得到预测值和实际值之间的误差。

接着，反向传播将会计算每个神经元的误差，并将误差通过链式法则向后传播，以更新每个神经元的权值。

这一步也被称为误差反向传播，它通过计算每个神经元对误差的贡献来更新神经元之间的权值。

总的来说，BP神经网络的优点在于其具有灵活性和较高的准确率。

但同时也存在着过拟合和运算时间过长等问题，因此在实际应用中需要根据实际情况加以取舍。

第二篇：BP神经网络的应用BP神经网络作为一种人工智能算法，其应用范围非常广泛。

以下是BP神经网络在不同领域的应用案例。

1. 图像处理BP神经网络在图像处理方面的应用主要有两个方面：图像分类和图像增强。

在图像分类方面，BP神经网络可以通过对不同特征之间的关系进行学习，从而对图像进行分类。

在图像增强方面，BP神经网络可以根据图像的特征进行修复和增强，从而提高图像的质量。

2. 股票预测BP神经网络可以通过对历史数据的学习来预测未来股市趋势和股票价格变化，对投资者提供参考依据。

3. 语音识别BP神经网络可以对人声进行测量和分析，从而识别出人说的话，实现语音识别的功能。

BP神经网络算法BP神经网络算法（BackPropagation Neural Network）是一种基于梯度下降法训练的人工神经网络模型，广泛应用于分类、回归和模式识别等领域。

它通过多个神经元之间的连接和权重来模拟真实神经系统中的信息传递过程，从而实现复杂的非线性函数拟合和预测。

BP神经网络由输入层、隐含层和输出层组成，其中输入层接受外部输入的特征向量，隐含层负责进行特征的抽取和转换，输出层产生最终的预测结果。

每个神经元都与上一层的所有神经元相连，且每个连接都有一个权重，通过不断调整权重来优化神经网络的性能。

BP神经网络的训练过程主要包括前向传播和反向传播两个阶段。

在前向传播中，通过输入层将特征向量引入网络，逐层计算每个神经元的输出值，直至得到输出层的预测结果。

在反向传播中，通过计算输出层的误差，逐层地反向传播误差信号，并根据误差信号调整每个连接的权重值。

具体来说，在前向传播过程中，每个神经元的输出可以通过激活函数来计算。

常见的激活函数包括Sigmoid函数、ReLU函数等，用于引入非线性因素，增加模型的表达能力。

然后，根据权重和输入信号的乘积来计算每个神经元的加权和，并通过激活函数将其转化为输出。

在反向传播过程中，首先需要计算输出层的误差。

一般采用均方差损失函数，通过计算预测值与真实值之间的差异来衡量模型的性能。

然后，根据误差信号逐层传播，通过链式法则来计算每个神经元的局部梯度。

最后，根据梯度下降法则，更新每个连接的权重值，以减小误差并提高模型的拟合能力。

总结来说，BP神经网络算法是一种通过多层神经元之间的连接和权重来模拟信息传递的人工神经网络模型。

通过前向传播和反向传播两个阶段，通过不断调整权重来训练模型，并通过激活函数引入非线性因素。

BP 神经网络算法在分类、回归和模式识别等领域具有广泛的应用前景。

BP神经网络BP神经网络，也称为反向传播神经网络（Backpropagation Neural Network），是一种常见的人工神经网络类型，用于机器学习和深度学习任务。

它是一种监督学习算法，用于解决分类和回归问题。

以下是BP神经网络的基本概念和工作原理：神经元（Neurons）：BP神经网络由多个神经元组成，通常分为三层：输入层、隐藏层和输出层。

输入层接收外部数据，隐藏层用于中间计算，输出层产生网络的最终输出。

权重（Weights）：每个连接两个神经元的边都有一个权重，表示连接的强度。

这些权重是网络的参数，需要通过训练来调整，以便网络能够正确地进行预测。

激活函数（Activation Function）：每个神经元都有一个激活函数，用于计算神经元的输出。

常见的激活函数包括Sigmoid、ReLU（Rectified Linear Unit）和tanh（双曲正切）等。

前向传播（Forward Propagation）：在训练过程中，输入数据从输入层传递到输出层的过程称为前向传播。

数据经过一系列线性和非线性变换，最终产生网络的预测输出。

反向传播（Backpropagation）：反向传播是BP神经网络的核心。

它用于计算网络预测的误差，并根据误差调整网络中的权重。

这个过程分为以下几个步骤：1.计算预测输出与实际标签之间的误差。

2.将误差反向传播回隐藏层和输入层，计算它们的误差贡献。

3.根据误差贡献来更新权重，通常使用梯度下降法或其变种来进行权重更新。

训练（Training）：训练是通过多次迭代前向传播和反向传播来完成的过程。

目标是通过调整权重来减小网络的误差，使其能够正确地进行预测。

超参数（Hyperparameters）：BP神经网络中有一些需要人工设置的参数，如学习率、隐藏层的数量和神经元数量等。

这些参数的选择对网络的性能和训练速度具有重要影响。

BP神经网络在各种应用中都得到了广泛的使用，包括图像分类、语音识别、自然语言处理等领域。

BP神经网络模型与学习算法BP（Back Propagation）神经网络模型是一种常用的人工神经网络模型，主要用于分类和回归问题。

BP网络由输入层、隐含层和输出层组成，利用反向传播算法进行学习和训练。

下面将详细介绍BP神经网络模型和学习算法。

-输入层：接受外界输入的数据，通常是特征向量。

-隐含层：对输入层特征进行非线性处理，并将处理后的结果传递给输出层。

-输出层：根据隐含层的输出结果进行分类或回归预测。

前向传播：从输入层到输出层逐层计算神经元的输出值。

对于每个神经元，输入信号经过带权和的线性变换，然后通过激活函数进行非线性变换，得到神经元的输出值，该值作为下一层神经元的输入。

-具有较强的非线性映射能力，可以用来解决复杂的分类和回归问题。

-学习能力强，能够从大量的训练样本中学习到隐藏在数据中的模式和规律。

-适用于处理多输入多输出问题，可以构建具有多个输入和输出的神经网络模型。

然而，BP神经网络模型也存在一些不足之处，包括：-容易陷入局部最优解，当网络层数较多时，很容易陷入局部极小点。

-对输入数据的数值范围敏感，需要对输入数据进行归一化处理，以避免权值的不平衡。

-训练时间较长，需要较大的训练集和较多的迭代次数才能达到较好的训练效果。

总结来说，BP神经网络模型是一种常用的人工神经网络模型，通过反向传播算法来实现网络的学习和训练。

BP神经网络模型具有较强的非线性映射能力和学习能力，适用于解决复杂的分类和回归问题。

然而，BP 神经网络模型也存在局部最优解问题和对输入数据的敏感性等不足之处。

因此，在实际应用中需要根据具体问题选择合适的算法和模型。

BP神经网络在函数逼近中的实现1.1 概述BP神经网络是目前人工神经网络模式中最具代表性,应用得最广泛的一种模型,具有自学习、自组织、自适应和很强的非线性映射能力,可以以任意精度逼近任意连续函数.近年来,为了解决BP网络收敛速度慢,训练时间长等不足,提出了许多改进算法.然而,在针对实际问题的BP网络建模过程中,选择多少层网络,每层多少个神经元节点,选择何种传递函数等,均无可行的理论指导,只能通过大量的实验计算获得.MATLAB中的神经网络工具箱(Neural NetworkToolbox,简称NNbox),为解决这一问题提供了便利的条件.神经网络工具箱功能十分完善,提供了各种MATLAB函数,包括神经网络的建立、训练和仿真等函数,以及各种改进训练算法函数,用户可以很方便地进行神经网络的设计和仿真,也可以在MATLAB源文件的基础上进行适当修改,形成自己的工具包以满足实际需要。

此项课题主要是针对MATLAB软件对BP神经网络的各种算法的编程，将神经网络算法应用于函数逼近和样本含量估计问题中，并分析比较相关参数对算法运行结果的影响。

人工神经网络（Artificial Neural Networks，NN）是由大量的、简单的处理单元（称为神经元）广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学系统。

神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力，特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。

神经网络的发展与神经科学、数理科学、认知科学、计算机科学、人工智能、信息科学、控制论、机器人学、微电子学、心理学、微电子学、心理学、光计算、分子生物学等有关，是一门新兴的边缘交叉学科。

神经网络具有非线性自适应的信息处理能力，克服了传统人工智能方法对于直觉的缺陷，因而在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。

BP神经⽹络　百度百科　在⼈⼯神经⽹络发展历史中，很长⼀段时间⾥没有找到隐层的连接权值调整问题的有效算法。

直到误差反向传播算法（BP 算法）的提出，成功地解决了求解⾮线性连续函数的多层前馈神经⽹络权重调整问题。

BP (Back Propagation)神经⽹络，即误差反传误差反向传播算法的学习过程，由信息的正向传播和误差的反向传播两个过程组成。

输⼊层各神经元负责接收来⾃外界的输⼊信息，并传递给中间层各神经元；中间层是内部信息处理层，负责信息变换，根据信息变化能⼒的需求，中间层可以设计为单隐层或者多隐层结构；最后⼀个隐层传递到输出层各神经元的信息，经进⼀步处理后，完成⼀次学习的正向传播处理过程，由输出层向外界输出信息处理结果。

当实际输出与期望输出不符时，进⼊误差的反向传播阶段。

误差通过输出层，按误差梯度下降的⽅式修正各层权值，向隐层、输⼊层逐层反传。

周⽽复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经⽹络学习训练的过程，此过程⼀直进⾏到⽹络输出的误差减少到可以接受的程度，或者预先设定的学习次数为⽌。

BP神经⽹络模型BP⽹络模型包括其输⼊输出模型、作⽤函数模型、误差计算模型和⾃学习模型。

（1）节点输出模型 隐节点输出模型：Oj=f(∑Wij×Xi-qj) (1) 输出节点输出模型：Yk=f(∑Tjk×Oj-qk) (2) f-⾮线形作⽤函数；q -神经单元阈值。

图1 典型BP⽹络结构模型 （2）作⽤函数模型 作⽤函数是反映下层输⼊对上层节点刺激脉冲强度的函数⼜称刺激函数，⼀般取为(0,1)内连续取值Sigmoid函数：f(x)=1/(1+e) （3） （3）误差计算模型 误差计算模型是反映神经⽹络期望输出与计算输出之间误差⼤⼩的函数： Ep=1/2×∑(tpi-Opi) (4) tpi- i节点的期望输出值；Opi-i节点计算输出值。

（4）⾃学习模型 神经⽹络的学习过程，即连接下层节点和上层节点之间的权重拒阵Wij的设定和误差修正过程。